一、查找算法的评价指标
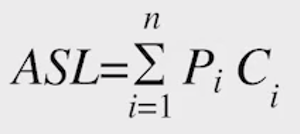
查找长度 :在查找运算中,需要对比关键字的次数称为查找长度
平均查找长度(ASL,Average Search Length) :所有查找过程中进行关键字的比较次数的平均值,ASL 的数量级反应了查找算法时间复杂度
二、顺序查找
2.1 算法思想
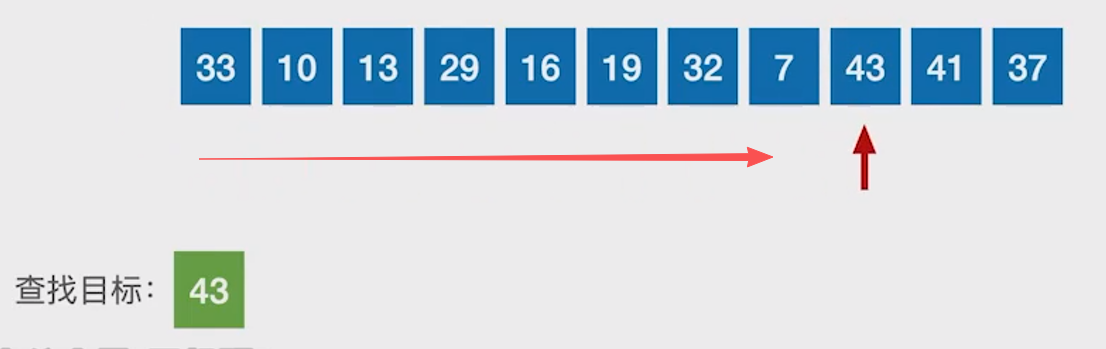
- 顺序查找,又叫"线性查找",适用于顺序表、链表,表中元素有序无序都OK
- 从头到脚(或者从脚到头)挨个找
- 可在0号位置存"哨兵 ",从尾部向头部挨个查找。优点 :循环时无需判断下标是否越界,哨兵理解(有哨兵时,就不能再往前了)
2.2 算法实现
不带哨兵 :
带哨兵 :0号位置存"哨兵 ",循环时无需判断下标是否越界

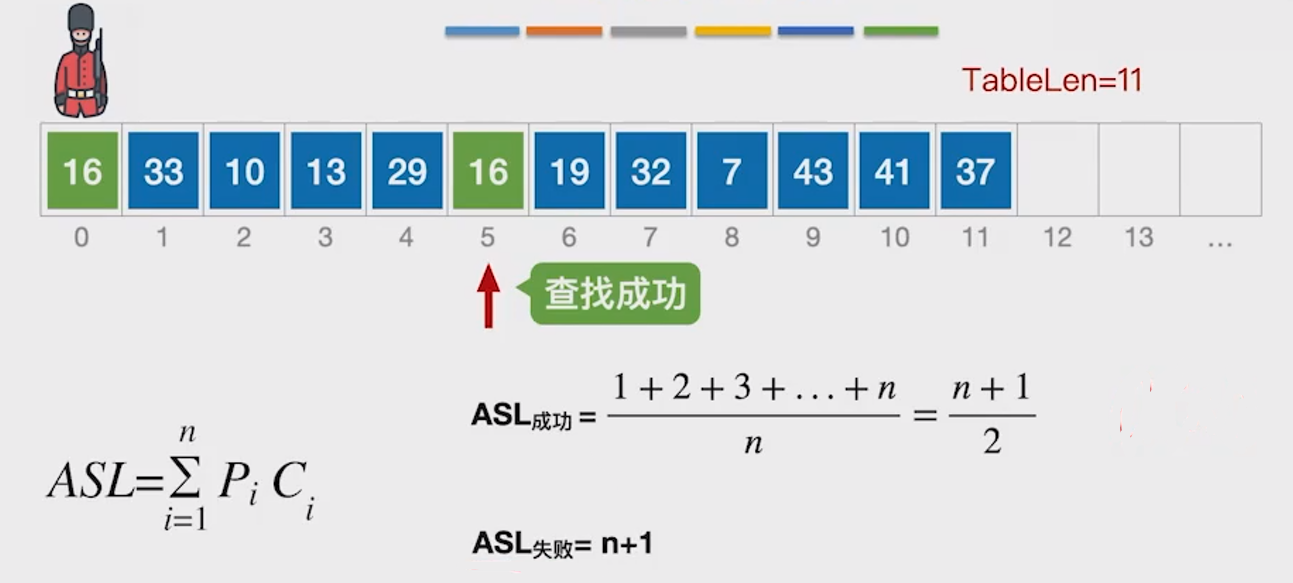
查找效率分析 :每次查找都是1/n等概率,查找对比次数为n
2.3 算法优化
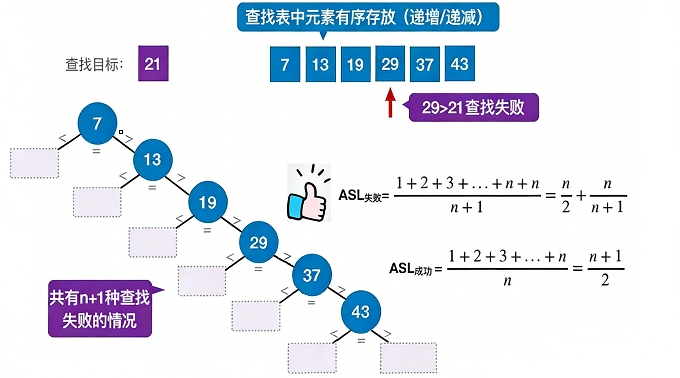
问题:为什么分子是 1+2+3+...+n+n
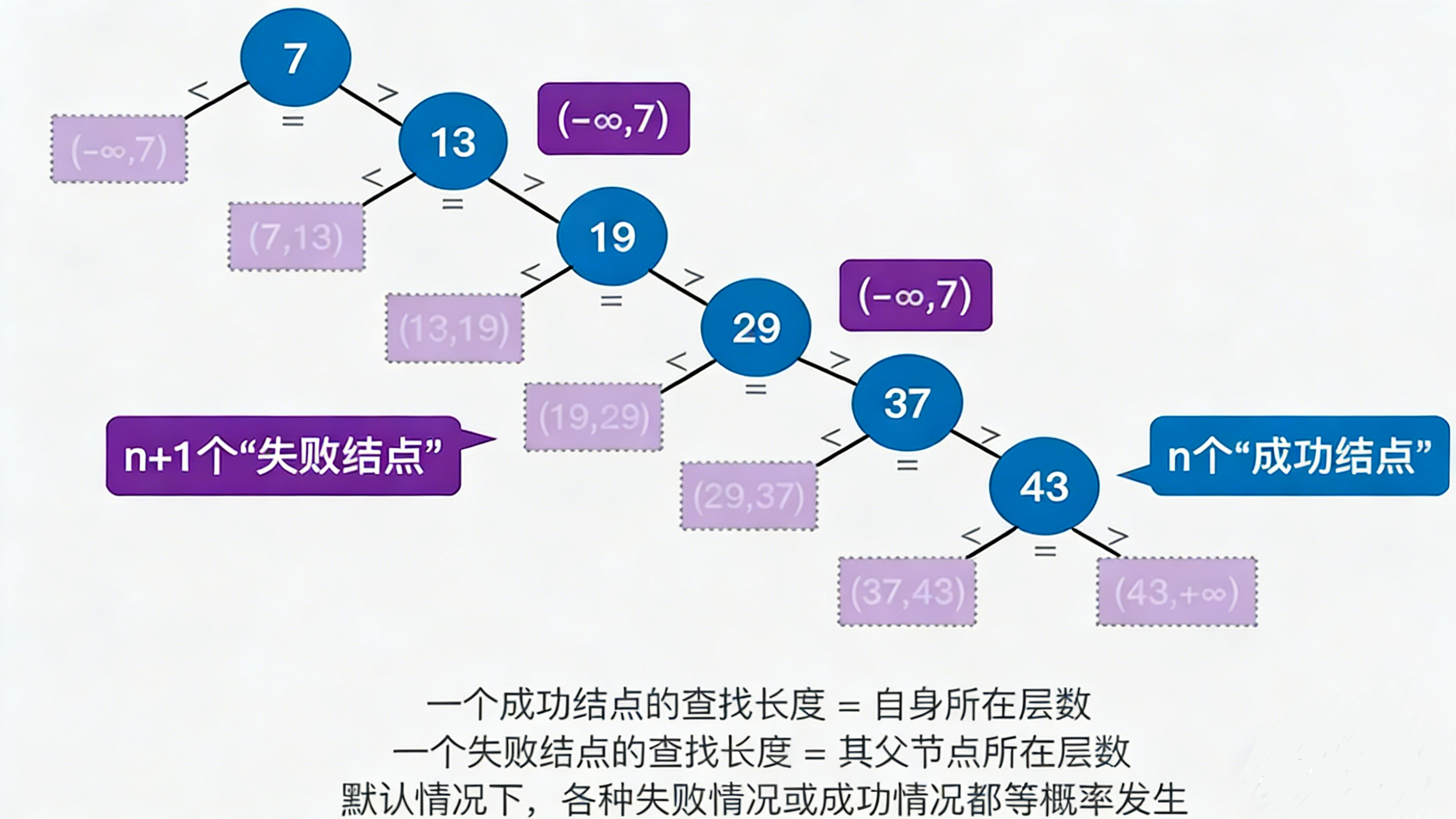
2.3.1 查找失败的位置
- 在有序表 [7,13,19,29,37,43](共 n=6 个元素)中,查找失败会发生在 n+1=7 个区间:
(-∞,7)、(7,13)、(13,19)、(19,29)、(29,37)、(37,43)、(43,+∞)。
2.3.2 各失败位置的比较次数
-
前 n 个失败位置(如 (-∞,7) 到 (37,43)),需要的比较次数分别是 1,2,3,...,n。
-
最后一个失败位置 (43,+∞),需要比较到表尾的 43,再判断大于它,所以比较次数也是 n(和第 n 个元素的比较次数相同)。
2.3.3 求和逻辑
- 把所有失败位置的比较次数相加: 1+2+3+...+(n-1)+n + n ,也就是 1+2+3+...+n + n,这就是分子的由来。
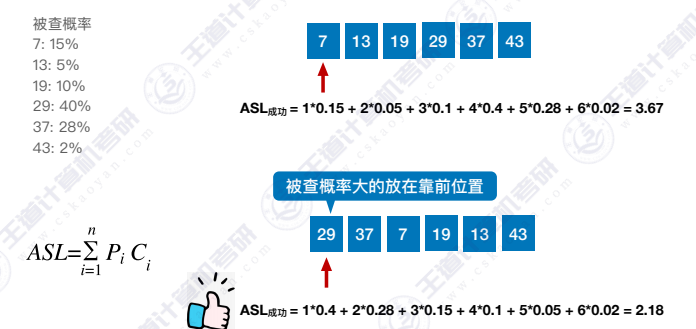
2.2.4 被查概率不相等
ASL成功 :将被查概率大的放在靠前位置,从而降低ASL值
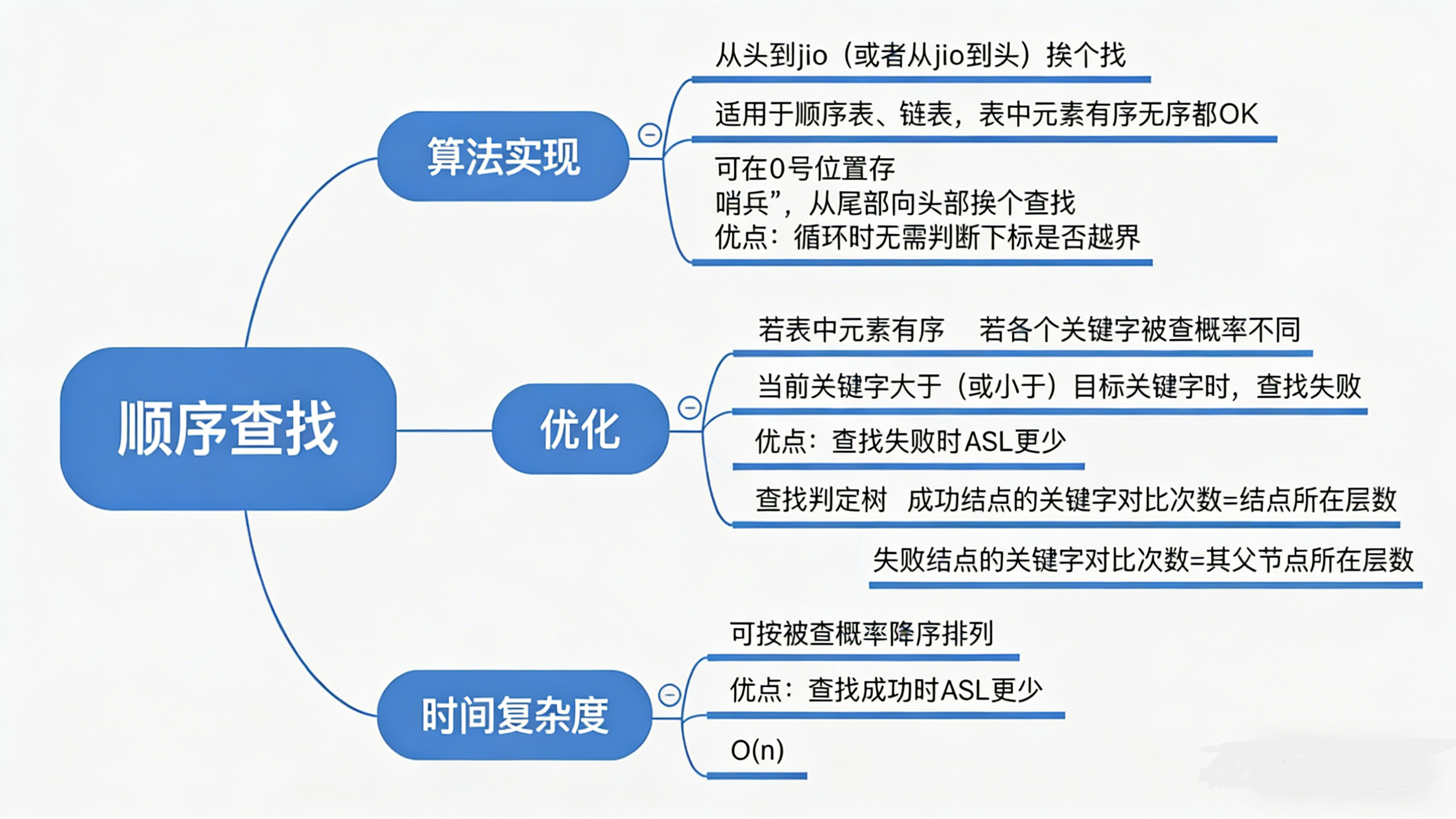
2.4 顺序查找总结
三、折半查找
3.1 算法思想
折半查找,又称"二分查找",仅适用于有序的顺序表。
步骤一 :

步骤二 :
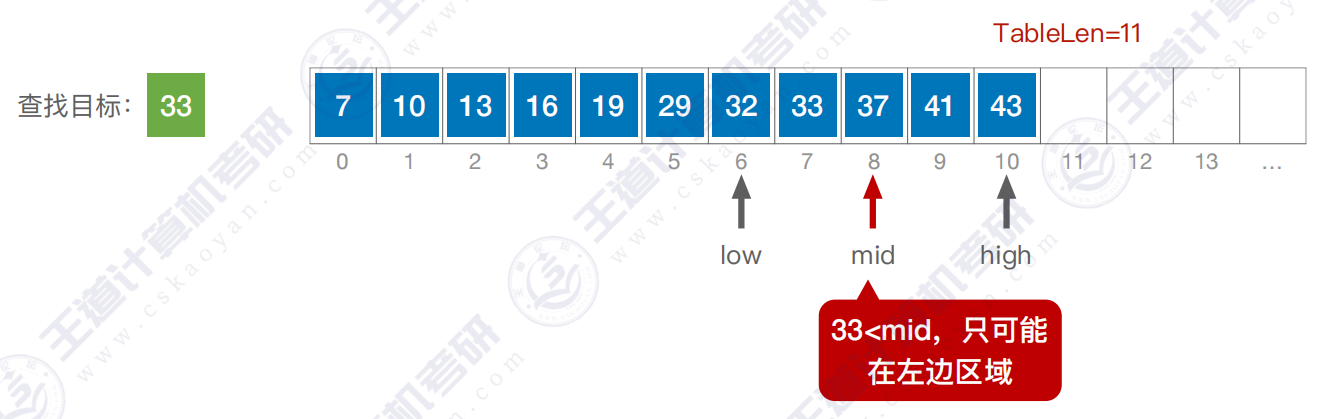
步骤三 :
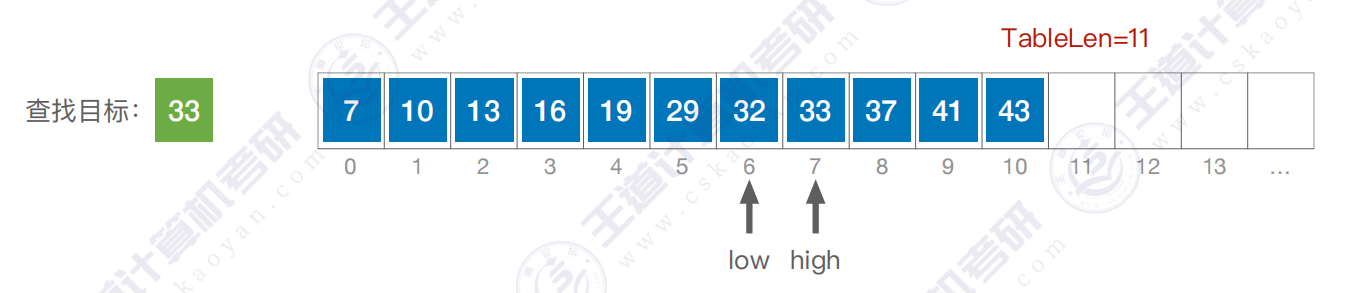
步骤四:
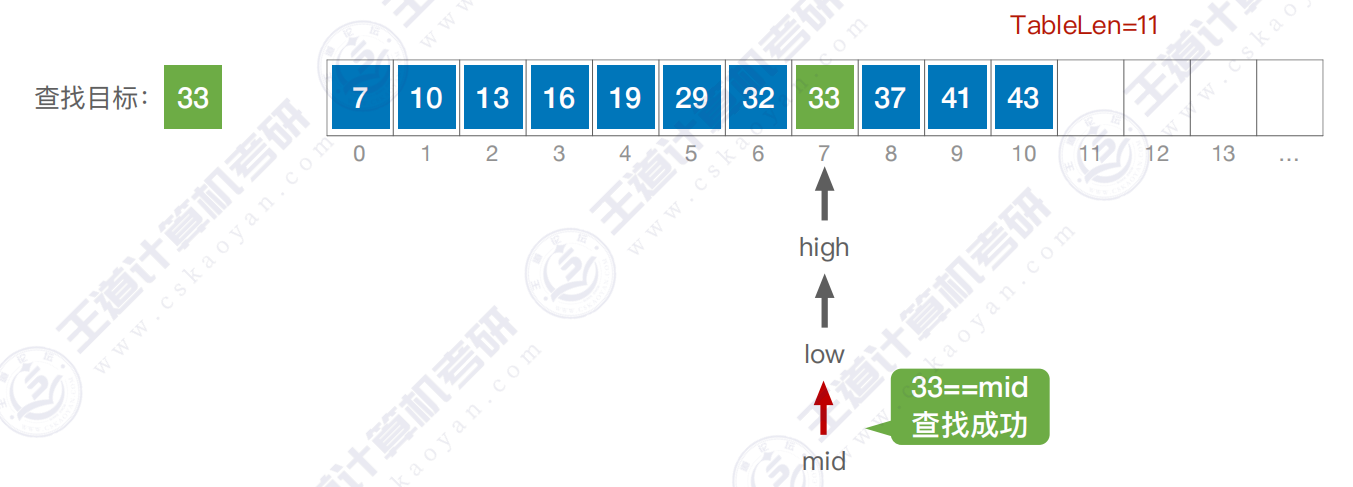
3.2 折半查找效率分析
初始序列 :
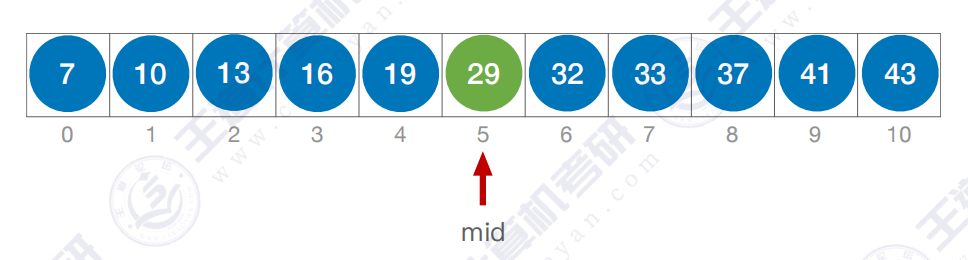
最终划分 :
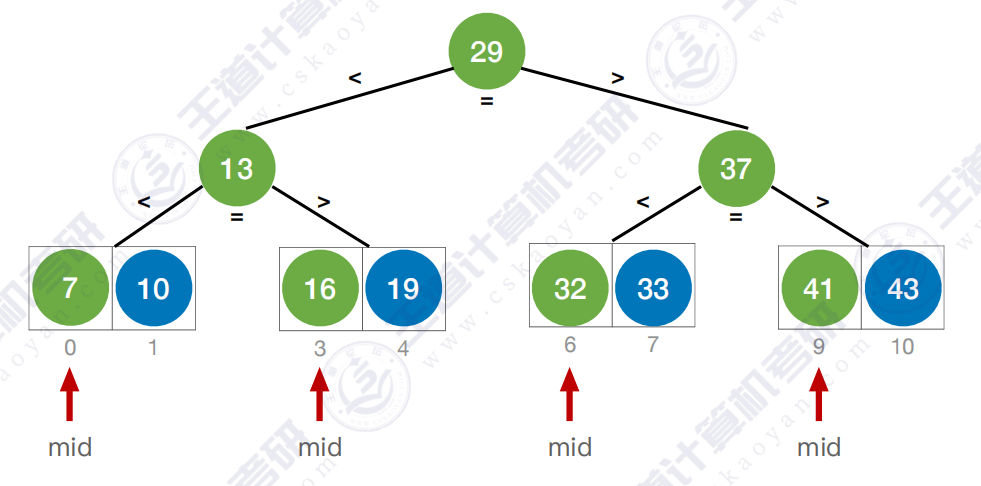
查找性能分析 :类似"层次遍历"计算ASL
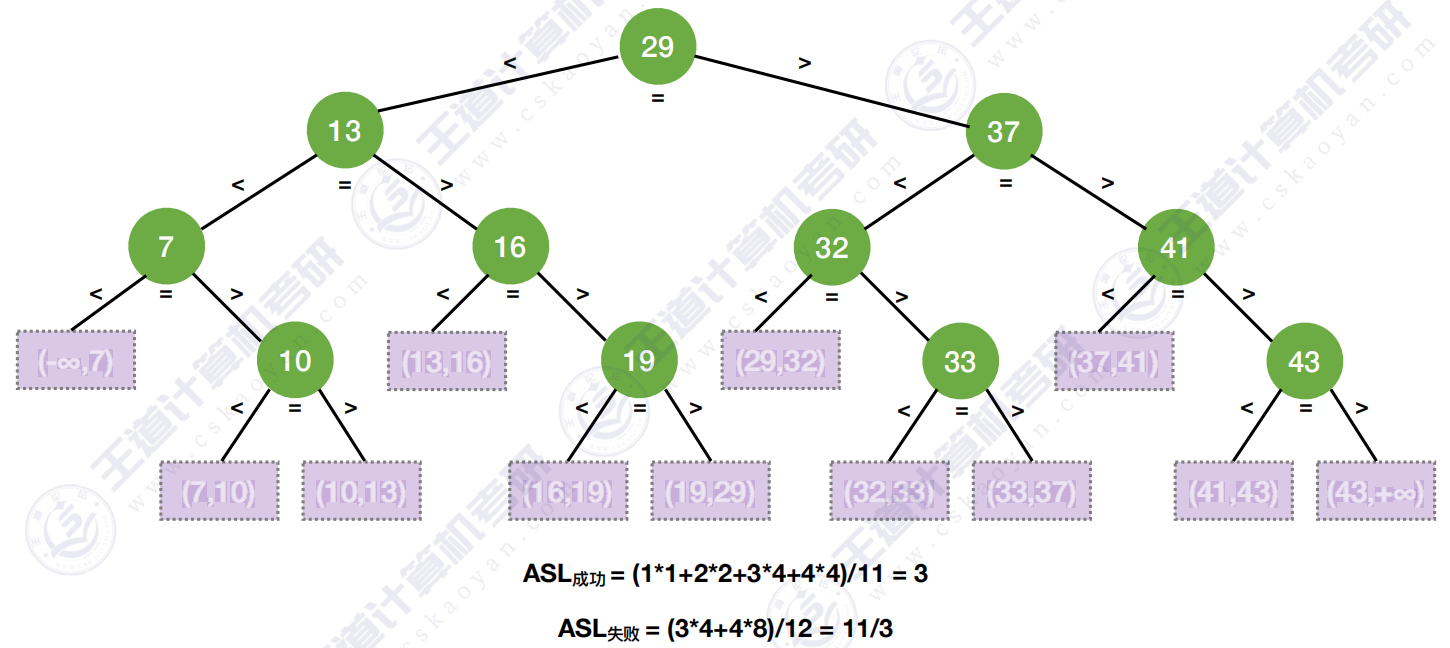
3.3 查找判定树的构造
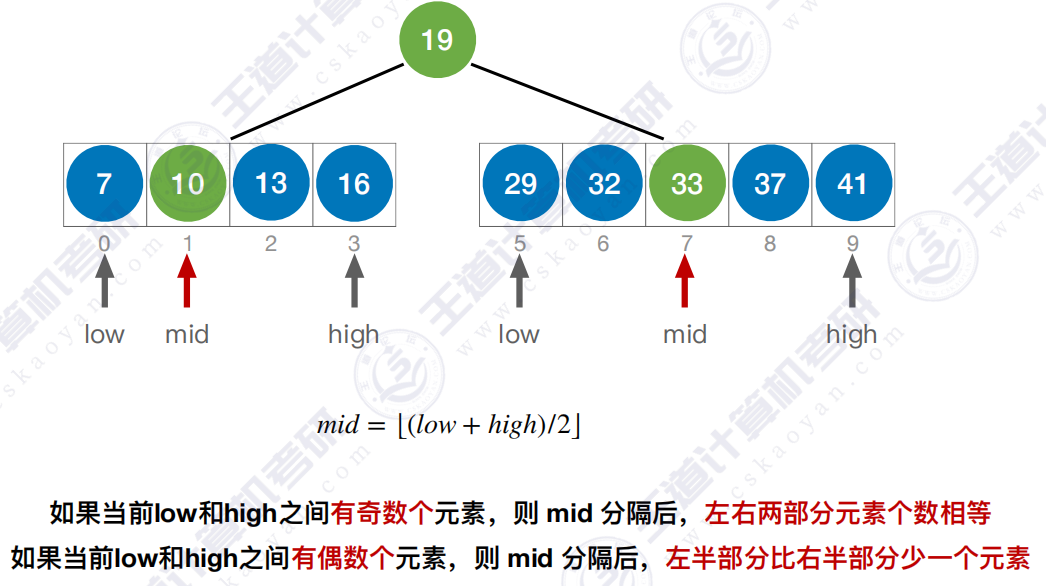
原始序列 :如果当前low和high之间有奇数 个元素,则mid分隔后,左右两部分 元素个数相等

开始划分 :

继续划分 :
最终结果 :
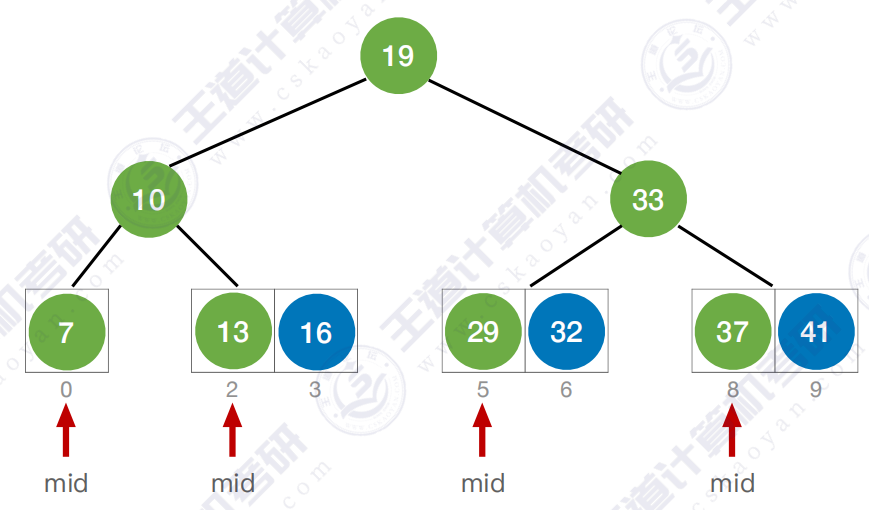
折半查找判定树 :
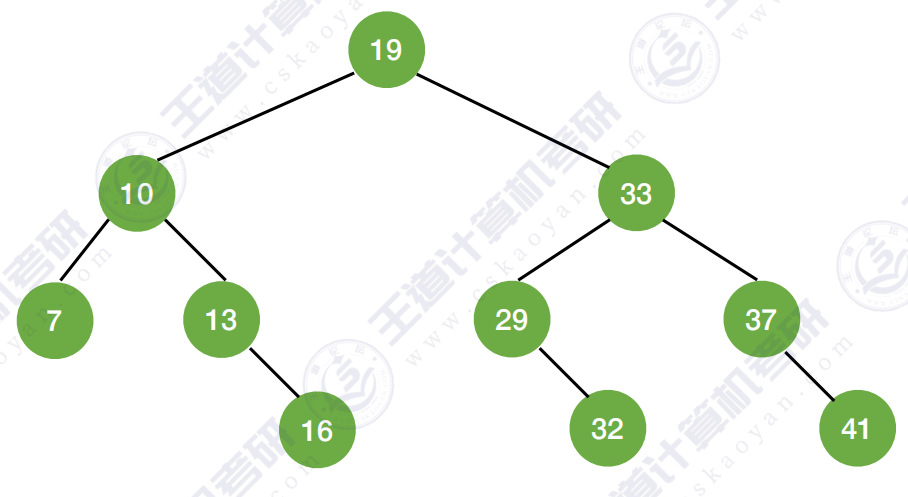
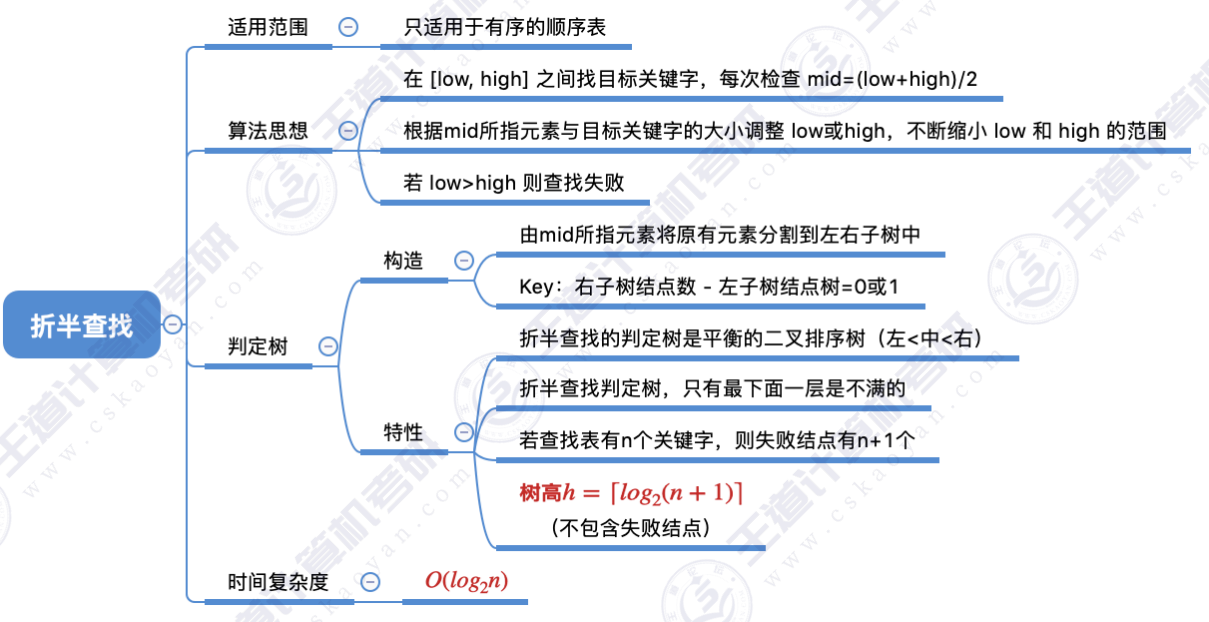
3.4 折半查找总结
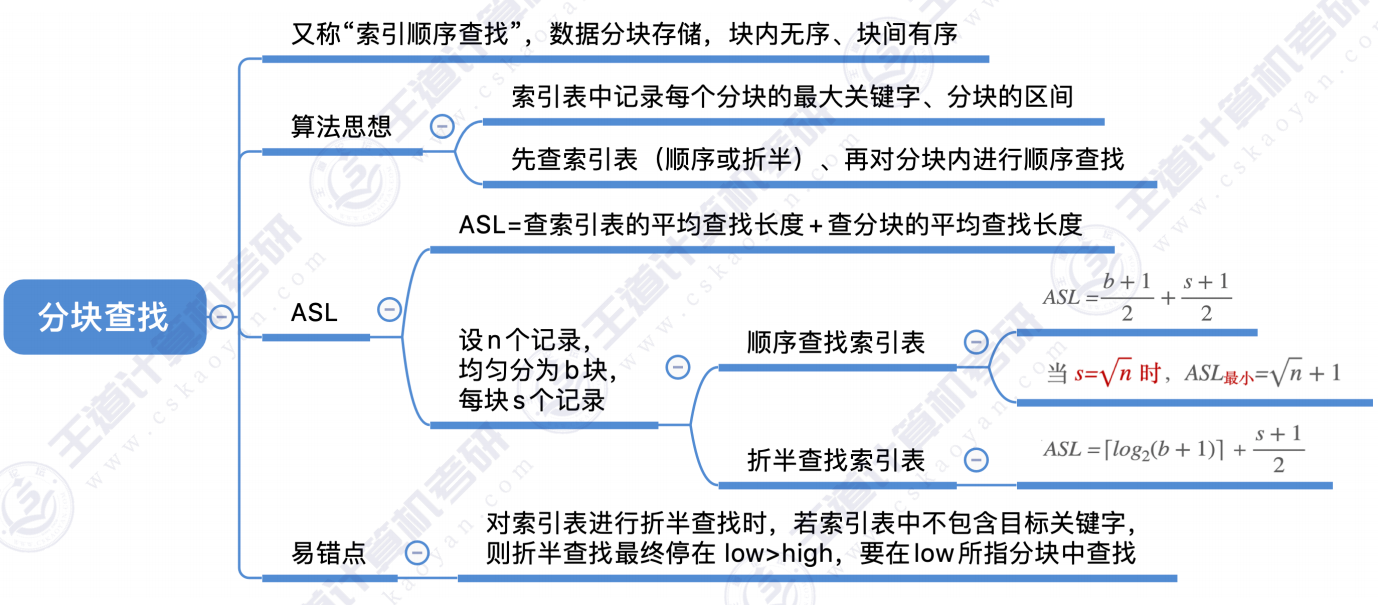
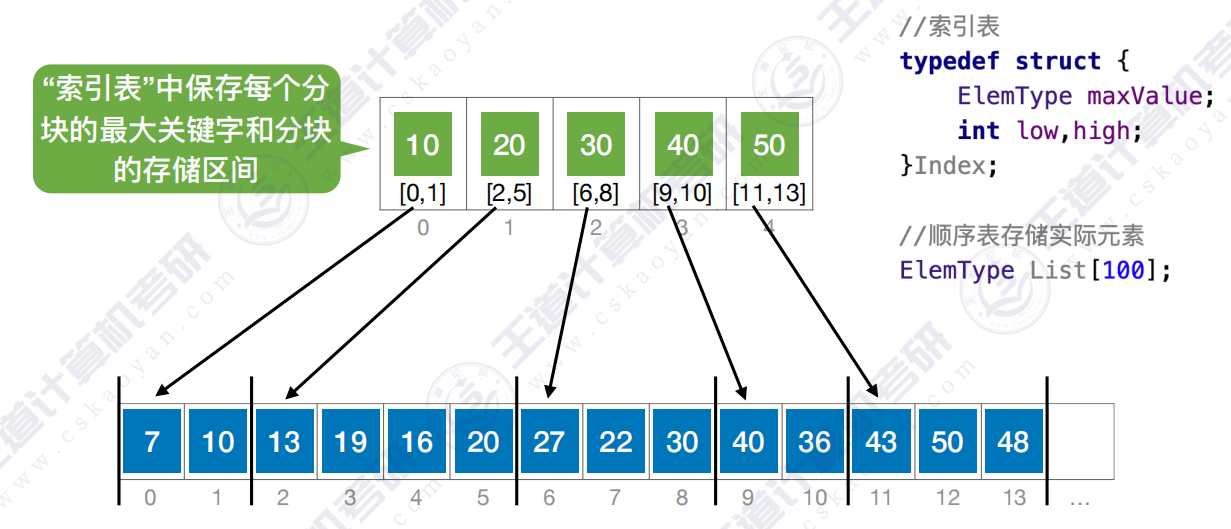
四、分块查找
4.1 算法思想
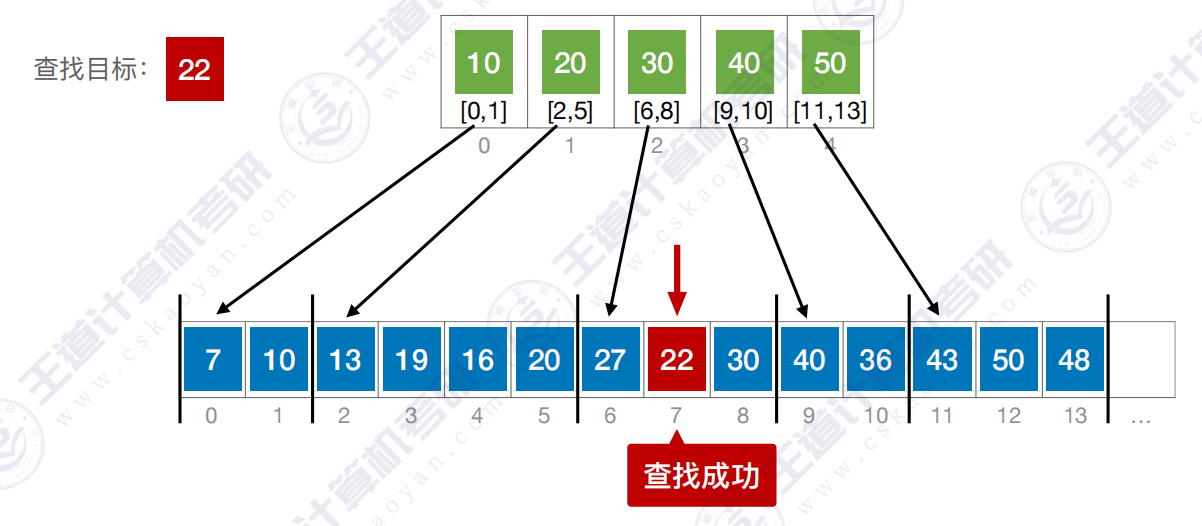
特点:块内无序、块间有序
- 在索引表中确定待查记录所属的分块(可顺序、可折半)
- 在块内顺序查找
开始查找 :
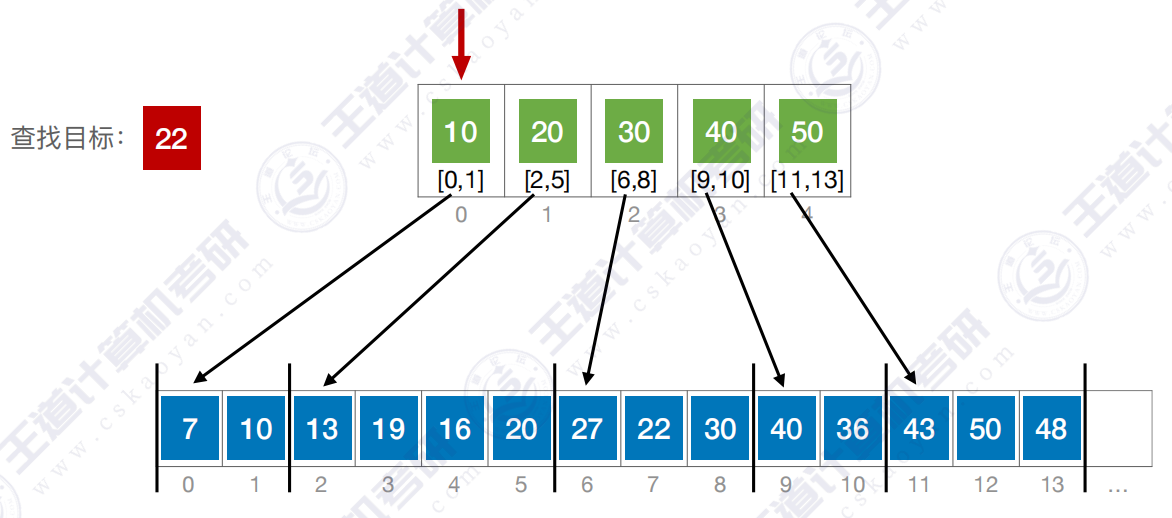
查找成功 :
4.2 查找效率分析
步骤一 :

步骤二 :
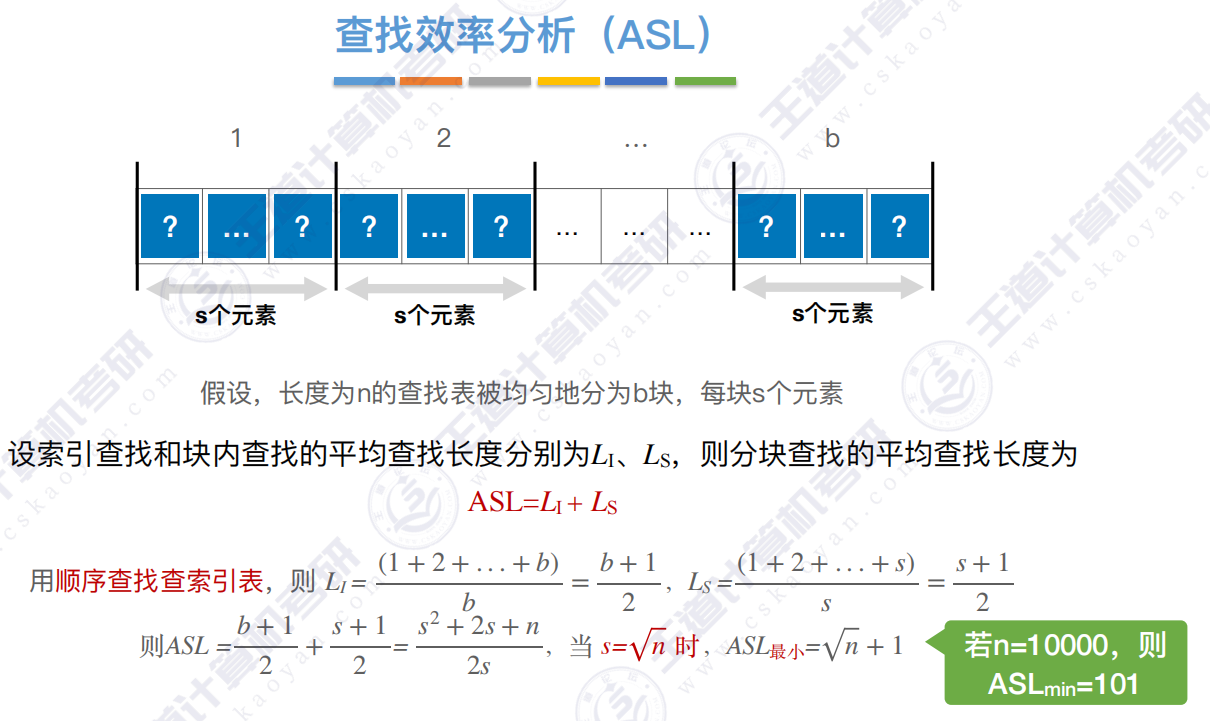
步骤三 :

4.3 总结