机器学习入门（二十）支持向量机SVM

（；￣ェ￣）。2026-02-04 12:58

支持向量机全称是Supported Vector Machine（支持向量机）

即寻找到一个超平面使样本分成两类，并且间隔最大。

• 是一种监督学习算法，主要用于分类，也可用于回归

• 与逻辑回归和决策树等其他分类器相比，SVM 提供了非常高的准确度

优缺点

• 优点：

（1）适合小样本、高纬度数据，比较强泛化能力

（2）可有效地处理高维数据；可使用不同的核函数来适应不同的数据类型

• 缺点：

计算复杂度较高，对于大规模数据的处理可能会存在困难

超平面最大间隔

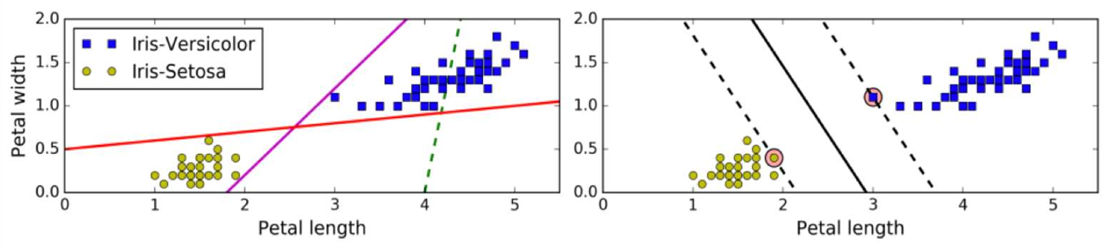
硬间隔Hard Margin

• 如果样本线性可分，在所有样本分类都正确的情况下，寻找最大间隔，这就是硬间隔

• 如果出现异常值、或者样本不能线性可分，此时硬间隔无法实现。

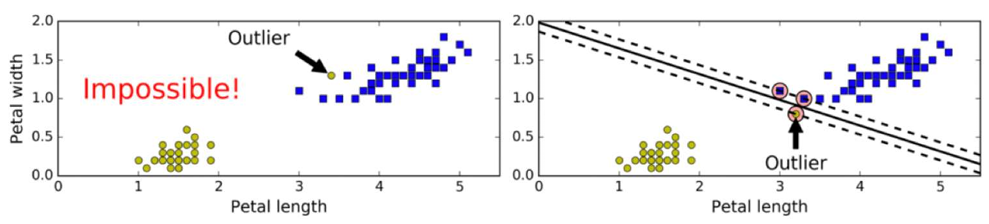
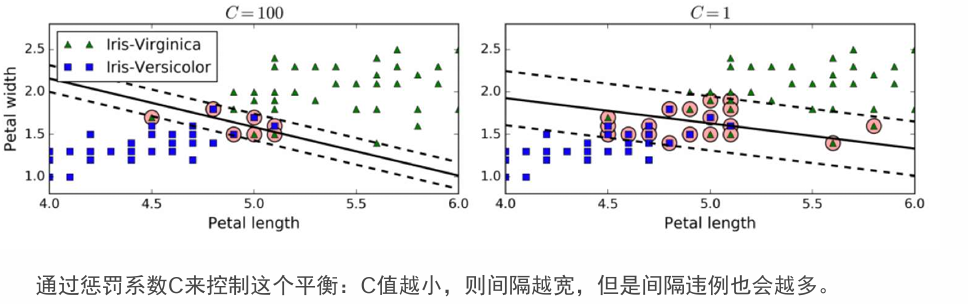
软间隔SoftMargin和惩罚系数

• 允许部分样本，在最大间隔之内，甚至在错误的一边，寻找最大间隔，这就是软间隔

• 目标是尽可能在保持间隔宽阔和限制间隔违例之间找到良好的平衡。

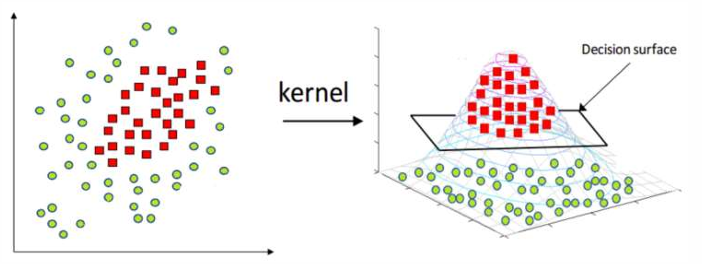
核函数Kernel

核函数将原始输入空间映射到新的特征空间，使得原本线性不可分的样本在核空间可分

使用LinearSVC探索鸢尾花分类 -- API初步使用

plot_util.py

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt


def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_map = ListedColormap(["#EF9A9A", "#FFF59D", "#90CAF9"])

    # plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)
    plt.contourf(x0, x1, zz, cmap=custom_map)


def plot_decision_boundary_svc(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1)
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_map = ListedColormap(["#EF9A9A", "#FFF59D", "#90CAF9"])

    # plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)
    plt.contourf(x0, x1, zz, cmap=custom_map)

    w = model.coef_[0]
    b = model.intercept_[0]
    # w0* x0 + w1* x1+ b = 0
    # =>x1 = -w0/w1 * x0 - b/w1
    plot_x = np.linspace(axis[0], axis[1], 200)
    up_y = -w[0] / w[1] * plot_x - b / w[1] + 1 / w[1]
    down_y = -w[0] / w[1] * plot_x - b / w[1] - 1 / w[1]
    up_index = (up_y >= axis[2]) & (up_y <= axis[3])
    down_index = (down_y >= axis[2]) & (down_y <= axis[3])
    plt.plot(plot_x[up_index], up_y[up_index], color="black")
    plt.plot(plot_x[down_index], down_y[down_index], color="black")
python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
from plot_util import plot_decision_boundary, plot_decision_boundary_svc


def dm01():
    X, y = load_iris(return_X_y=True)
    print('X.shape --> ', X.shape)
    print('y.shape --> ', y.shape)

    X = X[y < 2, :2]
    y = y[y < 2]
    print('x.shape-->', X.shape)
    print('y.shape-->', y.shape)

    plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red')
    plt.scatter(X[y == 1, 0], X[y == 1, 1], color='blue')
    plt.show()

    transformer = StandardScaler()
    X_std = transformer.fit_transform(X)

    svc = LinearSVC(dual='auto', C=30)
    svc.fit(X_std, y)

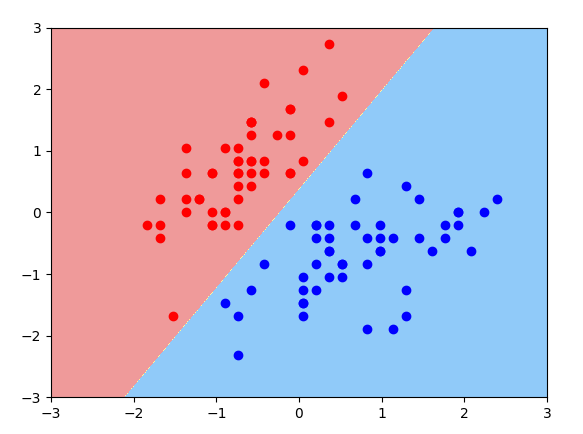
    plot_decision_boundary(svc, axis=[-3, 3, -3, 3])
    plt.scatter(X_std[y == 0, 0], X_std[y == 0, 1], c='red')
    plt.scatter(X_std[y == 1, 0], X_std[y == 1, 1], c='blue')
    # plt.scatter(X_standard[:, 0], X_standard[:, 1], c=y)
    plt.show()


dm01()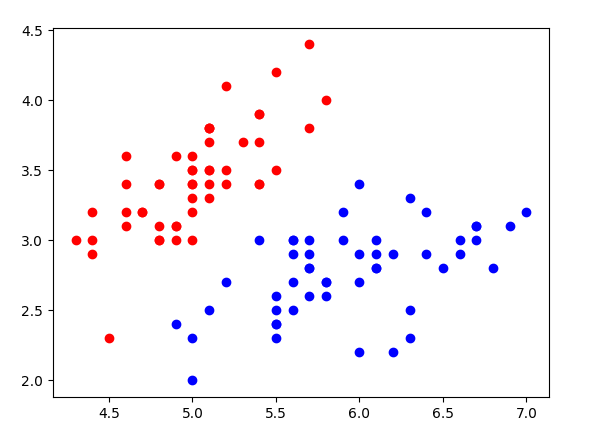

使用LinearSVC探索鸢尾花分类 -- 惩罚参数C对超平面的影响

python 复制代码 
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from plot_util import plot_decision_boundary_svc


def dm01():
    X, y = load_iris(return_X_y=True)
    print('x.shape -->', X.shape)
    print('y.shape -->', y.shape)

    X = X[y < 2, :2]
    y = y[y < 2]
    print('x.shape-->', X.shape)
    print('y.shape-->', y.shape)

    plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red')
    plt.scatter(X[y == 1, 0], X[y == 1, 1], color='blue')
    plt.show()

    transformer = StandardScaler()
    X_std = transformer.fit_transform(X)

    svc = LinearSVC(dual='auto', C=0.1)
    svc.fit(X_std, y)
    print(svc.score(X_std, y))

    plot_decision_boundary_svc(svc, axis=[-3, 3, -3, 3])
    plt.scatter(X_std[y == 0, 0], X_std[y == 0, 1], c='red')
    plt.scatter(X_std[y == 1, 0], X_std[y == 1, 1], c='blue')
    # plt.scatter(X_standard[:, 0], X_standard[:, 1], c=y)
    plt.show()

    svc2 = LinearSVC(dual='auto', C=30)
    svc2.fit(X_std, y)
    print(svc2.score(X_std, y))

    plot_decision_boundary_svc(svc2, axis=[-3, 3, -3, 3])
    plt.scatter(X_std[y == 0, 0], X_std[y == 0, 1], c='red')
    plt.scatter(X_std[y == 1, 0], X_std[y == 1, 1], c='blue')
    # plt.scatter(X_standard[:, 0], X_standard[:, 1], c=y)
    plt.show()


dm01()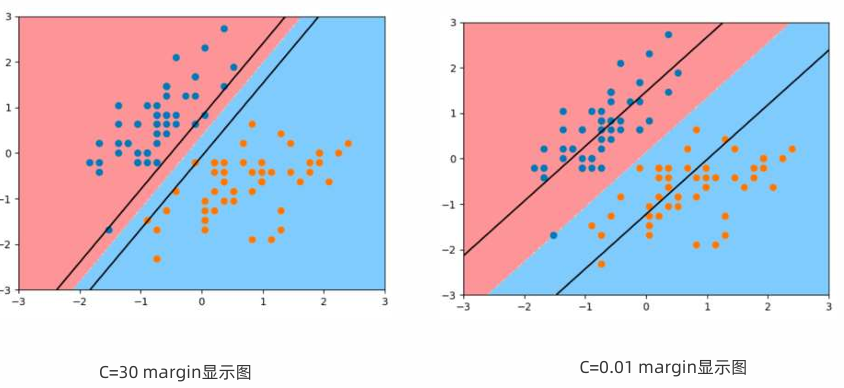

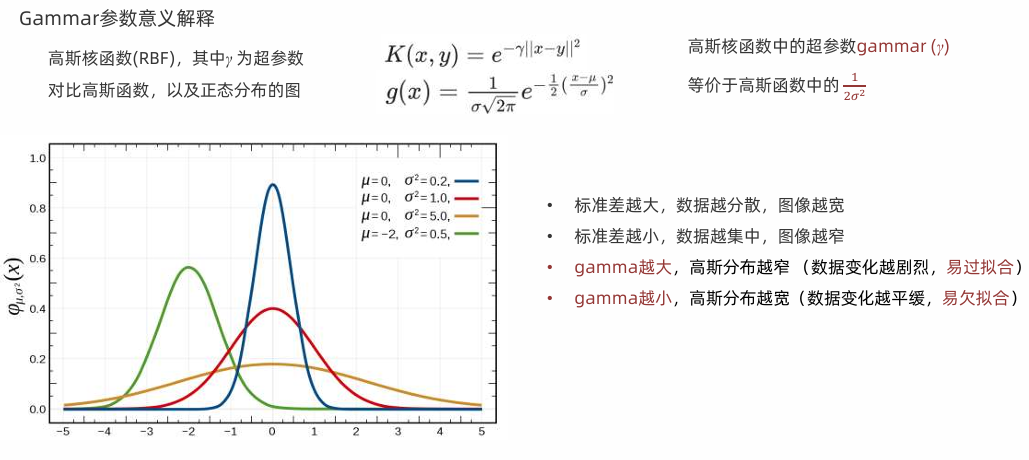
高斯核函数

高斯核 Radial Basis Function Kernel (径向基函数，又称RBF核)

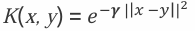
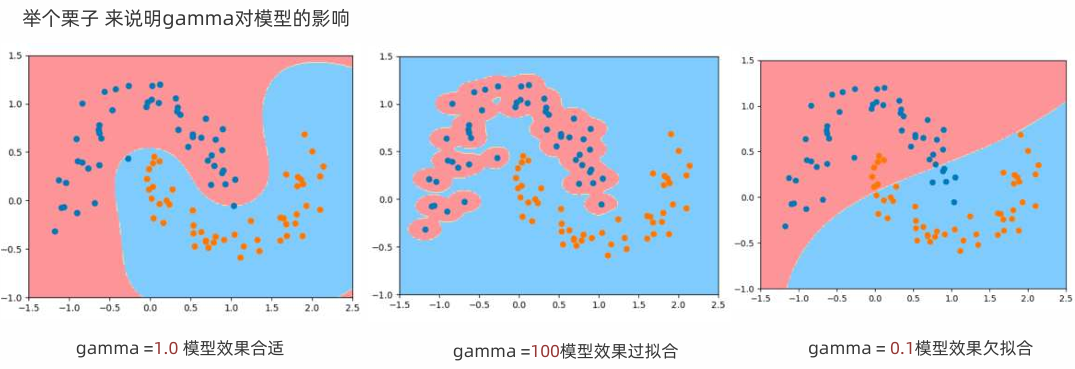
结论：gamma越大，高斯分布越窄，gamma越小，高斯分布越宽

代码实现上述案例

python 复制代码 
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from plot_util import plot_decision_boundary
import numpy as np


def dm01():
    X, y = make_moons(noise=0.15)
    print('x.shape -->', X.shape)
    print('y.shape -->', y.shape)
    plt.scatter(X[y == 0, 0], X[y == 0, 1])
    plt.scatter(X[y == 1, 0], X[y == 1, 1])
    plt.show()

    def RBFKernelSVC(gamma=1.0):
        return Pipeline([
            ('std_scaler', StandardScaler()),
            ('svc', SVC(kernel='rbf', gamma=gamma))
        ])

    print('x.shape -->', X.shape)
    print('y.shape -->', y.shape)

    svc1 = RBFKernelSVC(gamma=1.0)
    svc1.fit(X, y)

    # 画图
    plot_decision_boundary(svc1, axis=[-1.5, 2.5, -1.0, 1.5])
    plt.scatter(X[y == 0, 0], X[y == 0, 1])
    plt.scatter(X[y == 1, 0], X[y == 1, 1])
    plt.show()

    # 4.2 实例化模型2 -过拟合
    svc2 = RBFKernelSVC(gamma=100)
    svc2.fit(X, y)
    plot_decision_boundary(svc2, axis=[-1.5, 2.5, -1.0, 1.5])
    plt.scatter(X[y == 0, 0], X[y == 0, 1])
    plt.scatter(X[y == 1, 0], X[y == 1, 1])
    plt.show()

    # 4.3 实例化模型3 -欠拟合
    svc3 = RBFKernelSVC(gamma=0.1)
    svc3.fit(X, y)
    plot_decision_boundary(svc3, axis=[-1.5, 2.5, -1.0, 1.5])
    plt.scatter(X[y == 0, 0], X[y == 0, 1])
    plt.scatter(X[y == 1, 0], X[y == 1, 1])
    plt.show()


dm01()

SVC和LinearSVC主要区别对比

特性 SVC(kernel='linear') LinearSVC
底层库 libsvm liblinear
优化算法 SMO 坐标下降法
正则化参数 C（惩罚系数） C（惩罚系数）
损失函数 铰链损失（hinge loss） 可选的损失函数
正则化形式 L2 正则化 L2 或 L1 正则化（通过 penalty）
截距（bias）处理 自动处理 可选择是否拟合截距
多分类策略 一对一（one-vs-one） 一对多（one-vs-rest）
速度（线性问题） 较慢 快很多（特别是大数据）
核函数 支持各种核 仅线性
支持稀疏数据 有限 更好

LinearSVC基于load_iris实现多分类

python 复制代码 
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
import numpy as np

plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei', 'KaiTi']
plt.rcParams['axes.unicode_minus'] = False


# 如果你没有plot_decision_boundary_svc，这里是实现
def plot_decision_boundary_svc(model, axis):
    """绘制SVM决策边界"""
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], 500),
        np.linspace(axis[2], axis[3], 500)
    )

    X_new = np.c_[x0.ravel(), x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#90CAF9', '#A5D6A7'])

    plt.contourf(x0, x1, zz, cmap=custom_cmap, alpha=0.3)


def dm01_iris_multiclass():
    """使用完整Iris数据集展示LinearSVC的多分类"""
    # 1. 加载完整数据
    X, y = load_iris(return_X_y=True)
    print('完整数据集:')
    print('X.shape -->', X.shape)  # (150, 4)
    print('y.shape -->', y.shape)  # (150,)
    print('类别分布:', np.bincount(y))  # [50, 50, 50]
    print('类别标签:', np.unique(y))  # [0, 1, 2]

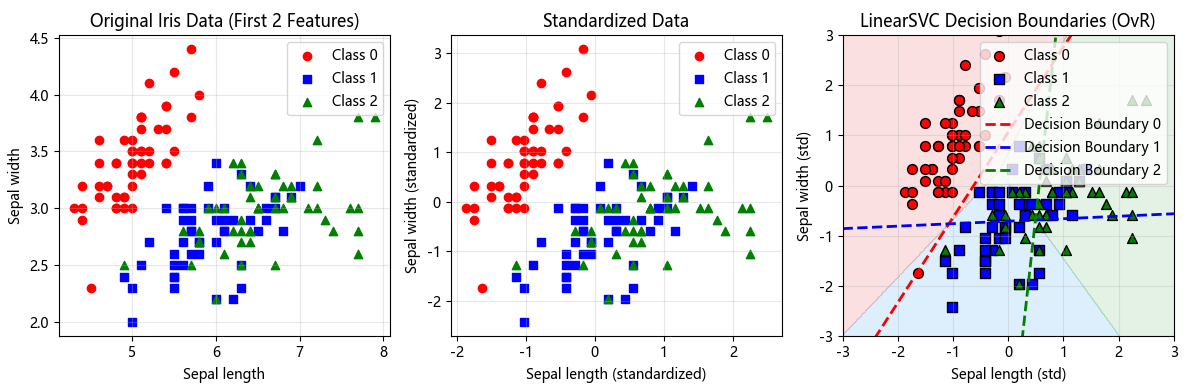
    # 2. 可视化前两个特征（便于绘图）
    plt.figure(figsize=(12, 4))

    # 原始数据可视化
    plt.subplot(131)
    colors = ['red', 'blue', 'green']
    markers = ['o', 's', '^']

    for i in range(3):
        plt.scatter(X[y == i, 0], X[y == i, 1],
                    color=colors[i], marker=markers[i],
                    label=f'Class {i}')
    plt.xlabel('Sepal length')
    plt.ylabel('Sepal width')
    plt.title('Original Iris Data (First 2 Features)')
    plt.legend()
    plt.grid(True, alpha=0.3)

    # 3. 标准化（重要！SVM对尺度敏感）
    scaler = StandardScaler()
    X_std = scaler.fit_transform(X)

    # 标准化后可视化
    plt.subplot(132)
    for i in range(3):
        plt.scatter(X_std[y == i, 0], X_std[y == i, 1],
                    color=colors[i], marker=markers[i],
                    label=f'Class {i}')
    plt.xlabel('Sepal length (standardized)')
    plt.ylabel('Sepal width (standardized)')
    plt.title('Standardized Data')
    plt.legend()
    plt.grid(True, alpha=0.3)

    # 4. 使用LinearSVC进行多分类
    print('\n=== LinearSVC多分类演示 ===')

    # LinearSVC默认使用One-vs-Rest策略
    svc = LinearSVC(
        C=1.0,  # 正则化参数
        dual='auto',  # 自动选择对偶或原始问题
        multi_class='ovr',  # One-vs-Rest策略
        random_state=42,
        max_iter=10000
    )

    # 只用前两个特征训练（为了可视化）
    svc.fit(X_std[:, :2], y)

    print(f'训练准确率: {svc.score(X_std[:, :2], y):.4f}')
    print(f'系数形状: {svc.coef_.shape}')  # (3, 2) - 3个分类器，每个有2个系数
    print(f'截距形状: {svc.intercept_.shape}')  # (3,) - 3个截距

    # 5. 可视化决策边界
    plt.subplot(133)

    # 绘制决策区域
    plot_decision_boundary_svc(svc, axis=[-3, 3, -3, 3])

    # 绘制数据点
    for i in range(3):
        plt.scatter(X_std[y == i, 0], X_std[y == i, 1],
                    color=colors[i], marker=markers[i],
                    edgecolor='k', s=50,
                    label=f'Class {i}')

    # 绘制决策边界线
    x_boundary = np.linspace(-3, 3, 100)

    # 对于One-vs-Rest，每条线是决策函数为0的地方
    # w1*x1 + w2*x2 + b = 0 => x2 = -(w1*x1 + b)/w2
    for i in range(3):
        w1, w2 = svc.coef_[i]
        b = svc.intercept_[i]

        # 注意：这里可能出现除以0的情况
        if abs(w2) > 1e-10:
            y_boundary = -(w1 * x_boundary + b) / w2
            plt.plot(x_boundary, y_boundary,
                     color=colors[i], linestyle='--',
                     linewidth=2, label=f'Decision Boundary {i}')

    plt.xlabel('Sepal length (std)')
    plt.ylabel('Sepal width (std)')
    plt.title('LinearSVC Decision Boundaries (OvR)')
    plt.legend(loc='upper right')
    plt.grid(True, alpha=0.3)
    plt.axis([-3, 3, -3, 3])

    plt.tight_layout()
    plt.show()

    # 6. 深入分析决策函数
    print('\n=== 决策函数分析 ===')

    # 获取三个分类器的决策值
    decision_values = svc.decision_function(X_std[:5, :2])  # 前5个样本
    print('前5个样本的决策值（每列对应一个分类器）:')
    print(decision_values)
    print(f'决策值形状: {decision_values.shape}')  # (5, 3)

    # 预测结果
    predictions = svc.predict(X_std[:5, :2])
    print('预测结果:', predictions)
    print('真实标签:', y[:5])

    # 7. 查看One-vs-Rest如何工作
    print('\n=== One-vs-Rest原理 ===')
    print('分类器0: 是类别0 vs 不是类别0')
    print('分类器1: 是类别1 vs 不是类别1')
    print('分类器2: 是类别2 vs 不是类别2')
    print('\n每个样本选择决策值最大的分类器作为最终类别')

    # 8. 使用不同C值对比
    print('\n=== 不同C值的影响 ===')

    C_values = [0.01, 0.1, 1, 10, 100]
    plt.figure(figsize=(15, 3))

    for idx, C in enumerate(C_values):
        svc_tmp = LinearSVC(C=C, dual='auto', max_iter=10000, random_state=42)
        svc_tmp.fit(X_std[:, :2], y)

        plt.subplot(1, len(C_values), idx + 1)
        plot_decision_boundary_svc(svc_tmp, axis=[-3, 3, -3, 3])

        for i in range(3):
            plt.scatter(X_std[y == i, 0], X_std[y == i, 1],
                        color=colors[i], marker=markers[i],
                        alpha=0.6, s=30)

        plt.title(f'C = {C}\n准确率: {svc_tmp.score(X_std[:, :2], y):.3f}')
        plt.axis([-3, 3, -3, 3])

    plt.tight_layout()
    plt.show()

    return svc, X_std, y


# 运行函数
if __name__ == '__main__':
    svc_model, X_standardized, y_labels = (dm01_iris_multiclass())
相关推荐
铁手飞鹰2 小时前
[深度学习]Vision Transformer
人工智能·pytorch·python·深度学习·transformer
Web3VentureView2 小时前
目标：覆盖全网主流公链，SYNBO 正式开启公链生态媒体合作矩阵计划
大数据·网络·人工智能·区块链·媒体·加密货币
香芋Yu2 小时前
【深度学习教程——02_优化与正则(Optimization)】09_为什么Dropout能防止过拟合？正则化的本质
人工智能·深度学习
易营宝2 小时前
Yandex广告投放效果怎么样？B2B外贸品牌实测报告
人工智能·seo
会飞的老朱2 小时前
专精特新科技企业，如何用数智化打通管理全链路？
人工智能·科技·oa协同办公
AI_56782 小时前
Git冲突治理白皮书：智能标记与可视化协同的下一代解决方案
大数据·人工智能·git·机器学习
InfiSight智睿视界2 小时前
当老字号遇上AI：阳坊涮肉的数字化运营转型之路
大数据·人工智能·连锁店智能巡检
张3蜂2 小时前
OpenClaw 深度解析：从个人 AI 助理到开源智能体平台
人工智能·开源
程序员欣宸2 小时前
LangChain4j实战之十六：RAG (检索增强生成)，Naive RAG
java·人工智能·ai·langchain4j
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03Claude Code Skills 实用使用手册042025 年大语言模型发展回顾：关键突破、意外转折与 2026 年展望05Clawdbot 中文汉化版 接入微信、飞书06一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示07Vue-skills的中文文档08Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services09在Trae中使用Pencil MCP10UV安装并设置国内源