模拟退火算法零基础快速入门

原理

模拟退火（SA(simulated annealing)）算法的名字起得很形象，退火（annealing）原本的意思是将金属加热到很高温度，然后缓慢冷却。在高温下，原子运动剧烈，能跳出不稳定的状态；随着缓慢冷却，原子最终会停留在能量最低的晶体结构中，使金属更有韧性。

从上面的解释中，我们会发现随着温度的降低，金属原子的晶体结构渐渐稳定，最终到达一个我们期望的状态，同理退火算法就是通过模拟退火的过程找到全局的最优解。

具体来说，我们把当前状态设置成一个山坡上的小球，初始时，这个小球非常有活力（设拥有初始活力 T 等于 2000），遇到向下的坡时，它理所当然的滚下去，遇到向上的坡时可以用力爬上去，随着时间流逝，小球渐渐失去了活力（设降温系数是 0.997），最终在一个地方一动不动（设此时的活力 T 小于等于），最后这个小球可能会被困在一个极小值点，不在全局最小值点，我们可以通过让小球初始时更有活力（增加 T）以及降温的速度更慢（增加降温系数）来到达全局最小值点，当然这样做会让一次模拟的时间加长，不能太大。

注：接下来我可能会提到活力和温度，他们指的都是 T 。

题目1

U644153 图的染色 - 洛谷https://www.luogu.com.cn/problem/U644153

AC代码

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

int n, m;
long long g[35][35];
int color[35];
long long current_ans = 0, final_ans = 0;

void sa() {
    memset(color, 0, sizeof(color));
    current_ans = 0;

    double T = 1e6;
    while (T > 1e-4) {
        int u = rand() % n + 1;

        long long delta = 0;
        for (int v = 1; v <= n; v++) {
            if (u == v || g[u][v] == 0) continue;
            if (color[u] == color[v]) delta += g[u][v]; 
            else delta -= g[u][v]; 
        }

        if (delta > 0 || exp(delta / T) > (double)rand() / RAND_MAX) {
            current_ans += delta;
            color[u] = 1 - color[u];
            final_ans = max(final_ans, current_ans);
        }
        T *= 0.9997;
    }
}

int main() {
    srand(time(0));
    if (!(cin >> n >> m)) return 0;
    for (int i = 0; i < m; i++) {
        int u, v; long long w;
        cin >> u >> v >> w;
        g[u][v] = g[v][u] = w;
    }

    for (int i = 0; i < 50; i++) sa();

    cout << final_ans << endl;
    return 0;
}

逐步分析

好，既然知道了原理，我们看一下代码是怎么实现退火的，首先根据题意建图，接着模拟 50 次退火，对于每次模拟，我们先让所有节点同色，并且重置当前结果为 0：

cpp 复制代码

    memset(color, 0, sizeof(color));
    current_ans = 0;

之后我们设置初始温度 T = 1e6，降温结束温度是 1e-4，现在这个小球开始滚动，我们随机一个滚动的方向 u，接着我们尝试朝这个方向移动：

cpp 复制代码

        int u = rand() % n + 1;

我们初始化 delta 为移动的后果：

cpp 复制代码

        long long delta = 0;

接着我们计算移动产生的后果：

cpp 复制代码

        for (int v = 1; v <= n; v++) {
            if (u == v || g[u][v] == 0) continue;
            if (color[u] == color[v]) delta += g[u][v]; 
            else delta -= g[u][v]; 
        }

核心判断

接着我们基于移动的结果判断是否真的要超方向 u 移动，我们分两种情况：

1，移动的结果是好的，也就是 delta > 0 。

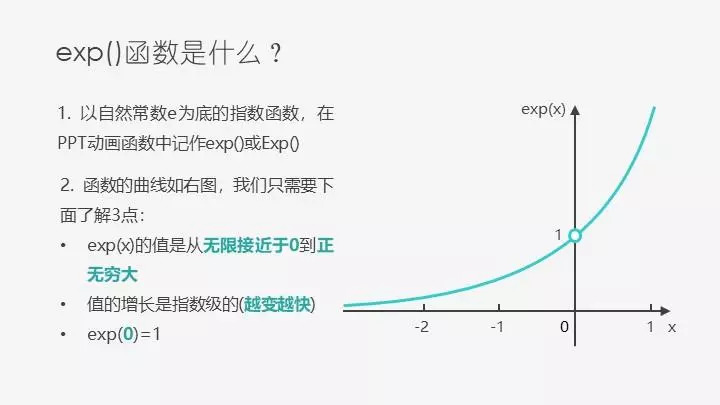
2，移动的结果是不好的，我们通过exp( delta / T ) 来代表我们采取这个移动的概率，接下来就是最精髓的地方了，根据下图可知，当 delta 越小概率越小，当前的活力 T 越大概率越大 ，这简直太贴合我们的上文介绍的原理了，如果我们把坏结果当成是一个上坡路，那么这个上坡路的路越陡（结果 delta 越坏），小球越难爬上去，小球越有活力（当前的活力 T 越大），越容易爬上去。

接下来我们只需要将概率转化为准确的 bool 值就行了，很直接的，我们随机生成一个（0，1）之间的数 ( double ) rand() / RAND_MAX ，如果我们计算的概率值 exp( delta / T ) 大于这个随机数，返回 1，否则返回 0 。

cpp 复制代码

        if (delta > 0 || exp(delta / T) > (double)rand() / RAND_MAX) {
            current_ans += delta;
            color[u] = 1 - color[u];
            final_ans = max(final_ans, current_ans);
        }

最后我们模拟退火，降低当前温度（活力）：

cpp 复制代码

        T *= 0.9997;

优化方案

然后我们就大功告成了，吗？

一般来说是没问题，首先模拟退火这个方法最大的优势是简化问题，对于一些很复杂的问题，我们可能用公式推不出来，但是直接用模拟退火随机查找这一特性就可以避免这一问题，就像黑承所说的那样，既然不知道谁才是替身使者，那就把所有人都揍一顿。

但是也正因为如此，这个算法的时间复杂度普遍较高，如果出现了被卡时间的情况，这个时候有两种解决方案：

1，加速退火算法本身：降低初始温度，加快降温速度，减少模拟次数（当然这也可能会导致被困在局部极小值）。

2，结合题目加入优化，这里不好说怎么优化，我们得具体题目具体分析，下一道题就存在这种优化。

题目2（存在优化）

P4035 [JSOI2008] 球形空间产生器 - 洛谷https://www.luogu.com.cn/problem/P4035

AC代码

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;

int n;
struct Point {
    double x[12];
} p[15], center = { 0 };

double get_dist(Point a, Point b) {
    double sum = 0;
    for (int i = 0; i < n; i++)
        sum += (a.x[i] - b.x[i]) * (a.x[i] - b.x[i]);
    return sqrt(sum);
}

void sa() {
    double T = 1.0;
    while (T > 1e-6) {
        double dists[15], avg = 0;
        for (int i = 0; i <= n; i++) {
            dists[i] = get_dist(center, p[i]);
            avg += dists[i];
        }
        avg /= (n + 1);

        double delta_move[12] = { 0 };
        for (int i = 0; i <= n; i++) {
            double len = dists[i] - avg; // 偏差
            for (int j = 0; j < n; j++) {
                // 根据该点到球心的位移向量进行修正
                delta_move[j] += ((p[i].x[j] - center.x[j]) / dists[i]) * len;
            }
        }

        // 将所有点的"拉力"和"推力"汇总，乘上步长 T
        for (int j = 0; j < n; j++) {
            center.x[j] += delta_move[j] * T;
        }

        T *= 0.99995;
    }
}

int main() {
    if (!(cin >> n)) return 0;
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j < n; j++) {
            cin >> p[i].x[j];
            center.x[j] += p[i].x[j];
        }
    }
    // 初始点设为重心
    for (int j = 0; j < n; j++) center.x[j] = center.x[j] / (n + 1);

    sa();

    for (int i = 0; i < n; i++)
        printf("%.3lf%c", center.x[i], i == n - 1 ? '\n' : ' ');
    return 0;
}


double delta_move[12] = { 0 };
for (int i = 0; i <= n; i++) {
    double factor = dists[i] - avg; // 偏差
    for (int j = 0; j < n; j++) {
        delta_move[j] += ((p[i].x[j] - center.x[j]) / dists[i]) * factor;
    }
}

...

for (int j = 0; j < n; j++) {
    center.x[j] += delta_move[j] * T;
}

逐步分析

优势，异同分析

这道题可以说很好的体现了模拟退火算法的优势，以下是两条提交记录，第一条提交记录用的是高斯消元法，第二条提交记录用的是模拟退火算法，可以看出高斯消元法的时间复杂度是模拟退火算法的十倍，但是这又怎么样呢，400ms对于AC来说仍然绰绰有余了，它的实现比高斯消元要简单的，最重要的是，你可能没学过高斯消元，但是你大概率学过模拟退火。

但是如果你这道题是用随机的方式找球心你最多只能得 80，至少我改了二十几次参数都是这样，这时候我们就要根据题意优化我们的算法，首先，我们可以从重心出发，把重心当作是我们的中心（一个完整且均匀的球的重心就是球心）：

cpp 复制代码

    // 初始点设为重心
    for (int j = 0; j < n; j++) center.x[j] = center.x[j] / (n + 1);

核心优化

接下来我们只需要不断移动我们的中心，直到中心点的活力消耗完( T <= 1e-6 ) 。

现在的问题就是我们该怎么移动我们的中心使得它能靠近球心，很简单，我们只需要让中心往合适的方向移动合适的长度 ，合适的长度就是当前点到中心的距离与所有点到中心点的平均距离的差（大于 0 说明离得远，小于 0 说明离得近），合适的方向就是一个单位向量（一个只有方向没有长度的向量）:，这样循环了每一个节点的每一个维度之后我们就得到了一个修改向量 delta_move[ ] ，我们只要原来的中心坐标加上了这个修改向量中心就会向球心靠近。

这样无疑大大提高了速度，因为现在的模拟退火的移动方向从随机变成了每一次都一定更优：

cpp 复制代码

double delta_move[12] = { 0 };
for (int i = 0; i <= n; i++) {
    double len = dists[i] - avg; // 偏差
    for (int j = 0; j < n; j++) {
        delta_move[j] += ((p[i].x[j] - center.x[j]) / dists[i]) * len;
    }
}

...

for (int j = 0; j < n; j++) {
    center.x[j] += delta_move[j] * T;
}

注意事项

需要注意的是这道题模拟退火的参数选择，T 在这里最多是 1 ，因为如果超过 1 就代表了过度修改，此时我们就可以减缓降温速度，降低截止温度来让这个过程变得更丝滑，更准确。