嗨~大家好,这里是春栀怡铃声 的博客~
"做你害怕的事,然后发现,不过如此~"
目录
"假如《哈利·波特》的分院帽是个程序员...
它不会念咒语,而是掏出一棵发光的树:'勇敢?→左枝|智慧?→右枝|野心?→左左枝...'
3次选择,精准分院!这棵'决策树',正是二叉树的魔法变体✨"
让我们坐稳发车!探索二叉树的奥秘~
树概念及结构
1.树的概念
树---非线性顺序结构
有一个根节点,剩下的都是子节点,因为长相像一个倒过来的树,所以被称为树
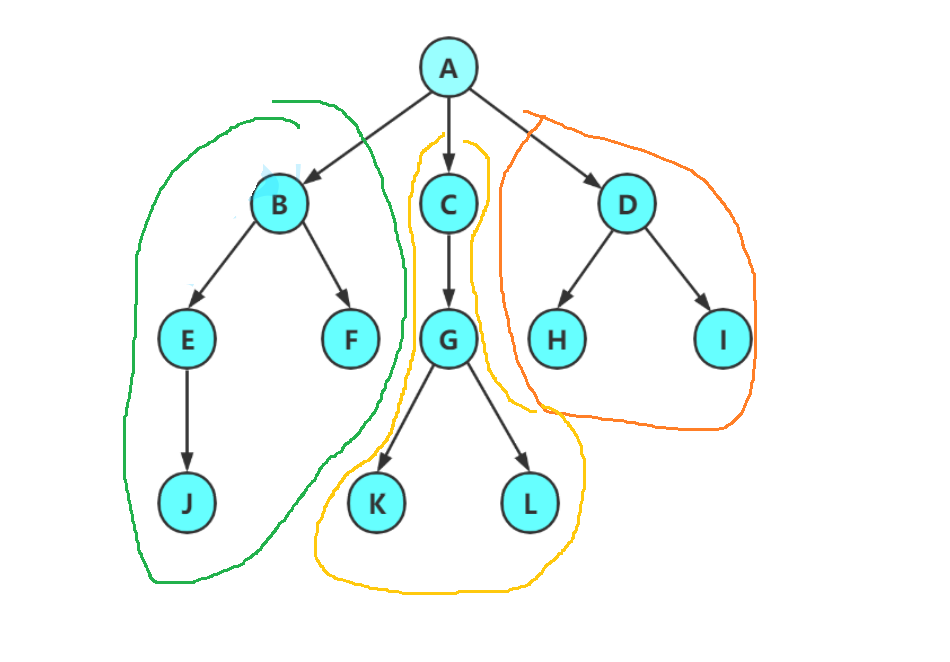
A--根节点
用不同颜色圈起来的是不同子树 注意 :树形结构中,子树之间不能有交集,否则就不是树形结构
不是树:
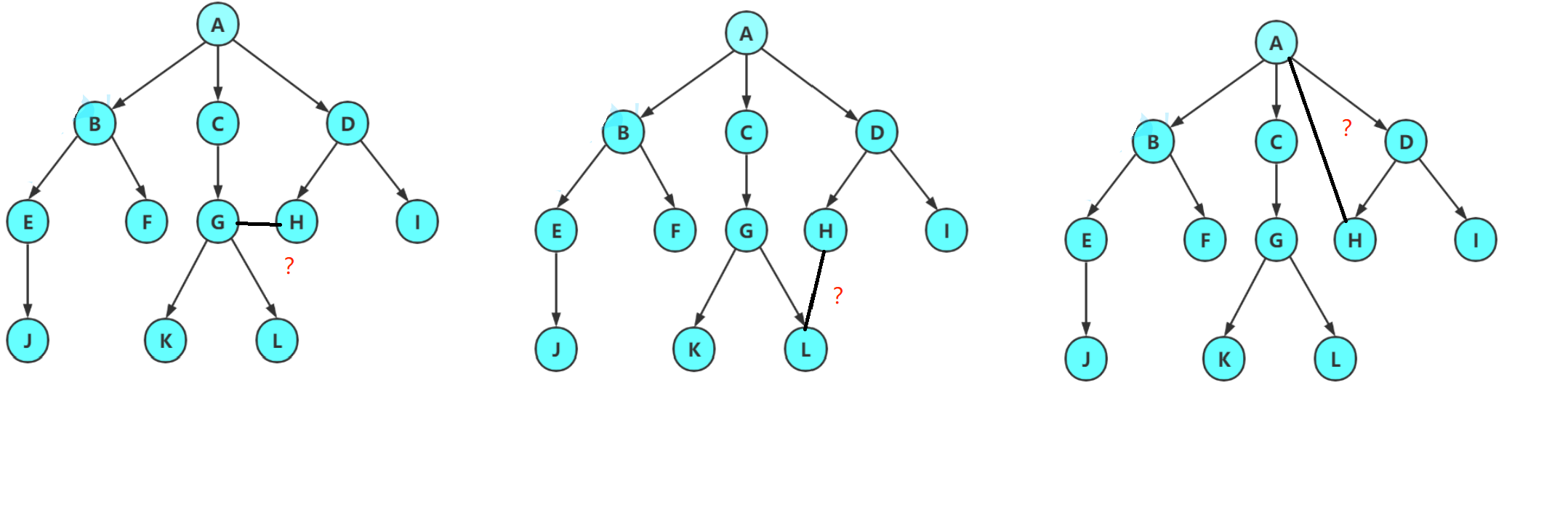
2.树的相关概念
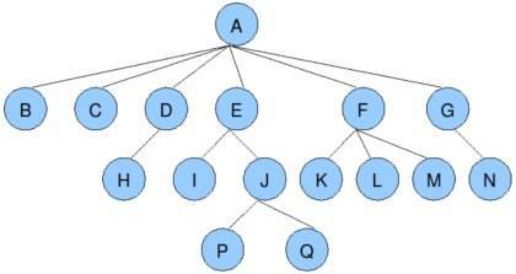
结点的度:一个结点含有的子树的个数称为该结点的度 例如:A的度为6,F的度为3
树的度:结点中最大的度即为树的度 例如图中树的度为6
叶子结点:度为0的结点为叶子节点。例如 B C H I......
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 图中:B是A的孩子结点
兄弟结点:具有相同父结点的结点互称为兄弟结点;图:B、C是兄弟结点
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
树的高度或深度:树中结点的最大层次; 如图:树的高度为4
3.树的表示
我们来了解比较简单的孩子兄弟表示法
typedef int DataType;
struct Node
{
struct Node* firstChild1; // 第一个孩子结点
struct Node* pNextBrother; // 指向其下一个兄弟结点
DataType data; // 结点中的数据域
};图形演示: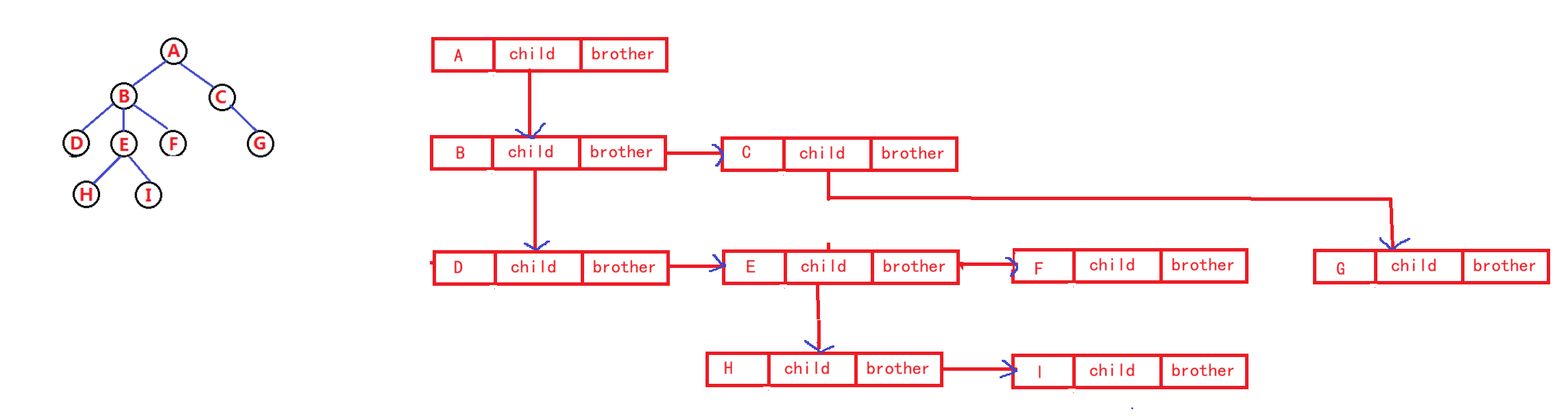
二叉树概念及结构
1.二叉树的概念
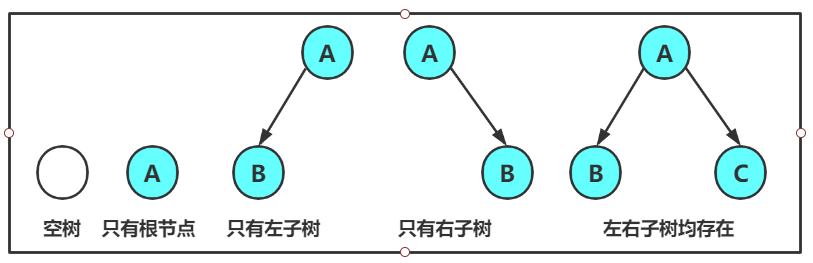
一棵二叉树是结点的一个有限集合,该集合: 1. 或者为空 2. 由一个根结点加上两棵别称为左子树和右子树的二叉树组成
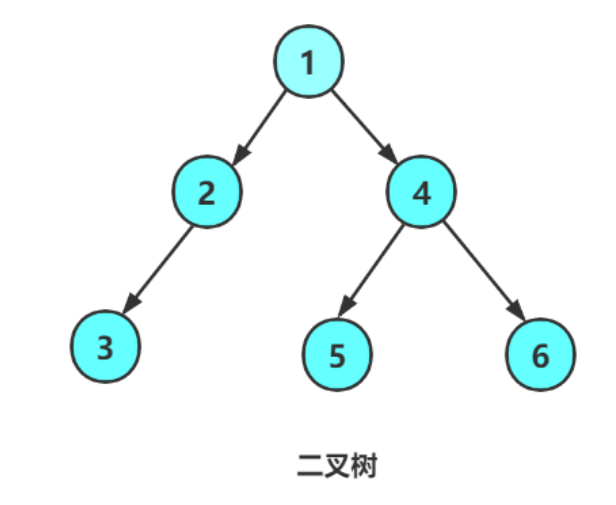
2.特殊的二叉树
1.满二叉树
每一个父结点都有2个子结点
满二叉树是一种特殊的完全二叉树。
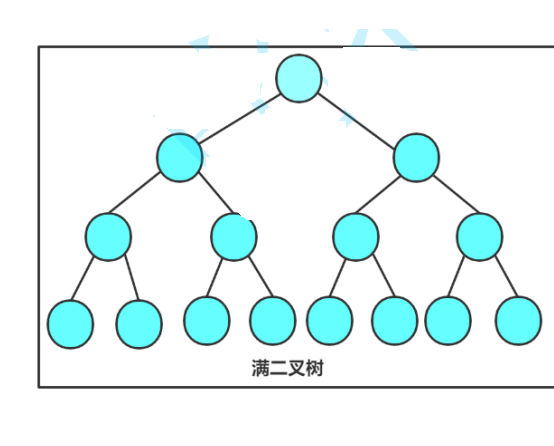
2.完全二叉树
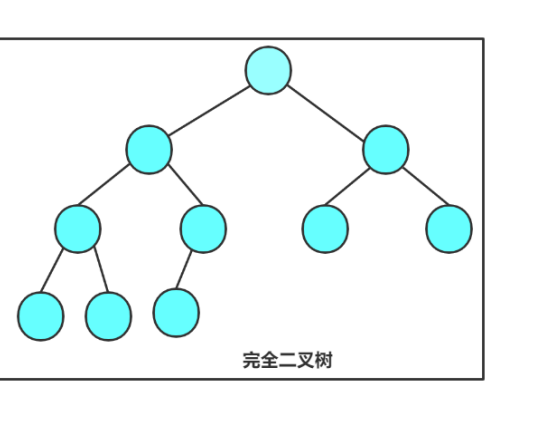
| 对比维度 | 满二叉树 | 完全二叉树 | 💡 关键洞察 |
|---|---|---|---|
| 节点分布 | 所有层节点数达最大(第i层=2ⁱ⁻¹) | 仅最后一层可能不满,且必须靠左连续 | ✅ 完全二叉树允许"最后一排没坐满",但禁止"3号座空着,4号座有人" |
| 叶子位置 | 仅出现在最后一层 | 可出现在最后一层或倒数第二层(最后一层叶子靠左) | 🌰 6个节点的完全二叉树:节点3只有左孩子(度为1),叶子在第2、3层 |
| 节点度特性 | 非叶子节点度全为2,无度为1节点 | 度为1的节点只能有0个或1个,且只能有左孩子(绝无"只有右孩子") | ⚠️ 强调:若遇"左空右不空",直接判定非完全二叉树! |
| 节点总数 | 必为奇数(2ᵏ-1) | 可奇可偶:偶数时有1个度为1节点,奇数时无 | 📐 深度公式: 满:k = log₂(n+1) |
3.二叉树的性质
1.若规定根结点的层数为1,则一棵非空二叉树的第 n 层上最多有 2^(n-1) 个结点.
-
若规定根结点的层数为1,则深度为h的二叉树的最大结点数是 2^h-1
-
若规定根结点的层数为1,具有n个结点的满二叉树的深度,h=log₂ (n+1)
(ps: 是log以2 为底,n+1为对数)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有结点从0开始编号,则对于序号为i的结点有: 1. 若i>0,i位置结点的双亲序号:(i-1)/2 ;i=0,i为根结点编号,无双亲结点 2. i结点的左孩子结点 :i*2+1 右孩子结点:i*2+2
4.二叉树的存储结构
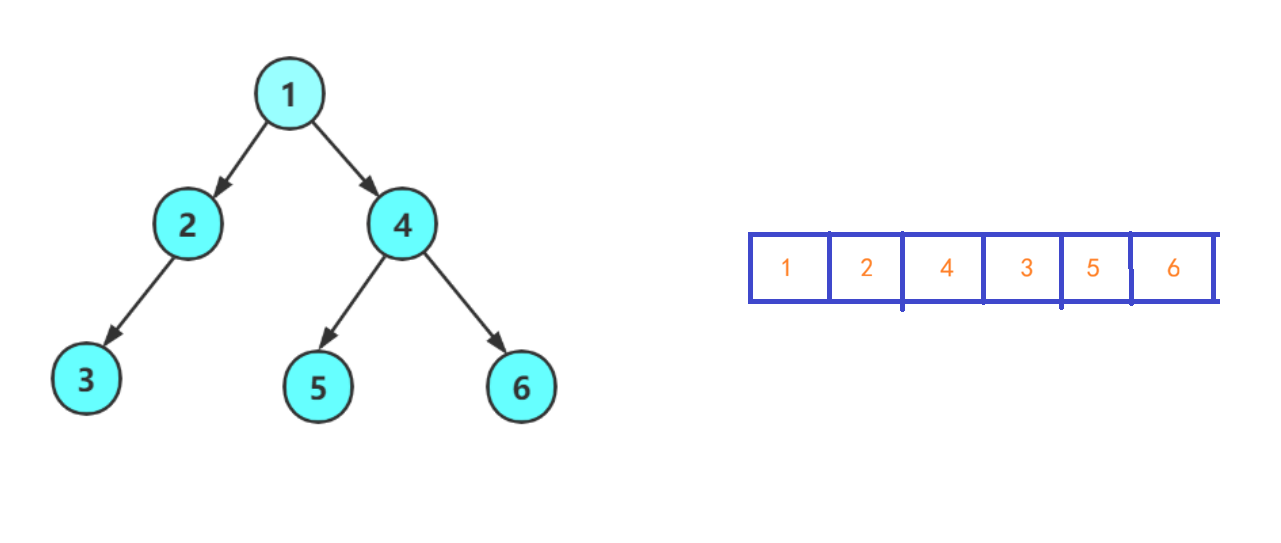
1.顺序存储
一般完全二叉树才用顺序存储,也就是数组存储,物理结构是数组,逻辑结构是二叉树
而现实中使用中只有堆才会使用数组来存储,关于堆我们下一章节会专门讲解。
2.链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是 链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。
二叉树顺序结构及实现
1.二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。
现实中我们通常把堆 (一种二叉树) 使用顺序结构的数组来存储,需要注意的是这里的堆 和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
2.堆的概念及结构
堆是一种特殊的数据结构,逻辑上是一棵完全二叉树,物理上用数组存储。它的核心特点是:父节点的值总是大于或小于子节点的值。
堆中某个结点的值总是不大于或不小于其父结点的值;
堆总是一棵完全二叉树。
更多堆的知识在这里~https://blog.csdn.net/wyx6666668888888/article/details/157655398?spm=1001.2014.3001.5501
二叉树链式结构及实现
前置说明
为了说明二叉树的遍历,我们先暂时用简单方式创建二叉树 在"二叉树的创建与销毁" 精讲怎么创建二叉树
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(int x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode)); //这里扩充的是整个结构体的大小
//不能写成 BTDataType 这个!!
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->data = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node2->left = node3;
node1->right = node4;
node4->left = node5;
node4->right = node6;
return node1;
}BuyNode函数负责新插入的结点创建
CreatBinaryTree函数负责将每个结点联系起来,形成二叉树
这样就创建了6个节点的二叉树
二叉树的遍历
前序
遍历一个二叉树时 :先访问当前节点(根)->遍历左子树->遍历右子树
这个规则会递归地应用到每个子树上。
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%d ",root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}访问根结点 1
继续访问左子树 以2为根,访问2的左子树3
以3为根,访问左子树,左子树为NULL 返回根为2的结点,访问2的右子树,2的右子树为空返回到1,继续访问1的右子树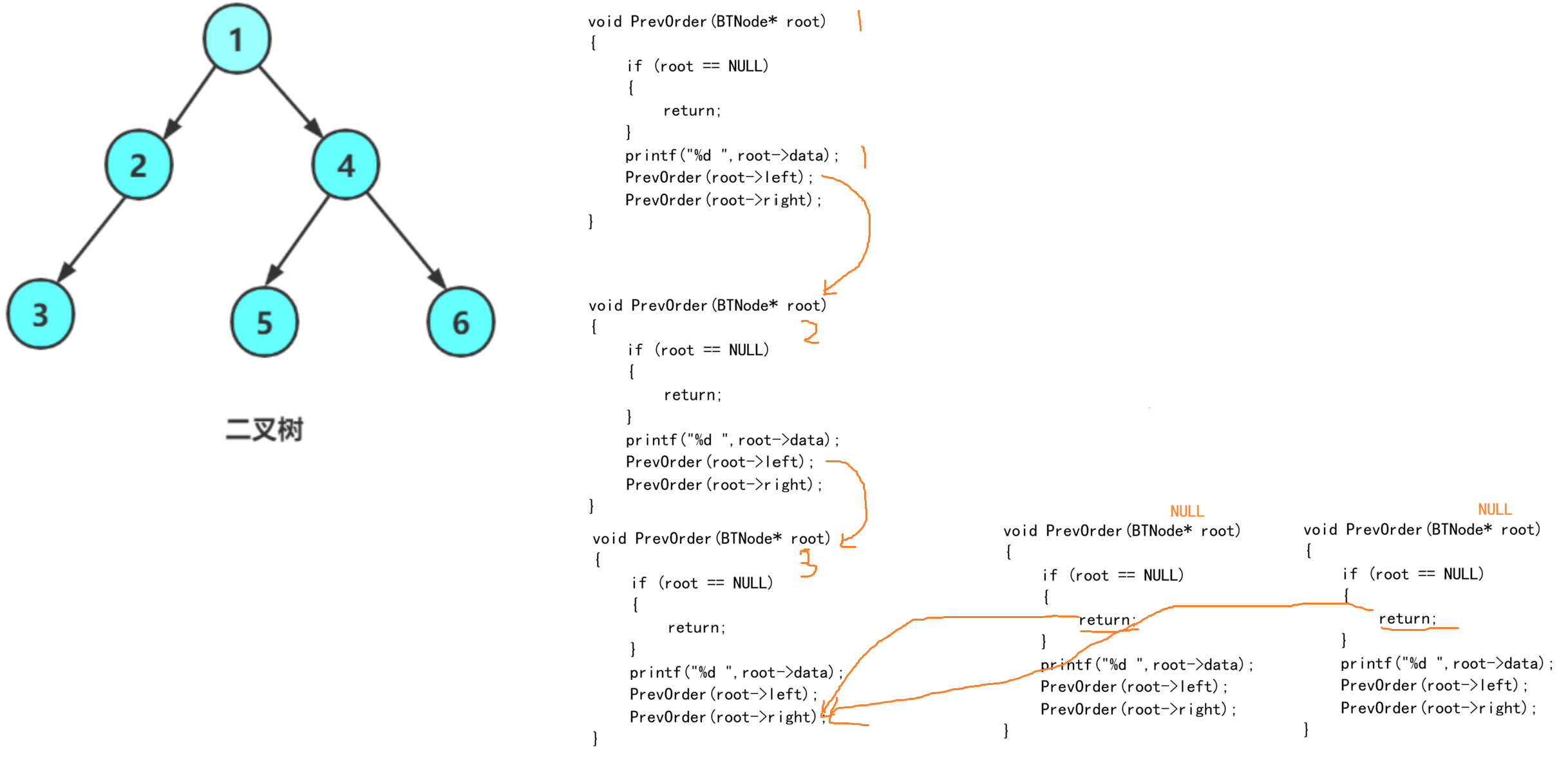
N 代表空 ,每一个框 框住的是一个小的树
中序
遍历一个二叉树时 :先遍历左子树-> 节点(根)->遍历右子树
这个规则会递归地应用到每个子树上。
void InOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}从1出发 → 先处理左子树(2为根)
处理2的左子树(3为根):
3无左子树 → 访问3
3无右子树 → 返回
访问2:
2无左子树 → 访问2
2无右子树 → 返回
访问1
处理1的右子树(4为根):
4有左子树 → 访问5
5无左子树 → 访问5
5无右子树 → 返回
访问4的右子树 6
6无左子树->访问6
6无右子树->返回
✅ 最终结果:3 → 2→ 1→ 5→ 4→ 6
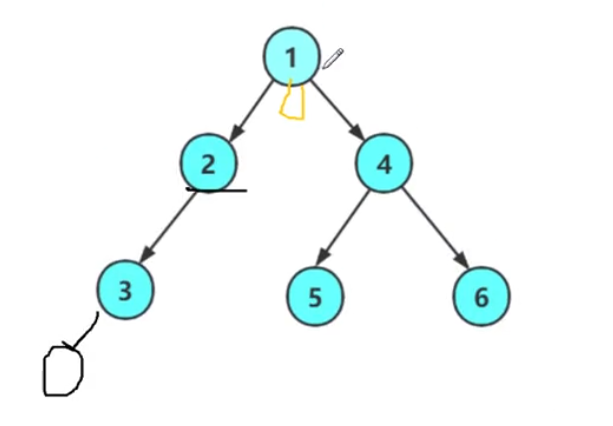
N 代表空 ,每一个框 框住的是一个小的树
后序
void BackOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
BackOrder(root->left);
BackOrder(root->right);
printf("%d ", root->data);
}遍历一个二叉树时 :先遍历左子树->遍历右子树->访问节点(根)
这个规则会递归地应用到每个子树上。
后序的解法与前序推导类似,希望大家可以自己讲给自己听~
结点个数以及高度等
二叉树结点个数
// 二叉树结点个数
int BinaryTreeSize(BTNode* root)
{
return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;
}使用递归,计算结点个数
二叉树叶子结点个数
// 二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}二叉树第k层结点个数
// 二叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}求k层节点个数,也就是求左子树和右子树的k-1层的结点个数之和
先判断如果根节点为空,说明为空堆
如果k==1 第一层只有根结点,返回为1
如果都不是,按照递归方式求左子树和右子树k-1层结点数之和
二叉树查找值为x的结点
//查找x
BTNode* BTFind(BTNode* root, BTData x)
{
if (root == NULL)
return NULL;
if (root->val == x)
return root;
BTNode* node1=BTFind(root->left, x);
if (node1) return node1;
BTNode* node2=BTFind(root->right, x);
if (node2) return node2;
return NULL;
}如果传入的二叉树为空,肯定没有要找的值
根节点找到就是x 返回根节点
如果根节点不是x 查找根节点的左结点,如果左结点找到了,返回,不用继续再右子树中找
所以需要记录node1 node2 可以用来判断有无找到x
二叉树的高度
//树的高度
int TreeHeight(BTNode*root)
{
if (root == NULL)
return 0;
return TreeHeight(root->left) > TreeHeight(root->right)?
TreeHeight(root->left)+1: TreeHeight(root->right)+1;
}二叉树的创建
通过前序遍历的数组构建二叉树
'#'--代表空 ,随意输入一串字符 "abc##de#g##f###"
typedef struct Binarytree
{
struct Binarytree* left;
struct Binarytree* right;
char val;
}BTNode;
BTNode* CreateBTNode(char* a, int* pi)
{
if (a[(*pi)] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->val = a[(*pi)++];
root->left = CreateBTNode(a, pi);
root->right = CreateBTNode(a, pi);
return root;
}
int main() {
char a[100];
scanf("%s", a);
int i = 0;
BTNode* root = CreateBTNode(a, &i);
return 0;
}设置字符数组a 存储输入数据,用'#' 代表空格
if (a[(*pi)] == '#')
{
(*pi)++;
return NULL;
}
如果在读取数组数据时,检测到了'#' 直接返回NULL 并且继续让下标+1
这里使用指针才能改变 i ,让 i 变化起来
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->val = a[(*pi)++];
root->left = CreateBTNode(a, pi);
root->right = CreateBTNode(a, pi);
return root;
动态申请空间创建二叉树结点,
root->val = a[(*pi)++]; 先使用后++,不用担心错误
接下来的逻辑是按照前序的方式创建二叉树
感谢花时间阅读这篇内容!
如果觉得有价值,欢迎点赞支持、收藏备用,或分享给同行。你的认可,是我持续输出高质量内容的最大动力。
我们下期再见喽!!!