【深度学习】：从神经网络到AI大模型的核心逻辑

一、什么是深度学习？------AI世界的"仿生大脑"

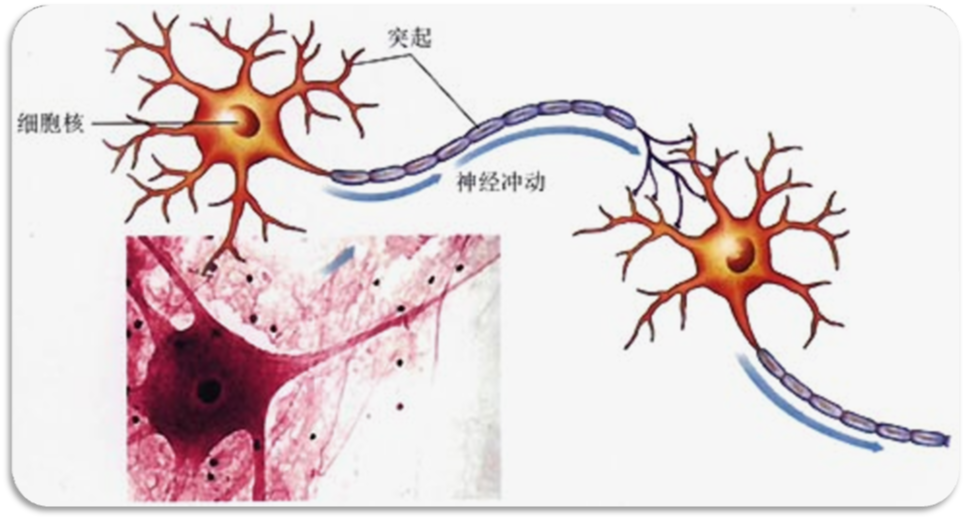
深度学习（DL, Deep Learning）并非凭空出现的技术，而是机器学习（ML, Machine Learning）领域的一个新研究方向，本质是人工智能的"子领域"。它的核心灵感来自人类大脑的神经元网络，通过模拟人脑处理信息的方式，让计算机具备自主学习的能力。

简单来说，深度学习有三个关键特征：

基于人工神经网络：以"神经元"为基本单元，通过节点间的连接传递信号，模拟生物神经的工作模式；
多层次结构：区别于传统机器学习，深度学习的神经网络包含多层隐藏层，能自动从数据中提取"浅特征→深特征"（比如从图像的像素点，逐步学习到边缘、形状、物体轮廓）；
反向传播优化：通过计算预测误差，反向调整网络中的参数，让模型越学越准。

如今，深度学习已在图像识别、语音识别、自然语言处理等领域取得突破性成果，成为AI技术落地的核心驱动力。

如果把深度学习比作一栋建筑，神经网络就是它的"钢筋骨架"。要理解深度学习，首先要搞懂神经网络的核心组成。

每个神经元就像一个简单的"信号处理器"，其工作原理可以用一个通俗的公式概括：

输出 = 激活函数（权重×输入 + 偏置）

输入（x1, x2, ..., xn）：外界传入的"原始信号"，比如图像的像素值、语音的声波数据；
权重（w1, w2, ..., wn）：每个输入信号的"重要程度系数"，相当于信号传递中的"损耗率"------权重越大，说明这个输入对结果的影响越显著；
偏置（b）：一个固定的"辅助参数"，本质是一个存储值恒为1的"偏置节点"，用于调整模型的输出基准（比如让模型在没有输入时也能有基础响应）；
激活函数（如sigmoid）：给线性计算加入"非线性"，让模型能处理复杂问题（比如区分"猫"和"狗"这种非线性分布的数据）。

举个例子：当识别一张猫的图片时，神经元会接收像素点的输入信号，通过权重筛选出"猫的胡须""猫的耳朵"等关键特征信号，再经过激活函数处理，输出"是否为猫"的判断。

神经网络的发展经历了"从简单到复杂"的过程：

感知器（Perceptron）：最基础的神经网络，只有"输入层+输出层"两层结构，本质是一个线性分类器（只能用一条直线划分数据）。比如判断"是否为苹果"，感知器只能处理颜色、形状等线性相关的特征；

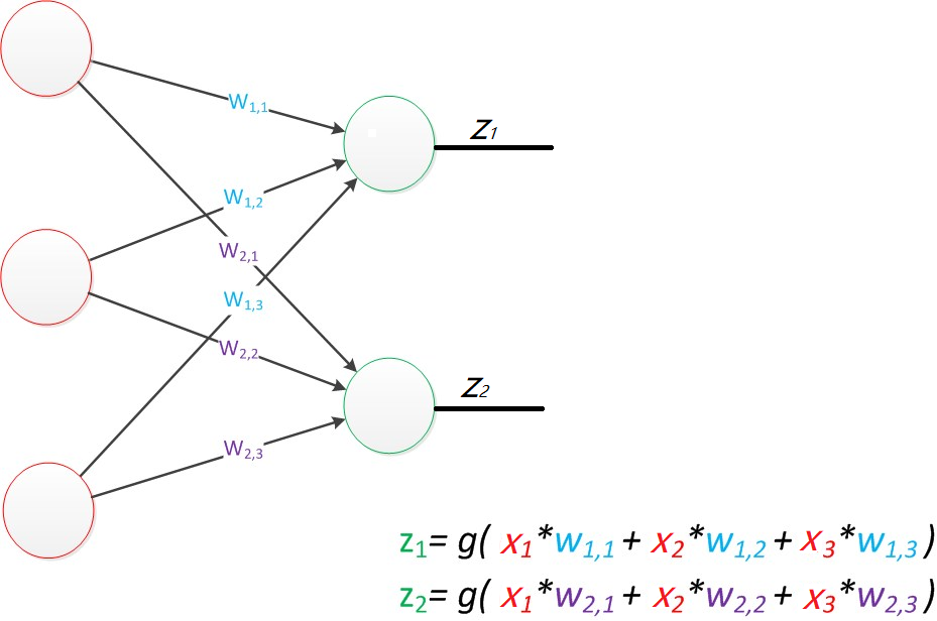
多层感知器（MLP）：在输入层和输出层之间加入了"隐藏层"------这是神经网络能处理非线性问题的关键！隐藏层就像"信号加工车间"，把输入的原始特征转化为更抽象的深层特征，比如从"像素点"加工成"物体轮廓"，再到"具体类别"，从而实现复杂的分类任务（比如区分不同品种的猫、识别手写文字）。

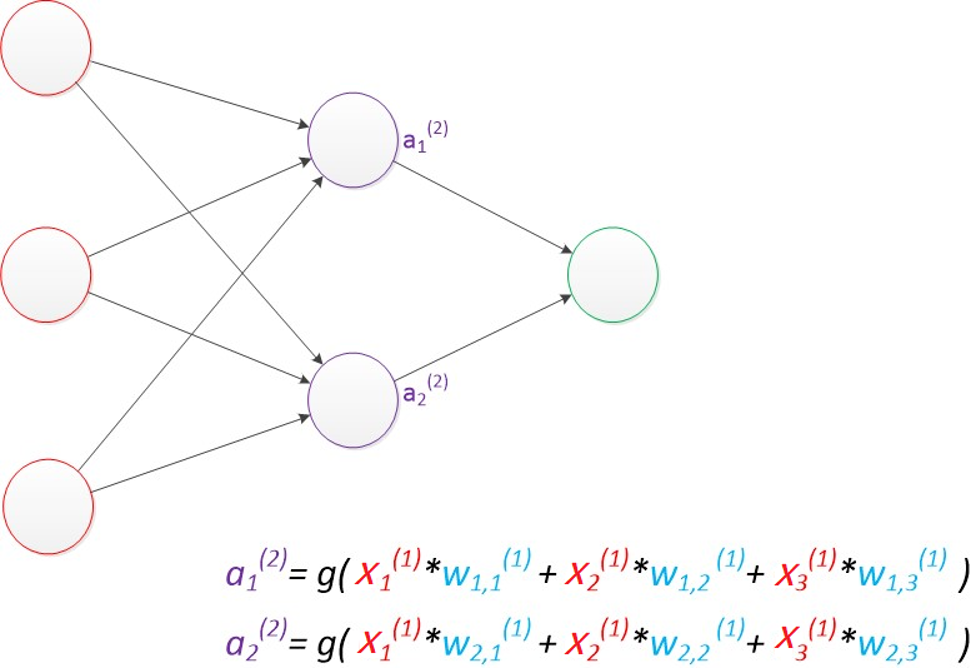
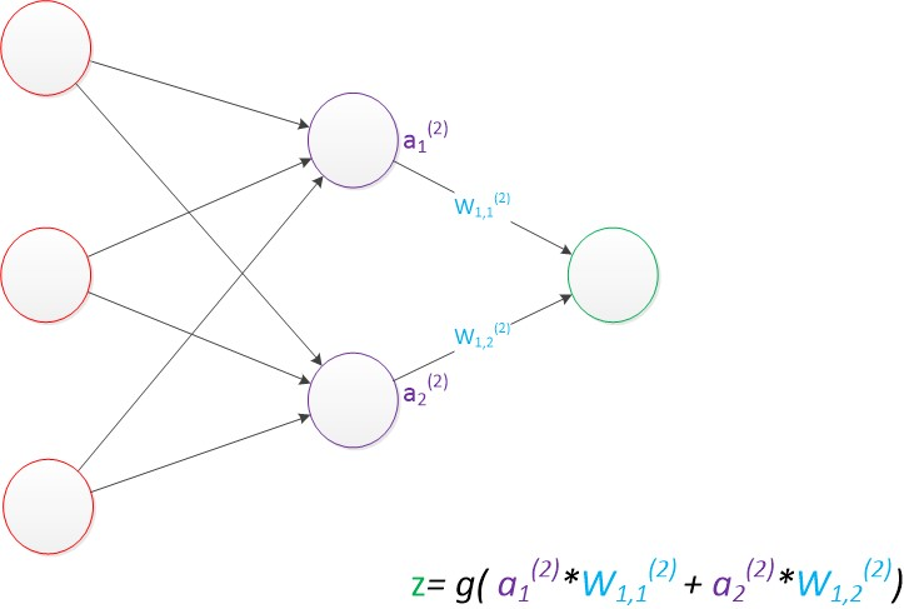
这里有个核心规律：输入层节点数=特征维度 ，输出层节点数=目标维度，而隐藏层的节点数没有固定标准，通常靠经验或测试筛选最优值。

神经网络的本质是一系列矩阵运算：输入数据是矩阵，权重是矩阵，层与层之间的信号传递就是矩阵相乘，再加上激活函数的处理。因此，实现深度学习最核心的工具，其实是线性代数库。

一个刚搭建好的神经网络，就像一个"空白大脑"，需要通过"训练"才能学会技能。训练的核心目标，是找到最优的权重参数，让预测结果尽可能接近真实值。

训练的第一步，是判断"预测得准不准"------这就需要损失函数（也叫代价函数）。它的作用是计算"预测值（yi）"和"真实值（y）"的差距，误差越小，模型效果越好。

常见的损失函数有：

训练中很容易出现一个问题：模型在训练集上表现良好，但在测试集上表现很差，这就是"过拟合"。

正则化的作用的就是"约束"模型的权重参数，避免它过度依赖某些特征。常见的有两种：

文档里有个很形象的例子：输入信号是[1,1,1,1]，权重w1=[1,0,0,0]只关注第一个输入，而w2=[0.25,0.25,0.25,0.25]关注所有输入。虽然两者的计算结果都是1，但w2能"雨露均沾"地学习所有特征，避免过拟合，效果更好------这正是正则化想要达到的目标。

找到了误差（损失函数），也有了约束（正则化），接下来就是"修正参数"------这就需要梯度下降和反向传播（BP）的配合。

梯度下降：相当于"找最小值的导航仪"。梯度是损失函数的偏导数向量，指向函数值增长最快的方向，而我们要找的是损失最小的点，所以需要"沿着梯度的反方向"调整参数。这里的"步长"（学习率）很关键：步长太大容易"跑过"最小值，步长太小则学习速度太慢；
反向传播 ：先通过"正向传播"（输入→隐藏层→输出层）计算预测结果，再根据损失值，从输出层反向推导每个权重对误差的影响，然后用梯度下降调整权重------这个"正向计算+反向修正"的循环，会一直持续到损失值小于允许范围，模型才算"训练完成"。