πRL是一款在线强化学习的VLA框架,适配π0、π0.5等基于流的VLA模型。
核心解决 "对数似然计算难" 和 "探索性不足" 两大问题:
- 提出 Flow-Noise(离散时间 MDP 建模 + 可学习噪声网络)
- 将去噪过程建模为离散时间 MDP,引入可学习噪声网络,实现对数似然精确计算;
- 提出 Flow-SDE(ODE 转 SDE + 双层 MDP)
- 将 ODE 去噪过程转化为 SDE,构建双层 MDP 耦合去噪与环境交互,提升探索效率。
优化算法:基于近端策略优化(PPO)实现政策优化
论文地址:πRL:Online RL Fine-tuning for Flow-based Vision-Language-Action Models
代码地址:https://github.com/RLinf/RLinf
πRL开源的代码中,使用RLinf框架实现模型微调和推理的:
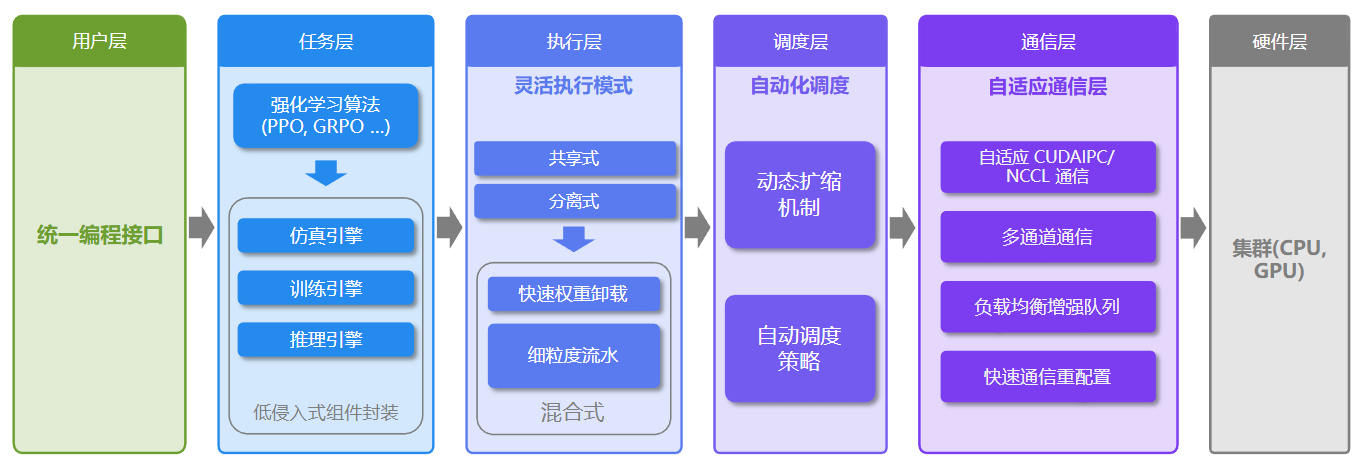
1、模型框架
基于流的VLA模型(如π0、π0.5)通过流匹配迭代优化生成动作,优势:高频动作块、高灵巧任务适配。
πRL的思路流程,从 预训练→SFT→RL 的完整链路:
- Pretraining(预训练):基于大规模多模态数据集预训练 VLM,获得基础的视觉-语言理解能力;
- SFT(监督微调):用特定任务数据集微调,得到初始的流基 VLA 模型(π0/π0.5)------ 但 SFT 受限于专家演示,性能有瓶颈;
- πRL(强化学习微调):通过「在线与环境交互(Policy Rollout)→收集数据到 Buffer→用 PPO/GPPO 更新 Actor」的流程,让模型突破 SFT 瓶颈,提升性能与泛化性。
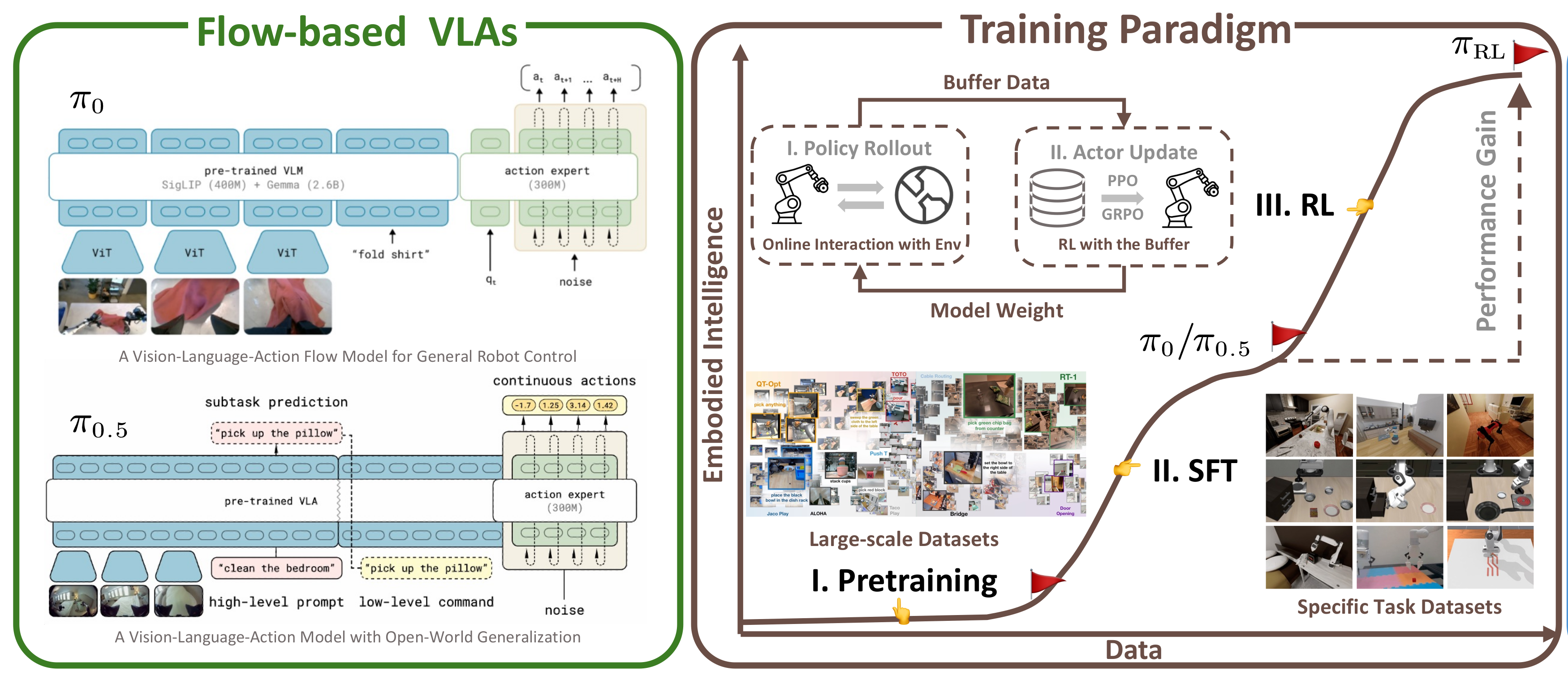
核心亮点:πRL 是「预训练→SFT」范式的延伸,通过环境交互实现从演示学习到自主学习的升级。
2、模型设计分析
核心围绕问题建模 与流式VLA模型原理展开,为后续Flow-Noise、Flow-SDE技术方案提供数学框架和概念铺垫,逻辑上遵循"问题形式化→模型基础定义"的递进关系,具体拆解如下:
一、问题建模:MDP框架定义(强化学习核心基础)
这部分将机器人操作任务抽象为标准马尔可夫决策过程(MDP),明确RL优化的目标与数学表达,是后续策略优化的前提。
1. MDP五要素定义
- 状态(State, s t s_t st) :由机器人观测( o t o_t ot,包括RGB图像、语言指令、机器人本体数据)构成,是模型决策的输入依据。
- 动作(Action, a t a_t at):流式VLA模型输出的机器人执行动作,属于连续动作空间(区别于自回归模型的离散动作)。
- 初始状态分布( P 0 P_0 P0):任务开始时的状态概率分布,决定初始观测的采样范围。
- 状态转移概率( P E N V P_{ENV} PENV) :给定当前状态 s t s_t st和动作 a t a_t at,转移到下一个状态 s t + 1 s_{t+1} st+1的概率,由环境动力学决定。
- 奖励函数( R E N V R_{ENV} RENV):环境对动作的反馈(如任务成功得1分,失败得0分),是RL优化的核心导向。
- 折扣因子( γ \gamma γ):平衡即时奖励与未来奖励的权重(默认0.99),避免短视决策。
2. 核心目标与优化公式
- 优化目标 :学习最优策略 π θ \pi_\theta πθ,最大化期望折扣累积奖励:
J ( π θ ) = E π θ , P 0 [ ∑ t = 0 T γ t R E N V ( s t , a t ) ] \mathcal{J}(\pi_{\theta})=\mathbb{E}{\pi{\theta}, P_{0}}\left[\sum_{t=0}^{T} \gamma^{t} R_{ENV}(s_{t}, a_{t})\right] J(πθ)=Eπθ,P0[t=0∑TγtRENV(st,at)]
其中 T T T为任务 horizon(最大时间步),期望基于策略 π θ \pi_\theta πθ和初始状态分布 P 0 P_0 P0计算。
- 策略梯度近似 :通过采样轨迹估计目标函数的梯度,核心依赖动作对数似然 log π θ ( a t ∣ s t ) \log \pi_\theta(a_t | s_t) logπθ(at∣st):
∇ θ J ( π θ ) = E π θ , P 0 [ ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) A ( s t , a t ) ] \nabla_{\theta} \mathcal{J}(\pi_{\theta})=\mathbb{E}{\pi{\theta}, P_{0}}\left[\sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}(a_{t} | s_{t}) A(s_{t}, a_{t})\right] ∇θJ(πθ)=Eπθ,P0[t=0∑T∇θlogπθ(at∣st)A(st,at)]
关键说明: A ( s t , a t ) = Q ( s t , a t ) − V ( s t ) A(s_t, a_t)=Q(s_t, a_t)-V(s_t) A(st,at)=Q(st,at)−V(st)为优势函数,衡量动作相对状态价值的优劣,是低方差的策略更新信号------而流式VLA的核心痛点正是无法直接计算 log π θ ( a t ∣ s t ) \log \pi_\theta(a_t | s_t) logπθ(at∣st),这也是后续技术方案的突破口。
二、流式VLA模型:动作生成原理与数学表达
基于流的VLA模型如何从多模态观测生成动作,核心是"条件流匹配(CFM)"机制,为后续修改去噪过程(Flow-Noise/Flow-SDE)提供靶点。
1. 模型核心功能
输入:多模态观测 o t o_t ot(RGB图像+语言tokens+本体感受数据);
输出:未来H个连续动作序列 A t = [ a t , 0 , . . . , a t , H − 1 ] A_t=[a_{t,0}, ..., a_{t,H-1}] At=[at,0,...,at,H−1],即"动作块",对应概率分布 p ( A t ∣ o t ) p(A_t | o_t) p(At∣ot)。
2. 核心机制:条件流匹配(CFM)
流模型的本质是"将标准高斯噪声通过学习到的向量场,逐步转化为目标动作",具体分为训练和推理两个阶段:
(1)训练阶段:最小化CFM损失
- 模型学习一个条件向量场 v θ ( A t τ , o t ) v_\theta(A_t^\tau, o_t) vθ(Atτ,ot),目标是对齐"预测向量场"与"真实向量场"。
- 真实向量场定义: u ( A t τ ∣ A t ) = A t − ϵ u(A_t^\tau | A_t)=A_t - \epsilon u(Atτ∣At)=At−ϵ,其中 A t τ A_t^\tau Atτ是"带噪动作"(由目标动作 A t A_t At、高斯噪声 ϵ ∼ N ( 0 , I ) \epsilon \sim N(0,I) ϵ∼N(0,I)、连续时间 τ ∈ [ 0 , 1 ] \tau \in [0,1] τ∈[0,1]生成: A t τ = τ A t + ( 1 − τ ) ϵ A_t^\tau=\tau A_t + (1-\tau)\epsilon Atτ=τAt+(1−τ)ϵ)。
- CFM损失公式(训练核心目标):
L C F M = E τ , p ( A t , o t ) , q ( A t τ ∣ A t ) [ ∥ v θ ( A t τ , o t ) − u ( A t τ ∣ A t ) ∥ 2 2 ] \mathcal{L}{CFM}=\mathbb{E}{\tau, p(A_t, o_t), q(A_t^\tau | A_t)}\left[\left\| v_\theta(A_t^\tau, o_t)-u(A_t^\tau | A_t) \right\|_2^2\right] LCFM=Eτ,p(At,ot),q(Atτ∣At)[∥vθ(Atτ,ot)−u(Atτ∣At)∥22]
意义:让模型学会"从带噪动作中还原目标动作"的映射关系。
(2)推理阶段:迭代去噪生成动作
- 初始采样:从标准高斯分布中采样噪声向量 A t 0 ∼ N ( 0 , I ) A_t^0 \sim N(0,I) At0∼N(0,I)( τ = 0 \tau=0 τ=0时的带噪动作);
- 迭代去噪:基于前向欧拉法,逐步更新动作向量,直到 τ = 1 \tau=1 τ=1(去噪完成):
A t τ + δ = A t τ + v θ ( A t τ , o t ) ⋅ δ A_t^{\tau+\delta}=A_t^\tau + v_\theta(A_t^\tau, o_t) \cdot \delta Atτ+δ=Atτ+vθ(Atτ,ot)⋅δ
其中 δ = 1 / K \delta=1/K δ=1/K( K K K为去噪步数,文中默认4-5步),每一步通过学习到的向量场 v θ v_\theta vθ修正动作,最终得到目标动作序列 A t 1 A_t^1 At1。
3. 关键痛点预埋
- 推理阶段的确定性ODE采样:迭代去噪过程完全由向量场决定,无随机性,导致RL所需的"探索性"缺失;
- 对数似然难以计算 :动作生成是迭代过程,无法直接推导 p ( A t ∣ o t ) p(A_t | o_t) p(At∣ot)的解析解,导致策略梯度公式中的 log π θ ( a t ∣ s t ) \log \pi_\theta(a_t | s_t) logπθ(at∣st)无法直接计算------这两个问题正是后续Flow-Noise、Flow-SDE要解决的核心。
πRL解决这些问题后,在流式VLA模型基础进行强化学习的效果:
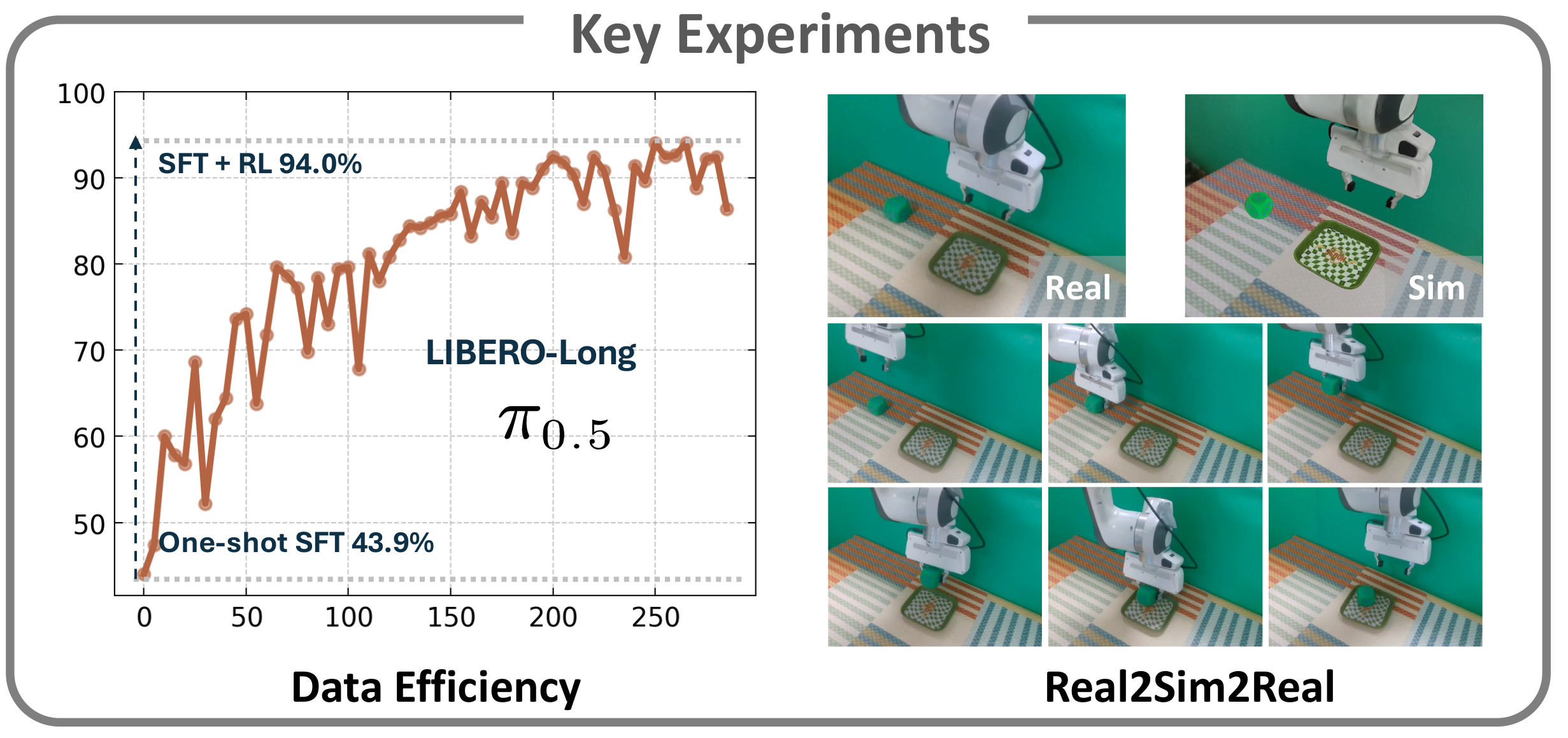
如上图所示,展示了πRL的优势
- Data Efficiency(数据效率):one-shot SFT 的成功率仅 43.9%,而 SFT+RL 能达到 94.0%,说明 πRL 在「少样本场景」下仍能有效提升性能;
- Real2Sim2Real(真实-模拟-真实迁移) :模拟环境训练的模型可零样本迁移至真实环境执行动作,证明 πRL 的优化结果具备跨环境适配性。
3、Flow-Noise 深度解析
Flow-Noise 是 πRL 框架中针对流式 VLA 的核心方案之一,核心目标是同时解决"对数似然难计算"和"探索性不足" 两个痛点,通过"离散化去噪过程+可学习噪声"实现流式模型与 RL 的适配。
以下从"核心逻辑→公式拆解→落地细节"三部分展开,重点用通俗语言解释公式含义:
一、核心逻辑
流式 VLA 的动作生成是"从高斯噪声逐步去噪得到目标动作"的连续过程(ODE驱动),但这个过程有两个问题:
- 连续过程无法直接计算"动作的对数似然"(RL 策略梯度必需);
- 确定性去噪没有随机性,RL 训练缺乏环境探索。
Flow-Noise 的解决方案:
- 把"连续去噪过程"拆成离散的步骤(像把"跑步"拆成"一步一步走"),每步的状态转移用高斯分布建模;
- 给每步注入可学习的噪声(噪声大小由模型自己学,不是固定值),既增加探索性,又能通过高斯分布的特性计算似然。
如下图所示,是Flow-Noise和Flow-SDE的思路流程。
展示了 "多模态观测→多模态理解→动作生成 + 噪声注入→最终动作输出"的链路,同时明确了 Flow-Noise 与 Flow-SDE 的核心差异
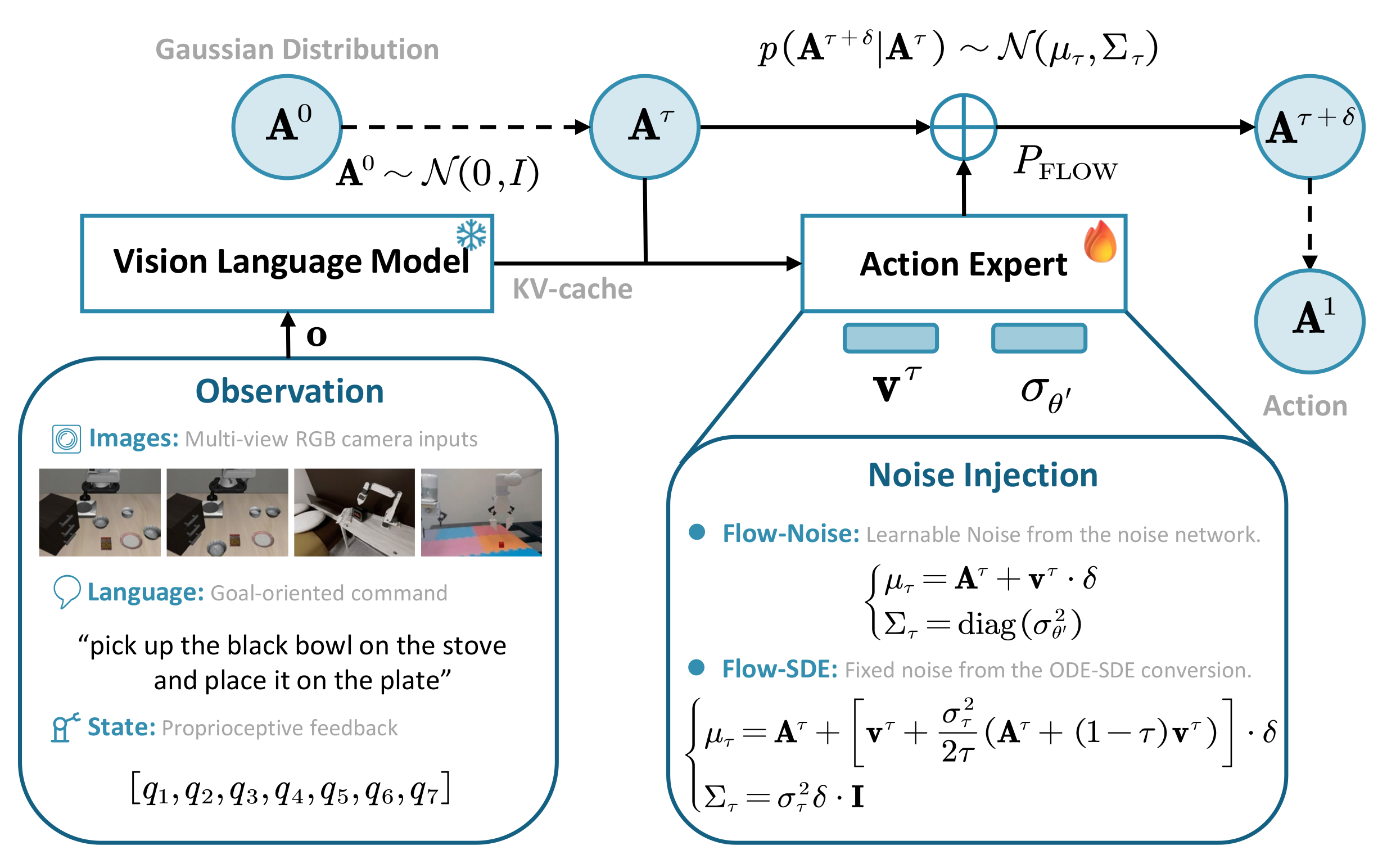
上图展示了核心流程:流式 VLA 的动作生成 + πRL 的噪声注入
- 输入层:收集多模态观测(图像、语言指令、机器人状态),提供任务的完整上下文;
- 理解层:VLM 融合多模态信息,通过 KV-cache 将语义特征传递给动作专家,完成 "任务需求 + 环境状态" 的理解;
- RL 适配层:动作专家结合向量场(引导去噪方向),通过 Flow-Noise(可学习噪声)/Flow-SDE(固定噪声)注入随机性(πRL 的核心,解决探索性不足);
- 生成层:从初始高斯噪声开始,迭代去噪得到最终机器人动作,完成 "噪声→有效动作" 的转化。
二、关键公式通俗拆解
Flow-Noise 核心是两个公式:公式(4)(随机性注入) 和 公式(5)(对数似然估计),下面逐个拆解符号、含义和作用:
1. 公式(4):随机性注入(给去噪过程加"可控噪声")
{ μ τ = A τ + v τ ⋅ δ ∑ τ = d i a g ( σ θ ′ 2 ) \left\{ \begin{array}{l} \mu_{\tau} = A^{\tau} + v^{\tau} \cdot \delta \\ \sum_{\tau} = diag\left(\sigma_{\theta'}^{2}\right) \end{array} \right. {μτ=Aτ+vτ⋅δ∑τ=diag(σθ′2)
这是 Flow-Noise 最核心的公式,定义了"每个去噪步骤的动作更新规则",本质是把"确定性去噪"改成"带噪声的概率性去噪"。
(1)先搞懂符号含义
| 符号 | 通俗含义 |
|---|---|
| τ \tau τ | 去噪时间(范围 [0,1]): τ = 0 \tau=0 τ=0 是纯噪声, τ = 1 \tau=1 τ=1 是最终动作 |
| δ \delta δ | 去噪步长(固定值): δ = 1 / K \delta=1/K δ=1/K,K 是总去噪步数(文中默认 K=4) |
| A τ A^{\tau} Aτ | 当前去噪步骤的动作状态(比如 τ = 0.25 \tau=0.25 τ=0.25 时的"半去噪动作") |
| v τ v^{\tau} vτ | 流模型学到的向量场( v θ ( A τ , o ) v_\theta(A^\tau, o) vθ(Aτ,o) 的简写):负责"引导动作去噪" |
| μ τ \mu_{\tau} μτ | 下一步动作的"均值"(去噪的核心方向) |
| σ θ ′ \sigma_{\theta'} σθ′ | 可学习的噪声标准差(由噪声网络 θ ′ \theta' θ′ 输出):控制噪声大小 |
| ∑ τ \sum_{\tau} ∑τ | 下一步动作的"方差矩阵"(diag 表示是对角矩阵,即各动作维度噪声独立) |
(2)公式的物理意义(通俗理解)
公式其实在说:"下一步的动作 = 按原方向去噪 + 随机噪声",分两部分解释:
-
第一行(均值 μ τ \mu_{\tau} μτ) :保证去噪的"大方向没错"。
A τ + v τ ⋅ δ A^{\tau} + v^{\tau} \cdot \delta Aτ+vτ⋅δ 是原流模型的确定性去噪更新(前向欧拉法),比如当前动作是 A 0.25 A^{0.25} A0.25,向量场 v 0.25 v^{0.25} v0.25 告诉模型"该往哪个方向调整才能更接近目标动作",乘以步长 δ \delta δ 就是"这一步该调整多少"------这部分确保动作不会因为加了噪声而偏离目标。 -
第二行(方差 ∑ τ \sum_{\tau} ∑τ) :注入"可控的探索噪声"。
噪声标准差 σ θ ′ \sigma_{\theta'} σθ′ 不是固定值(比如不是一直加 0.5 的噪声),而是由一个专门的"噪声网络"学习得到,这个网络会根据当前的动作 A τ A^\tau Aτ 和观测 o o o 动态调整:比如任务简单时少加噪声(避免瞎探索),任务复杂时多加噪声(多尝试不同动作)。
对角矩阵 diag ( σ θ ′ 2 ) \text{diag}(\sigma_{\theta'}^2) diag(σθ′2) 表示"每个动作维度的噪声独立"(比如机器人的"平移"和"旋转"动作的噪声互不影响),符合实际机器人控制场景。
(3)为什么要这么设计?
- 解决"探索性不足":噪声让动作生成有随机性,RL agent 能尝试不同动作,找到更好的策略;
- 保证"动作有效性":均值部分沿用原流模型的去噪方向,避免噪声导致动作完全失控;
- 适配 RL 计算 :动作的转移服从高斯分布 p ( A τ + δ ∣ A τ ) ∼ N ( μ τ , ∑ τ ) p(A^{\tau+\delta} | A^\tau) \sim N(\mu_\tau, \sum_\tau) p(Aτ+δ∣Aτ)∼N(μτ,∑τ),而高斯分布的似然可以直接计算(这是后续对数似然估计的基础)。
2. 公式(5):对数似然估计(解决"似然难计算"痛点)
log π ( A ∣ o ) = log ( π ( A 0 ∣ o ) ∏ k = 0 K − 1 π ( A τ k + 1 ∣ A τ k , o ) ) \log \pi(\mathcal{A} | o) = \log \left( \pi(A^{0} | o) \prod_{k=0}^{K-1} \pi(A^{\tau_{k+1}} | A^{\tau_k}, o) \right) logπ(A∣o)=log(π(A0∣o)k=0∏K−1π(Aτk+1∣Aτk,o))
这是 Flow-Noise 最巧妙的设计:把"连续去噪过程的整体似然",拆成"离散步骤的似然乘积",让原本不可计算的量变得可算。
(1)符号含义补充
| 符号 | 通俗含义 |
|---|---|
| A \mathcal{A} A | 整个去噪序列: ( A 0 , A δ , A 2 δ , . . . , A 1 ) (A^0, A^\delta, A^{2\delta}, ..., A^1) (A0,Aδ,A2δ,...,A1)(从纯噪声到最终动作) |
| π ( A 0 ∣ o ) \pi(A^0 \mid o) π(A0∣o) | 初始噪声的概率: A 0 ∼ N ( 0 , I ) A^0 \sim N(0,I) A0∼N(0,I),似然就是标准高斯分布的概率密度 |
| π ( A τ k + 1 ∣ A τ k , o ) \pi(A^{\tau_{k+1}} \mid A^{\tau_k}, o) π(Aτk+1∣Aτk,o) | 第 k 步到第 k+1 步的转移似然:即公式(4)中高斯分布的概率密度 |
| ∏ \prod ∏ | 乘积符号:表示"所有步骤的转移似然相乘" |
(2)公式的物理意义(通俗理解)
我们可以用"从家到公司的概率"来类比:
- 连续过程(原流模型):相当于"从家到公司走了一条连续的路",要计算"走完整条路的概率",没法直接算(因为路径是无限多的);
- 离散过程(Flow-Noise):相当于"把路拆成 K 步(比如家→路口1→路口2→...→公司)","走完整条路的概率"="家到路口1的概率"×"路口1到路口2的概率"×...×"路口K-1到公司的概率"------每个步骤的概率都是高斯分布的似然(可直接计算),乘积就是整体似然。
再进一步,对公式两边取对数( log \log log),乘积会变成求和(对数的性质: log ( a b ) = log a + log b \log(ab)=\log a + \log b log(ab)=loga+logb),最终整体对数似然为:
log π ( A ∣ o ) = log π ( A 0 ∣ o ) + ∑ k = 0 K − 1 log π ( A τ k + 1 ∣ A τ k , o ) \log \pi(\mathcal{A} | o) = \log \pi(A^0 | o) + \sum_{k=0}^{K-1} \log \pi(A^{\tau_{k+1}} | A^{\tau_k}, o) logπ(A∣o)=logπ(A0∣o)+k=0∑K−1logπ(Aτk+1∣Aτk,o)
这就完美适配了 RL 的策略梯度公式(策略梯度需要计算 log π ( a t ∣ s t ) \log \pi(a_t | s_t) logπ(at∣st))------现在这个对数似然可以通过"求和"直接计算,没有任何近似误差。
(3)关键细节:为什么离散化后似然就可算了?
因为每个步骤的转移都是高斯分布,而高斯分布的概率密度函数(似然)有解析解:
π ( x ∣ μ , ∑ ) = 1 ( 2 π ) d ∣ ∑ ∣ exp ( − 1 2 ( x − μ ) T ∑ − 1 ( x − μ ) ) \pi(x | \mu, \sum) = \frac{1}{\sqrt{(2\pi)^d |\sum|}} \exp\left( -\frac{1}{2}(x - \mu)^T \sum^{-1} (x - \mu) \right) π(x∣μ,∑)=(2π)d∣∑∣ 1exp(−21(x−μ)T∑−1(x−μ))
其中 d 是动作维度, ∣ ∑ ∣ |\sum| ∣∑∣ 是方差矩阵的行列式。虽然这个公式看起来复杂,但计算机可以直接计算------这也是 Flow-Noise 选择高斯分布建模转移的核心原因。
三、Flow-Noise 的作用
-
噪声网络的训练与丢弃 :
噪声网络(输出 σ θ ′ \sigma_{\theta'} σθ′)和流模型的向量场 v θ v_\theta vθ 一起训练,训练时通过噪声增强探索,帮助 RL 找到更好的策略;但推理时(机器人实际执行任务时),噪声网络会被丢弃,动作生成回到"确定性去噪"(只保留 μ τ \mu_{\tau} μτ 部分),避免噪声影响任务执行精度。
-
去噪步数 K 的选择 :
K 是离散化的步数(文中默认 K=4),K 越大,离散化越接近连续过程,似然计算越精确,但计算成本越高;K 越小,计算越快,但可能引入离散误差------文中通过实验验证 K=4 是"精度-速度"的平衡点。
-
与 RL 策略优化的衔接 :
公式(5)计算出的 log π ( A ∣ o ) \log \pi(\mathcal{A} | o) logπ(A∣o),就是 RL 策略梯度公式中需要的 log π θ ( a t ∣ s t ) \log \pi_\theta(a_t | s_t) logπθ(at∣st)(这里的 a t a_t at 是最终动作 A 1 A^1 A1, s t s_t st 是观测 o t o_t ot)。将其代入 PPO 的策略梯度公式,就能实现对"流式 VLA 策略"的优化。
四、核心总结(Flow-Noise 公式的逻辑闭环)
- 公式(4):通过"均值(原方向去噪)+ 方差(可学习噪声)",解决"探索性不足",同时让每个步骤的转移似然可计算;
- 公式(5):通过"离散化拆解+对数求和",解决"整体似然难计算",完美适配 RL 的策略梯度要求;
- 两个公式协同:既保证了动作生成的有效性(不偏离目标),又提供了 RL 所需的探索性和似然计算能力,最终让流式 VLA 能被 RL 微调。
4、Flow-SDE 深度解析
Flow-SDE 是 πRL 框架的另一核心方案,与 Flow-Noise 目标一致(解决"对数似然难计算"和"探索性不足"),但采用"ODE转SDE+双层MDP"的思路,更侧重"探索效率"和"计算成本平衡"。
以下从"核心逻辑→公式拆解→落地细节"展开,用生活化例子讲透公式含义,避免复杂推导。
一、核心逻辑
流基 VLA 原有的动作生成是"确定性ODE过程"(像"按固定路线开车",没有偏离),Flow-SDE 的核心想法是:
- 把"确定性ODE"改成
"随机性SDE"(像"开车时允许轻微偏离路线探索"),既加噪声又不破坏动作的有效性; 把"去噪过程"和"机器人与环境交互"拆成"内外两层任务"(双层MDP),让去噪和探索互不干扰;- 用"混合采样"减少计算量(只在部分步骤加噪声,其余步骤仍用确定性更新)。
简单说:Flow-SDE 是"给动作生成加'可控随机偏差',同时用分层逻辑简化计算"。
如下图所示,针对Flow-Noise/Flow-SDE设计不同 MDP 结构,实现流式 VLA 与 RL 的适配。
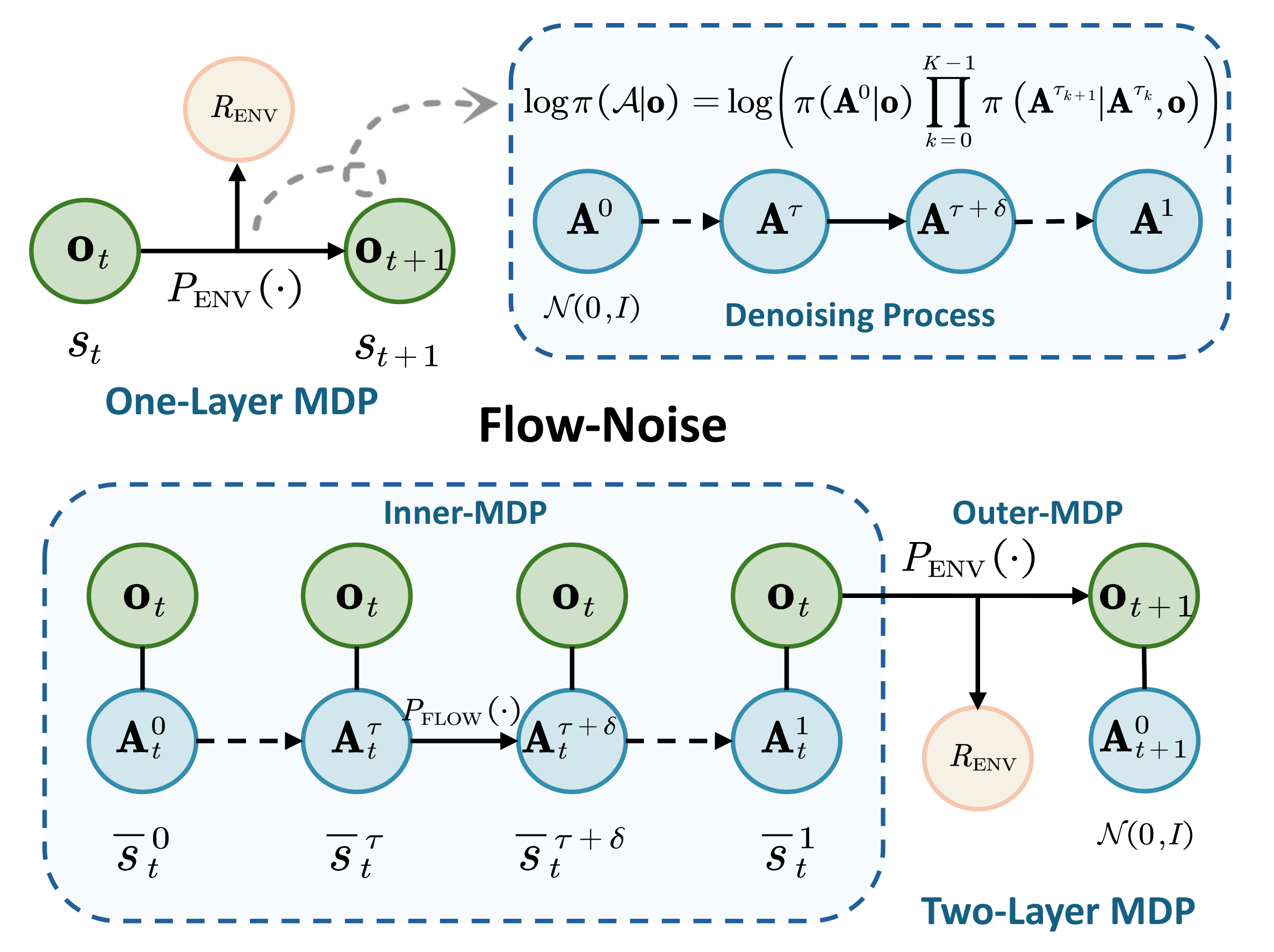
流基VLA与RL的适配实现:
- Flow-Noise(单层 MDP) :将「去噪过程 + 环境交互」合并为单层 MDP------以观测 (o_t) 作为状态,环境转移至 (o_{t+1});同时把去噪的对数似然拆分为初始噪声似然 × 各步骤转移似然,通过单层 MDP 简化计算,直接关联动作生成与环境奖励。
- Flow-SDE(双层 MDP):将「去噪」和「环境交互」拆分为内外层 MDP------内层 MDP 负责去噪(观测不变,迭代更新动作),内层完成后进入外层 MDP(环境转移、获取奖励、重置动作),通过分层机制兼顾去噪的完整性与 RL 的环境反馈逻辑。
两者均通过 MDP 建模,解决流基 VLA 的 RL 适配核心问题(似然计算、探索性)。
二、关键公式通俗拆解
Flow-SDE 的核心公式按"ODE→SDE转化→离散化→双层MDP"的顺序排列,重点拆解 4 个核心公式:公式(6)(原ODE)、公式(7)(SDE转化)、公式(8)(最终SDE)、公式(9)(离散化转移),以及双层MDP的定义式。
1. 公式(6):原流模型的ODE(确定性去噪,对比基准)
d A τ = v τ d τ d A^{\tau} = v^{\tau} d \tau dAτ=vτdτ
这是流基 VLA 原本的动作生成公式,先看懂它才能理解"为什么要转SDE"。
(1)符号含义
| 符号 | 通俗含义 |
|---|---|
| d A τ d A^{\tau} dAτ | 去噪过程中"动作的微小变化量"(比如 τ = 0.3 \tau=0.3 τ=0.3 到 τ = 0.31 \tau=0.31 τ=0.31 的动作差异) |
| v τ v^{\tau} vτ | 流模型学到的向量场(和 Flow-Noise 一致):指引"动作该往哪个方向调整" |
| d τ d \tau dτ | 去噪时间的微小增量(比如从 0.3 到 0.31, d τ = 0.01 d\tau=0.01 dτ=0.01) |
(2)公式的物理意义
这个公式本质是:"动作的微小变化 = 去噪方向 × 时间增量" 。
比如:向量场 v τ v^{\tau} vτ 告诉模型"当前动作要向左调整10个单位"(去噪方向),时间增量 d τ = 0.01 d\tau=0.01 dτ=0.01(走一小步),那么动作就会向左调整 10 × 0.01 = 0.1 10×0.01=0.1 10×0.01=0.1 个单位------整个过程没有任何随机性,动作完全按固定路线生成,这就是"探索性不足"的根源。
2. 公式(7):ODE转SDE(注入随机性,核心改造)
d A τ = ( v τ − 1 2 g 2 ( τ ) ∇ log q τ ( A τ ) ) d τ ⏟ Drift Term + g ( τ ) d w ⏟ Diffusion Term d A^{\tau} = \underbrace{\left(v^{\tau}-\frac{1}{2} g^{2}(\tau) \nabla \log q_{\tau}\left(A^{\tau}\right)\right) d \tau}{\text{Drift Term}} + \underbrace{g(\tau) d w}{\text{Diffusion Term}} dAτ=Drift Term (vτ−21g2(τ)∇logqτ(Aτ))dτ+Diffusion Term g(τ)dw
这是 Flow-SDE 最关键的改造:把"确定性ODE"变成"随机性SDE",核心是加了"漂移项"和"扩散项"。
(1)符号含义(新增符号重点讲)
| 符号 | 通俗含义 |
|---|---|
| Drift Term(漂移项) | "修正方向的项":保证动作不会因为加噪声而偏离目标(相当于"方向盘") |
| Diffusion Term(扩散项) | "加噪声的项":注入随机性,提升探索性(相当于"轻微晃动方向盘") |
| g ( τ ) g(\tau) g(τ) | 噪声调度函数:控制不同去噪阶段的噪声大小( τ \tau τ 越小噪声越大,符合"从噪声到动作"的逻辑) |
| ∇ log q τ ( A τ ) \nabla \log q_{\tau}(A^{\tau}) ∇logqτ(Aτ) | 分数函数(score function):衡量"当前带噪动作离目标动作有多远"(由流模型特性推导得出) |
| d w d w dw | 维纳过程(Wiener process):简单理解为"随机噪声"(每次采样的噪声值不同,服从高斯分布) |
(2)公式的物理意义(通俗类比)
把动作生成比作"从起点(纯噪声)走到终点(目标动作)":
- 原ODE(公式6):只能走一条固定路线,不能偏离;
- 新SDE(公式7):可以走"主路线附近的小范围区域",既不会迷路(漂移项控制),又能探索不同路径(扩散项控制)。
分两部分详细说:
-
漂移项(Drift Term):"方向盘+修正器"
核心作用是"抵消噪声带来的偏差"。原来的 v τ d τ v^{\tau} d\tau vτdτ 是"主路线方向",后面加的 − 1 2 g 2 ( τ ) ∇ log q τ ( A τ ) d τ -\frac{1}{2} g^2(\tau) \nabla \log q_{\tau}(A^\tau) d\tau −21g2(τ)∇logqτ(Aτ)dτ 是"修正项"------分数函数 ∇ log q τ ( A τ ) \nabla \log q_{\tau}(A^\tau) ∇logqτ(Aτ) 会告诉模型"当前动作偏得太远了",修正项会把动作拉回主路线,保证最终生成的动作仍然有效(不会因为加噪声而变成"无效动作")。
-
扩散项(Diffusion Term):"随机探索器"
g ( τ ) d w g(\tau) d w g(τ)dw 是直接注入的噪声: g ( τ ) g(\tau) g(τ) 控制"噪声强度"(比如去噪初期 τ = 0 \tau=0 τ=0时噪声大,后期 τ = 1 \tau=1 τ=1时噪声小,避免快到目标时还乱晃), d w d w dw 是"随机噪声值"(每次探索的偏差不同)。这部分完美解决了"探索性不足"的问题。
(3)为什么要这么设计?
- 只加噪声会导致动作失控(比如机器人本来要抓杯子,加噪声后可能去抓桌子);
- 只加修正项会回到确定性ODE(没有探索性);
- 漂移项+扩散项的组合:既保证"大方向没错",又允许"小范围探索",完美适配RL的需求。
3. 公式(8):最终SDE(代入分数函数,落地计算)
d A τ = [ v τ + σ τ 2 2 τ ( A τ + ( 1 − τ ) v τ ) ] d τ + σ τ d w τ d A^{\tau} = \left[ v^{\tau} + \frac{\sigma_{\tau}^{2}}{2\tau} \left( A^{\tau} + (1-\tau) v^{\tau} \right) \right] d\tau + \sigma_{\tau} d w_{\tau} dAτ=[vτ+2τστ2(Aτ+(1−τ)vτ)]dτ+στdwτ
公式(7)里的"分数函数"是抽象概念,公式(8)是把它替换成"可计算的流模型参数"( v τ v^\tau vτ、 A τ A^\tau Aτ 等),让模型能实际训练。
(1)符号含义补充
| 符号 | 通俗含义 |
|---|---|
| σ τ \sigma_{\tau} στ | 噪声强度(替代公式7的 g ( τ ) g(\tau) g(τ)):文中定义为 σ τ = a τ 1 − τ \sigma_{\tau}=a \sqrt{\frac{\tau}{1-\tau}} στ=a1−ττ ( a a a 是超参数,默认0.5) |
| 其他符号 | 和之前一致( v τ v^\tau vτ 是向量场, A τ A^\tau Aτ 是当前动作, τ \tau τ 是去噪时间) |
(2)公式的物理意义
不用纠结推导过程,核心记住:这是"可落地的SDE公式" ------把抽象的"分数函数"换成了流模型已经学到的 v τ v^\tau vτ 和当前动作 A τ A^\tau Aτ,计算机可以直接计算。
关键变化:漂移项更复杂,但本质还是"修正方向+抵消噪声偏差",扩散项明确了"噪声强度怎么随去噪阶段变化"( τ \tau τ 从0到1时, τ 1 − τ \sqrt{\frac{\tau}{1-\tau}} 1−ττ 从0升至无穷大,实际训练通过超参数 a a a 限制后期噪声)。
4. 公式(9):SDE离散化(适配RL迭代训练)
{ μ τ = A τ + [ v τ + σ τ 2 2 τ ( A τ + ( 1 − τ ) v τ ) ] ⋅ δ Σ τ = σ τ 2 δ ⋅ I \begin{cases} \mu_{\tau} = A^{\tau} + \left[ v^{\tau} + \frac{\sigma_{\tau}^{2}}{2\tau} \left( A^{\tau} + (1-\tau) v^{\tau} \right) \right] \cdot \delta \\ \Sigma_{\tau} = \sigma_{\tau}^{2} \delta \cdot \mathbf{I} \end{cases} {μτ=Aτ+[vτ+2τστ2(Aτ+(1−τ)vτ)]⋅δΣτ=στ2δ⋅I
SDE是"连续过程",RL训练是"一步一步迭代"(离散的),所以需要把SDE拆成"离散步骤",公式(9)就是干这个的。
(1)符号含义补充
| 符号 | 通俗含义 |
|---|---|
| δ \delta δ | 离散步长(和 Flow-Noise 一致: δ = 1 / K \delta=1/K δ=1/K,K是去噪步数,默认4-5) |
| μ τ \mu_{\tau} μτ | 下一步动作的"均值"(相当于"离散后的漂移项",大方向) |
| Σ τ \Sigma_{\tau} Στ | 下一步动作的"方差"(相当于"离散后的扩散项",噪声大小) |
| I \mathbf{I} I | 单位矩阵:表示各动作维度的噪声独立(比如"平移"和"旋转"的噪声互不影响) |
(2)公式的物理意义
这个公式和 Flow-Noise 的公式(4)很像,本质是:"离散步骤的动作更新 = 按SDE方向走一步 + 固定方差的噪声"。
- 第一行(均值 μ τ \mu_\tau μτ):把连续的SDE离散为单步更新量,保证动作大方向不跑偏;
- 第二行(方差 Σ τ \Sigma_\tau Στ):离散噪声大小由噪声强度 σ τ \sigma_\tau στ 和步长 δ \delta δ 共同决定,步长越大噪声越大。
关键优势:离散后动作转移服从高斯分布 p ( A τ + δ ∣ A τ ) ∼ N ( μ τ , Σ τ ) p(A^{\tau+\delta} | A^\tau) \sim \mathcal{N}(\mu_\tau, \Sigma_\tau) p(Aτ+δ∣Aτ)∼N(μτ,Στ),对数似然可直接计算,适配RL策略梯度。
5. 双层MDP相关定义(非纯公式,数学表达标准化)
Flow-SDE 把"去噪"和"环境交互"拆成两层MDP,以下是核心定义的通俗解释(对应文中公式10-12):
(1)状态
s ‾ t τ = ( o t , A t τ ) \overline{s}{t}^{\tau} = (o{t}, A_{t}^{\tau}) stτ=(ot,Atτ)
- 通俗含义:当前状态 = 机器人观测(图像+语言指令)+ 当前去噪阶段动作;
- 示例:观测到"桌上有杯子"( o t o_t ot)+ 半去噪动作( A t 0.5 A_t^{0.5} At0.5)构成双层MDP完整状态。
(2)动作
a ‾ t τ = { A t τ + δ , τ < 1 A t 1 , τ = 1 \overline{a}{t}^{\tau} = \begin{cases} A{t}^{\tau+\delta}, & \tau<1 \\ A_{t}^{1}, & \tau=1 \end{cases} atτ={Atτ+δ,At1,τ<1τ=1
- 通俗含义:去噪未完成时为下一步去噪动作,完成时为最终执行动作。
(3)状态转移
s ‾ t ′ τ ′ = { ( o t , a ‾ t τ ) , τ < 1 ( o t + 1 , A t + 1 0 ) , τ = 1 \overline{s}{t'}^{\tau'} = \begin{cases} \left(o{t}, \overline{a}{t}^{\tau}\right), & \tau<1 \\ \left(o{t+1}, A_{t+1}^{0}\right), & \tau=1 \end{cases} st′τ′={(ot,atτ),(ot+1,At+10),τ<1τ=1
- 通俗含义:去噪中仅更新动作、观测不变;去噪完成后环境观测更新,动作重置为初始噪声。
(4)奖励函数
R ‾ ( s ‾ t τ , a ‾ t τ ) = { 0 , τ < 1 R ENV ( o t , A t 1 ) , τ = 1 \overline{R}\left(\overline{s}{t}^{\tau}, \overline{a}{t}^{\tau}\right) = \begin{cases} 0, & \tau<1 \\ R_{\text{ENV}}\left(o_{t}, A_{t}^{1}\right), & \tau=1 \end{cases} R(stτ,atτ)={0,RENV(ot,At1),τ<1τ=1
- 通俗含义:仅去噪完成、执行最终动作时给予环境奖励,去噪过程奖励为0。
三、Flow-SDE 的作用
-
混合ODE-SDE采样(降成本) :
双层MDP会增加训练步骤,采用混合采样 :每个环境步随机选去噪时间 τ t \tau_t τt,仅该步用SDE加噪声,其余步用ODE确定性更新,兼顾探索性与训练效率(效率提升约2倍)。
-
噪声强度超参数 a a a 的选择 :
噪声强度 σ τ = a τ 1 − τ \sigma_\tau = a \sqrt{\frac{\tau}{1-\tau}} στ=a1−ττ 中, a a a 为全局噪声缩放系数(默认0.5):
- a a a 过小:噪声不足,探索能力弱;
- a a a 过大:噪声过载,动作失控、训练震荡。
-
与PPO的衔接 :
公式(9)的高斯分布似然即为PPO策略梯度所需的 log π ( a ‾ t τ ∣ s ‾ t τ ) \log \pi(\overline{a}_t^\tau | \overline{s}_t^\tau) logπ(atτ∣stτ),直接代入PPO目标函数即可完成策略优化。
四、核心总结(Flow-SDE 公式的逻辑闭环)
- 公式(6):原ODE为基准,暴露确定性生成的探索缺陷;
- 公式(7):SDE改造为核心,通过漂移+扩散项实现可控随机探索;
- 公式(8):落地化SDE,将抽象分数函数替换为可计算模型参数;
- 公式(9):离散化适配RL,高斯似然可直接用于策略梯度;
- 双层MDP:分层解耦去噪与环境交互,降低计算冗余。
整套方案同时解决对数似然难计算 、探索性不足问题,并通过混合采样平衡计算成本。
5、模型效果
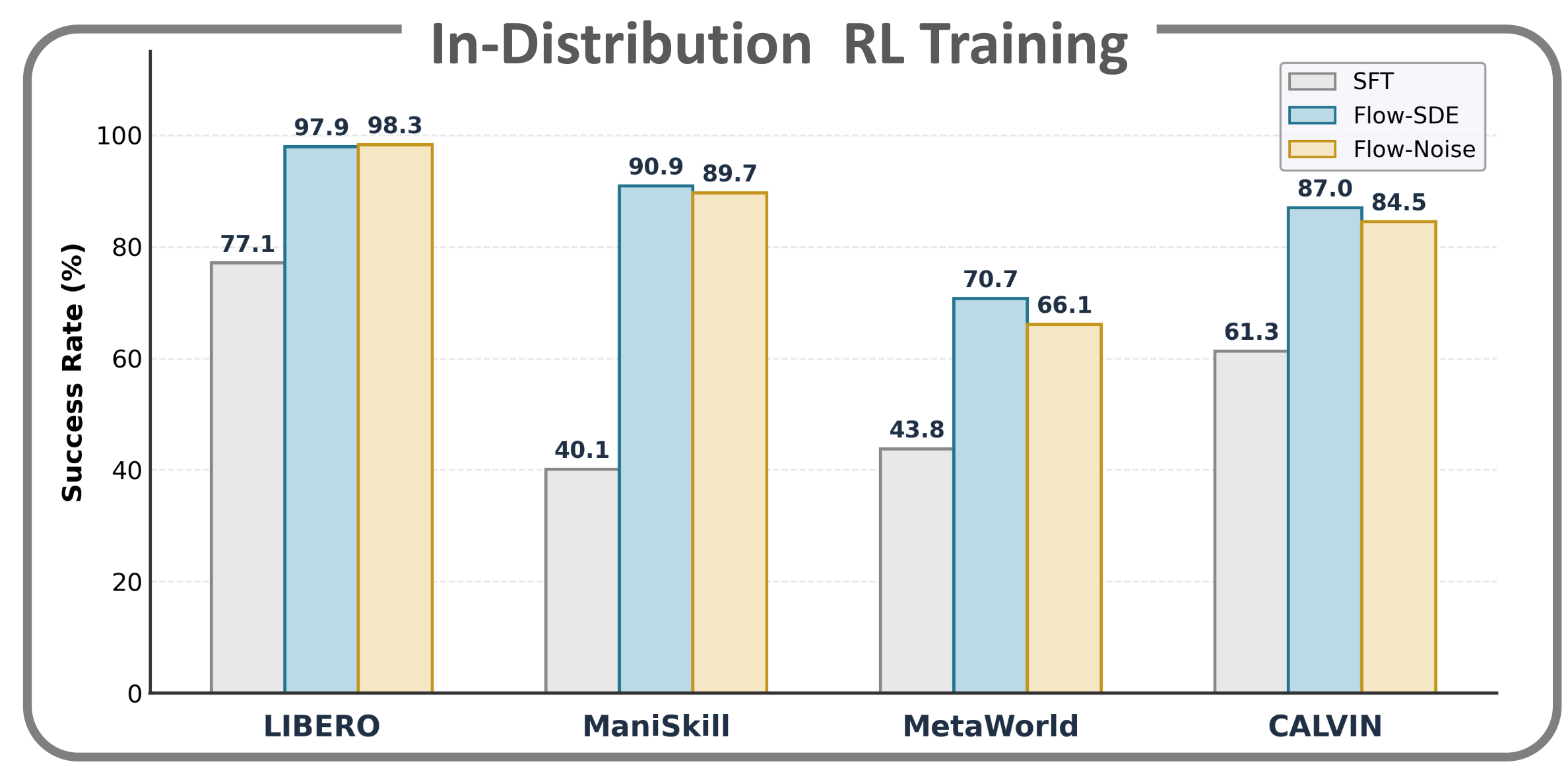
πRL性能提升,柱状图对比了 SFT、Flow-SDE、Flow-Noise 在 4 大基准的任务成功率:
- LIBERO:SFT(77.1)→ Flow-SDE(97.9)/Flow-Noise(98.3),提升超 20%
- ManiSkill:SFT(40.1)→ Flow-SDE(90.9)/Flow-Noise(89.7),提升超 40%
- MetaWorld、CALVIN:均取得显著性能提升
- 整体平均提升幅度 :27.6% - 31.0%
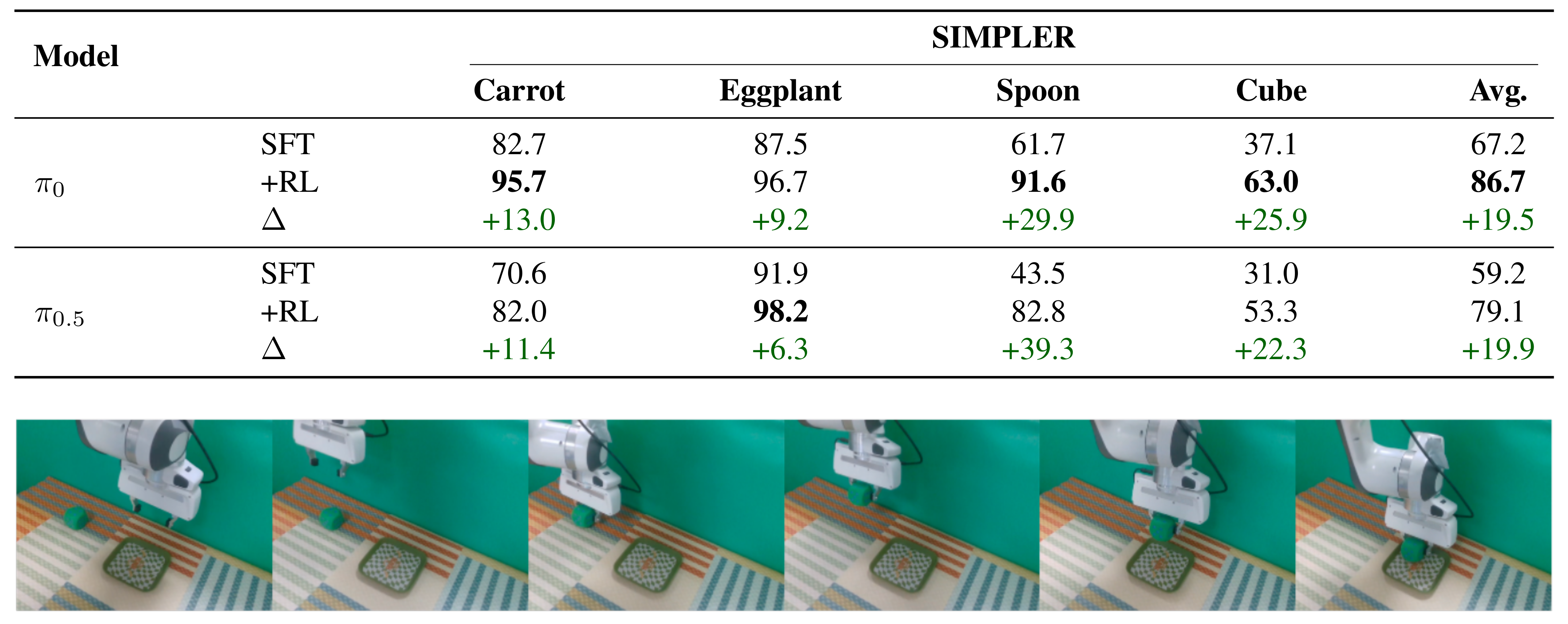
采用 Flow-Noise 方法的 π₀与 π₀.₅在 SIMPLER 基准测试上的评估结果,如下图所示:
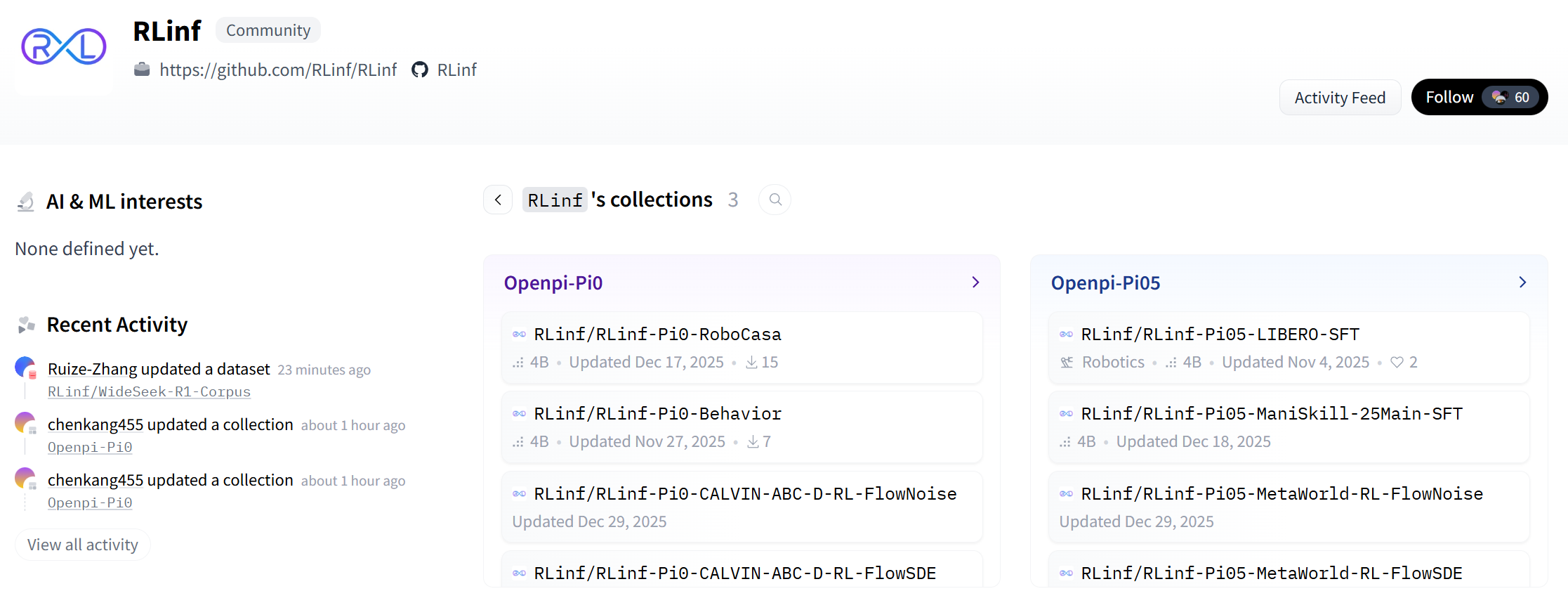
支持多款流匹配的VLM模型,比如常规π0和π0.5等
后面文章再介绍复现情况
分享完成~