从概念到实现：深入解析七大经典排序算法

念越2026-02-05 9:19

文章目录

1、 排序的概念

排序：是将一组关键字按照大小，递增或递减的排列起来。

稳定性：在原本的关键字序列中，r[i] = r[j] ,且r[i]在r[j]前面，拍完序后，r[i]依然在r[j]前面，相对次序保持不变，这种排序算法就是稳定的，反之，则是不稳定的。

2、常见的排序算法

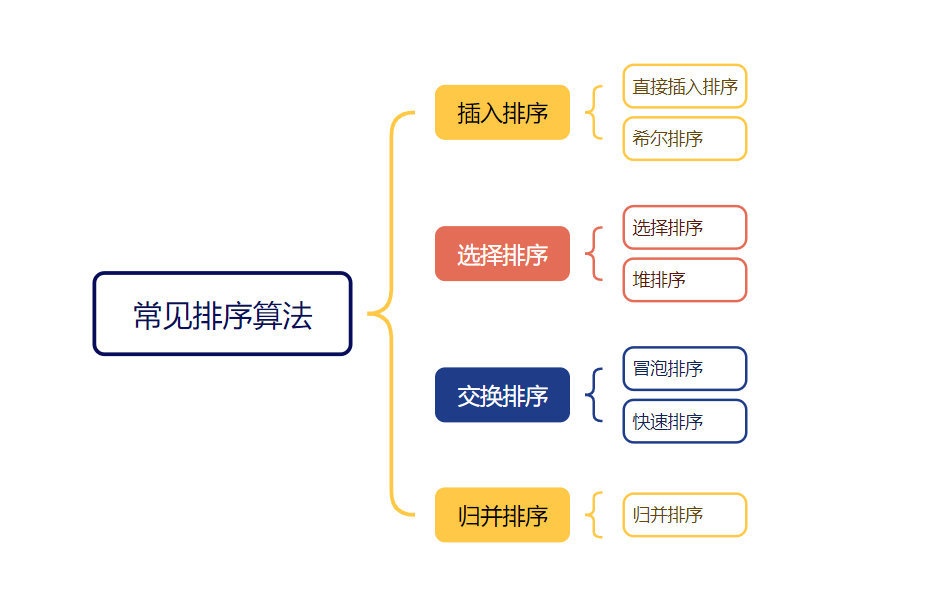
3、常见排序算法的实现

3.1插入排序

3.1.1直接插入排序

基本思想：把待排序的关键码值按大小逐个插入到已排好序的有序序列中，直到所有的记录插完为止，得到一个新的有序序列。

3.1.1.1 直接插入排序代码实现

Sort类

在此算法中， 让i指向数组的1下标的元素，让j指向数组i下标的前一个元素，定义一个临时变量存储i下标指向的值，如果array[j]的值大于tmp，就让array[j]的值赋值给array[j+1]，往后移一位，再让j--，

java 复制代码 
public class Sort {
    public static void insertSort(int[] array){
        for (int i = 1; i < array.length ; i++) {
            int tmp = array[i];
            int j = i-1;
            for( ; j>=0; j--){
                if(array[j]>tmp){
                    array[j+1] =array[j];
                }else {
                    array[j+1] = tmp;
                    break;
                }
            }
            array[j+1] = tmp;
        }
    }
}

Test测试类

java 复制代码 
public class Test {
    public static void main(String[] args) {
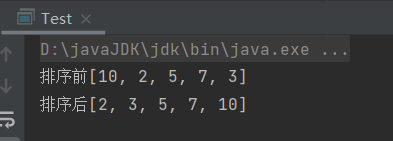
      int[] array = new int[]{10,2,5,7,3};
        System.out.println("排序前"+Arrays.toString(array));
      Sort.insertSort(array);
        System.out.println("排序后"+Arrays.toString(array));
    }
}

排序结果

3.1.1.2直接插入排序特性总结

1.元素越有序，直接插入排序的算法的时间效率越高。

2.时间复杂度为O(n^2)，元素逆序的时候。

3.空间复杂为O(1)

4.稳定性：稳定

3.1.2希尔排序

基本思想：采用分组排序的思想，组内进行插入排序，让组内元素有序。选定一个整数作为增量，用这个整数对元素进行分组，组内进行排序，让组内有序，再缩小增量，重复上述过程，当增量为1时，所有关键字在同一组内排好序。

3.1.2.1希尔排序的算法实现

Sort类

java 复制代码 
public static void shellSort(int[] array){
        int gap = array.length;
        while (gap >1){
             gap/= 2;
             shell(array,gap);
        }
    }
    private static void shell(int[] array , int gap){
        for (int i = gap; i < array.length; i++) {
            int tmp = array[i];
            int j = i - gap;
            for(; j >= 0 ; j -= gap){
                if(array[j] > tmp){
                   array[j+gap] = array[j];
                }else {
                    array[j+gap] = tmp;
                    break;
                }
            }
              array[j+gap] = tmp;
        }
    }

Test测试类

java 复制代码 
public class Test {
    public static void main(String[] args) {
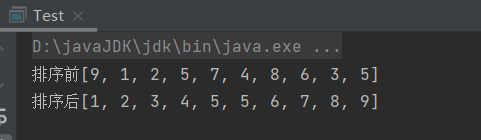
      int[] array = new int[]{9,1,2,5,7,4,8,6,3,5};
        System.out.println("排序前"+Arrays.toString(array));
        Sort.shellSort(array);
        System.out.println("排序后"+Arrays.toString(array));
      
    }
}

测试结果

3.1.2.2希尔排序特性总结

1.希尔排序是对直接插入排序的优化。

2.当gap>1时，都是预排序，目的是让数组更接近于有序，当gap=1时，数组已经非常接近有序了，在整体进行排序，就会很快。

3.稳定性：不稳定

3.2选择排序

3.2.1直接选择排序

基本思想：每次在待排序的元素中选择最大或者最小的一个元素，放在序列起始位置。

3.2.1.1直接选择排序代码实现

每次把当前排序的第一个元素看做是最小值的下标i，定义一个下标j从i+1开始，找有没有比i下标更小的元素，如果有，则更新最小值下标，然后与i下标对应的元素进行交换元素。

Sort类

java 复制代码 
 public static void selectSort(int[] array){
        for (int i = 0; i < array.length; i++) {
            int midIndex = i;
            int j = i+1;
            for(; j<array.length;j++){
                if(array[j]<array[midIndex]){
                    midIndex = j; //更新最小值下标
                }
            }
            swap(array,i,midIndex);
        }
    }
    private static void swap(int[] array ,int i ,int j){
        int tmp = array[j];
        array[j] = array[i];
        array[i] = tmp;
    }
}

Test测试类

java 复制代码 
public class Test {
    public static void main(String[] args) {
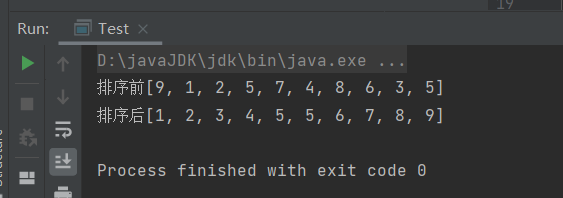
      int[] array = new int[]{9,1,2,5,7,4,8,6,3,5};
        System.out.println("排序前"+Arrays.toString(array));
        Sort.selectSort(array);
        System.out.println("排序后"+Arrays.toString(array));

    }
}

测试结果

3.2.1.2直接选择排序代码优化

一次遍历，可以找到数组中的最大值和最小值。

java 复制代码 
 private static void swap(int[] array ,int i ,int j){
        int tmp = array[j];
        array[j] = array[i];
        array[i] = tmp;
    }
    public static void selectSort(int[] array){
        int left = 0;  //数组第一个元素
        int right = array.length-1;  //数组最后一个元素
       while (left < right){
               int minIndex =left;
               int maxIndex = left;
               for(int j = left+1; j<= right;j++){
                   if(array[minIndex]>array[j]){
                       minIndex = j;
                   }
                   if(array[maxIndex]<array[j]){
                       maxIndex = j;
                   }

           }
           swap(array,left,minIndex);
           if(maxIndex == left){         //如果第一个元素是最大值，需要进行把下标换回来
               maxIndex = minIndex;
           }
           swap(array,right,maxIndex);
           left++;
           right--;
       }
    }
3.2.1.3直接选择排序特性总结

1.时间复杂度：O(n^2)

2.空间复杂度为：O(1)

3.稳定性：不稳定

3.2.2堆排序

基本思想：先把待排序序列构建成大根堆，再大根堆上进行排序。升序排序需要建立大根堆，降序排序需要建立小根堆。

3.2.2.1堆排序代码实现
java 复制代码 
 public static void heapSort(int[] array){
      //创建大根堆
        createHeap(array);
        //进行排序
        int end = array.length-1;
        while (end>0){
            swap(array,0,end);
            siftDown(array,0,end); //调整为大根堆
            end--;
        }
    }
    private static void createHeap(int[] array){
        for(int parent = (array.length-1-1)/2; parent >= 0;parent--){
            siftDown(array,parent,array.length);
        }
    }

    private static void siftDown(int[] array, int parent, int length) {
        int child = 2*parent+1;
        while (child<length){
            if(child+1<length && array[child]<array[child+1]){ //有有孩子且当右孩子比左孩子大
                    child++;
            }
            if(array[parent]<array[child]){
                swap(array,parent,child);
                parent = child;  
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }
    private static void swap(int[] array ,int i ,int j){
        int tmp = array[j];
        array[j] = array[i];
        array[i] = tmp;
    }
3.2.2.2堆排序特性总结

1.时间复杂度：O(n*log^n)

2.空间复杂度为：O(1)

3.稳定性：不稳定

3.3交换排序

3.3.1冒泡排序

基本思想：相邻元素之间两两进行比较和交换，使较大的元素向后移，使较小的元素向前移。

3.3.1.1冒泡排序代码实现
java 复制代码 
 public static void bubbleSort(int[] array){
      for (int i = 0; i < array.length-1; i++) { //控制趟数
          boolean flg = false;
          for(int j = 0; j<array.length-1-i;j++){  //控制比较次数
              if(array[j]> array[j+1]){
                  swap(array,j,j+1);
                    flg = true;
              }
              if(!flg){ //没有进行交换
                  break;
              }
          }

      }
  }
    private static void swap(int[] array ,int i ,int j){
        int tmp = array[j];
        array[j] = array[i];
        array[i] = tmp;
    }
3.3.1.2冒泡排序特性总结

1.时间复杂度：O(n^2),没有优化前

2.空间复杂度为：O(1)

3.稳定性：稳定

3.3.2快速排序

快速排序使用分治策略，其基本思想是：

  1. 选择一个元素作为基准（pivot）
  2. 将数组分为两部分：
    · 左边：所有元素 ≤ 基准
    · 右边：所有元素 ≥ 基准
  3. 对左右两部分递归地执行相同操作
3.3.2.1快速排序Hoare版代码实现
java 复制代码 
public static void quickSort(int[] array){
  quick(array,0,array.length-1);
}
private static void quick(int[] array,int start,int end){
      if(start>=end){         //start > end ,没有右子树   start==end,只有一个元素
         return;
      }
      int pivot = partition(array,start,end);
      quick(array,start,pivot-1);    //递归左边
      quick(array,pivot+1,end);     //递归右边
}

  private static int partition(int[] array, int left, int right) {
      int tmp = array[left];
      int tmpLeft = left;
    while (left<right){     //没有相遇
      while (left<right && array[right] >= tmp){ //从后往前找，比基准小的值,必须要取等号，因为当数组中第一个数和最后一个数相等时，会陷入死循环
          right--;
      }
        while (left<right && array[left] <= tmp){ //从前往后找，比基准大的值
            left++;
        }
        swap(array,left,right);

    }
    swap(array,left,tmpLeft); //当第一个数为数组中最大的数时，当left和right相遇以后，需要把基准值交换到正确位置，使得基准值的左边都比它小，右边都比它大
    return left;
  }

  private static void swap(int[] array ,int i ,int j){
      int tmp = array[j];
      array[j] = array[i];
      array[i] = tmp;
  }
3.3.2.2快速排序挖坑版代码实现
java 复制代码 
 public static void quickSort(int[] array){
 quick(array,0,array.length-1);
}
private static void quick(int[] array,int start,int end){
     if(start>=end){         //start > end ,没有右子树   start==end,只有一个元素
        return;
     }
     int pivot = partition(array,start,end);
     quick(array,start,pivot-1);    //递归左边
     quick(array,pivot+1,end);     //递归右边
}

 private static int partition(int[] array,int left,int right){
     int tmp = array[left];
     while (left<right){
         while (left<right && array[right] >= tmp){ //从后往前找，比基准小的值,必须要取等号，因为当数组中第一个数和最后一个数相等时，会陷入死循环
             right--;
         }
         array[left] = array[right];
         while (left<right && array[left] <= tmp){
             left++;
         }
         array[right] = array[left];
     }
     array[left] = tmp;
     return left;
 }

 private static void swap(int[] array ,int i ,int j){
     int tmp = array[j];
     array[j] = array[i];
     array[i] = tmp;
 }
3.3.2.3快速排序代码优化实现（三数取中法选key）
java 复制代码 
public static void quickSort(int[] array){
  quick1(array,0,array.length-1);
}
  private static void quick1(int[] array,int start,int end){
      if(start>=end){         //start > end ,没有右子树   start==end,只有一个元素
          return;
      }
      int middleIndex = findMiddleNum(array,start,end);
      swap(array,start,middleIndex);


      int pivot = partition(array,start,end);
      quick(array,start,pivot-1);    //递归左边
      quick(array,pivot+1,end);     //递归右边
  }
private  static int findMiddleNum(int[] array,int left,int right){
      int mid = (left+right)/2;
      if(array[left] < array[right]){
          if(array[left]>array[mid]){
              return left;
          }else if(array[right]<array[mid]){
              return right;
          }else {
              return mid;
          }
      }else {
          if(array[mid]<array[right]){
              return right;
          }else if(array[mid]>array[left]){
              return left;
          }else {
              return left;
          }
      }
}
  private static int partition(int[] array,int left,int right){
      int tmp = array[left];
      while (left<right){
          while (left<right && array[right] >= tmp){ //从后往前找，比基准小的值,必须要取等号，因为当数组中第一个数和最后一个数相等时，会陷入死循环
              right--;
          }
          array[left] = array[right];
          while (left<right && array[left] <= tmp){
              left++;
          }
          array[right] = array[left];
      }
      array[left] = tmp;
      return left;
  }

  private static void swap(int[] array ,int i ,int j){
      int tmp = array[j];
      array[j] = array[i];
      array[i] = tmp;
  }

测试结果

3.3.2.4快速排序特性总结

1.时间复杂度：一般为O(n*logn)

2.空间复杂度为：O(logn)

3.稳定性：不稳定

3.4归并排序

3.4.1基本思想

该算法采用的是分治法，将已有的子序列合并，得到完全有序的序列，即先让每个子序列有序，再让子序列段间有序。

3.4.1.1归并排代码实现
java 复制代码 
 public static void mergeSort(int[] array){
     mergeSortTmp(array,0,array.length-1);
    }
    private static void mergeSortTmp(int[] array,int left,int right){
        if(left>=right){           //递归结束的条件
            return;
        }
       int mid = (left+right) / 2;
        mergeSortTmp(array,left,mid);
        mergeSortTmp(array,mid+1,right);  //走到这里全部分解完毕
        //合并
        merge(array,left,mid,right);

    }

    private static void merge(int[] array, int left, int mid, int right) {
        int[] tmp = new int[right-left+1];
        int k = 0;
        int s1 = left;
      //  int e1 = mid;
        int s2 = mid+1;
      //  int e2 = right;
        while (s1<=mid && s2<=right){
            if(array[s1] <= array[s2]){
                tmp[k++] = array[s1++];
            }else {
                tmp[k++] = array[s2++];
            }
        }
        while (s1 <= mid){         //一边还没有走完，另外一边走完了
            tmp[k++] = array[s1++];
        }
        while (s2 <= right){
            tmp[k++] = array[s2++];
        }
        //写入array数组
        for (int i = 0; i < k; i++) {
            array[i+left] = tmp[i];
        }
    }

测试结果

3.4.1.2快速排序特性总结

1.时间复杂度：一般为O(n*logn)

2.空间复杂度为：O(n)

3.稳定性：稳定

3.5排序算法性能对比表

排序算法 最好时间复杂度 平均时间复杂度 最坏时间复杂度 空间复杂度 稳定性
冒泡排序 O(n) O(n²) O(n²) O(1) 稳定
插入排序 O(n) O(n²) O(n²) O(1) 稳定
选择排序 O(n²) O(n²) O(n²) O(1) 不稳定
希尔排序 O(n) O(n¹·³) O(n²) O(1) 不稳定
堆排序 O(n*log n) O(n*log n) O(n*log n) O(1) 不稳定
快速排序 O(n*log n) O(n*log n) O(n²) O(log n) ~ O(n) 不稳定
归并排序 O(n*log n) O(n*log n) O(n log n) O(n) 稳定
相关推荐
shilei_c2 小时前
qt qDebug无输出问题解决
开发语言·c++·算法
像少年啦飞驰点、2 小时前
零基础入门 Spring Boot：从“Hello World”到可部署微服务的完整学习指南
java·spring boot·微服务·编程入门·后端开发
乌蒙山连着山外山2 小时前
idea中的工程，import有问题
java·ide·intellij-idea
秋深枫叶红2 小时前
嵌入式C语言阶段复习——函数
c语言·数据结构·算法
We་ct2 小时前
LeetCode 49. 字母异位词分组：经典哈希解法解析+易错点规避
前端·算法·leetcode·typescript·哈希算法
梵刹古音2 小时前
【C语言】 数组函数与排序算法
c语言·算法·排序算法
1candobetter2 小时前
JAVA后端开发——Maven 依赖传递 ≠ Spring 自动装配
java·spring·maven
生命不息战斗不止(王子晗)2 小时前
2026面试大纲 - java数据结构与集合专题
java·数据结构·面试
若鱼19192 小时前
SpringBoot4.0新特性-Null-safety消灭空指针
java·spring
热门推荐
01GitHub 镜像站点02一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示03Claude Code Skills 实用使用手册04Vue-skills的中文文档05在Trae中使用Pencil MCP06OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)07UV安装并设置国内源08OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书09让 Trae IDE 智能体 “读懂”文档 Excel+PDF+DOCX ：mcp-documents-reader 工具使用指南10Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services