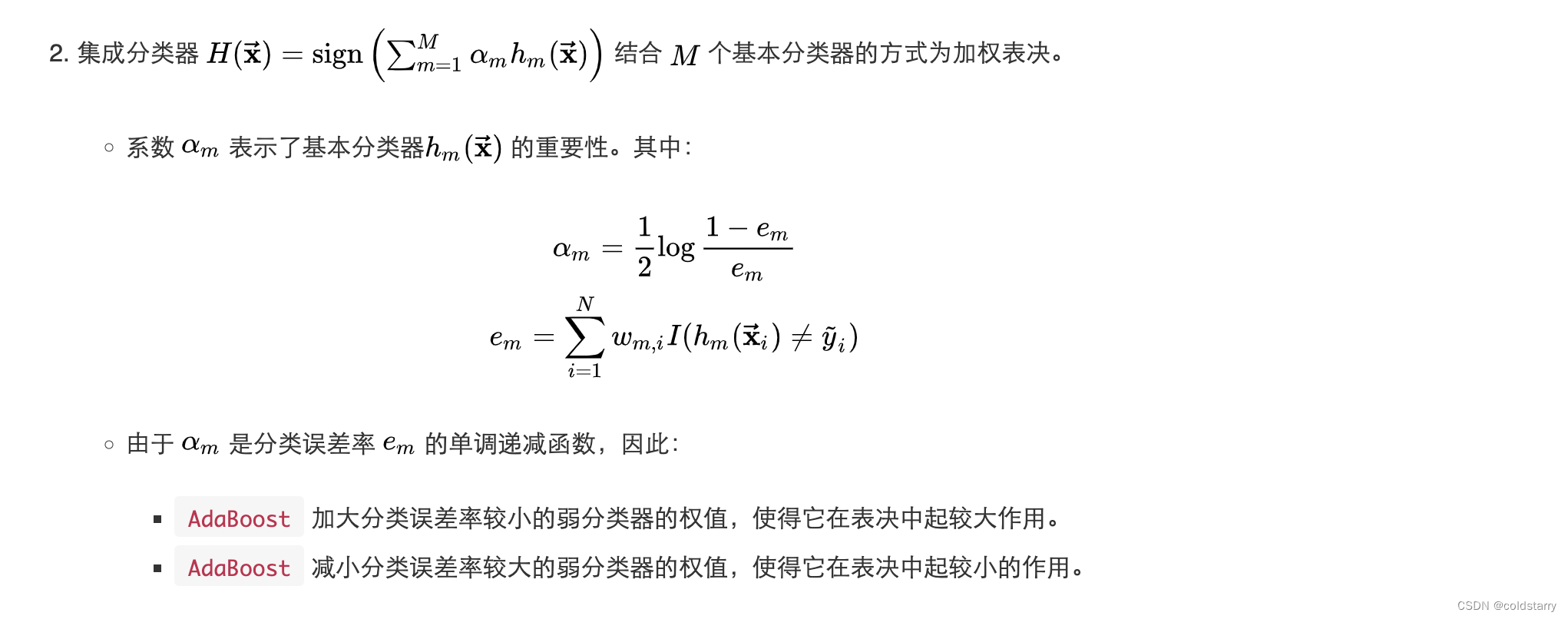
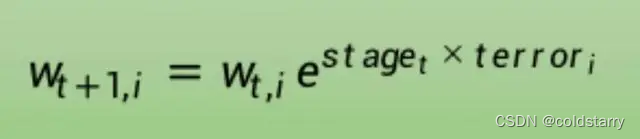前置知识:
sheng的学习笔记-AI-集成学习(bagging,随机森林,堆叠法)
目录
[AdaBoost 算法](#AdaBoost 算法)
[Adaboost 集成](#Adaboost 集成)
AdaBoost 算法
AdaBoost,是英文"Adaptive Boosting"(自适应增强)
AdaBoost的核心就是求当前分类器的权重和更新样本的误差。它可以用于提高任何机器学习算法的性能。最好与弱学习器一起使用。
这意味着难以分类的样本会收到越来越大的权重,直到算法识别出正确分类这些样本的模型。
与AdaBoost一起使用的最合适也是最常见的算法是具有一层的决策树。因为这些树很短,并且只包含一个用于分类的决策,所以它们通常被称为决策树桩。
AdaBoost示意图

训练数据集中的每个实例都被加权。初始权重设置为:Weight(Xi) = 1/N
其中Xi是第i个训练实例,N是训练实例的总数。(训练实例:即用于训练模型的样本数据)
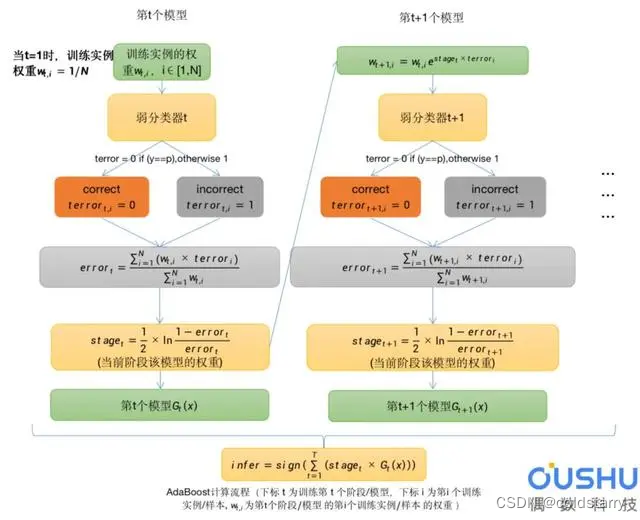
流程解析:
错误分类率error
每个实例都有自己独立的权重w,通常我们会对w进行归一化,使得w之和sum(w)=1。
使用加权之后的样本作为训练数据,以弱分类器(决策树桩)进行训练。仅支持二元(两类)分类问题,因此每个决策树桩对一个输入变量做出一个决策,并为第一类或第二类输出+1或-1值。
为训练后的模型计算错误分类率。传统的计算方式如下:
其中error是误分类率,correct是模型正确预测的训练实例数,N是训练实例总数。例如,如果模型正确预测了100个训练实例中的68个,则错误率或误分类率为(100-68)/100或0.32 。
将以上方式修改为加权训练实例:
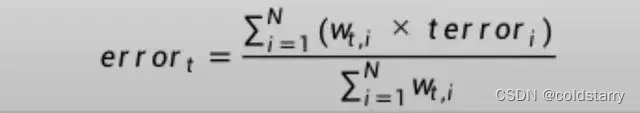
这是误分类率的加权和,w是训练实例i的权重,terror是训练实例i的预测误差,terror为1时是误分类,为0时是正确分类,sum是对N个实例的求和
例如,如果我们有三个训练实例,权重分别为0.01、0.5和0.2.预测值为-1、-1和-1,实例中的真实输出变量为-1、1和-1,则terror为0、1和0。误分类率将计算为:
error = (0.01*0 + 0.5*1 + 0.2*0)/(0.01+0.5+0.2) = 0.704
权重
为经过训练的模型计算阶段权值,该值为模型做出的任何预测提供权重。训练模型的阶段值计算如下:
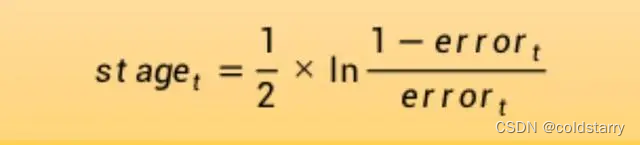
其中stage是用于对模型的预测进行加权的阶段值,即当前阶段模型的权重,ln()是自然对数,error是模型的误分类率。阶段权重stage的作用是,更准确的模型对最终预测的权重贡献更大
stage的图像如下:横轴是error,纵轴是stage,小于0.5值为正,大于0.5值为负
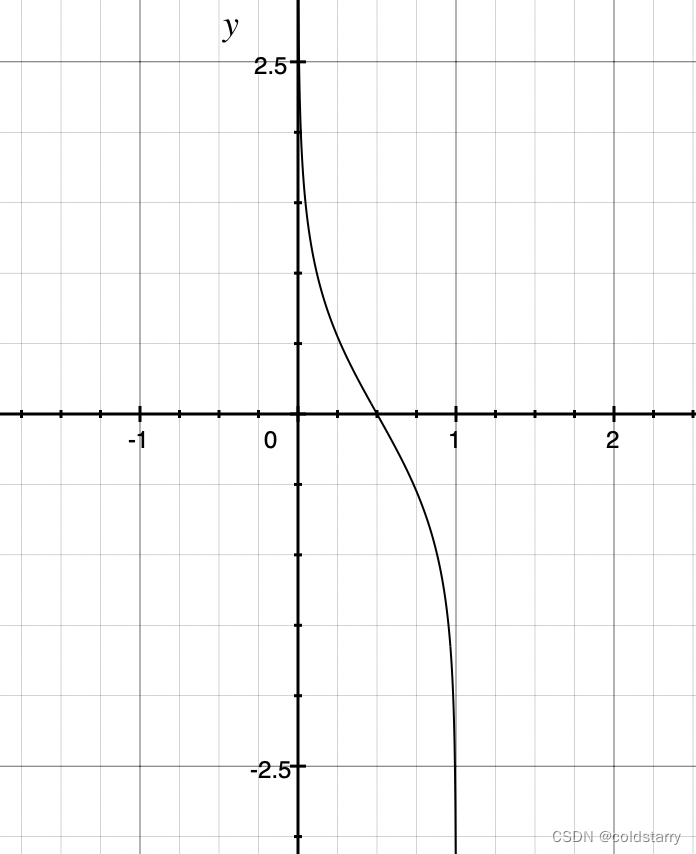
其中w是特定训练实例的权重,e是数值常数,stage是弱分类器的误分类率,terror是弱分类器预测输出变量的错误训练实例,评估为: terror = 0 if (y==p), otherwise 1
e的x方的图像如下
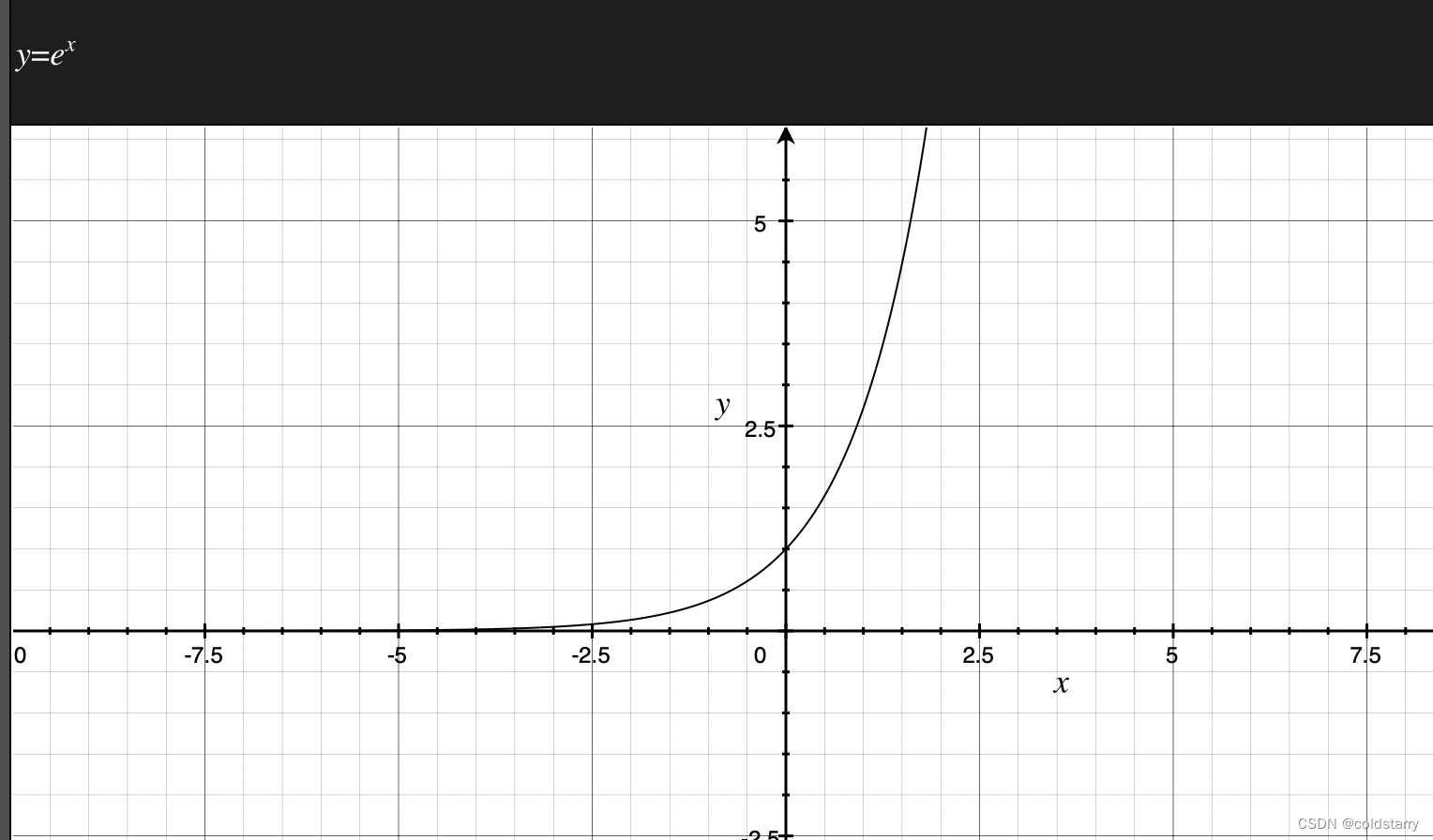
其中y是训练实例的输出变量,p是弱学习器的预测结果。
如果训练实例被正确分类,则权重不发生改变,如果被错误分类,则增大权重
Adaboost 集成
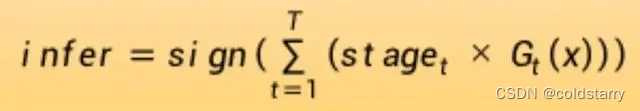
算法
西瓜书的算法
西瓜书的算法,解释的比较隐晦,大概看看


其他资料补充算法
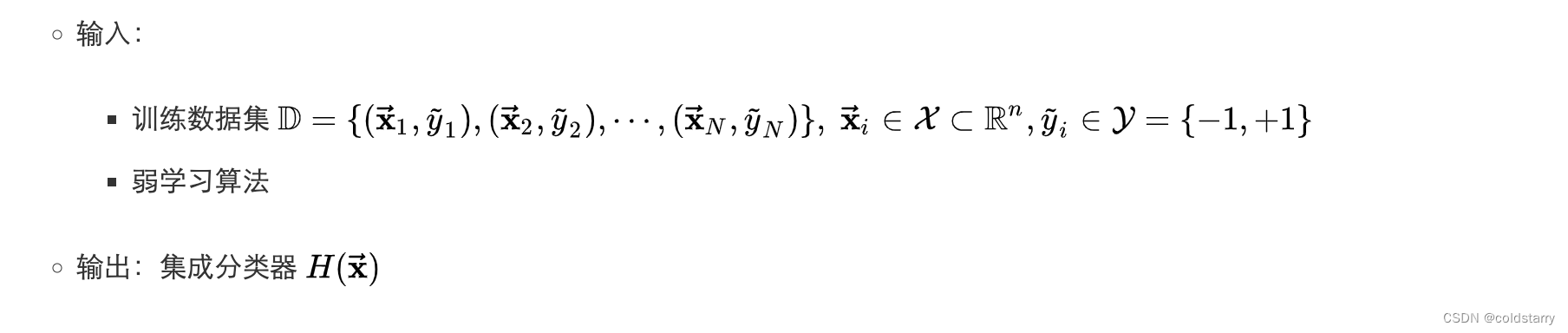

算法解释
其中exp就是e的指数,图像上面有对于w的计算,如果正确分类样本,变量取-a,值会很少,如果错误分类样本,变量取a,exp(a)值会大
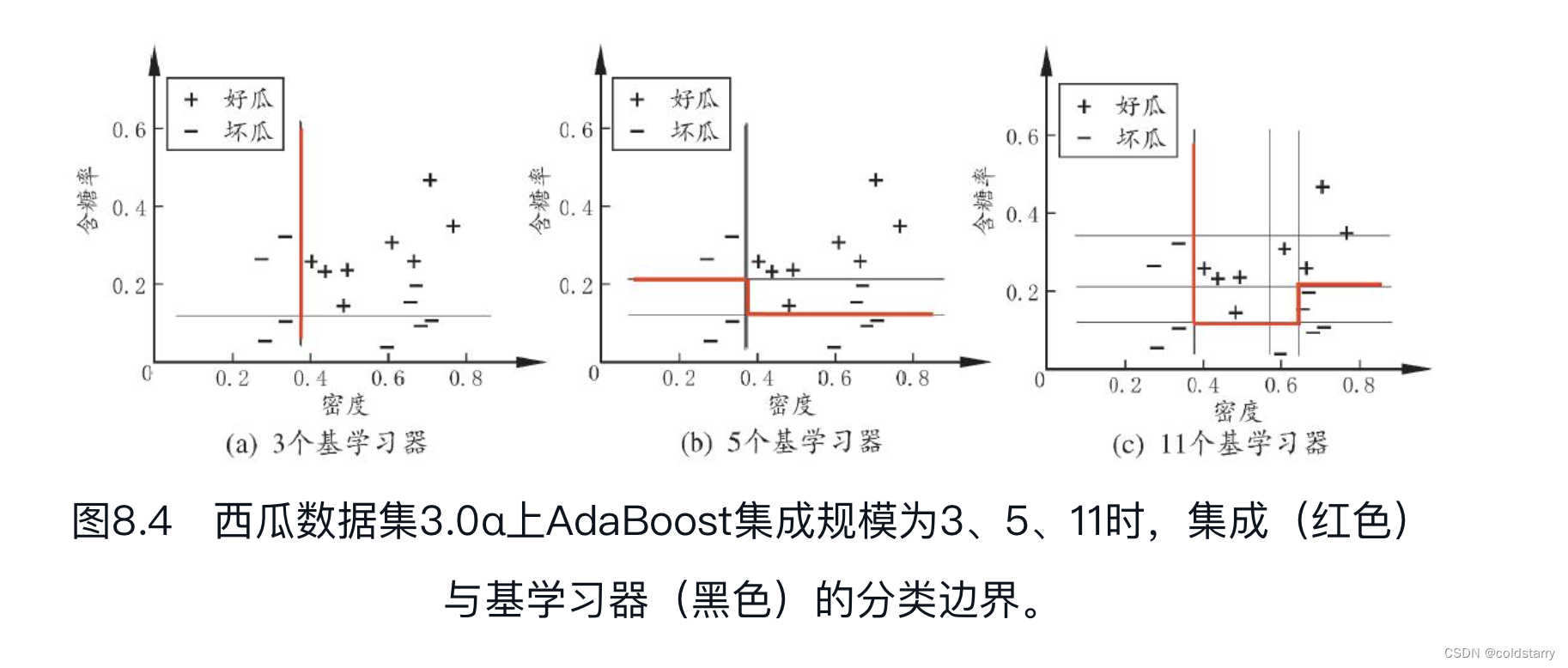
从偏差-方差分解的角度看,Boosting主要关注降低偏差,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。我们以决策树桩为基学习器,在表4.5的西瓜数据集3.0α上运行AdaBoost算法,不同规模(size)的集成及其基学习器所对应的分类边界如图8.4所示
分类器
每个分类器都是弱分类器,大多数用决策桩,意思是:
只用 1 个属性
只分 1 次
形式上:
if 触感 == 硬滑:
+1
else:
-1
决策桩完整流程:

纯度分析
adaboost不做属性纯度分析,在决策桩内部做纯度分析
常用的gini指数
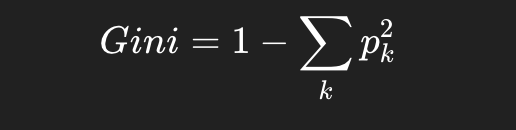
adaboost内的加权纯度(信息增益/entropy),每个样本不再是 1 票,而是 wi票
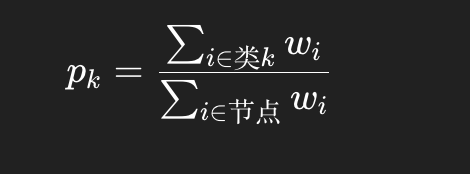
有些教材直接用加权错误率,选择最小的 err 即可。
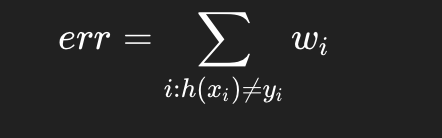
所以"加权增益"可以用 Gini、信息增益,也可以直接用加权错误率(最常见)
举个例子:
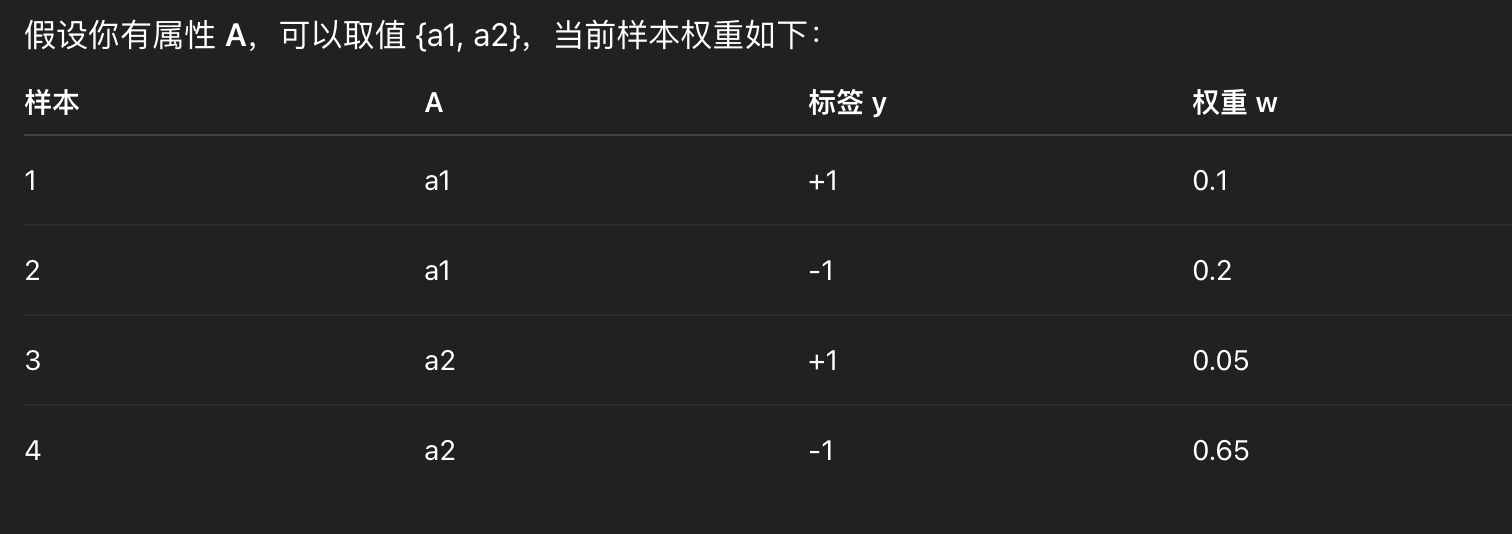

总结