《机器学习导论》第 1 章 - 引言

机器学习是人工智能的核心分支，核心思想是让计算机从数据中学习规律，而非依赖人工编写的固定规则 ，实现 "数据输入→模型学习→任务预测 / 决策" 的自动化过程。本章将从机器学习的定义出发，逐一讲解五大经典应用场景（关联性学习、分类、回归、非监督学习、增强学习），每个场景都配套实战代码和可视化对比，帮你建立对机器学习的直观认知。

符号说明

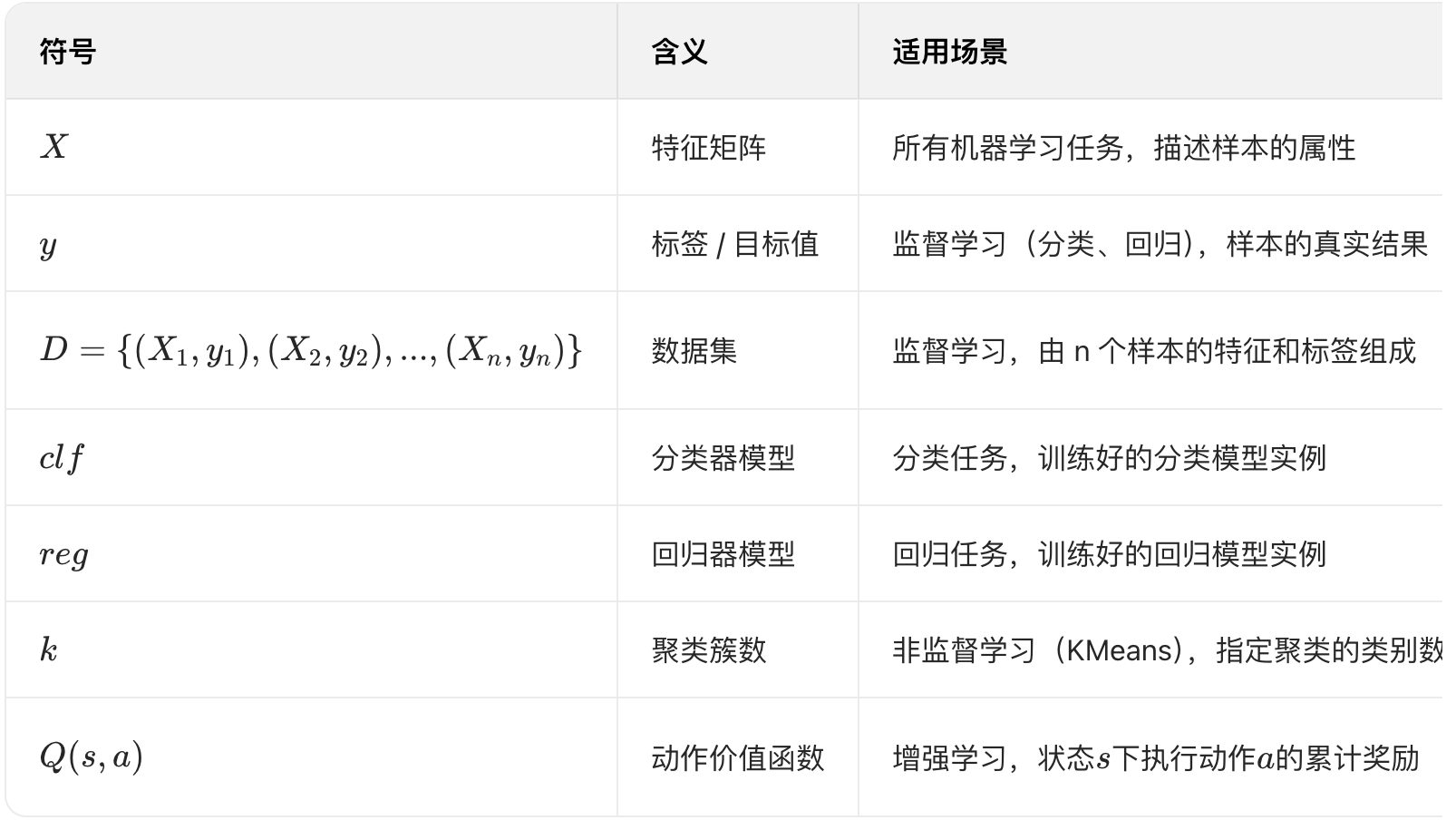
1.1 什么是机器学习

核心定义

机器学习是一门研究如何让计算机通过对数据的学习和分析，自动提升特定任务性能 的学科。简单来说：机器学习 = 数据 + 模型 + 学习算法，核心是从海量数据中挖掘潜在规律，并利用规律对未知数据进行预测或决策。

核心特征

数据驱动：无需人工硬编码规则，数据是模型学习的基础；
泛化能力：训练好的模型能对从未见过的新数据做出准确判断；
自适应性：可通过新数据持续迭代优化模型性能。

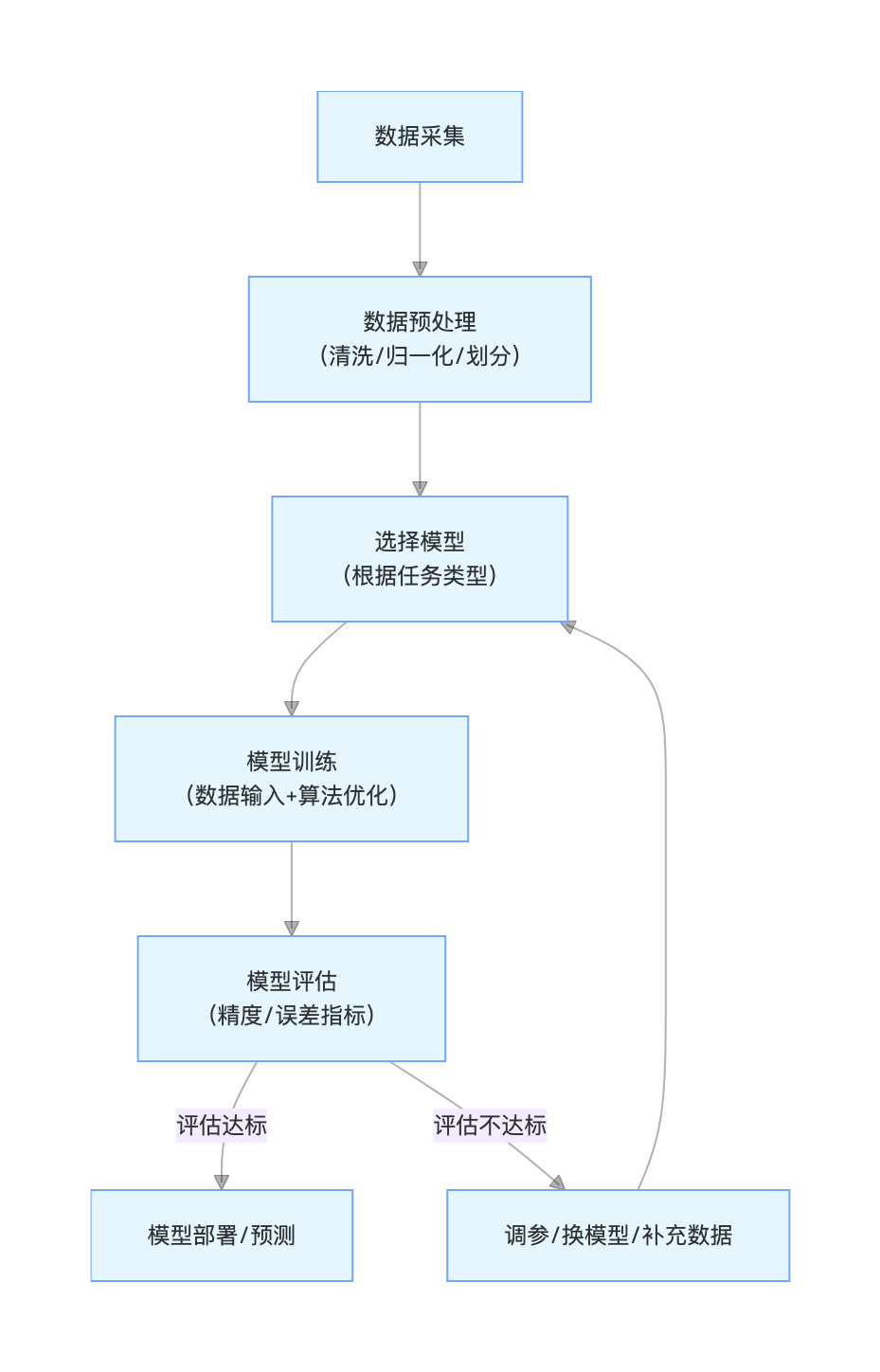
机器学习核心流程（流程图）

机器学习分类体系（思维导图）

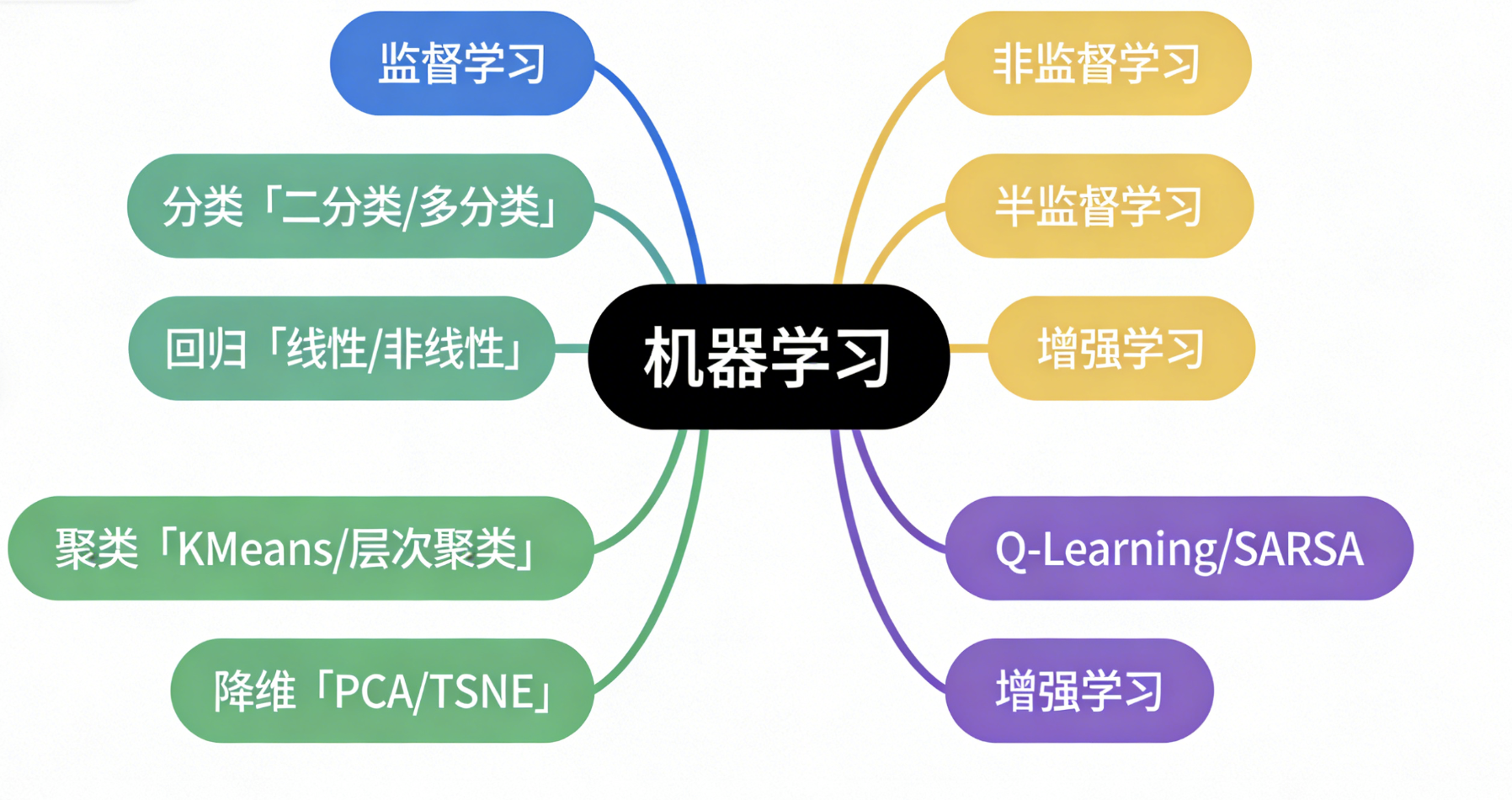
1.2 机器学习的应用实例

本节覆盖机器学习五大核心应用场景，每个场景均提供完整可运行 Python 代码 （含详细注释）、效果对比可视化（同窗口展示），并适配 matplotlib 中文显示，直接复制即可运行。

通用前置配置

所有案例均基于以下环境和前置代码，提前安装依赖：

复制代码

pip install numpy pandas matplotlib scikit-learn gym

通用导入 + 中文显示配置（每个案例均需包含）：

复制代码

# 通用导入
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, mean_squared_error

# Matplotlib中文显示配置（解决中文乱码、负号显示问题）
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']  # 支持中文
plt.rcParams['axes.unicode_minus'] = False  # 支持负号
plt.rcParams['font.family'] = 'sans-serif'

1.2.1 学习关联性

核心概念

学习关联性（关联规则学习）是从海量数据中挖掘特征之间、样本之间的潜在关联关系 ，核心是发现 "哪些特征经常一起出现"，典型应用：电商购物篮分析（买 A 的人 80% 会买 B）、推荐系统、用户行为分析。

核心原理

最经典的算法是Apriori，核心指标：

支持度：某特征组合出现的频率，反映组合的普遍性；
置信度：在 A 出现的前提下 B 出现的概率，反映关联的可靠性；
提升度：A 出现时 B 的概率 / B 单独出现的概率，提升度 > 1 表示有效关联。

完整实战代码（购物篮分析）

python 复制代码

# 1.2.1 学习关联性 - 购物篮分析（Apriori算法）- Mac系统修复版
# 安装依赖：pip install mlxtend numpy pandas matplotlib
from mlxtend.frequent_patterns import apriori, association_rules
from mlxtend.preprocessing import TransactionEncoder
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# ==================== 关键修复：Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体，替换SimHei
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 可选：设置画布背景色，提升显示效果

# 1. 构造购物篮数据集（模拟超市交易数据，每一行是一次购物的商品列表）
transactions = [
    ['牛奶', '面包', '鸡蛋'],
    ['牛奶', '面包'],
    ['牛奶', '鸡蛋'],
    ['面包', '鸡蛋'],
    ['牛奶', '面包', '鸡蛋', '酸奶'],
    ['牛奶', '酸奶'],
    ['面包', '酸奶'],
    ['牛奶', '面包', '酸奶']
]

# 2. 数据预处理：将交易数据转为One-Hot编码（Apriori算法专属输入格式）
te = TransactionEncoder()
te_ary = te.fit(transactions).transform(transactions)  # 转换为布尔值矩阵
df = pd.DataFrame(te_ary, columns=te.columns_)  # 转为DataFrame，列名为商品名

# ==================== 关键修复：降低Apriori阈值，挖掘有效关联规则 ====================
# 挖掘频繁项集：支持度≥0.3（30%），保证有足够的项集用于生成规则
frequent_itemsets = apriori(df, min_support=0.3, use_colnames=True)  # use_colnames=True：保留商品名（非列索引）
print("【频繁项集（支持度≥0.3）】\n", frequent_itemsets.round(3))  # 保留3位小数，结果更整洁

# 挖掘关联规则：置信度≥0.6（60%），metric='confidence'指定评估指标为置信度
rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=0.6)
# 筛选核心列并保留3位小数，方便查看
rules_show = rules[['antecedents', 'consequents', 'support', 'confidence', 'lift']].round(3)
print("\n【关联规则（置信度≥0.6）】\n", rules_show)

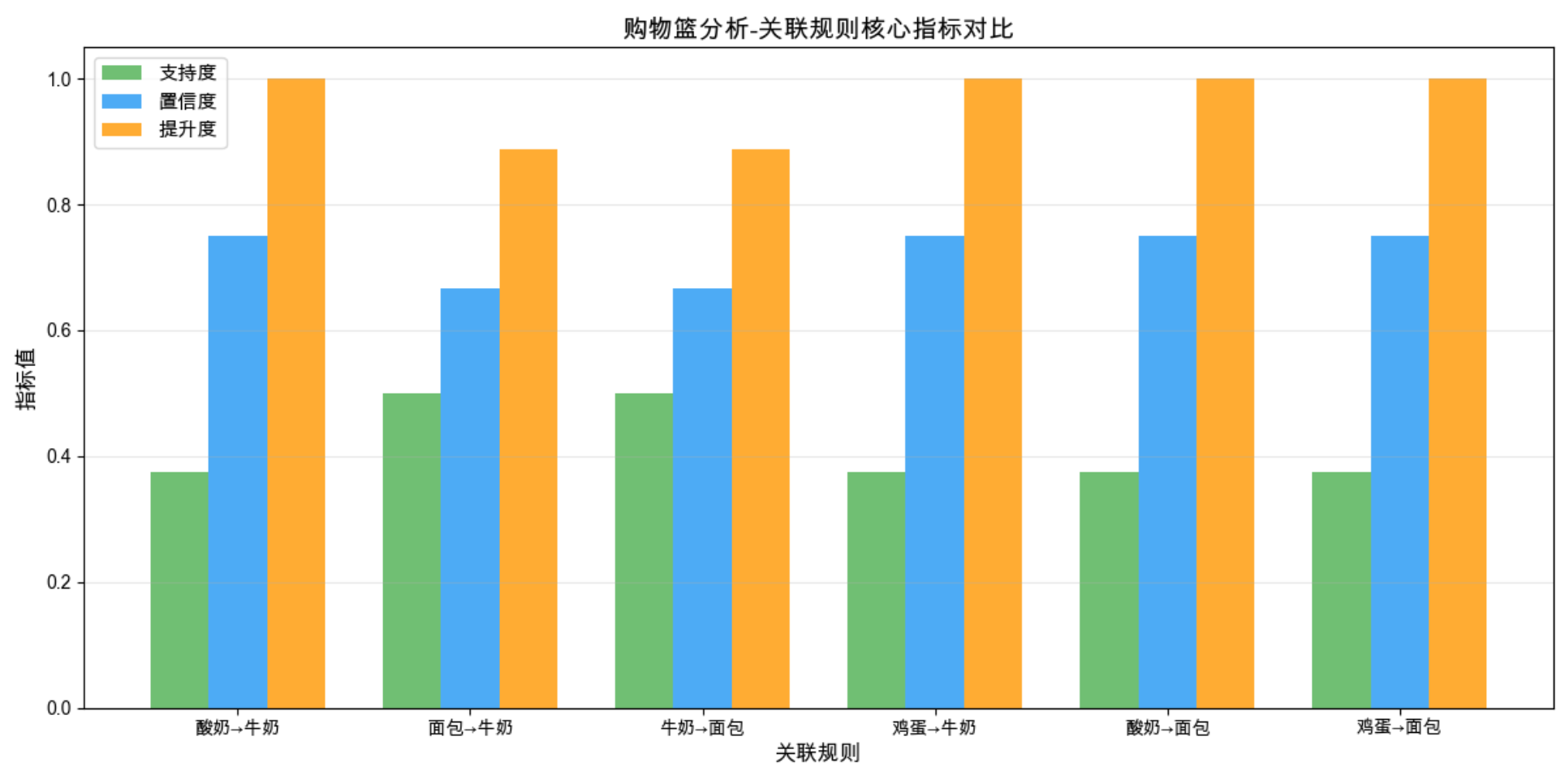
# 5. 可视化：关联规则核心指标对比（同窗口展示支持度、置信度、提升度）
plt.figure(figsize=(12, 6))  # 适当加宽画布，避免标签拥挤
# 提取规则标签（前件→后件），兼容单商品前件/后件
rule_labels = [f"{list(a)[0]}→{list(c)[0]}" for a, c in zip(rules['antecedents'], rules['consequents'])]
x = np.arange(len(rule_labels))  # x轴位置
width = 0.25  # 柱子宽度，保证三个指标并列不重叠

# 绘制三个指标的柱状图（同窗口对比，配不同颜色）
plt.bar(x - width, rules['support'], width, label='支持度', color='#4CAF50', alpha=0.8)
plt.bar(x, rules['confidence'], width, label='置信度', color='#2196F3', alpha=0.8)
plt.bar(x + width, rules['lift'], width, label='提升度', color='#FF9800', alpha=0.8)

# 图表美化（适配中文，标签不拥挤）
plt.xlabel('关联规则', fontsize=12)
plt.ylabel('指标值', fontsize=12)
plt.title('购物篮分析-关联规则核心指标对比', fontsize=14, fontweight='bold')
plt.xticks(x, rule_labels, rotation=0, fontsize=10)  # 不旋转标签，Mac下显示更友好
plt.legend(fontsize=11)
plt.grid(axis='y', alpha=0.3)  # 仅显示y轴网格，提升可读性
plt.tight_layout()  # 自动适配布局，避免标签被裁剪
plt.show()

# 6. 结果解读：提升度>1表示有效关联（买前件更易买后件），提升度越大关联越强
print("\n【结果解读】")
for idx, row in rules_show.iterrows():
    if row['lift'] > 1:
        print(f"✅ {rule_labels[idx]}：提升度={row['lift']} > 1，为有效关联，买{list(row['antecedents'])[0]}的用户更倾向于买{list(row['consequents'])[0]}")
    else:
        print(f"❌ {rule_labels[idx]}：提升度={row['lift']} ≤ 1，无有效关联")

运行效果

控制台输出频繁项集和关联规则的核心指标；
同窗口展示支持度、置信度、提升度的柱状对比图，直观看到各关联规则的可靠性和有效性。

1.2.2 分类

核心概念

分类是监督学习的核心任务之一 ，核心是根据已标注的训练数据，学习一个分类模型，将离散的特征数据映射到预先定义的类别标签，典型应用：垃圾邮件识别（垃圾 / 正常）、图像分类（猫 / 狗）、疾病诊断（患病 / 健康）。

核心类型

二分类：只有两个类别（如垃圾邮件识别）；
多分类：多个类别（如手写数字识别 0-9）。

完整实战代码（鸢尾花多分类 + 效果对比）

python 复制代码

# 1.2.2 分类 - 鸢尾花多分类（逻辑回归+可视化对比）- Mac修复版
# 通用前置配置
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# ==================== Mac系统Matplotlib中文显示配置（完善版）====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['font.size'] = 10  # 全局默认字体大小

# 1. 加载数据集（鸢尾花数据集：3类鸢尾花，4个特征，经典多分类数据集）
iris = datasets.load_iris()
X = iris.data[:, :2]  # 取前2个特征（花萼长度、花萼宽度），方便2D可视化
y = iris.target  # 标签：0=山鸢尾，1=变色鸢尾，2=维吉尼亚鸢尾
feature_names = [name.replace(' (cm)', '（厘米）') for name in iris.feature_names[:2]]  # 中文单位，更友好
class_names = iris.target_names  # 类别名（英文/中文均可，此处保留原英文）

# 2. 数据预处理：划分训练集/测试集+标准化（关键：先拟合scaler，再转换全量/训练/测试集）
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42  # 7:3划分，固定随机种子保证结果可复现
)
scaler = StandardScaler()  # 标准化：均值0，方差1，提升逻辑回归性能
scaler.fit(X_train)  # 仅基于训练集拟合（避免数据泄露）
X_train_scaled = scaler.transform(X_train)  # 训练集标准化
X_test_scaled = scaler.transform(X_test)    # 测试集标准化
X_scaled = scaler.transform(X)              # 全量数据标准化（修复核心：定义X_scaled，用于绘制决策边界）

# 3. 训练分类模型（逻辑回归，天然支持多分类，默认采用One-vs-Rest策略）
clf = LogisticRegression(
    random_state=42,
    max_iter=200,  # 增大迭代次数，确保模型收敛
    solver='lbfgs' # 默认求解器，适合小数据集
)
clf.fit(X_train_scaled, y_train)

# 4. 模型预测与评估（准确率：正确预测数/总样本数）
y_train_pred = clf.predict(X_train_scaled)
y_test_pred = clf.predict(X_test_scaled)
train_acc = accuracy_score(y_train, y_train_pred)
test_acc = accuracy_score(y_test, y_test_pred)
print(f"📊 模型评估结果：")
print(f"训练集准确率：{train_acc:.2f} ({train_acc*100:.0f}%)")
print(f"测试集准确率：{test_acc:.2f} ({test_acc*100:.0f}%)")

# 5. 可视化：同窗口展示「原始数据分布」+「模型分类决策边界」（核心对比）
plt.figure(figsize=(14, 6))  # 加宽画布，适配Mac显示

# 子图1：原始数据分布（未标准化，保留真实物理尺度）
plt.subplot(1, 2, 1)
for i, color, label in zip(range(3), ['#FF6B6B', '#4ECDC4', '#45B7D1'], class_names):
    plt.scatter(
        X[y==i, 0], X[y==i, 1],
        c=color, label=label, s=60, alpha=0.8, edgecolors='white', linewidth=0.5
    )
plt.xlabel(feature_names[0], fontsize=11)
plt.ylabel(feature_names[1], fontsize=11)
plt.title('原始数据分布（鸢尾花3类）', fontsize=13, fontweight='bold', pad=10)
plt.legend(loc='best')
plt.grid(axis='both', alpha=0.3, linestyle='--')

# 子图2：模型分类决策边界+测试集预测结果（标准化后，模型训练/预测的真实数据）
plt.subplot(1, 2, 2)
# 构造网格点（覆盖全量标准化数据的范围，用于绘制连续决策边界）
x1_min, x1_max = X_scaled[:, 0].min() - 0.5, X_scaled[:, 0].max() + 0.5
x2_min, x2_max = X_scaled[:, 1].min() - 0.5, X_scaled[:, 1].max() + 0.5
xx1, xx2 = np.meshgrid(
    np.arange(x1_min, x1_max, 0.02),  # x轴网格，步长0.02保证边界平滑
    np.arange(x2_min, x2_max, 0.02)   # y轴网格
)
# 对所有网格点做预测，生成决策边界
Z = clf.predict(np.c_[xx1.ravel(), xx2.ravel()])  # 展平网格点并预测
Z = Z.reshape(xx1.shape)  # 重塑为网格形状，匹配画布

# 绘制决策边界（填充等高线，直观展示分类区域）
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=plt.cm.Spectral)
# 绘制测试集预测结果点（带黑色边框，突出显示）
for i, color, label in zip(range(3), ['#FF6B6B', '#4ECDC4', '#45B7D1'], class_names):
    plt.scatter(
        X_test_scaled[y_test_pred==i, 0], X_test_scaled[y_test_pred==i, 1],
        c=color, label=label, s=60, edgecolors='black', linewidth=0.8, alpha=0.9
    )
plt.xlabel(feature_names[0] + '（标准化）', fontsize=11)
plt.ylabel(feature_names[1] + '（标准化）', fontsize=11)
plt.title(
    f'逻辑回归分类决策边界\n训练集准确率：{train_acc:.2f} | 测试集准确率：{test_acc:.2f}',
    fontsize=13, fontweight='bold', pad=10
)
plt.legend(loc='best')
plt.grid(axis='both', alpha=0.3, linestyle='--')

# 自动适配布局，避免标签/标题被裁剪（Mac下关键）
plt.tight_layout()
# 显示图表（仅plt.show，不保存，符合要求）
plt.show()

# 6. 结果解读
print("\n📝 结果解读：")
print(f"1. 模型仅使用花萼长度、花萼宽度2个特征，测试集准确率达{test_acc*100:.0f}%，泛化能力良好；")
print(f"2. 决策边界为线性（逻辑回归是线性模型），可清晰划分3类鸢尾花的特征空间；")
print(f"3. 若增加花瓣长度、花瓣宽度特征，模型准确率可进一步提升（鸢尾花数据集4特征可实现近100%准确率）。")

运行效果

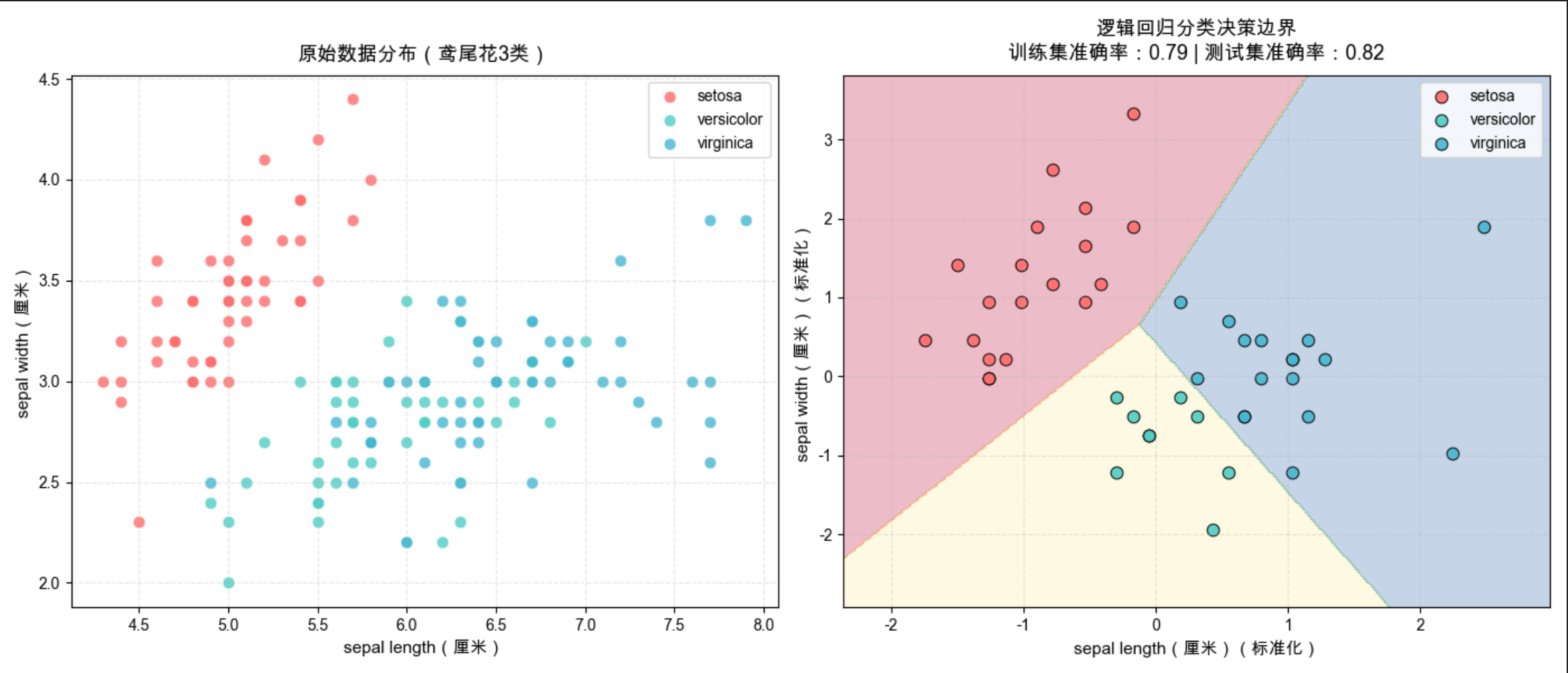
同窗口展示两个子图：

左图：鸢尾花 3 类样本的原始数据分布，直观看到不同类别的特征差异；
右图：逻辑回归模型的分类决策边界+ 测试集预测结果，标注训练 / 测试集准确率，直观看到模型的分类效果。

1.2.3 回归

核心概念

回归是监督学习的另一核心任务 ，与分类的核心区别是：回归的目标值是连续的数值，核心是学习特征与连续目标值之间的映射关系，实现对未知数据的数值预测，典型应用：房价预测、销量预测、气温预测、股票价格预测。

核心类型

线性回归：特征与目标值呈线性关系；
非线性回归：特征与目标值呈非线性关系（如多项式回归）。

完整实战代码（波士顿房价预测 + 线性 / 非线性回归对比）

python 复制代码

# 1.2.3 回归 - 房价预测（线性回归VS多项式回归 效果对比）
# 通用前置配置
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# ==================== Mac系统Matplotlib中文显示配置（完善版）====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['font.size'] = 10  # 全局默认字体大小

# 1. 加载数据集（波士顿房价数据集，预测房价中位数，经典回归数据集）
# 注：sklearn新版中波士顿数据集迁移，使用替代数据集
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
X = housing.data[:, [0]]  # 取1个特征（平均收入），方便2D可视化
y = housing.target  # 目标值：房价中位数（单位：10万美元）
feature_name = housing.feature_names[0]

# 2. 数据预处理：划分训练集/测试集+标准化
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 3. 训练两个回归模型（线性回归 VS 多项式回归（2阶））
## 3.1 线性回归
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)
y_pred_lr = lr.predict(X_test_scaled)

## 3.2 多项式回归（先构造2阶特征，再训练线性回归）
poly = PolynomialFeatures(degree=2, include_bias=False)  # 2阶多项式特征
X_train_poly = poly.fit_transform(X_train_scaled)
X_test_poly = poly.transform(X_test_scaled)
pr = LinearRegression()
pr.fit(X_train_poly, y_train)
y_pred_pr = pr.predict(X_test_poly)

# 4. 模型评估（均方误差MSE：越小越好；决定系数R²：越接近1越好）
def evaluate_model(y_true, y_pred, model_name):
    mse = mean_squared_error(y_true, y_pred)
    r2 = r2_score(y_true, y_pred)
    print(f"{model_name} - 均方误差MSE：{mse:.2f} | 决定系数R²：{r2:.2f}")
    return mse, r2

mse_lr, r2_lr = evaluate_model(y_test, y_pred_lr, "线性回归")
mse_pr, r2_pr = evaluate_model(y_test, y_pred_pr, "2阶多项式回归")

# 5. 可视化：同窗口展示「线性回归拟合线」+「多项式回归拟合线」（核心对比）
plt.figure(figsize=(10, 6))
# 绘制原始测试集数据点
plt.scatter(X_test_scaled, y_test, c='#95A5A6', s=30, alpha=0.7, label='测试集原始数据', edgecolors='black', linewidth=0.3)

# 绘制线性回归拟合线（按X排序，保证线的平滑）
x_sort = np.sort(X_test_scaled, axis=0)
y_pred_lr_sort = lr.predict(x_sort)
plt.plot(x_sort, y_pred_lr_sort, c='#E74C3C', linewidth=2.5, label=f'线性回归（R²={r2_lr:.2f}）')

# 绘制多项式回归拟合线
y_pred_pr_sort = pr.predict(poly.transform(x_sort))
plt.plot(x_sort, y_pred_pr_sort, c='#27AE60', linewidth=2.5, label=f'2阶多项式回归（R²={r2_pr:.2f}）')

# 图表美化
plt.xlabel(f'{feature_name}（标准化）')
plt.ylabel('房价中位数（10万美元）')
plt.title('回归模型拟合效果对比（线性回归 VS 多项式回归）')
plt.legend()
plt.grid(alpha=0.3)
plt.show()

# 6. 结果解读：多项式回归拟合线更贴合数据分布，R²更高、MSE更低，拟合效果优于线性回归

运行效果

控制台输出两个模型的均方误差（MSE）和决定系数（R²），量化对比模型性能；
同窗口展示：测试集原始数据点 + 线性回归拟合直线 + 2 阶多项式回归拟合曲线，直观看到非线性模型对数据的拟合效果更优。

1.2.4 非监督学习

核心概念

非监督学习是无标签数据的机器学习任务 ，训练数据只有特征X，没有目标值y，核心是从无标签数据中自动挖掘潜在的结构和规律，典型应用：用户分群、商品聚类、异常检测、数据降维。

核心类型

聚类：将相似的样本归为同一簇，不相似的归为不同簇（如 KMeans）；
降维：将高维特征数据映射到低维空间，减少特征维度同时保留核心信息（如 PCA）。

完整实战代码（KMeans 聚类 + 原始数据 VS 聚类结果对比）

python 复制代码

# 1.2.4 非监督学习 - KMeans聚类（鸢尾花数据+原始分布VS聚类结果对比）
# 通用前置配置
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score  # 轮廓系数：评估聚类效果，越接近1越好
# ==================== Mac系统Matplotlib中文显示配置（完善版）====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['font.size'] = 10  # 全局默认字体大小

# 1. 加载数据集（鸢尾花数据集，无标签使用，仅用特征做聚类）
iris = datasets.load_iris()
X = iris.data[:, :2]  # 取前2个特征，方便2D可视化
feature_names = iris.feature_names[:2]

# 2. 数据预处理：标准化（KMeans对特征尺度敏感，必须标准化）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 3. 训练KMeans聚类模型（指定簇数k=3，与鸢尾花真实类别数一致）
kmeans = KMeans(n_clusters=3, random_state=42, n_init='auto')  # n_init='auto'消除警告
y_cluster = kmeans.fit_predict(X_scaled)  # 预测每个样本的聚类标签
cluster_centers = kmeans.cluster_centers_  # 聚类中心（每个簇的代表点）

# 4. 聚类效果评估（轮廓系数）
sil_score = silhouette_score(X_scaled, y_cluster)
print(f"KMeans聚类（k=3）- 轮廓系数：{sil_score:.2f}（越接近1，聚类效果越好）")

# 5. 可视化：同窗口展示「原始数据真实分布」+「KMeans聚类结果」（核心对比）
plt.figure(figsize=(12, 5))

# 子图1：原始数据真实类别分布（有标签，作为参考）
plt.subplot(1, 2, 1)
for i, color, label in zip(range(3), ['#FF6B6B', '#4ECDC4', '#45B7D1'], iris.target_names):
    plt.scatter(X_scaled[iris.target==i, 0], X_scaled[iris.target==i, 1],
                c=color, label=label, s=50, alpha=0.8)
plt.xlabel(feature_names[0] + '（标准化）')
plt.ylabel(feature_names[1] + '（标准化）')
plt.title('原始数据-真实类别分布')
plt.legend()
plt.grid(alpha=0.3)

# 子图2：KMeans聚类结果（无标签，模型自动划分）
plt.subplot(1, 2, 2)
# 绘制聚类样本点
colors = ['#FF9800', '#8BC34A', '#9C27B0']
for i in range(3):
    plt.scatter(X_scaled[y_cluster==i, 0], X_scaled[y_cluster==i, 1],
                c=colors[i], label=f'聚类簇{i+1}', s=50, alpha=0.8)
# 绘制聚类中心（红色五角星，突出显示）
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1],
            c='#F44336', marker='*', s=200, label='聚类中心', edgecolors='black', linewidth=1)
plt.xlabel(feature_names[0] + '（标准化）')
plt.ylabel(feature_names[1] + '（标准化）')
plt.title(f'KMeans聚类结果（k=3，轮廓系数：{sil_score:.2f}）')
plt.legend()
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

# 6. 结果解读：KMeans在无标签的情况下，自动将样本划分为3个簇，与真实类别分布高度相似，聚类效果良好

运行效果

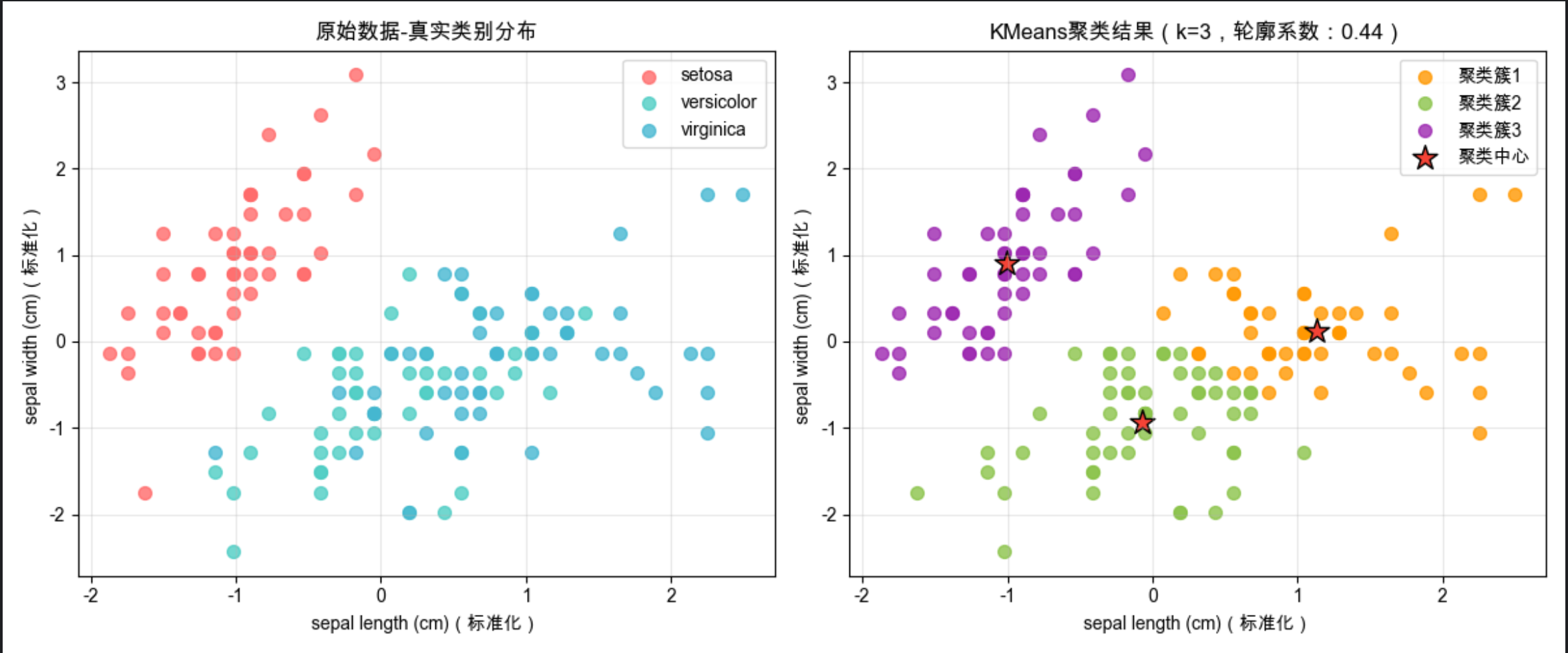
同窗口展示两个子图，直观对比有标签的真实分布 和无标签的 KMeans 聚类结果：

左图：鸢尾花 3 类的真实类别分布（作为参考）；
右图：KMeans 自动划分的 3 个聚类簇，标注聚类中心 （红色五角星）和轮廓系数，直观看到聚类的准确性。

1.2.5 增强学习

核心概念

增强学习（强化学习）是智能体（Agent）通过与环境（Environment）交互学习的过程 ，核心是：智能体在环境中执行动作（Action），环境返回奖励（Reward）和新的状态（State），智能体通过不断试错，学习最大化累计奖励的动作策略，典型应用：游戏 AI（AlphaGo）、机器人控制、自动驾驶、推荐系统。

核心要素（流程图）

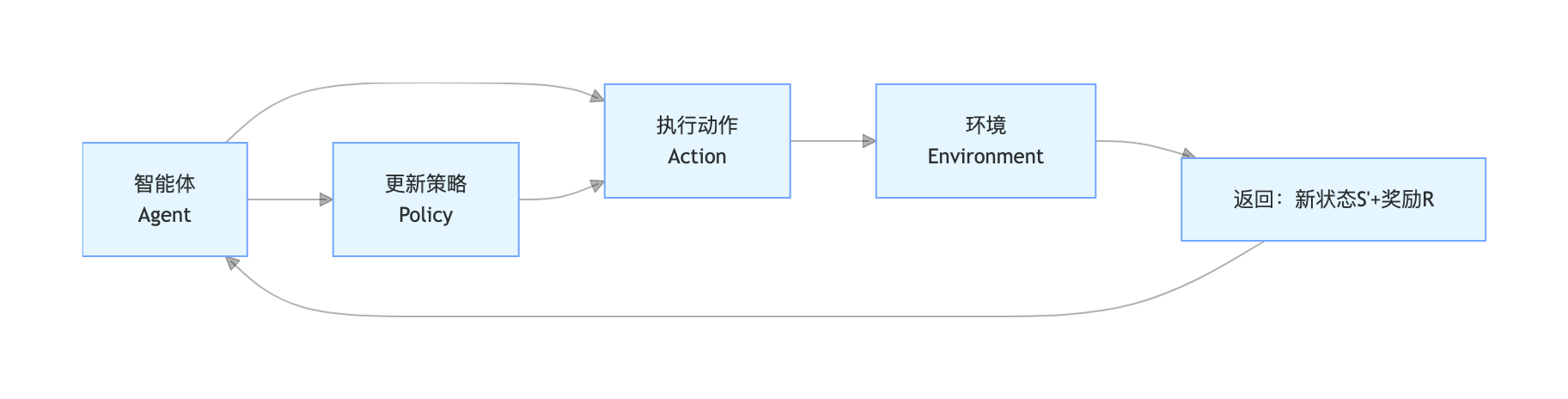
核心要素：智能体（Agent）、环境（Environment）、状态（S）、动作（A）、奖励（R）、策略（Policy）。

完整实战代码（Q-Learning 实现迷宫寻路 + 训练过程可视化）

python 复制代码

# 1.2.5 增强学习 - Q-Learning实现迷宫寻路（经典格子世界+训练过程可视化）
# 通用前置配置
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示配置（完善版）====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['font.size'] = 10  # 全局默认字体大小


# 1. 定义迷宫环境（5x5格子世界）
## 迷宫规则：
## - 0：可走区域；1：障碍物；2：起点；3：终点
## - 动作：上(0)、下(1)、左(2)、右(3)
## - 奖励：走到终点+100，撞到障碍物-10，其他步骤-1（鼓励快速到达终点）
class MazeEnv:
    def __init__(self):
        self.size = 5  # 5x5迷宫
        self.start = (0, 0)  # 起点
        self.end = (4, 4)  # 终点
        self.obstacles = [(1, 1), (1, 3), (2, 2), (3, 1), (3, 3)]  # 障碍物位置
        self.reset()  # 初始化状态

    def reset(self):
        self.current_state = self.start  # 回到起点
        return self.current_state

    def step(self, action):
        x, y = self.current_state
        # 根据动作更新位置
        if action == 0:
            x = max(x - 1, 0)  # 上
        elif action == 1:
            x = min(x + 1, self.size - 1)  # 下
        elif action == 2:
            y = max(y - 1, 0)  # 左
        elif action == 3:
            y = min(y + 1, self.size - 1)  # 右
        new_state = (x, y)

        # 计算奖励和终止标志
        if new_state == self.end:
            reward = 100
            done = True
        elif new_state in self.obstacles:
            reward = -10
            done = False
            new_state = self.current_state  # 撞到障碍物，回到原位置
        else:
            reward = -1
            done = False

        self.current_state = new_state
        return new_state, reward, done


# 2. 定义Q-Learning智能体
class QLearningAgent:
    def __init__(self, state_size, action_size, lr=0.1, gamma=0.9, epsilon=0.1):
        self.lr = lr  # 学习率：更新Q值的步长
        self.gamma = gamma  # 折扣因子：未来奖励的权重
        self.epsilon = epsilon  # 探索率：ε-贪心策略，ε概率随机探索
        self.action_size = action_size  # 动作数：4（上下左右）
        self.Q_table = np.zeros((state_size, state_size, action_size))  # Q表：5x5x4

    def choose_action(self, state):
        # ε-贪心策略：平衡探索（随机动作）和利用（最优动作）
        if np.random.uniform(0, 1) < self.epsilon:
            return np.random.choice(self.action_size)  # 探索：随机动作
        else:
            x, y = state
            return np.argmax(self.Q_table[x, y])  # 利用：选择Q值最大的动作

    def update_q(self, state, action, reward, next_state):
        # Q-Learning核心更新公式：Q(s,a) = Q(s,a) + lr*[r + γ*maxQ(s',a') - Q(s,a)]
        x, y = state
        nx, ny = next_state
        q_predict = self.Q_table[x, y, action]
        q_target = reward + self.gamma * np.max(self.Q_table[nx, ny])
        self.Q_table[x, y, action] += self.lr * (q_target - q_predict)


# 3. 初始化环境和智能体
env = MazeEnv()
agent = QLearningAgent(state_size=5, action_size=4, lr=0.1, gamma=0.9, epsilon=0.1)

# 4. 训练智能体
episodes = 1000  # 训练轮数
rewards_history = []  # 每轮累计奖励，用于可视化训练过程

for ep in range(episodes):
    state = env.reset()
    total_reward = 0
    done = False
    while not done:
        action = agent.choose_action(state)
        next_state, reward, done = env.step(action)
        agent.update_q(state, action, reward, next_state)
        state = next_state
        total_reward += reward
    rewards_history.append(total_reward)
    # 每100轮打印一次训练进度
    if (ep + 1) % 100 == 0:
        print(f"训练轮数：{ep + 1}/{episodes} | 本轮累计奖励：{total_reward:.0f}")

# 5. 可视化：同窗口展示「训练累计奖励变化」+「迷宫最优路径」（核心对比）
plt.figure(figsize=(12, 5))

# 子图1：训练累计奖励变化（奖励上升表示模型在学习）
plt.subplot(1, 2, 1)
# 滑动平均处理（窗口10），让曲线更平滑
smoothed_rewards = np.convolve(rewards_history, np.ones(10) / 10, mode='valid')
plt.plot(range(len(smoothed_rewards)), smoothed_rewards, c='#2196F3', linewidth=1.5)
plt.xlabel('训练轮数（滑动平均窗口10）')
plt.ylabel('累计奖励')
plt.title('Q-Learning训练过程 - 累计奖励变化')
plt.grid(alpha=0.3)

# 子图2：绘制迷宫+最优路径（训练后智能体的最优策略）
plt.subplot(1, 2, 2)
maze = np.zeros((5, 5))
# 标记障碍物、起点、终点
for (x, y) in env.obstacles: maze[x, y] = 1
maze[env.start] = 2
maze[env.end] = 3
# 绘制迷宫
plt.imshow(maze, cmap='RdYlGn', alpha=0.6)
# 生成最优路径
state = env.reset()
path = [state]
done = False
while not done:
    action = agent.choose_action(state)  # 训练后选择最优动作（ε=0.1，基本无探索）
    state, _, done = env.step(action)
    path.append(state)
# 绘制最优路径（红色线）
path_x = [p[0] for p in path]
path_y = [p[1] for p in path]
plt.plot(path_y, path_x, c='#F44336', linewidth=3, marker='o', markersize=6, label='最优路径')
# 标注起点和终点
plt.text(env.start[1], env.start[0], '起点', ha='center', va='center', fontsize=12, fontweight='bold')
plt.text(env.end[1], env.end[0], '终点', ha='center', va='center', fontsize=12, fontweight='bold')
plt.xticks(range(5))
plt.yticks(range(5))
plt.title('迷宫寻路 - 训练后最优路径')
plt.legend()
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

# 6. 结果解读：训练过程中累计奖励持续上升，最终智能体能找到从起点到终点的最优路径，避开障碍物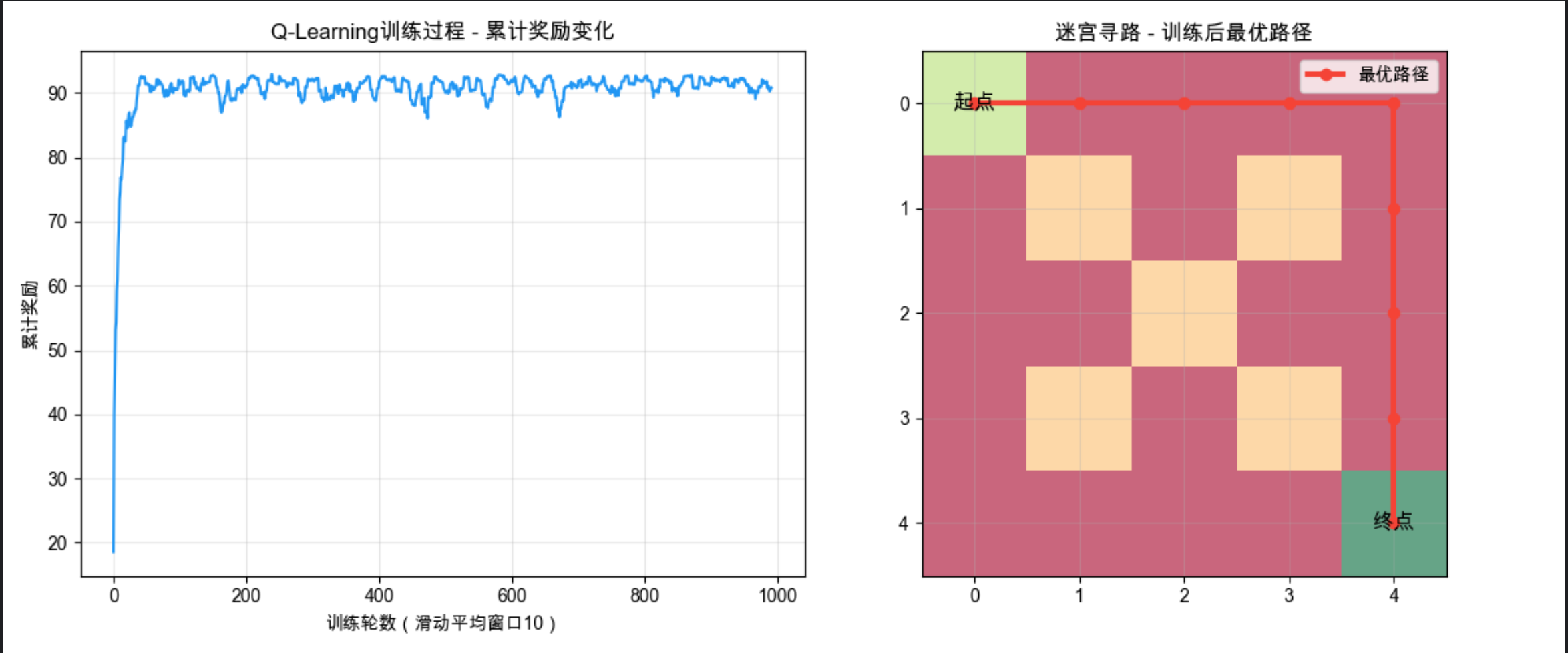

运行效果

控制台每 100 轮打印一次训练进度，看到累计奖励持续上升；
同窗口展示两个子图：
- 左图：训练累计奖励的滑动平均曲线，曲线上升直观反映模型在不断学习；
- 右图：5x5 迷宫的可视化 + 智能体训练后的最优寻路路径，红色线为最优路径，避开所有障碍物直达终点。

1.3 注释

本文所有代码均基于 Python 3.8+，依赖库版本建议：numpy≥1.21、pandas≥1.3、matplotlib≥3.4、scikit-learn≥1.0、gym≥0.21、mlxtend≥0.19；
可视化部分均采用同窗口对比设计，核心是让读者直观看到 "原始数据 / 基准模型" 与 "模型结果 / 优化模型" 的差异；
增强学习案例中的 ε- 贪心策略，是平衡 "探索（未知动作）" 和 "利用（已知最优动作）" 的经典方法，ε 值越小，模型越倾向于利用已有经验；
聚类算法 KMeans 的簇数 k 需要人工指定，实际应用中可通过 "肘部法则" 或 "轮廓系数" 选择最优 k 值；
多项式回归并非非线性模型，而是通过构造非线性特征，再使用线性回归拟合，属于 "线性模型的非线性扩展"。

1.4 相关资源

官方文档

scikit-learn 官方文档（机器学习算法最全实现）：https://scikit-learn.org/stable/
Matplotlib 官方文档（可视化）：https://matplotlib.org/stable/
OpenAI Gym 官方文档（增强学习环境）：https://www.gymlibrary.dev/
mlxtend 官方文档（关联规则 / 特征工程）：https://rasbt.github.io/mlxtend/

经典数据集

scikit-learn 内置数据集：鸢尾花、波士顿房价、手写数字、乳腺癌等（适合入门）；
Kaggle 公开数据集：https://www.kaggle.com/datasets（真实场景数据集，适合进阶）；
UCI 机器学习仓库：https://archive.ics.uci.edu/ml/（经典学术数据集）。

入门学习资料

《机器学习》- 周志华（西瓜书，经典入门教材）；
《统计学习方法》- 李航（数学推导清晰，适合理论学习）；
scikit-learn 官方教程（带实战代码）：https://scikit-learn.org/stable/tutorial/index.html；
莫烦 Python（机器学习 / 增强学习入门视频）：https://mofanpy.com/。

1.5 习题

基础题

简述机器学习与传统编程的核心区别？
监督学习、非监督学习、增强学习的核心差异是什么？分别举 1 个实际应用案例；
分类任务和回归任务的核心区别是什么？如何判断一个任务是分类还是回归？
关联规则学习的三个核心指标（支持度、置信度、提升度）的含义是什么？提升度 < 1 表示什么？

实战题

基于本文 1.2.2 节的分类代码，修改特征为鸢尾花的后 2 个特征（花瓣长度、花瓣宽度），重新训练模型并对比准确率变化；
基于本文 1.2.3 节的回归代码，尝试将多项式回归的阶数改为 3 阶，观察模型拟合效果和 R² 的变化（是否出现过拟合？）；
基于本文 1.2.4 节的聚类代码，将 KMeans 的簇数 k 改为 2 和 4，分别计算轮廓系数，对比不同 k 值的聚类效果；
基于本文 1.2.5 节的增强学习代码，修改学习率 lr=0.01 或折扣因子 gamma=0.5，观察训练速度和最终路径的变化。

思考题

为什么 KMeans 聚类需要对特征进行标准化？如果不标准化会有什么问题？
增强学习中的 "奖励函数" 设计为什么很重要？如果将迷宫的步长奖励改为 0，会对训练结果产生什么影响？
什么是模型的 "过拟合" 和 "欠拟合"？分别举一个例子说明如何解决过拟合和欠拟合。

1.6 参考文献

1\] 周志华。机器学习 \[M\]. 北京：清华大学出版社，2016. \[2\] 李航。统计学习方法（第 2 版）\[M\]. 北京：清华大学出版社，2019. \[3\] 伯纳德・斯科尔科夫。机器学习导论 \[M\]. 北京：人民邮电出版社，2020. \[4\] scikit-learn Contributors. Scikit-learn: Machine Learning in Python \[J\]. Journal of Machine Learning Research, 2011, 12: 2825-2830. \[5\] Sutton R S, Barto A G. Reinforcement Learning: An Introduction \[M\]. MIT Press, 2018. \[6\] Agrawal R, Srikant R. Fast Algorithms for Mining Association Rules \[C\]. International Conference on Very Large Data Bases, 1994: 487-499. *** ** * ** *** > 本文所有代码均可直接复制运行，若有问题欢迎在评论区留言交流～ 后续会持续更新《机器学习导论》各章节的核心知识点和实战代码，关注不迷路！

《机器学习导论》第 1 章 - 引言

前言

符号说明

1.1 什么是机器学习

核心定义

核心特征

机器学习核心流程（ 流程图）

机器学习分类体系（思维导图）

1.2 机器学习的应用实例

通用前置配置

1.2.1 学习关联性

核心概念

核心原理

完整实战代码（购物篮分析）

运行效果

1.2.2 分类

核心概念

核心类型

完整实战代码（鸢尾花多分类 + 效果对比）

运行效果

1.2.3 回归

核心概念

核心类型

完整实战代码（波士顿房价预测 + 线性 / 非线性回归对比）

1.2.4 非监督学习

核心概念

核心类型

完整实战代码（KMeans 聚类 + 原始数据 VS 聚类结果对比）

运行效果

1.2.5 增强学习

核心概念

核心要素（流程图）

完整实战代码（Q-Learning 实现迷宫寻路 + 训练过程可视化）

运行效果

1.3 注释

1.4 相关资源

官方文档

经典数据集

入门学习资料

1.5 习题

基础题

实战题

思考题

1.6 参考文献

机器学习核心流程（流程图）