题目
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中"相邻"单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
数据范围
m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length<= 15
board 和 word 仅由大小写英文字母组成
测试用例
示例1
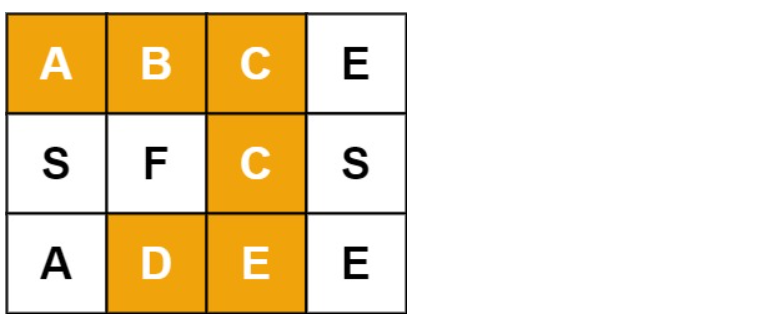
java
输入:board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "ABCCED"
输出:true示例2
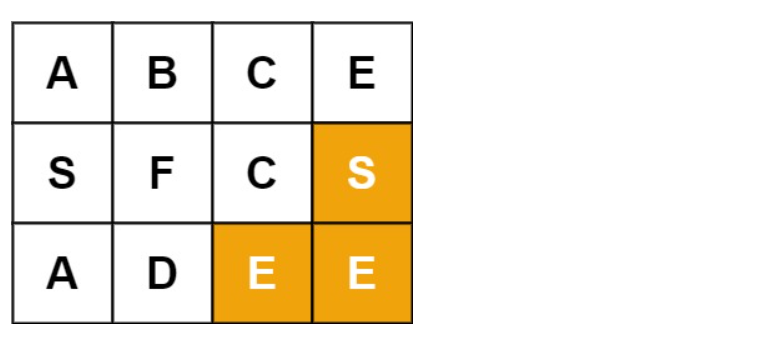
java
输入:board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "SEE"
输出:true示例3
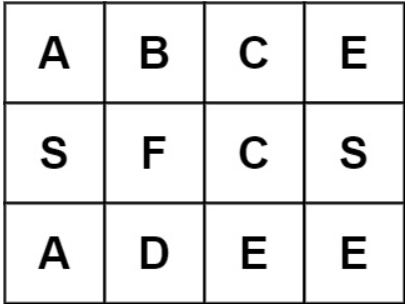
java
输入:board = [['A','B','C','E'],['S','F','C','S'],['A','D','E','E']], word = "ABCB"
输出:false题解1(博主版本,时间ONM*3L)
java
class Solution {
// 全局变量记录最终结果,只要找到一条路径就变为 true
boolean res = false;
// 定义四个移动方向:右、左、下、上 (注意:这里的顺序和坐标对应关系视具体定义而定)
int move[][] = {{0, 1, 0, -1}, {1, 0, -1, 0}};
// 辅助数组,用于记录网格是否被访问过 (Memory/Visited)
int mry[][];
// c 代表行数 (count/rows), r 代表列数 (rows/columns) - *注:命名有点反直觉*
int c, r;
public boolean exist(char[][] board, String word) {
char w[] = word.toCharArray();
char head = w[0];
c = board.length; // 获取行数
r = board[0].length; // 获取列数
// 遍历整个棋盘寻找起点
for(int i = 0; i < c; i++){
for(int j = 0; j < r; j++){
// 只有当当前字符等于单词首字母时,才开始搜索
if(board[i][j] == head){
// 初始化访问数组 (注意:这里每次匹配头字符都new一次数组,开销较大)
mry = new int[c][r];
mry[i][j] = 1; // 标记起点已访问
// 开始 DFS,参数:当前的二维坐标被压缩成了一维 (i*r+j)
dfs(board, w, mry, 1, i * r + j);
// 如果在 DFS 中找到了路径,直接返回 true
if(res){
return res;
}
}
}
}
return false; // 遍历完都没找到
}
// DFS 递归函数
// stage: 当前匹配到了单词的第几个字符
// curr: 当前坐标的一维表示
public void dfs(char[][] board, char[] word, int mry[][], int stage, int curr){
// 递归终止条件:如果匹配长度等于单词长度,说明找到了
if(stage == word.length){
res = true;
return;
}
// 将一维坐标还原回二维坐标 x, y
int x = curr / r;
int y = curr % r;
// 尝试向四个方向移动
for(int k = 0; k < 4; k++){
// 剪枝:如果已经找到了结果,不需要继续搜索
if(res == true){
return;
}
// 计算下一个坐标
int tx = x + move[0][k];
int ty = y + move[1][k];
// 边界检查 && 检查是否已访问 && 检查字符是否匹配
if(tx >= 0 && tx < c && ty >= 0 && ty < r &&
mry[tx][ty] != 1 && board[tx][ty] == word[stage]){
mry[tx][ty] = 1; // 标记访问
// 递归进入下一层
dfs(board, word, mry, stage + 1, tx * r + ty);
mry[tx][ty] = 0; // 回溯:恢复状态,以便其他路径可以使用该格子
}
}
}
}官解(时空同上)
java
class Solution {
public boolean exist(char[][] board, String word) {
int h = board.length, w = board[0].length;
boolean[][] visited = new boolean[h][w];
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
boolean flag = check(board, visited, i, j, word, 0);
if (flag) {
return true;
}
}
}
return false;
}
public boolean check(char[][] board, boolean[][] visited, int i, int j, String s, int k) {
if (board[i][j] != s.charAt(k)) {
return false;
} else if (k == s.length() - 1) {
return true;
}
visited[i][j] = true;
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
boolean result = false;
for (int[] dir : directions) {
int newi = i + dir[0], newj = j + dir[1];
if (newi >= 0 && newi < board.length && newj >= 0 && newj < board[0].length) {
if (!visited[newi][newj]) {
boolean flag = check(board, visited, newi, newj, s, k + 1);
if (flag) {
result = true;
break;
}
}
}
}
visited[i][j] = false;
return result;
}
}题解3(题解1优化,使用原始数组 ,时间相同,空间OL)
java
class Solution {
public boolean exist(char[][] board, String word) {
int m = board.length;
int n = board[0].length;
char[] w = word.toCharArray();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 如果找到入口,直接开始 DFS
if (dfs(board, w, i, j, 0)) {
return true;
}
}
}
return false;
}
private boolean dfs(char[][] board, char[] word, int i, int j, int k) {
// 1. 终止条件:如果不匹配,或者越界
if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] != word[k]) {
return false;
}
// 2. 成功条件:匹配到了最后一个字符
if (k == word.length - 1) {
return true;
}
// 3. 标记当前格子已访问(用特殊字符覆盖,省去 mry 数组)
char temp = board[i][j];
board[i][j] = '#';
// 4. 向四个方向递归
boolean found = dfs(board, word, i + 1, j, k + 1) ||
dfs(board, word, i - 1, j, k + 1) ||
dfs(board, word, i, j + 1, k + 1) ||
dfs(board, word, i, j - 1, k + 1);
// 5. 回溯:还原当前格子
board[i][j] = temp;
return found;
}
}思路
这道题的思路大差不差都是回溯算法,但具体实现有点差别,题解1大家看个乐就好不要学,虽然与官解时空一样,但终究差一些,因为每次都创建了一个新的mry,这对于回溯算法是不需要的,按官解的回溯还原就行了,博主没有直接传xy,传的是组合信息,这里纯是博主想写写这个代码了,实际效果不如直接传xy,因为需要做一次计算。
但前两种方法都还没有做到完全信任回溯法,只要我们定一个临时变量存储当前格子的值,我们就可以用回溯法还原,记录操作就可以在原数组中完成。