逻辑回归作为机器学习中最经典的分类算法之一,以其简洁的数学原理、可解释性强的优势,广泛应用于风控、医疗、推荐系统等多个领域。它本质上是通过线性模型拟合数据,再通过sigmoid函数将输出映射到[0,1]区间,实现二分类(或多分类)预测。但在实际实战中,仅掌握基础公式远远不够------数据不平衡、模型泛化能力不足等问题,往往会让模型效果大打折扣。
今天这篇博客,将从逻辑回归核心公式回顾入手,重点拆解实战中必备的三个关键技巧:交叉验证(解决泛化能力问题)、下采样(解决数据不平衡的"减法"思路)、过采样(解决数据不平衡的"加法"思路),帮你避开实战坑,让逻辑回归模型更稳健、更精准(文中实战例子可自行替换为自身数据)。
一、先回顾:逻辑回归核心公式与核心逻辑
在深入实战技巧前,我们先快速回顾逻辑回归的核心知识点,为后续内容做好铺垫------毕竟所有实战技巧,都是围绕"优化模型拟合效果"展开的。
1. 核心公式(二分类为例)
逻辑回归的本质是"线性回归+非线性映射",核心分为两步:
第一步:构建线性预测函数,拟合特征与标签的线性关系:
其中,是单个样本的n个特征,
是模型需要学习的参数(
为截距项),z是线性回归的输出,取值范围为(-∞,+∞)。
第二步:通过sigmoid函数,将线性输出z映射到[0,1]区间,得到样本属于正类的概率:
sigmoid函数的特性的是:当z→+∞时,(判定为正类);当z→-∞时,
(判定为负类);当z=0时,
(临界值,可自定义阈值调整分类结果)。
二、核心铺垫:正则化损失函数的来历与核心用途
在逻辑回归实战中,正则化是避免过拟合的关键手段,其底层原理源自线性回归的损失函数优化,也是本次实战案例中LogisticRegression(penalty='l2')的核心理论支撑。结合实战中常用的线性回归损失函数,我们拆解基础损失函数 与L2 正则化损失函数的来历、用途,理解正则化的核心逻辑。
1. 线性回归基础损失函数(无正则化)
公式:
来历
该公式是最小二乘损失(MSE,均方误差),源自 "最小化预测值与真实值的平方误差和" 的核心思想,是线性回归的原生损失函数,也是所有回归类模型损失函数的基础原型。
公式中的21是数学优化小技巧:后续对损失函数求导时,平方项的系数 2 会与21抵消,让求导结果更简洁,不影响最终 "最小化损失" 的优化目标。
用途
核心作用是衡量模型对训练数据的拟合程度,损失函数值越小,说明模型的预测值与真实值越接近,对训练集的拟合效果越好。
但该公式存在明显短板:仅用它训练模型时,若数据集特征维度高、样本量少,或训练集中存在噪声,模型会过度学习训练集的细节特征,导致过拟合,在新数据上的泛化能力极差。
2. 线性回归 L2 正则化损失函数
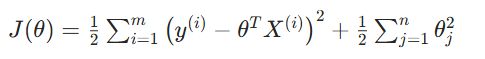
来历
该公式是在基础最小二乘损失 的基础上,增加了L2 正则化惩罚项 (也常简写为
,代表所有参数的平方和)。
正则化的核心思想是:在 "最小化拟合误差" 和 "约束模型复杂度" 之间找平衡------ 模型的参数值越大,代表模型的拟合越复杂,越容易捕捉训练集的噪声;通过给参数增加平方惩罚,强制模型选择更小的参数值,让模型更 "简单",从而抑制过拟合。
用途
- 核心作用:防止过拟合惩罚项会对过大的参数值进行 "扣分",模型为了最小化总损失,会主动选择更小的参数,避免过度学习训练集的噪声特征,从而提升模型在新数据上的泛化能力。
3. 实战核心痛点
掌握上述公式,就能训练出逻辑回归模型,但实际应用中,我们常会遇到两个核心问题:
-
模型泛化能力差:训练集上效果很好(准确率高、损失小),但测试集上效果急剧下降,出现"过拟合"(模型过度学习训练集噪声,无法适应新数据);
-
数据不平衡:样本中正负类比例悬殊(如风控场景中,"违约用户"仅占1%,"正常用户"占99%),模型会偏向多数类,导致少数类(关键类)预测准确率极低。
而我们今天重点讲的「交叉验证」「下采样」「过采样」,正是分别解决这两个痛点的核心技巧------交叉验证解决泛化能力问题,下采样与过采样解决数据不平衡问题。
二、重点一:交叉验证(Cross Validation)------ 让模型泛化能力更稳健
很多新手训练逻辑回归时,习惯将数据直接分成"训练集"和"测试集"(如7:3拆分),用训练集训练模型,用测试集评估效果。这种方法简单,但存在一个致命问题:测试集的划分具有随机性,如果测试集恰好包含较多"特殊样本"(如异常值、极端值),评估结果会严重偏离模型真实性能,导致我们误判模型效果。
交叉验证的核心思路,就是「多次划分数据、多次训练评估」,用"平均性能"衡量模型的真实泛化能力,避免单次划分的随机性带来的误差。
1. 交叉验证的核心原理
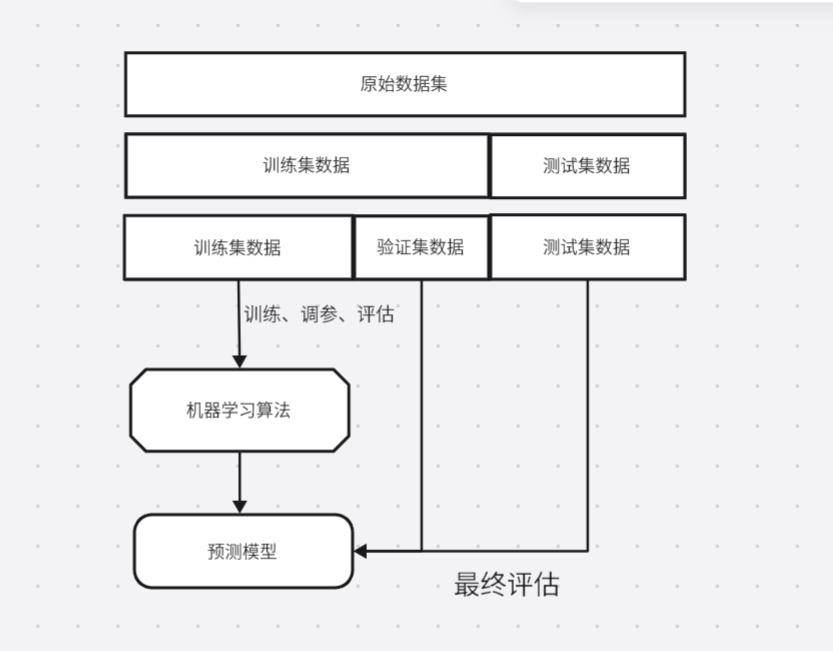
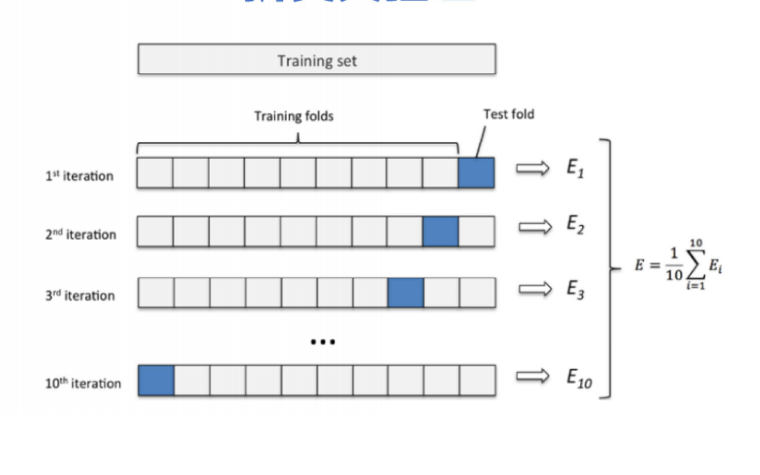
交叉验证的本质是"利用有限数据,最大化发挥数据的评估价值"。最常用的是「K折交叉验证」(K-Fold Cross Validation),其核心步骤如下(以K=5为例):
-
将全部数据集(排除最终测试集)随机打乱,均匀分成K个大小相等的子集(折);
-
第一次训练:用第1-4折作为训练集,训练逻辑回归模型;用第5折作为验证集,评估模型性能(如准确率、召回率、AUC值);
-
第二次训练:用第1-3、5折作为训练集,第4折作为验证集,再次训练并评估;
-
重复上述过程,共进行K次训练和评估(每次用不同的1折作为验证集,其余K-1折作为训练集);
-
计算K次评估结果的平均值(如平均AUC、平均准确率),作为模型的最终泛化能力评估指标。
补充:除了K折交叉验证,实战中还会用到「留一交叉验证」(LOOCV,K=m,m为样本数,适合小样本)、「分层K折交叉验证」(Stratified K-Fold,保持每折中正负类比例与原数据一致,适合不平衡数据)------ 其中分层K折,是逻辑回归处理不平衡数据时的首选交叉验证方式。
2. 逻辑回归中交叉验证的核心作用
逻辑回归中,交叉验证不仅能评估模型泛化能力,还能辅助完成「参数选择」(如正则化参数λ的选择),避免过拟合:
-
避免过拟合误判:如果模型在训练集上准确率很高,但K次交叉验证的平均准确率很低,说明模型存在过拟合,需要调整参数(如增加正则化强度);
-
优化模型参数:通过交叉验证,我们可以对比不同参数(如正则化类型L1/L2、参数λ的不同取值)下的平均评估指标,选择最优参数组合;
-
提升评估可靠性:多次划分、多次评估的平均值,能有效抵消单次测试集划分的随机性,更真实反映模型在新数据上的表现。
3. 实战实例(关于银行信用卡信誉实例):
python
import pandas as pd
import numpy as np
# 绘制可视化混淆矩阵
def cm_plot(y, yp):
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
cm = confusion_matrix(y, yp)
plt.matshow(cm, cmap=plt.cm.Blues)
plt.colorbar()
for x in range(len(cm)):
for y in range(len(cm)):
plt.annotate(cm[x, y], xy=[y, x], horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label')
plt.xlabel('Predicted label')
return plt
'''数据处理'''
data = pd.read_csv('creditcard.csv')
'''Z标准化'''
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
a = data[['Amount']] # 返回表格数据
data['Amount'] = scaler.fit_transform(data[['Amount']])
data = data.drop(['Time'], axis=1) #删除无用列
'''对数据进行切分'''
from sklearn.model_selection import train_test_split
X = data.drop('Class', axis=1) # 删除cLass列,其余数据作为特征集
y = data.Class
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
from sklearn.linear_model import LogisticRegression
#交叉验证的函数
from sklearn.model_selection import cross_val_score
# 交叉验证
# 选择较优惩罚因子
scores = []
c_param_range = [0.01, 0.1, 1, 10, 100] # 参数
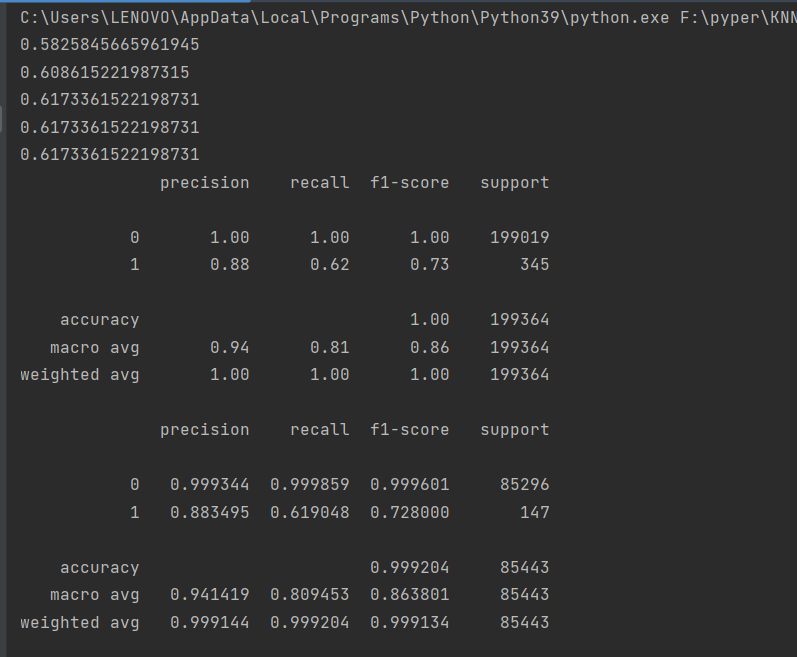
for i in c_param_range: # 第1次循环的时候c=0.01,5个逻辑回归模型
lr = LogisticRegression(C=i, penalty='l2', solver='lbfgs', max_iter=1000)
score = cross_val_score(lr, x_train, y_train, cv=8, scoring='recall')
score_mean = sum(score)/len(score)# 交叉验证后的值召回率
scores.append(score_mean)# 保存所有召回率
print(score_mean) #讲不同的c参数分别传入模型,分别看看那个模型效果更好,就选哪个
best_c = c_param_range[np.argmax(scores)]# 寻找到scores中最大值的对应的c参数
'''建立最优模型'''
lr = LogisticRegression(C=best_c, penalty='l2', max_iter=1000)
lr.fit(x_train, y_train) #fit训练集进行,深度学习
# 绘制混淆矩阵
from sklearn import metrics # 函数是专门用来做测试的
train_predicted = lr.predict(x_train) # 测试进行
print(metrics.classification_report(y_train, train_predicted)) # 自测
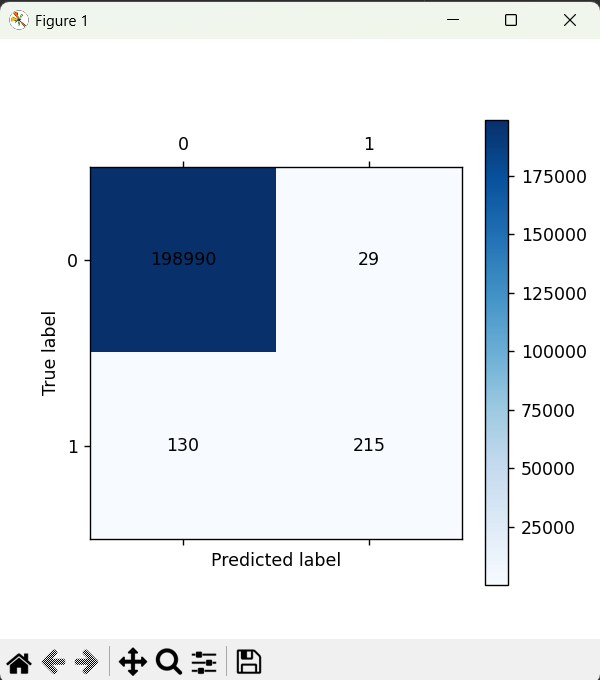
cm_plot(y_train, train_predicted)
'''使用测试集数据进行测试'''
test_predicted = lr.predict(x_test)
print(metrics.classification_report(y_test, test_predicted, digits=6))
cm_plot(y_test, test_predicted).show()混淆矩阵图
三、最后总结
逻辑回归看似简单,但实战中的"泛化能力"和"数据不平衡",是决定模型能否落地的关键。交叉验证让我们能正确评估模型的真实性能,避免"纸上谈兵"。怎样解决数据不平衡的问题呢?下一篇文章会仔细介绍
本文的知识点的都是围绕实战展开,没有过多复杂的公式推导,重点是让你理解"为什么要用""怎么用"。接下来,你可以把自己的例子代入这个流程,亲自实操一遍------毕竟,机器学习的核心,从来都是"理论+实操",只有动手练,才能真正掌握这些技巧。