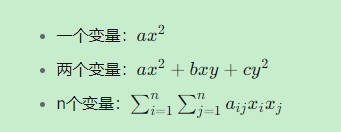二次型：从线性代数到测量平差的桥梁

一、二次型的核心概念

1.1 什么是二次型？

二次型是关于多个变量的二次齐次多项式，没有一次项和常数项。

基本形式：

特点：每一项都是二次的（变量的总次数为2）。

1.2 为什么需要矩阵表示？

1.3 简单示例

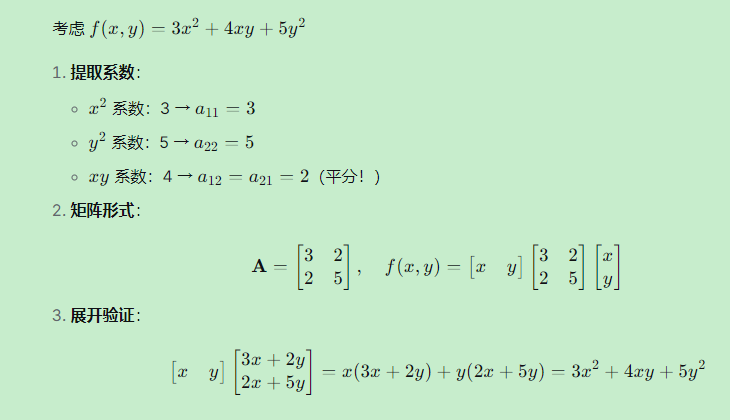
二、二次型的几何意义

二次型是线性代数中一个核心概念，但其本质是几何的 。简单来说，二次型的几何意义就是描述了一个n维空间中的"二次曲面"（或曲线）的形状和取向。

我们可以从低维到高维，层层深入地理解：

1. 核心思想：从函数到图形

一个二次型本质上是一个二次齐次多项式。例如，在二维和三维空间中：

二维 (x, y) ： Q(x, y) = ax² + 2bxy + cy²。令 Q(x, y) = 常数，就得到一条平面二次曲线（椭圆、双曲线或抛物线）。
三维 (x, y, z) ： Q(x, y, z) = ax² + by² + cz² + 2dxy + 2exz + 2fyz。令 Q(x, y, z) = 常数，就得到一个空间二次曲面（椭球面、单/双叶双曲面、抛物面等）。

这个"常数"（通常是1）就像一个等高线 或等值面。研究二次型，就是研究这些等高线/等值面的几何形状。

2. 矩阵表示：抓住形状的关键

任何二次型都可以写成矩阵形式：
Q(𝐱) = 𝐱ᵀA𝐱

其中 𝐱 是列向量，A 是一个实对称矩阵。

这个对称矩阵 A 是理解几何意义的关键，因为它包含了图形的所有内在信息：

矩阵A的特征值 → 决定了图形沿主轴方向的伸缩程度（是拉长、压扁还是反向）。
矩阵A的特征向量 → 决定了图形的主轴方向。
矩阵A的正定性 → 决定了图形的整体类型。

3. 几何意义的详细分解

a) 主轴定理（谱定理）------ 找到"正视角度"

这是最深刻的几何解释。任何二次型 𝐱ᵀA𝐱 都可以通过一个旋转（或更一般地，正交变换） 𝐱 = P𝐲 化为标准形（仅有平方项，没有交叉项）：
Q = λ₁y₁² + λ₂y₂² + ... + λ_ny_n²

其中 P 的列向量就是 A 的特征向量（主轴方向），λ_i 就是对应的特征值。

几何意义 ：无论原来的二次曲面在坐标系中多么"歪斜"（有交叉项 xy 等），总存在一个新的直角坐标系（由主轴构成），从这个角度看过去，这个曲面就是正着放的，其方程只剩下平方项。这就好比一个倾斜的椭圆，旋转到与坐标轴对齐后，方程就变得简洁。

b) 特征值的符号------决定形状的类型（分类）

在标准形 λ₁y₁² + λ₂y₂² + ... = 常数 中，特征值 λ_i 的符号至关重要。以二维为例 (λ₁y₁² + λ₂y₂² = 1)：

特征值符号	二次型正定性	曲线 `=1` 的形状	三维曲面 `=1` 的类比
λ₁>0， λ₂>0	正定	椭圆	椭球面
λ₁<0， λ₂<0	负定	无图像（`-1=1` 时是椭圆）	无图像
λ₁>0， λ₂<0	不定	双曲线	单叶双曲面
λ₁>0， λ₂=0	半正定	两条平行直线	椭圆柱面

几何意义：

所有特征值为正：图形在所有主轴方向上都"开口向上"（像碗状），等高线是封闭的椭圆（椭球）。
特征值有正有负：图形在某些方向上"向上"，某些方向上"向下"（像马鞍面），等高线是不封闭的双曲线。
特征值有零：图形沿该主轴方向是"平坦延伸"的（像柱面或抛物面）。

c) 矩阵的正定性------能量与极值

二次型常常代表一种"能量"或"代价"。

正定二次型 (𝐱ᵀA𝐱 > 0， ∀𝐱≠0)：其图形像一个向上开口的碗 。在原点取唯一的极小值。这在优化问题中至关重要，意味着目标函数有唯一的最小值点。
半正定 ：像一个槽或平坦的通道，有最小值线或面。
不定：像一个马鞍面 ，原点是一个鞍点，既非极大也非极小。

4. 实际应用中的几何意义

优化与机器学习：在损失函数中，二次型近似描述函数在极值点附近的曲率。正定的Hessian矩阵意味着局部最小值。
物理与工程：
- 在刚体力学中，转动惯量张量就是一个二次型，其对应的椭球叫惯性椭球，描述了刚体在不同轴向上旋转惯性的分布。
- 在弹性力学中，应变能函数常用二次型表示。
多元统计分析：
- 多元正态分布的指数部分 (𝐱-𝛍)ᵀΣ⁻¹(𝐱-𝛍) 就是一个二次型，其等值面是椭球，描述了数据的分布范围和相关结构。协方差矩阵的逆 Σ⁻¹ 决定了这个椭球的形状和方向。
微分几何：曲面的第二基本形式就是一个二次型，用来描述曲面的局部弯曲程度。

总结

二次型的几何意义，可以概括为：它是描述n维空间中二次曲面"形状DNA"的代数工具。

矩阵A 存储了这份DNA信息。
特征分解（主轴定理） 是解读这份DNA的密钥，它将曲面旋转到"标准姿态"。
特征值的符号和大小 直接告诉我们这个曲面是椭球、双曲面、柱面还是抛物面，以及它各个方向的陡峭程度。
正定性 则从整体上判断了这个曲面是"碗状"、"马鞍状"还是"平坦状"，从而决定了其在优化问题中的极值性质。

理解了这个几何图像，很多关于二次型的代数性质（如合同变换、惯性定理等）就会变得非常直观。

2.1 等值面的形状

二次型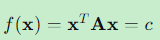（常数）定义了空间中的等值面。

二维情况（两个变量）：

正定：椭圆（或圆）
不定：双曲线
半正定：抛物线或直线

三维情况：

正定：椭球面
不定：双曲面或马鞍面

2.2 在测量中的直接对应

误差椭圆就是二次型等值面的直接体现！

三、二次型的标准形与合同变换

3.1 为什么需要标准形？

原始二次型包含交叉项，几何形状可能是倾斜的。通过坐标变换，可以消除交叉项，使几何形状"摆正"。

目标：找到新坐标系，使二次型变为：

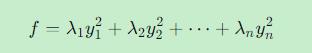
只有平方项，没有交叉项。

3.2 两种主要方法

方法一：配方法（代数方法）

逐步配方消除交叉项。

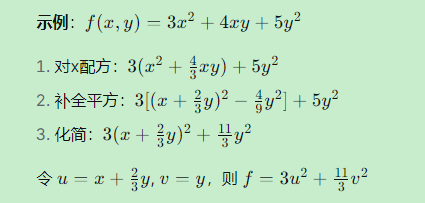
方法二：正交变换法（特征值法）

这是更系统的方法，基于矩阵的特征值分解。

步骤：

几何意义：特征向量给出了等值面的主轴方向，特征值的平方根给出了主轴长度。

3.3 在测量中的意义

误差椭圆的主轴方向 正是协方差矩阵的特征向量方向，主轴长度与特征值的平方根成正比。

复制代码

# 计算误差椭圆的主轴
import numpy as np

# 假设协方差矩阵
D = np.array([[0.25, 0.12],
              [0.12, 0.16]])

# 特征分解
eigenvalues, eigenvectors = np.linalg.eig(D)

print("协方差矩阵D:")
print(D)
print("\n特征值（主轴长度的平方）:", eigenvalues)
print("特征向量（主轴方向）:")
print(eigenvectors)

# 计算主轴长度（假设k=1，1σ椭圆）
axis_lengths = np.sqrt(eigenvalues)
print("\n误差椭圆主轴长度:", axis_lengths)

# 主轴方向角（从x轴逆时针）
theta = np.arctan2(eigenvectors[1, 0], eigenvectors[0, 0])
print("长轴方向角（度）:", np.degrees(theta))

四、正定二次型与正定矩阵

4.1 正定的定义

几何意义 ：等值面是封闭的椭球面 ，在原点处有严格最小值。

4.2 判断正定的方法

方法1：特征值判断

方法2：主子式判断（Sylvester准则）

方法3：平方和分解

4.3 在测量平差中的重要性

4.4 半正定矩阵

特点：

所有特征值 ≥ 0
等值面可能是椭球面、椭圆柱面或更退化的形状
在平差中，当参数存在线性相关时，法方程矩阵可能半正定（奇异）

五、二次型的导数与极值

5.1 导数公式

对于对称矩阵 A：

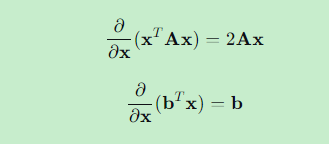
5.2 最小二乘问题的推导

5.3 极值性质

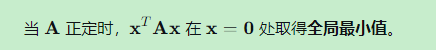
在平差中，这意味着：在正确的模型下，最小二乘解确实使目标函数最小。

六、在测量平差中的核心应用

6.1 最小二乘准则的本质

6.2 精度评定中的二次型

6.3 假设检验的统计量

6.4 误差椭圆的数学基础

七、数值计算与实际编程

7.1 二次型的数值计算

复制代码

import numpy as np

# 方法1：直接计算
def quadratic_form_direct(x, A):
    """直接计算二次型 x^T A x"""
    return x.T @ A @ x

# 方法2：利用对称性（更高效）
def quadratic_form_efficient(x, A):
    """利用对称性的高效计算"""
    # A是对称的，可以优化
    return np.sum(A * np.outer(x, x))

# 方法3：Cholesky分解（最稳定，A正定时）
def quadratic_form_cholesky(x, A):
    """通过Cholesky分解计算"""
    L = np.linalg.cholesky(A)  # A = L L^T
    y = L.T @ x
    return np.sum(y**2)

# 示例
A = np.array([[4, 1], [1, 3]])  # 对称正定矩阵
x = np.array([2, 3])

print("直接计算:", quadratic_form_direct(x, A))
print("高效计算:", quadratic_form_efficient(x, A))
print("Cholesky方法:", quadratic_form_cholesky(x, A))

7.2 平差中的实际计算

复制代码

class LeastSquaresAdjustment:
    """最小二乘平差类"""
    
    def __init__(self, A, P, l):
        """
        A: 设计矩阵
        P: 权矩阵
        l: 常数项向量
        """
        self.A = A
        self.P = P
        self.l = l
        self.n, self.t = A.shape
    
    def solve(self):
        """解法方程"""
        # 法方程系数矩阵
        N = self.A.T @ self.P @ self.A
        
        # 法方程常数项
        U = self.A.T @ self.P @ self.l
        
        # 求解参数
        x_hat = np.linalg.solve(N, U)
        
        # 计算残差
        V = self.A @ x_hat - self.l
        
        # 单位权方差
        VTPV = V.T @ self.P @ V  # 二次型！
        sigma0_sq = VTPV / (self.n - self.t)
        
        # 参数协因数阵
        Q_xx = np.linalg.inv(N)
        
        return {
            'parameters': x_hat,
            'residuals': V,
            'sigma0_sq': sigma0_sq,
            'Q_xx': Q_xx,
            'VTPV': VTPV  # 二次型值
        }
    
    def error_ellipse(self, index1=0, index2=1, confidence=0.95):
        """计算两个参数的误差椭圆"""
        Q_sub = self.result['Q_xx'][[index1, index2], :][:, [index1, index2]]
        
        # 特征分解
        eigenvalues, eigenvectors = np.linalg.eig(Q_sub)
        
        # 卡方值 (2个自由度)
        from scipy import stats
        k_sq = stats.chi2.ppf(confidence, 2)
        k = np.sqrt(k_sq)
        
        # 椭圆参数
        axis_lengths = k * np.sqrt(eigenvalues * self.result['sigma0_sq'])
        orientation = np.arctan2(eigenvectors[1, 0], eigenvectors[0, 0])
        
        return {
            'semi_major': np.max(axis_lengths),
            'semi_minor': np.min(axis_lengths),
            'orientation': np.degrees(orientation),
            'axis_lengths': axis_lengths,
            'eigenvectors': eigenvectors
        }

# 使用示例
A = np.array([[1, 0], [0, 1], [1, 1]])
P = np.diag([1, 1, 0.5])
l = np.array([2.1, 3.2, 5.0])

adjustment = LeastSquaresAdjustment(A, P, l)
result = adjustment.solve()
print("参数估计:", result['parameters'])
print("单位权方差:", result['sigma0_sq'])
print("V^T P V =", result['VTPV'])

ellipse = adjustment.error_ellipse()
print("\n误差椭圆参数:")
print(f"长半轴: {ellipse['semi_major']:.4f}")
print(f"短半轴: {ellipse['semi_minor']:.4f}")
print(f"方位角: {ellipse['orientation']:.2f}°")