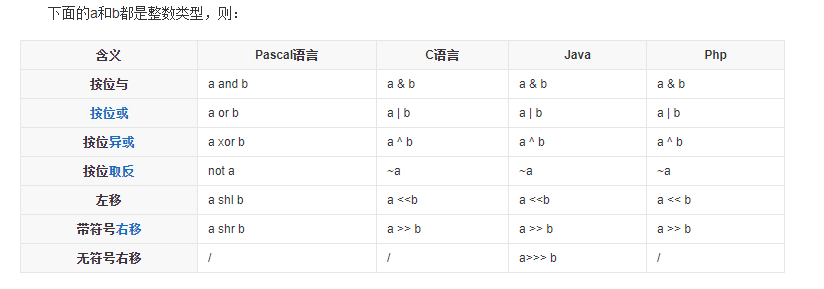
位运算和进制

位运算
与运算符 & and

and运算通常用于二进制的取位操作，例如一个数 and 1的结果就是取二进制的最末位。这可以用来判断一个整数的奇偶，二进制的最末位为0表示该数为偶数，最末位为1表示该数为奇数。

相同位的两个数字都为1，则为1；若有一个不为1，则为0。

或运算 | or

or运算通常用于二进制特定位上的无条件赋值，例如一个数or 1的结果就是把二进制最末位强行变成1。如果需要把二进制最末位变成0，对这个数or 1之后再减一就可以了，其实际意义就是把这个数强行变成最接近的偶数。

一个数或上0，还是该数，也就是说，一个数字或上0并不会改变此数字的大小。

相同位只要一个为1即为1。

异或运算 ^ xor （无进位加法）

异或的符号是^。按位异或运算, 对等长二进制模式按位执行逻辑按位异或操作. 操作的结果是如果某位不同则该位为1, 否则该位为0.

xor运算的逆运算是它本身，也就是说两次异或同一个数最后结果不变，即(a xor b) xor b = a。xor运算可以用于简单的加密，比如你想对你MM说1314520，但怕别人知道，于是双方约定拿你的生日19880516作为密钥。1314520 xor 19880516 = 20665500，你就把20665500告诉MM。MM再次计算20665500 xor 19880516的值，得到1314520。

相同位不同则为1，相同则为0。

非运算 ~ not

not运算的定义是把内存中的0和1全部取反。使用not运算时要格外小心，你需要注意整数类型有没有符号。如果not的对象是无符号整数（不能表示负数），那么得到的值就是它与该类型上界的差，因为无符号类型的数是用00到$FFFF依次表示的。

反码补码和原码
原码

原码：是最简单的机器数表示法。用最高位表示符号位，'1'表示负号，'0'表示正号。其他位存放该数的二进制的绝对值。
反码

正数的反码还是等于原码负数的反码就是他的原码除符号位外，按位取反。
补码：正数的补码等于他的原码　　　负数的补码等于反码+1。　　（这只是一种算补码的方式，很多相关书籍对于补码就是这句话）

然后说负数的补码等于他的原码自低位向高位开始数的第一个 '1' 及其右边的 '0' 保持不变，左边的各位按位取反，符号位不变。

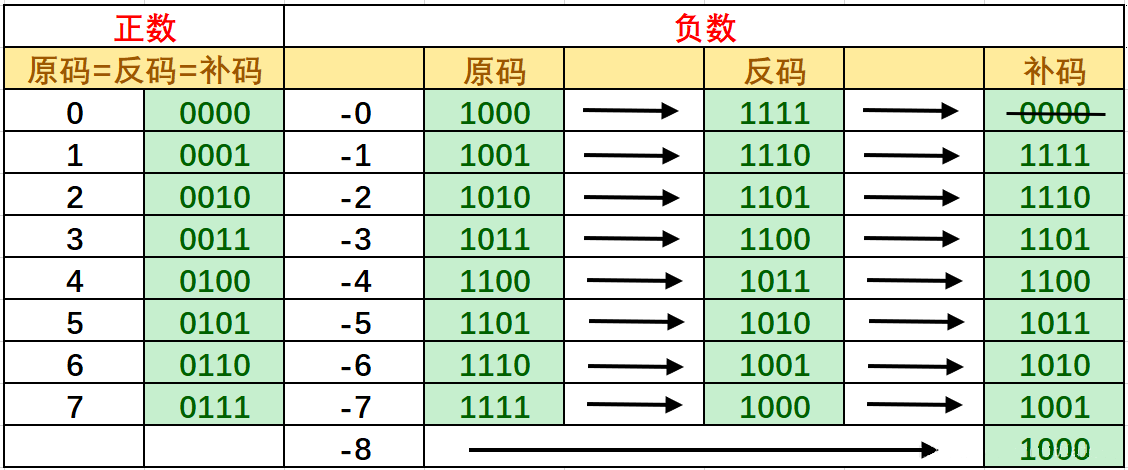
在补码中也不存在负零了，因为1000表示-8
模是指一个计量系统的计数范围。如时钟等。计算机也可以看成一个计量机器，它也有一个计量范围，即都存在一个"模"。例如：时钟的计量范围是0～11，模=12。表示n位的计算机计量范围是0～2 ^(n)-1，模=2 ^(n)。"模"实质上是计量器产生"溢出"的量，它的值在计量器上表示不出来，计量器上只能表示出模的余数。任何有模的计量器，均可化减法为加法运算。(把减去一个数等价转化为加上一个正数)

在这里，我们再次强调原码，反码，补码的引入是为了解决做减法的问题。在原码，反码表示法中，我们把减法化为加法的思维是减去一个数，等于加上一个数的相反数，结果发现引入了符号位，却因为符号位造成了各种意向不到的问题。

但是从上面的例子中，我们可以看到：对于数值有限制、有溢出的运算（模运算）来说，减去一个数，其实也相当于加上这个数的同余数。

也就是说，我们不引入负数的概念，就可以把减法当成加法来算。所以接下来我们聊4位二进制数的运算，也不必急于引入符号位。因为补码的思想，把减法当成加法时并不是必须要引入符号位的。
位运算的简单应用

功能	示例	位运算 (x为int例子的变量名)
去掉最后一位	110011 -> 11001	x >> 1
在最后加一个0	110011 -> 1100110	x << 1
在最后加一个1	110011 -> 1100111	(x << 1) + 1
把最后一位变成1	101100 -> 101101	x
把最后一位变成0	101101 -> 101100	(x
最后一位取反	101101 -> 101100	x ^ 1
把右数第k位变成1	101001 -> 101101, k = 3	x ^ (1 << (k - 1))
把右数第k位变成0	101101 -> 101001, k = 3	x & (~(1 << (k - 1)))
取末三位	101101 -> 101	x & 7
取右数第k位	1101101 -> 1, k = 4	x >> (k - 1) & 1
把末k位变成1	101001 -> 101111, k = 4	x
末k位取反	101001 -> 100110, k = 4	x ^ ((1 << k ) - 1)
把右边连续的1变成0	100101111 -> 100100000	x & (x + 1)
把右起第一个0变成1	100101111 -> 100111111	x
把右边连续的0变成1	11011000 -> 11011111	x
取右边连续的1	100101111 -> 1111	(x ^ (x + 1)) >> 1
去掉右起第一个1的左边	100101000 -> 1000	x & (-x)
从右边开始，把最后一个1改写成0	100101000 -> 100100000	x & (x - 1)

201.数字范围按位与

cpp 复制代码

class Solution {
public:
    int rangeBitwiseAnd(int left, int right) {
        int shift = 0;
        // 寻找公共前缀
        while(left < right)
        {
            left >>= 1;
            right >>= 1;
            ++shift;
        }
        return left << shift;
        
    }
};
// 或者
class Solution {
    public int rangeBitwiseAnd(int left, int right) {
        while (left < right) {
            // 抹去最右边的 1
            right = right & (right - 1);
        }
        return right;
    }
}

class Solution {
  public int rangeBitwiseAnd(int left, int right) {
    int res = 0;
    for (int i = 30; i >= 0; i -- ) {
      if ((left >> i & 1) != (right >> i & 1)) break;
      if ((left >> i & 1) == 1) res += 1 << i;
     }
    return res;
   }
}

注意左移右移 >> <<的使用