人工智能：深度学习：1.pytorch概述(1)

&星痕&2026-02-06 8:10

1.pytorch 简介

PyTorch 自 2017 年发布以来，以其简洁的语法和简单的上手难度，风靡全球。作为 Meta 人工智能研究院研发的开源深度学习框架，它采用 Python 原生编程风格，搭配动态计算图机制，让模型编写、调试与迭代都更加直观高效。兼顾科研灵活性与工业级性能，支持 GPU 加速、自动微分与模块化网络搭建，现已广泛应用于计算机视觉、自然语言处理、大模型训练等主流 AI 领域，成为全球开发者与研究人员的首选框架之一。

pytorch 安装请见。

2. 张量

1. 张量的定义

张量本质上是高维数组，支持 CPU 与 GPU 的跨硬件高效计算，同时内置自动微分功能，为深度学习模型的反向传播、梯度求解提供核心支撑。

在 PyTorch 中，张量的创建方式灵活多样，常用的创建方法主要分为以下三类：

一、根据已有数据（Python 原生类型、NumPy 类型）转化为张量

该方式是将已有的 Python 列表、元组，或 NumPy 数组直接封装为张量，完整保留原始数据的数值与维度结构，是从现有数据快速构建张量的最直观方式，适配各类已有数据集的张量转换场景。

python 复制代码 
import torch
import numpy as np
# torch.tensor(data)：Python列表转张量-一维示例
# 参数：data为必填原始数据，支持列表、元组等Python原生可迭代类型
print(torch.tensor([1, 2, 3]))
# torch.tensor(data)：Python列表转张量-二维示例
print(torch.tensor([[1, 2], [3, 4]]))
# torch.from_numpy(ndarray)：NumPy数组转张量
# 参数：ndarray为必填NumPy数组，转换后与原数组共享内存
print(torch.from_numpy(np.array([[5, 6], [7, 8]])))
# tensor([1, 2, 3])
# tensor([[1, 2],
#         [3, 4]])
# tensor([[5, 6],
#         [7, 8]], dtype=torch.int32)

NumPy 数组转张量基于零复制技术实现，转换时不拷贝数据，PyTorch 张量仅存储指向 NumPy 数组的内存指针，二者共享同一块内存区域，修改一方数据会同步影响另一方，需特别注意。

python 复制代码 
import torch
import numpy as np
# 1. NumPy数组转张量
arr = np.array([1, 2, 3, 4])
t = torch.from_numpy(arr)
print("原始数据：")
print("NumPy数组：", arr)  # [1 2 3 4]
print("PyTorch张量：", t)  # tensor([1, 2, 3, 4], dtype=torch.int32)

# 2. 修改NumPy数组，张量同步被修改
arr += 1
print("\n修改NumPy数组后：")
print("NumPy数组：", arr)  # [2 3 4 5]
print("PyTorch张量：", t)  # tensor([2, 3, 4, 5], dtype=torch.int32)

# 3. 张量原地修改（_表示原地操作），NumPy数组同步被修改
t.add_(2)
print("\n张量原地自增2后：")
print("NumPy数组：", arr)  # [4 5 6 7]
print("PyTorch张量：", t)  # tensor([4, 5, 6, 7], dtype=torch.int32)
# 原始数据：
# NumPy数组： [1 2 3 4]
# PyTorch张量： tensor([1, 2, 3, 4], dtype=torch.int32)
# 
# 修改NumPy数组后：
# NumPy数组： [2 3 4 5]
# PyTorch张量： tensor([2, 3, 4, 5], dtype=torch.int32)
# 
# 张量原地自增2后：
# NumPy数组： [4 5 6 7]
# PyTorch张量： tensor([4, 5, 6, 7], dtype=torch.int32)

若需将张量转换回 NumPy 数组，直接调用张量的 numpy () 方法即可，同样基于零复制技术，与原张量共享内存，修改同步生效：

python 复制代码 
import torch
import numpy as np
# 张量转NumPy数组
t = torch.tensor([1, 2, 3, 4])
arr = t.numpy()
print("张量类型：", type(t))  # <class 'torch.Tensor'>
print("转换后NumPy数组类型：", type(arr))  # <class 'numpy.ndarray'>
print("NumPy数组：", arr)  # [1 2 3 4]
# 张量类型： <class 'torch.Tensor'>
# 转换后NumPy数组类型： <class 'numpy.ndarray'>
# NumPy数组： [1 2 3 4]
总结：三类核心转换方法汇总
  1. Python 列表 / 元组转张量：torch.tensor(data)（一维 / 二维均适用，直接封装原始数据）
  2. NumPy 数组转张量：torch.from_numpy(ndarray)（零复制，与原数组共享内存）
  3. 张量转回 NumPy 数组：张量.numpy()（零复制，与原张量共享内存）

二、根据形状生成张量

通过指定维度尺寸直接创建张量，无需提前准备数据，分为类构造初始化 和函数构造初始化两种，二者用法与底层逻辑存在明显区别：

  • torch.Tensor(shape)：首字母大写为张量类的构造器，传入形状参数即可创建张量，默认值为内存随机浮点数；
  • torch.tensor(data)：小写为张量构造函数，必须传入具体数据，会根据输入数据生成对应张量，是更常用的安全创建方式。
python 复制代码 
import torch
# torch.Tensor（首字母大写：张量类初始化，仅指定形状）
print(torch.Tensor(2, 3))
# torch.tensor（小写：张量构造函数，需传入具体数据值）
print(torch.tensor([[1, 2], [3, 4]]))
# tensor([[0.0000e+00, 0.0000e+00, 1.4013e-45],
#         [0.0000e+00, 0.0000e+00, 0.0000e+00]])
# tensor([[1, 2],
#         [3, 4]])

三、生成固定值张量

该类方法用于创建数值全为 0、全为 1 等固定值的张量，支持直接指定形状创建 ，或参照已有张量形状创建两种形式，常用于初始化模型参数、构建掩码矩阵等场景。

python 复制代码 
import torch
# 定义参考张量
a = torch.tensor([[1, 2], [3, 4]])
# torch.zeros：直接指定形状，创建全0张量
print(torch.zeros(3, 2))
# torch.zeros_like：参照已有张量的形状，创建同形状全0张量
print(torch.zeros_like(a))
# torch.ones：直接指定形状，创建全1张量
print(torch.ones(3, 2))
# torch.ones_like：参照已有张量的形状，创建同形状全1张量
print(torch.ones_like(a))
# tensor([[0., 0.],
#         [0., 0.],
#         [0., 0.]])
# tensor([[0, 0],
#         [0, 0]])
# tensor([[1., 1.],
#         [1., 1.],
#         [1., 1.]])
# tensor([[1, 1],
#         [1, 1]])

2. 张量的类型

在未显式声明数据类型的情况下，整数型数据创建的张量默认类型为 torch.int64，浮点型数据默认生成 torch.float32 类型。若需自定义张量数据类型，主要有两种常用方式：

一是创建张量时，通过 dtype 参数直接指定所需数据类型；

二是对已创建的张量，调用类型转换方法将其转化为目标数据类型。（一般使用 Python 对象中的 type 方法。）

注：PyTorch 中的张量数据类型和 C++ 中的数值类型定义基本一致，命名与取值规则可相互参考。深度学习中，浮点型张量默认优先使用 float32，仅当大模型训练 / 推理面临内存资源不足时，才会选用精度更低的 float16，甚至极致压缩的 float8 以节省内存。

python 复制代码 
import torch

# 示例1：未声明类型，整数列表创建张量，默认torch.int64类型
a = torch.tensor([1, 2, 3])
print(a.dtype)  # torch.int64

# 示例2：创建时通过dtype参数指定数据类型（指定为torch.float32）
b = torch.tensor([1, 2, 3], dtype=torch.float32)
print(b.dtype)  # torch.float32

# 示例3：对已创建张量统一使用type方法做类型转换（int64转float64、float32转int32）
c = a.type(torch.float64)
d = b.type(torch.int32)
print(c.dtype)  # torch.float64
print(d.dtype)  # torch.int32
# torch.int64
# torch.float32
# torch.float64
# torch.int32

3. 张量的基本操作

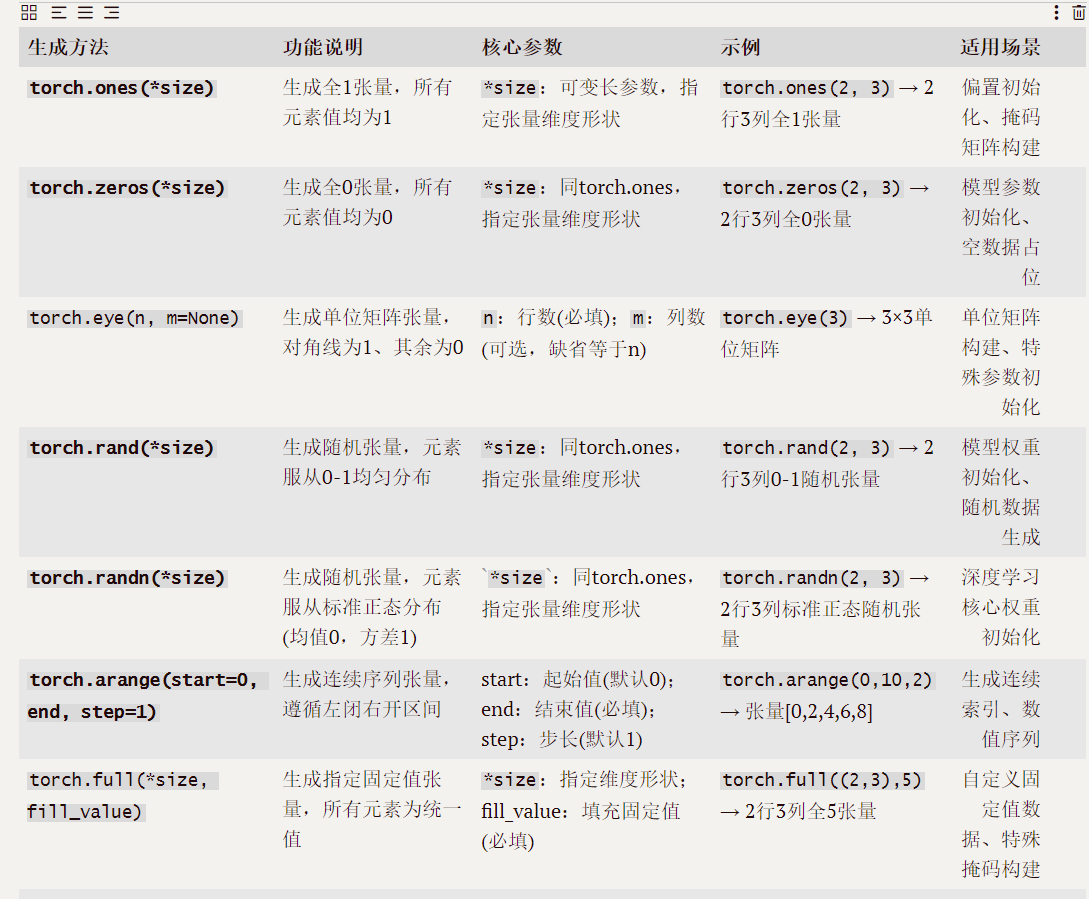
一，常见生成操作

二、获取基本属性

可通过专属方法 / 函数获取张量的形状、维度、元素总数等核心属性，也可对张量形状进行重塑，还能计算张量的元素和、平均值，操作如下：

.shape：返回张量各维度尺寸，深度学习中一般对应通道数、行、列；

len(张量)：获取张量的维度数，等价于张量 shape 属性的第一个数字；

.numel()：计算张量中元素的总数，结果为 shape 中所有维度数据的乘积；

.reshape()：重塑张量的形状，仅改变维度排列方式，不会更改张量中的元素内容；

.sum()：计算张量元素的总和，支持指定维度求和、保持维度等参数配置；

.mean()：计算张量元素的平均值，参数规则与.sum()一致。

.sum () 参数

python 复制代码 
import torch
# 定义示例张量（模拟通道数2、行3、列4，固定随机种子保证结果可复现）
torch.manual_seed(0)
t = torch.randn(2, 3, 4)
print("原始张量：\n", t)
print("张量形状：", t.shape)          # 获取形状
print("张量维度数：", len(t))        # len(张量)获取维度数
print("张量元素总数：", t.numel())   # numel()获取元素总数
# reshape重塑形状（2,3,4→2,12，元素内容不变）
t_reshape = t.reshape(2, 12)
print("重塑后形状：", t_reshape.shape)
print("重塑后元素总数：", t_reshape.numel()) # 元素总数不变

# 1. 无参数：对所有元素求和
sum_all = t.sum()
# 2. 指定dim=2：对最后一维（列维度）求和，压缩该维度
sum_dim2 = t.sum(dim=2)
# 3. 指定dim=1 + keepdim=True：对行维度求和，保持原维度数（求和维度变为1）
sum_dim1_keep = t.sum(dim=1, keepdim=True)
# 4. 计算所有元素平均值
mean_all = t.mean()

print("所有元素总和：", sum_all)
print("dim=2求和结果形状：", sum_dim2.shape, "结果：\n", sum_dim2)
print("dim=1+keepdim=True求和结果形状：", sum_dim1_keep.shape, "结果：\n", sum_dim1_keep)
print("所有元素平均值：", mean_all)

# 运行结果：
# 原始张量：
#  tensor([[[ 1.5410, -0.2934, -2.1788,  0.5684],
#          [-1.0845, -1.3986,  0.4033,  0.8380],
#          [-0.7193, -0.4033, -0.5966,  0.1820]],
# 
#         [[ 0.8033, -0.8063, -1.2220,  0.2082],
#          [-0.9080, -1.0480,  1.2277, -0.5631],
#          [ 0.3635, -0.6724,  0.1026, -0.1719]]])
# 张量形状： torch.Size([2, 3, 4])
# 张量维度数： 2
# 张量元素总数： 24
# 重塑后形状： torch.Size([2, 12])
# 重塑后元素总数： 24
# 所有元素总和： tensor(-6.2119)
# dim=2求和结果形状： torch.Size([2, 3]) 结果：
#  tensor([[-0.3628, -1.2418, -1.5372],
#         [-0.9968, -1.2914, -0.3782]])
# dim=1+keepdim=True求和结果形状： torch.Size([2, 1, 4]) 结果：
#  tensor([[[-0.2628, -2.0953, -2.3721,  1.5884]],
# 
#         [[ 0.2588, -2.5267,  0.1083, -0.5268]]])
# 所有元素平均值： tensor(-0.2588)

三、运算

1.按元素计算

PyTorch 中常见的加减乘除、幂运算，以及指数运算（exp）均为按元素计算 （逐元素运算），运算后张量的shape（形状）保持不变，仅张量内的元素数值发生改变。

python 复制代码 
import torch
# 定义基础张量（保证形状一致，支持按元素运算）
a = torch.tensor([1, 2, 3], dtype=torch.float32)
b = torch.tensor([4, 5, 6], dtype=torch.float32)
print("原始张量a：", a, "形状：", a.shape)
print("原始张量b：", b, "形状：", b.shape)

# 1. 加法运算
add_res = a + b
print("加法结果：", add_res, "形状：", add_res.shape)

# 2. 减法运算
sub_res = a - b
print("减法结果：", sub_res, "形状：", sub_res.shape)

# 3. 乘法运算（按元素）
mul_res = a * b
print("按元素乘法结果：", mul_res, "形状：", mul_res.shape)

# 4. 除法运算（按元素）
div_res = a / b
print("按元素除法结果：", div_res, "形状：", div_res.shape)

# 5. 幂运算（按元素，a的b次幂）
pow_res = a ** b
print("按元素幂运算结果：", pow_res, "形状：", pow_res.shape)

# 6. 指数运算exp（按元素，计算自然常数e的张量元素次幂，e^x）
exp_res = torch.exp(a)
print("指数运算exp结果：", exp_res, "形状：", exp_res.shape)

# 原始张量a： tensor([1., 2., 3.]) 形状： torch.Size([3])
# 原始张量b： tensor([4., 5., 6.]) 形状： torch.Size([3])
# 加法结果： tensor([5., 7., 9.]) 形状： torch.Size([3])
# 减法结果： tensor([-3., -3., -3.]) 形状： torch.Size([3])
# 按元素乘法结果： tensor([ 4., 10., 18.]) 形状： torch.Size([3])
# 按元素除法结果： tensor([0.2500, 0.4000, 0.5000]) 形状： torch.Size([3])
# 按元素幂运算结果： tensor([   1.,   32., 729.]) 形状： torch.Size([3])
# 指数运算exp结果： tensor([ 2.7183,  7.3891, 20.0855]) 形状： torch.Size([3])

注

  1. 按元素运算要求参与运算的张量形状完全一致（单目运算如exp无此要求），否则会触发形状不匹配错误；
  2. 也可通过 PyTorch 专属方法实现（效果与运算符一致）：torch.add(a,b)、torch.sub(a,b)、torch.mul(a,b)、torch.div(a,b)、torch.pow(a,b)，指数运算仅支持torch.exp(x)；
  3. 所有按元素运算后，张量的维度、尺寸均与原张量保持一致，仅元素数值更新；
  4. torch.exp(x)为自然指数运算，计算 ex（e 为自然常数，约等于 2.71828），是深度学习中激活函数、概率计算等场景的常用操作。

2、广播机制

在张量计算中，若参与运算的张量形状不同，可通过广播机制实现按元素运算：广播机制会自动复制元素对张量进行虚拟扩展，使所有张量最终拥有相同形状，再对扩展后的张量执行按元素操作，无需手动复制，节省内存且简化代码。

python 复制代码 
import torch
# 2行3列矩阵
a = torch.tensor([[1,2,3], 
                  [4,5,6]])  # shape: [2,3]
print("张量a：",a)
# 长度3的向量（广播时自动匹配列维度，虚拟扩为2行3列）
b = torch.tensor([10,20,30]) # shape: [3]
print("张量b：",b)
# 广播相加（不用手动把b变成2行3列！）
res1 = a + b
print("广播结果：")
print(res1)

# 手动复制对比（结果完全一样，只是多占内存）
b_copy = b.repeat(2,1)  # 手动复制成2行3列
print("b_copy:",b_copy)
res2 = a + b_copy
print("\n手动复制结果：")
print(res2)  # 和res1完全相同

# 运行结果：
# 张量a： tensor([[1, 2, 3],
#         [4, 5, 6]])
# 张量b： tensor([10, 20, 30])
# 广播结果：
# tensor([[11, 22, 33],
#         [14, 25, 36]])
# b_copy: tensor([[10, 20, 30],
#         [10, 20, 30]])
# 
# 手动复制结果：
# tensor([[11, 22, 33],
#         [14, 25, 36]])

可以看到。 b由一行三列复制成了两行三列，并与a进行按元素相加。

注：进行广播的条件:

  1. 假设有两个张量的形状为 (a,b) 和 (c,d) 等维度形式，当 a!=c 且 a,c!=1、b!=d 且 b,d!=1 时，广播可以 进行。也就是说：从两个张量的最后一个维度开始向前依次匹配，对应维度需满足二者相等，或其中一个维度为 1；维度数少的张量会在最左侧自动补 1 后再参与匹配。

四，元素分割

1.索引和切片

  • 逗号是 Torch 多维张量维度分割符，不同维度的索引 / 切片通过逗号分隔，按「从左到右」对应张量的各个维度；
  • 单个维度内的操作规则与 Python 数组完全一致：索引从 0 开始，切片start:end遵循左闭右开，:表示取该维度全部元素；
  • 适配任意维度张量：二维[行, 列]、三维[通道, 行, 列]，更高维度按维度顺序依次用逗号分割即可；
  • 索引 / 切片为张量视图操作，不额外占用内存，修改切片结果会同步影响原张量。
python 复制代码 
import torch
# 定义2行3列二维示例张量
t = torch.tensor([[1, 2, 3],
                  [4, 5, 6]])  # shape: [2, 3]
print("原始二维张量：\n", t)

# 1. 单元素索引：逗号分割行、列维度，索引从0开始
print("第1行第2列元素：", t[0, 1])  # 行索引0，列索引1
print("第2行第3列元素：", t[1, 2])  # 行索引1，列索引2

# 2. 维度切片：逗号分割不同维度，各维度独立使用切片规则（左闭右开）
print("所有行，前2列：\n", t[:, :2])  # 行取全部(:)，列取0-1列(:2)
print("第2行，所有列：\n", t[1, :])   # 行取索引1，列取全部(:)
print("第1-2行，第2-3列：\n", t[0:2, 1:3])  # 行0-1，列1-2

# 3. 三维张量示例：逗号分割通道、行、列维度
t3 = torch.tensor([[[1,2], [3,4]],
                   [[5,6], [7,8]]])  # shape: [2, 2, 2]
print("\n原始三维张量：\n", t3)
print("第2个通道，所有行，第1列：\n", t3[1, :, 0])  # 通道1，行全部，列0

# 运行结果：
# 原始二维张量：
#  tensor([[1, 2, 3],
#         [4, 5, 6]])
# 第1行第2列元素： tensor(2)
# 第2行第3列元素： tensor(6)
# 所有行，前2列：
#  tensor([[1, 2],
#         [4, 5]])
# 第2行，所有列：
#  tensor([4, 5, 6])
# 第1-2行，第2-3列：
#  tensor([[2, 3],
#         [5, 6]])
# 
# 原始三维张量：
#  tensor([[[1, 2],
#          [3, 4]],
#         [[5, 6],
#          [7, 8]]])
# 第2个通道，所有行，第1列：
#  tensor([5, 7])

2. split 分割

若需对张量进行不均等分割 ，可使用split方法，支持按指定长度在目标维度上完成任意长度的分割，是张量分割的常用方法。

split 核心参数
代码示例
python 复制代码 
import torch
# 定义示例张量：1维张量（长度8）、2维张量（4行3列）
t1 = torch.tensor([1,2,3,4,5,6,7,8])  # shape: [8]
t2 = torch.tensor([[1,2,3], [4,5,6], [7,8,9], [10,11,12]])  # shape: [4,3]
print("原始1维张量：", t1)
print("原始2维张量：\n", t2)

# 1. 1维张量不均等分割：按[3,2,3]分割（列表和=8），默认dim=0
split_t1 = t1.split([3,2,3])
print("\n1维张量不均等分割结果：", split_t1)

# 2. 2维张量行维度（dim=0）均等分割：按固定长度2分割
split_t2_0 = t2.split(2, dim=0)
print("\n2维张量dim=0均等分割结果：")
for i in split_t2_0:
    print(i)

# 3. 2维张量列维度（dim=1）不均等分割：按[1,2]分割（列表和=3）
split_t2_1 = t2.split([1,2], dim=1)
print("\n2维张量dim=1不均等分割结果：")
for i in split_t2_1:
    print(i)

# 运行结果：
# 原始1维张量： tensor([1, 2, 3, 4, 5, 6, 7, 8])
# 原始2维张量：
#  tensor([[ 1,  2,  3],
#         [ 4,  5,  6],
#         [ 7,  8,  9],
#         [10, 11, 12]])
# 
# 1维张量不均等分割结果： (tensor([1, 2, 3]), tensor([4, 5]), tensor([6, 7, 8]))
# 
# 2维张量dim=0均等分割结果：
# tensor([[1, 2, 3],
#        [4, 5, 6]])
# tensor([[ 7,  8,  9],
#        [10, 11, 12]])
# 
# 2维张量dim=1不均等分割结果：
# tensor([[ 1],
#        [ 4],
#        [ 7],
#        [10]])
# tensor([[ 2,  3],
#        [ 5,  6],
#        [ 8,  9],
#        [11, 12]])

注：

  1. split返回张量元组 ，每个元素为分割后的子张量，可通过索引提取（如split_t1[0]）；
  2. 不均等分割时，整数列表的元素和必须等于目标维度的总长度，否则会报错；
  3. 均等分割传入单个整数时，若目标维度长度无法被该整数整除，最后一个子张量长度会小于指定值（如长度 8 按 3 分割，结果为 [3,3,2]）；
  4. 分割后所有子张量的非分割维度形状与原张量一致，仅分割维度按规则拆分。

4. 张量的代数运算

1. 哈达玛积（Hadamard Product）

哈达玛积是张量按元素相乘的代数运算，数学符号为 ⊙，核心作用是对两个张量的对应位置元素进行乘法融合，能更好地融合两个张量的特征信息，是深度学习中特征融合的常用基础运算。

核心特性

  1. 哈达玛积不会改变张量的形状，运算后张量的shape与原张量完全一致；
  2. 运算要求参与计算的两个张量形状完全相同（或满足广播机制），否则无法执行按元素相乘；
  3. 哈达玛积为逐元素独立运算，每个位置的结果仅由两个张量对应位置的元素相乘得到，无维度间的交叉计算。
python 复制代码 
import torch
# 基础哈达玛积：形状相同的张量按元素相乘
x = torch.tensor([[1, 2], [3, 4]], dtype=torch.float32)
y = torch.tensor([[5, 6], [7, 8]], dtype=torch.float32)
print("特征张量x：\n", x)
print("特征张量y：\n", y)
# 哈达玛积实现（两种方式效果一致）
hadamard_prod = x * y  # 简洁写法，推荐使用
# hadamard_prod = torch.mul(x, y)  # 方法调用写法
print("哈达玛积(x⊙y)结果：\n", hadamard_prod)
print("基础运算结果形状：", hadamard_prod.shape)

# 广播机制下的哈达玛积：形状不同但满足广播条件
a = torch.tensor([[1, 2], [3, 4]], dtype=torch.float32)  # shape: [2,2]
b = torch.tensor([[2, 3]], dtype=torch.float32)          # shape: [1,2]
print("\n广播运算-张量a：\n", a)
print("广播运算-张量b：\n", b)
broadcast_prod = a * b
print("广播后哈达玛积结果：\n", broadcast_prod)
print("广播运算结果形状：", broadcast_prod.shape)

# 运行结果：
# 特征张量x：
#  tensor([[1., 2.],
#         [3., 4.]])
# 特征张量y：
#  tensor([[5., 6.],
#         [7., 8.]])
# 哈达玛积(x⊙y)结果：
#  tensor([[ 5., 12.],
#         [21., 32.]])
# 基础运算结果形状： torch.Size([2, 2])
# 
# 广播运算-张量a：
#  tensor([[1., 2.],
#         [3., 4.]])
# 广播运算-张量b：
#  tensor([[2., 3.]])
# 广播后哈达玛积结果：
#  tensor([[ 2.,  6.],
#         [ 6., 12.]])
# 广播运算结果形状： torch.Size([2, 2])

与矩阵乘法的区别

需注意哈达玛积（⊙）与普通矩阵乘法（×）的核心差异：

  • 哈达玛积：按元素相乘，形状不变，要求形状相同 / 满足广播，用x * y或torch.mul(x,y)实现；
  • 矩阵乘法：按矩阵运算规则计算（行 × 列），形状由原矩阵行列数决定，要求前一矩阵列数 = 后一矩阵行数，用torch.matmul(x,y)或x @ y实现。

2.矩阵向量积和矩阵乘矩阵

矩阵与向量相乘使用torch.mv，矩阵与矩阵相乘使用torch.mm，二者均为 PyTorch 针对二维张量线性运算的专属方法，规则严格匹配线性代数学理。

（1）矩阵向量积：torch.mv

复制代码 
torch.mv(mat, vec)
参数介绍
  • mat：输入二维矩阵张量，形状为[m,n]（m 行 n 列），要求为二维张量，不可为一维 / 三维及以上；
  • vec：输入向量张量，形状为[n]（一维张量）或[n,1]（二维列向量），需满足矩阵列数 = 向量维度。

（2）矩阵乘矩阵：torch.mm

复制代码 
torch.mm(mat1, mat2)
参数介绍
  • mat1：第一个输入二维矩阵张量，形状为[m,n]（m 行 n 列），要求为二维张量；
  • mat2：第二个输入二维矩阵张量，形状为[n,k]（n 行 k 列），要求为二维张量，需满足前矩阵列数 = 后矩阵行数。
python 复制代码 
import torch
# ===================== 矩阵向量积：torch.mv =====================
# 定义3行2列矩阵、2维一维向量（形状匹配）
mat = torch.tensor([[1,2], [3,4], [5,6]], dtype=torch.float32)  # shape: [3,2]
vec = torch.tensor([7,8], dtype=torch.float32)                  # shape: [2]
mv_res = torch.mv(mat, vec)
print("【矩阵向量积】结果：", mv_res, " 形状：", mv_res.shape)

# ===================== 矩阵乘矩阵：torch.mm =====================
# 定义3行2列矩阵mat1、2行4列矩阵mat2（形状匹配）
mat1 = torch.tensor([[1,2], [3,4], [5,6]], dtype=torch.float32) # shape: [3,2]
mat2 = torch.tensor([[1,2,3,4], [5,6,7,8]], dtype=torch.float32)# shape: [2,4]
mm_res = torch.mm(mat1, mat2)
print("【矩阵乘矩阵】结果：\n", mm_res, " 形状：", mm_res.shape)

# 运行结果：
# 【矩阵向量积】结果： tensor([23., 53., 83.])  形状： torch.Size([3])
# 【矩阵乘矩阵】结果：
#  tensor([[11., 14., 17., 20.],
#         [23., 30., 37., 44.],
#         [35., 46., 57., 68.]])  形状： torch.Size([3, 4])
注：
  1. torch.mv和torch.mm仅支持二维张量 （矩阵）参与运算，一维张量仅可作为torch.mv的 vec 参数，三维及以上张量需使用torch.matmul；
  2. 二者均要求形状严格匹配，不满足匹配规则会直接触发形状不匹配错误，无广播机制；
相关推荐
JQLvopkk2 小时前
C# 实践AI 编码：Visual Studio + VSCode 组合方案
人工智能·c#·visual studio
新缸中之脑2 小时前
基于PageIndex的文档问答
人工智能
普通网友2 小时前
解决rfid系统安全的逻辑方法
人工智能
七夜zippoe2 小时前
时间序列分析实战：从平稳性检验到Prophet与LSTM预测
人工智能·python·机器学习·arima·时间序列·prophet
OpenLoong 开源社区2 小时前
合作官宣 | 技术协同新标杆！openKylin 适配具身智能人形机器人计划正式启动
人工智能·机器人·开源
说私域2 小时前
开源AI智能名片链动2+1模式S2B2C商城小程序驱动下的电商裂变增长路径研究
人工智能·小程序·开源·流量运营·私域运营
说私域2 小时前
六度人脉视域下信息价值传递的创新路径——基于AI智能名片链动2+1模式小程序的实践研究
人工智能·小程序·流量运营·私域运营
新新学长搞科研2 小时前
【CCF主办 | 高认可度会议】第六届人工智能、大数据与算法国际学术会议(CAIBDA 2026)
大数据·开发语言·网络·人工智能·算法·r语言·中国计算机学会
多恩Stone2 小时前
【3D-AICG 系列-2】Trellis 2 的O-voxel (上) Shape: Flexible Dual Grid
人工智能·python·算法·3d·aigc
热门推荐
01GitHub 镜像站点02Vue-skills的中文文档03Claude Code Skills 实用使用手册04一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示05Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services06UV安装并设置国内源07让 Trae IDE 智能体 “读懂”文档 Excel+PDF+DOCX ：mcp-documents-reader 工具使用指南08Linux下V2Ray安装配置指南09OpenClaw Chrome扩展使用教程 - 浏览器中继控制10OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书