【洛谷】记忆化搜索 原理剖析与经典例题详解

文章目录

• 引入记忆化搜索
• Function
• 天下第一
• 滑雪

---

记忆化搜索也是⼀种剪枝策略。

通过⼀个"备忘录"，记录第⼀次搜索到的结果，当下⼀次搜索到这个状态时，直接在"备忘录"⾥⾯找 结果。

记忆化搜索，有时也叫动态规划。

引入记忆化搜索

我们先从一道题切入：斐波那契数

这道题我们在第一次学习递归时就见到过，实现方式很简单，要拿到n的斐波那契数就用一个dfs函数实现，只用把n传进去它就会自动把n对应的斐波那契数算出来。

//算出n的斐波那契数 
int dfs(int n)
{
    if(n == 0 || n == 1) return n;
    return dfs(n - 1) + dfs(n - 2);
}

class Solution {
public:
    int fib(int n) {
        return dfs(n);
    }
};

不管上面的原始代码效率是比较低的，整体时间复杂度的O(n^2)，因为递归过程中含有大量重复工作，比如下图计算f(3)，f(3)递归展开图和计算出的结果都一样，假如f(3)计算出的结果是x，如果我们能创建一个备忘录，把存进这个备忘录里，当我们下一此递归到f(3)时就不用继续往下递归了，直接return备忘录里的x就行了，这样时间复杂度就能优化为O(n)。

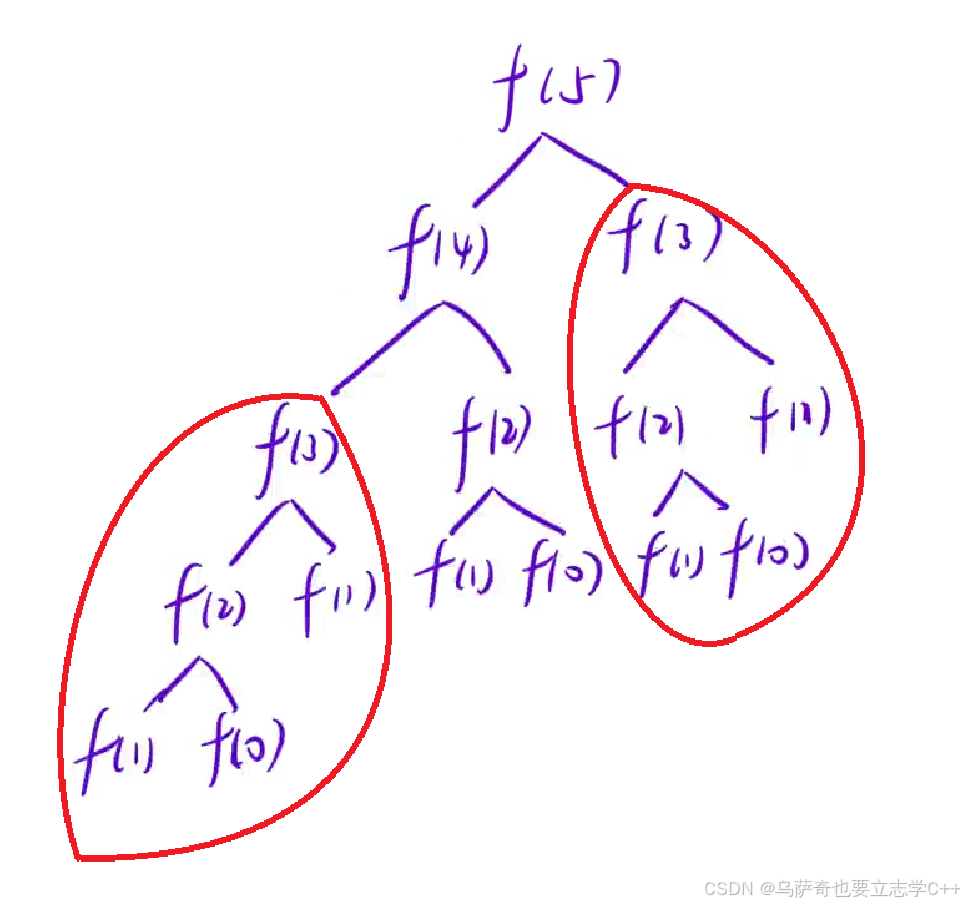
对于本题，我们可以用一个整型数组f充当备忘录。 实现记忆化搜索分三步走：

1、创建备忘录，并且备忘录的初始值是在递归过程中不会出现的值，因为在递归过程中需要判断f[i]是否被修改过，如果没被修改过那么f[i]还保持初始值。

2、递归返回之前需要把值存入备忘录。

3、递归刚开始先检查备忘录中是否有对应值，如果有就不再往下递归，直接用备忘录的值。
记忆化搜索只有当dfs类题目中出现重复相同问题是时才能使用。
下面是优化后的代码：

int f[35];

//算出n的斐波那契数 
int dfs(int n)
{
    if(f[n] != -1)
            return f[n];
    if(n == 0 || n == 1) return n;
    f[n] = dfs(n - 1) + dfs(n - 2);
    return f[n];
}

class Solution {
public:
    int fib(int n) {
        memset(f, -1, sizeof(f));
        return dfs(n);
    }
};

Function

题目描述

题目解析

本题本质就是一个加强版的斐波那契数，并且在搜索搜索过程中会出现重复的问题，比如下图左边两个分支一定都会走到w(18,19,20)，所以我们开一个三维数组来充当备忘录，虽然题目中a b c的值范围很大，但是只要abc中有一个大于20就会递归dfs(20, 20, 20)，所以三维数组开25就够了。

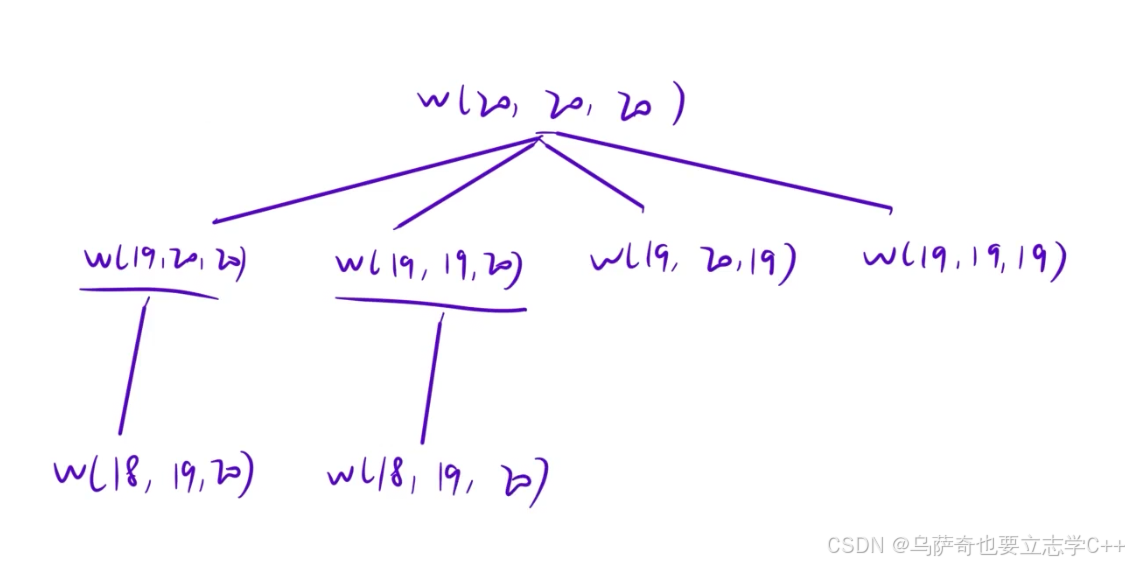
注意：本题虽有多组测试数据，但是每组数据开始不用对f数组做初始化。

代码

#include <iostream>
using namespace std;

typedef long long LL;

const int N = 25;

LL a, b, c;
LL f[N][N][N]; //备忘录

int dfs(LL a, LL b, LL c)
{
	if (a <= 0 || b <= 0 || c <= 0)
	{
		return 1;
	}
	if (a > 20 || b > 20 || c > 20)
	{
		return dfs(20, 20, 20);
	}

	if (f[a][b][c])
		return f[a][b][c];

	if (a < b && b < c)
	{
        f[a][b][c] = dfs(a, b, c - 1) + dfs(a, b - 1, c - 1) - dfs(a, b - 1, c);
		return f[a][b][c];
	}
	else 
	{
		f[a][b][c]  = dfs(a - 1, b, c) + dfs(a - 1, b - 1, c) + dfs(a - 1, b, c - 1) - dfs(a - 1, b - 1, c - 1);
		return f[a][b][c];
	}
}

int main()
{
	int i = 1;
	while (cin >> a >> b >> c)
	{
		if (a == -1 && b == -1 && c == -1)
			break;
		printf("w(%lld, %lld, %lld) = %lld\n", a, b, c, dfs(a, b, c));
	}
	return 0;
}

天下第一

题目描述

题目解析

没写出正确答案原因：

1、平局如何判断？如何处理递归死循环也就是递归过程中如何判断x,y值是否重复出现了？

2、如何实现递归，如何递归传参，需要传回合数吗？ 不需要，因为可以推出x y的递归更新公式，不用判断奇回合、偶回合。
解题思路：

1、本题有个关键点，模数都为p，所以依旧使用记忆化搜索，用一个二维数组充当备忘录，并且多组数据也不用初始化，但是需要注意本题的数据范围比较大，二维数组类型如果是整型空间会不够，因为本题只用输出获胜和平局，所以二维数组用字符类型即可。

2、递归进行模运算思路如下：

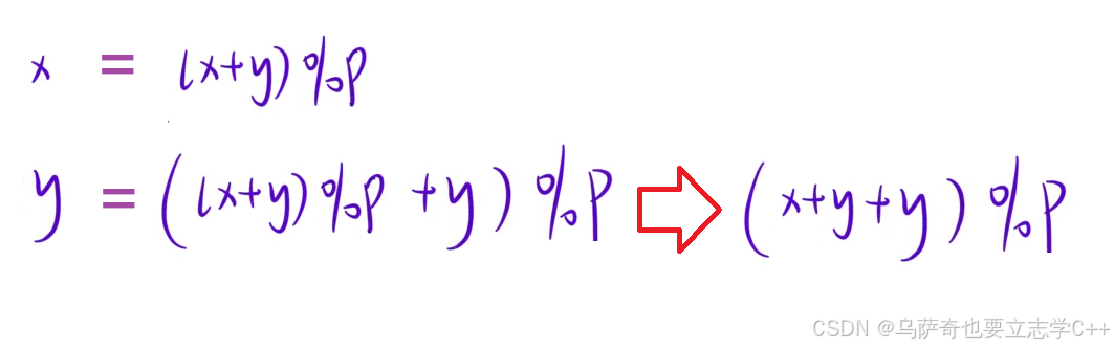
之前我们介绍过无论是加法还是乘法，连续的模运算都可以合并为一次模运算：

加法链：((a+b)%p+c)%p=(a+b+c)%p

乘法链：((a×b)%p×c)%p=(a×b×c)%p

3、本题某一方获胜很好判断，平局处理需要一点手法，我们的思路是递归到一种x

y状态就把对应的f[x][y]置为3，默认是平局，然后继续往下递归，当递归当底后有两种返回情况，一种是分出胜负了也就是x y其中一个变为0了，此时会将f[x][y]该位获胜方的数字，然后递归返回，并在回溯过程中： return f[x][y] = dfs((x + y) % p, (x + 2 * y) % p); 把每一个结点状态的f[x][y]都置为获胜方的数字，因为该递归分支的每一个结点包括最开始的x y都会走到同一个底结点，返回同一个结果。

还有一种情况是递归死循环了，也就是x y又递归到了一开始f[x][y]置为3的状态，此时会因为if (f[x][y]) 不为0（因为被置为3了·）而递归返回，也会将路径上的所有结点的f[x][y]置为3。

代码

#include <iostream>
using namespace std;

const int N = 1e4 + 10;

int T, p, x, y;
char f[N][N]; //备忘录

char dfs(int x, int y)
{
	if (f[x][y])
		return f[x][y];

	//标记该状态访问过，若后续回溯没有将'3'修改，
	// 说明递归死循环了，又重复递归到了该状态，
	// 在if (f[x][y])分支就返回了，返回值为'3'
	f[x][y] = '3'; 

	if (x == 0)
		return f[x][y] = '1';
	if (y == 0)
		return f[x][y] = '2';
	//继续往下递归
	return f[x][y] = dfs((x + y) % p, (x + 2 * y) % p);
}

int main()
{
	cin >> T >> p;
	while (T--)
	{
		cin >> x >> y;
		char ret = dfs(x, y);
		if (ret == '1')
		{
			cout << 1 << endl;
		}
		else if (ret == '2')
		{
			cout << 2 << endl;
		}
		else
		{
			cout << "error" << endl;
		}
	}
	return 0;
}

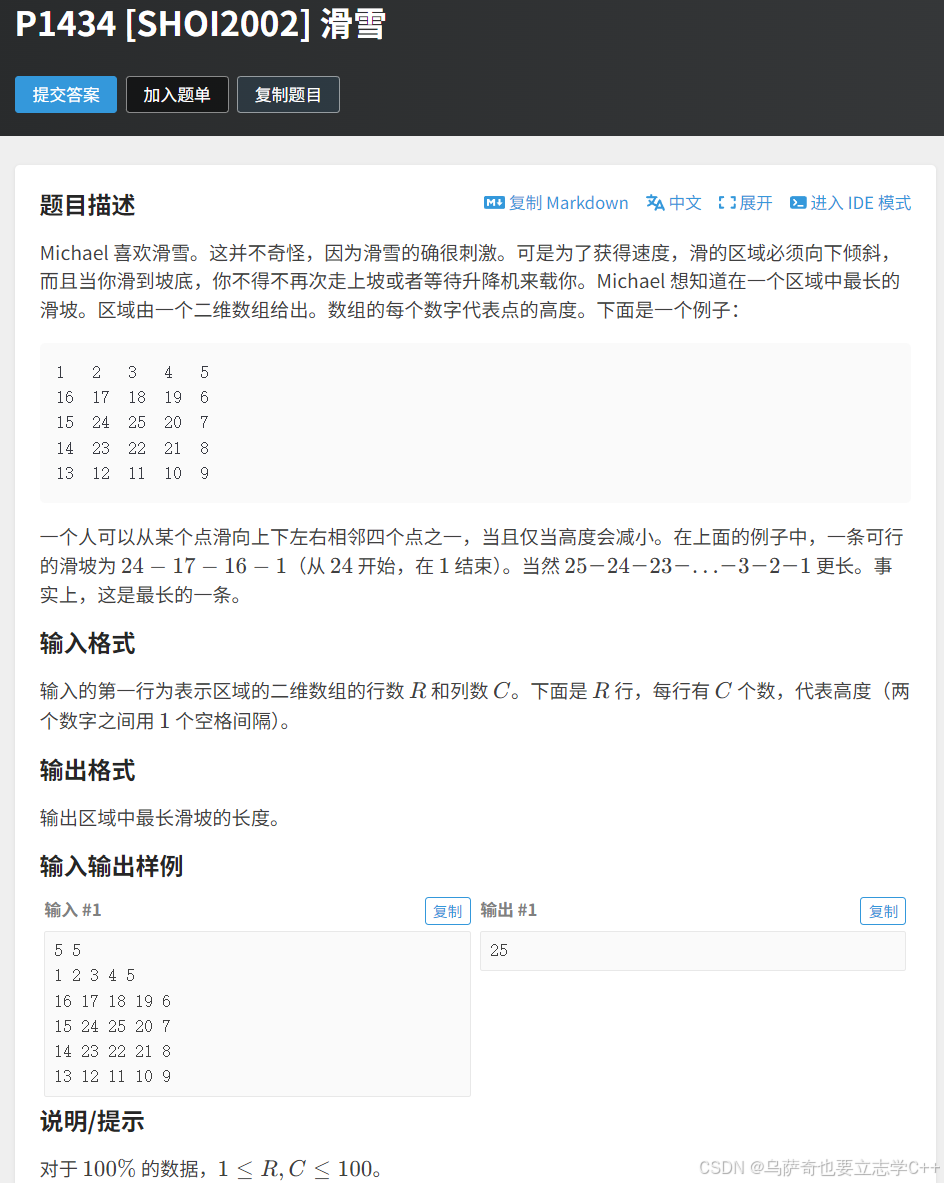
滑雪

题目描述

题目解析

本题思路是枚举递归每一个格子，找出每个格子的最长滑坡长度，本题也需要用记忆化搜索优化时间复杂度，因为在枚举递归所有格子时会递归上下左右四个格子，这时如果有的格子已经递归过了就可以直接在备忘录中找到结果返回。

除了记忆化搜索还需要可行性剪枝，第一是数组越界剪枝，第二是下一个递归的格子a[x][y]数字要小于当前的格子a[m][n]。

递归上下左右格子依旧用方向向量，方向向量 dx/dy 分别表示上下左右四个方向的坐标偏移，详细介绍在模拟专题的蛇形方阵。
注意，在计算len时要把len初始化为1，因为递归格子本身也算一个距离。

代码

#include <iostream>
using namespace std;

const int N = 110;

//方向向量
int dx[4] = { 0, 0, -1, 1 };
int dy[4] = { 1, -1, 0, 0 };

int r, c;
int a[N][N]; //原数据
int f[N][N]; //备忘录
int ret; //最长滑坡

int dfs(int m, int n)
{
	if (f[m][n])
	{
		return f[m][n];
	}
	int len = 1; //len初始化为1，因为本身也算一个距离
	//递归上下左右四个格子
	for (int i = 0; i < 4; i++)
	{
		int x = m + dx[i];
		int y = n + dy[i];
		//可行性剪枝
		if (x < 1 || x > r || y < 1 || y > c || a[x][y] >= a[m][n])
		{
			continue;
		}
		len = max(len, dfs(x, y) + 1); // +1因为需要加上本身
	}
	f[m][n] = len;
	return len;
}

int main()
{
	//初始化数据
	cin >> r >> c;
	for (int i = 1; i <= r; i++)
	{
		for (int j = 1; j <= c; j++)
		{
			cin >> a[i][j];
		}
	}
	//依次递归每一个格子
	for (int i = 1; i <= r; i++)
	{
		for (int j = 1; j <= c; j++)
		{
			ret = max(ret, dfs(i, j));
		}
	}
	cout << ret << endl;
	return 0;
}

以上就是小编分享的全部内容了，如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言，感谢您的大力支持。
一键三连好运连连哦~~