题目一:

算法原理:
题意很简单,解决策略就是模拟题目要求的步骤,而模拟的过程中使用堆这个数据结构则更为方便,因为是要选出最重的两块石头,所以要采用大根堆才方便拿最大的两块石头,因此将所有石头都放进大根堆、
然后连续拿出堆顶的两个元素a,b,进行碰撞,因为a先拿出来,所以a一定是大于等于b的,如果相等则什么也不放回堆,否则就说明a>b,将a-b放回堆中,如此循环,直到堆里的元素只剩下不到2个则停止
最后判断一下堆里的元素个数,如果剩下一个,则返回这一个,如果没有元素,则返回0
代码:
java
class Solution {
public int lastStoneWeight(int[] stones) {
//创建大根堆
PriorityQueue<Integer> q=new PriorityQueue<>((a,b)->b-a);
//将所有石头全部放进堆
for(int stone:stones){
q.offer(stone);
}
//模拟石头碰撞
while(q.size()>1){
int x=q.poll();
int y=q.poll();
if(x>y){
q.offer(x-y);
}
}
//如果撞完一个石头都不剩了
if(q.size()==0){
return 0;
}
//返回最后的一块石头
return q.poll();
}
}题目二:
算法原理:
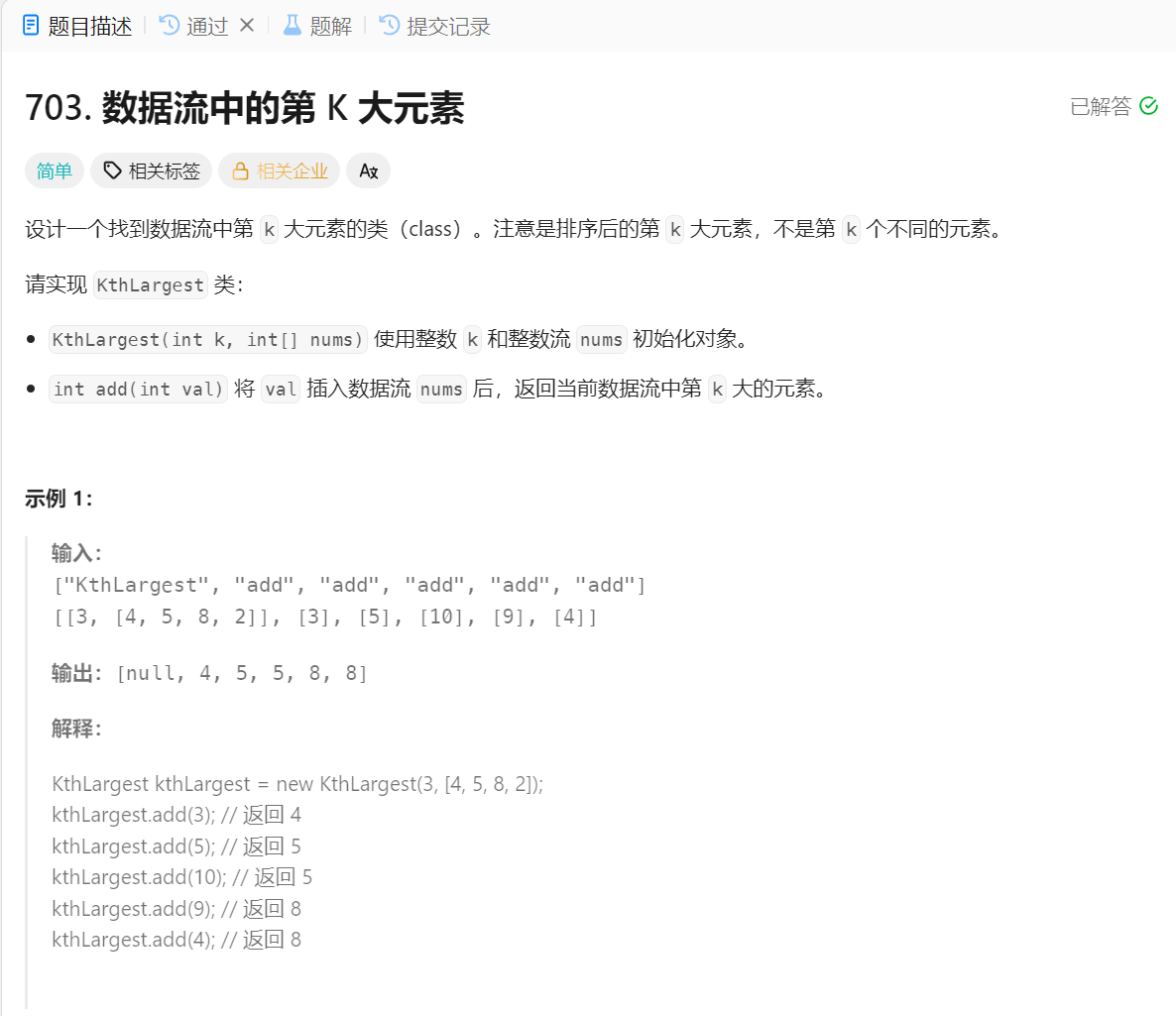
经典的TOPK问题,结论是找第K大就创建小根堆,找第K小就创建大根堆,反着来的
然后控制堆的大小为k,当堆为k的大小之后,每扔一个进去,就再出一个堆顶,这样就会保持堆顶的那个元素为第K大的元素
代码:
java
class KthLargest {
//找第K大就创建小根堆
PriorityQueue<Integer> q=new PriorityQueue<>();
int _k;
public KthLargest(int k, int[] nums) {
_k=k;
//全部扔进去
for(int x:nums){
q.offer(x);
//如果超过k的大小
if(q.size()>k){
q.poll();
}
}
}
public int add(int val) {
//扔进去
q.offer(val);
//如果超过k的大小
if(q.size()>_k){
q.poll();
}
//堆顶元素就是第K大
return q.peek();
}
}题目三:

算法原理:
原理不难,就是先用哈希表统计一下每个单词出现的次数,再创建一个小根堆,然后这个小根堆的比较规则如题目所示,然后用TOPK流程走一遍,最后剩下的就是符合要求的,然后题目要求返回的是最大的在前面,而堆顶元素是第K大的(也就是K个里面最小的)
但是代码会有一定难度
首先是数据类型,HashMap是一个集合类,而子元素的类型是Map.Entry,然后Map.Entry必须依赖Map才能创建,Pair也是一个键值对类型,可以直接创建
然后是比较器的创建,因为是取高频的,也就是次数多的,那么就创建小根堆,当次数一样时,按字典序升序排序(排在后面的会先出去),字典序升序是b在前,a在后,字典序降序是a在前,b在后,小根堆是a在前,b在后,大根堆是b在前,a在后
大小根堆用多了,这个记得比较熟,但是字典序很少用,很难记
记忆字典序的方法就是,字典序升序就是字典序大的排在堆顶,因为这样才会先出去,那么就是大根堆,所以就是b在前,a在后,反之就是a在前,b在后
最后堆顶的是出现频次第K大的,而题目要求返回顺序是从大到小,所以还要将列表翻转一遍,使用Collection.reverse()进行翻转
代码:
java
class Solution {
public List<String> topKFrequent(String[] words, int k) {
//统计单词频次
HashMap<String,Integer> map=new HashMap<>();
for(String s:words){
map.put(s,map.getOrDefault(s,0)+1);
}
//创建小根堆,类型为Pair------{"String":1}这种键值对数据类型
PriorityQueue<Pair<String,Integer>> q=new PriorityQueue<>(
(a,b)->
{
//按照字典序升序
if(a.getValue().equals(b.getValue())){
return b.getKey().compareTo(a.getKey());
}
//小根堆
return a.getValue().compareTo(b.getValue());
}
);
//TOPK流程走一遍
for(Map.Entry<String,Integer> e:map.entrySet()){
q.offer(new Pair<String,Integer>(e.getKey(),e.getValue()));
if(q.size()>k){
q.poll();
}
}
List<String> ret=new ArrayList<>();
while(!q.isEmpty()){
ret.add(q.poll().getKey());
}
//翻转一下
Collections.reverse(ret);
return ret;
}
}题目四:

算法原理:
第一反应是创建一个数组,然后将所有元素放进去,要找中位数的时候,再进行一次排序,最后返回数组长度一半的那个数即可,但是会超时,其中排序的时间复杂度为O(NlogN)
代码1(数组排序):
java
class MedianFinder {
ArrayList<Integer> list;
public MedianFinder() {
list=new ArrayList<>();
}
public void addNum(int num) {
list.add(num);
}
public double findMedian() {
//排序
list.sort(null);
//下标的中位数
int mid=list.size()/2;
//如果为偶数
if(list.size()%2==0){
return (list.get(mid-1)+list.get(mid))/2.0;
}else{//如果为奇数
return list.get(mid);
}
}
}优化:
使用插入排序算法,可将排序的复杂度降为O(N),但还是会超时
大小堆:
将数组(已排好序)分为两半,左边的数都全部扔进大根堆,右边的数都全部扔进小根堆,那么此时大小根堆的堆顶元素就是数组的中位数,如果数组长度是偶数,就将两个堆顶元素相加再除2,如果是奇数,那么我们默认左边比右边多1,因此左边的大根堆的元素就是中位数
而排序过程就由堆来完成,来一个就扔进堆里,时间复杂度为O(logN)
其中这个过程需要动态调整大小根堆的个数,使得大小根堆的元素个数要么相等,要么左边个数比右边个数多1
而这个调整的策略模拟一下,很快就出来了,就是大的往大放,小的往小放,具体逻辑如代码所示,拿1,2,3为例子走一遍代码就明白了
代码2(大小堆):
java
class MedianFinder {
//大小堆
PriorityQueue<Integer> left,right;
public MedianFinder() {
//左边是大根堆,右边是小根堆
left=new PriorityQueue<>((a,b)->b-a);
right=new PriorityQueue<>();
}
public void addNum(int num) {
//当个数为偶数时
if(left.size()==right.size()){
//为空或小于左边堆顶的值
if(left.isEmpty()||num<=left.peek()){
left.offer(num);
}else{//大于左边堆顶的值
right.offer(num);
//保持左边个数始终大于等于右边,且只大于1
left.offer(right.poll());
}
}else{//左边个数=右边个数+1
if(num<=left.peek()){//小于左边堆顶的值
left.offer(num);
//此时左边个数=右边个数+2,匀一个给右边,使得左右相等
right.offer(left.poll());
}else{//大于左边堆顶的值
right.offer(num);
}
}
}
public double findMedian() {
//如果为偶数
if(left.size()==right.size()){
//返回平均值
return (left.peek()+right.peek())/2.0;
}else{//为奇数
return left.peek();//返回中位数
}
}
}