排序
插入排序
直接插入排序
实现
直接插入排序是一种简单的插入排序法,其基本思想 是:把待排序的数据 按其值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
- 巧记:打扑克牌时整理牌的方法
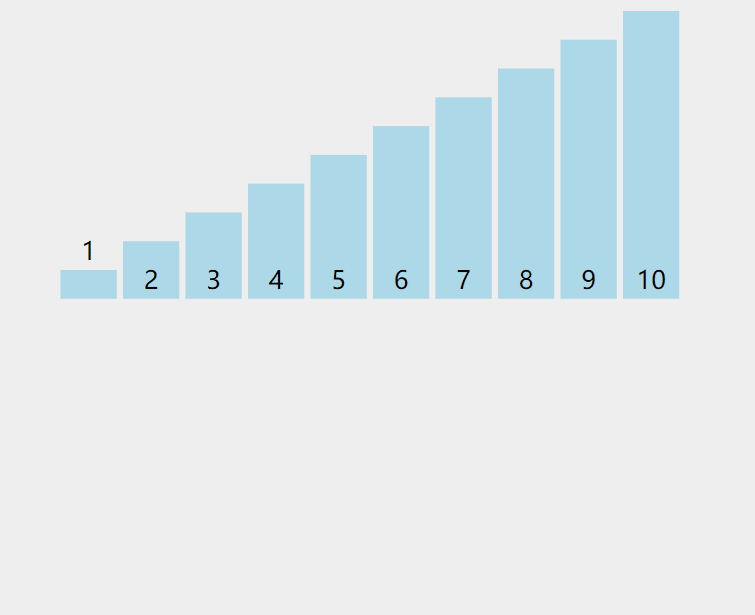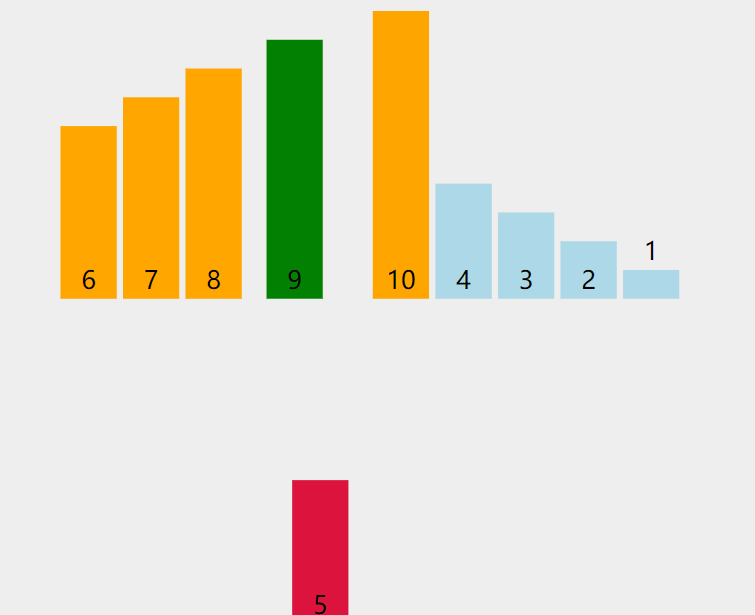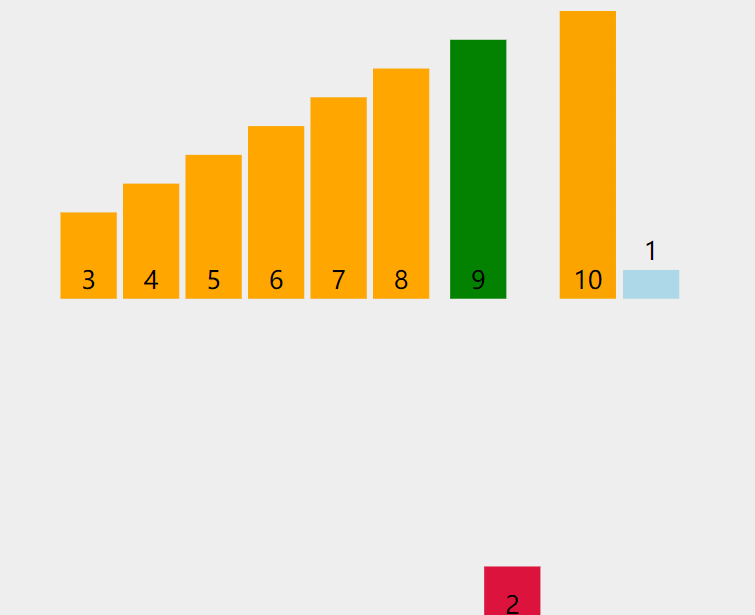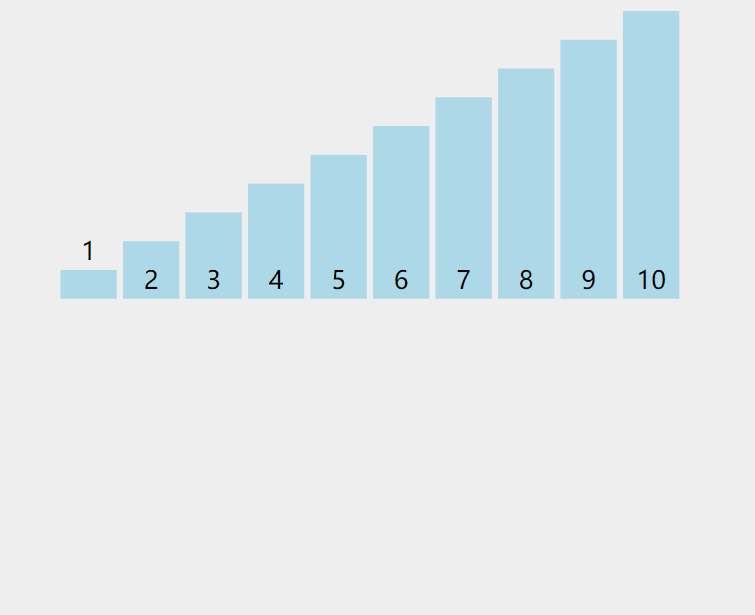
指针:
- end:标识有序序列的最后一个位置
- tmp:当前的待排序数据
c
void InsertSort(int* arr, int n)
{
for (int i = 0;i < n - 1;i++) {
int end = i;
int tmp = arr[end + 1];
while (end >= 0) {
if (arr[end] > tmp) {
arr[end + 1] = arr[end];
end--;
}
else {
break;
}
}
arr[end + 1] = tmp;
}时间复杂度分析
- 最差情况:数组完全降序
c
for (int i = 0; i < n - 1; i++) { // 执行 n-1 次
int end = i;
int tmp = arr[end + 1];
while (end >= 0) { // 最坏执行 i+1 次
if (arr[end] > tmp) {
arr[end + 1] = arr[end];
end--;
} else {
break;
}
}
arr[end + 1] = tmp;
}循环次数:
外层循环:n-1 次
内层循环(最坏):1 + 2 + 3 + ... + (n-1) 次
即:
外层循环第 1 次执行时(i=0),内层循环最多执行 1 次
外层循环第 2 次执行时(i=1),内层循环最多执行 2 次
外层循环第 3 次执行时(i=2),内层循环最多执行 3 次
...
外层循环第 n-1 次执行时(i=n-2),内层循环最多执行 n-1 次
- 不要直接把外层循环和内层循环的次数相乘了!在这个外层循环次数决定内层循环次数的情况下是绝对错误的!只有内外层循环次数互不关联才可以相乘!(相互独立事件)
bash
T(n) = 1 + 2 + 3 + ... + (n-1)
= n(n-1)/2
= O(n²)- 平均情况:小于 O(n²) 大于O(n)
- 最好情况: 数组有序且为升序------ O(n)
关于插入排序与冒泡排序的时间复杂度对比
虽然插入排序和冒泡排序在最坏情况下(输入完全逆序)的时间复杂度都是 O(n²),但在实际性能表现上有重要差异:
- 最好情况对比:
- 插入排序:当输入数组已完全有序时,内层循环立即break,时间复杂度为 O(n)
- 冒泡排序:同样在完全有序时,通过优化(设置交换标志)可以达到 O(n),但标准实现仍需 O(n²)
- 平均情况对比:
- 插入排序:平均情况仍为 O(n²),但常数因子较小
- 冒泡排序:平均情况为 O(n²),且交换操作更频繁
- 最差情况发生概率:
- 插入排序的最差情况相对较少(仅完全逆序或特定模式)
- 冒泡排序的最差情况范围更广,除完全有序外的多数情况都比较接近 O(n²)

希尔排序
实现
目的在于优化直接插入排序时间复杂度较差的情况(即大数在前,小数在后的这种情况)。
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数(通常是gap = n/3+1),把待排序文件所有记录分成各组,所有的距离相等的记录分在同一组内,并对每一组内的记录进行排序,然后gap=gap/3+1得到下一个整数,再将数组分成各组,进行插入排序。
当gap=1时,就相当于直接插入排序。------这意味着希尔排序可以在直接插入排序的代码基础上实现。
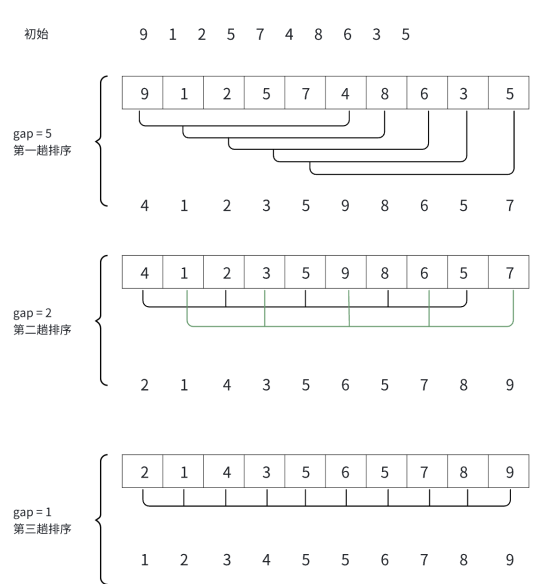
gap:既是分组的数量,也是组内元素编号的间隔大小,每组有n/gap个数据。
希尔排序的特性总结
- 希尔排序是对直接插入排序的优化。
- 当 gap > 1 时都是预排序,目的是让数组更接近于有序(小数在前大数在后)。
当 gap == 1 时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。
c
//希尔排序
void ShellSort(int* arr, int n)
{
int gap = n;
while (gap > 1) {
gap = gap / 3 + 1; //最常用的gap算法,除3是因为分组数会比较少,加1是确保最终有gap=1
//如果除数是2的话,就不需要再加1了,否则会一直循环
for (int i = 0;i < n - gap;i++) {
int end = i;
int tmp = arr[end + gap];
while (end >= 0) {
if (arr[end] > tmp) {
arr[end + gap] = arr[end];
end -= gap;
}
else {
break;
}
}
arr[end + gap] = tmp;
}
}
}时间复杂度分析
一、时间复杂度估算
外层循环
- 时间复杂度为: O ( log 2 n ) O(\log_2 n) O(log2n) 或 O ( log 3 n ) O(\log_3 n) O(log3n),即 O ( log n ) O(\log n) O(logn)
- 这是因为增量
gap每次以除以2或3的方式递减,循环次数是对数级的。
内层循环
假设共有 n n n 个数据,当前增量为 gap:
- 数据被分为
gap组,每组有 n g a p \frac{n}{gap} gapn 个元素。 - 每组进行插入排序,最坏情况下移动次数为 1 + 2 + 3 + ⋯ + ( n g a p − 1 ) 1+2+3+\dots+(\frac{n}{gap}-1) 1+2+3+⋯+(gapn−1)。
- 总移动次数为:
g a p × [ 1 + 2 + 3 + ⋯ + ( n g a p − 1 ) ] gap \times \left[1+2+3+\dots+\left(\frac{n}{gap}-1\right)\right] gap×[1+2+3+⋯+(gapn−1)]
示例(以 gap 每次除以3为例)
- 当 g a p = n 3 gap = \frac{n}{3} gap=3n 时,移动总数为:
n 3 × ( 1 + 2 ) = n \frac{n}{3} \times (1+2) = n 3n×(1+2)=n - 当 g a p = n 9 gap = \frac{n}{9} gap=9n 时,移动总数为:
n 9 × ( 1 + 2 + ⋯ + 8 ) = n 9 × 8 × 9 2 = 4 n \frac{n}{9} \times (1+2+\dots+8) = \frac{n}{9} \times \frac{8 \times 9}{2} = 4n 9n×(1+2+⋯+8)=9n×28×9=4n - 当 g a p = 1 gap = 1 gap=1 时,退化为直接插入排序,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
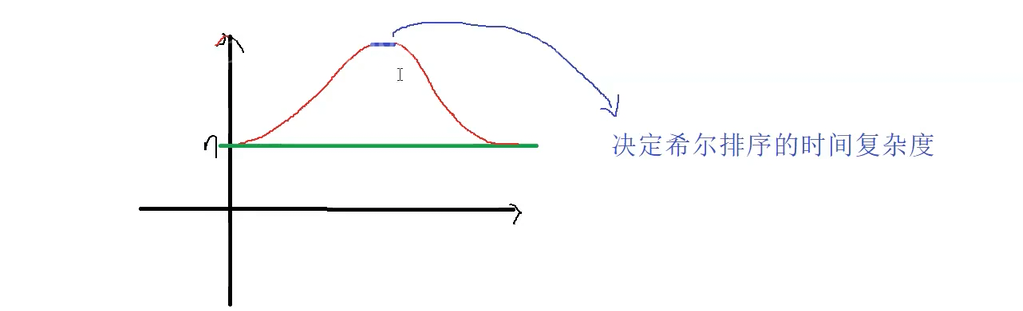
二、趋势曲线(抛物线形式)
- 在
gap从 n 3 \frac{n}{3} 3n 到 1 的过程中,比较次数先上升后下降。 - 初始和最终阶段的比较次数均为 n n n。
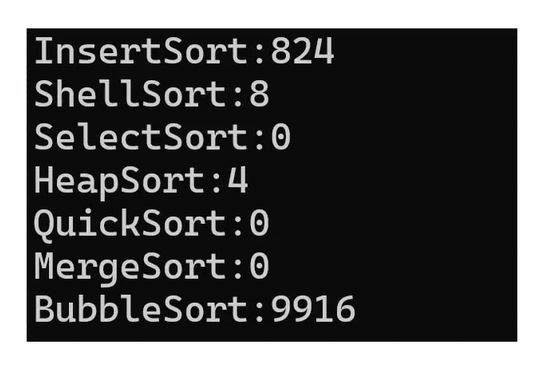
最大值决定了希尔排序的时间复杂度,但是具体的数值不得而知。

选择排序
直接选择排序
实现
选择排序的基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
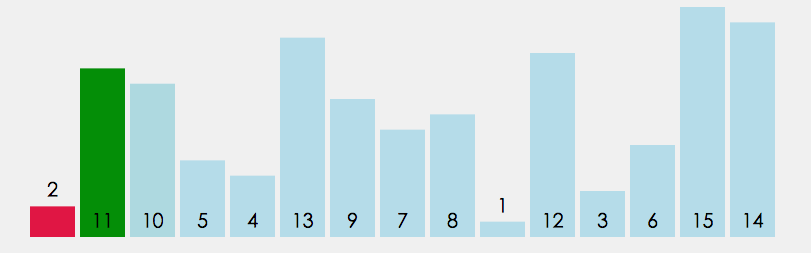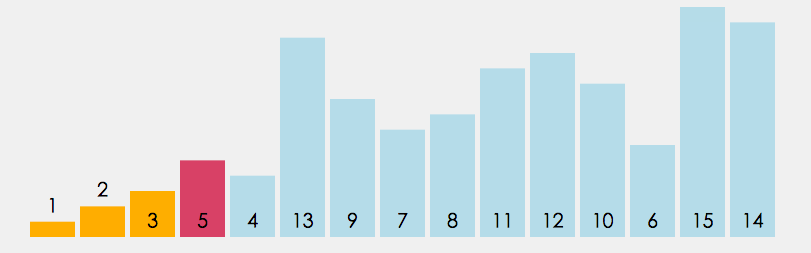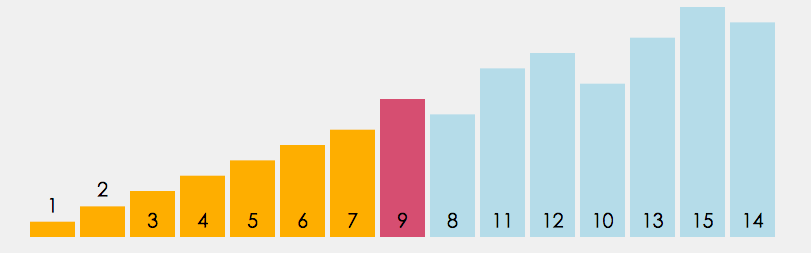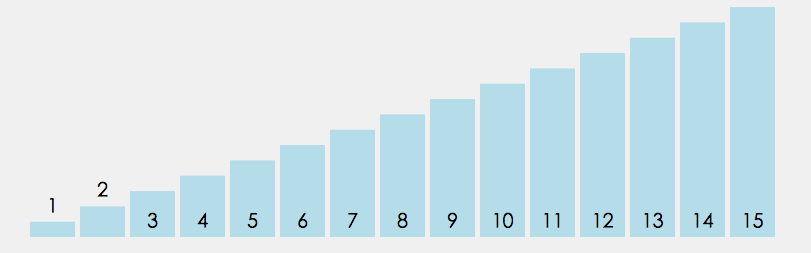
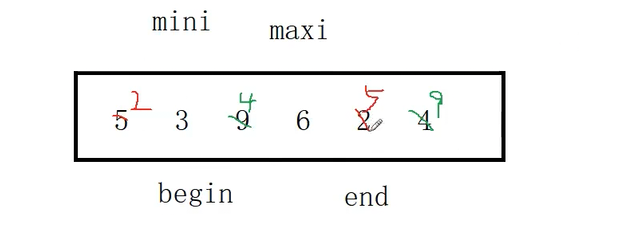
优化:不仅找最小交换,也找最大交换
c
//直接选择排序
void SelectSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1;i <= end;i++) {
//同时找到最小值和最大值
if (arr[i] < arr[mini])
{
mini = i;
}
if (arr[i] > arr[maxi])
{
maxi = i;
}
}
Swap(&arr[mini], &arr[begin]);//把最小值换到最前面
Swap(&arr[maxi], &arr[end]);//把最大值换到最后面
begin++;
end--;
}
}此代码出现的问题:

出现的原因:当begin==maxi时,如果Swap(&arr[mini], &arr[begin]) 先一步把begin的数据换走了,也就是说真正的最大值移动到了mini指向的位置。
Swap(&arr[maxi], &arr[end])的作用就也会受到影响:交换的不是最大值而是最小值
所以当begin==maxi时,应该使maxi直接指向mini。
c
void SelectSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1;i <= end;i++) {
//特殊情况的修正
if (maxi == begin)
{
maxi = mini;
}
//同时找到最小值和最大值
if (arr[i] < arr[mini])
{
mini = i;
}
if (arr[i] > arr[maxi])
{
maxi = i;
}
}
Swap(&arr[mini], &arr[begin]);
Swap(&arr[maxi], &arr[end]);
begin++;
end--;
}
}时间复杂度分析
交换次数之和:(n-2)+(n-4)+(n-6)+......+0
计算结果时间复杂度为恒定的 O ( n 2 ) O(n^2) O(n2)
时间复杂度很差,所以实际应用中也不常见。
快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值 ,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
实现
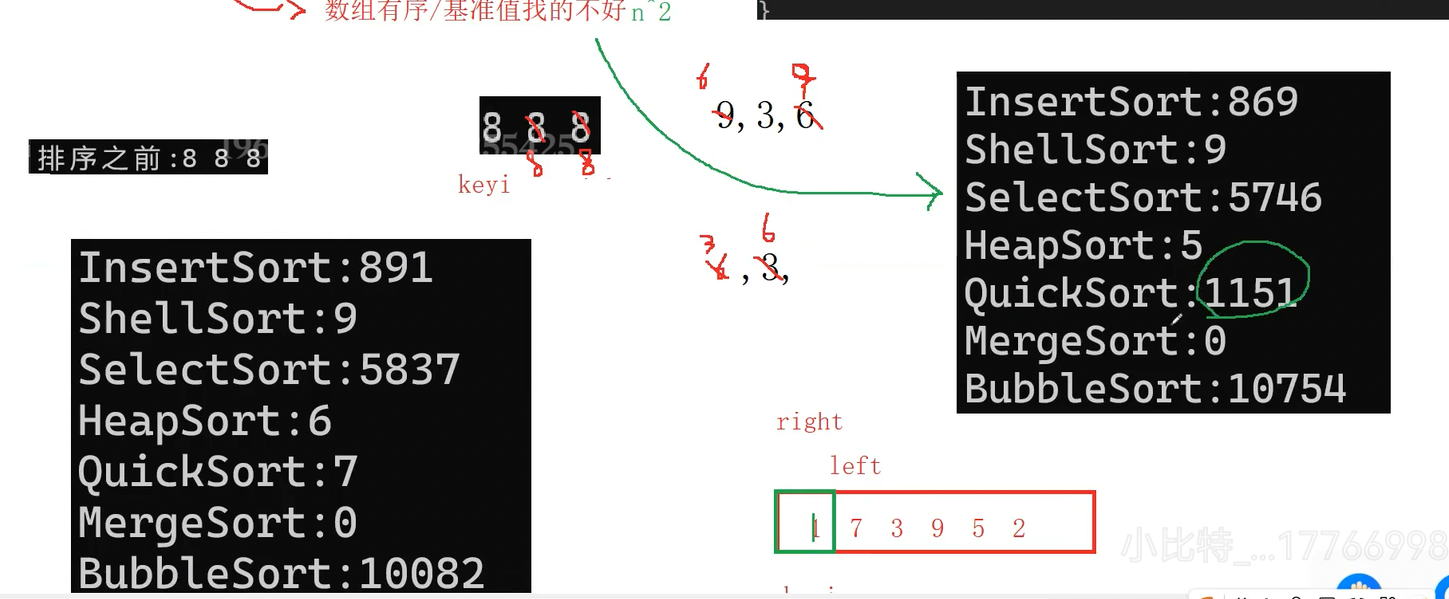
Hoare方法
keyi:基准值位置序号
right:从右往左走找比基准值要小的数据
left:从左往右走找比基准值要大的数据
找到后让right和left数据交换
当left>right,keyi和right数据交换,完成一轮快速排序

- 代码实现:注意注释中重点1、2的讨论,是代码实现非常容易出错的点
c
//找基准值位置
int _QuickSort(int* arr, int left, int right)
{
int keyi = left; // 选择区间最左元素作为基准值(pivot)
left++; // 从 pivot 右侧开始扫描,避免基准值参与比较
while (left <= right)
//重点1:如果条件是left < right,假设left==right时,arr[right]>arr[keyi],此时Swap(&arr[keyi], &arr[right])不能获得正确的排序序列(显然比基准值大的到基准值左侧去了)
//如果加上等号,发现这个问题就可以解决了
{
// right:从右向左扫描
// 寻找第一个 <= 基准值 的元素
while (left <= right && arr[right] > arr[keyi])
//重点2:为什么条件是arr[right] > arr[keyi],难道相等时也要交换吗?这是否是一种浪费?
//答:条件差异导致的是递归次数的区别,如果相等时交换,递归次数为logn,不交换递归次数为n,具体分析见下方图片
{
right--;
}
// left:从左向右扫描
// 寻找第一个 >= 基准值 的元素
while (left <= right && arr[left] < arr[keyi])
{
left++;
}
// 此处若 left <= right,可交换 arr[left] 与 arr[right]
if (left <= right)
{
Swap(&arr[left++], &arr[right--]);
//重点3:如果这里不做自增减的话,当arr[left]==arr[right]时,代码会进入死循环
}
}
// 将基准值交换到分区完成后的最终位置(right)
// 此时:right 左侧元素 <= pivot,右侧元素 >= pivot
Swap(&arr[keyi], &arr[right]);
return right; // 返回基准值的最终下标
}
//快速排序需要知道基准值的范围
void QuickSort(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
//有多个数的区间需要排序
//找基准值位置
int keyi = _QuickSort(arr, left, right);
//根据基准值位置将待排序集合分割成左右两子序列再进行快速排序
QuickSort(arr, left, keyi - 1);//左序列[left,keyi-1]
QuickSort(arr, keyi + 1, right);//右序列[keyi+1,right]
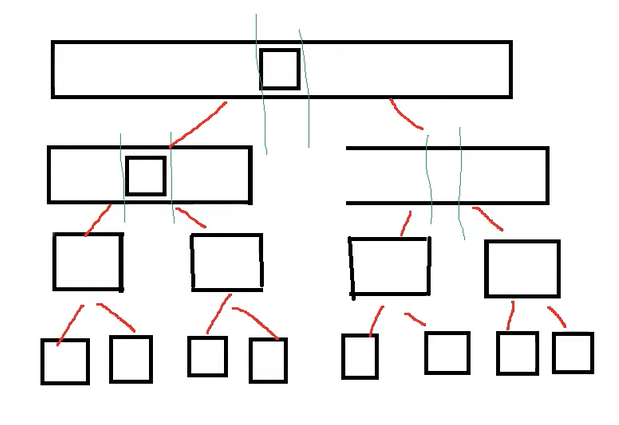
}重点2分析:

对应这部分代码的次数计算
下图左:相等元素交换:最终返回的基准值位置在arr内部位置------递归次数为logn(二叉树的高度)
下图右:相等元素不交换:最终基准值位置在arr[0]------递归次数为n

挖坑法
思路:
创建左右指针。首先从右向左找出比基准小的数据,找到后立即放入左边坑中,当前位置变为新的"坑",然后从左向右找出比基准大的数据,找到后立即放入右边坑中,当前位置变为新的"坑",结束循环后将最开始存储的分界值放入当前的"坑"中,返回当前"坑"下标(即分界值下标)

c
int _QuickSort(int* a, int left, int right)
{
int hole = left;
int key = a[hole];
while (left < right)
{
while (left < right && a[right] > key)
{
--right;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] < key)
{
++left;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}lomuto前后指针法
思路:
- 创建两个前后指针prev、cur,初始都指向arr[0]
- cur从左往右找比基准值小的数据
1)cur指向数据小于基准值:prev++,prev与cur指向的数据交换
2)cur指向数据大于基准值:不处理 - cur继续移动直至越界
- prev所指位置就是基准值的位置
c
//前后指针法
int _QuickSort2(int* arr, int left, int right)
{
int keyi = left;
int prev = left, cur = prev + 1;
while (cur <= right)
{
if (arr[cur] < arr[keyi]&&++prev != cur)//优化:减少prev和cur指向元素相等时带来的无效交换
{
Swap(&arr[prev], &arr[cur]);
}
++cur;
}
Swap(&arr[prev], &arr[keyi]);
return prev;
}时间复杂度分析
外层:递归次数logn
内层:_QuickSort交换次数认为是n n/2 n/4......
时间复杂度为O(nlogn)
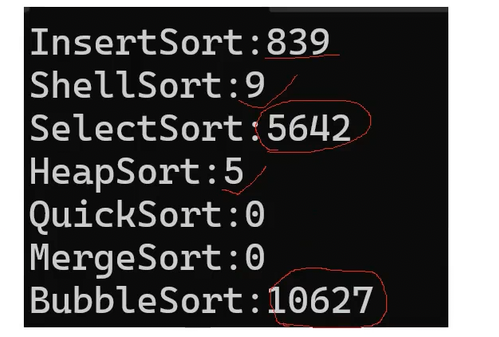
当数组有序/基准值找的不好时(比如{1.7.3.9.5.2})------ 基准值位置总是在arr[0],时间复杂度会达到 O ( n 2 ) O(n^2) O(n2)
针对基准值问题的优化方法:三数取中(暂不实现)
非递归版本的快速排序
借助数据结构------栈
用于存储需要排序的区间,右区间先进栈,左区间后进栈------这样出栈的时候可以先得到左区间
c
//非递归版本的快速排序
void QuickSortNonR(int* arr, int left, int right)
{
ST st;
STinit(&st);
//区间入栈
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
//取栈顶两次
int begin = StackTop(&st);
StackPop(&st);
int end = StackTop(&st);
StackPop(&st);
//前后指针法找基准值
int keyi = begin;
int prev = begin, cur = prev + 1;
while (cur <= end)
{
if (arr[cur] < arr[keyi] && ++prev != cur)//优化:减少prev和cur指向元素相等时带来的无效交换
{
Swap(&arr[prev], &arr[cur]);
}
++cur;
}
Swap(&arr[prev], &arr[keyi]);
keyi = prev;
//左序列[left,keyi-1] 右序列[keyi+1,right]
//要考虑序列无效 or 不用排序的情况
if (keyi + 1 < end)
{
StackPush(&st, end);
StackPush(&st, keyi+1);
}
if (begin < keyi - 1)
{
StackPush(&st, keyi-1);
StackPush(&st, begin);
}
}
STDestroy(&st);
}归并排序
实现
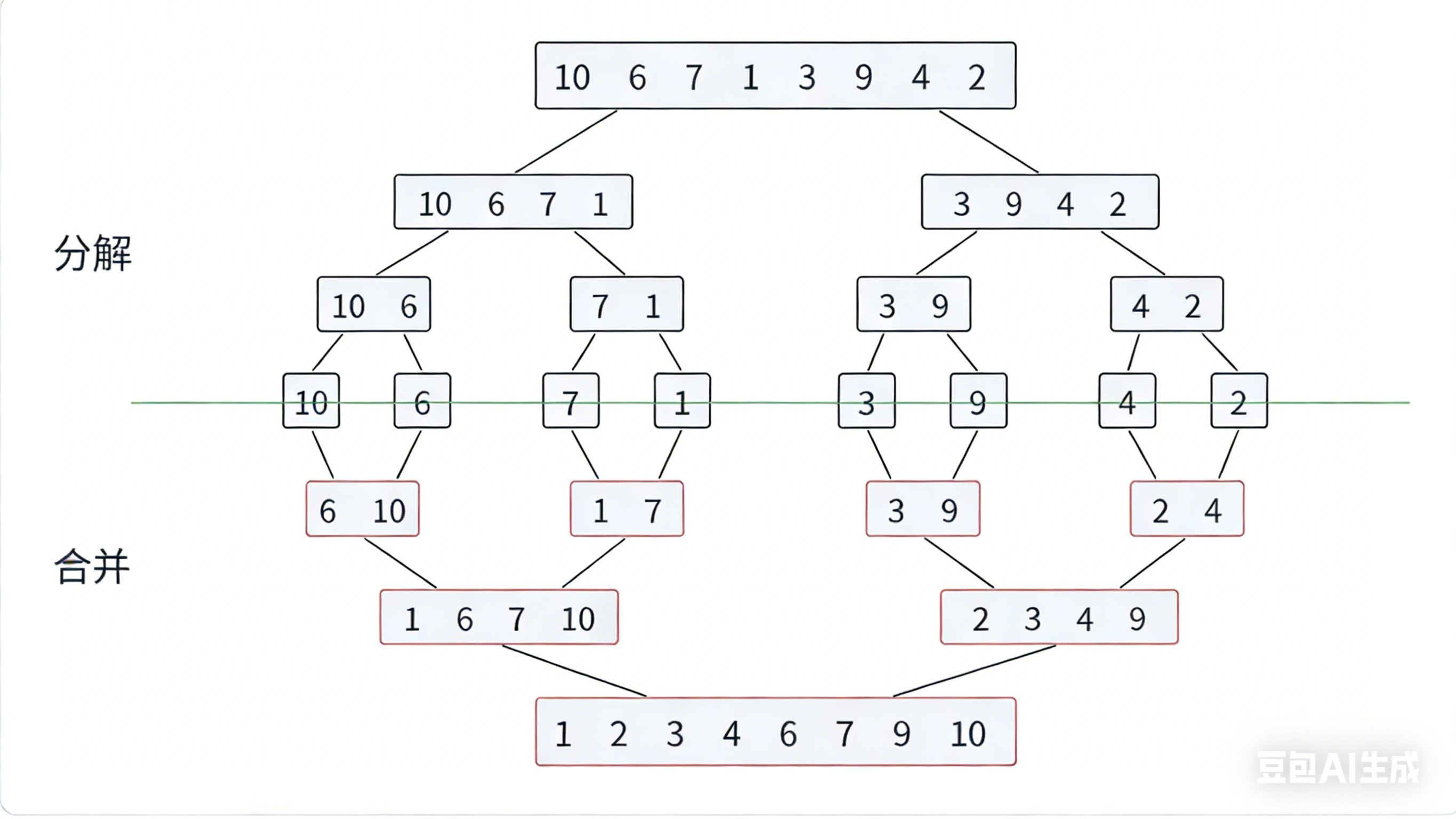
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序核心步骤:
c
void _MergeSort(int* arr, int left, int right,int* tmp)
{
//分解
//只有一个数据时不再二分
if(left >= right) return;
int mid = (left + right) / 2;
//根据mid划分左右两个序列:[left, mid] [mid+1, right]
_MergeSort(arr, left, mid,tmp);
_MergeSort(arr, mid+1, right,tmp);
//合并两个序列 [left, mid] [mid+1, right]
//使用tmp来合并排序避免直接改变arr
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] <= arr[begin2]){
tmp[index++] = arr[begin1++];
}
else {
tmp[index++] = arr[begin2++];
}
}
//退出循环,但有可能左or右序列的元素还没全部放入tmp中
while (begin1 <= end1) {
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2) {
tmp[index++] = arr[begin2++];
}
//将tmp元素导入原数组
for (int i = left;i <= right;i++) {
arr[i] = tmp[i];
}
}
void MergeSort(int* arr, int n)
{
//分解
//开辟与原数组大小相同的原始数组
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}时间复杂度分析
时间复杂度=函数递归次数 * 单次递归时间复杂度
显然递归的方式呈现为二叉树,即递归次数为logn
单次递归比较次数为n
时间复杂度为nlogn,与快速排序、堆排序相同
非比较排序
前面讲到的排序算法,在排序过程中都需要进行数据大小的比较,因此这些算法统称为比较排序。对应的,在排序过程中不进行数据大小的比较的排序算法就是非比较排序。
计数排序
实现
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数,用count数组保存
- 根据统计的结果将数字排布到原来的序列中
count数组大小的选择
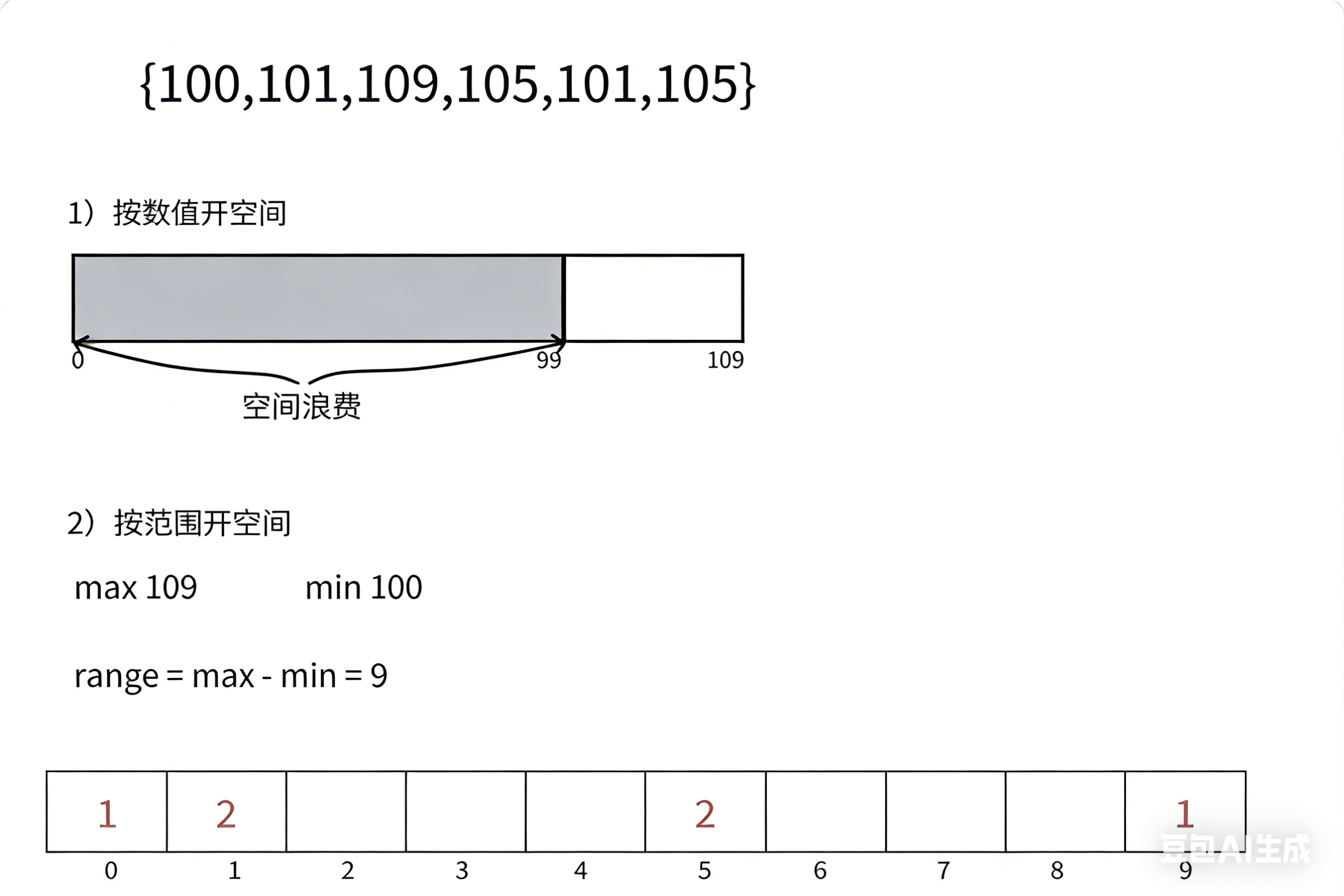
c
void CountSort(int* arr, int n)
{
int min = arr[0], max = arr[0];
for (int i = 0;i < n;i++) {
if (arr[i] < min)
{
min = arr[i];
}
if (arr[i] > max)
{
max = arr[i];
}
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int*) * range);
if (count == NULL)
{
perror("malloc fail!");
}
//将 count 指向的内存区域中,连续 sizeof(int) * range 个字节的内容全部设置为 0
memset(count, 0, sizeof(int) * range);
//统计相同元素出现次数,用count数组保存
for (int i = 0;i < n;i++) {
count[arr[i] - min]++;
}
//将次数还原到原数组中
int index = 0;
for (int i = 0;i < range;i++) {
//还原数字
arr[index] = i + min;
//重新排布
while (count[i]--) {
arr[index++] = i + min;
}
}
}时间复杂度分析
计数排序的特性:
计数排序在数据范围集中时,效率很高,但是当数据范围分散时(max-min=range-1越大,时间复杂度和空间复杂度都越差),效果就不太好。
时间复杂度: O(n + range) 因为不知道n和range谁大,不能消去
空间复杂度: O(range)
排序算法复杂度与稳定性分析
稳定性 :假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的
相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。

辅助空间---空间复杂度
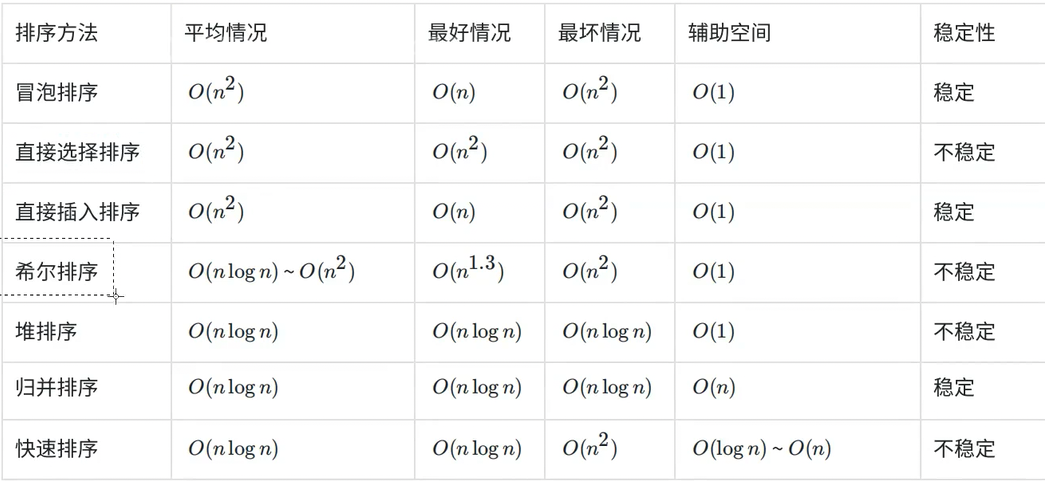
- 稳定性验证案例
直接选择排序:5 8 5 2 9
希尔排序:5 8 2 5 9
堆排序:2 2 2 2
快速排序:5 3 3 4 3 8 9 10 11