一，模型训练(Trainning)
机器学习模型训练三大步骤：
- 建模（找函数）：Function with Unknown Parameters
- 定义损失函数（Loss Function）：Define Loss from Training Data
- 优化（Optimization）
以预测明日文章订阅量的任务(Regression，回归)为例。在此例中，机器学习的过程就是通过前几个月甚至几年的数据，机器找到一个函数能够预测明日的订阅情况，即
1.Function with Unknown Parameters
第一步需要我们写出一个代表未知参数的函数式，简单来说就是先猜测一下这个能预测明日订阅情况的函数式。以最简单的线性形式为例(guess based on domain knowledge)，我们假设这个式子是
是明日的订阅量，准备预测的数值
2.Define Loss from Training Data
Loss称为损失函数，写作。它通过计算模型预测值和真实目标值(label)的差距，给函数的拟合效果打分(判断参数选择的好坏)。值越小表示参数选择的越好。
Loss函数实际上根据任务的不同有多种不同的形式，这里的回归任务(Regression)通常使用MSE/MAE，MAE全称Mean Absolute Error，写为，
是真实值，称为label。MSE全称Mean Square Error，写为
。
假设，则
，
。接下来利用过去数据计算此函数式预测的每日的误差，然后都加起来取平均：
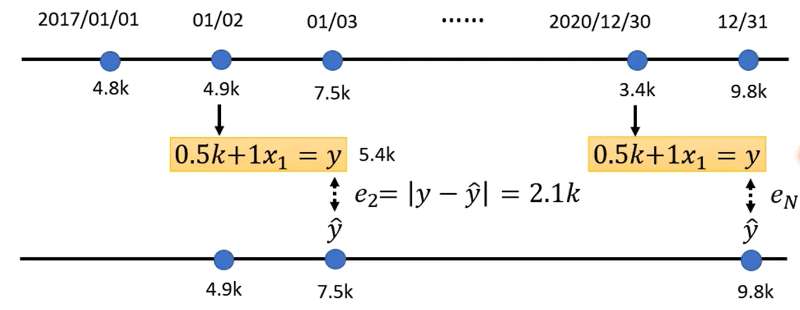
我们可以选取不同的，计算得到不同的Loss，Loss值最小的那个
就是我们要找的。如下图不同
组合得到的Loss值，颜色越浅代表Loss越小。
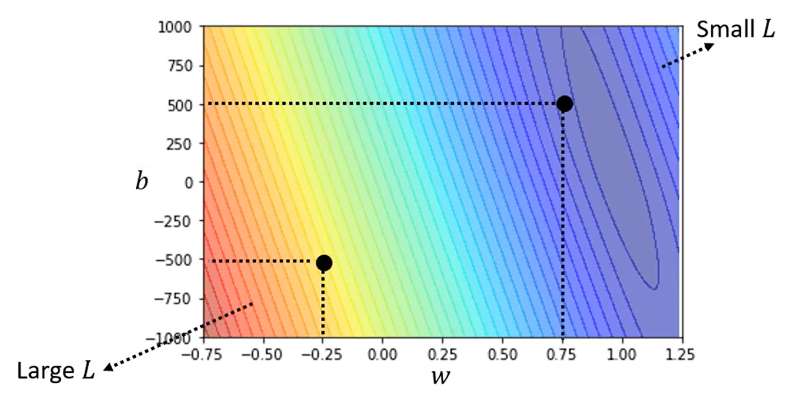
3.Optimization
在此案例中，Optimization的目的就是找一个最佳的使
最小，即
要找到最佳，最常用的方法是梯度下降(Gradient Desent)。对
分别进行Gradient Desent，下面以
为例：
与
的数值对应关系如下曲线所示。
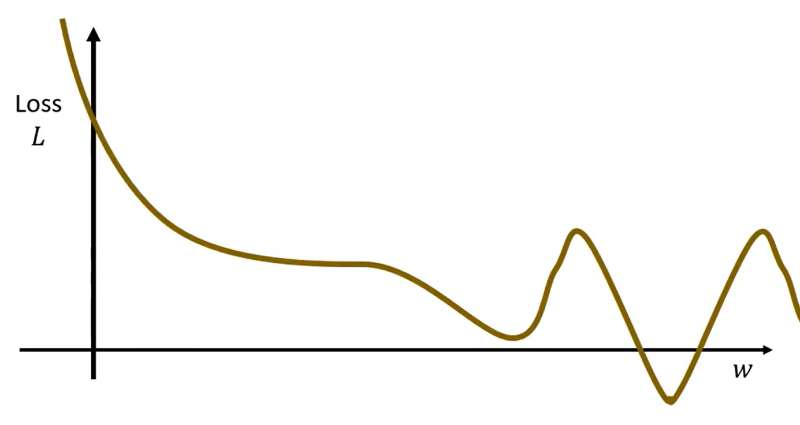
第一步要随机选取初始点(此处为随机选取，之后可能会有更多的方法来选取一个合适的初始点)：
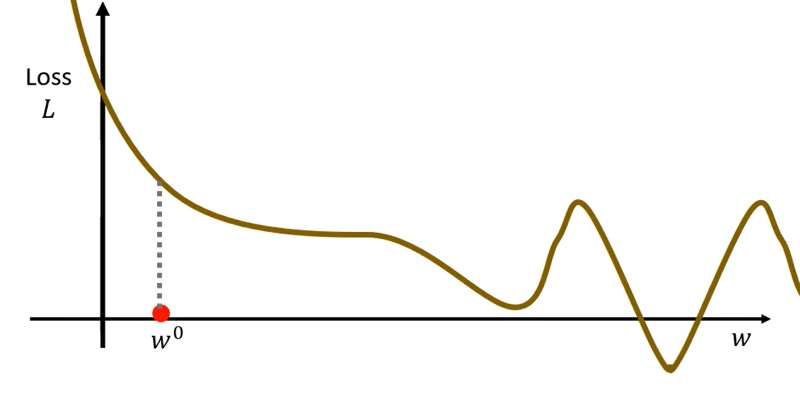
第二步计算处
对
的微分，即
。如果计算出来是负数表示左高右低，则将
增加。
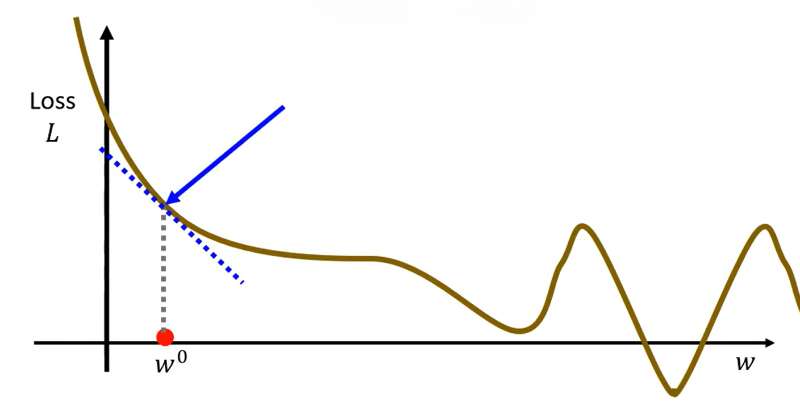
第三步更新的值。更新长度为
，也就是取决于微分大小和
(Learning Rate，学习率)。(
是一个超参数(hyperparameters)，所谓超参数是指在模型训练开始前，由人工预先设定、无法通过训练数据自动学习得到的参数，用于控制模型的训练流程、结构设计与优化策略，是调控模型性能和训练行为的外部配置项)
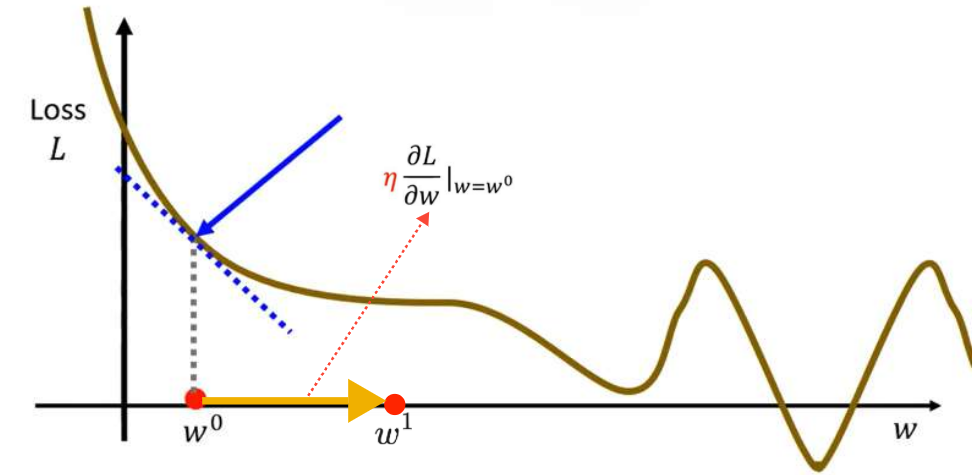
接下来重复上述操作，计算处梯度，根据梯度值再更新
。最终会停止更新(两种情况下会停止，第一种情况是自己设定要参数更新几次停止，这也是一个hyperparameters；第二种情况是更新到最小值处，最小值处梯度为0，不再更新)
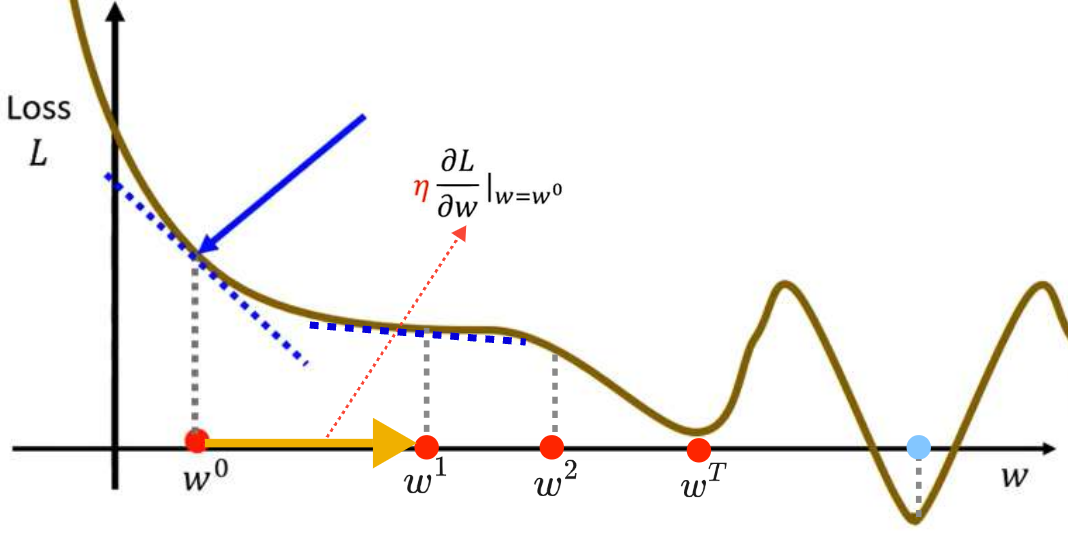
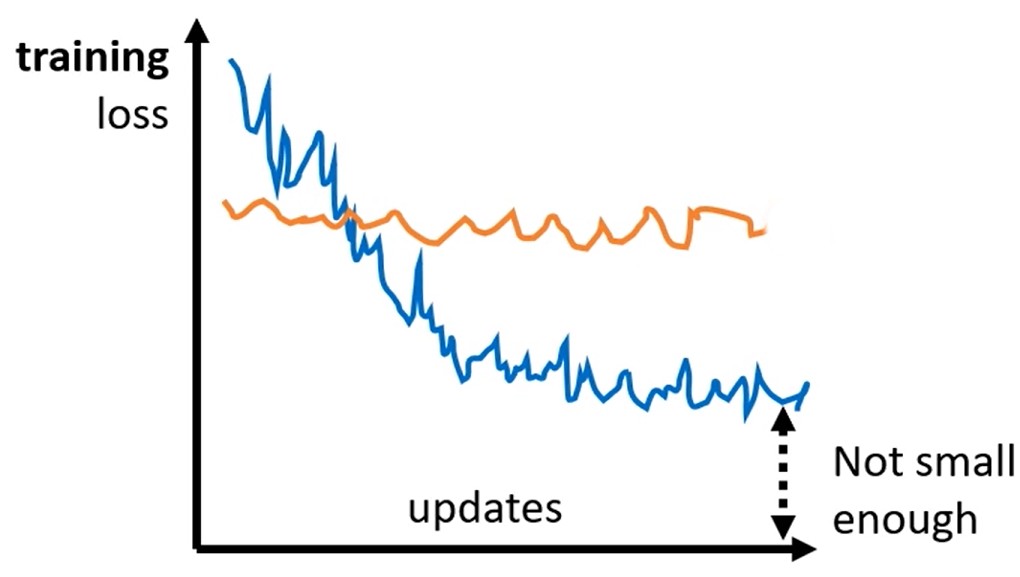
⭐但是Gradient Desent这个方法会有两个**临界点(critical point)**问题，导致Loss不下降或者下降到一定程度就不再下降：
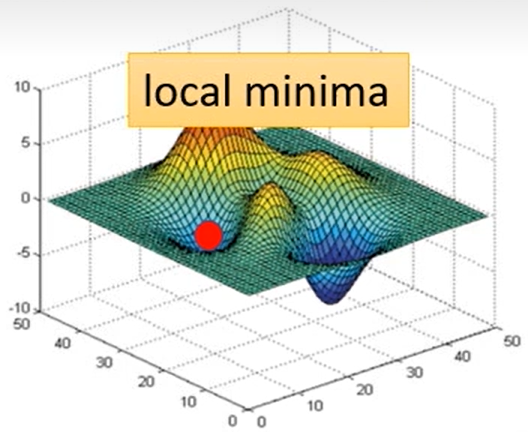
局部最优问题(local minima)： 看上图介绍的更新过程就可以发现蓝点才是真正最优的点，但是我们找到局部最优的
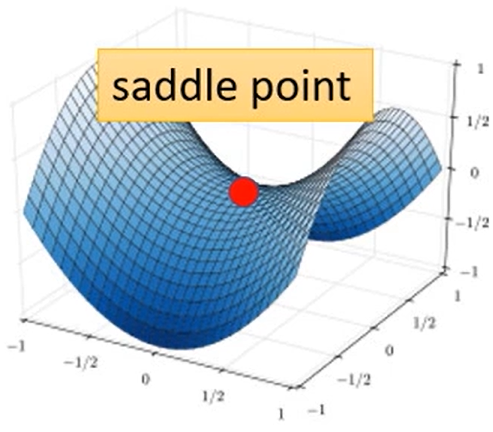
鞍点问题(saddle point)： 鞍点同样是损失函数梯度
在深度学习神经网络中，高维参数空间出现的局部最优点很少，并且绝大多数局部极小值的损失值、模型性能与全局最优高度接近，极少出现 "劣质局部最优"；而参数维度越高，鞍点数量呈指数级增长，并且鞍点的平坦区会让梯度模长趋近于 0， vanilla 梯度下降会陷入长期停滞，是训练收敛缓慢的核心原因之一。后续学习过程中会介绍解决方法。
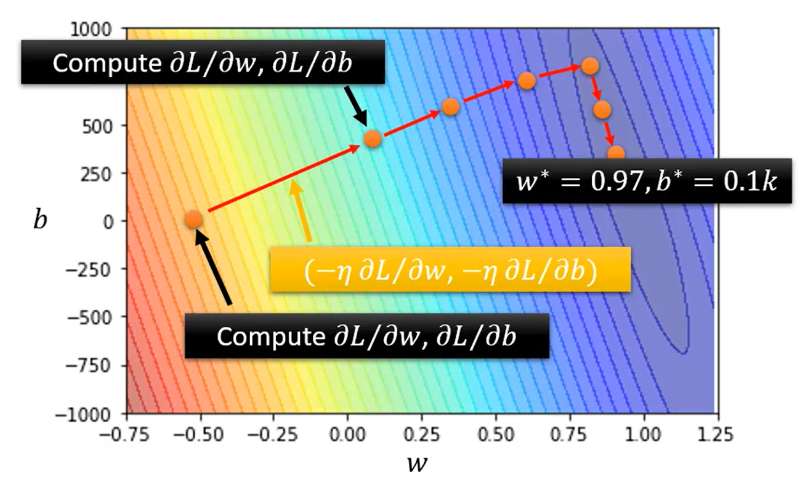
两个参数的Optimization的过程和上述是一样的：
- (Randomly) Pick initial values
- Compute:
- Update
二，模型改进与优化
线性模型(Linear models)改进
按照训练数据推导出的最佳模型是：
经过计算，此数据在训练集上的误差，在测试集上的误差
。下面是预测测试集2021.1.1-2021.2.14几天的订阅数据，红线为真实数据，蓝线为上述模型预测的数据。
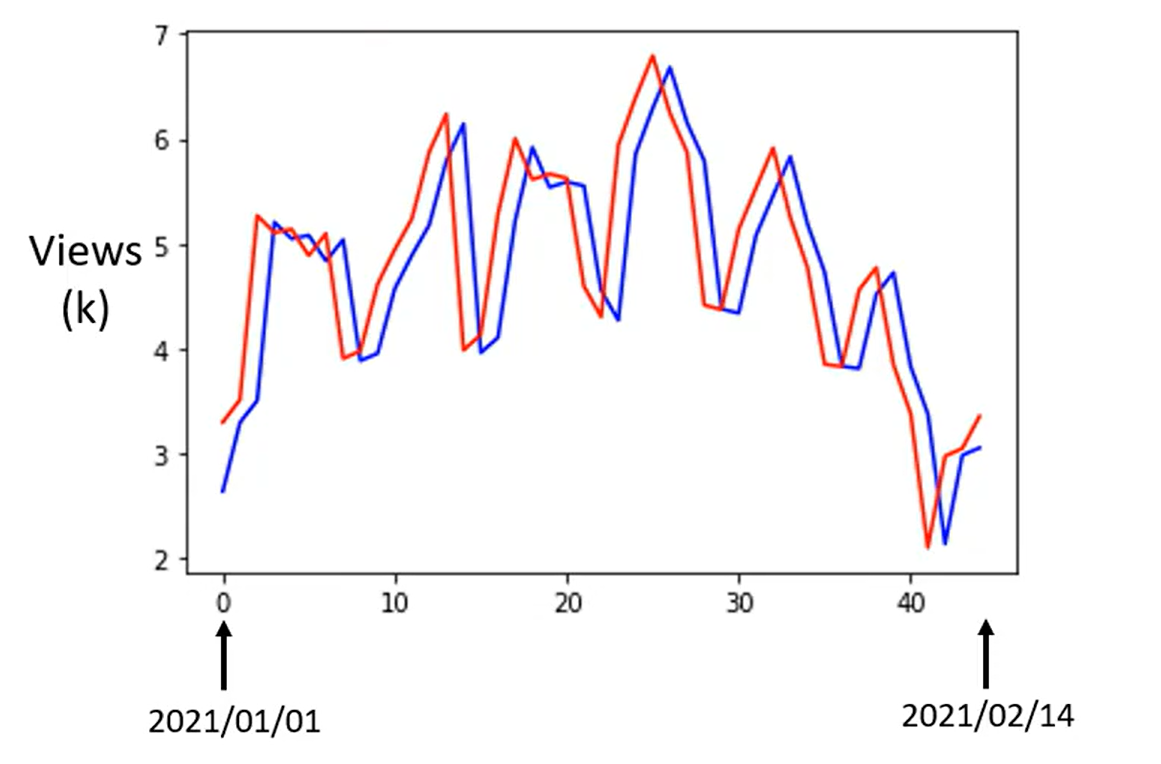
通过上图可以看到订阅数有一个明显的周期性(周期为7)，为了进一步减小预测误差，我们可以考虑改进模型，改进思路是通过前7日的数据来预测明日的数据。改进模型：
经过计算，此模型在训练集上的误差，在测试集上的误差
。其中
与
的最佳值如下：
接下来继续改进模型考虑前28天：
经过计算，此模型在训练集上的误差，在测试集上的误差
继续改进模型考虑前56天：
经过计算，此模型在训练集上的误差，在测试集上的误差
可以看到误差几乎没有变化了，再考虑天数来改进模型的思路不会有太大效果了。
非线性模型（进入深度学习）
Linear models可以很好表示符合直线分布的数据，选取不同的和不同的
就可以表示不同的斜率、高度。
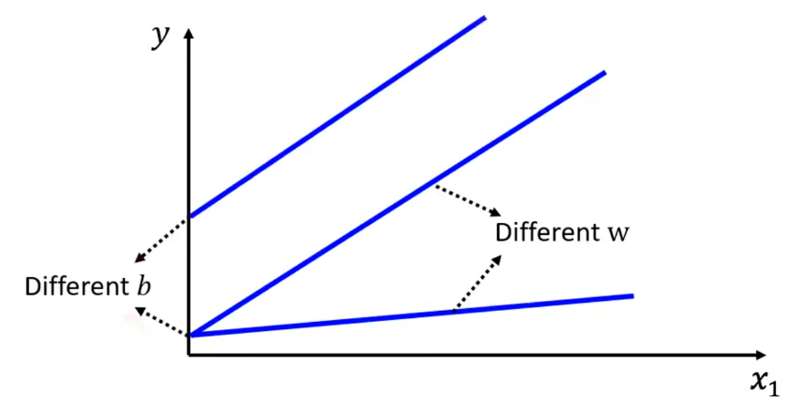
但是对于折线、曲线使用Linear models就会出现很大的偏差。(Linear models有很大的限制，称为Linear Bias) 我们需要一个更复杂更有弹性的model去表示更复杂的折线、曲线。
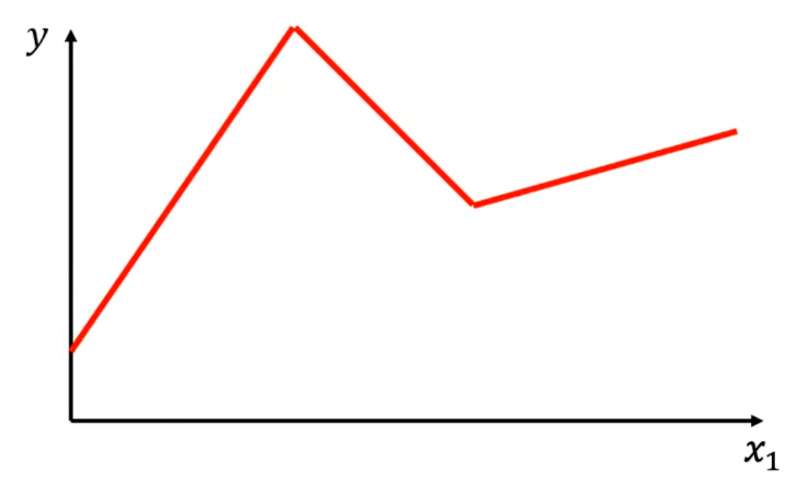
任意的折线都可以用常数 + 一段特殊折线表示，即：
以上图红色折线为例，选取常数项(标号0)、特殊折线1、特殊折线2、特殊折线3(每段特殊折线的中间部分的斜率与其对应红色折线的斜率相等)。将这几段折线加到一起即可得到红色折线。(折线有几段线段就需要几个特殊折线拼出)
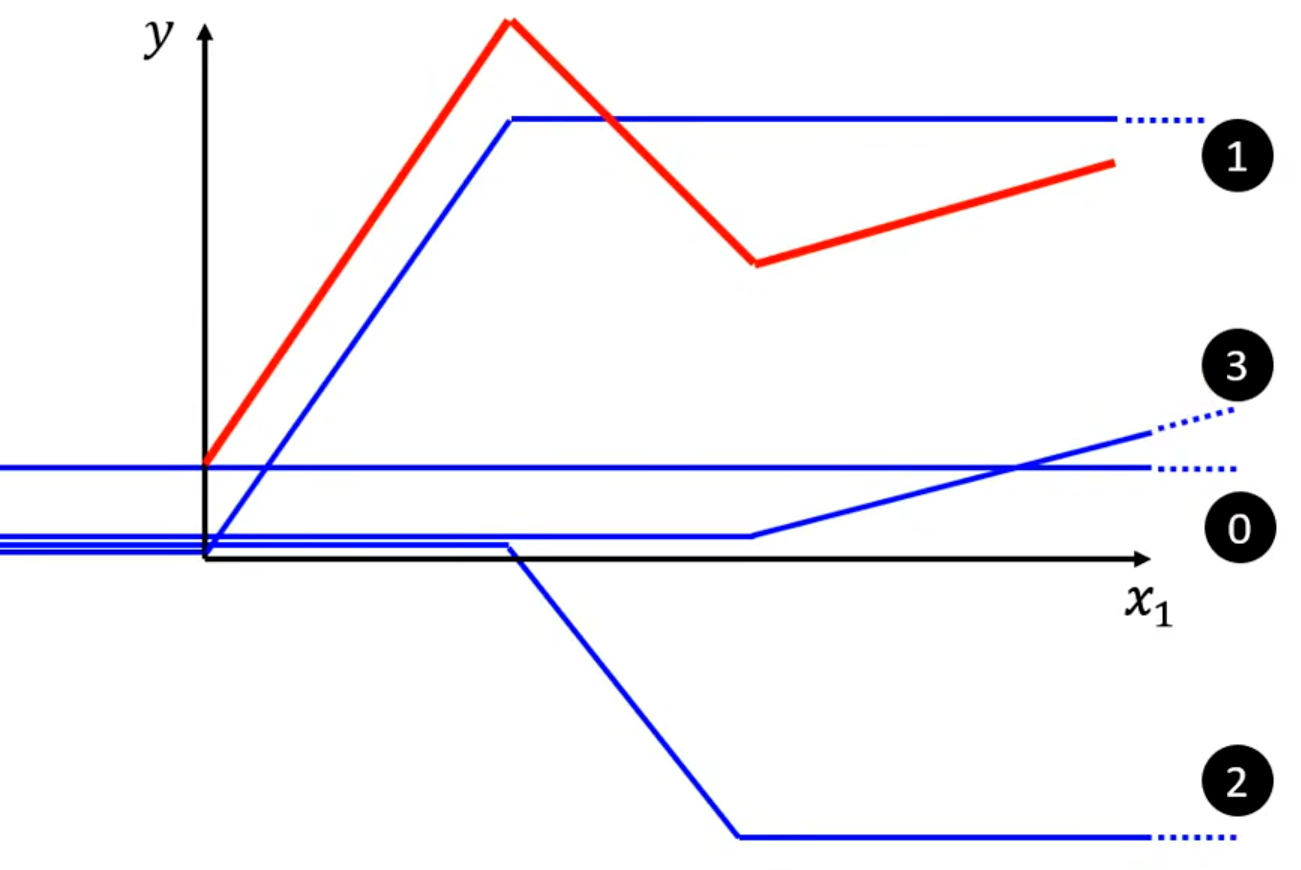
对于曲线，可以看成是由很多段折线组成。只要点取的越多，最终的图像就越逼近曲线，同时需要的特殊折线也就更多(也是一个hyperparameters)。
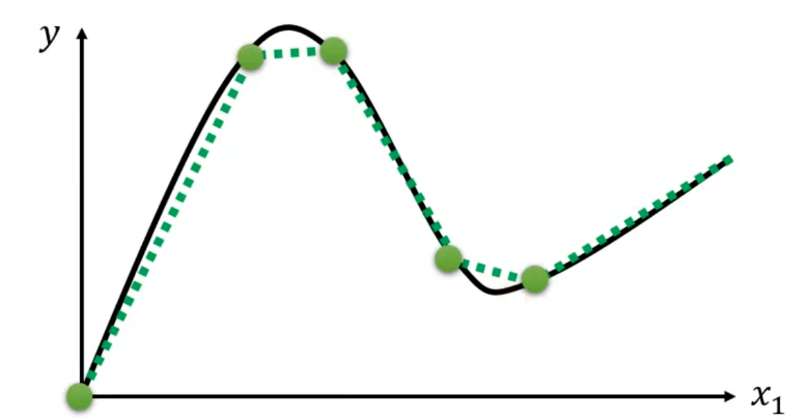
这段特殊折线(Hard Sigmoid)通常用一段类似的曲线函数(Sigmoid或ReLU)来近似表示(以Sigmoid Function为例)：
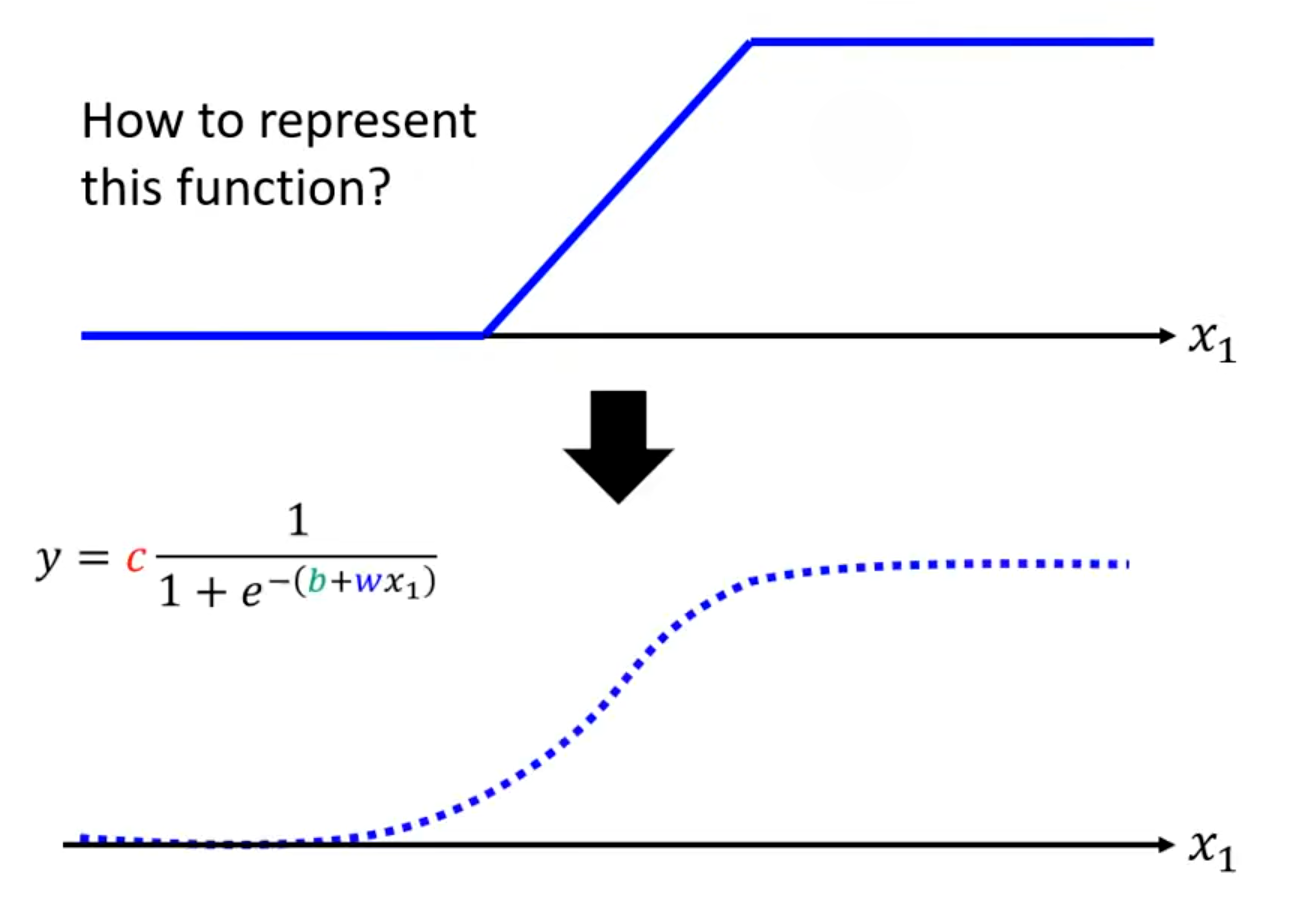
。不同的
分别决定了Hard Sigmoid的斜率、平移、高度。
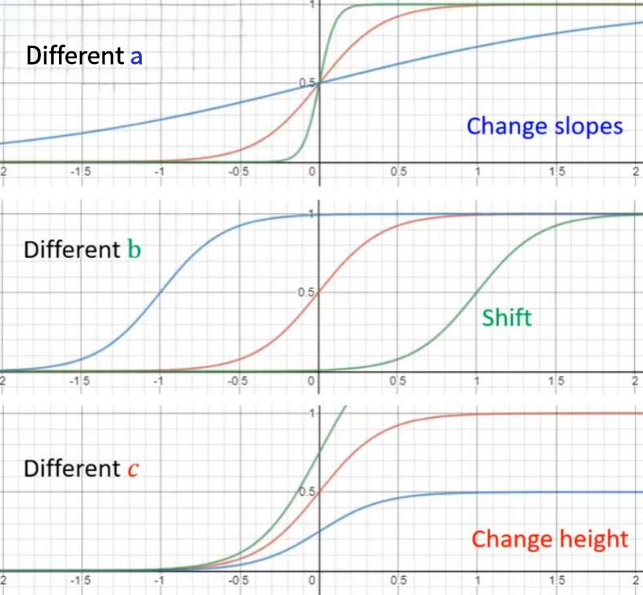
仍以下图折线为例，将Hard Sigmoid1、Hard Sigmoid2、Hard Sigmoid3加起来后得到：
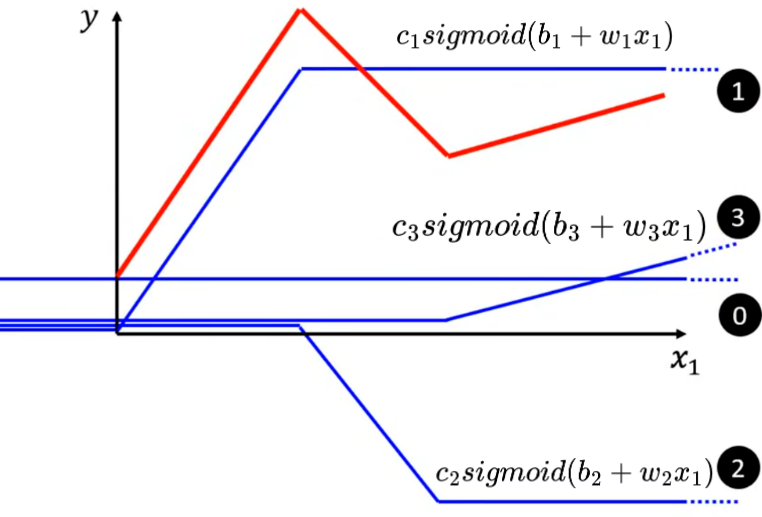
补充：ReLU
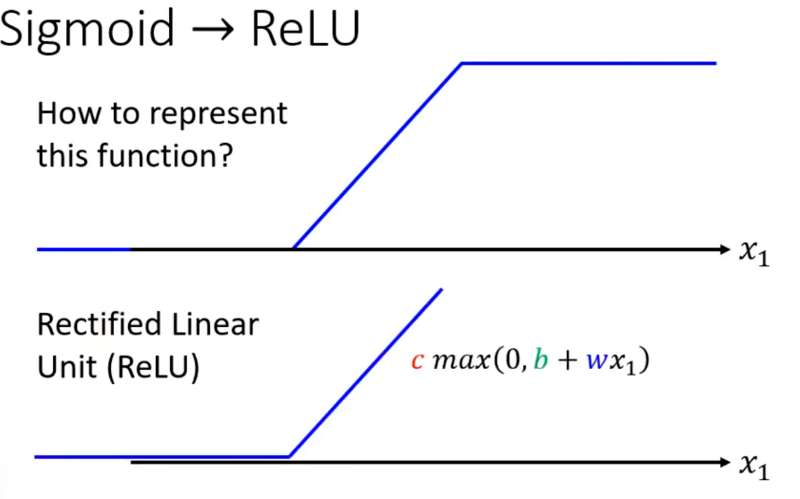
Sigmoid和ReLU在机器学习里称为激活函数(Activation function)
通过Sigmoid得到New Model：
假设，
：
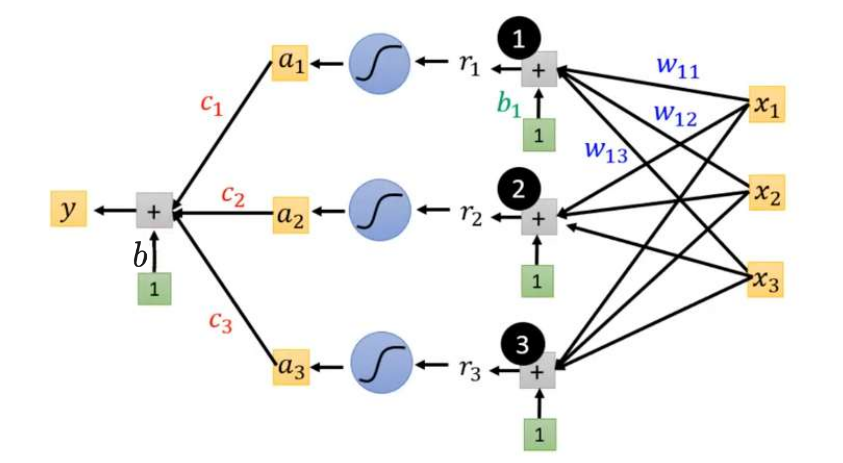
其中：
用矩阵表示为：
用向量表示为：
所以上述图像可以表示为：
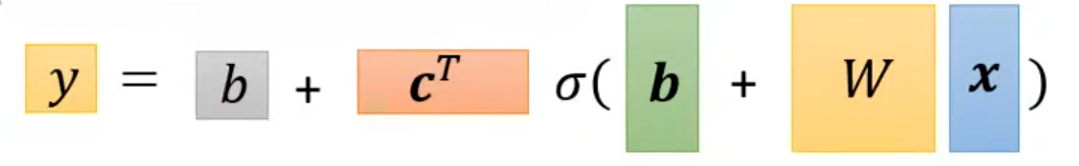
未知参数(Unknown parameters)为：
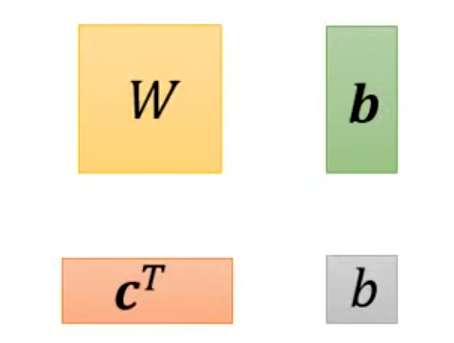
将这些参数排成一列，统一用表示：
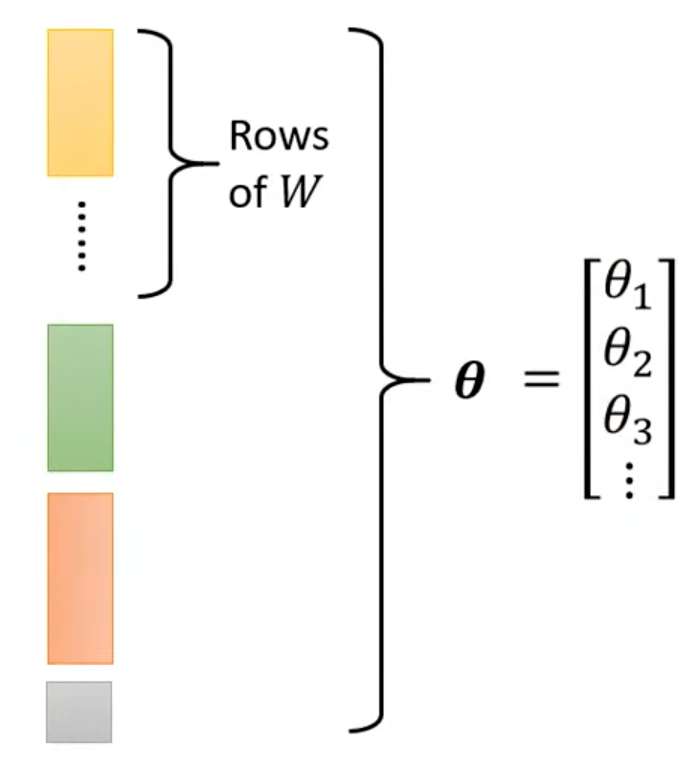
在New Model上的损失函数，计算方法与之前一样；Optimization的步骤也与之前相同，求解：
- 1.(Randomly) Pick initial values
- 2.Compute:
- 3.Update
⭐实际上进行Gradient Descent时并不是直接使用这种 "全数据集算梯度→一次性更新参数"的批量梯度下降(Batch Gradient Descent，BGD)，而是使用随机梯度下降(Stochastic Gradient Descent，SGD)和小批量SGD(Mini-batch SGD)。
不管是 BGD 还是 SGD，核心目的都是最小化损失函数（比如预测房价的误差、分类图片的错误率），通过沿着损失函数的负梯度方向更新模型参数，逐步让模型的预测结果越来越准。两者的唯一区别是用多少样本计算梯度
批量梯度下降(BGD)每次更新参数时，用全部训练样本计算损失函数的梯度，即
随机梯度下降(SGD)每次更新参数时，随机抽取 1 个训练样本计算梯度，用单个样本的梯度代替全量样本的平均梯度，即
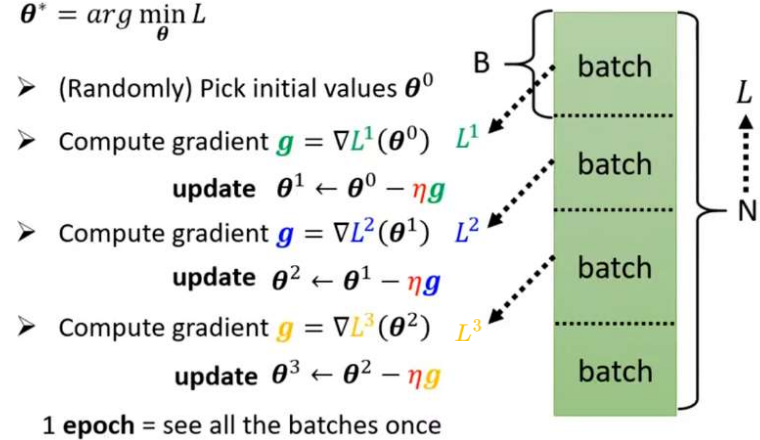
小批量随机梯度下降(Mini-Batch SGD)工程中最常用的折中方案（也常被直接称作 SGD），每次随机抽取 一小批样本（如 32/64/128 个）计算梯度。如下图所示，将N个数据随机分成一组一组的batch，每个batch里有B个数据。每一组batch计算梯度并进行更新(Update)。所有batch均梯度下降更新一轮称为一个epoch。
BGD梯度准确，更新一步就离真实值很近，但需要计算所有样本的梯度，样本多了极慢。使用SGD代替BGD可以大幅降低计算量，提升训练速度，适配大数据集；除此之外，它还可以引入梯度噪声，帮助跳出鞍点 / 平坦区 / 局部最优。
使用New Model得到的最小误差如下：
|-----|--------|-----------|------------|-------------|
| | Linear | 10Sigmoid | 100Sigmoid | 1000Sigmoid |
| 数据集 | 0.32K | 0.32K | 0.28K | 0.27K |
| 测试集 | 0.46K | 0.45K | 0.43K | 0.43K |
可以看到叠加再多的Sigmoid效果也不会显著，甚至不变化。于是继续改进模型：将Sigmoid嵌套做几次，如下图所示。要做几次是一个hyperparameters。
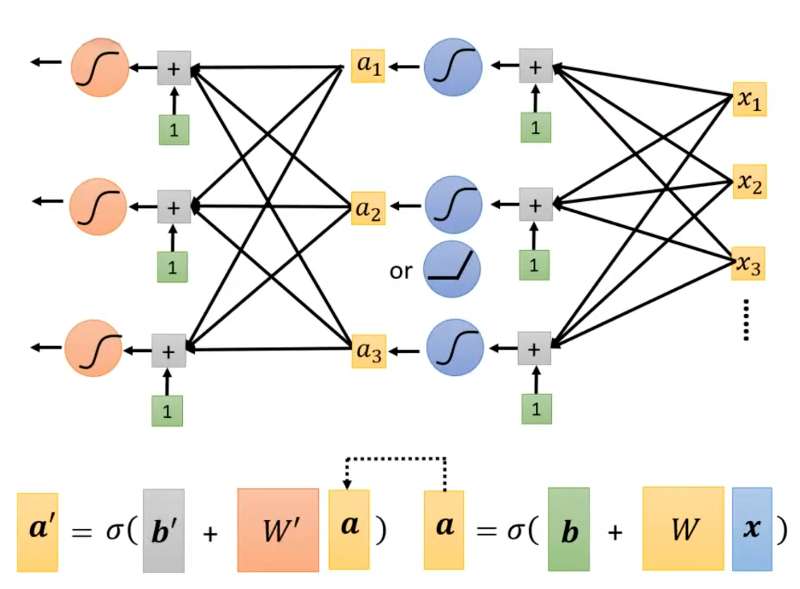
改进Model得到的最小误差如下：
|-----|--------|--------|--------|--------|
| | 1layer | 2layer | 3layer | 4layer |
| 数据集 | 0.28K | 0.18K | 0.14K | 0.10K |
| 测试集 | 0.43K | 0.39K | 0.38K | 0.44K |
上述Sigmoid嵌套的过程称为Neural Network(神经网络) ，Neural Network的Layer(层数) 就是Sigmoid运算了几次。每一步Sigmoid称为一个Neuron(神经元) 。输入经过多层神经元计算得到输出，这整个过程称为深度学习(Deep Learning) 。深度学习发展过程中，神经网络层越叠越多，错误率也从16.4%减少到6.7%。但并不是层数越多越好，上述数据在Layer达到4层时，在数据集误差进一步减小，但在测试集误差却增加了，这称为过拟合(Overfitting)。
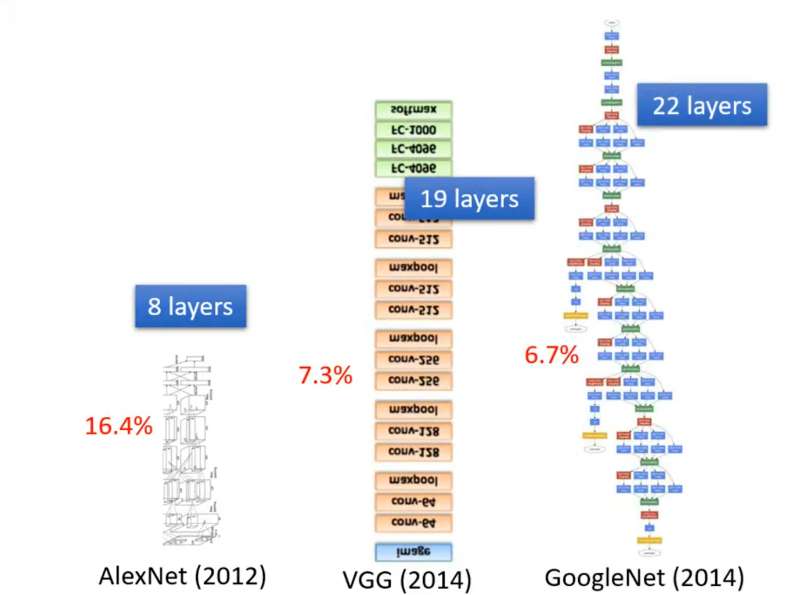
反向传播（Backpropagation, BP）
反向传播(Backpropagation, BP)用于多层神经网络计算参数梯度，它是在神经网络正向传播得到预测值与损失后，依托链式求导法则从输出层向输入层反向逐层计算损失函数对所有权重、偏置的梯度，为梯度下降更新参数提供梯度数据的算法。是神经网络训练的"梯度计算器"，和梯度下降配合完成模型参数优化。
**"正向传播算损失 → 反向传播算梯度 → 梯度下降更新参数"**三步构成神经网络完整训练流程。
反向传播数学根基是链式求导法则：
若函数嵌套为，则复合函数导数为：
而神经网络是多层函数嵌套，BP 就是把这个法则从输出层反向递推到每一层参数，拆解复杂梯度为多层简单梯度的乘积。
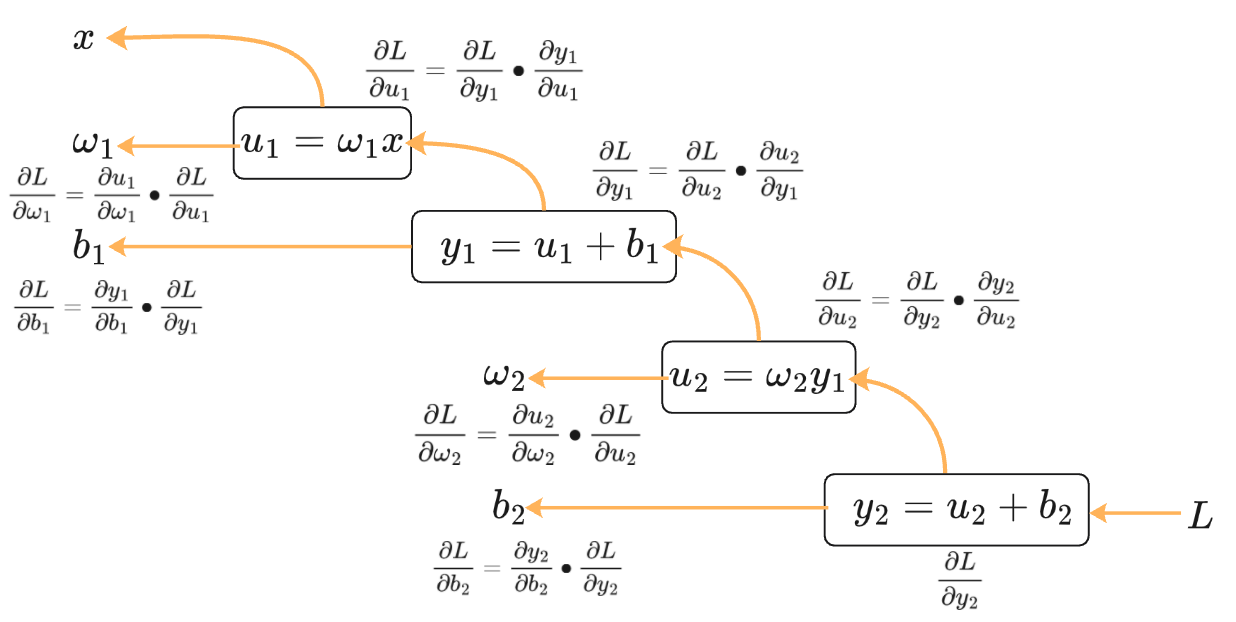
如下两层神经网络(两层Linear Model)计算图。下图为正向传播过程 ，输入数据逐层前向计算，得到模型预测值，计算损失。
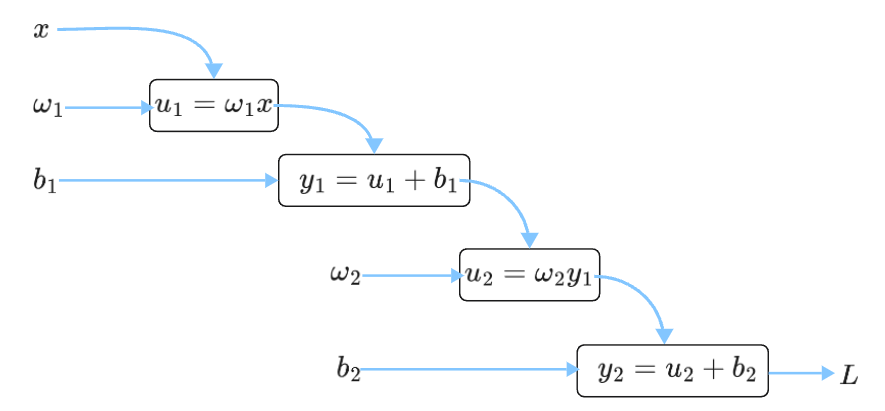
为了更新参数来减小损失函数
。采用梯度下降法必须求出
，使用反向传播求解：
