排序-快速排序

免费版Java学习笔记（28w字）链接：https://www.yuque.com/aoyouaoyou/sgcqr8

免费版Java面试题（20w字）链接：https://www.yuque.com/aoyouaoyou/wh3hto

完整版Java学习笔记200w字，附有代码实现，图解清楚，仅需9.9

完整版Java面试题，150w字，高频面试题，内容详细，仅需9.9

完整版：

https://www.xiaohongshu.com/user/profile/63c2d512000000002601232c

祝您新的一年事事马到成功，身体健康，阖家幸福，大展宏图！

一、快速排序介绍

1. 定位

快速排序和冒泡排序同属交换排序，均通过元素间的比较与交换实现排序，但快速排序是对冒泡排序的极致优化------冒泡排序每轮仅归位1个元素，而快速排序每轮能将数组拆分为两个子区间，大幅减少排序轮次。

2. 思想：分治法（Divide and Conquer）

快速排序的是分治+基准元素划分，步骤可概括为「选基准、划区间、递归治」：

选基准 ：从待排序数组中挑选一个元素作为基准元素（pivot），作为划分区间的依据；
划区间 ：遍历数组，将所有小于基准 的元素移到基准左侧，大于基准的元素移到基准右侧，基准元素最终归位到其排序后的正确位置；
递归治：以基准元素为分界，将数组拆分为左、右两个子区间，分别对两个子区间重复执行「选基准、划区间」操作，直到子区间长度为0或1（天然有序）。

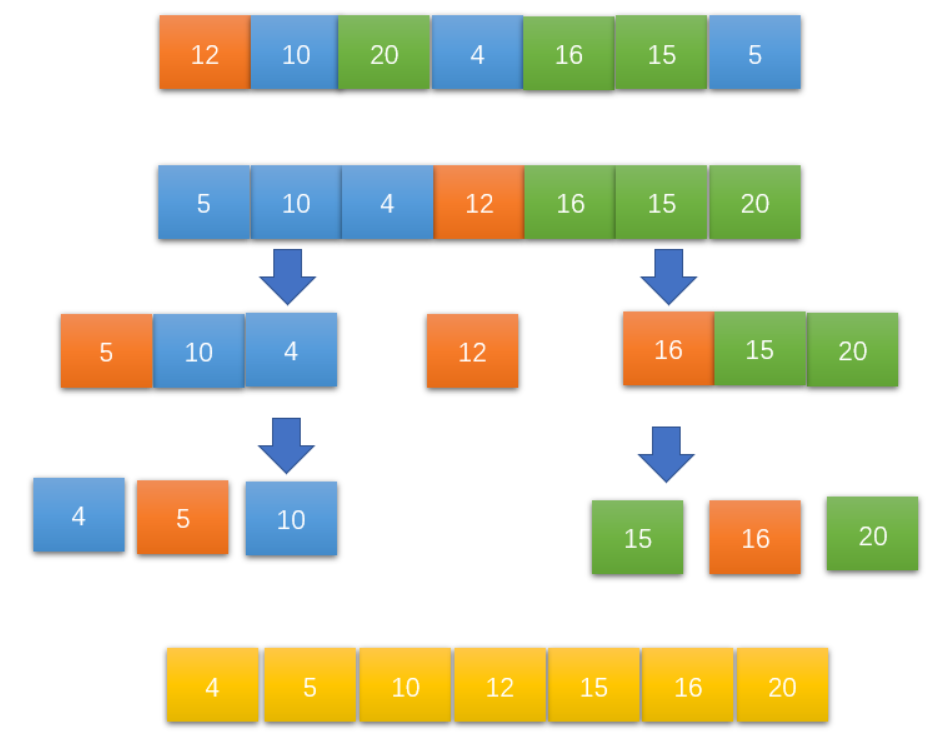
注：橙色为基准元素，蓝色为比基准元素小的元素，绿色比基准元素大的元素。

3. 关键特点

分治思想的典型应用，通过递归将大问题拆解为小问题解决；
属于原地排序（仅需少量临时变量），空间利用率高；
未做特殊处理时为不稳定排序（相同值元素的相对位置可能改变）；
时间复杂度为O(nlogn)，排序效率远高于冒泡排序等O(n²)级算法。

二、快速排序的两个细节

1. 基准元素（pivot）的选择

基准元素的选择直接影响快速排序的效率，理想的基准是能将数组均匀划分为两个等长子区间的元素，常用选择方式：

固定位置：选数组起始位置 或末尾位置的元素（代码实现最简单，本文示例采用）；
随机选择：随机挑选数组中的一个元素，与起始/末尾元素交换位置后再使用（避免数组有序时的效率退化）；
三数取中：选数组起始、中间、末尾三个位置的元素，取其值的中位数作为基准（更易划分为均匀区间）。

2. 区间划分的两种方法

划分区间是快速排序的步骤，实现方式主要有双边循环法 和单边循环法，两者最终目的都是将基准元素归位，并划分出左右子区间，仅实现思路不同。

三、区间划分实现一：双边循环法

1. 思路

从数组左右两侧同时遍历，通过两个指针（left、right）的移动与元素交换，实现区间划分，是「右指针找小值，左指针找大值，找到后交换，最终基准归位」。

2. 具体步骤（基准选起始位置元素，升序排序）

初始化：将基准元素pivot设为数组[startIndex]，左指针left指向startIndex，右指针right指向endIndex；
循环遍历（left ≠ right时）：

- 先移动right指针：若arr[right] > pivot，指针左移；若arr[right] ≤ pivot，right指针停止；
- 再移动left指针：若arr[left] ≤ pivot，指针右移；若arr[left] > pivot，left指针停止；
- 若left < right，交换arr[left]和arr[right]的值，继续循环；

基准归位：当left == right时，交换arr[startIndex]（原基准）和arr[left]（指针重合位置）的值，此时left（right）即为基准的最终位置；
返回结果：返回基准的最终位置pivotIndex，作为左右子区间的分界点。

3. 关键注意点

必须先移动right指针，否则会导致指针重合位置的元素值大于基准，基准归位后划分区间错误；
循环条件需严格判断left < right，避免指针越界。

4. 代码实现

复制代码

import java.util.Arrays;

/**
 * 快速排序 - 双边循环法实现
 */
public class QuickSortDouble {
    // 快速排序主方法，递归实现
    public static void quickSort(int[] arr, int startIndex, int endIndex) {
        // 递归终止条件：子区间长度≤1（天然有序）
        if (startIndex >= endIndex) {
            return;
        }
        // 双边循环划分区间，得到基准元素的最终位置
        int pivotIndex = partition(arr, startIndex, endIndex);
        // 递归排序左子区间（基准左侧，小于基准）
        quickSort(arr, startIndex, pivotIndex - 1);
        // 递归排序右子区间（基准右侧，大于基准）
        quickSort(arr, pivotIndex + 1, endIndex);
    }

    /**
     * 双边循环法 - 区间划分方法
     * @param arr 待排序数组
     * @param startIndex 子区间起始下标
     * @param endIndex 子区间结束下标
     * @return 基准元素的最终位置
     */
    private static int partition(int[] arr, int startIndex, int endIndex) {
        // 选起始位置元素作为基准（可优化为随机选择/三数取中）
        int pivot = arr[startIndex];
        int left = startIndex;  // 左指针
        int right = endIndex;   // 右指针

        while (left != right) {
            // 第一步：移动右指针，找小于等于pivot的元素
            while (left < right && arr[right] > pivot) {
                right--;
            }
            // 第二步：移动左指针，找大于pivot的元素
            while (left < right && arr[left] <= pivot) {
                left++;
            }
            // 第三步：交换左右指针指向的元素
            if (left < right) {
                int temp = arr[left];
                arr[left] = arr[right];
                arr[right] = temp;
            }
        }

        // 基准元素归位：交换起始位置和指针重合位置的元素
        arr[startIndex] = arr[left];
        arr[left] = pivot;

        return left; // 返回基准最终位置
    }

    // 测试主方法
    public static void main(String[] args) {
        int[] arr = new int[]{4,7,3,5,6,2,8,1};
        quickSort(arr, 0, arr.length - 1);
        System.out.println("双边循环法排序结果：" + Arrays.toString(arr));
    }
}

运行结果：双边循环法排序结果：[1, 2, 3, 4, 5, 6, 7, 8]

四、区间划分实现二：单边循环法

1. 思路

从数组一侧（基准下一个位置）单向遍历，通过mark指针标记「小于基准元素的区域边界」，遍历过程中不断扩大该边界，最终实现区间划分，思路比双边循环法更简洁。

2. 具体步骤（基准选起始位置元素，升序排序）

初始化：将基准元素pivot设为数组[startIndex]，mark指针指向startIndex（代表小于pivot的区域初始边界为起始位置）；
单向遍历：从i = startIndex + 1开始，遍历至endIndex：

- 若arr[i] > pivot，直接继续遍历下一个元素；
- 若arr[i] < pivot，先将mark指针右移1位（扩大小于pivot的区域边界），再交换arr[mark]和arr[i]的值；

基准归位：遍历结束后，交换arr[startIndex]（原基准）和arr[mark]的值，此时mark即为基准的最终位置；
返回结果：返回基准的最终位置pivotIndex，作为左右子区间的分界点。

3. 关键注意点

mark指针的作用是界定小于基准的元素区域，仅当找到更小元素时才移动；
遍历从startIndex + 1开始，避免基准元素自身参与比较。

4. 代码实现

复制代码

import java.util.Arrays;

/**
 * 快速排序 - 单边循环法实现（思路更简洁）
 */
public class QuickSortSingle {
    // 快速排序主方法，递归实现
    public static void quickSort(int[] arr, int startIndex, int endIndex) {
        // 递归终止条件：子区间长度≤1
        if (startIndex >= endIndex) {
            return;
        }
        // 单边循环划分区间，得到基准元素的最终位置
        int pivotIndex = partition(arr, startIndex, endIndex);
        // 递归排序左、右子区间
        quickSort(arr, startIndex, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, endIndex);
    }

    /**
     * 单边循环法 - 区间划分方法
     * @param arr 待排序数组
     * @param startIndex 子区间起始下标
     * @param endIndex 子区间结束下标
     * @return 基准元素的最终位置
     */
    private static int partition(int[] arr, int startIndex, int endIndex) {
        // 选起始位置元素作为基准
        int pivot = arr[startIndex];
        int mark = startIndex; // 小于基准的区域边界指针

        // 从基准下一个位置开始单向遍历
        for (int i = startIndex + 1; i <= endIndex; i++) {
            // 找到小于基准的元素，扩大边界并交换
            if (arr[i] < pivot) {
                mark++;
                int temp = arr[mark];
                arr[mark] = arr[i];
                arr[i] = temp;
            }
        }

        // 基准元素归位：交换起始位置和mark指针位置的元素
        arr[startIndex] = arr[mark];
        arr[mark] = pivot;

        return mark; // 返回基准最终位置
    }

    // 测试主方法
    public static void main(String[] args) {
        int[] arr = new int[]{4,7,3,5,6,2,8,1};
        quickSort(arr, 0, arr.length - 1);
        System.out.println("单边循环法排序结果：" + Arrays.toString(arr));
    }
}

运行结果：单边循环法排序结果：[1, 2, 3, 4, 5, 6, 7, 8]

五、时间复杂度与空间复杂度

1. 时间复杂度

快速排序的时间复杂度与基准元素的选择直接相关，为分治的层数×每轮的遍历次数：

最好情况 ：基准每次都能将数组均匀划分为两个等长子区间 ，分治层数为log₂n，每轮遍历n个元素，时间复杂度为 O(nlogn)；
最坏情况 ：数组完全有序/逆序 ，且基准选固定起始/末尾元素，此时数组被划分为「n-1个元素」和「0个元素」的子区间，分治层数为n，时间复杂度退化为 O(n²)（可通过随机选基准/三数取中避免）；
平均情况 ：工程中最常见的场景，时间复杂度为 O(nlogn)（快速排序的时间复杂度）。

2. 空间复杂度

快速排序的空间消耗主要来自递归调用的栈空间：

最好情况：递归层数为log₂n，空间复杂度为 O(logn)；
最坏情况：递归层数为n，空间复杂度为 O(n)；
平均情况：空间复杂度为 O(logn)。

优化：可通过「尾递归优化」或「非递归实现（手动模拟栈）」减少栈空间消耗。

六、特性与适用场景

1. 优点

效率极高：时间复杂度O(nlogn)，在随机数据下排序速度优于归并排序、堆排序，是实际开发中最常用的排序算法；
原地排序：仅需少量临时变量，空间复杂度低（O(logn)），无需额外开辟数组；
实现灵活：区间划分有多种方式，基准选择可根据场景优化，适配不同数据特点。

2. 缺点

不稳定排序：相同值的元素在排序后可能改变相对位置（若需稳定，可在交换时增加等值判断，或选择归并排序）；
极端情况效率退化：固定选基准时，有序数组会导致效率退化为O(n²)（可通过随机选基准/三数取中解决）；
递归实现：数据量极大时可能触发栈溢出（可通过非递归实现解决）。

3. 适用场景

快速排序是工业级主流排序算法，适用于：

处理大规模随机数据的排序（如百万/千万级数据）；
对空间利用率要求较高的场景（原地排序）；
无需保持相同值元素相对位置的场景（非稳定排序可接受）。

JDK中的应用 ：JDK 1.8的Arrays.sort()方法中，对基本数据类型数组的排序采用双轴快速排序（快速排序的优化版，选两个基准元素，划分为三个区间），效率比传统快速排序更高。

七、快速排序与冒泡排序的对比

作为同属交换排序的算法，两者的差异体现在效率、思路、适用场景等方方面面，是O(nlogn)与O(n²)级算法的典型对比：

|-------|------------------------|-------------------------|
| 对比维度 | 快速排序 | 冒泡排序 |
| 思想 | 分治法+基准划分，每轮归位1个基准并拆分区间 | 相邻元素两两交换，每轮仅归位1个最大/最小元素 |
| 时间复杂度 | O(nlogn) | O(n²) |
| 空间复杂度 | O(logn)（递归栈） | O(1)（纯原地） |
| 排序稳定性 | 不稳定（可优化为稳定） | 稳定 |
| 遍历方式 | 分治递归，按需遍历子区间 | 双层循环，全量遍历 |
| 适用场景 | 大规模、随机数据排序（工业主流） | 小规模、基本有序数据排序（入门教学） |

八、总结

快速排序是交换排序 的高效实现，思想为分治法，通过「选基准、划区间、递归治」实现排序，每轮归位1个基准并拆分数组；
区间划分是步骤，有双边循环法 （左右双指针）和单边循环法（单指针+边界标记）两种实现，单边循环法思路更简洁；
基准元素的选择影响效率，固定选起始/末尾易导致有序数组效率退化，工程中常用随机选择 或三数取中优化；
快速排序为原地、不稳定排序，时间复杂度O(nlogn)，空间复杂度O(logn)，是工业开发中处理大规模随机数据的主流排序算法；
与冒泡排序相比，快速排序通过分治大幅减少了比较和交换次数，效率提升数个量级，是O(nlogn)级算法的典型代表。