52.携带研究材料（卡码网）
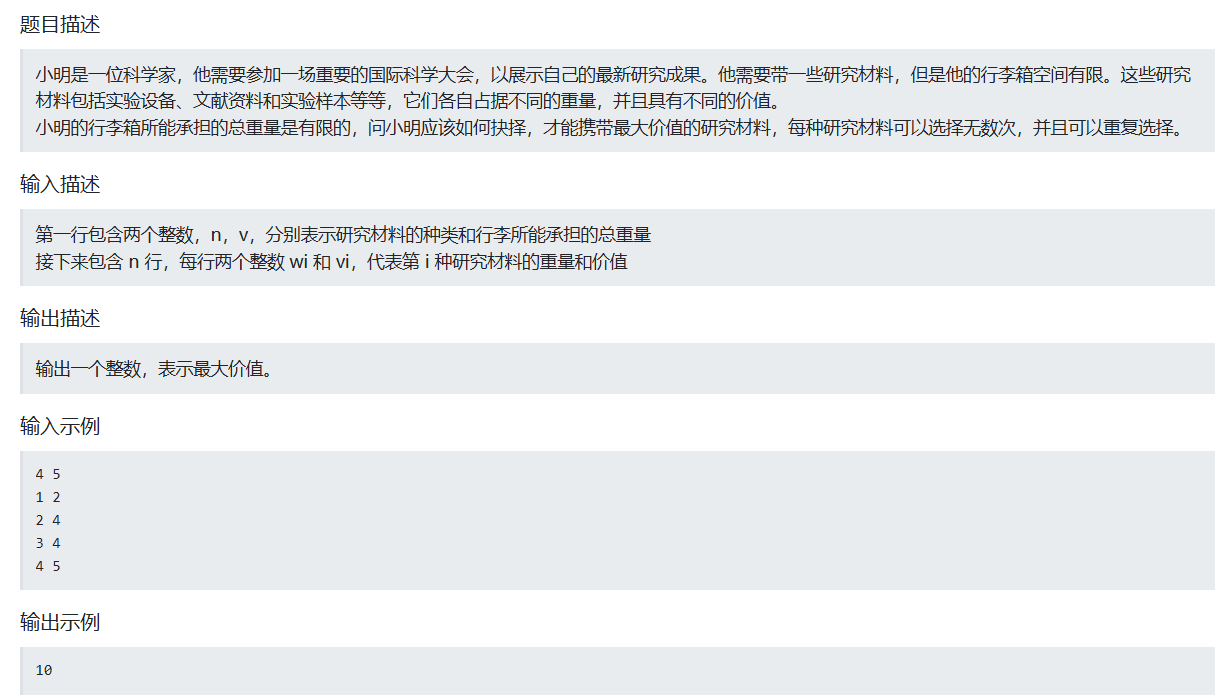
题目链接
携带研究材料
https://kamacoder.com/problempage.php?pid=1052
核心思路
1，确定dp数组及其下标含义
定义一个一维dp数组，下标表示背包大小。
2，确定递推公式
因为完全背包的物品是无限个，所以放完了一个，还能在同一层找。
二维递推公式写法：dp i j = max(dp i - 1 j , dp i j - w\[ i ] + v i )
一维递推公式写法：dp j = max(dp j , dp j - w\[ i ] + v i )
4，初始化数组
全部为0
3，确定循环顺序
因为完全背包物品有无限个，所以遍历背包可以正序遍历，这样正好默认是在同一层
易错点
一维递推公式写法：dp j = max(dp j , dp j - w\[ i ] + v i )
518.零钱兑换||
题目链接
零钱兑换||https://leetcode.cn/problems/coin-change-ii/description/
核心思路
1，定义一维dp数组，dp j 为填满背包大小为 j 的背包的组合数有dp j 种。
2，确定递推公式
因为求的是方法有多少种，所以用累加的形式：
dp j = dp j + dp j - w\[ i ];
表示填满当前背包有两种来源：
不放物品 i ，那么就是dp j 。
放物品 i ，那么就是dp j - w\[ i ]。
3，初始化dp数组
dp0 = 1;
4，确定遍历方向
先遍历物品，再遍历背包。背包是正序遍历
易错点
1,背包大小要从w i 开始，放不进就默认dp j
2,dp数组的类型为unsigned long long
377.组合总和IV
题目链接
组合总和IVhttps://leetcode.cn/problems/combination-sum-iv/description/
核心思路
1，定义一个一维dp数组，dp j 表示当背包为 j 时，排列数为多少个
2，确定递推公式dp j = dp j + dp j - w\[ i ];
3，初始化dp数组
dp 0 = 0
4，确定遍历顺序
因为求的是排列数，对顺序有要求，那我们就考虑填满每个背包大小的最后一个值是什么。因为每个背包大小都要考虑，所以物品在内层循环。
易错点
1,dp数组的类型为unsigned long long
2，遍历顺序为，背包在外，物品在内
57.爬楼梯（卡码网）
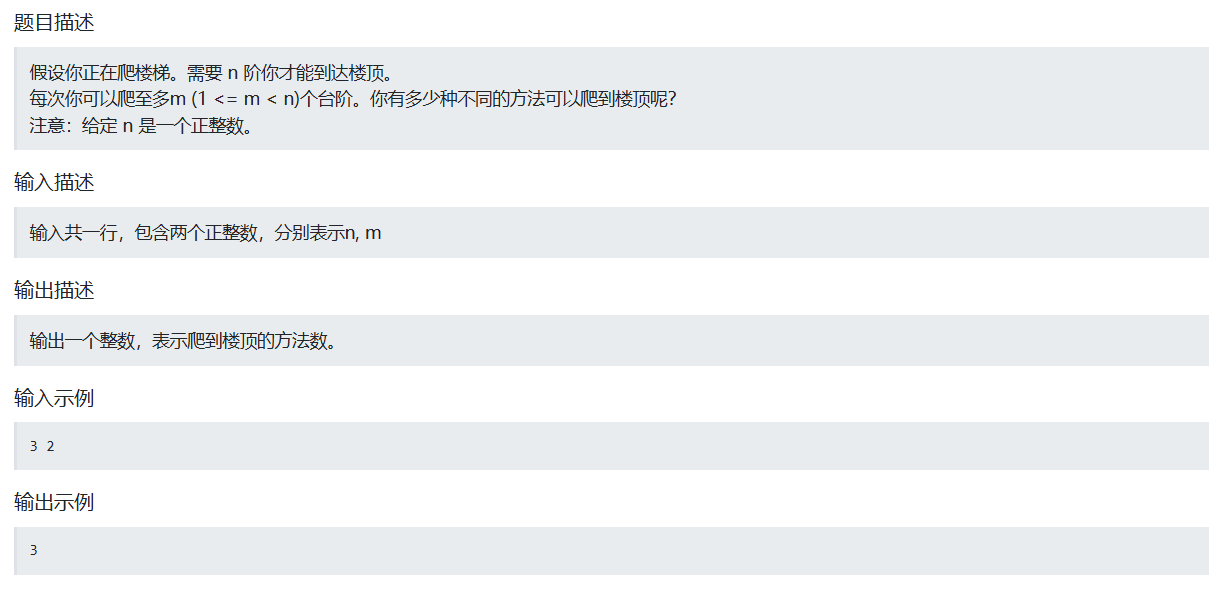
题目链接
爬楼梯（卡码网）https://kamacoder.com/problempage.php?pid=1067
核心思路
1，确定一维dp数组及其下标含义
dp j 表示爬上台阶为 j 总共有 dp j 种方法
2，推导递推公式dp j = dp j + dp j - w\[ i ];
3,初始化数组
dp0 = 0
4，确定遍历顺序
因为是排列数，所以物品放内，背包放外
易错点
1，台阶个数是背包大小，一次可以爬多少个台阶是物品。
2，初始化了台阶个数为0时的方法，所以背包从1开始
3，物品从1开始，小于等于m。