官方文档链接:https://developer.mozilla.org/zh-CN/docs/Web/SVG/Reference/Attribute/d#path
路径命令是对要绘制的路径的说明。每一个命令由代表命令的字母和代表参数的数字组成。
SVG 定义了六种路径命令类型,一共 20 条命令:
MoveTo:M、m
LineTo:L、l、H、h、V、v
三次贝塞尔曲线:C、c、S、s
二次贝塞尔曲线:Q、q、T、t
椭圆曲线:A、a
ClosePath:Z、z
备注:命令是大小写敏感的。大写的命令指定绝对坐标,而小写命令指定相对(于当前位置的)坐标。
备注:命令是大小写敏感的。大写的命令指定绝对坐标,而小写命令指定相对(于当前位置的)坐标。
始终可以将负值作为命令的参数:
负的角度是逆时针的;
绝对坐标中,负的 x 和 y 将被解释为负坐标;
相对坐标中,负的 x 值为向左移动,负的 y 值为向上移动。

Lineto 路径命令
Lineto 指令将绘制一条直线段。这个直线段从当前位置 (Po ; {xo , yo })移到指定位置 (Pn ; {xn , yn })。然后,指定位置 (Pn )将变成下一个命令中的当前位置 (Po′)。
| 命令 | 参数 | 备注 |
| L | (x, y)+ | 在当前位置 和指定位置 x,y 之间绘制一条线段。后续子坐标序列将被解释为隐式的绝对位置的 LineTo(L)命令的参数。 公式: Po′ = Pn = {x, y} |
| l | (dx, dy)+ | 在当前位置 和指定位置 之间绘制一条线段,指定位置 为当前位置 沿 x 轴偏移 dx 以及沿 y 轴偏移 dy 处。后续子坐标序列将被解释为隐式的相对位置的 LineTo(L)命令的参数。 公式: Po′ = Pn = {xo + dx, yo + dy} |
| H | x+ | 在当前位置 与指定位置 之间绘制一条水平线段。指定位置 由 x 参数和当前位置 的 y 坐标指定。后续子序列的值将被解释为隐式的绝对位置的 LineTo(H)命令的参数。 公式: Po′ = Pn = {x, yo} |
| h | dx+ | 在当前位置 与指定位置 之间绘制一条水平线段。指定位置 由当前位置 沿 x 轴偏移 dx 的 x 坐标和当前位置 的 y 坐标指定。后续子序列的值将被解释为隐式的相对位置的 LineTo(h)命令的参数。 公式: Po′ = Pn = {xo + dx, yo} |
| V | y+ | 在当前位置 与指定位置 之间绘制一条垂直线段。指定位置 由 y 参数和当前位置 的 x 坐标指定。后续子序列的值将被解释为隐式的绝对位置的 LineTo(V)命令的参数。 公式: Po′ = Pn = {xo, y} |
| v | dy+ |
在当前位置 与指定位置 之间绘制一条垂直线段。指定位置 由当前位置 沿 y 轴偏移 dy 的 y 坐标和当前位置 的 x 坐标指定。后续子序列的值将被解释为隐式的相对位置的 LineTo(v)命令的参数。 公式: Po′ = Pn = {xo, yo + dy} |
|---|
示例
html
<svg viewBox="0 0 200 100" xmlns="http://www.w3.org/2000/svg">
<!-- 使用绝对坐标的 LineTo 命令 -->
<path
fill="none"
stroke="red"
d="M 10,10
L 90,90
V 10
H 50" />
<!-- 使用相对坐标的 LineTo 命令 -->
<path
fill="none"
stroke="red"
d="M 110,10
l 80,80
v -80
h -40" />
</svg>
三次贝塞尔曲线
三次 贝塞尔曲线是使用四个点定义的平滑曲线:
(Po = {xo , yo})
(Pn = {xn , yn})
(Pcs = {xcs , ycs})(控制在起点附近的曲线的曲率)
(Pce = {xce , yce})(控制在终点附近的曲线的曲率)
绘制后,终点 (Pn )将成为下一个命令中的当前位置 (Po′)。
| 命令 | 参数 | 备注 |
| C | (x1,y1, x2,y2, x,y)+ | 在当前位置 和终点 x,y 之间绘制一条三次贝塞尔曲线。起始控制点 通过 x1,y1 指定,而终点控制点 通过 x2,y2 指定。后续的三元组坐标序列将被解释为隐式的绝对位置的三次贝塞尔曲线(C)命令的参数。 公式: Po′ = Pn = {x, y} ; Pcs = {x1, y1} ; Pce = {x2, y2} |
| c | (dx1,dy1, dx2,dy2, dx,dy)+ | 在当前位置 和终点 (终点 为当前位置 沿 x 轴偏移 dx 以及沿 y 轴偏移 dy 处)之间绘制一条三次贝塞尔曲线。起始控制点 为当前位置 沿 x 轴偏移 dx1 以及沿 y 轴偏移 dy1 处;而终点控制点 为当前位置 沿 x 轴偏移 dx2 以及沿 y 轴偏移 dy2 处。后续的三元组坐标序列将被解释为隐式的相对位置的三次贝塞尔曲线(c)命令的参数。 公式: Po′ = Pn = {xo + dx, yo + dy} ; Pcs = {xo + dx1, yo + dy1} ; Pce = {xo + dx2, yo + dy2} |
| S | (x2,y2, x,y)+ | 在当前位置 和终点 x,y 之间绘制一条平滑的三次贝塞尔曲线。终点控制点 通过 x2,y2 指定。起始控制点 是上一条曲线命令的终点控制点 在当前位置 上的反射点;若上一条命令不是曲线命令,则其与曲线的起始点(当前位置 )相同。后续成对的坐标序列将被解释为隐式的绝对位置的平滑三次贝塞尔曲线(S)命令的参数。 |
| s | (dx2,dy2, dx,dy)+ |
在当前位置 和终点 (终点 为当前位置 沿 x 轴偏移 dx 以及沿 y 轴偏移 dy 处)之间绘制一条平滑的三次贝塞尔曲线。终点控制点 为当前位置 沿 x 轴偏移 dx2 以及沿 y 轴偏移 dy2 处。起始控制点 是上一条曲线命令的终点控制点 在当前位置 上的反射点;若上一条命令不是曲线命令,则其与曲线的起始点(当前位置 )相同。后续成对的坐标序列将被解释为隐式的相对位置的平滑三次贝塞尔曲线(s)命令的参数。 |
|---|
示例
html
<svg
viewBox="0 0 200 100"
xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink">
<!-- 使用绝对坐标的三次贝塞尔曲线 -->
<path
fill="none"
stroke="red"
d="M 10,90
C 30,90 25,10 50,10
S 70,90 90,90" />
<!-- 使用相对坐标的三次贝塞尔曲线 -->
<path
fill="none"
stroke="red"
d="M 110,90
c 20,0 15,-80 40,-80
s 20,80 40,80" />
<!-- 高亮显示曲线顶点和控制点 -->
<g id="ControlPoints">
<!-- 第一段三次贝塞尔曲线的控制点 -->
<line x1="10" y1="90" x2="30" y2="90" stroke="lightgrey" />
<circle cx="30" cy="90" r="1.5" />
<line x1="50" y1="10" x2="25" y2="10" stroke="lightgrey" />
<circle cx="25" cy="10" r="1.5" />
<!-- 第二段平滑三次贝塞尔曲线的控制点(第一个是隐式的) -->
<line
x1="50"
y1="10"
x2="75"
y2="10"
stroke="lightgrey"
stroke-dasharray="2" />
<circle cx="75" cy="10" r="1.5" fill="lightgrey" />
<line x1="90" y1="90" x2="70" y2="90" stroke="lightgrey" />
<circle cx="70" cy="90" r="1.5" />
<!-- 曲线顶点 -->
<circle cx="10" cy="90" r="1.5" />
<circle cx="50" cy="10" r="1.5" />
<circle cx="90" cy="90" r="1.5" />
</g>
<use xlink:href="#ControlPoints" x="100" />
</svg>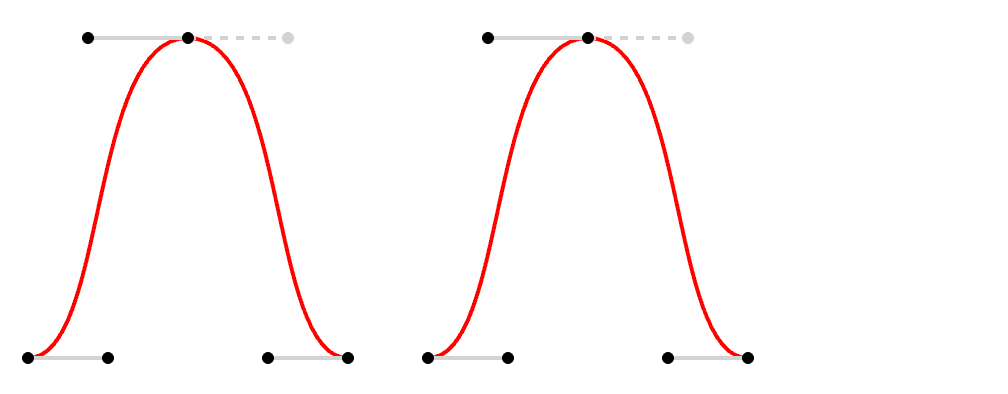
二次贝塞尔曲线
二次 贝塞尔曲线是使用三个点定义的平滑曲线:
Po = {xo , yo}
Pn = {xn , yn}
Pc = {xc , yc}(控制曲率)
绘制后,终点 (Pn )将成为下一个命令中的当前位置 (Po′)。
| 命令 | 参数 | 备注 |
| Q | (x1,y1, x,y)+ | 在当前位置 和终点 x,y 之间绘制一条二次贝塞尔曲线。控制点 通过 x1,y1 指定。后续成对的坐标序列将被解释为隐式的绝对位置的二次贝塞尔曲线(Q)命令的参数。 公式: Po′ = Pn = {x, y} ; Pc = {x1, y1} |
| q | (dx1,dy1, dx,dy)+ | 在当前位置 和终点 (终点 为当前位置 沿 x 轴偏移 dx 以及沿 y 轴偏移 dy 处)之间绘制一条二次贝塞尔曲线。控制点 为当前位置 (曲线的起始点)沿 x 轴偏移 dx1 以及沿 y 轴偏移 dy1 处。后续成对的坐标序列将被解释为隐式的相对位置的二次贝塞尔曲线(q)命令的参数。 公式: Po′ = Pn = {xo + dx, yo + dy} ; Pc = {xo + dx1, yo + dy1} |
| T | (x,y)+ | 在当前位置 和终点 x,y 之间绘制一条平滑的二次贝塞尔曲线。控制点 是上一条曲线命令的控制点 在当前位置 上的反射点;若上一条命令不是曲线命令,则其与曲线的起始点(当前位置 )相同。后续的坐标序列将被解释为隐式的绝对位置的平滑二次贝塞尔曲线(T)命令的参数。 公式: Po′ = Pn = {x, y} |
| t | (dx,dy)+ |
在当前位置 和终点 (终点 为当前位置 沿 x 轴偏移 dx 以及沿 y 轴偏移 dy 处)之间绘制一条平滑的二次贝塞尔曲线。控制点 是上一条曲线命令的控制点 在当前位置 上的反射点;若上一条命令不是曲线命令,则其与曲线的起始点(当前位置 )相同。后续的坐标序列将被解释为隐式的相对位置的平滑二次贝塞尔曲线(t)命令的参数。 公式: Po′ = Pn = {xo + dx, yo + dy} |
|---|
示例
html
<svg
viewBox="0 0 200 100"
xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink">
<!-- 二次贝塞尔曲线,带有隐式重复 -->
<path
fill="none"
stroke="red"
d="M 10,50
Q 25,25 40,50
t 30,0 30,0 30,0 30,0 30,0" />
<!-- 高亮显示曲线顶点和控制点 -->
<g>
<polyline points="10,50 25,25 40,50" stroke="rgba(0,0,0,.2)" fill="none" />
<circle cx="25" cy="25" r="1.5" />
<!-- 曲线顶点 -->
<circle cx="10" cy="50" r="1.5" />
<circle cx="40" cy="50" r="1.5" />
<g id="SmoothQuadraticDown">
<polyline
points="40,50 55,75 70,50"
stroke="rgba(0,0,0,.2)"
stroke-dasharray="2"
fill="none" />
<circle cx="55" cy="75" r="1.5" fill="lightgrey" />
<circle cx="70" cy="50" r="1.5" />
</g>
<g id="SmoothQuadraticUp">
<polyline
points="70,50 85,25 100,50"
stroke="rgba(0,0,0,.2)"
stroke-dasharray="2"
fill="none" />
<circle cx="85" cy="25" r="1.5" fill="lightgrey" />
<circle cx="100" cy="50" r="1.5" />
</g>
<use xlink:href="#SmoothQuadraticDown" x="60" />
<use xlink:href="#SmoothQuadraticUp" x="60" />
<use xlink:href="#SmoothQuadraticDown" x="120" />
</g>
</svg>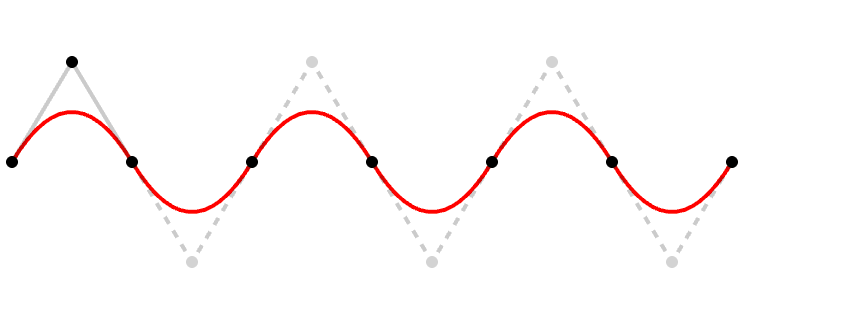
椭圆曲线
椭圆曲线是定义为椭圆的一部分的曲线。有时,使用椭圆曲线绘制高度规则的曲线会比使用贝塞尔曲线更容易。
| 命令 | 参数 | 备注 |
| A | (rx ry angle large-arc-flag sweep-flag x y)+ | 在当前位置和坐标 x,y 之间绘制一条椭圆曲线。用于绘制圆弧的椭圆中心根据命令的其他参数确定: * rx 和ry 是椭圆的两个半径; * angle 表示椭圆相对于 x 轴的旋转角度; * large-arc-flag 和 sweep-flag 允许选择必须绘制的弧线,因为其他参数可以绘制 4 条可能的弧线。 * large-arc-flag 允许选择一个大弧线(1)或一个小弧线(0), * sweep-flag 允许选择一条顺时针旋转的弧线(1)或一条逆时针旋转的弧线(0) 坐标 x,y 将成为下一个命令中的当前位置。后续参数集合的序列将被解释为隐式的绝对位置的椭圆曲线(A)命令的参数。 |
| a | (rx ry angle large-arc-flag sweep-flag dx dy)+ |
在当前位置和指定位置之间绘制一条椭圆曲线。指定位置为当前位置沿 x 轴偏移 dx 以及沿 y 轴偏移 dy 处。用于绘制圆弧的椭圆中心根据命令的其他参数确定: * rx 和 ry 是椭圆的两个半径; * angle 表示椭圆相对于 x 轴的旋转角度; * large-arc-flag 和 sweep-flag 允许选择必须绘制的弧线,因为其他参数可以绘制 4 条可能的弧线。 * large-arc-flag 允许选择一个大弧线(1)或一个小弧线(0), * sweep-flag 允许选择一条顺时针旋转的弧线(1)或一条逆时针旋转的弧线(0) 当前位置沿 x 轴偏移 dx 以及沿 y 轴偏移后的位置将成为下一个命令中的当前位置。后续参数集合的序列将被解释为隐式的相对位置的椭圆曲线(a)命令的参数。 |
|---|
示例
html
<svg viewBox="0 0 20 20" xmlns="http://www.w3.org/2000/svg">
<!-- 通过弧形标志绘制不同的弧形路径 -->
<path
fill="none"
stroke="red"
d="M 6,10
A 6 4 10 1 0 14,10" />
<path
fill="none"
stroke="lime"
d="M 6,10
A 6 4 10 1 1 14,10" />
<path
fill="none"
stroke="purple"
d="M 6,10
A 6 4 10 0 1 14,10" />
<path
fill="none"
stroke="pink"
d="M 6,10
A 6 4 10 0 0 14,10" />
</svg>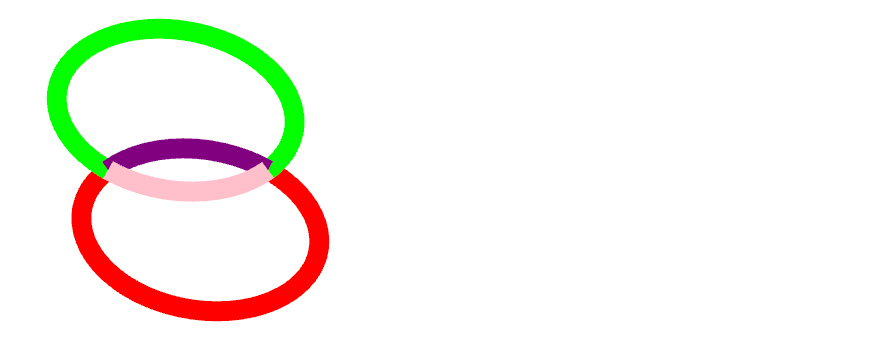
ClosePath
ClosePath 命令将从当前位置绘制一条直线到路径中的第一个点。
| 命令 | 参数 | 备注 |
| Z, z | 通过连接路径的最后一个点与路径的起始点来闭合当前的子路径。如果这两个点的坐标不同,则在两者之间绘制一条直线。 |
|---|
备注: 使用 ClosePath 命令闭合的形状的外观可能与使用其他命令向起始点绘制一条线而闭合的形状不同,因为前者是将线条的末端连接在一起(根据 stroke-linejoin 的设置),而不是仅仅绘制到坐标点上。
示例
html
<svg viewBox="0 -1 30 11" xmlns="http://www.w3.org/2000/svg">
<!--
一个起点和终点不同的开放形状
-->
<path
stroke="red"
d="M 5,1
l -4,8 8,0" />
<!--
一个起点和终点相同的开放形状
-->
<path
stroke="red"
d="M 15,1
l -4,8 8,0 -4,-8" />
<!--
一个起点和终点不同的闭合形状
-->
<path
stroke="red"
d="M 25,1
l -4,8 8,0
z" />
</svg>