- 前言
- 数组和指针
-
- 概念
- 指针数组和数组指针
- 函数指针和函数指针数组
- 数组和指针的关系
- [const 和 指针](#const 和 指针)
- strlen和字符数组
- 一些练习题
- 库函数模拟实现
- 内存对齐
- 数据存储
- 编译链接
前言
博主之前也写过很多C语言的文章,但都是一两年前的事情了。当初的文章还是很青涩,内容也有一些差错。如今学习完C/C++核心内容再回头去总结他们的重点。接下来按重要程度逐个回顾。
数组和指针
概念
- 数组
数组是一种线性数据结构,用于存储相同类型的元素集合。元素通过索引(通常从0开始)访问,内存中连续分配,支持高效随机访问。
- 指针
指针是一种变量,用于存储另一个变量的内存地址。通过指针可以直接访问或修改该地址的数据,常用于动态内存分配、数组操作和函数参数传递等场景。
指针数组和数组指针
要判断指针数组和数组指针我们先回到操作符的优先级:[]的优先级高于*。
因为不加括号的情况下type * arrname[] 是指针数组。
cpp
//指针数组
int main() {
int a, b, c;
int* arr[] = { &a,&b,&c };
for (auto e : arr)cout << e << ' ';
cout << endl;
return 0;
}输出:
000000A09D95FB54 000000A09D95FB74 000000A09D95FB94加了括号则是数组指针:
cpp
int main() {
int arr[] = { 1,2,3,4,5 };
int (*ptr)[5] = &arr;
cout << ptr << endl;
cout << **ptr << ' ' << *(*ptr + 1) << ' ' << (*ptr)[2] << endl;
cout << endl;
return 0;
}输出:
0000000BEB17F798
1 2 3函数指针和函数指针数组
继续回到操作符的优先级。()的优先级高于*
- 因此不加括号就是返回指针的函数:
cpp
int* ptr() {
int* a = new int(4);
return a;
}
int main() {
cout << ptr() << endl;
return 0;
}输出:
cpp
000002C1B1227F10- 加了括号就是函数指针:
cpp
void test() {
cout << "hello world" << endl;
}
int main() {
void (*ptr)() = test;
ptr();
return 0;
}输出:
hello world- 函数指针数组
首先他既然是一个数组,那么我们就要先和[]结合,其次他是(xx指针)数组,因此我们要和*结合,再给出xx的类型:
cpp
void test1() {
cout << 1 << endl;
}
void test2() {
cout << 2 << endl;
}
int main() {
void(*arr[])() = {test1,test2};
for (auto e : arr) {
e();
}
return 0;
}输出:
1
2这里arr就是所谓的转接表。如果你类型太复杂,我们可以进行typedef:
cpp
typedef void(*Test)();
void test1() {
cout << 1 << endl;
}
void test2() {
cout << 2 << endl;
}
int main() {
Test arr[] = {test1,test2};
for (auto e : arr) {
e();
}
return 0;
}输出:
1
2数组和指针的关系
一维数组名大多时候能看作指针:
cpp
int arr[5] = {1,2,3,4,5};
int* p = arr; // 合法:arr隐式转换为&arr[0],p指向首元素
// 以下操作完全等价,数组的下标访问本质是指针偏移
cout << arr[2] << endl; // 3:数组下标访问
cout << *(arr+2) << endl;// 3:数组名转指针后,指针+偏移解引用
cout << p[2] << endl; // 3:指针也支持下标访问(语法糖)
cout << *(p+2) << endl; // 3:指针标准偏移解引用但他们的类型是不同的:
cpp
int main() {
int arr[5] = { 1,2,3,4,5 };
int* p = arr;
cout << typeid(arr).name() << endl;
cout << typeid(p).name() << endl;
return 0;
}输出
int [5]
int * __ptr64类型不同能带来非常多的不同:
cpp
int arr[5] = {1,2,3,4,5};
int* p = arr;
// 场景1:sizeof(数组名) ------ 计算整个数组的内存大小(字节)
cout << sizeof(arr) << endl; // 20(5*4):arr是数组,计算整体大小
cout << sizeof(p) << endl; // 8(64位):p是指针,仅计算指针本身大小
// 场景2:&数组名 ------ 获取整个数组的地址(类型为int (*)[5],数组指针)
cout << &arr << endl; // 数组首地址(如0x7ffeefbff560)
cout << arr << endl; // 首元素地址(同上面值,类型不同)
cout << &arr[0] << endl; // 首元素地址(同上面值)
// 关键:&arr + 1 偏移整个数组大小,arr + 1 偏移一个元素大小
cout << &arr + 1 << endl; // 0x7ffeefbff560 + 20 = 0x7ffeefbff574
cout << arr + 1 << endl; // 0x7ffeefbff560 + 4 = 0x7ffeefbff564
// 场景3:decltype(数组名) ------ 推导类型为数组类型(int[5])
decltype(arr) a; // 合法:a的类型是int[5],定义一个同类型数组
decltype(p) b; // 合法:b的类型是int*,定义一个同类型指针此外还有一个关键陷阱:数组传参自动退化为指针,函数内无法用 sizeof 求真实长度,必须额外传长度
const 和 指针
const和指针的关系让人又恨又恨,三种排列:
cpp
const int *;
int const *;
int * const;要区分这三者,我们只需要知道,const的修饰原则:
const 修饰其「左侧紧邻」的对象;若 const 在最左侧,默认修饰其右侧紧邻的类型。
速看:


以及:

那么const int *修饰的变量就一定不能修改吗,也不尽然:
cpp
int main() {
int a = 10;
const int * p = &a;
*(int *)p = 1;
cout << a << endl;
return 0;
}1strlen和字符数组
我们直接上代码:
cpp
int main() {
const char str1[] = "miss";
const char* str2 = "you!";
cout << "str1 sizeof:" << sizeof(str1) << " strlen:" << strlen(str1) << endl;
cout << "str2 sizeof:" << sizeof(str2) << " strlen:" << strlen(str2) << endl;
return 0;
}str1 sizeof:5 strlen:4
str2 sizeof:8 strlen:4因为我们每个字符串结尾都有终止符\0.所以sizeof算出来是5,而strlen算出来是4.
一些练习题
- 一维数组
cpp
int a[] = {1,2,3,4};
printf("%d\n",sizeof(a));
printf("%d\n",sizeof(a+0));
printf("%d\n",sizeof(*a));
printf("%d\n",sizeof(a+1));
printf("%d\n",sizeof(a[1]));
printf("%d\n",sizeof(&a));
printf("%d\n",sizeof(*&a));
printf("%d\n",sizeof(&a+1));
printf("%d\n",sizeof(&a[0]));
printf("%d\n",sizeof(&a[0]+1));输出:
16
8
4
8
4
8
16
8
8
8为了凸显不同,这里是x64。
- 字符数组
cpp
char arr[] = { 'a','b','c','d','e','f' };
printf("%d\n", sizeof(arr));
printf("%d\n", sizeof(arr + 0));
printf("%d\n", sizeof(*arr));
printf("%d\n", sizeof(arr[1]));
printf("%d\n", sizeof(&arr));
printf("%d\n", sizeof(&arr + 1));
printf("%d\n", sizeof(&arr[0] + 1));6
8
1
1
8
8
8
cpp
char arr[] = { 'a','b','c','d','e','f' }
printf("%d\n", strlen(arr));
printf("%d\n", strlen(arr + 0));
printf("%d\n", strlen(*arr));
printf("%d\n", strlen(arr[1]));
printf("%d\n", strlen(&arr));
printf("%d\n", strlen(&arr + 1));
printf("%d\n", strlen(&arr[0] + 1));这个一堆类型不匹配,一堆随机值。
cpp
char arr[] = "abcdef";
printf("%d\n", sizeof(arr));
printf("%d\n", sizeof(arr+0));
printf("%d\n", sizeof(*arr));
printf("%d\n", sizeof(arr[1]));
printf("%d\n", sizeof(&arr));
printf("%d\n", sizeof(&arr+1));
printf("%d\n", sizeof(&arr[0]+1));7
8
1
1
8
8
8- 二维数组
cpp
int main() {
int a[3][4] = { 0 };
printf("%d\n", sizeof(a));
printf("%d\n", sizeof(a[0][0]));
printf("%d\n", sizeof(a[0]));
return 0;
}48
4
16- 指针运算
cpp
int main()
{
int a[5] = { 1, 2, 3, 4, 5 };
int* ptr = (int*)(&a + 1);
printf("%d,%d", *(a + 1), *(ptr - 1));
return 0;
}2,5x86环境下:
cpp
struct Test
{
int Num;
char* pcName;
short sDate;
short sBa[4];
}*p = (struct Test*)0x100000;
int main()
{
printf("%p\n", p + 0x1);
printf("%p\n", (unsigned long)p + 0x1);
printf("%p\n", (unsigned int*)p + 0x1);
return 0;
}00100014
00100001
00100004小端字节序:
cpp
int main()
{
int a[4] = { 1, 2, 3, 4 };
int* ptr1 = (int*)(&a + 1);
int* ptr2 = (int*)((int)a + 1);
printf("%x,%x", ptr1[-1], *ptr2);
return 0;
}4,2000000
cpp
int main()
{
int a[3][2] = { (0, 1), (2, 3), (4, 5) };
int* p;
p = a[0];
printf("%d", p[0]);
return 0;
}1注意逗号表达式哦。
x86下:
cpp
int main()
{
int a[5][5];
int(*p)[4];
p = (decltype(p))a;
printf("%p,%d\n", &p[4][2] - &a[4][2], &p[4][2] - &a[4][2]);
return 0;
}FFFFFFFC,-4这里要注意指针减法的本质不是求地址值差,而是元素个数差。
cpp
int main()
{
int aa[2][5] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int* ptr1 = (int*)(&aa + 1);
int* ptr2 = (int*)(*(aa + 1));
printf("%d,%d", *(ptr1 - 1), *(ptr2 - 1));
return 0;
}10,5
cpp
int main()
{
const char* a[] = { "work","at","alibaba" };
const char** pa = a;
pa++;
printf("%s\n", *pa);
return 0;
}at最难的一道:
cpp
int main()
{
const char* c[] = { "ENTER","NEW","POINT","FIRST" };
const char** cp[] = { c + 3,c + 2,c + 1,c };
const char*** cpp = cp;
printf("%s\n", **++cpp);
printf("%s\n", *-- * ++cpp + 3);
printf("%s\n", *cpp[-2] + 3);
printf("%s\n", cpp[-1][-1] + 1);
return 0;
}POINT
ER
ST
EW库函数模拟实现
我们这里直接来实现:
memcpy
cpp
void* memcpy(void* dest, const void* src, size_t num) {
if (dest == src)return dest;
for (size_t i = 0; i < num; i++) {
((char*)dest)[i] = ((const char*)src)[i];
}
return dest;
}memmove
memmove和memcpy的区别在于,memmove能安全拷贝dest和src重叠区域。
cpp
void* memmove(void* dest, const void* src, size_t num) {
if (dest == src)return dest;
if ((unsigned long long)dest < (unsigned long long)src) {
for (size_t i = 0; i < num; i++) {
((char*)dest)[i] = ((const char*)src)[i];
}
}
else {
for (size_t i = 0; i < num; i++) {
((char*)dest)[num - i - 1] = ((const char*)src)[num - i - 1];
}
}
return dest;
}strstr
kmp
复习都复习了,自然不能写bf。在钻研了很久kmp之后,我终于明白了他的原理。首先我们先看普通的字符串匹配:
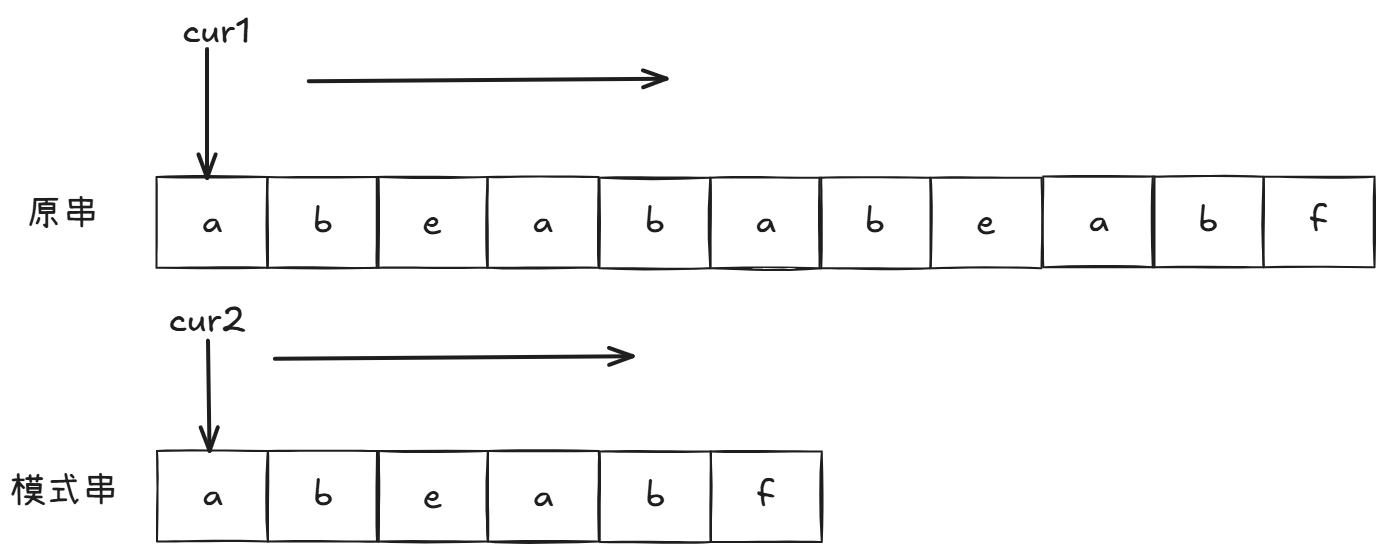
一个一个比对,遇到不相同字符则模式串返回起点,原串返回起点的下一个位置开始匹配:
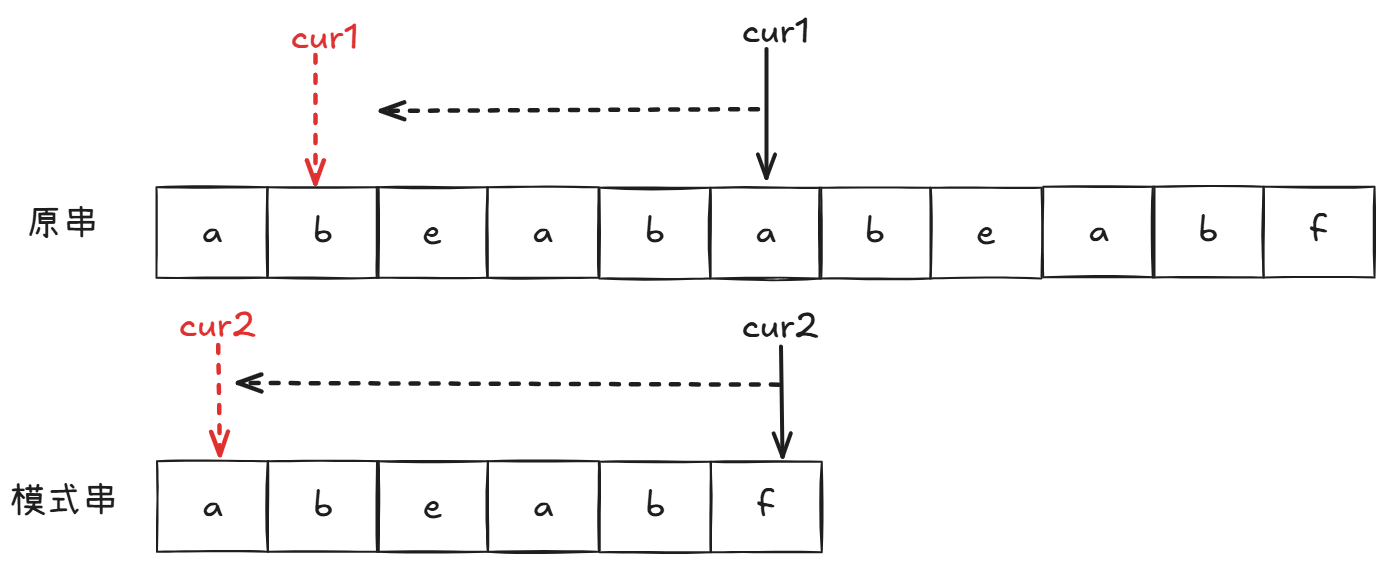
而KMP算法:
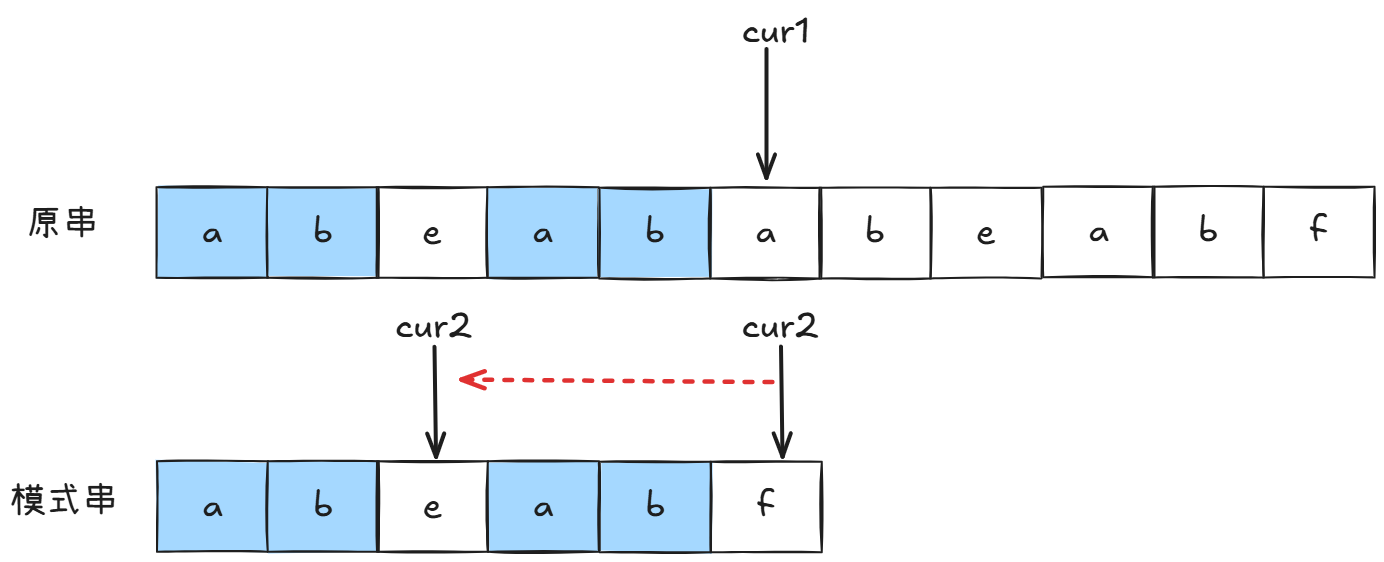
我们用肉眼能够看到,模式串f,前面有一部分和模式串开头"重复的",这说明我们不用在比较开头部分。进而cur1不动继续比较:
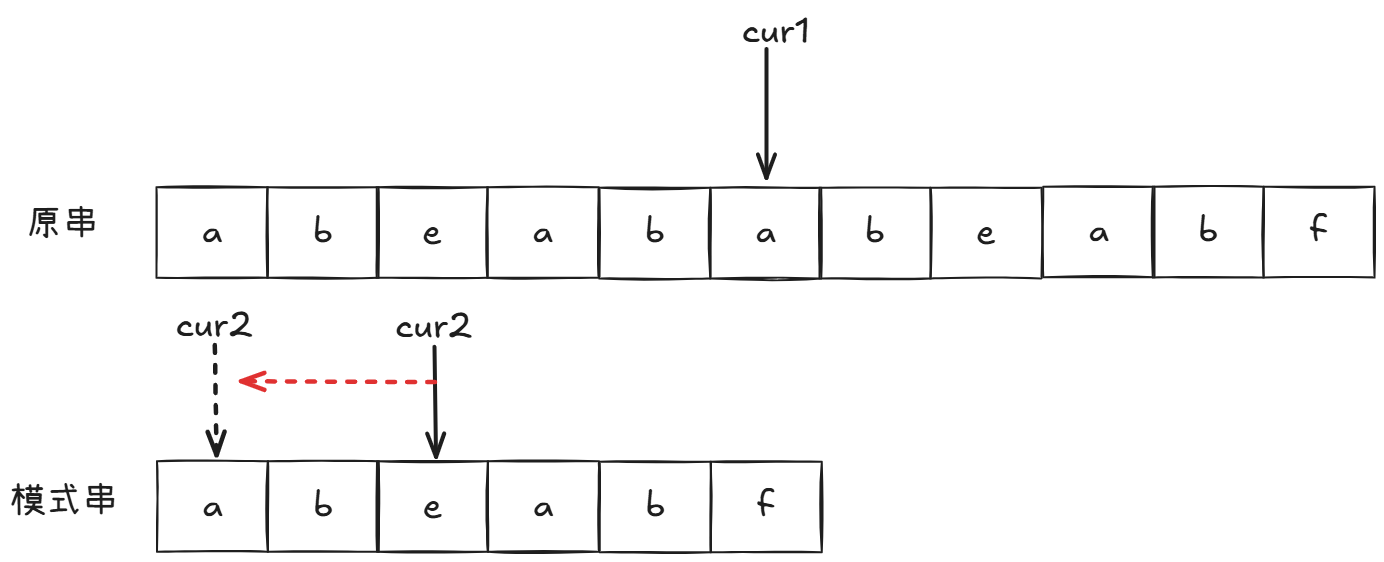
此时模式串e,前面没有重复部分,因此回到起点重新比较:
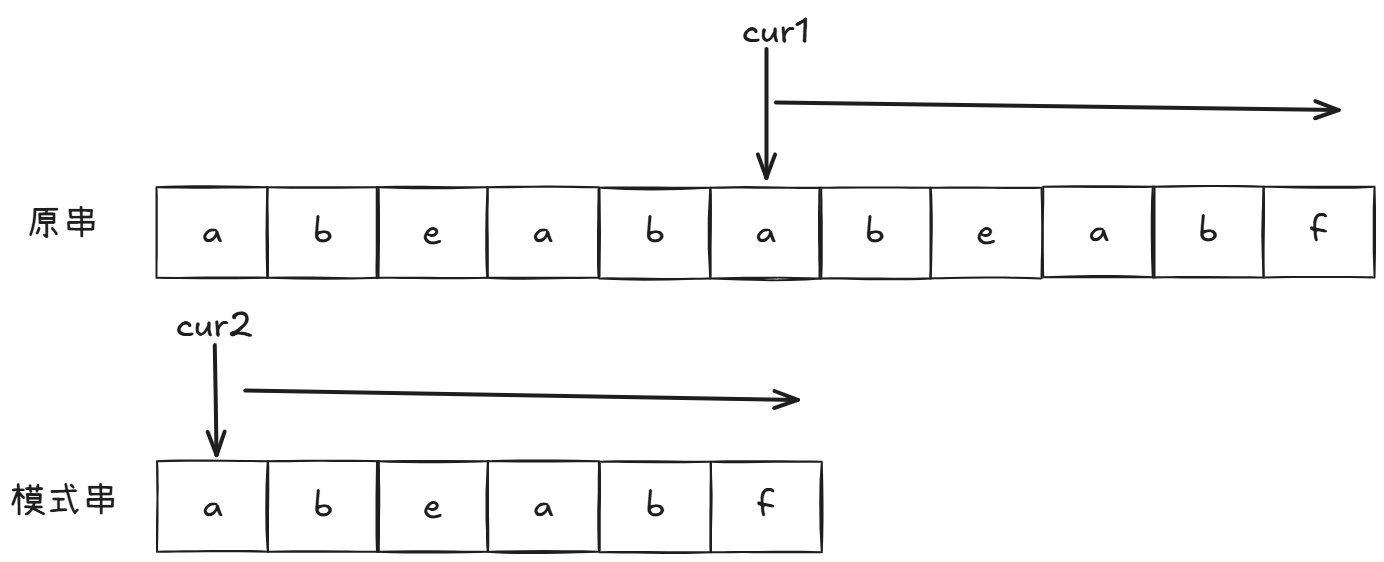
最后就一鼓作气比较完毕。
那么我们回到第一个不同的地方,KMP算法是什么回退逻辑?
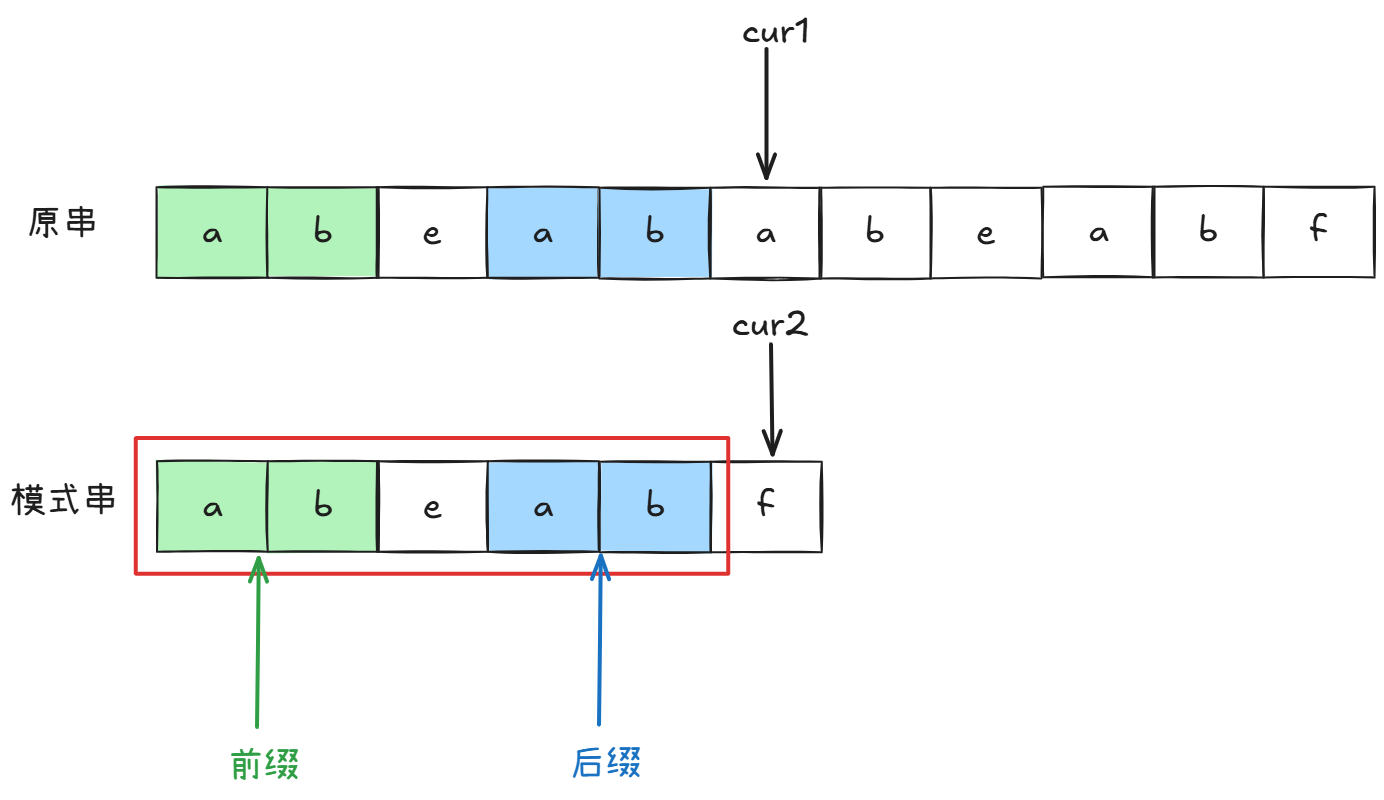
我们看f前的子串abeab,我们将axxx称作子串前缀(不包括最后一个字符),xxxb称作子串后缀(不包括第一个字符)。
图中圈出的是其中一个前缀和后缀,并且他们是相等的。
我们思考一下,原串cur1之前部分和模式串cur2之前部分是不是应该相等。
所以cur2的前缀和后缀相等,cur1的后缀是不是就等于cur2的前缀。我们是不是免去了cur1回退和cur2前缀的比较。
这时候有个问题,cur1不回退会不会错过解?
我们来看没有相等前缀和后缀情况:
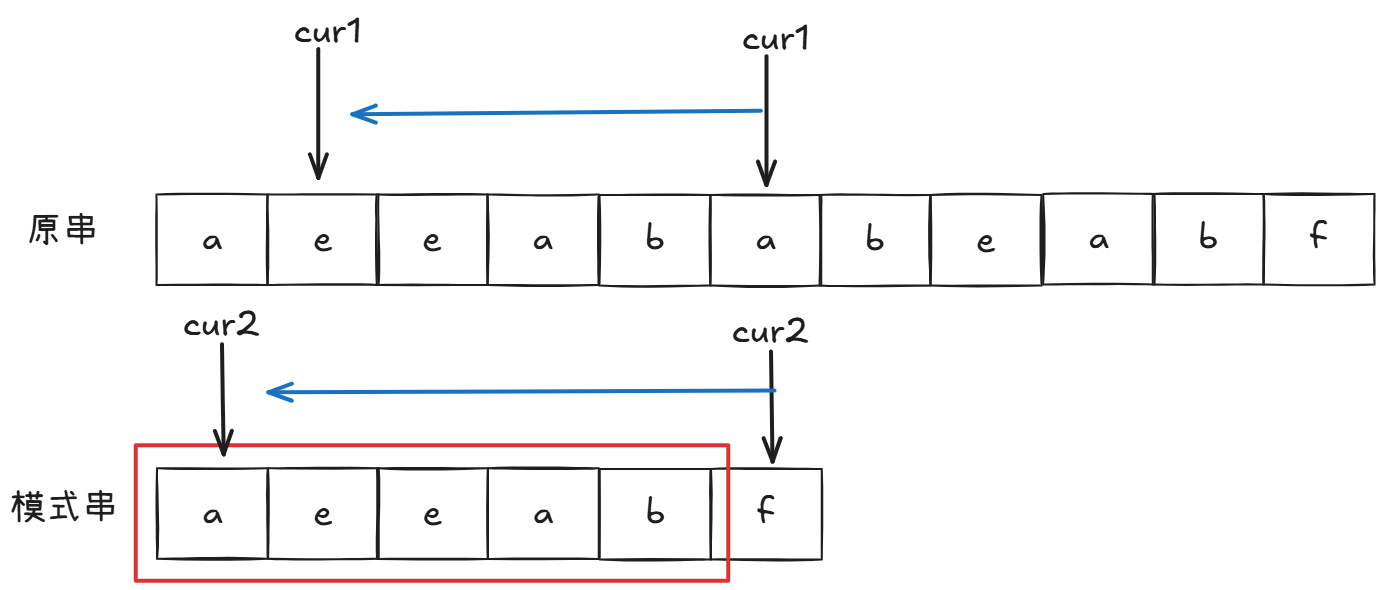
这是回退,我们思考cur1回退之后,再到没回退位置有没有正确答案的可能。
如果有:
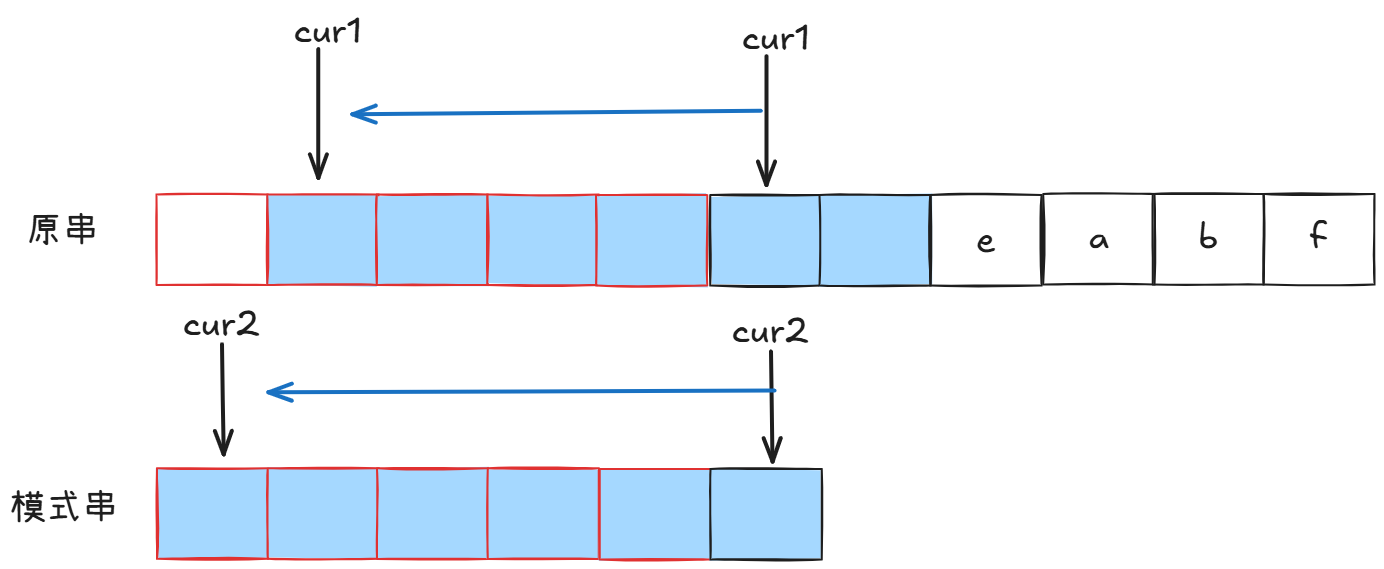
意味着蓝色部分是相等的,但是我们一开始cur1从扫扫描过的红色部分,叶和模式串相等:
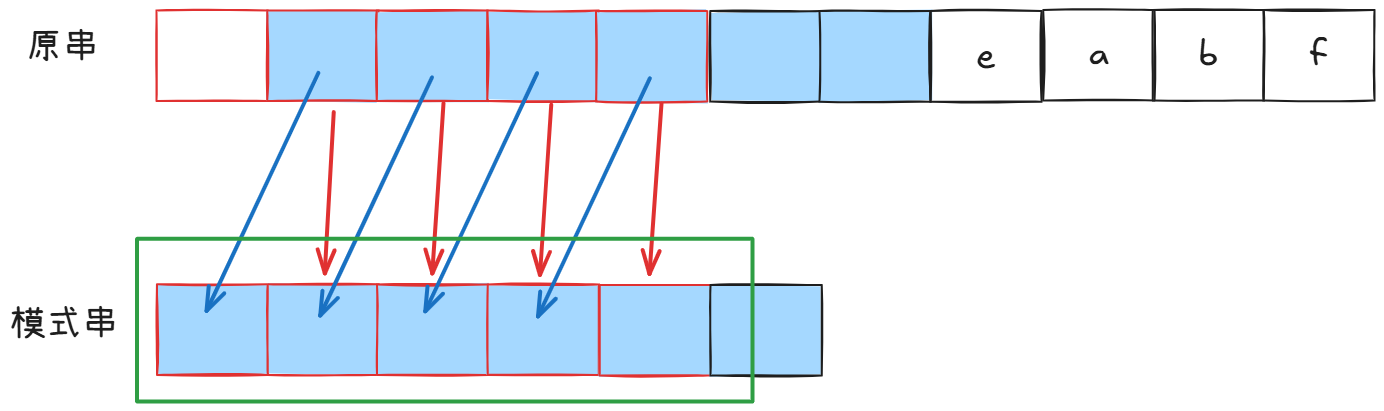
看到了吗,绿色部分的前四个字符,等于后四个字符。这与一开始假设的没有相等前后缀矛盾。
这意味着我们回退之后是必不可能有正确解的,除非有相等前后缀,但是有了相等前后缀我们就不必回退了。
那么我们的cur1不用回退,cur2要回退到什么地方呢?
实际上我们要用一个数组nxt[i]记录,以i结尾的模式串的最大相等前后缀大小:
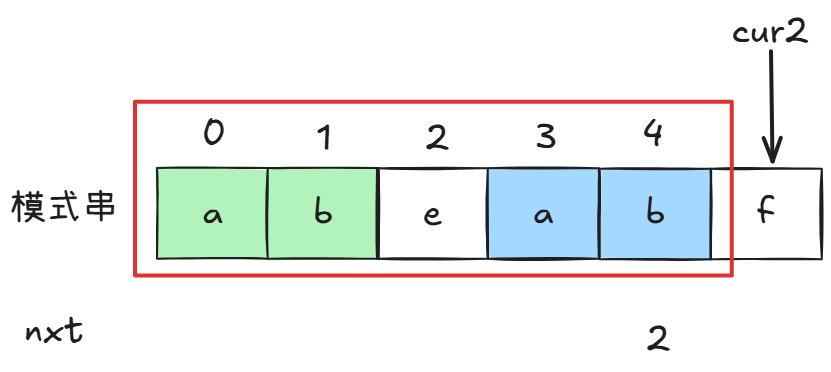
比如这里cur2前面的模式子串,最大前后缀是2.cur2不就是回退到2了吗。
那么接下来就是kmp问题最大的难点求nxt数组。
这是一个动态规划问题,我们先初始化nxt[0]为0.
我们先看一种情况:
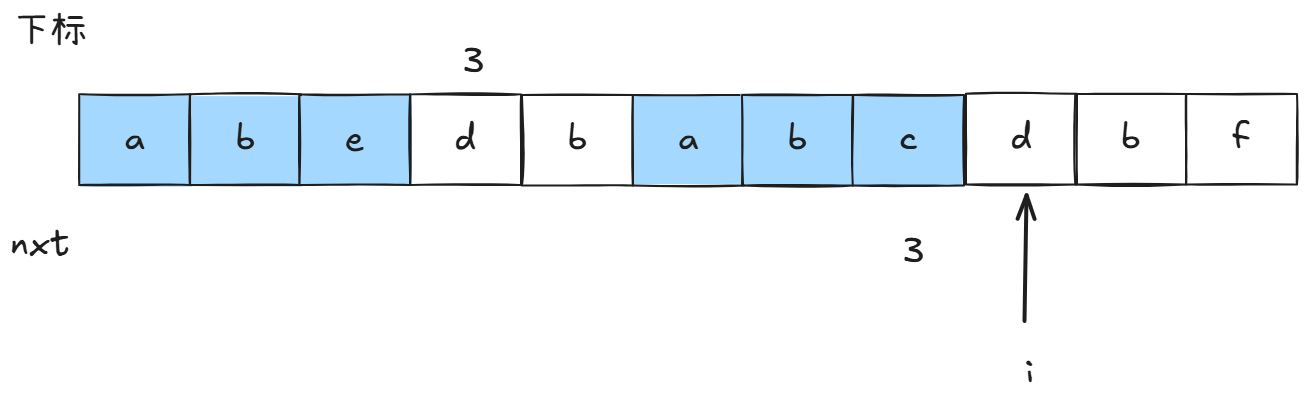
我们现在求nxt[i],我们很自然想到,string[i]能不能和前面的后缀结合变得更大。
所以我们让string[i]和string[nxt[i-1]]比较:
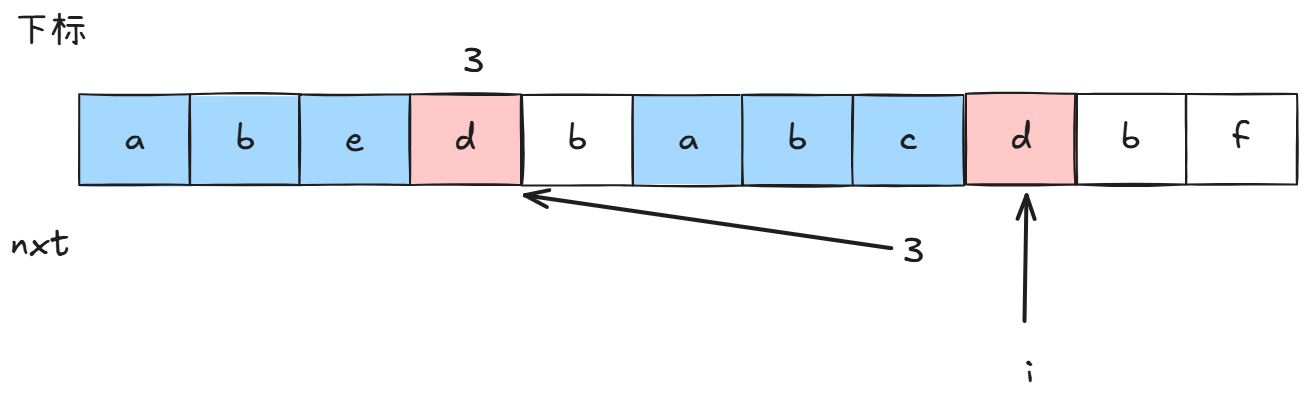
相等,那么nxt[i]=nxt[i-1]+1.
如果不相等呢?
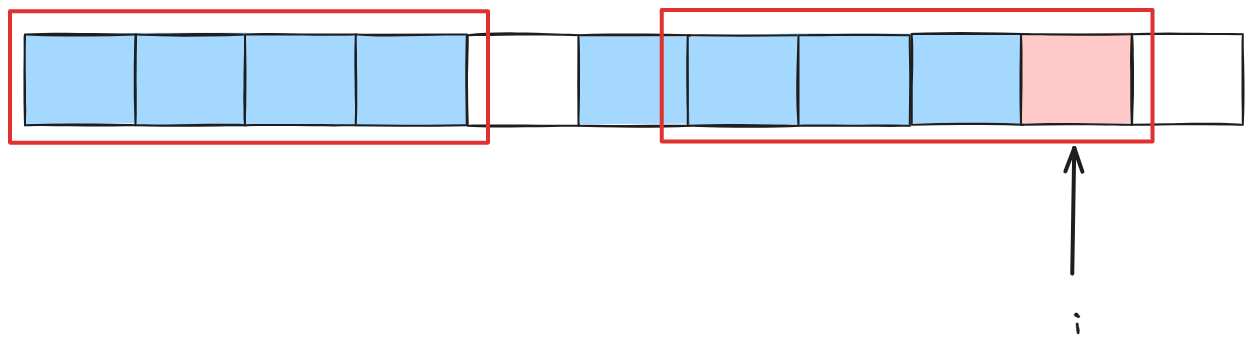
我们势必要舍弃一个相等的,找到使得红色部分相等的最大值。当然他未必是我现在框着的样子,还可能是:
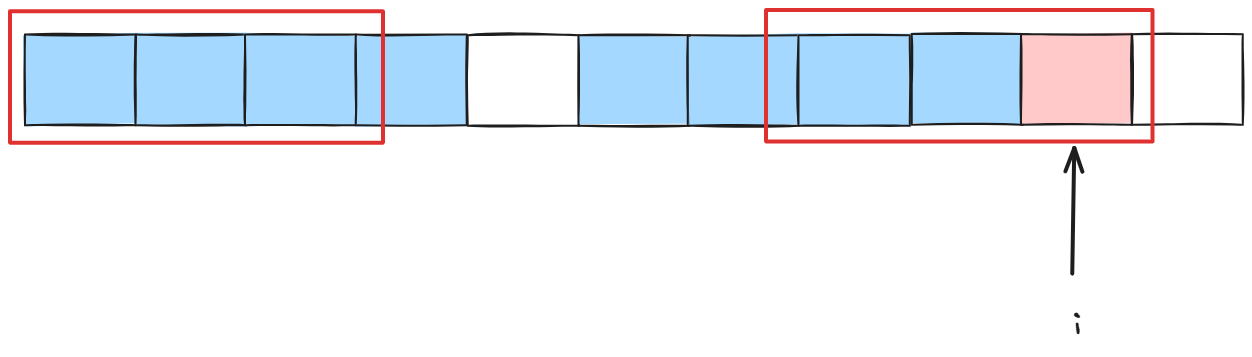
但是他们都有共同点:
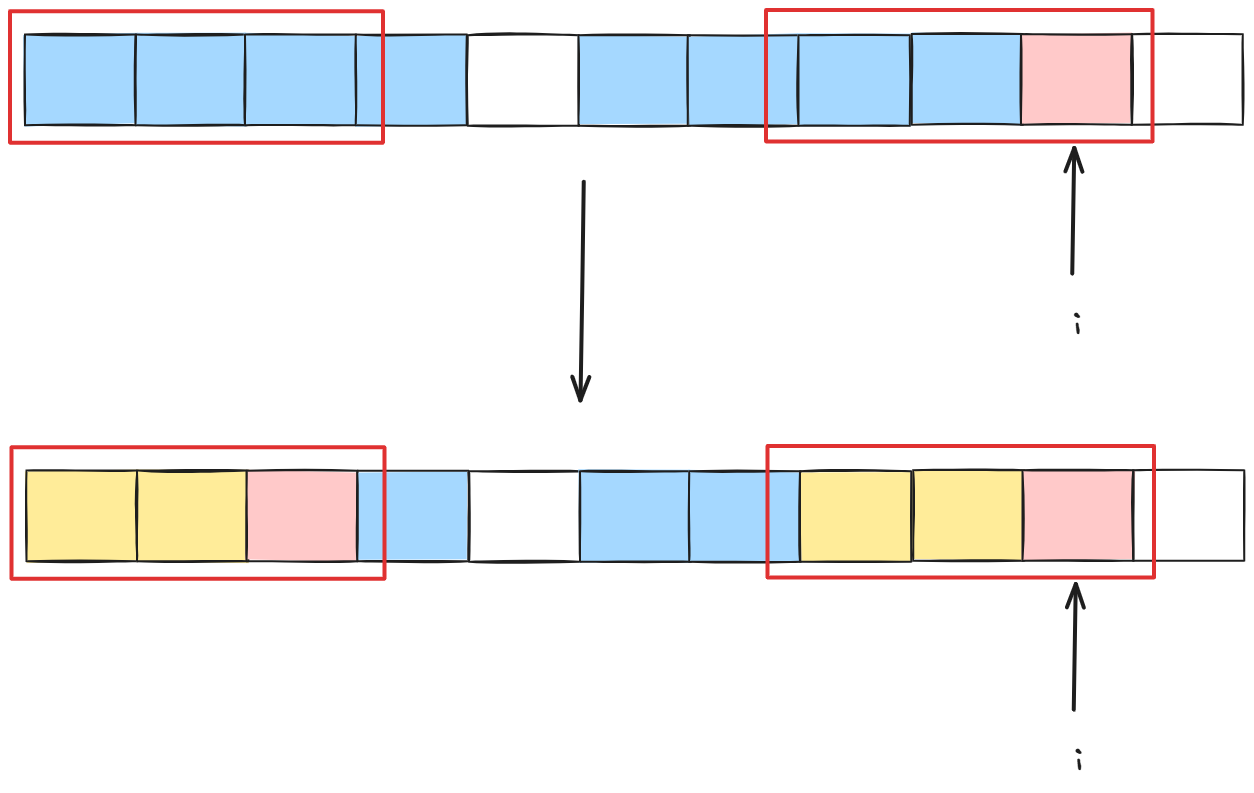
那就是黄色部分相等,红色部分相等。这时候我们不要忘记一个特别重要的点!蓝色部分原来是相等的:
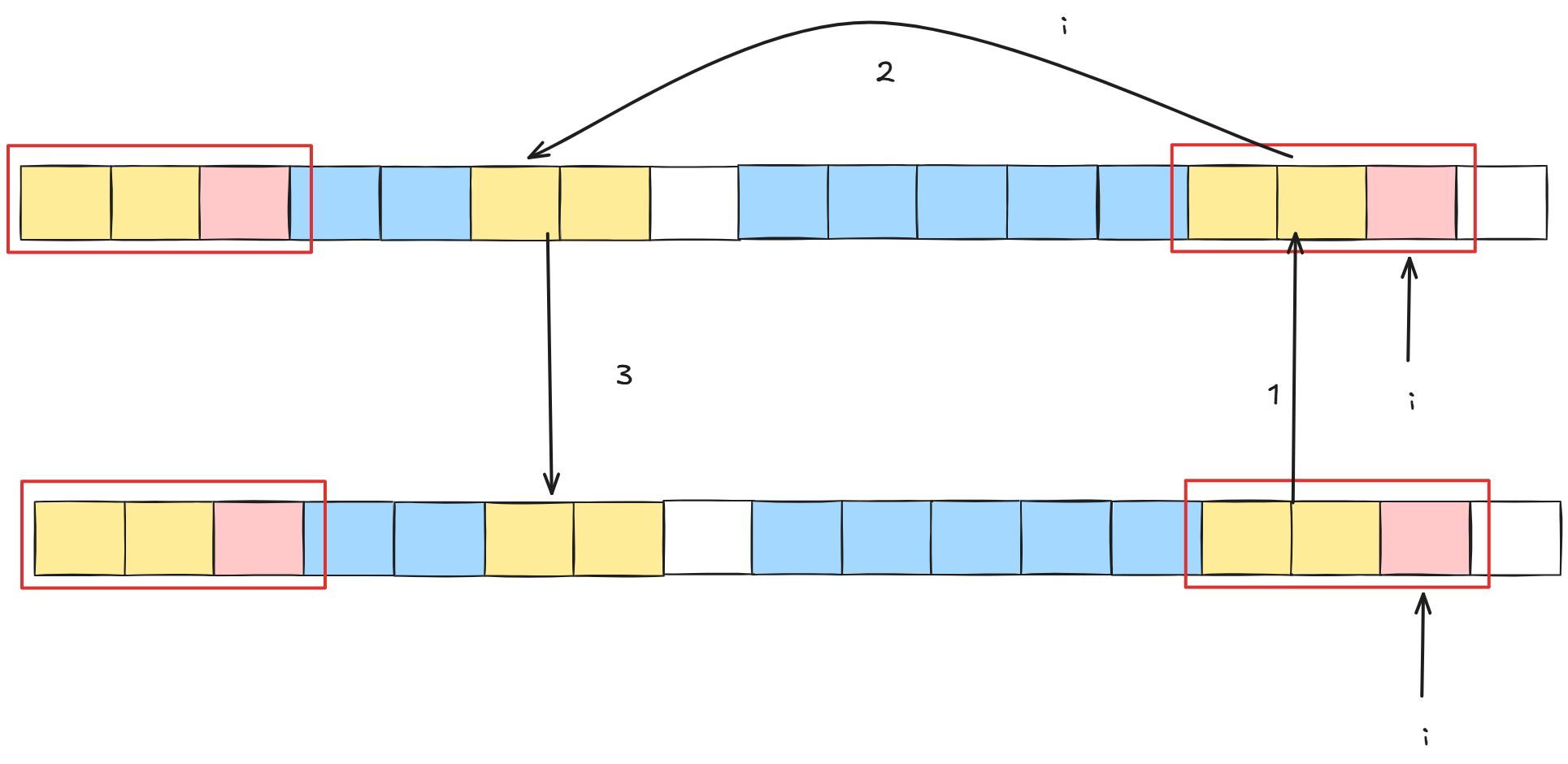
刚刚图太小,我们过大一下。这下看到了吗,黄色部分都是相等。这不就是要我们求白色格子前的最大前缀和,并且红色格子相等吗,那么白色格子是谁呢:

没错白色格子的下标就是nxt[i-1].
于是我们就得到了递推:
L e t j = n x t [ i − 1 ] Let \space j=nxt[i-1] Let j=nxt[i−1]
i f s [ i ] = = s [ j ] , s [ i ] = j + 1 ( 1 ) if\space s[i]==s[j],\space s[i]=j+1(1) if s[i]==s[j], s[i]=j+1(1)
e l s e l e t j = n e t [ j − 1 ] , r e t u r n ( 1 ) else\space let\space j=net[j-1],return (1) else let j=net[j−1],return(1)
当然如果j走到了0,那么nxt[i]就是与首元素是否相等了,是则1,否则0。
实现
那么我们现在来实现strstr吧:
cpp
char* strstr(const char* str1, const char* str2) {
if (!str1 || !str2)return nullptr;
size_t n = strlen(str1), m = strlen(str2);
if (!m)return (char*)str1;
size_t* nxt = (size_t*)malloc(m * sizeof(size_t));
nxt[0] = 0;
for (size_t i = 1; i < m; i++) {
size_t j = nxt[i - 1];
while (j && str2[i] != str2[j])j = nxt[j - 1];
if (str2[i] == str2[j])++j;
nxt[i] = j;
}
for (size_t i = 0, j = 0; i < n;) {
if (str1[i] == str2[j]) {
++i;
++j;
}else if (j != 0) {
j = nxt[j - 1];
}else {
++i;
}
if (j == m) {
return (char*)(str1 + i - m);
}
}
free(nxt);
nxt = nullptr;
return nullptr;
}memset
cpp
void* memset(void* ptr, int value, size_t num) {
for (size_t i = 0; i < num; i++) {
((unsigned char*)ptr)[i] = (unsigned char)value;
}
return ptr;
}memcmp
cpp
int memcmp(const void* ptr1, const void* ptr2, size_t num) {
unsigned char* p1 = (unsigned char*)ptr1, * p2 = (unsigned char*)ptr2;
for (size_t i = 0; i < num; i++) {
if (p1[i] != p2[i])return p1[i] - p2[i];
}
return 0;
}strlen
cpp
size_t strlen(const char* str) {
size_t len = 0;
while (str[len])++len;
return len;
}strcpy
cpp
char* strcpy(char* dest, const char* src) {
if (dest == src)return dest;
size_t i = 0;
for (; src[i]; i++) {
dest[i] = src[i];
}
dest[i] = 0;
return dest;
}内存对齐
回顾之前结构体部分,我们先给出内存对齐规则:
- 结构体的第一个成员对齐到相对结构体变量起始位置偏移量为0的地址处
- 其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。对齐数 = 编译器默认的一个对齐数与该成员变量大小的较小值。
- VS中默认的值为8
- Linux中没有默认对齐数,对齐数就是成员自身的大小
- 结构体总大小为最大对齐数(结构体中每个成员变量都有一个对齐数,所有对齐数中最大的的)整数倍。
- 如果嵌套了结构体的情况,嵌套的结构体成员对齐到自己的成员中最大对齐数的整数倍处,结构体的整体大小就是所有最大对齐数(含嵌套结构体中成员的对齐数)的整数倍。
理论现在这里,我们要理解为什么会存在结构体内存对齐。实际上内存对齐不是结构体特有的,而是每个类型都有内存对齐。我们以int和double为例:
x64环境下:
cpp
int main() {
int a, b, c;
double e, f, g;
cout << &a << ' ' << &b << ' ' << &c << ' ' << endl;
cout << ((unsigned long long) & a) % 4 << ' '
<< ((unsigned long long) & b) % 4 << ' ' << ((unsigned long long) & c) % 4 << endl;
cout << &e << ' ' << &f << ' ' << &g << ' ' << endl;
cout << ((unsigned long long) & e) % 8 << ' '
<< ((unsigned long long) & f) % 8 << ' ' << ((unsigned long long) & g) % 8 << endl;
return 0;
}000000582E8FFC64 000000582E8FFC84 000000582E8FFCA4
0 0 0
000000582E8FFCC8 000000582E8FFCE8 000000582E8FFD08
0 0 0我们发现int的起始地址是4的整数倍,double的起始地址是8的整数倍。这是操作系统精心设计的"巧合"。
首先我们需要知道操作系统的读取操作是以字长为单位的。比如x86下就是4字节。
每次读取的起始地址必须是4的整数倍 ,一次读取四个字节或者2个字节。
那么我们的整型如果不是内存对齐:
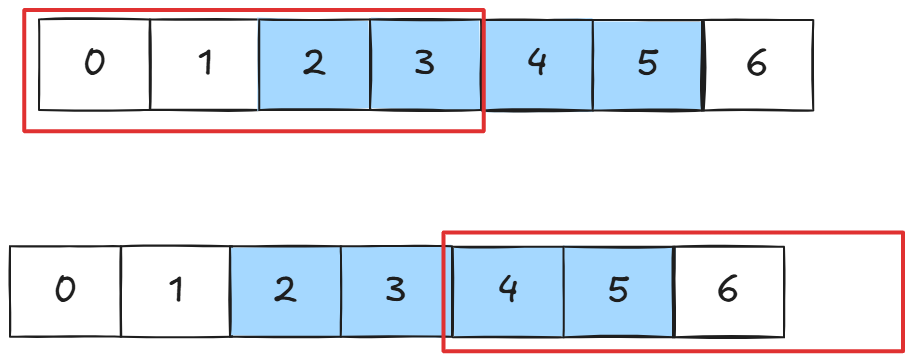
那么他就需要读取两次,效率低下。
- 总的来说,内存对齐的原因有两个:
- 刚刚提到的,效率问题。内存不对齐的数据需要多读取一次,效率低下。
- 移植原因:不是所有的硬件平台都能访问任意地址上的任意数据的;某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。
那么我们就知道了:
- 为什么结构体成员有内存对齐规则:
维护成员的内存对齐规则。 - 结构体自身的内存对齐数:
结构体自身对齐数自然就是最大的成员对齐数。
譬如:
cpp
struct test{
double b;
int a;
};这里如果test的起始地址只是4的整数倍如4,那么double的起始地就是4.直接违反了double的对齐规则。因此结构体的对齐数是8.
- 为什么结构体的大小是最大对齐数的整数倍。
像下面情况:
cpp
struct test{
int a;
char b;
};
test arr[2];这里如果test的大小不是4的整数倍,那就是6。那么arr第二个元素起始地址就是 4的整数倍+6,势必不是4的整数倍,违反了int的内存对齐规则。
数据存储
整型存储
整型存储的形式有原、反、补码。
计算机中整型以补码形式存储。
正数的原、反、补都是自身。
在继续讲负数补码如何计算,我们要知道,为什么要有补码:
因为计算机可以实现加减法,但是如果只有加法运算就会快很多。所以我们将减去一个数变为加上一个数,那么这个要加的数就是原数的补码。
我们以四位为例,1的二进制存储:0001。
想让一个数x代替-1,使得x+1=0,如果仅仅是将1取反:1110,两者相加就是1111,并非是0.因此我们还需要加上1.
故负数的补码就是负数的反码+1。
那么负数的反码就是将除了符号位,其余取反。
比如-1:1001,反码:1110,补码:1111.
大小端字节序
我们常见的类型中,除了char是一个字节以外,其他类型都是两个及两个以上的字节。那么,就会有个按什么顺序存储这些字节的问题,比如:0x11223344,在内存中我们既可以从高地址到低地址存储11223344,也可以从低地址向高地址存储11223344,这样就形成了大小端字节序。
- 大端序(Big-Endian):数据的高位字节存储在低地址,低位字节存储在高地址。例如,十六进制数 0x12345678 在大端序中的存储顺序为 12 34 56 78。
- 小端序(Little-Endian):数据的低位字节存储在低地址,高位字节存储在高地址。例如,0x12345678 在小端序中的存储顺序为 78 56 34 12。
我们只需记住一个口诀小小小,小端字节序的权值小的字节存放在小地址。
验证大小端字节序,我们可以拿一个联合体验证:
cpp
union test {
int a;
char b;
};
void Endian() {
test t = { 1 };
if (t.b) cout << "小端字节序" << endl;
else cout << "大端字节序" << endl;
}浮点数存储
编译链接
编译链接是衔接后面学习的一个重要知识点。
在任何ANSI C的实现中,都包含两种环境:翻译环境和运行环境。
编译环境用于将高级语言编写的源代码转换为机器代码或中间代码,生成可执行文件或库文件。
翻译环境通过解释器逐行执行源代码,无需预先编译为机器码。
编译细分为:预处理、编译、汇编。
最后经过将汇编文件链接形成可执行程序。
结合Linux gcc的使用来看
- 预处理
- 核心作用:处理源码中的预处理指令(#开头的指令),生成纯 C 代码。
- 具体操作:
展开#include头文件(把stdio.h等内容直接拷贝到当前文件);
替换#define宏定义(如#define MAX 100会把代码中所有MAX换成 100);
处理#ifdef/#if条件编译(保留符合条件的代码,删除不符合的);
删除注释(//、/* */);
添加行号和文件标识(方便后续调试报错)。 - 指令:
bash
gcc -E test.c -o test.i # -E:只执行预处理,-o指定输出文件- 编译
- 核心作用:把预处理后的纯 C 代码翻译成汇编语言代码。
- 具体操作:
词法分析 :把代码拆成一个个 "单词"(如关键字int、变量名a、运算符+);
语法分析 :检查代码语法是否符合 C 标准,生成语法树;
语义分析 :检查逻辑合理性(如变量未定义就使用、类型不匹配);
优化 :简化代码(如常量折叠1+2直接换成3)、调整执行顺序提升效率;
生成汇编代码:把语法树转成汇编指令(如mov、add)。 - 指令:
bash
gcc -S test.i -o test.s # -S:只编译到汇编,不汇编- 汇编
- 核心作用:把汇编代码翻译成机器能直接执行的二进制机器码,生成目标文件。
- 具体操作:
把汇编指令(如mov eax, 1)对应到 CPU 的机器码(如0xB8 0x01 0x00 0x00 0x00);
生成目标文件(.o/.obj):包含机器码、符号表 (变量 / 函数名和地址的映射)、重定位信息(待链接的地址标记)。 - 指令:
bash
gcc -c test.s -o test.o # -c:只汇编,不链接- 链接
- 核心作用:把多个目标文件(自己写的.o + 系统库的.o)合并,解决符号引用,生成可执行文件。
- 静态链接(Static Linking)
原理:把用到的库代码(如printf)直接拷贝到可执行文件中;
优点:可执行文件独立运行,不依赖外部库;
缺点:文件体积大,库更新后需要重新编译;
GCC 默认静态链接部分库,显式静态链接:
bash
gcc test.o -static -o test- 动态链接
原理:不拷贝库代码,只在可执行文件中记录库的路径和函数地址;
优点:文件体积小,多个程序共享同一个库,库更新后无需重新编译;
缺点:运行时需要依赖系统中的动态库(如libc.so/msvcrt.dll);
GCC 默认动态链接:
bash
gcc test.o -o test-
链接的关键步骤:
符号解析 :找到所有未定义的符号(如printf),匹配库中的定义;
重定位 :把符号的虚拟地址替换成实际内存地址;
合并段 :把多个目标文件的代码段、数据段合并成一个;
添加程序入口:设置main函数为程序启动入口(实际是_start/mainCRTStartup调用main)。 -
各阶段的错误:
预处理错误:头文件找不到(fatal error: stdio.h: No such file or directory);
编译错误:语法错误(error: expected ';' before 'return')、类型错误;
汇编错误:非法汇编指令(少见,通常是编译器 bug);
链接错误:符号未定义(undefined reference to 'printf')、重复定义(multiple definition of 'main')。
宏函数
我们还要记得如何实现一些简单的宏函数:
cpp
#define Add(x,y) ((x)+(y))
int main() {
cout << Add(10, 20) << ' ' << Add(20.7, 12, 2) << ' ' << endl;
return 0;
}