Python入门：Python3 statistics模块全面学习教程

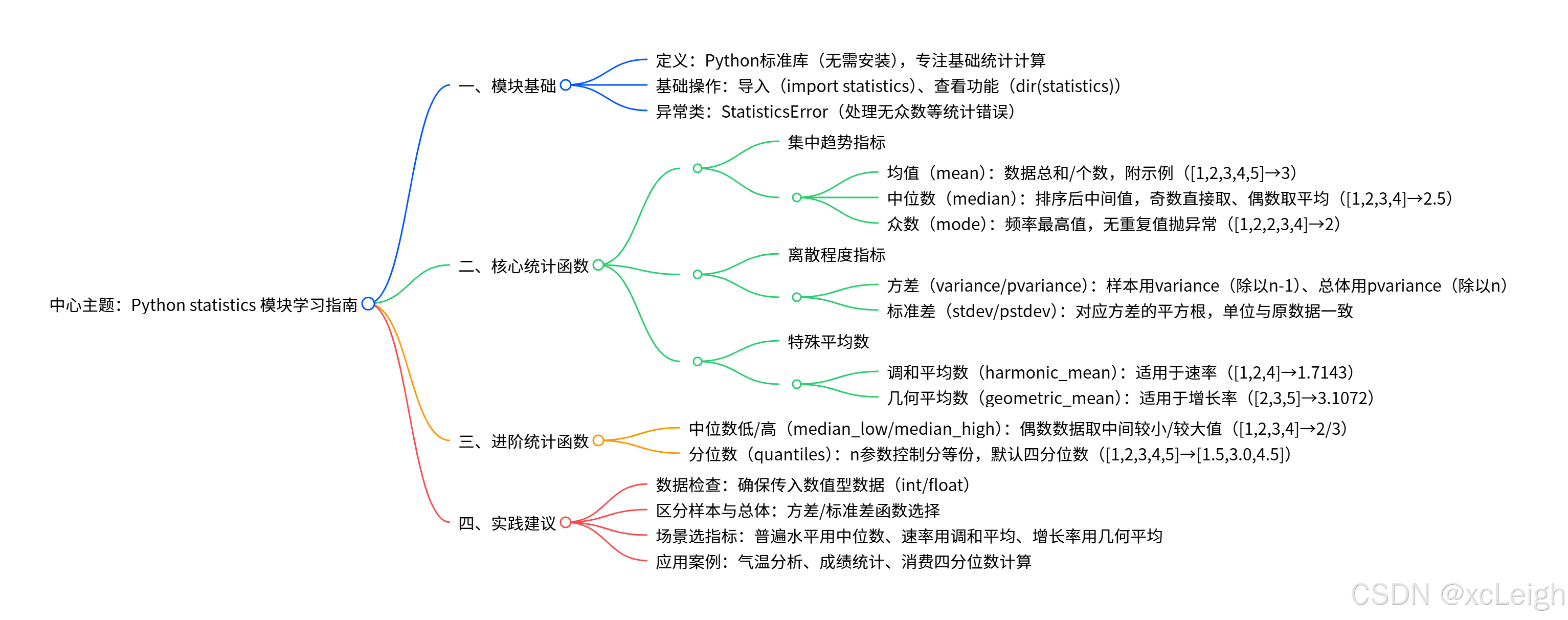
Python入门：Python3 statistics模块全面学习教程

Python入门：Python3 statistics模块全面学习教程，该模块属标准库无需额外安装，是初学者与数据分析师进行基础统计分析的实用工具。文章先介绍模块定位与基础操作（导入模块、用 dir () 查看功能），再结合代码实例与结果解释，详细讲解核心统计函数 ------ 涵盖均值（mean）、中位数（median）、众数（mode）等集中趋势指标，方差（variance）、标准差（stdev）等离散程度指标，以及调和平均数（harmonic_mean）、几何平均数（geometric_mean），还有中位数低 / 高、分位数（quantiles）等进阶函数，同时提示众数计算的异常处理。最后给出实践建议，如区分样本与总体选择对应方差 / 标准差函数、依场景选合适统计指标，帮助读者高效用该模块完成数据统计任务。

前言

Python作为一门简洁、易读、功能强大的编程语言，其基础语法是入门学习的核心。掌握好基础语法，能为后续的编程实践打下坚实的基础。本文将全面讲解Python3的基础语法知识，适合编程初学者系统学习。Python以其简洁优雅的语法和强大的通用性，成为当今最受欢迎的编程语言。本专栏旨在系统性地带你从零基础入门到精通Python核心。无论你是零基础小白还是希望进阶的专业开发者，都将通过清晰的讲解、丰富的实例和实战项目，逐步掌握语法基础、核心数据结构、函数与模块、面向对象编程、文件处理、主流库应用（如数据分析、Web开发、自动化）以及面向对象高级特性，最终具备独立开发能力和解决复杂问题的思维，高效应对数据分析、人工智能、Web应用、自动化脚本等广泛领域的实际需求。

---

🥇 点击进入Python入门专栏，Python凭借简洁易读的语法，是零基础学习编程的理想选择。本专栏专为初学者设计，系统讲解Python核心基础：变量、数据类型、流程控制、函数、文件操作及常用库入门。通过清晰示例与实用小项目，助你快速掌握编程思维，打下坚实根基，迈出自动化办公、数据分析或Web开发的第一步。

🥇 点击进入Python小游戏实战专栏， 寓教于乐，用Python亲手打造经典小游戏！本专栏通过开发贪吃蛇、飞机大战、猜数字、简易版俄罗斯方块等趣味项目，在实践中掌握Python核心语法、面向对象编程、事件处理、图形界面（如Pygame）等关键技能，将枯燥的代码学习转化为可见的成果，让学习编程充满乐趣与成就感，快速提升实战能力。

🥇 点击进入Python小工具实战专栏，告别重复劳动，用Python打造效率神器！本专栏教你开发文件批量处理、自动邮件通知、简易爬虫、桌面提醒、密码生成器、天气查询等实用小工具。聚焦os、shutil、requests、smtplib、schedule等核心库，通过真实场景案例，快速掌握自动化脚本编写技巧，解放双手，显著提升工作与生活效率，让代码真正服务于你的日常。

🥇 点击进入Python爬虫实战专栏，解锁网络数据宝库！本专栏手把手教你使用Python核心库（如requests、BeautifulSoup、Scrapy）构建高效爬虫。从基础网页解析到动态页面抓取、数据存储（CSV/数据库）、反爬策略应对及IP代理使用，通过实战项目（如电商比价、新闻聚合、图片采集、舆情监控），掌握合法合规获取并利用网络数据的核心技能，让数据成为你的超能力。

🥇 点击进入Python项目实战专栏，告别碎片化学习，挑战真实项目！本专栏精选Web应用开发（Flask/Django）、数据分析可视化、自动化办公系统、简易爬虫框架、API接口开发等综合项目。通过需求分析、架构设计、编码实现、测试部署的全流程，深入掌握工程化开发、代码复用、调试排错与团队协作核心能力，积累高质量作品集，真正具备解决复杂问题的Python实战经验。

---

---

🌐 前篇文章咱们练习了 Python3 random模块全面学习教程 ，如果忘记了，可以去重温一下，不停的重复敲击基础代码，有助于让你更加熟练掌握一门语言。今天咱们继续学习 ，Python3 statistics模块全面学习教程，下面开始吧！

在数据分析、科学计算甚至日常数据处理中，统计学指标 （如均值、中位数、标准差）是描述数据特征的核心工具。手动计算这些指标不仅繁琐，还容易出错。Python 内置的 statistics 模块恰好解决了这个问题------它封装了所有常用的基础统计函数，让我们无需重复造轮子，一行代码就能完成专业计算。

本文将从基础到实战，详细讲解 statistics 模块的使用方法，适合Python初学者、数据分析师入门学习。所有代码均可直接复制运行，建议边看边练！

1. 什么是 Python statistics 模块？

statistics 是 Python 标准库（无需额外安装）中的一个模块，专门用于处理基础统计计算。它支持多种常用统计指标，包括：

• 集中趋势指标：均值、中位数、众数
• 离散程度指标：方差、标准差
• 特殊平均数：调和平均数、几何平均数
• 分位数、分组中位数等进阶功能

无论是学生作业、数据分析报告，还是简单的业务数据处理，statistics 模块都能满足你的基础统计需求。

2. 基础准备：导入模块与查看内容

使用任何模块前，都需要先导入。statistics 模块的导入方式非常简单，同时我们可以通过 dir() 函数查看模块包含的所有功能。

2.1 导入模块

import statistics  # 导入statistics模块

2.2 查看模块所有功能

通过 dir(statistics) 可以列出模块内的所有类、函数和变量，帮助我们快速了解模块的能力：

import statistics

# 查看statistics模块的所有内容
print(dir(statistics))

输出（关键功能截取）：

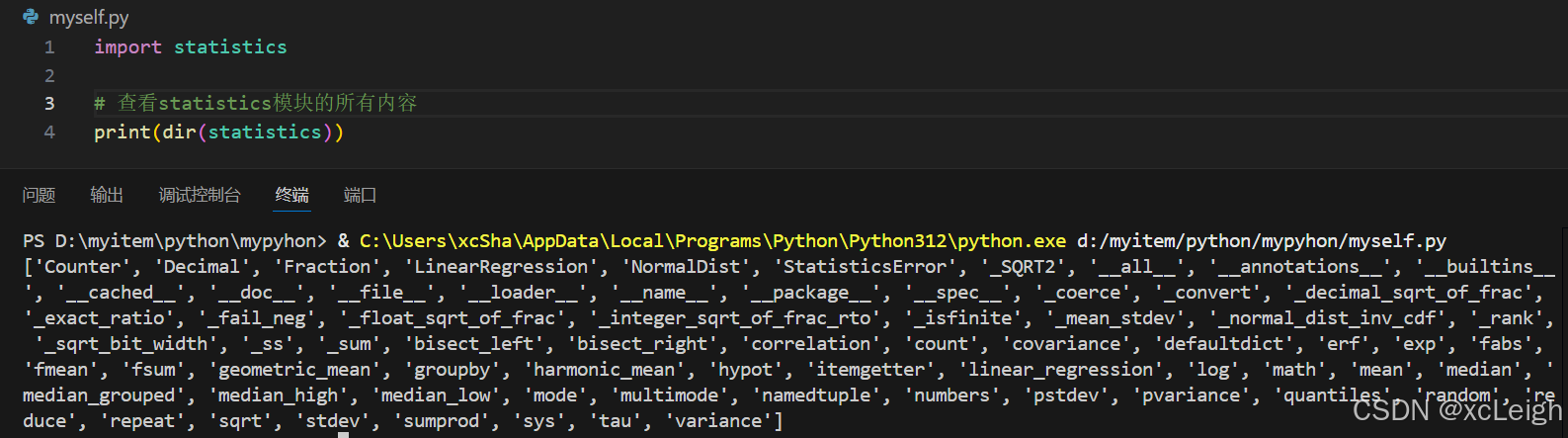
['Counter', 'NormalDist', 'StatisticsError', 'fmean', 'fsum', 'geometric_mean', 'harmonic_mean', 'mean', 'median', 'median_grouped', 'median_high', 'median_low', 'mode', 'multimode', 'pstdev', 'pvariance', 'quantiles', 'stdev', 'variance']

其中，带小写字母的（如 mean、median）就是我们常用的统计函数，StatisticsError 是模块专属的异常类（用于处理统计计算中的错误）。

3. 常用统计函数详解（附代码实例）

本节将逐个讲解 statistics 模块中最常用的统计函数，每个函数都包含「功能定义 + 代码实例 + 结果解释」，确保你能理解并复用。

3.1 均值（Mean）：statistics.mean(data)

定义 ：数据集中所有数值的算术平均值，计算公式为「总和 / 数据个数」。
适用场景：描述数据的"中心趋势"，如班级学生的平均成绩、每月平均销售额。

实例代码

import statistics

# 示例数据（5个整数）
data = [1, 2, 3, 4, 5]
# 计算均值
mean_value = statistics.mean(data)
# 输出结果
print(f"数据集 {data} 的均值为：{mean_value}")

运行结果

数据集 [1, 2, 3, 4, 5] 的均值为：3

计算逻辑：(1+2+3+4+5)/5 = 15/5 = 3，与代码结果一致。

3.2 中位数（Median）：statistics.median(data)

定义：将数据集按从小到大排序后，位于「中间位置」的数值。

• 若数据个数为奇数：直接取中间的数；
• 若数据个数为偶数 ：取中间两个数的平均值。
  适用场景：避免极端值影响（如工资数据，少数高薪者会拉高均值，中位数更能反映"普遍水平"）。

实例1：数据个数为奇数

import statistics

data = [1, 2, 3, 4, 5]  # 5个数据（奇数）
median_value = statistics.median(data)
print(f"数据集 {data} 的中位数为：{median_value}")

运行结果：

数据集 [1, 2, 3, 4, 5] 的中位数为：3

实例2：数据个数为偶数

import statistics

data = [1, 2, 3, 4]  # 4个数据（偶数）
median_value = statistics.median(data)
print(f"数据集 {data} 的中位数为：{median_value}")

运行结果：

数据集 [1, 2, 3, 4] 的中位数为：2.5

计算逻辑：中间两个数是 2 和 3，平均值为 (2+3)/2 = 2.5。

3.3 众数（Mode）：statistics.mode(data)

定义 ：数据集中出现「频率最高」的数值（若有多个数值频率相同，mode() 仅返回第一个）。
注意 ：若数据集中所有数值仅出现一次（无重复值），会触发 StatisticsError 异常。

实例1：有明确众数

import statistics

data = [1, 2, 2, 3, 4]  # 数值2出现2次（频率最高）
mode_value = statistics.mode(data)
print(f"数据集 {data} 的众数为：{mode_value}")

运行结果：

数据集 [1, 2, 2, 3, 4] 的众数为：2

实例2：处理无众数的异常

import statistics

data = [1, 2, 3, 4, 5]  # 所有数值仅出现1次
try:
    mode_value = statistics.mode(data)
    print(f"数据集 {data} 的众数为：{mode_value}")
except statistics.StatisticsError as e:
    print(f"计算众数时出错：{e}")

运行结果：

计算众数时出错：no mode found; all values appear exactly once

【提示】实际使用中，建议用 try-except 捕获 StatisticsError，避免程序崩溃。

3.4 方差（Variance）：statistics.variance(data) / statistics.pvariance(data)

定义：衡量数据集中数值与「均值」的离散程度（方差越大，数据波动越剧烈）。

• variance(data)：计算样本方差 （除以 n-1，适用于从总体中抽取的样本数据）；
• pvariance(data)：计算总体方差 （除以 n，适用于整个总体数据）。

实例代码

import statistics

data = [1, 2, 3, 4, 5]  # 示例数据
mean_value = statistics.mean(data)  # 先看均值（3）

# 计算样本方差（除以n-1=4）
sample_var = statistics.variance(data)
# 计算总体方差（除以n=5）
pop_var = statistics.pvariance(data)

print(f"数据集 {data} 的样本方差为：{sample_var}")
print(f"数据集 {data} 的总体方差为：{pop_var}")

运行结果：

数据集 [1, 2, 3, 4, 5] 的样本方差为：2.5
数据集 [1, 2, 3, 4, 5] 的总体方差为：2.0

计算逻辑：

• 每个数据与均值的差的平方和：(1-3)² + (2-3)² + (3-3)² + (4-3)² + (5-3)² = 4+1+0+1+4=10；
• 样本方差：10/(5-1) = 2.5；
• 总体方差：10/5 = 2.0。

3.5 标准差（Standard Deviation）：statistics.stdev(data) / statistics.pstdev(data)

定义：方差的平方根，作用与方差一致，但单位与原始数据相同（更易解释）。

• stdev(data)：样本标准差 （对应 variance）；
• pstdev(data)：总体标准差 （对应 pvariance）。

实例代码

import statistics

data = [1, 2, 3, 4, 5]
# 样本标准差（方差2.5的平方根）
sample_std = statistics.stdev(data)
# 总体标准差（方差2.0的平方根）
pop_std = statistics.pstdev(data)

print(f"数据集 {data} 的样本标准差为：{sample_std:.4f}")
print(f"数据集 {data} 的总体标准差为：{pop_std}")

运行结果：

数据集 [1, 2, 3, 4, 5] 的样本标准差为：1.5811
数据集 [1, 2, 3, 4, 5] 的总体标准差为：1.4142135623730951

3.6 调和平均数（Harmonic Mean）：statistics.harmonic_mean(data)

定义 ：适用于「速率、比率」类数据的平均值，计算公式为「数据个数 / 各数据倒数的和」。
适用场景：计算平均速度（如往返路程的平均速度）、平均转化率等。

实例：计算平均速度

假设一段路程分3段，速度分别为 1m/s、2m/s、4m/s，求全程平均速度：

import statistics

speeds = [1, 2, 4]  # 3段路程的速度
avg_speed = statistics.harmonic_mean(speeds)
print(f"3段路程的平均速度为：{avg_speed:.4f} m/s")

运行结果：

3段路程的平均速度为：1.7143 m/s

计算逻辑：3/(1/1 + 1/2 + 1/4) = 3/(1.75) ≈ 1.7143，符合调和平均数的物理意义。

3.7 几何平均数（Geometric Mean）：statistics.geometric_mean(data)

定义 ：适用于「增长率、比例」类数据的平均值，计算公式为「所有数据乘积的 n 次方根」（n 为数据个数）。
适用场景：计算年均增长率、投资回报率等（避免增长率过高/过低对均值的影响）。

实例：计算年均增长率

假设某公司3年的销售额增长率分别为 100%（即2倍）、200%（3倍）、400%（5倍），求年均增长率：

import statistics

growth_rates = [2, 3, 5]  # 增长率（以倍数表示，而非百分比）
avg_growth = statistics.geometric_mean(growth_rates)
print(f"3年销售额的年均增长倍数为：{avg_growth:.4f}")
print(f"年均增长率为：{((avg_growth - 1) * 100):.2f}%")

运行结果：

3年销售额的年均增长倍数为：3.1072
年均增长率为：210.72%

计算逻辑：(2×3×5) 的 3 次方根 ≈ 3.1072，即年均增长 210.72%。

4. 其他实用函数

除了上述核心函数，statistics 模块还提供了几个常用的进阶函数，适用于更精细的统计需求。

4.1 中位数低/高：median_low(data) / median_high(data)

• median_low(data)：数据个数为偶数时，返回「中间两个数中较小的那个」；
• median_high(data)：数据个数为偶数时，返回「中间两个数中较大的那个」。

实例代码

import statistics

data = [1, 2, 3, 4]  # 偶数个数据
low_median = statistics.median_low(data)
high_median = statistics.median_high(data)

print(f"数据集 {data} 的中位数低为：{low_median}")
print(f"数据集 {data} 的中位数高为：{high_median}")

运行结果：

数据集 [1, 2, 3, 4] 的中位数低为：2
数据集 [1, 2, 3, 4] 的中位数高为：3

4.2 分位数：statistics.quantiles(data, n=4)

定义 ：将数据集按从小到大排序后，分成 n 等份的数值（默认 n=4，即四分位数）。

• 四分位数（n=4）：将数据分为4段，返回 [下四分位数Q1, 中位数Q2, 上四分位数Q3]。

实例代码

import statistics

data = [1, 2, 3, 4, 5]  # 5个数据
# 计算四分位数（n=4）
quartiles = statistics.quantiles(data, n=4)
print(f"数据集 {data} 的四分位数为：{quartiles}")

# 计算三分位数（n=3）
tertiles = statistics.quantiles(data, n=3)
print(f"数据集 {data} 的三分位数为：{tertiles}")

运行结果：

数据集 [1, 2, 3, 4, 5] 的四分位数为：[1.5, 3.0, 4.5]
数据集 [1, 2, 3, 4, 5] 的三分位数为：[2.0, 4.0]

解释：

• 四分位数中，1.5（Q1）表示25%的数据小于它，4.5（Q3）表示75%的数据小于它；
• 三分位数中，2.0（Q1）表示33%的数据小于它，4.0（Q2）表示66%的数据小于它。

5. 总结与实践建议

statistics 模块是 Python 处理基础统计的"瑞士军刀"，它的优势在于：

1. 无需安装：属于标准库，导入即可使用；
2. 简单易用 ：函数名直观（如 mean、median），参数仅需传入数据列表；
3. 异常友好 ：提供 StatisticsError 统一处理统计计算中的错误。

实践建议

1. 数据类型检查 ：确保传入 statistics 函数的数据是「数值型」（int/float），若包含字符串会报错；
2. 区分样本与总体 ：计算方差/标准差时，根据数据是"样本"还是"总体"，选择 variance/stdev 或 pvariance/pstdev；
3. 结合实际场景选指标 ：
   • 描述"普遍水平"：优先用中位数（避免极端值）；
   • 描述"平均速率"：用调和平均数；
   • 描述"增长率"：用几何平均数。

尝试用 statistics 模块分析你身边的数据吧！比如：

• 分析一周的气温数据（均值、标准差）；
• 统计班级考试成绩的中位数、众数；
• 计算自己每月消费的四分位数（了解消费分布）。

如果遇到问题，欢迎在评论区留言讨论！

💡下一篇咱们学习 Python入门：Python3 hashlib模块全面学习教程！

附录：扩展学习资源

1. 官方资源 ：
   • Python官网：https://www.python.org
   • PyPI：https://pypi.org（查找第三方库）
   • 安装包等相关文件（另附带pycharm工具），网盘下载地址：https://pan.quark.cn/s/649af731037c
   • 学习资料视频和文档资源，网盘下载地址： https://pan.quark.cn/s/ee16901a8954
2. 本专栏特色资源 ：
   • 代码资源仓库：CSDN专属资源在线获取
   • 海量Python教程 ：关注公众号：xcLeigh，获取网盘地址
   • 一对一答疑 ：添加微信与博主在线沟通（备注"Python专栏"）

联系博主

xcLeigh 博主，全栈领域优质创作者，博客专家，目前，活跃在CSDN、微信公众号、小红书、知乎、掘金、快手、思否、微博、51CTO、B站、腾讯云开发者社区、阿里云开发者社区等平台，全网拥有几十万的粉丝，全网统一IP为 xcLeigh。希望通过我的分享，让大家能在喜悦的情况下收获到有用的知识。主要分享编程、开发工具、算法、技术学习心得等内容。很多读者评价他的文章简洁易懂，尤其对于一些复杂的技术话题，他能通过通俗的语言来解释，帮助初学者更好地理解。博客通常也会涉及一些实践经验，项目分享以及解决实际开发中遇到的问题。如果你是开发领域的初学者，或者在学习一些新的编程语言或框架，关注他的文章对你有很大帮助。

亲爱的朋友，无论前路如何漫长与崎岖，都请怀揣梦想的火种，因为在生活的广袤星空中，总有一颗属于你的璀璨星辰在熠熠生辉，静候你抵达。

愿你在这纷繁世间，能时常收获微小而确定的幸福，如春日微风轻拂面庞，所有的疲惫与烦恼都能被温柔以待，内心永远充盈着安宁与慰藉。

至此，文章已至尾声，而您的故事仍在续写，不知您对文中所叙有何独特见解？期待您在心中与我对话，开启思想的新交流。

---

💞 关注博主 🌀 带你实现畅游前后端！

🏰 大屏可视化 🌀 带你体验酷炫大屏！

💯 神秘个人简介 🌀 带你体验不一样得介绍！

🥇 从零到一学习Python 🌀 带你玩转Python技术流！

🏆 前沿应用深度测评 🌀 前沿AI产品热门应用在线等你来发掘！

💦 注 ：本文撰写于CSDN平台 ,作者：xcLeigh （所有权归作者所有） ，https://xcleigh.blog.csdn.net/，如果相关下载没有跳转，请查看这个地址，相关链接没有跳转，皆是抄袭本文，转载请备注本文原地址。

---

📣 亲，码字不易，动动小手，欢迎 点赞 ➕ 收藏，如 🈶 问题请留言（或者关注下方公众号，看见后第一时间回复，还有海量编程资料等你来领！），博主看见后一定及时给您答复 💌💌💌