JAVA进阶之路——数据结构之线性表（顺序表、链表）

数据结构之------线性表

引言
- 线性表的基本概念与定义
- - [1. 线性表的逻辑结构特点：什么是"线性"？](#1. 线性表的逻辑结构特点：什么是“线性”？)
  - [2. 抽象数据类型（ADT）定义：我们要什么功能？](#2. 抽象数据类型（ADT）定义：我们要什么功能？)
  - - [A. 构造与销毁（生与死）](#A. 构造与销毁（生与死）)
    - [B. 查看状态（只读操作）](#B. 查看状态（只读操作）)
    - [C. 修改数据（增与删）](#C. 修改数据（增与删）)
  - 3.线性表的两种存储结构
- 顺序表（顺序存储结构）
- - 1.啥是顺序表
  - [2. 基本操作的代码+时间复杂度分析](#2. 基本操作的代码+时间复杂度分析)
  - - JAVA代码实现
    - 时间复杂度分析
  - [3. 优缺点对比](#3. 优缺点对比)
- 链表（链式存储结构）
- - [1. 单链表的结构与实现](#1. 单链表的结构与实现)
  - - 核心概念
    - [Java 代码实现](#Java 代码实现)
  - [2. 链表的变体结构](#2. 链表的变体结构)
  - - [A. 双向链表 (Doubly Linked List)](#A. 双向链表 (Doubly Linked List))
    - [B. 循环链表 (Circular Linked List)](#B. 循环链表 (Circular Linked List))
  - [3. 时间复杂度深度分析](#3. 时间复杂度深度分析)
  - - [查找 (Search / Access) ------ **O(n)**](#查找 (Search / Access) —— O(n))
    - [插入 (Insert) ------ **O(1)** (前提是知道位置)](#插入 (Insert) —— O(1) (前提是知道位置))
    - [删除 (Delete) ------ **O(1)** (前提是知道位置)](#删除 (Delete) —— O(1) (前提是知道位置))
- 线性表的应用场景

引言

JAVA进阶之路里面的数据结构是本人作为复习来写的，第一篇其实很简单，但是仔细一想当初学的时候又是处处碰壁，所以这篇还是写的细致一点希望用大家能听懂的话讲明白

线性表是数据结构梦开始的地方，但有个前提你得先会结构体，如果有孩子不知道啥是结构体建议先知道结构体再来看本篇文章~

话不多说，开始正题！

线性表的基本概念与定义

1. 线性表的逻辑结构特点：什么是"线性"？

首先，我们要把逻辑结构 和物理存储分开。逻辑结构是你"想象中"的样子，物理存储是计算机内存中"实际"的样子。

逻辑上的线性表，就像是一条笔直的绳子，上面串着珠子。

它的核心特点可以归纳为以下四点：

有且仅有一个"排头兵"（第一个元素）
- 逻辑结构中，存在唯一的一个数据元素，它没有前驱（没有"老大"罩着它）。这个元素通常被称为表头。
有且仅有一个"收尾人"（最后一个元素）
- 存在唯一的一个数据元素，它没有后继（没有"小弟"跟在它后面）。这个元素通常被称为表尾。
中间的"单线联系"（一对一关系）
- 除了第一个和最后一个，其他所有元素都处于"前有古人，后有来者"的状态。
- 每个中间元素，有且仅有一个 直接前驱，有且仅有一个直接后继。
严格的次序性（序列）
- 元素之间是有绝对顺序的。 ( a , b , c ) (a, b, c) (a,b,c) 和 ( c , b , a ) (c, b, a) (c,b,a) 在线性表中是两个完全不同的表。

逻辑结构只关心"谁是谁的前一个，谁是谁的后一个"，不关心它们在内存里是不是挨着坐的。这一点直接引出了下面的两种存储方式。

2. 抽象数据类型（ADT）定义：我们要什么功能？

抽象数据类型（ADT）就像是线性表的"功能说明书"。不管你是用数组实现还是用链表实现，只要你叫"线性表"，你就必须提供以下这些基本操作。这些是计算机科学家定好的"规矩"。

我们可以把这些操作分为三类：

A. 构造与销毁（生与死）

InitList(&L) ：初始化 。造一个空的线性表 L L L。就像刚买回来的空书架。
DestroyList(&L) ：销毁。把表 L L L 彻底干掉，释放内存。书架拆了，书卖了。

B. 查看状态（只读操作）

Length(L) ：求长度 。问表 L L L："你现在存了多少个元素？"
Empty(L) ：判空。检查表 L L L 是不是空的（长度为0）。
GetElem(L, i, &e) ：按位查找 。给定一个位置 i i i（比如第3个），把那个位置的元素值取出来给 e e e。
LocateElem(L, e) ：按值查找 。给定一个值 e e e，问表："这玩意儿在哪个位置？"（返回位序）。

C. 修改数据（增与删）

ListInsert(&L, i, e) ：插入。在表 L L L 的第 i i i 个位置上，把元素 e e e 插进去。插进去之后，原来第 i i i 个及后面的元素都要往后挪一位。
ListDelete(&L, i, &e) ：删除。把表 L L L 中第 i i i 个位置的元素删掉。删完后，后面的元素要往前补位。被删掉的那个值，通过 e e e 返回给你留作纪念。

PS：

在数学和算法描述中，位置（位序）通常从 1 开始（第1个、第2个...）。但在编程实现中，下标通常从 0 开始。

3.线性表的两种存储结构

顺序存储（数组）与链式存储（链表）

说了那么多你可能懵了，那么我们接下来给大家具体讲讲这两类线性表，也就是顺序表和链表，帮助大家理解~

顺序表（顺序存储结构）

1.啥是顺序表

同志，你知道啥是数组吧，如图就是数组：

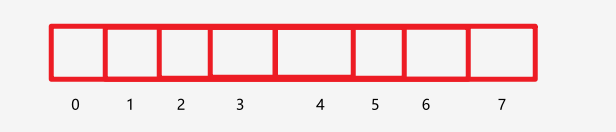
现在你知道了数组，也知道了结构体，那么线性表就是在数组里面放一个又一个的结构体！

如图：

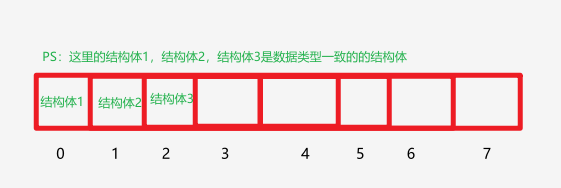
注意这里的结构体是来放你要存的数据和线性表的长度的，结构体定义一般如下：

c 复制代码

typedef struct {
    ElementType data[MAX_SIZE]; // 存放的数据元素
    int length;                 // 当前顺序表的长度
} SeqList; // 通常叫顺序表 (Sequential List)

因此：顺序表的实现原理是连续内存空间存储元素

2. 基本操作的代码+时间复杂度分析

JAVA代码实现

java 复制代码

public class SeqList {
    private int[] data;      // 存储元素的数组
    private int size;        // 当前元素个数
    private int capacity;    // 容量

    // 构造函数，初始化顺序表
    public SeqList(int capacity) {
        this.data = new int[capacity];
        this.size = 0;
        this.capacity = capacity;
    }

    // 随机访问元素
    public int get(int index) {
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException("Index out of bounds");
        }
        return data[index];
    }

    // 在指定位置插入元素
    public void insert(int index, int element) {
        if (size == capacity) {
            resize();
        }
        if (index < 0 || index > size) {
            throw new IndexOutOfBoundsException("Index out of bounds");
        }
        for (int i = size; i > index; i--) {
            data[i] = data[i - 1];
        }
        data[index] = element;
        size++;
    }

    // 删除指定位置的元素
    public int delete(int index) {
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException("Index out of bounds");
        }
        int deletedElement = data[index];
        for (int i = index; i < size - 1; i++) {
            data[i] = data[i + 1];
        }
        size--;
        return deletedElement;
    }

    // 扩容
    private void resize() {
        int newCapacity = capacity * 2;
        int[] newData = new int[newCapacity];
        System.arraycopy(data, 0, newData, 0, size);
        data = newData;
        capacity = newCapacity;
    }

    // 获取当前元素个数
    public int size() {
        return size;
    }
}

功能说明

get(int index)方法实现随机访问，时间复杂度为O(1)

insert(int index, int element)方法在指定位置插入元素，平均时间复杂度为O(n)

delete(int index)方法删除指定位置元素，平均时间复杂度为O(n)

resize()方法在容量不足时自动扩容，保证顺序表可动态增长

使用示例

java 复制代码

public class Main {
    public static void main(String[] args) {
        SeqList list = new SeqList(5);
        
        // 插入元素
        list.insert(0, 10);
        list.insert(1, 20);
        list.insert(2, 30);
        
        // 随机访问
        System.out.println("Element at index 1: " + list.get(1));
        
        // 删除元素
        list.delete(1);
        System.out.println("Element at index 1 after deletion: " + list.get(1));
    }
}

时间复杂度分析

随机访问O(1)：由于数组元素在内存中是连续存储的，通过下标可以直接计算出元素的内存地址进行访问。例如访问arr[5]，只需计算基地址+5×元素大小即可定位。
插入/删除O(n)：在数组中间插入或删除元素时，需要移动其后所有元素以保持连续性。例如在长度为n的数组第k个位置插入元素，需要将k到n-1位置的元素都向后移动一位。

3. 优缺点对比

优点：
- 支持快速随机访问：适合需要频繁按索引读取的场景，如实现哈希表、缓存等
- 内存局部性好：连续存储有利于CPU缓存预取
缺点：
- 扩容成本高：当容量不足时需要分配新数组并拷贝所有元素，典型实现是倍增策略(如Java ArrayList)
- 插入删除效率低：不适合频繁修改的场景，如实现队列时效率不如链表
- 固定大小限制：静态数组声明后无法改变容量

链表（链式存储结构）

既然你点名要 Java 代码，那咱们就直接上手干！相比 C 语言，Java 实现链表会少去很多指针的操作，但多了对象引用的概念，逻辑是一模一样的。

咱们按照你要求的三个维度，从最基础的单链表开始，一层层递进。

1. 单链表的结构与实现

核心概念

节点 (Node) ：链表的基石。每个节点包含两部分：
- 数据域 ：存放实际的数据（比如 int data）。
- 指针域 ：存放下一个 节点的引用（在 Java 里叫 next）。
头指针 (Head) ：这是链表的"命门"。它不存数据（或者你可以设计它存数据，但通常不存），它只保存第一个节点的地址。没有头指针，你就找不到整条链表。
尾指针 (Tail) ：指向最后一个节点。最后一个节点的 next 指向 null（空），表示链表到此为止。

其实就是结构体里面多存了个指向下一个结构体地址的这么一个变量，如图：

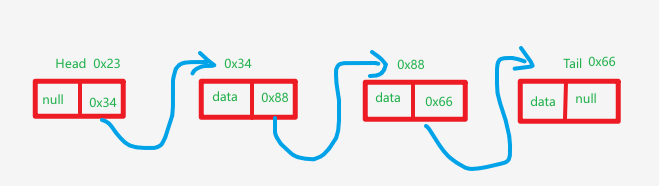
Java 代码实现

java 复制代码

// 1. 定义节点类
class ListNode {
    int val;        // 数据域，这里假设存整数
    ListNode next;  // 指针域，指向下一个节点

    // 构造函数
    ListNode(int val) {
        this.val = val;
        this.next = null; // 初始时指向空
    }
}

// 2. 定义链表操作类
public class LinkedList {
    private ListNode head; // 头指针，指向链表的第一个节点

    // 构造函数，初始化空链表
    public LinkedList() {
        this.head = null;
    }

    // --- 基本操作示例 ---

    // 在链表头部插入新节点 (最简单，时间复杂度 O(1))
    public void addFirst(int val) {
        ListNode newNode = new ListNode(val); // 1. 创建新节点
        newNode.next = head;                  // 2. 新节点的next指向原来的头节点
        head = newNode;                     // 3. 头指针指向新节点
        System.out.println("头部插入: " + val);
    }

    // 删除第一个节点 (演示删除操作)
    public void deleteFirst() {
        if (head == null) {
            System.out.println("链表为空，无法删除");
            return;
        }
        int deletedVal = head.val;
        head = head.next; // 头指针直接跳到下一个节点，原来的节点没人引用，会被Java垃圾回收
        System.out.println("头部删除: " + deletedVal);
    }

    // 遍历链表 (演示查找/访问操作)
    public void display() {
        if (head == null) {
            System.out.println("链表为空");
            return;
        }
        System.out.print("链表内容: ");
        ListNode current = head; // 从头节点开始
        while (current != null) {
            System.out.print(current.val + " -> ");
            current = current.next; // 移动到下一个节点
        }
        System.out.println("null");
    }

    // --- 测试 ---
    public static void main(String[] args) {
        LinkedList list = new LinkedList();

        list.addFirst(30);
        list.addFirst(20);
        list.addFirst(10);
        list.display(); // 输出: 10 -> 20 -> 30 -> null

        list.deleteFirst();
        list.display(); // 输出: 20 -> 30 -> null
    }
}

2. 链表的变体结构

单链表只能往前走（顺着 next），如果我们需要更强的功能，就需要升级结构。

A. 双向链表 (Doubly Linked List)

痛点解决 ：单链表只能从前往后找，如果我想知道"上一个是谁"怎么办？
结构变化：

每个节点多了一个 prev（previous）指针，指向前一个节点。
这样就可以双向行走了。

结构示意图 ：

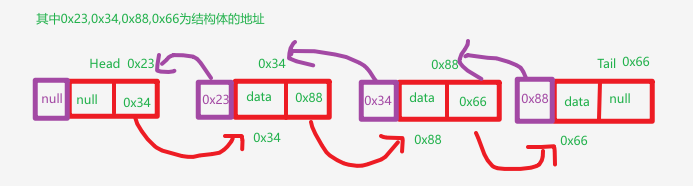
B. 循环链表 (Circular Linked List)

痛点解决 ：单链表走到尾巴就结束了（遇到 null）。如果我想让数据像贪吃蛇一样首尾相连怎么办？
结构变化：

最后一个节点的 next 不指向 null，而是指向头节点。【大家可以自己画一画】
这样就没有真正的"结尾"了，遍历的时候要小心别死循环。

3. 时间复杂度深度分析

这是面试必问的问题。为什么我们要用链表？就是为了一句话：牺牲查找速度，换取插入删除的自由。

查找 (Search / Access) ------ O(n)

原因：链表在内存中是散落的，不像数组那样连续。你不能通过下标直接计算地址。
过程：如果你想查找第 5 个元素，你必须从头指针开始，一个一个顺着 next 往下找，数到第 5 个才行。
最坏情况 ：要找的元素在尾巴上，或者根本不存在，那你得把整个链表走一遍。所以时间复杂度是 O(n)。

插入 (Insert) ------ O(1) (前提是知道位置)

原因：链表插入不需要像数组那样搬移元素。
过程：
- 如果是在头部插入：只需要修改头指针和新节点的 next 指针。
- 如果是在中间（已知前一个节点）：只需要修改两个指针（前一个节点指向新节点，新节点指向原来的下一个）。
注意：这里有个陷阱。如果题目说"在第 i 个位置插入"，那你得先花 O(n) 的时间找到第 i 个位置，然后再花 O(1) 插入。总时间复杂度还是 O(n)。但如果我们已经拿到了那个位置的指针，插入就是瞬间的 O(1)。

删除 (Delete) ------ O(1) (前提是知道位置)

原因：同理，不需要搬移数据。
过程：修改前一个节点的 next 指针，跳过要删除的节点即可。被跳过的节点因为没有引用指向它，会被垃圾回收器回收。

线性表的应用场景

顺序表适用场景

顺序表（数组实现）由于其连续存储的特性，特别适合以下场景：

元素数量固定：如存储固定长度的配置参数表、预先确定大小的哈希表
频繁随机访问 ：时间复杂度O(1)的访问特性使其适用于：
- 静态查找表（如字典序存储的关键字表）
- 图像处理中的像素矩阵存储
- 科学计算中的向量/矩阵运算
缓存友好性：CPU缓存预取机制对连续存储有优化，如游戏开发中的实体组件系统(ECS)

典型应用示例：

学生成绩管理系统中的静态成绩表
嵌入式系统中的硬件寄存器映射表

链表适用场景

链表（动态存储结构）的优势场景包括：

频繁增删操作 ：
- 实时系统中的消息队列（插入/删除时间复杂度O(1)）
- 文本编辑器的撤销操作链
内存灵活管理 ：
- 操作系统内存池管理（避免内存碎片）
- 动态增长的数据库索引
非连续存储需求 ：
- 文件系统中的磁盘块链式存储
- 图形处理中的多边形顶点存储

实现案例：

QQ 好友列表，经常有人上线（插入）、下线（删除），但很少需要遍历所有人的详细信息

典型实际应用

数组实现堆栈：
- 函数调用栈（固定大小的栈帧存储）
- 算术表达式求值（操作数栈）
- 具体实现步骤：
  c 复制代码
```
#define MAX_SIZE 100
typedef struct {
    int data[MAX_SIZE];
    int top;
} ArrayStack;
```
链表实现LRU缓存：
- 浏览器页面缓存淘汰
- 数据库查询缓存管理
- 实现要点：
  - 哈希表+双向链表（O(1)访问与移动）
  - 最近访问移至链表头部
  - 容量满时淘汰尾部节点
- 应用示例：
  python 复制代码
```
class LRUCache:
    def __init__(self, capacity):
        self.cache = OrderedDict()
        self.capacity = capacity
```
混合应用案例：
- MySQL的B+树索引（叶子节点链表串联）
- 区块链结构（哈希指针链表+交易数据数组）

这篇还是先给大家把最基础的讲到，后续由于学习的深入，这块知识要反复使用！

希望对大家有所帮助