

**前引:**在处理数组、字符串的子串 / 子数组问题时,你是否也曾陷入 "暴力遍历" 的泥潭?比如找最长无重复子串、最小覆盖子串,或是区间和满足条件的最短长度 ------ 暴力解法往往需要嵌套循环,时间复杂度飙升至 O (n²),面对大数据量时直接 "超时"。而滑动窗口算法,正是为解决这类 "区间查询" 问题而生的 "高效工具":它通过两个指针模拟一个 "可伸缩的窗口",在一次线性遍历中完成区间筛选,将时间复杂度直接优化到 O (n)。本文将从核心原理出发,拆解滑动窗口的 "窗口收缩 / 扩张" 逻辑,带你掌握固定窗口、可变窗口的通用模板,从此告别嵌套循环的低效困境!
目录
"滑动窗口"算法介绍
废话不多说,直接介绍:
"滑动窗口"也是依赖两个指针的移动,如果两个指针同向移动,那么可称为滑动窗口
比如一个毛毛虫,向一方移动,身体长度在移动的情况下不断变化!
【一】长度最小的子树组
(1)链接
https://leetcode.cn/problems/minimum-size-subarray-sum

(2)算法解析
要求:通过找一段区间,满足区间内的数字之和 >= target,求最短区间
暴力解法:强力枚举,从第一个数字 left 开始,让 right 不断向右,直达和满足要求
再从第二个数字开始,right回到left位置,重新求和.....不断循环
算法:
假设一段数组:【2,3,1,2,4,3】,定义left、right=0;target=7;
此时第一段有效区间是【2,3,1,2】,即left指向位置为2(0),right指向位置位2(3)
从第二次查找开始,暴力解法是让left和right都回到3(1)的位置,但是满足如下规律:

即left和right直接有一部分元素是重复的,right不需要回到left位置,如果此时【left,right】范围内的和满足要求继续右移left,否则right右移,right移动到数组末尾,更新为最后一次结果即完成
(3)代码
cpp
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums)
{
if(nums.size()==0)return 0;
int left = 0;
int right = left;
int len = INT_MAX;
int sum = 0;
while (right < nums.size())
{
sum += nums[right];
//进窗口,如果一直进不了循环呢
while (sum >= target)
{
if (sum >= target)
{
if (right - left < len)
{
len = right - left + 1;
}
}
sum-=nums[left++];
}
right++;
}
if(len==INT_MAX)return 0;
return len;
}
};(4)常用接口:max/min
求最大值或者最小值,可以直接使用接口:max/min(x1,x2),返回x1和x2对应的最值
通常整型最大值为INT_MAX,最小值在算法题中通常设置为-1
【二】无重复长度最长子串
(1)链接
https://leetcode.cn/problems/longest-substring-without-repeating-characters

(2)算法解析
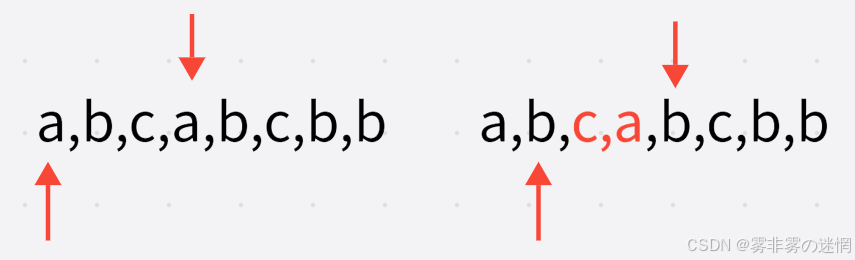
暴力枚举:left与right从0下标开始,left固定,right不断向后移动,碰到范围重复的就停下来
left++,right回到left位置,继续依次循环,如下图:

算法解析:我们看图,找到重复之后,left++,right就没必要回来了,反正right一定移动到上一次结尾的下一个位置,所以遇到重复的就left++,否则right一直向前。范围里的元素出现次数都为1
(3)代码
cpp
class Solution {
public:
int lengthOfLongestSubstring(string s)
{
//如果是空串返回0
if(s.empty())return 0;
//建立哈希表
unordered_set<char> V;
//双指针
int left=0;
int right=0;
int len=0;
while(right<s.size())
{
//只要窗口包含当前right的字符,就收缩left
while (V.count(s[right]))
{
V.erase(s[left++]);
}
//插入当前字
V.insert(s[right++]);
if (right - left > len)
{
len = right - left;
}
}
return len;
}
};(4)重要接口:
有两个容器是滑动窗口用的最多的:unordered_set<T> unordered_map<T,T>
其中**【】**根据key(没有就创建)返回value是 map 容器常用的接口
其中有一个接口可以判断是否重复,在本题很实用:count(key),key重复就返回非0
【三】最小覆盖子串(重要)
(1)链接
https://leetcode.cn/problems/minimum-window-substring

(2)算法解析
暴力枚举:left、right开始为0,先让right++,一直找到该范围包含全部的子串,主要是如何找?
借助unordered_map<char,int> 和【】(准备俩个该容器对象)最简单的就是 find ,如果hash1能find(s[right])且在 hash2 中找到对应字符且对应 value 相等,说明单个元素是符合条件
(1)单个元素符合条件:借助map和【】,确定单个元素是否一致
(2)比如 t = AA,有效元素个数为1,t = BA,有效元素个数为2,即不重复的字符数量相等
满足上面两个条件之后,那么范围就被确定下来了,此时left右移之后,重新划分范围
算法解析:算法解析也就是不让right每次回来,即一直向右,这没什么好说的,因为有重复的元素
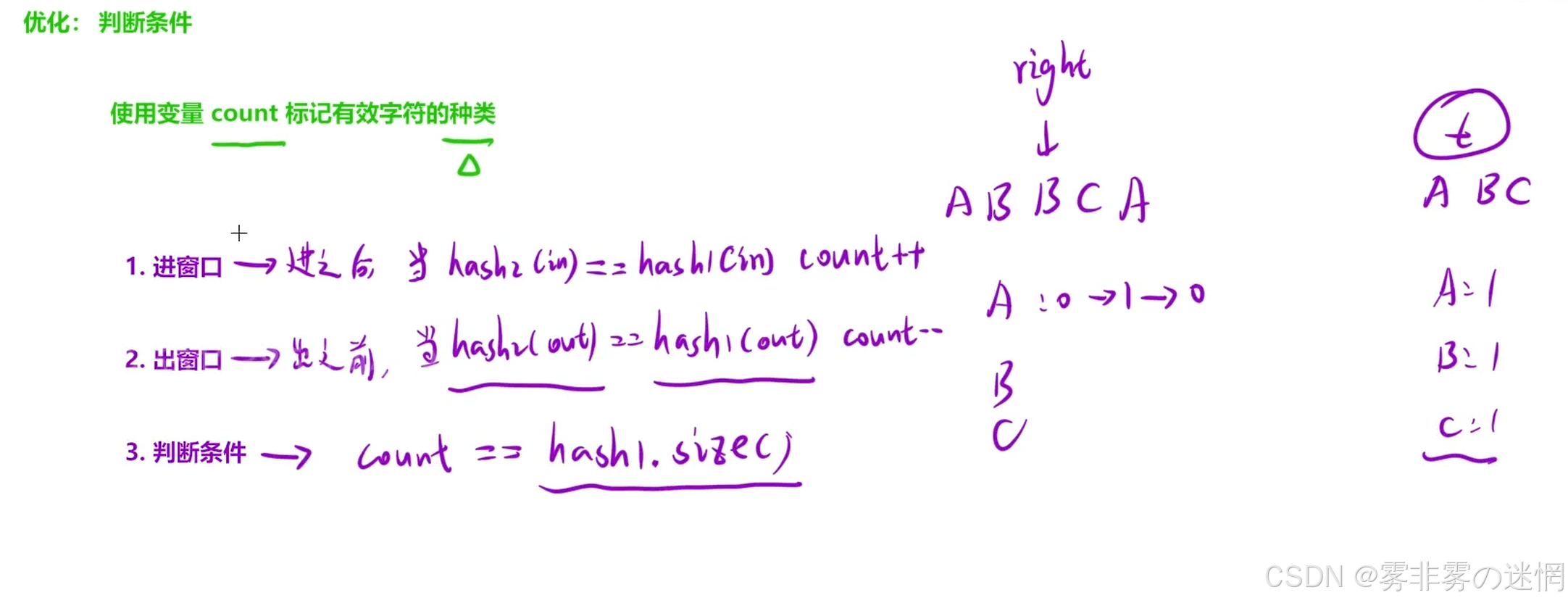
(3)优化(核心)
这题的主要困难就是 t 中的元素可能重复,否则直接被 **unordered_map<char,int>**秒杀,因此要解决重复的情况,可以引入一个变量 count ,先用 hash2 【】遍历 t 中的元素,获得有效元素个数,当 right 每次找到一个元素就让 hash1 【】该元素,如果该元素【】的value和hash2的相等,就count++,当count和"获得有效元素个数"相等,即单次范围划分完毕!count是种类不是个数
(4)代码
cpp
class Solution
{
public:
string minWindow(string s, string t)
{
int hash1[128] = { 0 }; // 统计字符串 t 中每⼀个字符的频次
int kinds = 0; // 统计有效字符有多少种
for(auto ch : t)
if(hash1[ch]++ == 0) kinds++;
int hash2[128] = { 0 }; // 统计窗⼝内每个字符的频次
int minlen = INT_MAX, begin = -1;
for(int left = 0, right = 0, count = 0; right < s.size(); right++)
{
char in = s[right];
if(++hash2[in] == hash1[in]) count++; // 进窗⼝ + 维护 count
while(count == kinds) // 判断条件
{
if(right - left + 1 < minlen) // 更新结果
{
minlen = right - left + 1;
begin = left;
}
char out = s[left++];
if(hash2[out]-- == hash1[out]) count--; // 出窗⼝ + 维护 count
}
}
if(begin == -1) return "";
else return s.substr(begin, minlen);
}
};