【声呐硬件设计】LFM信号处理中前级有源滤波器设计的关键考量与原理分析

摘要：

线性调频（LFM）信号因其优秀的脉冲压缩特性和抗干扰能力，被广泛应用于现代声呐系统中。在声呐接收机的模拟前端设计中，滤波器的选择至关重要。本文将重点探讨在使用有源滤波器处理LFM模拟回波信号时需要注意的核心事项，从群延时特性 、运放增益带宽积 、动态范围等维度深入分析其原理，并给出选型建议。

一、背景概述

声呐系统接收到的模拟回波信号通常混杂着环境噪声和干扰。在经过ADC采样之前，我们需要一个模拟滤波器（通常作为抗混叠滤波器或带通滤波器）来预处理信号。

对于LFM（Chirp）信号 ，其数学表达式通常为：
s(t)=A⋅rect(tT)⋅exp⁡(j(2πf0t+πkt2)) s(t) = A \cdot \text{rect}(\frac{t}{T}) \cdot \exp(j(2\pi f_0 t + \pi k t^2)) s(t)=A⋅rect(Tt)⋅exp(j(2πf0t+πkt2))

其中 kkk 为调频斜率。由于LFM信号的信息承载于频率随时间的变化 中，且后续DSP处理依赖于匹配滤波（脉冲压缩） ，这对模拟滤波器的相位线性度提出了比单频脉冲信号严苛得多的要求。

二、有源滤波器设计的四大注意事项

在选择和设计有源滤波器（如基于运算放大器的Sallen-Key或多重反馈MFB拓扑）时，必须注意以下四点：

1. 相位线性度与群延时平坦度（最重要！）

注意事项 ：

切勿只关注幅频响应（通带是否平坦、阻带衰减是否够快），必须将 群延时（Group Delay） 作为第一指标。

原理分析 ：

LFM信号是一个宽带信号。根据傅里叶变换性质，时域的延时对应频域的线性相移。

理想情况：滤波器在整个LFM带宽内的群延时是常数，信号只是整体被延迟，波形不变。
非理想情况 ：如果滤波器的相位是非线性的（即群延时随频率变化），那么LFM信号中不同频率分量的延迟时间将不同。
- 后果：这会导致脉冲压缩后的主瓣展宽 （降低距离分辨率）和旁瓣升高（容易掩盖弱目标），严重破坏LFM的增益优势。

选型建议：

首选：贝塞尔（Bessel）滤波器。它具有最佳的线性相位特性，能够最大限度地保持LFM的波形完整性，适合时域脉冲信号。
次选：巴特沃斯（Butterworth）滤波器。幅频响应最平坦，但相频响应不如贝塞尔。若使用，需确保截止频率远大于信号带宽，让信号落在相位相对线性的区域。
慎用：切比雪夫（Chebyshev）滤波器。虽然它滚降快，但其剧烈的相位非线性会严重畸变LFM信号。

2. 运放的增益带宽积（GBW）限制

注意事项 ：

LFM声呐的工作频率可能较高（如几十kHz到几百kHz）。选择运放时，GBW必须留有足够的余量。

原理分析 ：

有源滤波器的滤波特性依赖于运放的开环增益。当信号频率升高，运放的开环增益下降。如果运放的GBW不足，在高频段（LFM的高频端），滤波器不仅无法维持预期的QQQ值，还会引入额外的、不可预测的相位滞后。

经验公式：对于二阶滤波器，要求 GBW≥10∼100×fc×QGBW \ge 10 \sim 100 \times f_c \times QGBW≥10∼100×fc×Q。

选型建议 ：

对于高频宽带LFM声呐，如果普通运放GBW不足，应考虑使用高速运放，或者改用无源LC滤波器加缓冲级的方案。

3. 压摆率（Slew Rate）与大信号失真

注意事项 ：

声呐回波动态范围极大（近场强回波 vs 远场弱回波）。有源滤波器必须能无失真地处理最大幅度的回波。

原理分析 ：

LFM信号是等幅信号。当近场强回波到达时，如果信号的变化率（dV/dtdV/dtdV/dt）超过了运放的压摆率（SR），运放输出将不再是正弦波，而是变成三角波。

后果：这是一种非线性失真，会产生大量的高次谐波。在LFM匹配滤波后，这些谐波会形成假目标（Ghost Targets），严重干扰检测。

选型建议 ：

计算所需最小SR：SRmin=2π⋅fmax⋅VpeakSR_{min} = 2\pi \cdot f_{max} \cdot V_{peak}SRmin=2π⋅fmax⋅Vpeak。实际选型时应至少留出2倍余量。

4. 噪声系数

注意事项 ：

有源滤波器中的电阻和运放本身都是噪声源。

原理分析 ：

虽然LFM通过脉冲压缩能获得处理增益（Processing Gain），提高输出SNR，但如果模拟前端引入的噪声过大，淹没了微弱信号，后续的处理增益也无法挽回。

电阻热噪声 ：Vn=4kTRBV_n = \sqrt{4kTRB}Vn=4kTRB 。阻值越大，噪声越大。
运放噪声：包括电压噪声密度和电流噪声密度。

选型建议：

在功耗允许的情况下，尽量选用低噪声运放。
在滤波器设计中，反馈电阻的阻值不宜过大（例如避免使用MΩ\OmegaΩ级别的电阻），以降低热噪声。

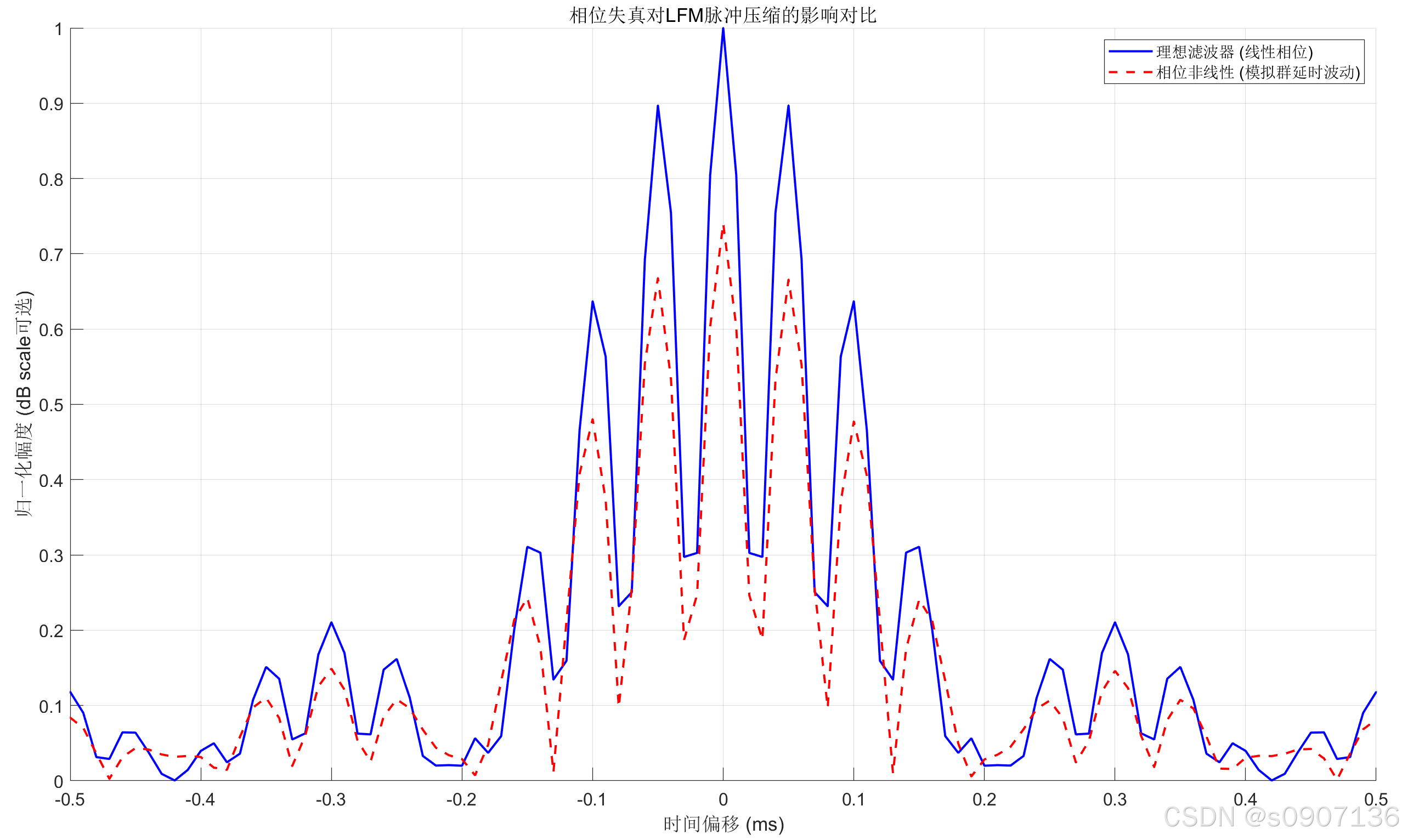
三、仿真验证：相位失真对脉冲压缩的影响

为了直观展示滤波器选择不当的后果，我们可以使用Python简单模拟一下。

场景假设

LFM带宽：5kHz
中心频率：10kHz
对比：无失真信号 vs 经过强非线性相位滤波器后的信号

matlab 复制代码

% 清空环境
clear; clc; close all;

%% 1. 参数设置与信号生成
fs = 100000;            % 采样率 100kHz
T = 0.01;               % 脉冲宽度 10ms
t = 0:1/fs:T-1/fs;      % 时间向量

f0 = 7500;              % 起始频率
f1 = 12500;             % 终止频率

% 生成理想LFM信号
% chirp函数生成线性调频信号
sig_ideal = chirp(t, f0, T, f1);

%% 2. 模拟相位失真 (模拟滤波器的非线性相位响应)
% 原理：时域信号做FFT -> 频域乘以相位误差项 -> IFFT还原
L = length(sig_ideal);
Y = fft(sig_ideal);
f = (-L/2:L/2-1)*(fs/L); % 生成以0为中心的频率向量
Y_shifted = fftshift(Y);

% 定义相位误差：模拟一个抛物线形的相位非线性
% 这种非线性相位对应着随频率线性变化的群延时
k_phase = 7e-9; 
phase_error = k_phase * f.^2; 

% 将误差应用到频域信号 (乘以 exp(j*phi))
Y_distorted_shifted = Y_shifted .* exp(1j * phase_error);
sig_distorted = real(ifft(ifftshift(Y_distorted_shifted)));

%% 3. 脉冲压缩 (匹配滤波)
% 使用xcorr进行互相关
[pc_ideal, lags] = xcorr(sig_ideal, sig_ideal);
[pc_distorted, ~] = xcorr(sig_distorted, sig_ideal);

% 转换为时间轴 (毫秒)
time_axis = lags/fs * 1000;

%% 4. 绘图对比
figure('Color','w');
hold on; grid on;

% 归一化处理：以理想信号的最大值为基准，观察失真信号的衰减
max_val = max(abs(pc_ideal));

plot(time_axis, abs(pc_ideal)/max_val, 'b', 'LineWidth', 1.5);
plot(time_axis, abs(pc_distorted)/max_val, 'r--', 'LineWidth', 1.5);

% 图表美化
xlim([-0.5, 0.5]); % 仅观察主瓣附近
xlabel('时间偏移 (ms)');
ylabel('归一化幅度 (dB scale可选)');
title('相位失真对LFM脉冲压缩的影响对比');
legend('理想滤波器 (线性相位)', '相位非线性 (模拟群延时波动)');
set(gca, 'FontSize', 12);

% 输出量化损失
loss_db = 20*log10(max(abs(pc_distorted))/max_val);
fprintf('由于相位失真导致的峰值损耗: %.2f dB\n', loss_db);

结果分析 ：

运行上述代码（逻辑示意）可以看到，红色虚线（相位失真后）的波峰虽然还在，但是：

峰值下降（SNR损失）。
主瓣变宽（距离分辨率变差）。
非对称旁瓣 出现。

四、总结与建议表

在设计LFM声呐的有源滤波器时，请参考下表进行决策：

考量维度	关键指标	推荐方案	避免方案
拓扑结构	群延时平坦度	Bessel 或低Q值的Butterworth	高阶Chebyshev
器件选型	增益带宽积 (GBW)	GBW>50⋅fmaxGBW > 50 \cdot f_{max}GBW>50⋅fmax	通用型低频运放 (如LM741等)
信号完整性	压摆率 (SR)	高SR运放，留足余量	轨到轨低功耗但SR低的运放
元器件	精度与稳定性	1%或0.1%金属膜电阻，NP0/C0G电容	碳膜电阻，Y5V电容（压电效应会导致颤噪）

结论：

LFM声呐的有源滤波器设计，本质上是在幅频特性 和相频特性 之间做权衡。对于LFM信号，保真度（相位线性）优于陡峭度（幅频滚降）。宁可牺牲一点带外噪声抑制能力（可以通过提高采样率和数字滤波弥补），也要保证通带内的群延时平坦，从而确保脉冲压缩的性能。

【声呐硬件设计】LFM信号处理中前级有源滤波器设计的关键考量与原理分析