PCL 法向量估计-PCA邻域点（经典 kNN 协方差）的协方差矩阵

1、数学原理：为什么 PCA 可以得到法向？

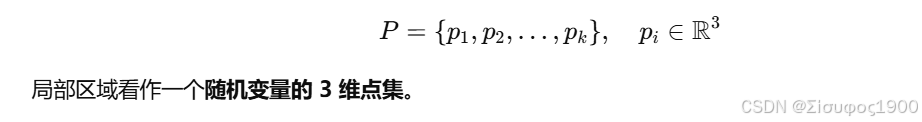
(1) 求几何中心

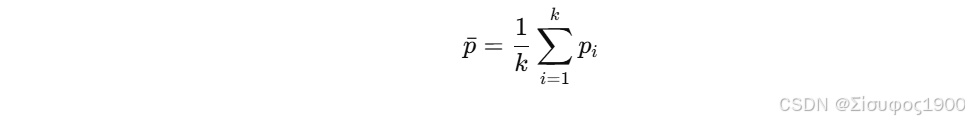
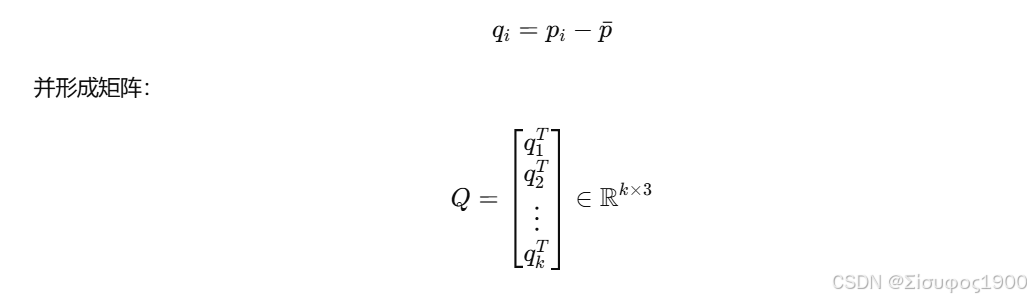
(2) 构建去中心化矩阵

(3) 协方差矩阵

PCL、Open3D、SLAM 全部采用

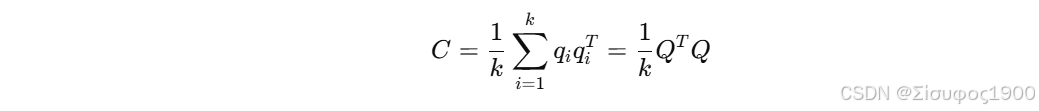
这个矩阵描述了在 x, y, z 方向的"离散程度"：

• 平面方向 → 大的特征值

• 法向方向 → 数据最不分散，因此特征值最小

所以：

局部平面法向 = 最小特征值对应的特征向量

(4) PCA 分解

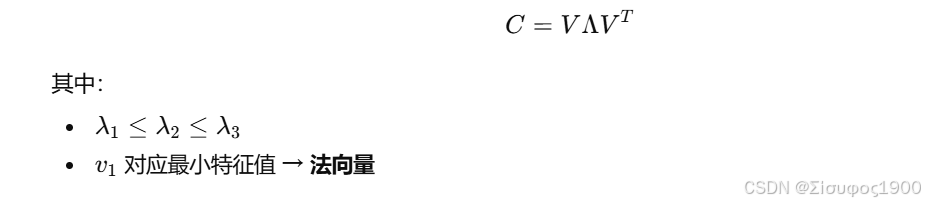
2. 为什么"最小特征值对应法向"？

因为：

• 局部邻域近似平面

• 平面中点分布在 2D 平面

• 法向方向数据"最不分散"（投影方差最小）

几何解释：

点云 → PCA 两个最大特征值 → 局部主方向 最小特征值方向 → 垂直于平面的方向

这是最经典、最重要的法向理论面试点。

3、协方差矩阵 C 的结构解释（高频考）

协方差矩阵：

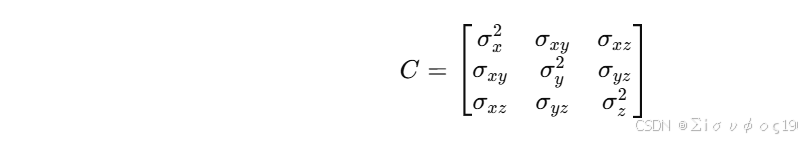
描述的是：

• 主方向（切平面方向） → 最大特征值

• 次主方向

• 法向（最微小方向） → 最小特征值

你可以直接告诉面试官：

PCA 的法向是"最不分散方向"。因此协方差矩阵的最小特征向量必定是法向。PCL 正是这么实现的。

4. MATLAB 完整实现

function N = pca_normals_albert(P, k)
% P: Nx3 点云
% k: 邻域点数量
% N: Nx3 法向矩阵

    N = zeros(size(P));
    Mdl = createns(P,'NSMethod','kdtree');

    for i = 1:size(P,1)
        % 1) 找k邻域
        idx = knnsearch(Mdl, P(i,:), 'K', k);
        pts = P(idx,:);

        % 2) 计算局部中心
        pbar = mean(pts,1);

        % 3) 去中心化
        Q = pts - pbar;

        % 4) 协方差矩阵 (PCL风格)
        C = (Q' * Q) / k;

        % 5) PCA 求法向
        [V, D] = eig(C);
        [~, j] = min(diag(D));
        normal = V(:, j);

        % 6) 方向统一
        if normal(3) < 0
            normal = -normal;
        end

        N(i,:) = normal';
    end
end

>> %% 1. 加载点云
ptCloud = pcread("bun000.ply");
P = ptCloud.Location;

%% 2. 计算 PCA 法向
N = pca_normals_albert(P, 30);

%% 3. 显示
figure; hold on; axis equal;
pcshow(P);
title("PCA (kNN) 法向量");

% 每隔一定数量画箭头
step = 200;
quiver3(P(1:step:end,1), P(1:step:end,2), P(1:step:end,3), ...
        N(1:step:end,1), N(1:step:end,2), N(1:step:end,3), 0.03, 'r');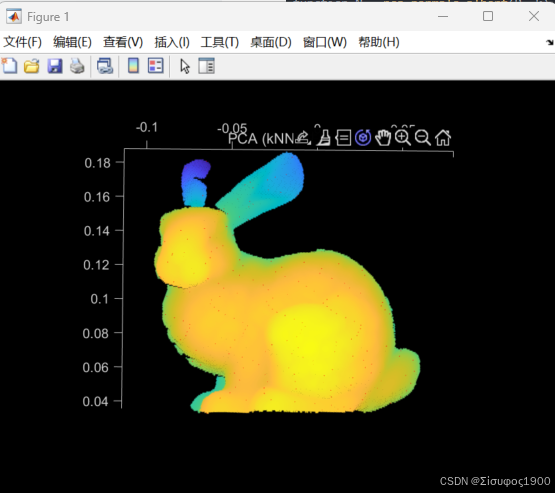

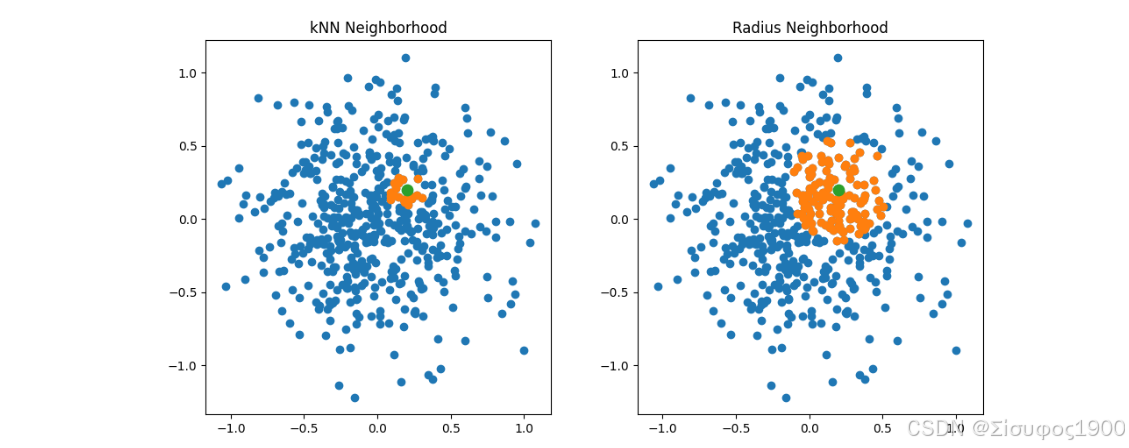
半径邻域 vs kNN 邻域对比图