transformer中的位置编码：从绝对位置编码到旋转位置编码

旋转位置编码
Transformer模型的关键组件之一是嵌入（embeddings）。你可能会问：为什么？因为Transformer中的自注意力机制是置换不变的（permutation-invariant）；它会计算序列中每个token相对其他token的注意力权重，但并未考虑token的顺序。实际上，注意力机制将序列视为token的无序集合。。因此，我们需要另一个称为位置嵌入（positional embedding）的组件，它考虑token的顺序并影响其嵌入表示。但是，有哪些不同类型位置嵌入？它们又是如何实现的？

在这篇文章将探讨三种主要的位置嵌入类型，并深入研究它们的实现方式。

本文的目录如下：

1. 背景和环境
2. 绝对位置嵌入

• 2.1 学习方法
• 2.2 固定方法（正弦波）
• 2.3 代码示例：RoBERTa 实现

1. 相对位置嵌入

• 3.1. 通俗解释
• 3.2 技术说明
• 3.3 代码示例：Transformer-XL 实现

1. 旋转定位嵌入（绳索）

• 4.1. 通俗解释
• 4.2 技术说明
• 4.3 相对论的数学证明
• 4.4 高维旋转矩阵
• 4.5 代码片段：Roformer 实现

1. 结论
2. 参考

1. 背景和语境

在自然语言处理（NLP）中，词序对于理解词义至关重要，就像对人类一样。如果词序被打乱，词义就会完全改变。例如，"Sam sits down on the mat" 和*"The mat sits down on Sam"，*仅仅一次词序的改变就完全改变了词义。

Transformer 是许多现代自然语言处理 (NLP) 系统的核心，它并行处理所有词。这种并行处理发生在注意力机制中，该机制计算每个词元从输入上下文中的其他词元获得的注意力分数。虽然并行处理本身极大地提高了效率，但它会导致模型丢失词序信息。因此，Transformer 引入了一个名为位置嵌入的附加组件，该组件创建包含词元在序列中位置或顺序信息的向量。

位置嵌入有很多不同的类型。其中三种主要的、广为人知的类型是绝对位置嵌入、相对位置嵌入和旋转位置嵌入（RoPE）。

2. 绝对位置嵌入

绝对位置嵌入就像给句子中的每个词元分配一个唯一的数字。实际上，我们为序列中的每个位置创建一个向量。最简单的情况下，每个词元的位置嵌入是一个独热向量，除了词元所在的索引位置外，其余位置的值为零。然后，我们将这些位置嵌入向量添加到词元嵌入向量中，再将它们输入到Transformer模型中。

例如，在句子*"I am a student"* 中，有4个词元。每个词元都有一个唯一的位置嵌入向量。假设嵌入维度为3。那么第一个词元*"I"* 的独热编码为[1, 0, 0]，第二个词元的独热编码为[0, 1, 0]，依此类推。

虽然one-hot编码是一种直接表达位置嵌入概念的方法，但在实践中，实现绝对位置嵌入还有更好的方法。所有不同的实现方式都简单有效，但它们在处理非常长的序列或长度超过训练集长度的序列时可能会遇到困难。下面来看看这些具体的实现方式。

绝对位置嵌入的实现通常涉及创建一个大小为 _vocabulary*embedding dim 的查找表。这意味着对于词汇表中的每个词元，查找表中都有一个条目，并且该条目的维度为 _embedding dim。

绝对位置嵌入主要有两种类型：学习型和固定式。

2.1 学习型方法

在学习型方法中，嵌入向量被随机初始化，然后在训练过程中进行训练。这种方法在最初的 Transformer 论文[5]以及 BERT、GPT 和 RoBERTa 等流行模型中均有应用。稍后我们将看到这种方法的代码示例。这种方法的缺点是，它可能无法很好地泛化到比训练过程中遇到的序列更长的序列，原因很简单，因为对于这些位置，查找表中不存在相应的条目。

2.2 固定式方法

位置编码：这种方法也称为正弦位置编码，最早在具有开创性的论文《注意力就是一切》[5] 中提出。该方法使用不同频率的正弦和余弦函数为每个位置创建独特的模式。该编码的公式如下：

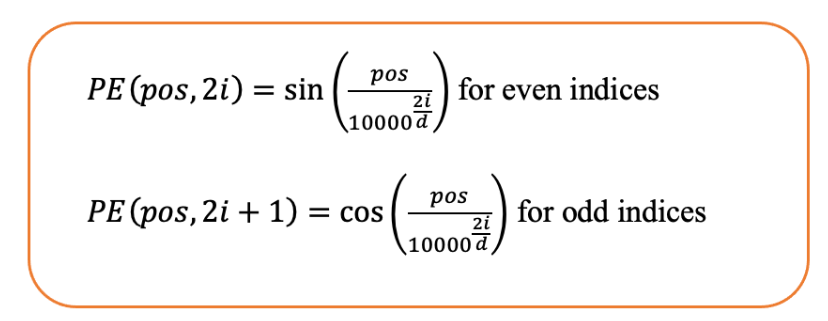
正弦位置编码

在上述公式中，PE 是位置嵌入，d是模型的维度，也称为嵌入维度。基本上，pos偶数索引位置的嵌入向量由 决定sin，奇数索引位置的嵌入向量由 决定cos。

这种方法的一个主要优点是能够推断训练期间未遇到的序列长度；这当然为处理不同的输入大小提供了很大的灵活性。

无论类型（学习型或固定型），一旦创建了绝对位置嵌入，它们就会被添加到词元嵌入中：

2.3 代码示例

以RoBERTa模型源代码中学习到的位置嵌入为例。源自HuggingFace代码库（链接在此）。

class RobertaEmbeddings(nn.Module):

    # Copied from transformers.models.bert.modeling_bert.BertEmbeddings.__init__
    def __init__(self, config):
        super().__init__()
        self.word_embeddings = nn.Embedding(config.vocab_size, config.hidden_size, padding_idx=config.pad_token_id)
        self.position_embeddings = nn.Embedding(config.max_position_embeddings, config.hidden_size)
        self.token_type_embeddings = nn.Embedding(config.type_vocab_size, config.hidden_size)

        # self.LayerNorm is not snake-cased to stick with TensorFlow model variable name and be able to load
        # any TensorFlow checkpoint file
        self.LayerNorm = nn.LayerNorm(config.hidden_size, eps=config.layer_norm_eps)
        self.dropout = nn.Dropout(config.hidden_dropout_prob)
        # position_ids (1, len position emb) is contiguous in memory and exported when serialized
        self.position_embedding_type = getattr(config, "position_embedding_type", "absolute")
        self.register_buffer(
            "position_ids", torch.arange(config.max_position_embeddings).expand((1, -1)), persistent=False
        )
        self.register_buffer(
            "token_type_ids", torch.zeros(self.position_ids.size(), dtype=torch.long), persistent=False
        )

        # End copy
        self.padding_idx = config.pad_token_id
        self.position_embeddings = nn.Embedding(
            config.max_position_embeddings, config.hidden_size, padding_idx=self.padding_idx
        )

    def forward(
        self, input_ids=None, token_type_ids=None, position_ids=None, inputs_embeds=None, past_key_values_length=0
    ):
        if position_ids is None:
            if input_ids is not None:
                # Create the position ids from the input token ids. Any padded tokens remain padded.
                position_ids = create_position_ids_from_input_ids(input_ids, self.padding_idx, past_key_values_length)
            else:
                position_ids = self.create_position_ids_from_inputs_embeds(inputs_embeds)

        if input_ids is not None:
            input_shape = input_ids.size()
        else:
            input_shape = inputs_embeds.size()[:-1]

        seq_length = input_shape[1]

        # Setting the token_type_ids to the registered buffer in constructor where it is all zeros, which usually occurs
        # when its auto-generated, registered buffer helps users when tracing the model without passing token_type_ids, solves
        # issue #5664
        if token_type_ids is None:
            if hasattr(self, "token_type_ids"):
                buffered_token_type_ids = self.token_type_ids[:, :seq_length]
                buffered_token_type_ids_expanded = buffered_token_type_ids.expand(input_shape[0], seq_length)
                token_type_ids = buffered_token_type_ids_expanded
            else:
                token_type_ids = torch.zeros(input_shape, dtype=torch.long, device=self.position_ids.device)

        if inputs_embeds is None:
            inputs_embeds = self.word_embeddings(input_ids)
        token_type_embeddings = self.token_type_embeddings(token_type_ids)

        embeddings = inputs_embeds + token_type_embeddings
        if self.position_embedding_type == "absolute":
            position_embeddings = self.position_embeddings(position_ids)
            embeddings += position_embeddings
        embeddings = self.LayerNorm(embeddings)
        embeddings = self.dropout(embeddings)
        return embeddings

需注意方法中的以下代码行__init__是如何用随机值初始化学习到的位置嵌入的：

self.position_embeddings = nn.Embedding(config.max_position_embeddings, config.hidden_size)

然后，在该forward方法中，将位置嵌入添加到词元嵌入中。

if self.position_embedding_type == "absolute":
    position_embeddings = self.position_embeddings(position_ids)
    embeddings += position_embeddings

在文本输入框中运行这段代码，结果如下：

from transformers import RobertaConfig

config = RobertaConfig()

print(config)

from transformers import RobertaConfig

config = RobertaConfig()

print(config)
RobertaConfig {
  "attention_probs_dropout_prob": 0.1,
  "bos_token_id": 0,
  "classifier_dropout": null,
  "eos_token_id": 2,
  "hidden_act": "gelu",
  "hidden_dropout_prob": 0.1,
  "hidden_size": 768,
  "initializer_range": 0.02,
  "intermediate_size": 3072,
  "layer_norm_eps": 1e-12,
  "max_position_embeddings": 512,
  "model_type": "roberta",
  "num_attention_heads": 12,
  "num_hidden_layers": 12,
  "pad_token_id": 1,
  "position_embedding_type": "absolute",
  "transformers_version": "4.31.0",
  "type_vocab_size": 2,
  "use_cache": true,
  "vocab_size": 50265
}

如上文打印的配置参数所示，我们有"position_embedding_type": "absolute",上下文窗口，其512长度为："max_position_embeddings": 512。让我们获取一个对象RobertaEmbedding：

emb = RobertaEmbeddings(config)
print(emb)

RobertaEmbeddings(
  (word_embeddings): Embedding(50265, 768, padding_idx=1)
  (position_embeddings): Embedding(512, 768, padding_idx=1)
  (token_type_embeddings): Embedding(2, 768)
  (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)
  (dropout): Dropout(p=0.1, inplace=False)
)

可以看到，在该RobertaEmbedding层上方，有一个(word_embeddings): Embedding(50265, 768, padding_idx=1)嵌入矩阵，其形状随机初始化50265*768；这意味着词汇表大小为50265，每个嵌入向量为，如果是768维的。

然后我们看到，(position_embeddings): Embedding(512, 768, padding_idx=1)位置嵌入向量也是随机初始化的，并且是768n维向量。注意这个嵌入矩阵的大小是n，512*768这意味着我们只能获得n个512位置的位置嵌入。因此，如果在推理时512出现一个长度超过n个标记的序列，我们将无法学习到它的位置嵌入！这是我们之前讨论过的学习绝对位置嵌入的缺点之一。

我们取一个序列并将其输入到嵌入层：

from transformers import RobertaTokenizer

# Initialize the tokenizer
tokenizer = RobertaTokenizer.from_pretrained("roberta-base")

sentence = "The quick brown fox jumps over the lazy dog."

# Tokenize the sentence
tokens = tokenizer.tokenize(sentence)

print(tokens)

# Get the input IDs
input_ids = tokenizer.encode(sentence, add_special_tokens=True)

print("nInput IDs:", input_ids)

它打印出以下内容：

['The', 'Ġquick', 'Ġbrown', 'Ġfox', 'Ġjumps', 'Ġover', 'Ġthe', 'Ġlazy', 'Ġdog', '.']

Input IDs: [0, 133, 2119, 6219, 23602, 13855, 81, 5, 22414, 2335, 4, 2]

注意，该序列由 12 个词元组成。我们将其传递给嵌入层：

input_tensor = torch.tensor(input_ids).reshape((1,-1))
emb(input_ids=input_tensor)

tensor([[[-0.7226, -2.3475, -0.5119,  ..., -1.3224, -0.0000, -0.9497],
         [-0.4094,  0.7778,  1.8330,  ...,  0.1183, -0.3897, -1.8805],
         [-0.7342, -1.6158,  0.2465,  ..., -0.0000, -1.4895, -0.8259],
         ...,
         [-0.2884, -3.0506,  0.6108,  ...,  0.8692,  0.9901,  0.6638],
         [ 0.6423, -2.1128,  1.2056,  ...,  0.2799,  0.5368, -1.0147],
         [-0.4305, -0.4462, -1.2317,  ...,  0.4016,  1.8494, -0.2363]]],
       grad_fn=<MulBackward0>)

输出张量是分别从相应的嵌入矩阵中检索到的词元嵌入和位置嵌入的总和。

3. 相对位置嵌入

相对位置嵌入关注序列中的标记如何以距离的方式相互关联，而不考虑标记的确切位置。

3.1 通俗解释

考虑句子*"I am a student" 。* "I" 的精确位置是1，"student" 的精确位置是4。这些是词元的绝对位置。相对位置嵌入没有考虑这些绝对位置，它只考虑*"I"与* "student" 的距离为3 ，与*"am"*的距离为1 。

相对位置嵌入在处理较长序列时具有优势，并且能够更好地泛化到训练过程中未遇到的序列长度。我们很快就会看到其中的原因。

一些使用相对位置嵌入的著名模型包括 Transformer-XL [1]、T5（文本到文本迁移 Transformer）[2]、DeBERTa（带有解耦注意力的解码增强型 BERT）[3] 和带有相对位置嵌入的 BERT [4]。可以阅读这些论文，了解它们是如何实现相对位置嵌入的。

3.2 技术说明

首先，与绝对位置嵌入（将位置嵌入添加到词元嵌入中）不同，相对位置嵌入创建的矩阵表示词元之间的相对距离。 例如，如果词元i 位于位置 2，词元j 位于位置 5，则相对位置为j−i=3。

然后，相对位置嵌入会修改注意力得分，使其包含相对位置信息。如上所知，在自注意力机制中，注意力得分是在词元对之间计算的。因此，相对位置嵌入会根据相对位置，或者通过为每个可能的相对距离引入一个可学习的嵌入，为注意力得分添加一个偏置项。

该方法的一种常见实现方式是在注意力得分中加入相对位置偏差。如果A 是注意力得分矩阵，则加入相对位置偏差矩阵B ：

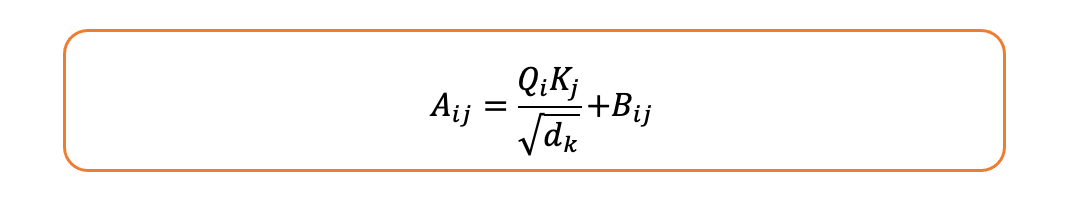
这里，Qi 和Kj​分别是标记 i 和j 的查询向量和键向量，_d k 是键向量的维度，Bij 是基于相对位置j−i的偏置项。

3.3 代码示例：Transformer-XL 实现

以下是在 PyTorch 中实现相对位置嵌入的简单代码。此实现与 Transformer-XL 的实现方式非常接近。要查看他们的代码库，请点击此处。

import torch
import torch.nn as nn

class RelativePositionalEmbedding(nn.Module):
    def __init__(self, max_len, d_model):
        super(RelativePositionalEmbedding, self).__init__()
        self.max_len = max_len
        self.d_model = d_model
        self.relative_embeddings = nn.Embedding(2 * max_len - 1, d_model)

    def forward(self, seq_len):
        # Generate relative positions
        range_vec = torch.arange(seq_len)
        range_mat = range_vec[None, :] - range_vec[:, None]
        clipped_mat = torch.clamp(range_mat, -self.max_len + 1, self.max_len - 1)
        relative_positions = clipped_mat + self.max_len - 1
        return self.relative_embeddings(relative_positions)

class RelativeSelfAttention(nn.Module):
    def __init__(self, d_model, num_heads, max_len):
        super(RelativeSelfAttention, self).__init__()
        self.num_heads = num_heads
        self.d_k = d_model // num_heads
        self.query = nn.Linear(d_model, d_model)
        self.key = nn.Linear(d_model, d_model)
        self.value = nn.Linear(d_model, d_model)
        self.relative_pos_embedding = RelativePositionalEmbedding(max_len, d_model)
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, x):
        batch_size, seq_len, d_model = x.size()
        Q = self.query(x).view(batch_size, seq_len, self.num_heads, self.d_k)
        K = self.key(x).view(batch_size, seq_len, self.num_heads, self.d_k)
        V = self.value(x).view(batch_size, seq_len, self.num_heads, self.d_k)

        # Compute standard attention scores
        scores = torch.einsum('bnqd,bnkd->bnqk', Q, K) / (self.d_k ** 0.5)

        # Get relative position embeddings
        rel_pos_embeddings = self.relative_pos_embedding(seq_len)
        rel_scores = torch.einsum('bnqd,rlkd->bnqk', Q, rel_pos_embeddings)

        # Add relative position scores
        scores += rel_scores
        attn_weights = self.softmax(scores)

        # Compute the final output
        output = torch.einsum('bnqk,bnvd->bnqd', attn_weights, V).contiguous()
        output = output.view(batch_size, seq_len, d_model)
        return output

我们可以使用以下参数调用它：

seq_len = 10
d_model = 512
num_heads = 8
max_len = 20

x = torch.randn(32, seq_len, d_model)  # Batch of sequences
attention = RelativeSelfAttention(d_model, num_heads, max_len)
output = attention(x)

请注意，seq_len（序列长度）指的是特定批次输入序列的实际长度，seq_len每个批次的长度都不同。

然而，max_len（最大长度）是一个预定义值，表示模型将考虑的最大相对位置距离。该值决定了模型将学习嵌入的相对位置范围。如果max_len设置为 20，则模型将拥有从-19到 的相对位置的嵌入19。

请注意，这就是为什么self.relative_embeddings = nn.Embedding(2 * max_len - 1, d_model)将其设置为此大小的原因，以便容纳由 定义的范围内的所有可能的相对位置max_len。

现在，我们来解释一下这段代码：

第一类如下，它创建了一个大小为的可学习嵌入矩阵2 * max_len - 1。在前向传播函数中，对于给定的序列，它从该relative_embeddings矩阵中检索相应的嵌入。

class RelativePositionalEmbedding(nn.Module):
    def __init__(self, max_len, d_model):
        super(RelativePositionalEmbedding, self).__init__()
        self.max_len = max_len
        self.d_model = d_model
        self.relative_embeddings = nn.Embedding(2 * max_len - 1, d_model)

    def forward(self, seq_len):
        # Generate relative positions
        range_vec = torch.arange(seq_len)
        range_mat = range_vec[None, :] - range_vec[:, None]
        clipped_mat = torch.clamp(range_mat, -self.max_len + 1, self.max_len - 1)
        relative_positions = clipped_mat + self.max_len - 1
        return self.relative_embeddings(relative_positions)

第二类（如下所示）接收一个序列（即x），并计算查询矩阵、键矩阵和值矩阵。请注意，每个注意力头都有自己的 Q、K 和 V；这就是为什么所有这些矩阵的形状都是(batch_size, seq_len, self.num_heads, self.d_k)。

class RelativeSelfAttention(nn.Module):
    def __init__(self, d_model, num_heads, max_len):
        super(RelativeSelfAttention, self).__init__()
        self.num_heads = num_heads
        self.d_k = d_model // num_heads
        self.query = nn.Linear(d_model, d_model)
        self.key = nn.Linear(d_model, d_model)
        self.value = nn.Linear(d_model, d_model)
        self.relative_pos_embedding = RelativePositionalEmbedding(max_len, self.d_k)
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, x):
        batch_size, seq_len, d_model = x.size()
        Q = self.query(x).view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)
        K = self.key(x).view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)
        V = self.value(x).view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)

        # Compute standard attention scores
        scores = torch.einsum('bhqd,bhkd->bhqk', Q, K) / (self.d_k ** 0.5)

        # Get relative position embeddings
        rel_pos_embeddings = self.relative_pos_embedding(seq_len)  # (seq_len, seq_len, d_k)
        rel_pos_embeddings = rel_pos_embeddings.transpose(0, 2).transpose(1, 2)  # (d_k, seq_len, seq_len)
        rel_scores = torch.einsum('bhqd,dqk->bhqk', Q, rel_pos_embeddings)

        # Add relative position scores
        scores += rel_scores
        attn_weights = self.softmax(scores)

        # Compute the final output
        output = torch.einsum('bhqk,bhvd->bhqd', attn_weights, V).contiguous()
        output = output.transpose(1, 2).reshape(batch_size, seq_len, d_model)
        return output

这行代码scores = torch.einsum('bhqd,bhkd->bhqk', Q, K) / (self.d_k ** 0.5)是一种简洁高效的复杂张量运算表示法。在本例中，它用于计算查询向量和键向量之间的点积。该等式'bhqd,bhkd->bhqk'可以解释如下：

• b批量大小。
• h注意力集中点的数量。
• q查询序列长度。
• k：键序列长度（在自注意力机制中，通常与查询序列长度相同）。
• d：每个头部的深度（即self.d_k）。

einsum 表示法'bhqd,bhkd->bhqk'规定，点积是在Q和 的最后一个维度之间计算的K，同时保持其他维度不变。

下一行代码rel_pos_embeddings = self.relative_pos_embedding(seq_len)检索序列中所有现有相对距离的相对位置嵌入；这就是它的形状为 的原因(seq_len, seq_len, d_k)。然后我们将其转置，使其形状变为(d_k, seq_len, seq_len)。下一行代码rel_scores = torch.einsum('bhqd,dqk->bhqk', Q, rel_pos_embeddings)计算相对位置嵌入对自注意力机制中注意力得分的贡献。这就是我们前面看到的公式中的相对位置偏置矩阵 B。

最后，我们将矩阵 B 添加到原始注意力分数中：

# Add relative position scores
scores 
+= rel_scores
attn_weights 
= self.softmax(scores)

然后乘以值矩阵V，即可得到输出：

# Compute the final output
output = torch.einsum('bhqk,bhvd->bhqd', attn_weights, V).contiguous()
output = output.transpose(1, 2).reshape(batch_size, seq_len, d_model)
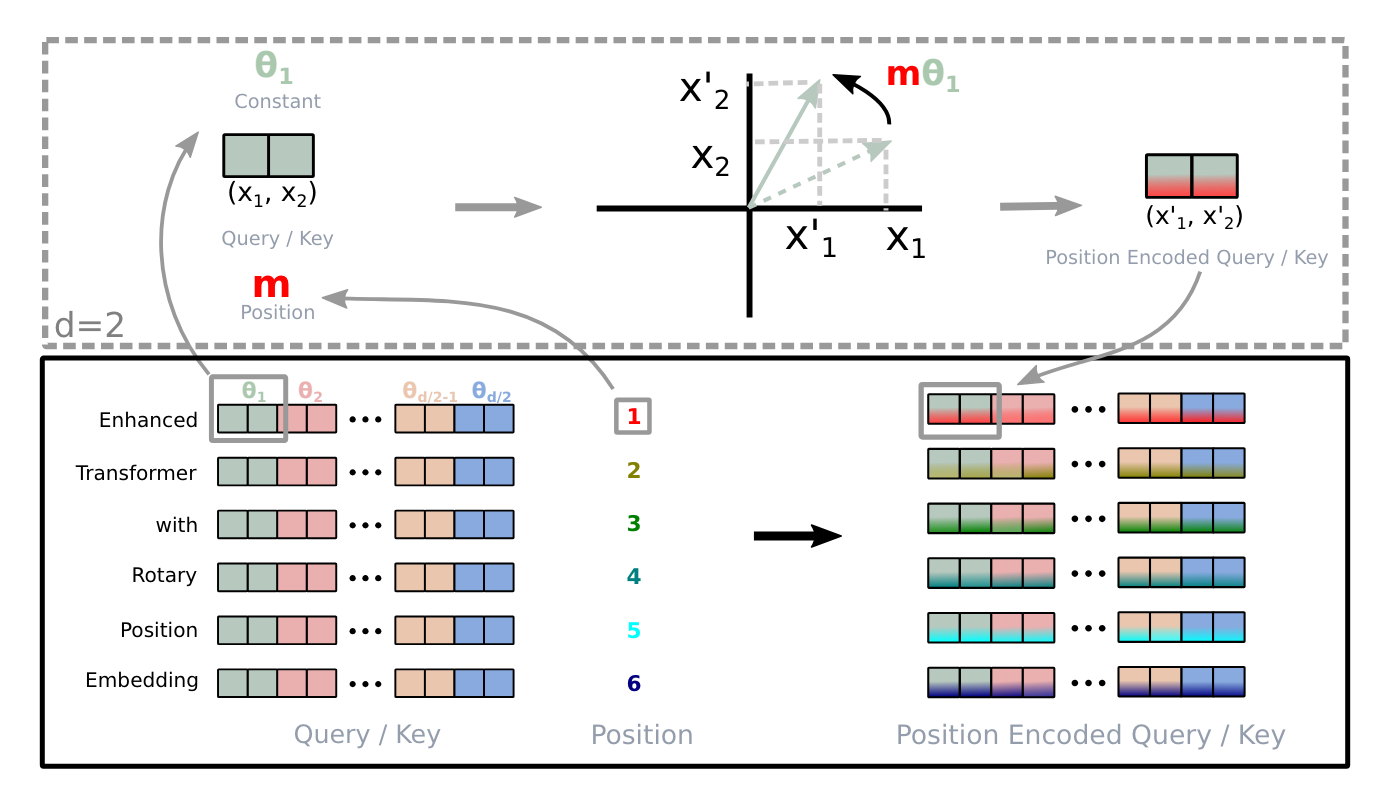
return output

4. 旋转定位嵌入

旋转位置嵌入（Rotary positional embedding，简称 RoPE）是一种巧妙的方法，它结合了绝对嵌入和相对嵌入的一些优点。该方法由 Roformer 在论文 [6] 中提出。

4.1 通俗解释：

RoPE 的核心思想是通过在高维空间中旋转词向量来编码位置信息。旋转的幅度取决于词或词元在序列中的位置。

这种旋转具有一个巧妙的数学特性：任意两个词之间的相对位置都可以通过一个词的向量相对于另一个词的旋转角度轻松计算出来。因此，虽然每个词都基于其绝对位置获得独特的旋转，但该模型也能够轻松计算出相对位置。

RoPE 具有以下几个优点：它比绝对位置嵌入更能有效地处理更长的序列；它自然地融合了绝对位置和相对位置信息；而且正如我们稍后将看到的，它计算效率高且易于实现。

4.2 技术说明：

给定一个词元嵌入及其位置（绝对位置嵌入），计算位置嵌入并将其添加到词元嵌入中：

然而，在旋转位置嵌入中，给定一个词元嵌入及其位置，它会生成一个新的嵌入，其中包含位置信息：

我们来看看它是如何计算的。简而言之（稍后我们会详细解释）：

给定一个词元，RoPE 会根据其在序列中的位置，对其对应的键向量和查询向量进行旋转。这种旋转是通过将向量乘以一个旋转矩阵来实现的。旋转后的键向量和查询向量随后会以常规方式（点积后接 softmax）用于计算注意力分数，Transformer 中的其余计算则照常进行。

让我们来看看什么是旋转矩阵，以及它如何应用于查询向量和键向量。

**旋转矩阵：**二维空间中的旋转矩阵（最简单的情况）如下所示，其中 θ 为任意角度：

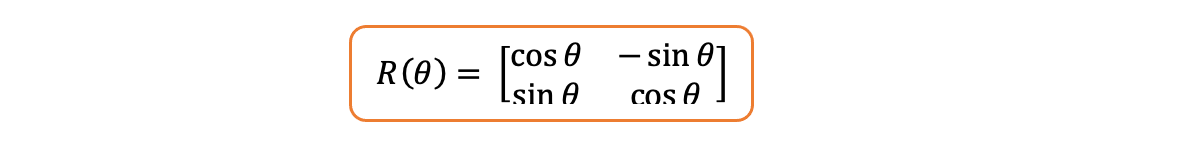
旋转矩阵（角度 θ）

如果将上述矩阵乘以一个二维向量，则只会改变向量的角度，而向量的长度保持不变。你同意吗？

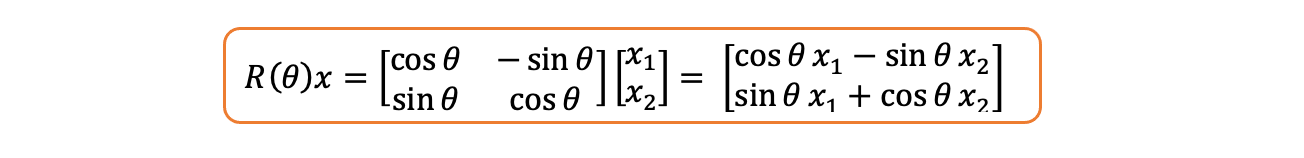
旋转矩阵与向量 x 的乘积

我们看到旋转后向量的范数与原向量的范数相同。让我们来计算一下：

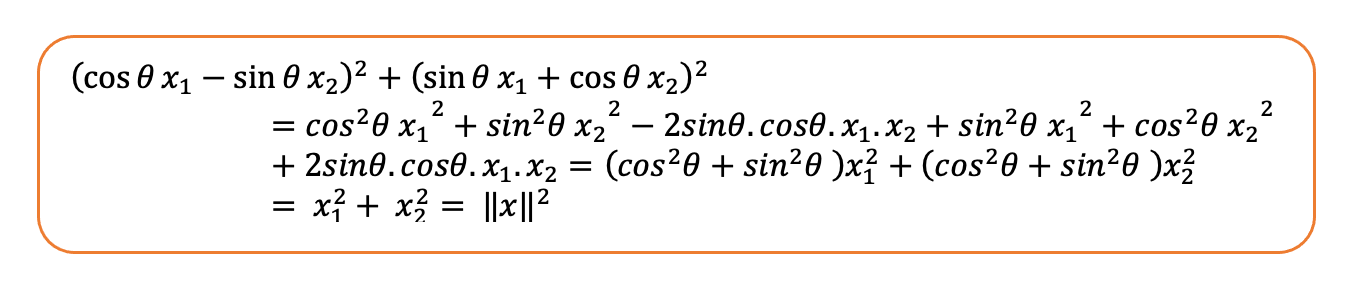
旋转矩阵保持向量范数不变

那么，它如何应用于键向量和查询向量呢？

请注意，查询向量是查询矩阵与词嵌入的乘积，即：

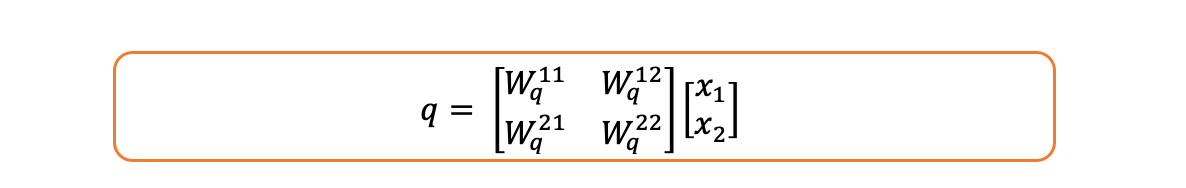
查询向量 -- 作者提供的图片

现在，如果我们对它应用旋转矩阵，我们就旋转了查询向量。

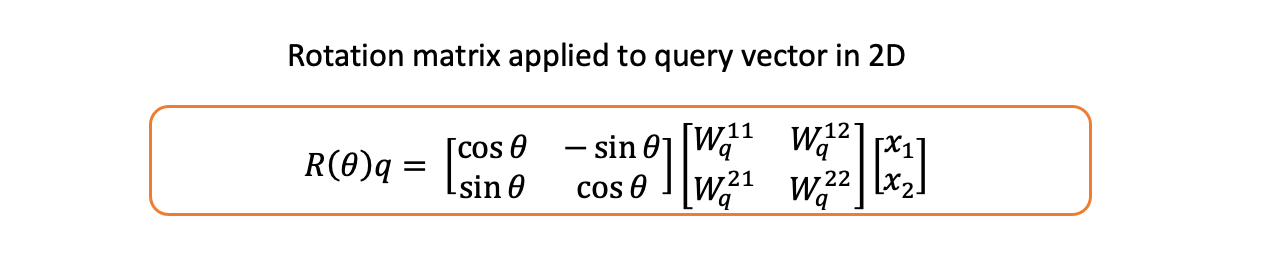
旋转矩阵与查询向量的乘积 -- 图片由作者提供

但是，它究竟是如何将位置信息包含在内呢？

问得好。以上所有数学推导都假设标记x 发生在位置 1！如果它发生在任意位置m， 那么旋转矩阵中将包含m：

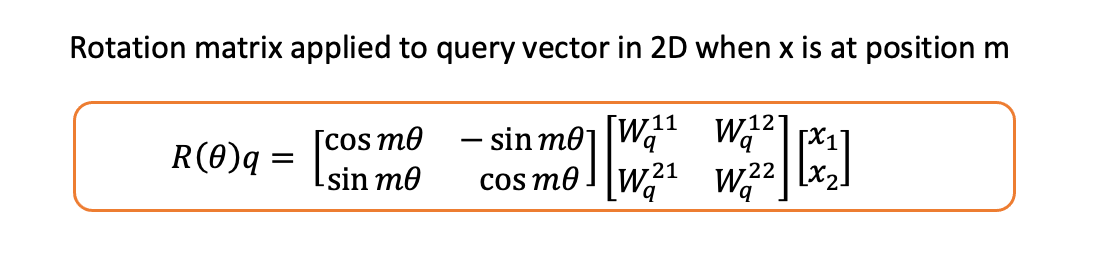
图片由作者提供

4.3 相对位置的数学证明

现在，**我们来证明旋转位置嵌入（RoPE）是相对的。**为此，我们需要证明两个词元之间的注意力得分仅取决于它们的相对位置，而与它们的绝对位置无关。

1. 让我们将 ROPE 操作定义如下：
   

ROPE 函数定义

2.考虑位置为和的两个标记n：

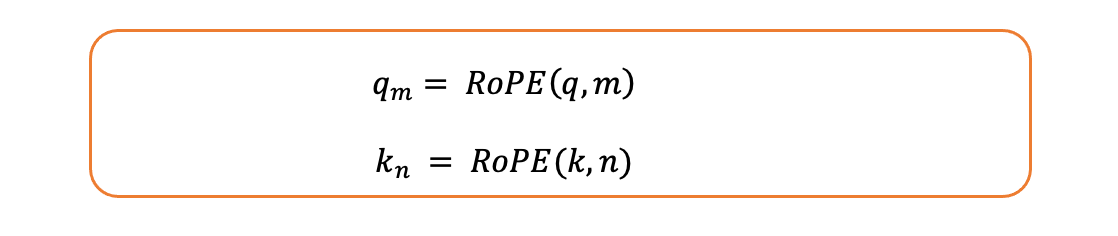
3.我们将注意力得分计算为它们的点积：

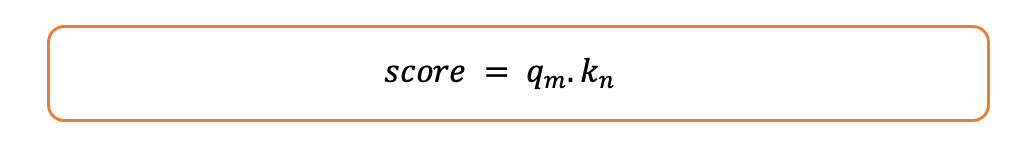
注意力得分

让我们将其展开如下：

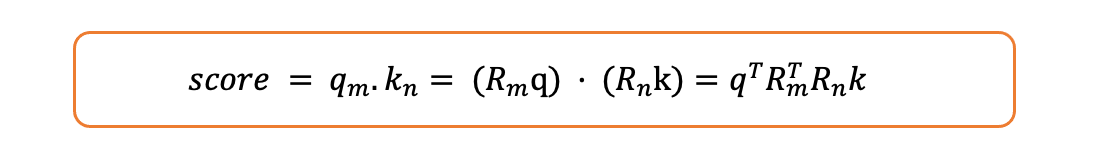
注意力得分

1. 旋转矩阵具有这样一个优良性质：

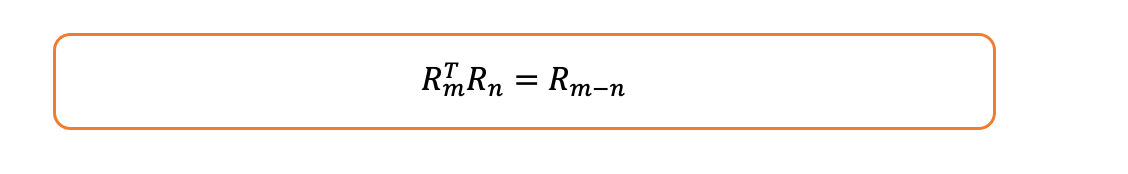
旋转矩阵的性质

1. 因此，注意力得分如下：

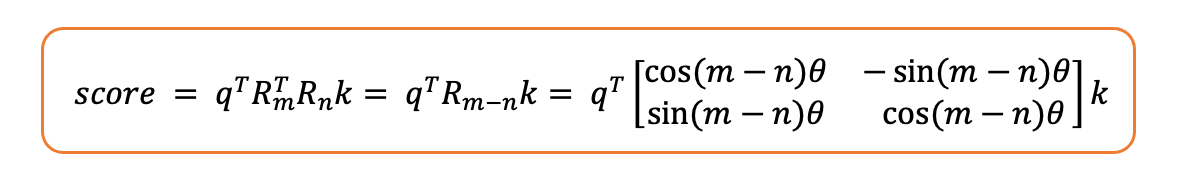
注意力得分

如其所见，得分是相对位置的函数，即位置之间的差异n。

4.4 高维旋转矩阵

模型的嵌入维度通常不是 2，而是远大于 2。那么旋转矩阵会如何变化呢？Roformer 论文 [6] 的作者提出了以下组合方式：

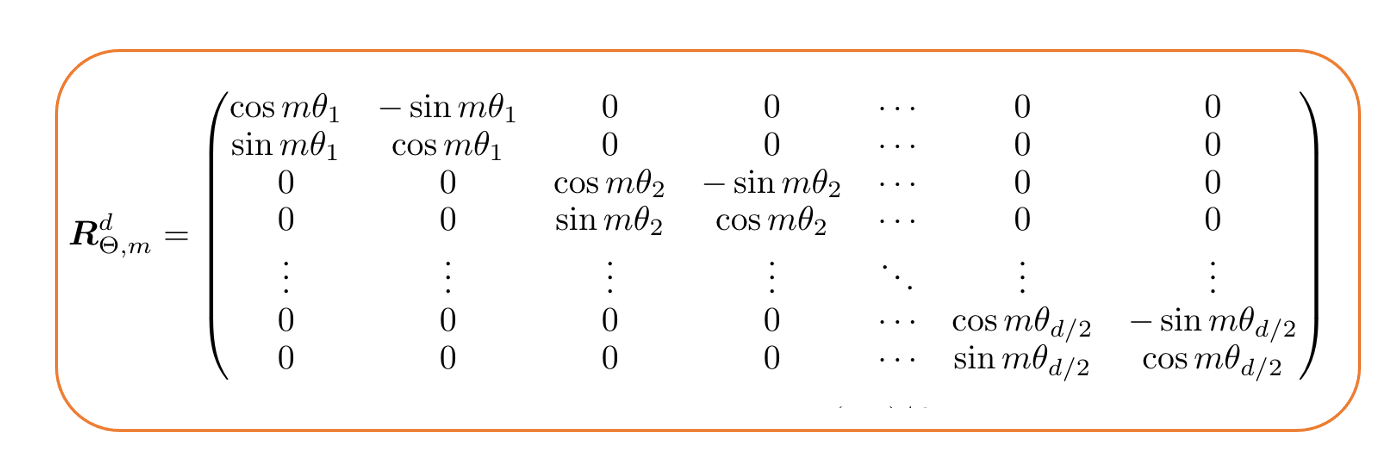
d维旋转矩阵

也就是说，对于位置m 和嵌入维度d，旋转矩阵由 d/2 个 2×2 的旋转矩阵组成。值得一提的是，由于这种构造是稀疏的，作者 [6] 推荐了一种计算效率高的方法，用标记嵌入向量x 来计算其乘积。

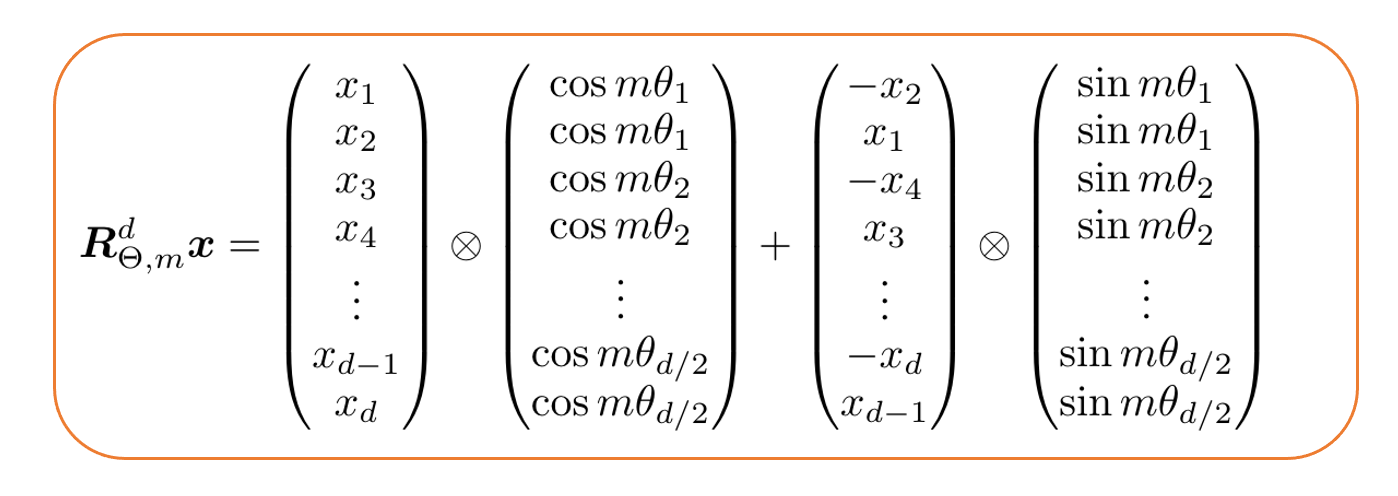
高效计算旋转矩阵乘以向量 x

4.5 代码片段：Roformer 实现

旋转位置嵌入（RoPE）的代码实现非常全面。详细概述请参见此处的完整代码库，但我想重点介绍负责计算 RoPE 的核心功能，该功能封装在以下方法中：

def apply_rotary_position_embeddings(sinusoidal_pos, query_layer, key_layer, value_layer=None):
    # https://kexue.fm/archives/8265
    # sin [batch_size, num_heads, sequence_length, embed_size_per_head//2]
    # cos [batch_size, num_heads, sequence_length, embed_size_per_head//2]
    sin, cos = sinusoidal_pos.chunk(2, dim=-1)
    # sin [θ0,θ1,θ2......θd/2-1] -> sin_pos [θ0,θ0,θ1,θ1,θ2,θ2......θd/2-1,θd/2-1]
    sin_pos = torch.stack([sin, sin], dim=-1).reshape_as(sinusoidal_pos)
    # cos [θ0,θ1,θ2......θd/2-1] -> cos_pos [θ0,θ0,θ1,θ1,θ2,θ2......θd/2-1,θd/2-1]
    cos_pos = torch.stack([cos, cos], dim=-1).reshape_as(sinusoidal_pos)
    # rotate_half_query_layer [-q1,q0,-q3,q2......,-qd-1,qd-2]
    rotate_half_query_layer = torch.stack([-query_layer[..., 1::2], query_layer[..., ::2]], dim=-1).reshape_as(
        query_layer
    )
    query_layer = query_layer * cos_pos + rotate_half_query_layer * sin_pos
    # rotate_half_key_layer [-k1,k0,-k3,k2......,-kd-1,kd-2]
    rotate_half_key_layer = torch.stack([-key_layer[..., 1::2], key_layer[..., ::2]], dim=-1).reshape_as(key_layer)
    key_layer = key_layer * cos_pos + rotate_half_key_layer * sin_pos
    if value_layer is not None:
        # rotate_half_value_layer [-v1,v0,-v3,v2......,-vd-1,vd-2]
        rotate_half_value_layer = torch.stack([-value_layer[..., 1::2], value_layer[..., ::2]], dim=-1).reshape_as(
            value_layer
        )
        value_layer = value_layer * cos_pos + rotate_half_value_layer * sin_pos
        return query_layer, key_layer, value_layer
    return query_layer, key_layer

请注意，本行query_layer = query_layer * cos_pos + rotate_half_query_layer * sin_pos是根据上一节中提到的高效计算方法进行计算的。

5.结论

本文回顾了三种主要的位置嵌入类型：绝对位置嵌入、相对位置嵌入和旋转位置嵌入。绝对位置嵌入提供了一种直接编码位置信息的方法，分为学习型和固定型两种。相对位置嵌入关注词元之间的相对距离。Transformer-XL 和 DeBERTa 等模型就采用了这种方法。最后，创新的旋转位置嵌入 (RoPE) 结合了绝对位置嵌入和相对位置嵌入的优势，为位置信息的编码提供了一种更高效、可扩展的解决方案。

参考：

1.Understanding Positional Embeddings in Transformers: From Absolute to Rotary

2. "Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context" by Zihang Dai et al.

3. "Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer" by Colin Raffel et al.

4. "DeBERTa: Decoding-enhanced BERT with Disentangled Attention" by Pengcheng He et al.

5. "Enhancing Pre-trained Language Representations with Rich Supervision" by Fangxiaoyu Feng et al.

6. "Attention Is All You Need" by Ashish Vaswani et al.

7. Roformer: Enhanced Transformer With Rotary Position Embedding

8. https://d2l.ai/chapter_attention-mechanisms-and-transformers/self-attention-and-positional-encoding.html