目录
[1、手动 SAGEConv 层](#1、手动 SAGEConv 层)
一、前言
本节主要会将下GraphSage的核心代码实战部分,理论部分,可以参考:
图神经网络分享系列-GraphSage(Inductive Representation Learning on Large Graphs) (一)
首先在简单说下,graphsage的出现主要创新点有以下几个
- 小批量训练 :通过采样邻居节点构建计算子图,支持mini-batch训练,降低内存消耗。
- 简单来说,之前看过gcn的同学应该可以发现,之前是全图计算的,落地会比较困难。
- 归纳式学习:传统图嵌入方法(如DeepWalk、Node2Vec)属于直推式(transductive)学习,只能处理训练时见过的固定节点。GraphSAGE通过设计可训练的聚合函数,能够为未见过的节点生成嵌入,适用于动态增长或变化的图数据。
- 灵活的聚合函数
再说一个题外话,大家知道为什么论文题目的缩写是GraphSage吗?文章最后给出答案~
二、算法核心代码讲解
以下面这个图为例
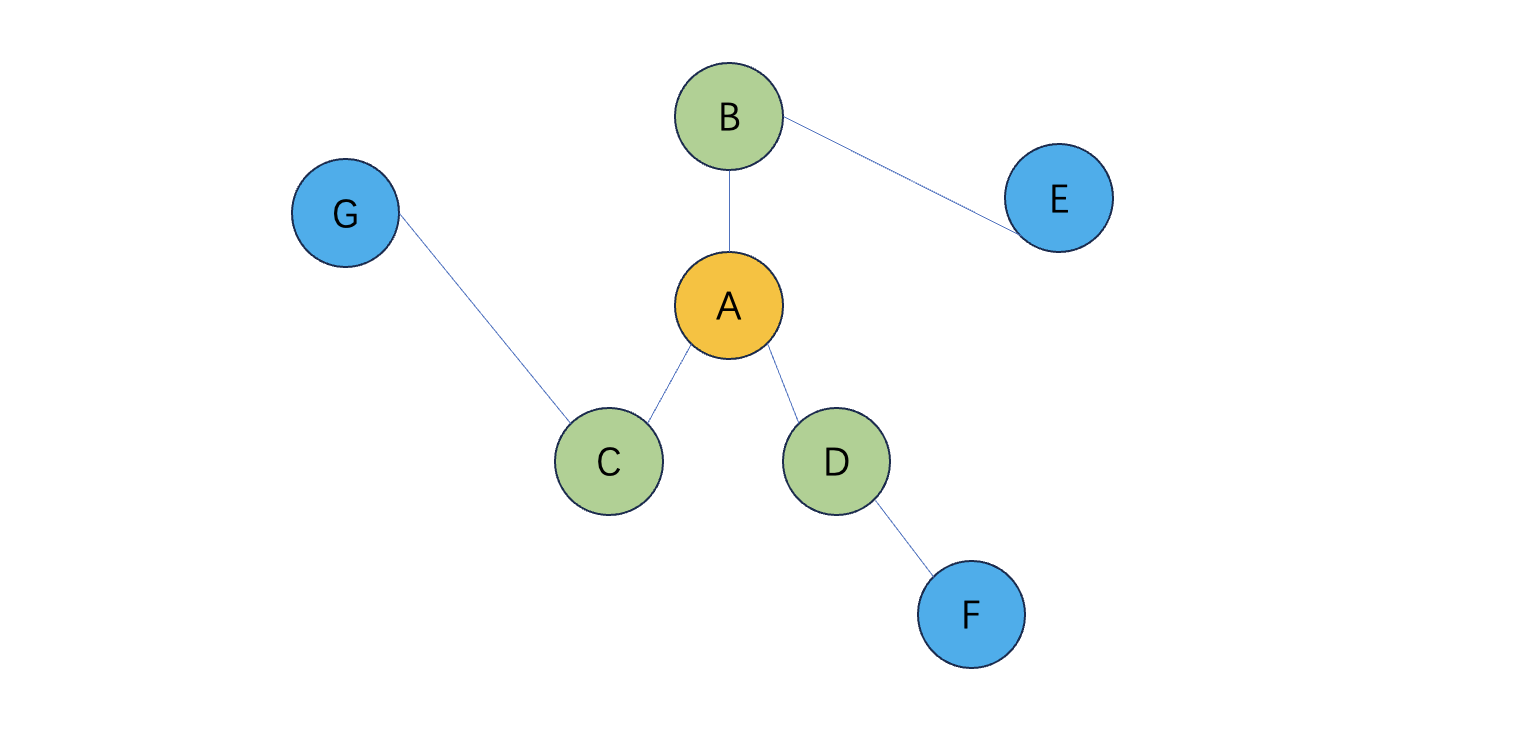
1、邻居采样
1、一阶采样
因为不会放进全图,所以需要采样,一阶采样为例,如上图:
(1)A:[B、C、D]
(2)B: [A、E]
(3)C: [A、G]
(4)D: [A、F]
(5)E: [B]
(6)F: [D]
(7)G: [C]
2、二阶采样
同上,不做过多描述,采样的过程中,存在,采样个数问题,如上,不同的节点,一阶邻居节点获多或少,这个时候会给定采样数,如果不够就有放回采样。
A->G分别对应1-7举个例子
以1为节点一阶采样2个,二阶采样3个结果如下
一阶采样两个,就是[3,2] 对应BC
二阶采样3个,就是[7, 1, 7, 5, 5, 5] 因为B的一阶邻居也就是A的二阶邻居,只有A、E也就是1和5,采样3个就是555.
2、聚合
以上图为例,共有7个节点,每个节点有8维度特征。
从A->G 分别对应1-7
import torch
import torch.nn as nn
import torch.nn.functional as F
# 输入数据
x = torch.randn(7, 8) # 7个节点,每个节点8维特征
adj = torch.tensor([
[0,1,1,1,0,0,0],
[1,0,0,0,1,0,0],
[1,0,0,0,0,0,1],
[1,0,0,0,0,1,0],
[0,1,0,0,0,0,0],
[0,0,0,1,0,0,0],
[0,0,1,0,0,0,0]
], dtype=torch.float)1、邻接矩阵

2、邻接列表
邻接列表主要是为了采样,如上面提到的采样主要有两种情况
- 当前邻居数少于采样数,需要有放回的重复采样
- 当前邻居数多余采样数,就无放回采样
本次为了展示没有做采样,直接保留原有的邻居数。
**🤔️思考,**这样会带来什么问题呢?
**答:**邻居过多会导致计算爆炸boom💥!,所以正常情况随机采样固定数量的邻居。
将邻接矩阵 adj 转换为邻接表 adj_list,方便遍历每个节点的邻居:
# 将邻接矩阵转换为邻接表(方便手动采样邻居)
adj_list = [[] for _ in range(7)]
for i in range(7):
for j in range(7):
if adj[i][j] == 1:
adj_list[i].append(j)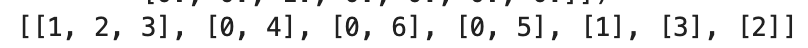
例如,adj_list[0] = [1, 2, 3] 表示节点 A 的邻居是 B, C, D
3、邻居聚合
1、手动 SAGEConv 层
-
邻居聚合 :对每个节点,聚合其邻居的特征(这里用
mean聚合):neighbor_embeddings = x[neighbors] # 获取邻居的特征
aggregated = torch.mean(neighbor_embeddings, dim=0) # 均值聚合 -
线性变换 :用
nn.Linear将聚合后的特征映射到新的维度:self.linear = nn.Linear(input_dim, output_dim)
output = self.linear(aggregated)
举个例子,A节点的特征是1*8维的,然后聚合后A节点的特征向量维度不变,数值会变成BCD加起来的均值。
🤔️思考,这里A节点的特征向量为什么只由邻居决定的,并没有自己的特征?
答:这里是简化版,其实看了理论部分,大家会发现是有带的,一般代码中会暴露出一个参数,来控制是否加入自身节点,看过我关于gcn的论文分享的小伙伴应该有印象,A'=A+I,简单来说,就是将自己也认为是自己的邻居。一般还是带上自身节点,原因如下:
- 信息完整性 :
邻居特征反映的是局部结构信息,而自身特征可能包含节点属性(如用户画像、分子属性等)。忽略自身特征会导致信息丢失。 - 避免梯度消失 :
如果仅聚合邻居特征,深层网络中节点自身的信息可能逐渐消失(类似 RNN 的梯度消失问题)。 - 任务需求 :
在节点分类任务中,节点自身标签或特征往往对预测至关重要。
| 实现方式 | 输入维度 | 是否保留自身特征 | 适用场景 |
|---|---|---|---|
| 标准 GraphSAGE | 2 * input_dim |
✅ 是 | 节点分类、推荐系统等 |
| 简化版(仅邻居) | input_dim |
❌ 否 | 异构图、图级别任务等 |
2、两轮聚合
🤔️思考,为什么要做两轮聚合?
答:
- 单层的局限性:
- 感受野受限
- 单层 GNN 只能直接聚合节点的一阶邻居(直接相连的节点)的信息。
- 问题:如果节点的类别标签依赖于更远距离的邻居(如二阶、三阶邻居),单层 GNN 无法捕捉这种依赖关系。
- 示例:在社交网络中,用户的兴趣可能受朋友的朋友(二阶邻居)影响,单层 GNN 会丢失这种信息。
- 表达能力不足
- 单层 GNN 的输出仅是节点自身特征和一阶邻居特征的线性组合,非线性变换能力有限。
- 问题:复杂图结构中的非线性关系(如异质性、层次性)难以通过单层线性变换建模
- 感受野受限
- 两层的作用 :
- 扩展感受野
- 效果 :
- 节点可以间接获取更远距离的邻居信息,增强全局信息捕捉能力。
- 在节点分类任务中,更广的感受野有助于利用图中的长距离依赖关系。
- 第二层 GNN 会聚合节点的二阶邻居的信息(即一阶邻居的邻居)。
- 效果 :
- 增强非线性建模能力
- 第二层引入额外的非线性变换(如 ReLU、Sigmoid 等),使模型能够学习更复杂的图结构模式。
- 效果 :
- 通过堆叠多层,模型可以拟合更复杂的函数(类似深度神经网络中的层数增加)。
- 例如,在异质图中(不同类别的节点连接模式不同),多层 GNN 可以区分不同子图的结构。
- 缓解过平滑问题(⚠️)
- 过平滑问题:随着层数增加,节点嵌入可能趋于相似(尤其是高阶邻居信息主导时)。
- 第二层的合理设计(如残差连接、跳跃连接)可以缓解这一问题,保留低阶信息的同时融合高阶信息。
- 扩展感受野
- 为什么需要两层(而非更多层)?
- 计算效率与过拟合权衡
- 两层 GNN 通常在感受野 和计算成本 之间取得平衡:
- 两层可以覆盖二阶邻居,适用于大多数社交网络、引文网络等场景。
- 更深层(如 3 层+)会显著增加计算量,且可能引入噪声(过平滑或过拟合)。
- 经验性结论:在许多基准数据集(如 Cora、Citeseer)上,两层 GNN 的性能接近或优于更深层模型。
- 两层 GNN 通常在感受野 和计算成本 之间取得平衡:
- 任务需求决定层数
- 节点分类任务:通常两层足够,因为类别标签的依赖关系多集中在局部邻域。
- 图级任务(如图分类):可能需要更深层以捕捉全局结构。
- 异质图或动态图:可能需要自适应层数或注意力机制。
- 计算效率与过拟合权衡
这个问题回答的有点多:
总结下
| 特性 | 单层 GNN | 两层 GNN |
|---|---|---|
| 感受野 | 一阶邻居 | 二阶邻居 |
| 表达能力 | 线性组合 | 非线性变换 |
| 适用场景 | 简单图结构 | 复杂图结构(如社交网络) |
🤔️思考,这里两层灰聚合二阶邻居,这里是真的直接聚合二阶邻居吗?
答:不是的
- 第一层聚合一阶邻居。
- 第二层聚合"已聚合一阶邻居信息的一阶邻居",相当于间接聚合二阶邻居。
总结感受野的区别
| 层数 | 直接聚合的邻居 | 间接聚合的邻居(通过嵌套) |
|---|---|---|
| 1层 | 一阶邻居 | 无 |
| 2层 | 一阶邻居 | 二阶邻居(通过 一阶聚合的嵌套) |
好,讲解到这里,差不多讲解完了,在回顾下,graphSage核心就是两步,采样,聚合。具体代码如下:
- ManualSAGEConv_simple:没有带自身节点,只使用了邻居节点
- ManualSAGEConv:带自身节点。
这里聚合的逻辑实现是用的mean,之后可以尝试其他的聚合方式~
# 手动实现 SAGEConv层+ 自身节点
class ManualSAGEConv(nn.Module):
def __init__(self, input_dim, output_dim):
super().__init__()
self.linear = nn.Linear(2 * input_dim, output_dim) # 拼接后维度翻倍
def forward(self, x, adj_list):
num_nodes = x.size(0)
new_embeddings = []
for node in range(num_nodes):
neighbors = adj_list[node]
if not neighbors:
neighbor_agg = torch.zeros(x.size(1), device=x.device) # 无邻居时补零
else:
neighbor_agg = torch.mean(x[neighbors], dim=0) # 均值聚合邻居
# 拼接自身特征和邻居聚合特征
concat_features = torch.cat([x[node], neighbor_agg], dim=0)
new_embeddings.append(concat_features)
new_embeddings = torch.stack(new_embeddings, dim=0)
output = self.linear(new_embeddings)
return output
# 手动实现 SAGEConv 层
class ManualSAGEConv_simple(nn.Module):
def __init__(self, input_dim, output_dim):
super(ManualSAGEConv, self).__init__()
self.linear = nn.Linear(input_dim, output_dim) # 线性变换
def forward(self, x, adj_list):
# x: [num_nodes, input_dim]
# adj_list: 邻接表,每个节点的邻居列表
num_nodes = x.size(0)
new_embeddings = torch.zeros((num_nodes, x.size(1)), device=x.device)
for node in range(num_nodes):
neighbors = adj_list[node]
if not neighbors: # 如果没有邻居(如孤立节点),则只聚合自身
neighbor_embeddings = x[node].unsqueeze(0)
else:
neighbor_embeddings = x[neighbors] # [num_neighbors, input_dim]
# 聚合邻居:Mean Aggregator
aggregated = torch.mean(neighbor_embeddings, dim=0)
new_embeddings[node] = aggregated
# 线性变换 + 激活函数
output = self.linear(new_embeddings)
return output
# 两层 GraphSAGE 模型
class GraphSAGE(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(GraphSAGE, self).__init__()
self.conv1 = ManualSAGEConv_simple(input_dim, hidden_dim)
self.conv2 = ManualSAGEConv_simple(hidden_dim, output_dim)
def forward(self, x, adj_list):
x = self.conv1(x, adj_list)
x = F.relu(x)
x = F.dropout(x, p=0.5, training=self.training)
x = self.conv2(x, adj_list)
return x
# 初始化模型
model = GraphSAGE(input_dim=8, hidden_dim=16, output_dim=8)
# 前向传播
node_embeddings = model(x, adj_list)
print("节点嵌入形状:", node_embeddings.shape) # 输出: torch.Size([7, 4])
print("节点表征:",node_embeddings)揭秘小时刻:
GraphSAGE(Graph SAmple and aggreGatE),相信大家看到这里也都可以理解了,其实正是它的过程,sample 采样+ aggregate 聚合~
好,目前gcn,gat,graphsage的实战都完成分享,后续会继续对图神经网络经典的论文进行分享,欢迎小伙伴评论交流哈~