论文题目：Modeling Relational Data with Graph Convolutional Networks（用图卷积网络建模关系数据）
会议：Extended Semantic Web Conference 2017
摘要：知识图支持各种各样的应用，包括问题回答和信息检索。尽管在它们的创建和维护上投入了巨大的努力，但即使是最大的(例如，Yago、DBPedia或Wikidata)也仍然不完整。我们引入了关系图卷积网络(R-GCNs)，并将其应用于两个标准的知识库补全任务:链接预测(缺失事实的恢复，即主-谓词-对象三元组)和实体分类(缺失实体属性的恢复)。RGCNs与最近一类在图上操作的神经网络相关，并且专门用于处理现实知识库的高度多关系数据特征。我们证明了R-GCNs作为实体分类的独立模型的有效性。我们进一步证明，用于链路预测的分解模型(如DistMult)可以通过使用编码器模型来丰富它们，从而在关系图中的多个推理步骤中积累证据，从而得到显著改进，证明在FB15k-237上比仅解码器基线提高了29.8%。
用图神经网络重构知识图谱：R-GCN论文深度解读
引言：知识图谱的困境
想象一下，你有一个包含数百万条知识的数据库------演员出演过哪些电影、城市位于哪个国家、人物在哪里接受教育等等。这就是知识图谱，它为问答系统、推荐引擎和信息检索提供了强大支撑。但是，即使是最大的知识图谱（如DBPedia、Wikidata）也面临一个严重问题：信息不完整。
2017年，来自阿姆斯特丹大学的研究团队在ESWC（欧洲语义网会议）上发表了一篇开创性论文：Modeling Relational Data with Graph Convolutional Networks，提出了关系图卷积网络（R-GCN），为解决知识图谱补全问题开辟了新路径。
今天，让我们深入解读这篇引用量超过3000次的经典论文。
一、问题背景：为什么需要R-GCN？
1.1 知识图谱的表示
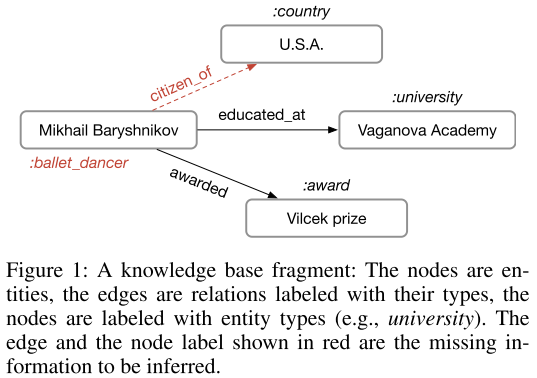
知识图谱本质上是一个有向标记多重图，由三元组（subject, predicate, object）构成。例如：
(Mikhail Baryshnikov, educated_at, Vaganova Academy)
(Vaganova Academy, type, university)
(Mikhail Baryshnikov, citizen_of, U.S.A.)在图中：
- 节点代表实体（如人物、地点、组织）
- 边代表关系（如"教育于"、"公民身份"）
- 每个实体可以有类型标签（如"舞蹈家"、"大学"）
1.2 两大核心任务
论文聚焦知识图谱的两个基础任务：
任务1：实体分类（Entity Classification）
- 目标：预测实体的缺失类型或属性
- 例如：给定Mikhail Baryshnikov的关系网络，推断他是"person"类型
任务2：链接预测（Link Prediction）
- 目标：预测缺失的三元组
- 例如：已知(Baryshnikov, educated_at, Vaganova Academy)，能否推断出(Baryshnikov, lived_in, Russia)？
1.3 现有方法的局限
传统方法主要分为两类：
张量分解方法（如DistMult、TransE、ComplEx）：
- 为每个实体学习一个固定的嵌入向量
- 通过优化三元组的评分函数来训练
- 问题：没有利用图的结构信息，缺乏多跳推理能力
路径特征方法：
- 提取实体间的路径作为特征
- 问题：计算开销大，难以扩展到大规模图
论文的核心洞察是：知识图谱中很多缺失信息可以通过邻域结构推断出来。如果知道Baryshnikov在俄罗斯的学校接受教育，就可以合理推断他可能在俄罗斯生活过，且应该被标记为"person"类型。
二、R-GCN方法详解
2.1 核心思想：关系感知的消息传递
R-GCN扩展了图卷积网络（GCN），专门设计用于处理多关系数据。其核心公式为：
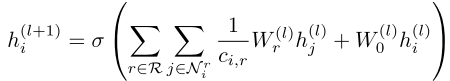
让我们拆解这个公式：
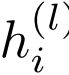：节点i在第l层的隐藏状态（特征向量）
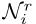：通过关系r连接到节点i的邻居集合
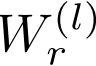：关系特定的权重矩阵（这是关键创新！）
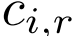：归一化常数，通常设为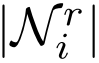
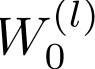：自连接的权重矩阵
：激活函数（如ReLU）
直观理解：
- 对于每种关系类型，使用不同的权重矩阵变换邻居特征
- 将所有关系的转换结果归一化求和
- 加上节点自身的特征（通过自连接）
- 应用非线性激活函数
这种设计允许模型学习"通过'educated_at'关系传递的信息应该如何转换"与"通过'citizen_of'关系传递的信息应该如何转换"是不同的。
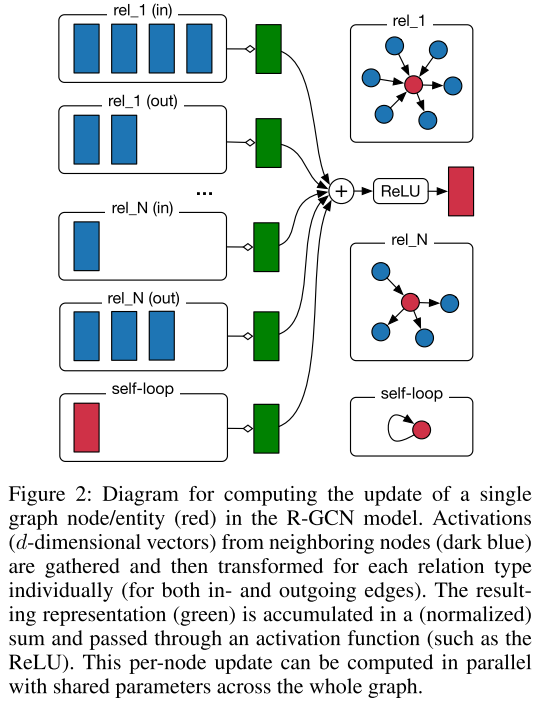
2.2 参数爆炸问题与正则化
多关系数据带来一个严重问题：如果知识图谱有1000种关系类型，每层就需要1000个权重矩阵，参数量会爆炸式增长！
论文提出两种正则化技术：
方法1：基函数分解（Basis Decomposition）
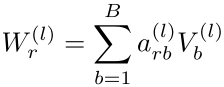
- 将每个关系的权重矩阵表示为B个基矩阵Vb的线性组合
- 只有组合系数a依赖于关系r
- 效果：实现关系间的权重共享，罕见关系可以从常见关系中学习
参数数量：
- 原始：
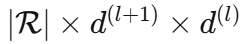
- 基分解后：
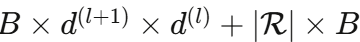
方法2：块对角分解（Block-Diagonal Decomposition）
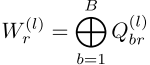
- 将权重矩阵约束为块对角形式
- 每个块Qbr是低维矩阵：
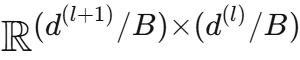
- 效果：施加稀疏性约束，将特征分组处理
参数数量：
- 块分解后：
2.3 任务1：实体分类架构
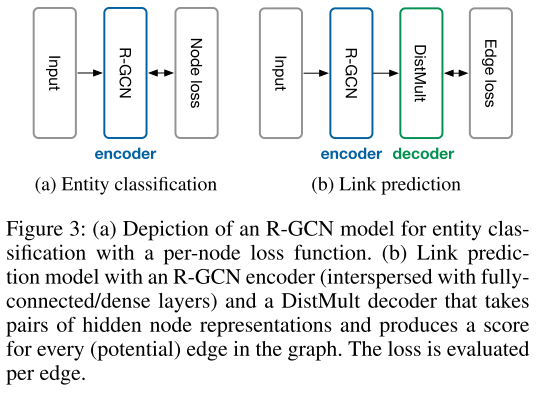
对于实体分类，R-GCN的使用非常直接：
- 输入层：每个实体用独特的one-hot向量表示（如果没有预定义特征）
- 隐藏层：堆叠多层R-GCN，传播邻域信息
- 输出层：在最后一层应用softmax激活函数
- 损失函数：交叉熵损失
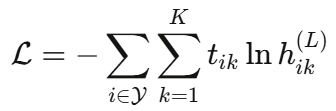
其中Y是有标签的节点集合，t ik是真实标签。
2.4 任务2：链接预测架构
链接预测采用自编码器框架：
编码器（Encoder）：
- R-GCN模型，将每个实体v_i编码为向量
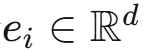
- 可以插入全连接层增强表达能力
解码器（Decoder）：
- 使用DistMult评分函数：
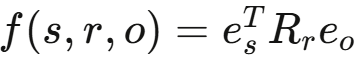
- Rr是关系r的对角矩阵
训练策略：
- 负采样：对每个正样本，随机破坏主语或宾语生成w个负样本
- 交叉熵损失：
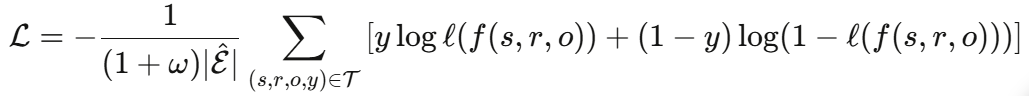
关键创新：不同于传统DistMult直接优化实体嵌入，R-GCN通过编码器从图结构中学习嵌入，实现了多跳推理。
三、实验结果
3.1 实体分类实验
论文在4个RDF格式数据集上评估：
| 数据集 | 实体数 | 关系数 | 边数 | 标注实体 | 类别数 |
|---|---|---|---|---|---|
| AIFB | 8,285 | 45 | 29,043 | 176 | 4 |
| MUTAG | 23,644 | 23 | 74,227 | 340 | 2 |
| BGS | 333,845 | 103 | 916,199 | 146 | 2 |
| AM | 1,666,764 | 133 | 5,988,321 | 1,000 | 11 |
实验设置：
- 2层R-GCN
- 16个隐藏单元（AM数据集用10个）
- 基函数分解
- Adam优化器，学习率0.01，训练50轮
结果对比（准确率%）：
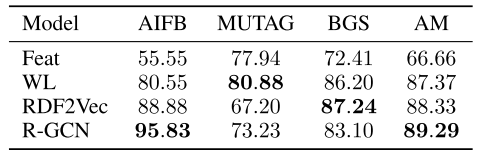
| 模型 | AIFB | MUTAG | BGS | AM |
|---|---|---|---|---|
| Feat（特征工程） | 55.55 | 77.94 | 72.41 | 66.66 |
| WL（图核方法） | 80.55 | 80.88 | 86.20 | 87.37 |
| RDF2Vec（图嵌入） | 88.88 | 67.20 | 87.24 | 88.33 |
| R-GCN（本文） | 95.83±0.62 | 73.23±0.48 | 83.10±0.80 | 89.29±0.35 |
关键发现：
- ✅ 在AIFB上，R-GCN比RDF2Vec提升了7个百分点，达到95.83%的准确率
- ✅ 在AM（最大数据集）上略优于RDF2Vec
- ❌ 在MUTAG和BGS上表现不如RDF2Vec
性能差异分析： 论文指出MUTAG和BGS的特殊性：
- MUTAG：分子图数据，关系编码原子键或特征存在性
- BGS：岩石类型数据，关系编码层次化特征
- 标注实体仅通过高度数枢纽节点连接
固定的归一化常数对高度数节点不友好。论文建议引入注意力机制替代固定归一化。
3.2 链接预测实验
数据集统计
| 数据集 | 实体数 | 关系数 | 训练边 | 验证边 | 测试边 |
|---|---|---|---|---|---|
| WN18 | 40,943 | 18 | 141,442 | 5,000 | 5,000 |
| FB15k | 14,951 | 1,345 | 483,142 | 50,000 | 59,071 |
| FB15k-237 | 14,541 | 237 | 272,115 | 17,535 | 20,466 |
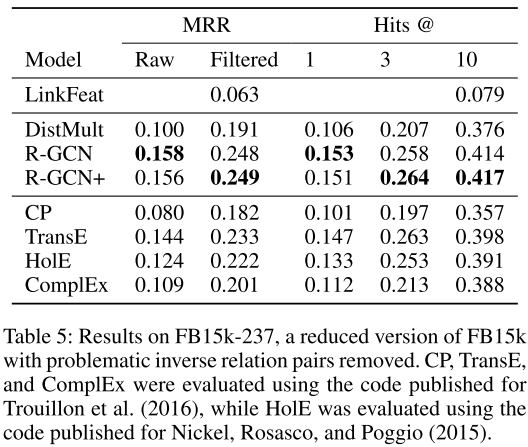
FB15k-237的重要性：
- Toutanova & Chen (2015)指出FB15k和WN18存在严重缺陷：训练集包含
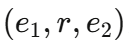，测试集包含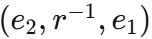
- 这使得任务变成记忆问题，简单的LinkFeat基线就能达到很高性能
- FB15k-237移除了所有逆关系对，是更真实的评估
FB15k-237结果（关键突破）
评估指标：
- MRR（Mean Reciprocal Rank）：倒数排名的平均值，越高越好
- Hits@K：正确答案排在前K位的比例
| 模型 | MRR (Filtered) | Hits@1 | Hits@3 | Hits@10 |
|---|---|---|---|---|
| LinkFeat | 0.079 | - | - | - |
| DistMult | 0.191 | 0.106 | 0.207 | 0.376 |
| CP | 0.182 | 0.101 | 0.197 | 0.357 |
| TransE | 0.233 | 0.147 | 0.263 | 0.398 |
| HolE | 0.222 | 0.133 | 0.253 | 0.391 |
| ComplEx | 0.201 | 0.112 | 0.213 | 0.388 |
| R-GCN | 0.248 | 0.153 | 0.258 | 0.414 |
| R-GCN+ | 0.249 | 0.151 | 0.264 | 0.417 |
惊人发现：
- 🚀 R-GCN的MRR比DistMult基线提升29.8%（0.191→0.248）
- 🚀 Hits@10从37.6%提升到41.4%
- ✨ 在这个更困难的数据集上，R-GCN超越了所有传统分解方法
为什么提升如此显著？ 因为FB15k-237移除了逆关系对，简单的局部模式不再有效，必须通过多跳推理来预测缺失链接------这正是R-GCN的优势！
FB15k和WN18结果
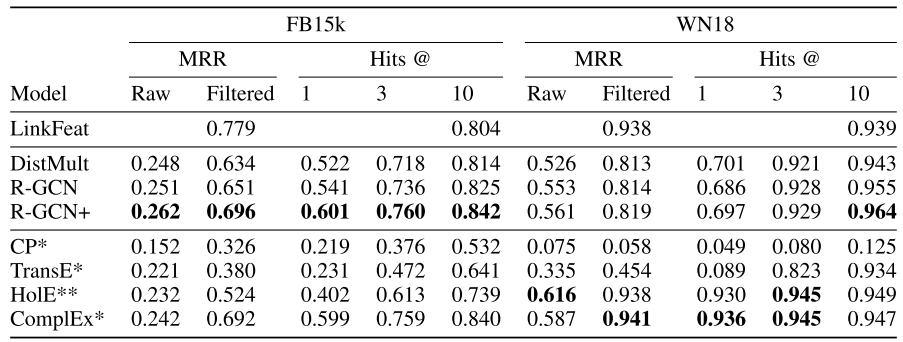
R-GCN+是什么？ 组合模型：
- 在FB15k上，
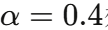效果最佳 - 结合了R-GCN的结构推理能力和DistMult的局部模式识别能力
有趣的观察： 论文绘制了FB15k上性能与节点度数的关系曲线（图4）：
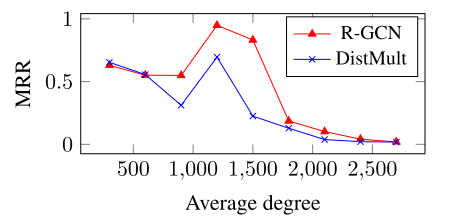
- 低度数节点：DistMult性能更好（局部信息充足）
- 高度数节点：R-GCN性能更好（丰富的上下文信息）
- 这解释了为什么组合模型R-GCN+表现最佳
3.3 实验配置细节
R-GCN超参数：
| 数据集 | 层数 | 隐藏维度 | 正则化 |
|---|---|---|---|
| FB15k | 1 | 200 | 基分解(B=2) |
| WN18 | 1 | 200 | 基分解(B=2) |
| FB15k-237 | 2 | 500 | 块分解(5×5) |
训练技巧：
- Edge Dropout：自连接0.2，其他边0.4（类似去噪自编码器）
- L2正则化：解码器权重惩罚0.01
- 负采样：每个正样本配1个负样本
- 优化器：Adam，学习率0.01
- 批处理：全批次梯度下降
四、方法论亮点与局限
4.1 核心贡献
-
首次将GCN应用于关系数据
- 开创性地将图神经网络引入知识图谱领域
- 为后续大量研究奠定基础（论文被引超3000次）
-
优雅的正则化设计
- 基函数分解实现跨关系知识迁移
- 块对角分解有效控制参数规模
- 使得模型可以扩展到数百种关系类型
-
编码器-解码器框架
- 将结构建模（编码器）与评分函数（解码器）解耦
- 解码器可灵活替换（DistMult、ComplEx、HolE等）
- 通用性强，易于扩展
-
FB15k-237上的突破
- 29.8%的提升证明了多跳推理的价值
- 在更真实的评估场景下显著优于传统方法
4.2 局限性与未来方向
论文诚实指出的局限：
-
固定归一化的问题
- 对高度数节点不友好
- 建议引入注意力机制（这启发了后续的GAT、R-GAT等工作）
-
可扩展性挑战
- 全批次训练限制了处理超大规模图的能力
- 论文建议探索采样技术（如GraphSAGE式邻居采样）
-
特征融合待加强
- 当前只用one-hot向量作为输入
- 可以整合实体的文本描述、属性等丰富特征
论文提出的研究方向：
- 与ComplEx等更强解码器结合
- 加入注意力机制
- 实现mini-batch训练
- 应用于关系抽取等其他任务
总结
R-GCN论文以优雅的方式将图卷积网络扩展到多关系数据，在知识图谱补全任务上取得了显著成果。其核心贡献不仅是算法本身，更在于提出了一个通用的编码器-解码器框架，为后续研究提供了清晰的范式。
关键数字回顾：
- ✨ AIFB数据集：**95.83%**准确率（提升7个百分点）
- 🚀 FB15k-237：MRR 0.248（提升29.8%）
- 📈 3000+引用，影响深远
论文也保持了学术诚实，坦率讨论局限性并指出改进方向。这些局限催生了大量后续研究，使得图神经网络在知识图谱领域持续发展。
如果你对知识图谱、图神经网络或链接预测感兴趣，R-GCN绝对是一篇必读论文。它证明了一个简单的道理：在关系数据中，你的邻居定义了你是谁。
希望这篇博客能帮助你深入理解R-GCN的精髓。如果有任何问题或想深入讨论某个部分，欢迎在评论区留言！