Online Process Reward Learning for Agentic Reinforcement Learning

abstract

大型语言模型(LLM)越来越多地通过强化学习(RL)被训练为自主智能体[autonomous agents] ，能够在交互式环境中进行长期推理和行动。然而，稀疏且有时无法验证的奖励使得时序信用分配[temporal credit assignment] 变得极具挑战性。最近的研究尝试将过程监督整合到智能体学习中，但存在标注偏差[biased annotation] 、奖励欺骗[reward hacking] 、过细粒度信号[overly fine-grained signals] 导致的高方差，以及在状态重叠罕见时失效等问题。因此，我们提出了在线过程奖励学习(Online Process Reward Learning, OPRL)，这是一种通用的智能体RL信用分配策略[credit-assignment strategy]，能够无缝集成到标准在策略(on-policy)算法中，无需额外的轨迹采样或显式的步骤标签。

在OPRL中，我们交替优化隐式过程奖励模型(an implicit process reward model, PRM) 和智能体策略，通过基于轨迹的DPO目标函数[a trajectory-based DPO objective] 将轨迹偏好转化为隐式步骤奖励。这些步骤奖励随后用于计算步骤级优势函数[episode-level advantages] ，与来自结果奖励的episode级优势函数相结合进行策略更新，形成一个自我强化循环[a self-reinforcing loop] 。理论分析保证了学习到的步骤奖励[the learned step rewards] 与轨迹偏好[trajectory preferences] 保持一致，并且充当基于势函数的奖励塑形[potential-based shaping rewards]，提供有界梯度以稳定训练过程。

在实证研究中，我们在三个不同的智能体基准测试上评估OPRL，包括WebShop和VisualSokoban，以及具有不可验证奖励的开放式社交交互环境SOTOPIA。关键的是，OPRL在各个领域均展现出优于前沿LLM和强RL基线的性能，以更高的样本效率和更低的训练方差实现了最先进的结果。进一步的分析还表明，OPRL通过使用更少的动作实现了高效探索，凸显了其在真实世界场景中用于智能体学习的潜力。

1 INTRODUCTION

LLM正在快速从被动生成器演化为能够进行推理、行动并在长时间跨度内调整策略的自主智能体[autonomous agents] ，包括搜索和研究智能体[search and research agents] (Jin et al., 2025; OpenAI, 2025a)、移动和网页导航器[mobile and web navigators] (Furuta et al., 2024; Bai et al., 2024)、软件工程助手[software engineering assistants ](Yang et al., 2025; Wei et al., 2025a)、游戏玩家(Wang et al., 2025)，以及社交或具身智能[social or embodied intelligence](Liu et al., 2025; Lu et al., 2025)。
与传统的针对静态单轮任务的LLM后训练强化学习(Ouyang et al., 2022; Shao et al., 2024)不同，在动态交互式环境[dynamic, interactive environments]中训练LLM智能体面临特殊挑战：
(1) 奖励通常是稀疏且延迟的，使得对中间动作[intermediate actions] 的信用分配[credit assignment]变得复杂；
(2) 轨迹长且在token级别上是非马尔可夫的[long and non-Markovian]，每个步骤由思维链(CoT)(Wei et al., 2022)和可执行动作组成，当信用[credit]被推送到单个token时会放大方差；
(3) 环境和对手是非平稳的、开放式的，并且通常伴随着无法验证的奖励(例如对话[dialogues])。
因此，仅使用单一结果奖励的轨迹级优化(Wang et al., 2025; Chen et al., 2025; Wei et al., 2025b)受到**时序信用分配[temporal credit assignment]问题的困扰，导致高方差的策略学习、脆弱的探索以及在智能体任务上的有限收益。
最近的研究尝试特别通过强化学习中的过程监督[process supervision in RL]**来解决这些问题。例如，Zeng等人(2025)、Zou等人(2025)、Zhang等人(2025b)在中间步骤提供了更密集的反馈，但需要人工标注或手工设计的启发式方法，这些方法成本高、存在偏差且容易受到奖励欺骗的影响。

生成式奖励模型(Generative reward models, GRM) (例如，LLM作为评判者[LLM-as-judge])(Liu等人, 2025; Zha等人, 2025)预测每个步骤的关键性或正确性，减少了标注开销，但可能存在噪声且在不同领域间不一致。从结果标签训练的token级过程奖励模型(PRM)在单轮任务中有所帮助(Yuan等人, 2025; Cui等人, 2025)，但它们提供的奖励对于智能体学习来说往往过于细粒度，随着轨迹增长会放大方差并使训练不稳定。

其他方法[Other approaches] (Feng等人, 2025; Choudhury, 2025)通过分组相同状态[grouping identical states] 来计算逐步优势[step-wise advantages]，但这一假设在状态重叠罕见的开放式语言环境中会失效。

综合来看，这些局限性为智能体强化学习提出了一个核心问题：我们如何设计一种信用分配策略[credit assignment strategy]，使其具有标签效率且稳定，能够扩展到长期、多轮交互，并在开放式环境中对可验证和不可验证的奖励都保持鲁棒性和泛化能力？

为了解决这个问题，我们提出了在线过程奖励学习(Online Learning Process Rewards, OPRL) ，这是一种用于LLM智能体的通用信用分配策略[a general credit assignment strategy]。OPRL仅使用在策略轨迹及其结果偏好，在训练策略的同时训练PRM。

在每个训练步骤中，当前策略生成轨迹[rollouts] ，这些轨迹通过基于规则的验证器[a rule-based verifier] 或结果奖励模型(outcome reward model, ORM)进行排序，形成正负轨迹对[positive--negative trajectory pairs] 。然后，我们使用基于DPO推导的目标函数在这些轨迹对上更新PRM 。更新后的PRM通过测量每个动作相对于**先前策略快照[the previous policy snapshot]**的相对偏好，为每个动作诱导出隐式奖励。由于这个奖励是按回合计算的，它提供了密集的反馈来引导探索，同时保持足够粗粒度以控制方差。

策略优化[Policy optimization] 随后结合了两种互补的优势：来自结果奖励的episode级优势[Episode-level advantage]和来自隐式步骤奖励的步骤级优势，同时捕获全局任务成功和单个动作的贡献。OPRL与标准的在策略强化学习算法兼容，如PPO(Schulman等人, 2017)、GRPO(Shao等人, 2024)、RLOO(Ahmadian等人, 2024)、REINFORCE++(Hu等人, 2025)，无需显式步骤标签或额外的采样成本。

Episode-level Advantage

含义：

• 是整条轨迹τ_i的结果奖励（outcome reward）
• 比如在WebShop中：任务成功=1，失败=0
• 比如在SOTOPIA中：对话的目标完成分数（0-10分）

关键特点：

• ✅ 稀疏信号：只在episode结束时给一次
• ✅ 全局评价：评判整个任务是否成功
• ❌ 无法区分：不知道哪一步好、哪一步坏

Step-level Advantage（步骤级优势）

不完全是每一步的reward ，而是每一步相对于其他步骤的相对质量。

含义：

• `` 是第t步动作的**隐式奖励**

• 通过PRM学习得到，表示"这一步相比旧策略有多好"

• 是**相对值**，不是绝对分数

关键特点：

• ✅ 密集信号：每一步都有反馈

• ✅ 局部评价：区分每个动作的贡献

• ✅ 可组合：多个好步骤 → 好轨迹
  OPRL（Episode + Step 结合）

# 轨迹1（成功）
A^E(τ_1) = +0.5  # 全局成功奖励

# 通过PRM学到的步骤奖励
r_φ(步骤1) = +0.8  ← PRM认为这步很关键！
r_φ(步骤2) = +0.6  ← 也不错
r_φ(步骤3) = +0.2  ← 中性
r_φ(步骤4) = +0.1  ← 常规操作

# 归一化后的步骤优势
A^S(步骤1) = +1.2
A^S(步骤2) = +0.6
A^S(步骤3) = -0.3
A^S(步骤4) = -0.5

# 最终优势（公式5）
A(步骤1) = A^E + α·A^S = +0.5 + 1×(+1.2) = +1.7  ← 强化！
A(步骤2) = +0.5 + (+0.6) = +1.1
A(步骤3) = +0.5 + (-0.3) = +0.2
A(步骤4) = +0.5 + (-0.5) = 0.0

# 轨迹2（失败）
A^E(τ_2) = -0.5  # 全局失败惩罚

# 但PRM可能发现某些步骤其实还可以
r_φ(步骤1) = -0.9  ← 太离谱了
r_φ(步骤2) = -0.7
r_φ(步骤3) = -0.1  ← 浏览本身不算太坏
r_φ(步骤4) = +0.2  ← 返回首页是合理的止损

A^S(步骤1) = -1.5
A^S(步骤2) = -0.8
A^S(步骤3) = +0.1
A^S(步骤4) = +0.4

# 最终优势
A(步骤1) = -0.5 + (-1.5) = -2.0  ← 重点惩罚！
A(步骤2) = -0.5 + (-0.8) = -1.3
A(步骤3) = -0.5 + (+0.1) = -0.4  ← 惩罚减轻
A(步骤4) = -0.5 + (+0.4) = -0.1  ← 几乎不惩罚

OPRL从多个维度解决了先前工作的局限性：
(1) 我们的方法通过将轨迹级偏好转换为步骤级指导，在无需步骤标签的情况下提供细粒度、偏好一致的步骤信用分配。理论分析表明，这些隐式步骤奖励与Bradley-Terry轨迹偏好具有贝叶斯一致性，并实现了保持最优策略集的基于势函数的塑形（见定理3.3）；
(2) OPRL通过使用隐式步骤奖励[implicit step rewards] 而非**逐token奖励[per-token rewards]**在回合级别进行优化，从而稳定多轮强化学习训练并降低方差。具体而言，策略最大化塑形目标相当于执行朝向PRM的KL下降步骤，产生有界梯度从而稳定训练（见命题3.4）；
(3) OPRL仅依赖于轨迹级偏好，这些偏好可以来自基于规则的验证器（例如成功信号）或不可验证的结果奖励模型（例如LLM评判者），适用于状态重叠罕见的开放式环境。
这使得跨领域的统一信用分配策略成为可能。
在三个具有挑战性的智能体基准测试中的实验表明，OPRL在多样化的多轮设置中是有效的、高效的且鲁棒的。在WebShop和VisualSokoban中，它持续优于闭源前沿模型和强基线强化学习方法，使用Qwen2.5-7B(-VL)（Yang等人，2024）作为基础模型实现了最先进的结果。在SOTOPIA这个具有不可验证奖励的开放式社交交互环境中，OPRL在自我对话中将目标完成率提高了14%，在与GPT-4o对话时提高了48%（OpenAI，2024）。进一步的分析表明，相比仅使用结果奖励或token级PRM的基线方法，OPRL具有更快的收敛速度和更低的方差，表明其具有高样本效率和稳定的训练过程。OPRL还同时提升了episode级和步骤级奖励，同时产生更短的episode，这表明它通过更少的不必要动作实现了更有用的探索。最后，消融实验表明，优势级融合是关键的，环境步骤惩罚仅提供了适度的收益，而token级PRM对于稳定的多轮训练来说过于细粒度。
我们的贡献有三个方面：

• 我们提出了OPRL，这是一种通用的细粒度信用分配方法，将轨迹级偏好转换为智能体强化学习的密集步骤级指导。
• 我们提供了理论保证，证明所得到的隐式步骤奖励是偏好一致的，并构成具有有界梯度的基于势函数的奖励塑形，以稳定多轮强化学习训练。
• 实证结果和分析表明，OPRL在样本效率、跨强化学习算法的鲁棒性以及对具有不可验证奖励的开放式环境的泛化能力方面均优于基线方法。

2 PRELIMINARIES 预备知识

Task formulation（任务形式化）

我们将LLM智能体任务视为一个多步骤决策过程，其中智能体与环境交互，通过给定任务提示 x ∈ p(X) 进行顺序决策来实现长期目标。在每个时间步[timestep] ，智能体接收一个观察[an observation] （例如，对手消息或环境反馈），并用文本动作 作出响应，其中 表示token词汇表[the token vocabulary] ， 是最大生成长度¹[the maximum generation length]。然后环境返回一个标量奖励[a scalar reward] 并提供下一个观察[the next observation] 。
直到最后一个时间步[the last timestep] ，完整的episode 由一条轨迹组成：。然而，在现实世界场景中（例如对话），奖励可能是稀疏或延迟的，例如仅在轨迹结束时提供反馈或中间步骤只有弱信号。因此，将信用分配[assign credit]给轨迹中的各个步骤是具有挑战性的，特别是当有许多交互回合时。
强化学习通过优化LLM的策略[the policy] 来解决智能体任务，目标是最大化交互过程中的期望累积奖励。为了估计期望奖励关于 的梯度，使用了策略梯度方法，如 PPO（Schulman等人，2017）、GRPO（Shao等人，2024）、RLOO（Ahmadian等人，2024）和 REINFORCE++（Hu等人，2025）。这些强化学习算法主要在估计策略更新的优势函数的方式[the manner of estimating advantages for policy update]上有所不同。

例如，PPO使用广义优势估计(generalized advantage estimation, GAE) 通过学习的价值函数来计算优势。GRPO和RLOO是无critic的，在同一提示的N个样本批次中形成相对优势------GRPO通过组均值对每个奖励进行中心化[relative advantages within a batch of N samples for the same prompt]（通常归一化），而RLOO使用留一法均值。

REINFORCE++则使用批次归一化奖励[batch-normalized rewards] 作为基线奖励。隐式奖励[Implicit reward modeling] 在LLM对齐的奖励建模中显示出有效性，它使模型能够在没有显式标签的情况下推断奖励结构。除了偏好学习（Rafailov等人，2024b；Ethayarajh等人，2024；Wu等人，2025；Zhang等人，2025a）之外，隐式奖励还被用作结果奖励来评估模型输出的质量（Hosseini等人，2024；Zhong等人，2025）。此外，Rafailov等人（2024a）证明了DPO可以自动学习Q函数[a Q-function]。

除了用作结果奖励模型或Q函数[ORMs or Q-functions] 外，最近的工作探索了从隐式奖励推导过程奖励模型，用于测试时重排序（Yuan等人，2025）或单轮强化学习训练（Cui等人，2025）。

在这种设置中，PRM仅用结果标签训练，并将每个token的过程奖励参数化为 ，其中 表示PRM， 表示参考模型。 表示响应 中的第个token。

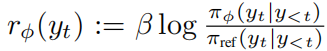
3 METHOD

在本节中，我们首先概述我们的方法，并为在线强化学习定义隐式步骤奖励[implicit step rewards for online RL]。然后，我们提供理论分析来证明这些步骤奖励为策略学习提供了可靠且稳定的指导。

实验配置

# WebShop 和 VisualSokoban
Policy Model (πθ):  Qwen2.5-7B-Instruct
PRM (πϕ):          Qwen2.5-7B-Instruct  # 从policy初始化

# 特殊情况：VisualSokoban（视觉+文本）
Policy Model (πθ):  Qwen2.5-VL-7B-Instruct  # 支持视觉
PRM (πϕ):          Qwen2.5-7B-Instruct     # 只需要文本

# SOTOPIA（社交对话）
Policy Model (πθ):  Qwen2.5-7B-Instruct
PRM (πϕ):          Qwen2.5-7B-Instruct

# 小模型实验（Table 4）
Policy Model (πθ):  Qwen2.5-1.5B-Instruct
PRM (πϕ):          Qwen2.5-1.5B-Instruct

两个Qwen模型，一个学"怎么做"，一个学"怎么评"！🎯

3.1 OVERVIEW

OPRL引入了一个与策略交替优化的在线PRM，将偏好更优动作的倾向转化为每个步骤的密集奖励[a dense reward for each step]，指导智能体的细粒度探索和改进。

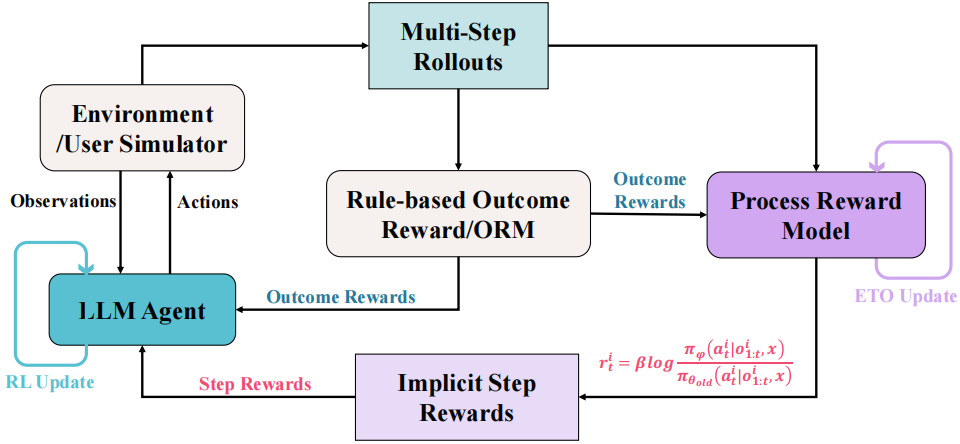
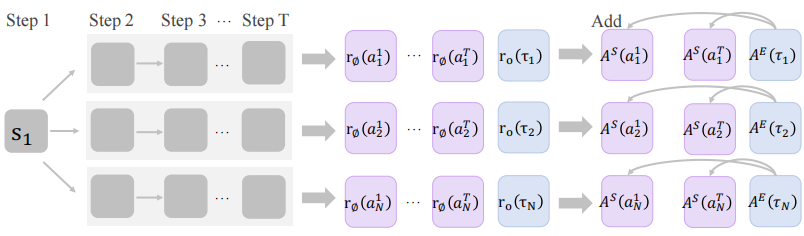
图1展示了我们方法的整体训练流程：

(1) 使用当前策略 采样on-policy rollouts；(2) 根据结果奖励 从相同的on-policy数据构建偏好对，并通过公式2中定义的DPO推导目标函数对PRM进行一个训练步骤的更新；(3) 使用更新后的PRM计算公式1中定义的隐式步骤奖励，并根据公式6对 进行一个训练步骤的优化。 和 的交替优化创建了一个自我强化循环，其中策略和PRM相互迭代增强。

• On-policy: 用"当前策略"生成的数据来训练"当前策略"
• Off-policy: 用"其他策略/过去策略"生成的数据来训练"当前策略"

下面我们首先提供隐式步骤奖励的定义，并详细说明每个模型的训练过程。有关OPRL的详细算法，请参阅附录A。

Definition 3.1 (Implicit step rewards) 定义3.1（隐式步骤奖励）

设 表示由当前策略 πθ 生成的轨迹。

对于轨迹中步骤 的动作 ，其隐式步骤奖励定义为

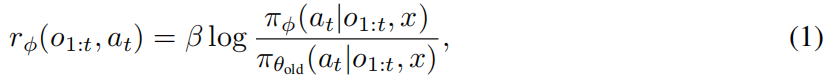
其中 表示在线更新的PRM， 是策略的先前快照[the previous snapshot of the policy] ， 是缩放奖励的温度参数。隐式步骤奖励衡量当前动作在新学习的PRM下相比旧策略下的概率增加程度。

正值表示 认为对近期改进负责的动作，而负值突出显示应该避免的动作。

Optimizing online PRM via DPO 通过DPO优化在线PRM

为了可扩展的在线PRM训练，我们简单地在由策略采样的正负轨迹对上优化 ，而不引入额外的轨迹采样，并推导出DPO风格的目标函数：

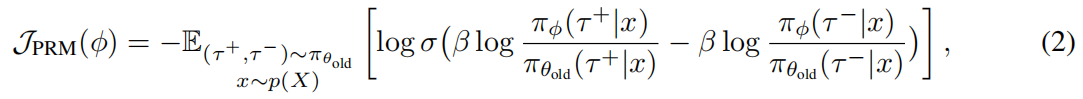
其中 σ 是逻辑sigmoid函数，β 与公式1一致； 是优于负样本 的正轨迹，两者都由结果奖励标注²。参见定理3.3，证明 是无偏的逐步奖励估计器。

² 在我们对WebShop和VisualSokoban的实验中，正轨迹是成功率大于0的轨迹，而对于SOTOPIA，正轨迹的目标完成分数大于6。

Policy learning with implicit step rewards 使用隐式步骤奖励进行策略学习

我们以GRPO为例说明如何将隐式步骤奖励整合到策略训练中，尽管我们的方法与任何策略梯度算法兼容。

如图2所示，对于每个任务提示 ，我们从当前策略 中采样 N 条轨迹 {}，并通过基于规则的验证器或结果奖励模型获得相应的结果奖励 {}。然后我们计算每条采样轨迹的episode级优势：

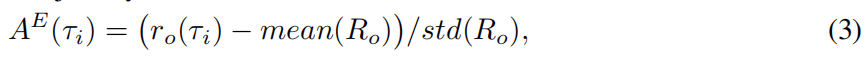
其中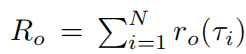

接下来，我们使用最新的PRM （来自前一个训练步骤）通过公式1获得每个动作 的隐式步骤奖励，并计算步骤级优势：

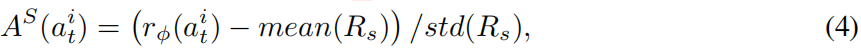
其中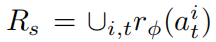 表示 N 条轨迹中所有步骤奖励的集合，以保持不同episode长度之间的尺度可比。

然后我们结合两级优势进行策略更新：

其中 α 是平衡全局正确性和局部质量的超参数，在我们所有实验中将其设置为1。

最后，策略使用Schulman等人(2017)、Shao等人(2024)、Ahmadian等人(2024)、Hu等人(2025)广泛使用的代理目标进行优化，但不包含KL散度惩罚：

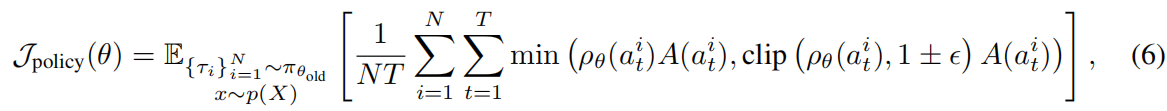
其中 是步骤级的重要性采样比率， 是控制重要性裁剪范围的超参数（在我们所有实验中设置为0.2）。

🎯 OPRL完整示例：WebShop购物任务

现在让我用一个具体例子走完OPRL的整个流程。

任务设定

目标： 买一双"红色耐克跑鞋，尺码42"

环境： WebShop网站模拟器

动作空间：

• search[query] - 搜索
• click[item_id] - 点击商品
• select[option] - 选择选项
• buy - 购买

初始状态

# 策略模型（刚开始训练）
π_θ = Qwen2.5-7B-Instruct  # 参数θ

# PRM模型（从策略初始化）
π_ϕ = copy(π_θ)  # 参数ϕ

# 旧策略快照
π_θ_old = copy(π_θ)

🔄 训练迭代第1步

Step 1: 采样轨迹（On-Policy Rollouts）

用当前策略 πθ 对同一个任务提示采样 N=8 条轨迹：

轨迹 τ1（成功）

o1: "Find red Nike running shoes size 42"
a1: search[red Nike running shoes]  
    CoT: "我需要搜索包含所有关键词的商品"

o2: "Results: [Nike Air Zoom..., Adidas Ultra...]"  
a2: click[item_1]  # Nike Air Zoom
    CoT: "第一个是耐克，应该点进去看"

o3: "Product page: Nike Air Zoom, Colors: red, blue"
a3: select[color=red]
    CoT: "选择红色"

o4: "Selected red. Sizes: 41, 42, 43"
a4: select[size=42]
    CoT: "选择42码"

o5: "Added to cart"
a5: buy
    CoT: "完成购买"

结果奖励: r_o(τ1) = 1.0 ✅（成功匹配所有要求）

轨迹 τ2（部分成功）

o1: "Find red Nike running shoes size 42"
a1: search[Nike shoes]  # 没搜"红色"

o2: "Results: [Nike shoes...]"
a2: click[item_5]

o3: "Product page: Nike Classic, Colors: white, black"
a3: select[color=white]  # 选错颜色

o4: "Sizes available..."
a4: select[size=42]  # 尺码对了

o5: "Added to cart"
a5: buy

结果奖励: r_o(τ2) = 0.3 ⚠️（只有品牌和尺码对）

轨迹 τ3（失败）

o1: "Find red Nike running shoes size 42"
a1: search[Adidas red]  # 品牌错了

o2: "Results: [Adidas products...]"
a2: click[item_2]

o3: "Product: Adidas Superstar red"
a3: select[size=40]  # 尺码也错了

o4: "Added to cart"
a4: buy

结果奖励: r_o(τ3) = 0.0 ❌（完全错误）

继续采样...

τ4: r_o = 0.7 (颜色和尺码对，品牌错)

τ5: r_o = 1.0 ✅

τ6: r_o = 0.0 ❌

τ7: r_o = 0.5

τ8: r_o = 0.2

Step 2: 更新PRM（公式2）

2.1 构建偏好对

根据结果奖励标注，正样本阈值 > 0：

正轨迹: [τ1, τ2, τ4, τ5, τ7, τ8]
负轨迹: [τ3, τ6]

偏好对:
(τ1+, τ3-), (τ1+, τ6-),  # τ1成功 vs 失败
(τ5+, τ3-), (τ5+, τ6-),  # τ5成功 vs 失败
(τ2+, τ3-), ...          # 部分成功 vs 失败

2.2 计算DPO损失

对偏好对 (τ1+, τ3-):

# τ1的轨迹概率
log π_ϕ(τ1|x) = log π_ϕ(a1|o1) + log π_ϕ(a2|o1,a1) + ...
log π_θ_old(τ1|x) = log π_θ_old(a1|o1) + ...

# τ3的轨迹概率  
log π_ϕ(τ3|x) = ...
log π_θ_old(τ3|x) = ...

# DPO目标（希望拉大差距）
loss = -log σ(
    β * [log π_ϕ(τ1)/π_θ_old(τ1)] 
    - β * [log π_ϕ(τ3)/π_θ_old(τ3)]
)

直觉： 训练πϕ使得：

• 对好轨迹τ1，πϕ(τ1) > π_θ_old(τ1) → 正奖励
• 对坏轨迹τ3，πϕ(τ3) < π_θ_old(τ3) → 负奖励

2.3 梯度更新

# 对所有偏好对计算损失
total_loss = sum([loss(τ+, τ-) for (τ+, τ-) in pairs])

# 更新PRM参数
ϕ = ϕ - lr_PRM * ∇_ϕ(total_loss)

结果： PRM学会了区分好坏动作的模式

Step 3: 计算隐式步骤奖励（公式1）

现在用更新后的πϕ给每个动作打分。

对τ1的每个动作：

# 步骤1: search[red Nike running shoes]
r_ϕ(a1) = β * log[π_ϕ(a1|o1) / π_θ_old(a1|o1)]
        = 0.05 * log[0.8 / 0.3]  # PRM认为这个搜索很好
        = 0.05 * 0.98 = +0.049

# 步骤2: click[item_1]  
r_ϕ(a2) = 0.05 * log[0.7 / 0.4]
        = 0.05 * 0.56 = +0.028

# 步骤3: select[color=red]
r_ϕ(a3) = 0.05 * log[0.9 / 0.5]  # 选对颜色，PRM很喜欢
        = 0.05 * 0.59 = +0.029

# 步骤4: select[size=42]
r_ϕ(a4) = 0.05 * log[0.85 / 0.6]
        = 0.05 * 0.35 = +0.017

# 步骤5: buy
r_ϕ(a5) = 0.05 * log[0.6 / 0.55]  # 常规操作
        = 0.05 * 0.09 = +0.004

对τ3的每个动作：

# 步骤1: search[Adidas red] - 品牌错了！
r_ϕ(a1) = 0.05 * log[0.2 / 0.4]  # PRM不喜欢
        = 0.05 * (-0.69) = -0.035

# 步骤2: click[item_2]
r_ϕ(a2) = 0.05 * log[0.3 / 0.5]
        = -0.026

# 步骤3: select[size=40] - 尺码错了！
r_ϕ(a3) = 0.05 * log[0.25 / 0.6]
        = -0.044

# 步骤4: buy
r_ϕ(a4) = 0.05 * log[0.5 / 0.55]
        = -0.005

观察： PRM已经学会了：

• 搜索要包含所有关键词 → +奖励
• 选错品牌/颜色/尺码 → -奖励

Step 4: 计算优势函数（公式3-5）

Episode级优势（公式3）

# 所有轨迹的结果奖励
R_o = [1.0, 0.3, 0.0, 0.7, 1.0, 0.0, 0.5, 0.2]
mean(R_o) = 0.46
std(R_o) = 0.38

# 每条轨迹的episode优势
A^E(τ1) = (1.0 - 0.46) / 0.38 = +1.42  # 成功！
A^E(τ2) = (0.3 - 0.46) / 0.38 = -0.42
A^E(τ3) = (0.0 - 0.46) / 0.38 = -1.21  # 失败！
A^E(τ4) = (0.7 - 0.46) / 0.38 = +0.63
A^E(τ5) = (1.0 - 0.46) / 0.38 = +1.42
...

步骤级优势（公式4）

# 收集所有8条轨迹的所有步骤奖励
R_s = [
    # τ1的步骤奖励
    +0.049, +0.028, +0.029, +0.017, +0.004,
    # τ2的步骤奖励  
    +0.015, -0.020, -0.035, +0.012, +0.003,
    # τ3的步骤奖励
    -0.035, -0.026, -0.044, -0.005,
    # ... τ4-τ8的所有步骤
]

mean(R_s) = 0.002
std(R_s) = 0.025

# τ1的每个动作的步骤优势
A^S(τ1, a1) = (0.049 - 0.002) / 0.025 = +1.88  # 搜索很好！
A^S(τ1, a2) = (0.028 - 0.002) / 0.025 = +1.04
A^S(τ1, a3) = (0.029 - 0.002) / 0.025 = +1.08  # 选红色很好！
A^S(τ1, a4) = (0.017 - 0.002) / 0.025 = +0.60
A^S(τ1, a5) = (0.004 - 0.002) / 0.025 = +0.08

# τ3的每个动作的步骤优势
A^S(τ3, a1) = (-0.035 - 0.002) / 0.025 = -1.48  # 搜错了！
A^S(τ3, a2) = (-0.026 - 0.002) / 0.025 = -1.12
A^S(τ3, a3) = (-0.044 - 0.002) / 0.025 = -1.84  # 选错尺码！
A^S(τ3, a4) = (-0.005 - 0.002) / 0.025 = -0.28

融合优势（公式5）

α = 1  # 超参数

# τ1的融合优势
A(τ1, a1) = A^E(τ1) + α * A^S(τ1, a1)
          = 1.42 + 1.0 * 1.88 = +3.30  ⭐⭐⭐

A(τ1, a2) = 1.42 + 1.04 = +2.46
A(τ1, a3) = 1.42 + 1.08 = +2.50  ⭐⭐
A(τ1, a4) = 1.42 + 0.60 = +2.02
A(τ1, a5) = 1.42 + 0.08 = +1.50

# τ3的融合优势
A(τ3, a1) = -1.21 + (-1.48) = -2.69  💀💀💀
A(τ3, a2) = -1.21 + (-1.12) = -2.33
A(τ3, a3) = -1.21 + (-1.84) = -3.05  💀💀💀💀
A(τ3, a4) = -1.21 + (-0.28) = -1.49

Step 5: 更新策略（公式6）

PPO-style目标

# 对τ1的第1个动作（搜索）
ρ_θ(a1) = π_θ(a1|o1) / π_θ_old(a1|o1)
        = 0.35 / 0.30 = 1.17  # 重要性比率

# PPO裁剪目标
L1 = ρ_θ(a1) * A(τ1, a1) = 1.17 * 3.30 = 3.86
L2 = clip(ρ_θ(a1), 0.8, 1.2) * A(τ1, a1) 
   = 1.17 * 3.30 = 3.86  # 没超出范围

objective = min(L1, L2) = 3.86

# 对τ3的第1个动作（搜错）
ρ_θ(a1) = 0.18 / 0.40 = 0.45

L1 = 0.45 * (-2.69) = -1.21
L2 = clip(0.45, 0.8, 1.2) * (-2.69)
   = 0.8 * (-2.69) = -2.15  # 被裁剪了

objective = max(L1, L2) = -1.21  # 最大化负数=惩罚

梯度更新

# 汇总所有轨迹、所有步骤的目标
J_policy = (1/NT) * Σ min(ρ * A, clip(ρ) * A)

# 更新策略参数
θ = θ + lr_policy * ∇_θ(J_policy)

结果：

• π_θ("search[red Nike running shoes]" | o1) ↑↑↑ # 大幅增加
• π_θ("search[Adidas red]" | o1) ↓↓↓ # 大幅减少
• π_θ("select[color=red]" | o3) ↑↑
• π_θ("select[size=40]" | ...) ↓↓

Step 6: 更新快照，进入下一轮

π_θ_old = copy(π_θ)  # 保存当前策略作为新的参考

# 下一个iteration重新开始
# 用新的πθ采样新轨迹...

3.2 THEORETICAL ANALYSIS 理论分析

现在我们证明公式1中定义的学习到的步骤奖励 rϕ 是：(1) 动作对潜在任务效用贡献的无偏估计器，以及 (2) 策略 πθ 的安全、良态的学习信号。

我们从成对轨迹的Bradley-Terry (BT) 偏好假设（Bradley & Terry, 1952）开始。

Assumption 3.2 (Trajectory-level preference model)

存在一个潜在效用函数 ，使得结果奖励验证器或模型以如下概率选择 τ+ 优于 τ−：

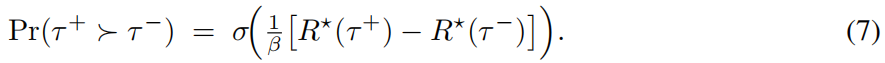
这是成对比较的经典BT似然。因此，最小化公式2中的PRM损失是对分数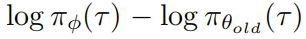 的精确极大似然估计，该分数与 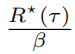相差一个常数。

定理3.3（基于势函数的奖励塑形） Theorem 3.3 (Potential-based reward shaping)

设PRM πϕ 是公式2中损失的全局最优解，设 πref 为DPO损失中使用的静态参考模型。则 ，其中 c(x) 是某个依赖于提示的常数。利用步骤奖励定义（公式1），我们得到伸缩恒等式：

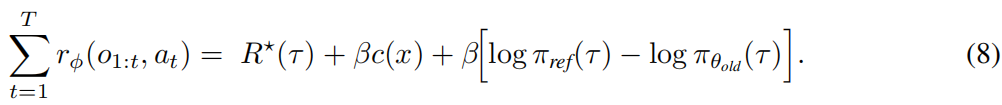
选择 θold = θ 可以消除最后一项。因此，rϕ 是 R⋆ 的基于势函数的塑形，它保持了最优策略集（Ng, 2003）。

定理3.3的核心含义

伸缩恒等式的直观理解：

所有步骤奖励之和 = 真实任务效用 + 常数项

ΣTt=1 rϕ(at) = R⋆(τ) + 常数
     ↓
步骤奖励正确地"分解"了轨迹的总价值

势函数塑形的保证：

• 不改变最优策略（哪个策略最好不变）
• 只是让学习更容易（提供密集信号）

Proposition 3.4 (Gradient alignment and boundedness) 命题3.4（梯度对齐与有界性）

Define the shaped objective 定义塑形目标函数

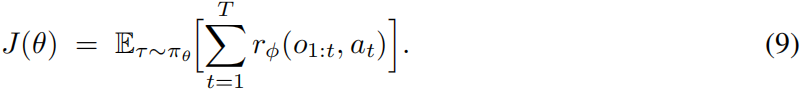
则策略梯度为：

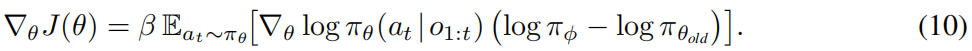
如果 θold = θ，这简化为 ∇θJ(θ) = −β ∇θ KL(πθ ∥ πϕ)，因此最大化 J 执行KL下降步骤，在信任域内将 πθ 向偏好对齐的PRM πϕ 移动。

设 ε = minat,o1:t πθold(at|o1:t, x) > 0。则

因此，策略梯度样本是一致有界的，保证了交替 {πϕ, πθ} 更新的稳定随机优化。

命题3.4的核心含义

KL下降的直观理解：

当 θold = θ 时：
最大化 J(θ) = 最小化 KL(πθ ∥ πϕ)
              ↓
           策略向PRM靠拢

有界性的重要性：

|rϕ| ≤ β log(1/ε)

意味着：步骤奖励不会爆炸
     → 梯度稳定
     → 训练稳定

总之，由于 πϕ 将概率集中在增加 R⋆ 的行为上，每个 rϕ 提供了动作对潜在任务效用贡献的近似无偏估计。密集且有界的步骤奖励相对于单一结果奖励也降低了方差，从而产生了有效的信用分配策略来加速策略学习。