《机器学习导论》第 11 章 - 多层感知器（MLP）

啊阿狸不会拉杆2026-02-10 8:41

目录

前言

[11.1 引言](#11.1 引言)

[11.1.1 理解人脑](#11.1.1 理解人脑)

[11.1.2 神经网络作为并行处理的典范](#11.1.2 神经网络作为并行处理的典范)

[11.2 感知器](#11.2 感知器)

代码实现：单个感知器

[11.3 训练感知器](#11.3 训练感知器)

代码实现：训练感知器（解决二分类问题）

[11.4 学习布尔函数](#11.4 学习布尔函数)

[代码实现：感知器 VS XOR 问题（对比可视化）](#代码实现：感知器 VS XOR 问题（对比可视化）)

[11.5 多层感知器](#11.5 多层感知器)

[代码实现：多层感知器（解决 XOR 问题）](#代码实现：多层感知器（解决 XOR 问题）)

[11.6 作为普适近似的 MLP](#11.6 作为普适近似的 MLP)

[代码实现：MLP 拟合非线性函数（可视化对比）](#代码实现：MLP 拟合非线性函数（可视化对比）)

[11.7 向后传播算法](#11.7 向后传播算法)

[11.7.1 非线性回归](#11.7.1 非线性回归)

[11.7.2 两类判别式](#11.7.2 两类判别式)

[11.7.3 多类判别式](#11.7.3 多类判别式)

[11.7.4 多个隐藏层](#11.7.4 多个隐藏层)

[11.8 训练过程](#11.8 训练过程)

[11.8.1 改善收敛性](#11.8.1 改善收敛性)

[11.8.2 过分训练（过拟合）](#11.8.2 过分训练（过拟合）)

[11.8.3 构造网络](#11.8.3 构造网络)

[11.8.4 线索](#11.8.4 线索)

[11.9 调整网络规模](#11.9 调整网络规模)

[11.10 学习的贝叶斯观点](#11.10 学习的贝叶斯观点)

[11.11 维度归约](#11.11 维度归约)

[代码实现：MLP 自编码器降维](#代码实现：MLP 自编码器降维)

[11.12 学习时间](#11.12 学习时间)

[11.12.1 时间延迟神经网络](#11.12.1 时间延迟神经网络)

[11.12.2 递归网络](#11.12.2 递归网络)

[11.13 深度学习](#11.13 深度学习)

[11.14 注释](#11.14 注释)

[11.15 习题](#11.15 习题)

[11.16 参考文献](#11.16 参考文献)

总结

本文配套完整可运行 Python 代码，包含可视化对比图，零基础也能轻松理解多层感知器核心原理！

前言

大家好！今天我们来深入学习《机器学习导论》第 11 章的核心内容 ------ 多层感知器（MLP）。MLP 作为神经网络的基础，是理解深度学习的关键。本文会用通俗易懂的语言拆解核心概念，搭配完整可运行的 Python 代码和直观的可视化对比图，让你真正吃透 MLP！

11.1 引言

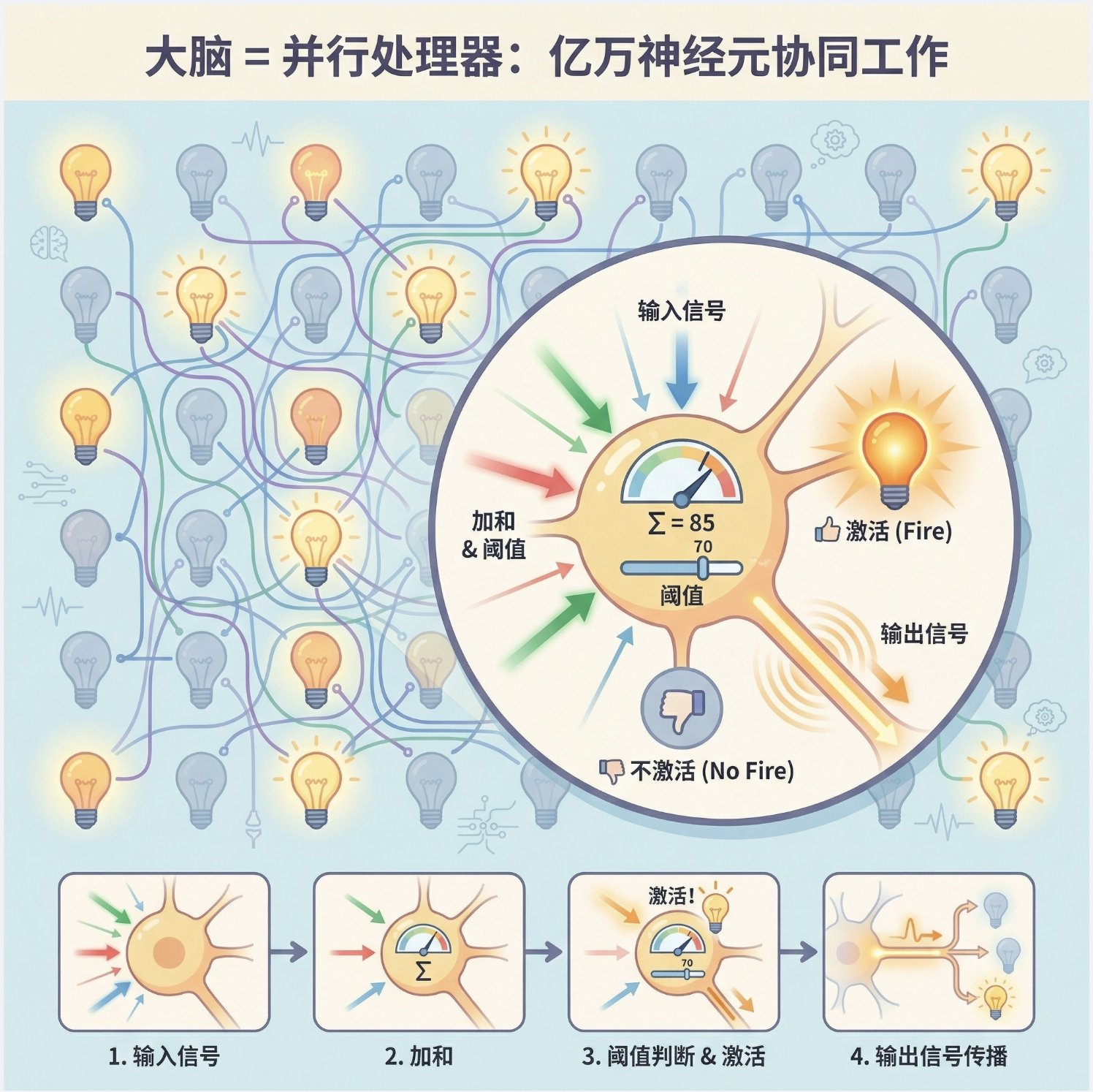
11.1.1 理解人脑

人脑就像一个超级复杂的 "并行处理器"，由上千亿个神经元相互连接组成。每个神经元接收来自其他神经元的信号，经过简单处理后再传递出去。我们可以把单个神经元想象成一个 "小型决策机"：收到足够多的 "正向信号" 就激活，否则保持沉默。

11.1.2 神经网络作为并行处理的典范

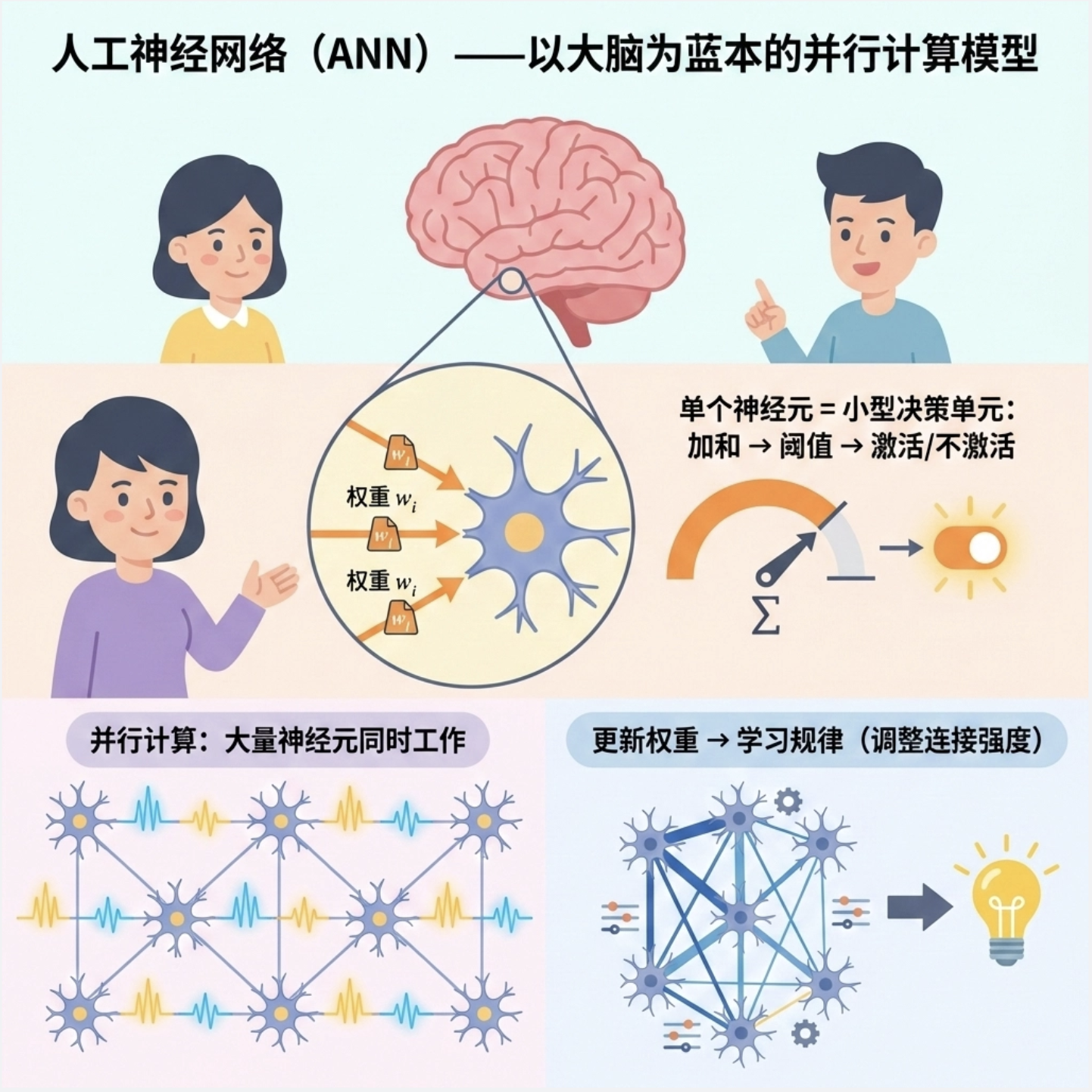
人工神经网络（ANN）就是模仿人脑结构设计的计算模型：

  • 把复杂任务拆分成多个简单的 "神经元计算"
  • 所有神经元可以同时（并行）处理数据
  • 通过调整神经元之间的连接强度（权重）来学习规律

11.2 感知器

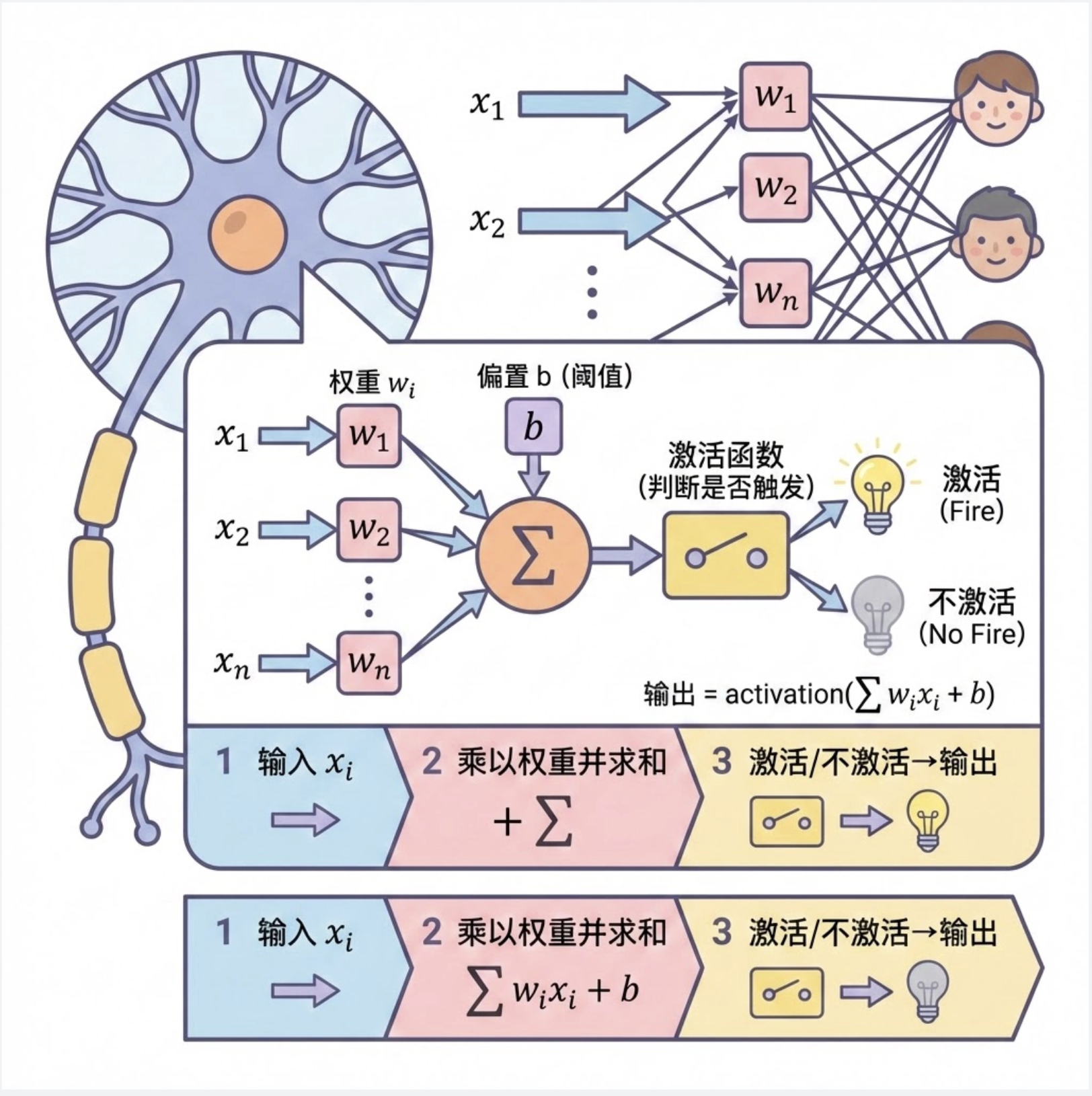
感知器是神经网络中最基础的 "积木"，相当于单个神经元的数学模型。我们可以把它理解成一个 "带门槛的开关"：

  1. 接收多个输入信号（x₁, x₂, ..., xₙ）
  2. 每个输入乘以对应的权重（w₁, w₂, ..., wₙ），求和
  3. 加上偏置项（b，相当于 "基础门槛"）
  4. 通过激活函数判断是否 "触发开关"

代码实现：单个感知器

复制代码 
import numpy as np
import matplotlib.pyplot as plt

# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

class Perceptron:
    """单个感知器实现"""
    def __init__(self, input_dim):
        # 初始化权重（随机）和偏置
        self.weights = np.random.randn(input_dim)
        self.bias = np.random.randn()
    
    def step_activation(self, x):
        """阶跃激活函数（感知器的核心）"""
        return 1 if x >= 0 else 0
    
    def forward(self, x):
        """前向计算：输入→加权求和→激活"""
        # 加权求和 + 偏置
        linear_output = np.dot(x, self.weights) + self.bias
        # 通过激活函数
        output = self.step_activation(linear_output)
        return output

# 测试单个感知器
if __name__ == "__main__":
    # 创建2输入感知器
    perceptron = Perceptron(input_dim=2)
    
    # 测试不同输入
    test_inputs = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    print("感知器输出测试：")
    for x in test_inputs:
        print(f"输入: {x}, 输出: {perceptron.forward(x)}")

11.3 训练感知器

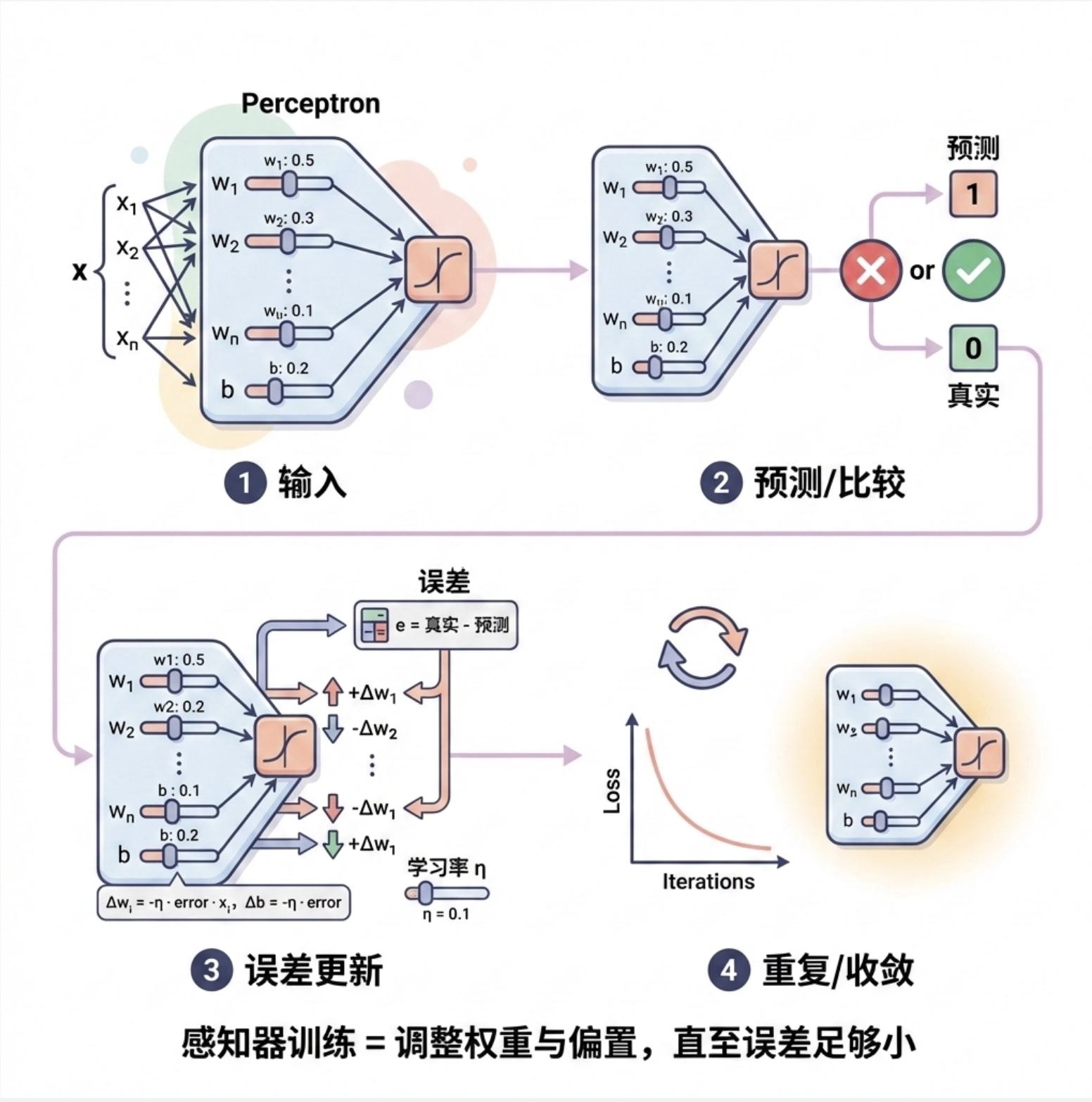
感知器的训练过程就像 "调整门槛和信号强度"：

  1. 给感知器输入数据，得到预测结果
  2. 对比预测结果和真实标签，计算误差
  3. 根据误差调整权重和偏置（权重更新规则）
  4. 重复上述步骤，直到误差足够小

代码实现：训练感知器（解决二分类问题）

python 复制代码 
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色


# ==================== 父类：基础感知器 ====================
class Perceptron:
    """单个感知器基础类"""

    def __init__(self, input_dim):
        # 初始化权重（随机正态分布）和偏置
        self.weights = np.random.randn(input_dim)
        self.bias = np.random.randn()

    def step_activation(self, x):
        """阶跃激活函数：感知器的核心激活函数"""
        return 1 if x >= 0 else 0

    def forward(self, x):
        """前向计算：输入→加权求和→激活"""
        # 加权求和 + 偏置
        linear_output = np.dot(x, self.weights) + self.bias
        # 通过激活函数得到输出
        output = self.step_activation(linear_output)
        return output


# ==================== 子类：可训练的感知器 ====================
class TrainablePerceptron(Perceptron):
    """可训练的感知器"""

    def __init__(self, input_dim, learning_rate=0.1):
        super().__init__(input_dim)
        self.lr = learning_rate  # 学习率：调整步长

    def train(self, X, y, epochs=100):
        """
        训练感知器
        X: 输入数据 (样本数, 特征数)
        y: 标签 (样本数,)
        epochs: 训练轮数
        """
        loss_history = []  # 记录每轮损失

        for epoch in range(epochs):
            total_loss = 0

            for xi, yi in zip(X, y):
                # 前向计算
                y_pred = self.forward(xi)
                # 计算误差
                error = yi - y_pred
                total_loss += abs(error)
                # 更新权重和偏置（感知器学习规则）
                self.weights += self.lr * error * xi
                self.bias += self.lr * error

            # 记录平均损失
            loss_history.append(total_loss / len(X))

            # 每10轮打印一次
            if (epoch + 1) % 10 == 0:
                print(f"Epoch {epoch + 1}, 平均误差: {loss_history[-1]:.4f}")

        return loss_history


# ==================== 测试代码：训练感知器解决AND问题 ====================
if __name__ == "__main__":
    # AND门数据（线性可分问题）
    X_and = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    y_and = np.array([0, 0, 0, 1])

    # 创建可训练感知器（2个输入特征，学习率0.1）
    perceptron = TrainablePerceptron(input_dim=2, learning_rate=0.1)
    # 训练感知器（50轮）
    loss_history = perceptron.train(X_and, y_and, epochs=50)

    # 可视化训练过程
    plt.figure(figsize=(10, 4))

    # 子图1：损失曲线（展示训练收敛过程）
    plt.subplot(1, 2, 1)
    plt.plot(loss_history, 'b-', linewidth=2)
    plt.xlabel("训练轮数")
    plt.ylabel("平均误差")
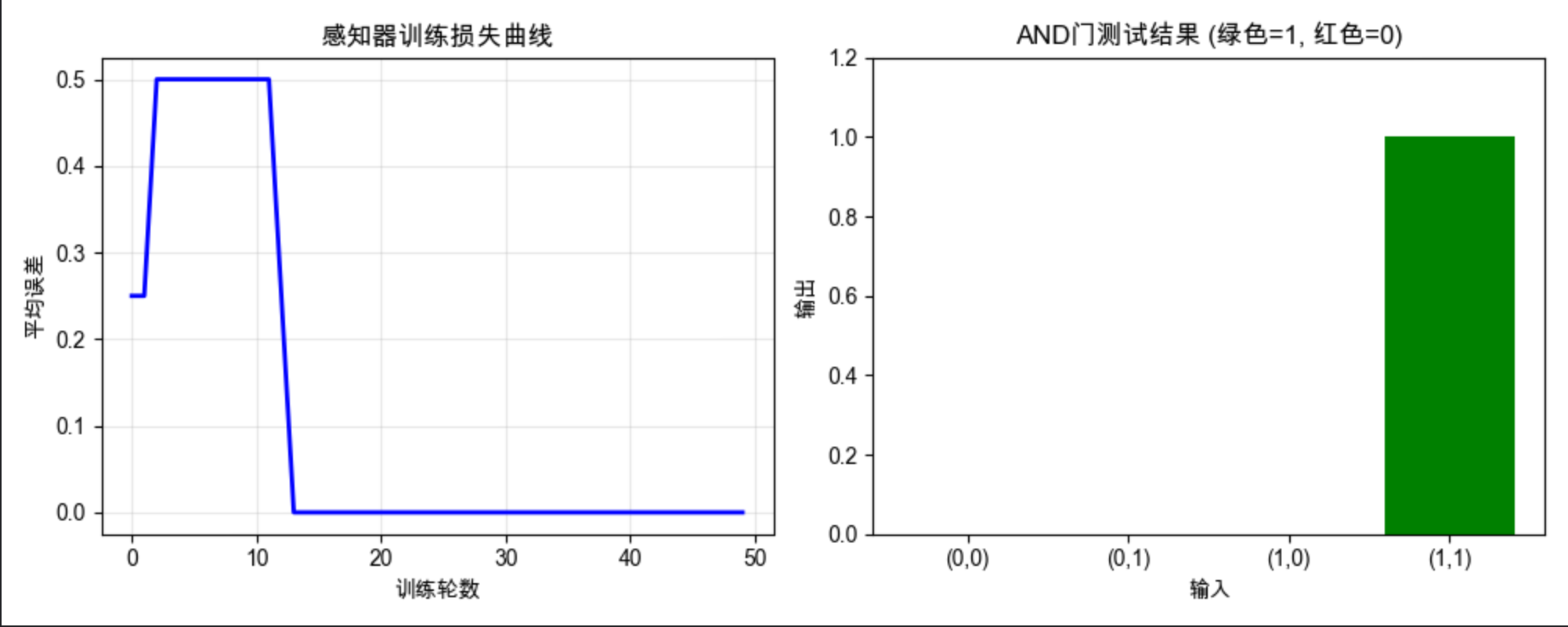
    plt.title("感知器训练损失曲线")
    plt.grid(True, alpha=0.3)

    # 子图2：AND门测试结果可视化
    plt.subplot(1, 2, 2)
    test_results = [perceptron.forward(x) for x in X_and]
    x_labels = [f"({x[0]},{x[1]})" for x in X_and]
    # 按输出值设置颜色：0为红色，1为绿色
    colors = ['red' if y == 0 else 'green' for y in test_results]
    plt.bar(x_labels, test_results, color=colors)
    plt.ylim(0, 1.2)  # 调整y轴范围，让图形更清晰
    plt.xlabel("输入")
    plt.ylabel("输出")
    plt.title("AND门测试结果 (绿色=1, 红色=0)")

    plt.tight_layout()  # 自动调整子图间距
    plt.show()

    # 打印最终训练得到的权重和偏置
    print(f"\n最终权重: {perceptron.weights}")
    print(f"最终偏置: {perceptron.bias}")

    # 额外验证：打印所有输入的预测结果
    print("\nAND门预测结果验证：")
    for xi, yi in zip(X_and, y_and):
        y_pred = perceptron.forward(xi)
        print(f"输入: {xi}, 真实值: {yi}, 预测值: {y_pred}")

11.4 学习布尔函数

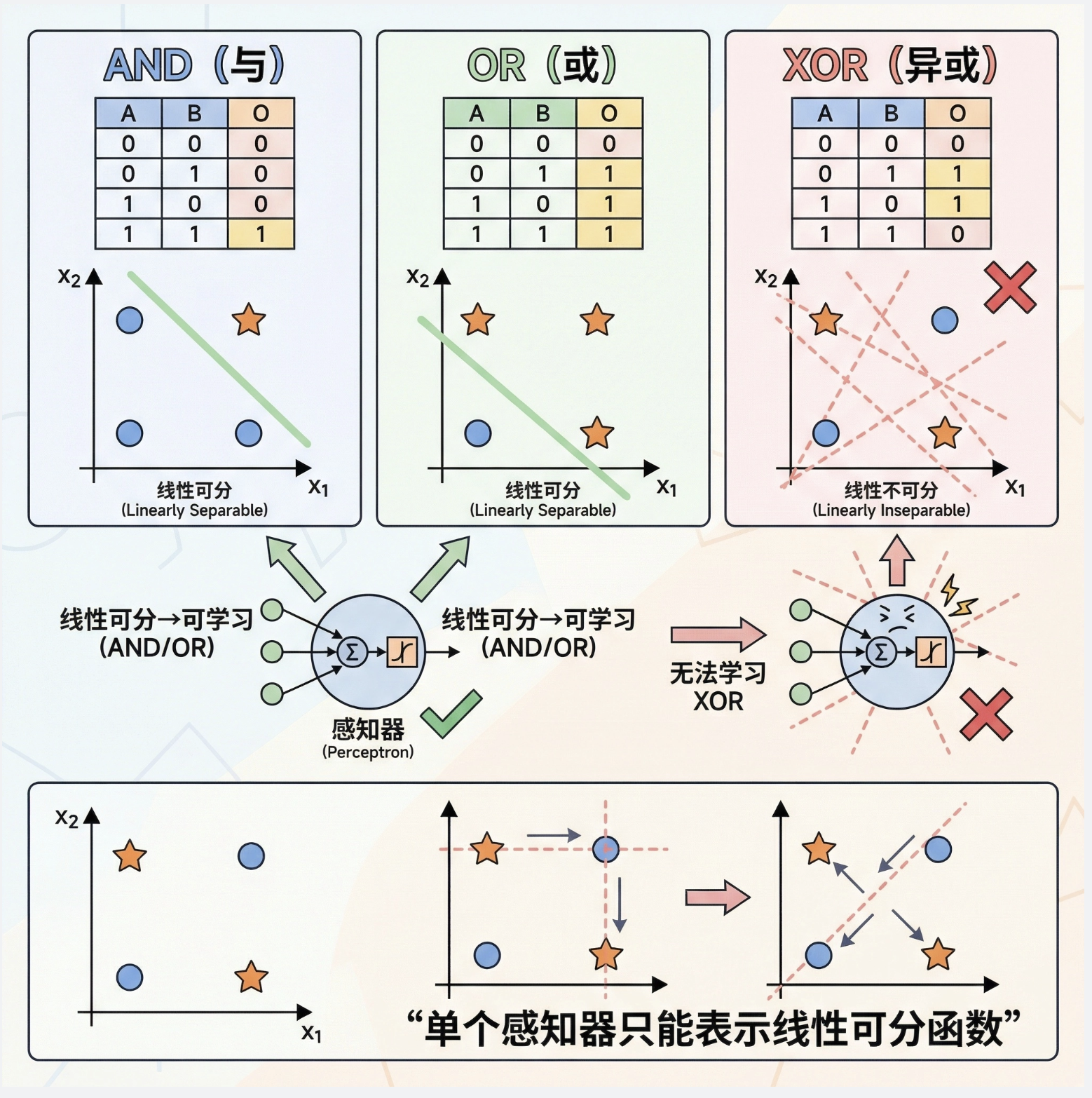
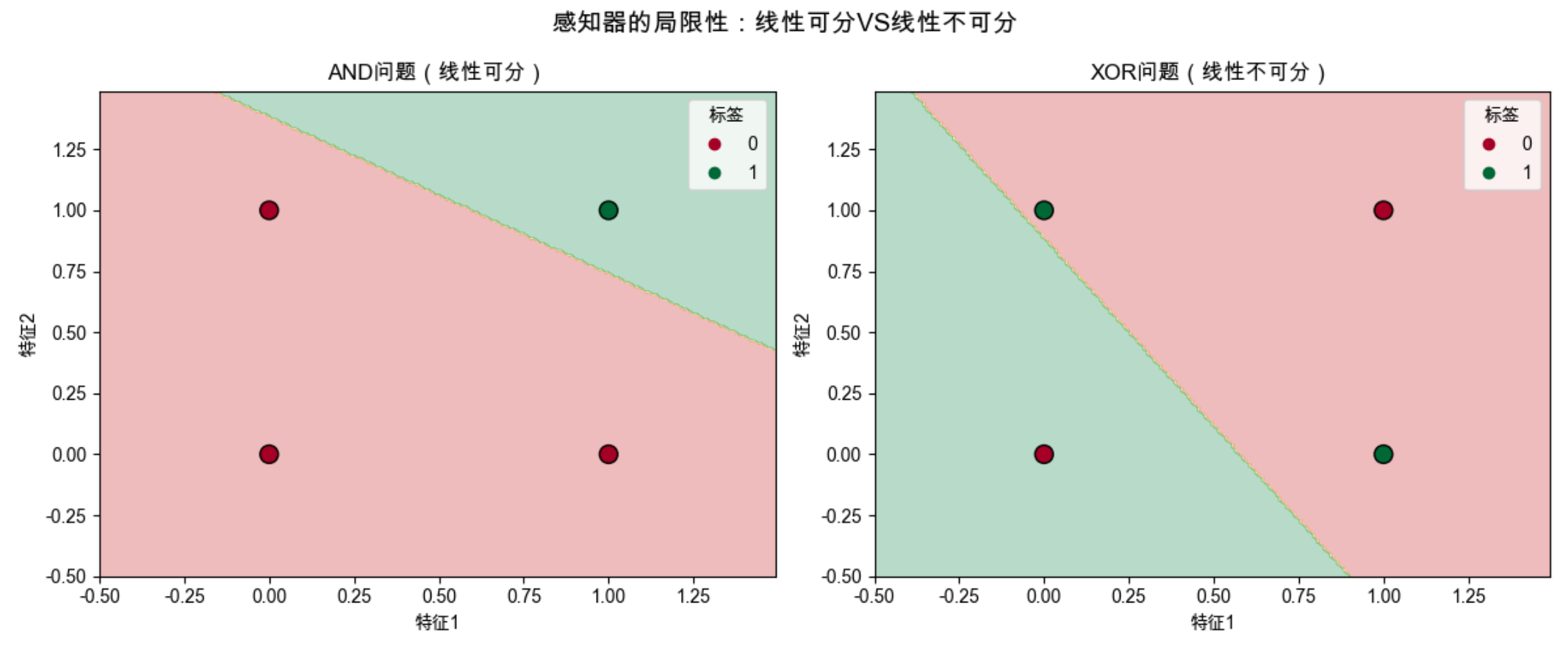
感知器可以学习简单的布尔函数（AND、OR），但无法学习异或（XOR）函数 ------ 这是感知器的最大局限性！

为什么？因为 XOR 问题是 "线性不可分" 的（无法用一条直线把 0 和 1 分开），而单个感知器只能处理线性可分问题。

代码实现：感知器 VS XOR 问题（对比可视化）

python 复制代码 
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色


# ==================== 基础感知器类 ====================
class Perceptron:
    """单个感知器基础类"""

    def __init__(self, input_dim):
        # 初始化权重（随机正态分布）和偏置
        self.weights = np.random.randn(input_dim)
        self.bias = np.random.randn()

    def step_activation(self, x):
        """阶跃激活函数：感知器的核心激活函数"""
        return 1 if x >= 0 else 0

    def forward(self, x):
        """前向计算：输入→加权求和→激活"""
        linear_output = np.dot(x, self.weights) + self.bias
        output = self.step_activation(linear_output)
        return output


# ==================== 可训练感知器类 ====================
class TrainablePerceptron(Perceptron):
    """可训练的感知器"""

    def __init__(self, input_dim, learning_rate=0.1):
        super().__init__(input_dim)
        self.lr = learning_rate  # 学习率：调整步长

    def train(self, X, y, epochs=100):
        """
        训练感知器
        X: 输入数据 (样本数, 特征数)
        y: 标签 (样本数,)
        epochs: 训练轮数
        """
        loss_history = []  # 记录每轮损失

        for epoch in range(epochs):
            total_loss = 0

            for xi, yi in zip(X, y):
                # 前向计算
                y_pred = self.forward(xi)
                # 计算误差
                error = yi - y_pred
                total_loss += abs(error)
                # 更新权重和偏置（感知器学习规则）
                self.weights += self.lr * error * xi
                self.bias += self.lr * error

            # 记录平均损失
            loss_history.append(total_loss / len(X))

            # 每10轮打印一次
            if (epoch + 1) % 10 == 0:
                print(f"Epoch {epoch + 1}, 平均误差: {loss_history[-1]:.4f}")

        return loss_history


# ==================== 决策边界绘制函数 ====================
def plot_decision_boundary(X, y, model, title, ax):
    """
    绘制感知器的决策边界
    X: 输入数据 (样本数, 特征数)
    y: 标签 (样本数,)
    model: 训练好的感知器模型
    title: 子图标题
    ax: 子图的坐标轴对象
    """
    # 创建网格（用于绘制决策边界）
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                         np.arange(y_min, y_max, 0.01))

    # 预测网格中每个点的输出
    Z = np.array([model.forward(np.array([x, y])) for x, y in zip(xx.ravel(), yy.ravel())])
    Z = Z.reshape(xx.shape)

    # 绘制决策边界填充图
    ax.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlGn)
    # 绘制样本点（带黑色边框，更清晰）
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdYlGn,
                         edgecolors='black', s=100)
    # 设置坐标轴标签和标题
    ax.set_xlabel("特征1")
    ax.set_ylabel("特征2")
    ax.set_title(title)
    # 添加图例
    ax.legend(*scatter.legend_elements(), title="标签")


# ==================== 测试代码：对比AND/XOR问题 ====================
if __name__ == "__main__":
    # 1. 准备XOR数据（线性不可分）
    X_xor = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    y_xor = np.array([0, 1, 1, 0])

    # 2. 创建感知器并训练XOR数据
    perceptron_xor = TrainablePerceptron(input_dim=2, learning_rate=0.1)
    print("===== 训练感知器处理XOR问题 =====")
    loss_history_xor = perceptron_xor.train(X_xor, y_xor, epochs=100)

    # 3. 创建画布，可视化对比AND/XOR问题
    plt.figure(figsize=(12, 5))

    # 子图1：AND问题（线性可分）
    plt.subplot(1, 2, 1)
    X_and = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    y_and = np.array([0, 0, 0, 1])
    and_perceptron = TrainablePerceptron(input_dim=2)
    and_perceptron.train(X_and, y_and, epochs=50)
    plot_decision_boundary(X_and, y_and, and_perceptron, "AND问题（线性可分）", plt.gca())

    # 子图2：XOR问题（线性不可分）
    plt.subplot(1, 2, 2)
    plot_decision_boundary(X_xor, y_xor, perceptron_xor, "XOR问题（线性不可分）", plt.gca())

    # 设置总标题和调整布局
    plt.suptitle("感知器的局限性：线性可分VS线性不可分", fontsize=14)
    plt.tight_layout()
    plt.show()

    # 4. 打印XOR问题的预测结果（验证感知器无法解决）
    print("\n===== XOR问题预测结果 =====")
    for xi, yi in zip(X_xor, y_xor):
        y_pred = perceptron_xor.forward(xi)
        print(f"输入: {xi}, 真实值: {yi}, 预测值: {y_pred}")

11.5 多层感知器

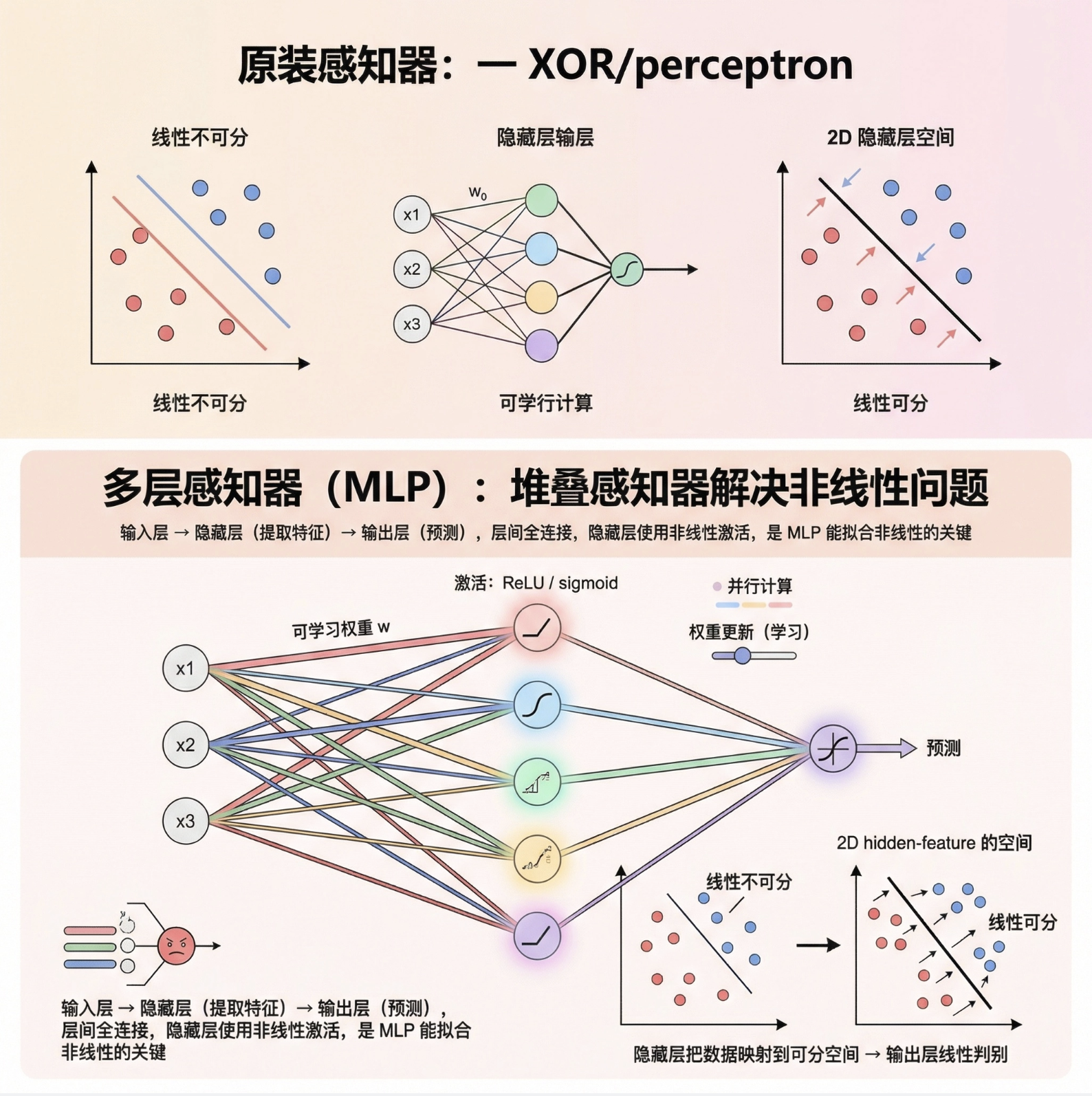
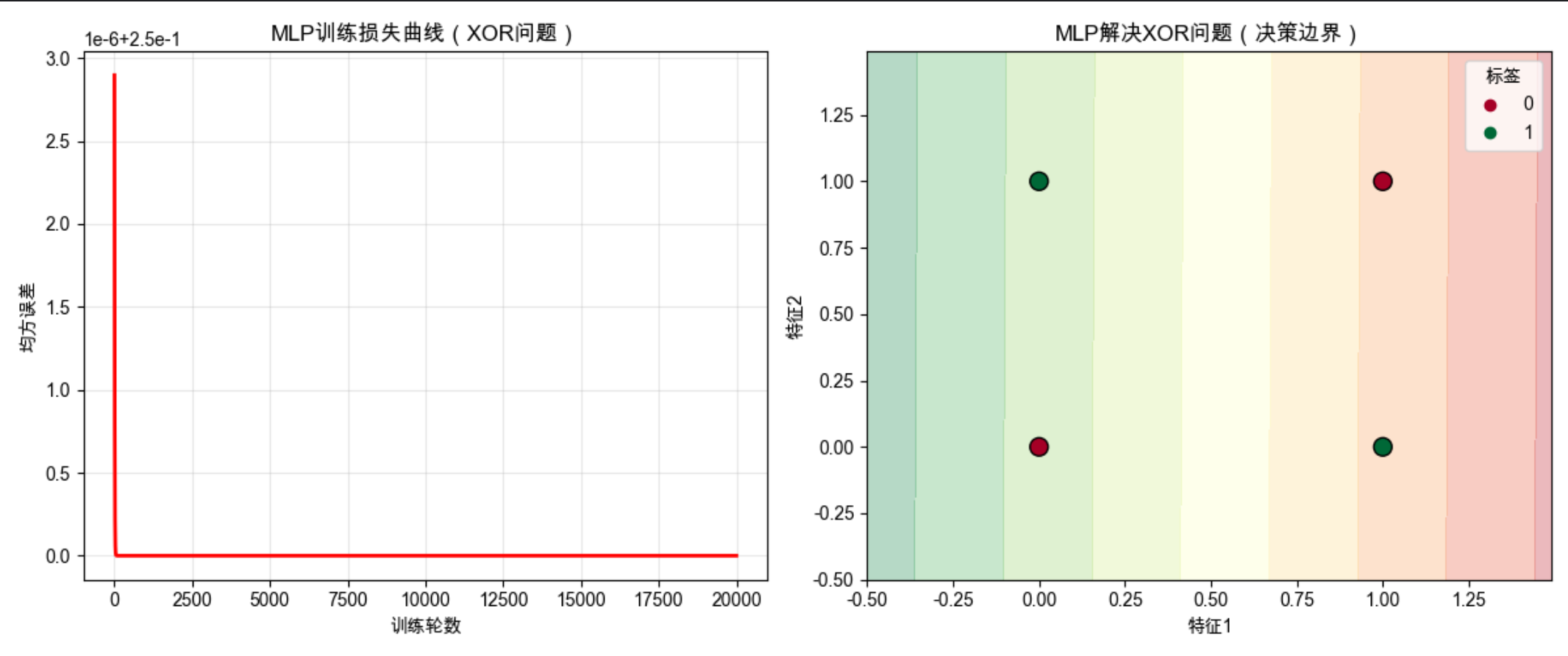
为了解决线性不可分问题，我们需要 "堆叠" 感知器 ------ 这就是多层感知器（MLP）！

MLP 就像 "多层流水线"：

  1. 输入层：接收原始数据
  2. 隐藏层：对数据进行 "特征提取"（可以有多层）
  3. 输出层：给出最终预测结果
  4. 每层之间全连接，层内无连接
  5. 隐藏层使用非线性激活函数 （如 sigmoid、ReLU）------ 这是 MLP 能处理非线性问题的关键！

用流程图展示 MLP 结构：

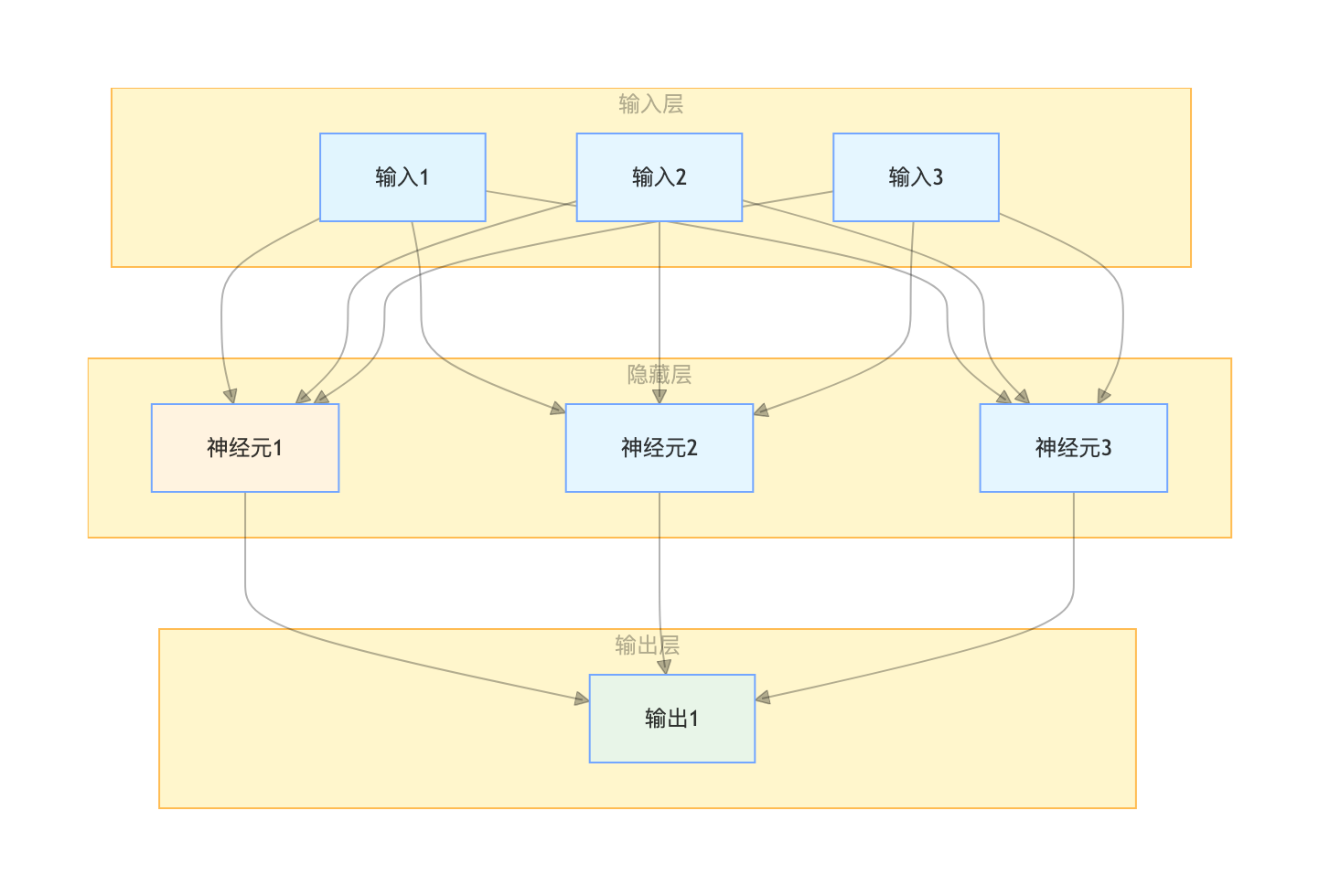
代码实现：多层感知器（解决 XOR 问题）

python 复制代码 
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色


# ==================== 多层感知器（MLP）类 ====================
class MLP:
    """多层感知器（1个隐藏层），用于解决线性不可分问题"""

    def __init__(self, input_dim, hidden_dim, output_dim):
        """
        初始化MLP权重和偏置
        input_dim: 输入维度（特征数）
        hidden_dim: 隐藏层神经元数量
        output_dim: 输出维度（分类/回归目标数）
        """
        # 输入层→隐藏层 权重（小随机数初始化）和偏置（全0）
        self.W1 = np.random.randn(input_dim, hidden_dim) * 0.01  # 缩放权重避免梯度消失
        self.b1 = np.zeros((1, hidden_dim))

        # 隐藏层→输出层 权重和偏置
        self.W2 = np.random.randn(hidden_dim, output_dim) * 0.01
        self.b2 = np.zeros((1, output_dim))

    def sigmoid(self, x):
        """sigmoid激活函数：将值压缩到0-1之间，引入非线性"""
        return 1 / (1 + np.exp(-x))

    def sigmoid_derivative(self, x):
        """sigmoid导数：用于反向传播计算梯度"""
        return x * (1 - x)

    def forward(self, X):
        """前向传播：从输入层到输出层的完整计算"""
        # 输入层→隐藏层：线性变换 + 激活
        self.z1 = np.dot(X, self.W1) + self.b1  # 线性输出
        self.a1 = self.sigmoid(self.z1)  # 隐藏层激活输出

        # 隐藏层→输出层：线性变换 + 激活
        self.z2 = np.dot(self.a1, self.W2) + self.b2  # 线性输出
        self.a2 = self.sigmoid(self.z2)  # 输出层激活输出

        return self.a2

    def backward(self, X, y, y_pred, learning_rate):
        """反向传播：计算梯度并更新权重/偏置"""
        m = X.shape[0]  # 样本数量，用于梯度归一化

        # 1. 计算输出层误差和梯度
        delta2 = (y_pred - y) * self.sigmoid_derivative(self.a2)  # 输出层误差项
        dW2 = np.dot(self.a1.T, delta2) / m  # W2的梯度
        db2 = np.sum(delta2, axis=0, keepdims=True) / m  # b2的梯度

        # 2. 计算隐藏层误差和梯度（反向传递）
        delta1 = np.dot(delta2, self.W2.T) * self.sigmoid_derivative(self.a1)  # 隐藏层误差项
        dW1 = np.dot(X.T, delta1) / m  # W1的梯度
        db1 = np.sum(delta1, axis=0, keepdims=True) / m  # b1的梯度

        # 3. 更新权重和偏置（梯度下降）
        self.W1 -= learning_rate * dW1
        self.b1 -= learning_rate * db1
        self.W2 -= learning_rate * dW2
        self.b2 -= learning_rate * db2

    def train(self, X, y, epochs=10000, learning_rate=0.1):
        """
        训练MLP
        X: 输入数据 (样本数, 特征数)
        y: 标签 (样本数, 输出维度)
        epochs: 训练轮数
        learning_rate: 学习率（梯度下降步长）
        """
        loss_history = []  # 记录每轮损失，用于可视化

        for epoch in range(epochs):
            # 前向传播得到预测值
            y_pred = self.forward(X)
            # 计算均方误差（回归/二分类损失）
            loss = np.mean((y_pred - y) ** 2)
            loss_history.append(loss)
            # 反向传播更新参数
            self.backward(X, y, y_pred, learning_rate)

            # 每1000轮打印一次训练进度
            if (epoch + 1) % 1000 == 0:
                print(f"Epoch {epoch + 1}, 损失: {loss:.6f}")

        return loss_history


# ==================== 测试代码：MLP解决XOR问题 ====================
if __name__ == "__main__":
    # 1. 准备XOR数据（线性不可分，单层感知器无法解决）
    X_xor = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    y_xor = np.array([[0], [1], [1], [0]])  # 调整为2维数组，匹配MLP输出维度

    # 2. 创建MLP模型（2输入特征，4个隐藏神经元，1个输出）
    mlp = MLP(input_dim=2, hidden_dim=4, output_dim=1)

    # 3. 训练模型（20000轮，学习率0.5）
    print("===== 开始训练MLP解决XOR问题 =====")
    loss_history = mlp.train(X_xor, y_xor, epochs=20000, learning_rate=0.5)

    # 4. 可视化训练结果
    plt.figure(figsize=(12, 5))

    # 子图1：训练损失曲线（展示收敛过程）
    plt.subplot(1, 2, 1)
    plt.plot(loss_history, 'r-', linewidth=2)
    plt.xlabel("训练轮数")
    plt.ylabel("均方误差")
    plt.title("MLP训练损失曲线（XOR问题）")
    plt.grid(True, alpha=0.3)

    # 子图2：MLP的决策边界（展示非线性分割能力）
    plt.subplot(1, 2, 2)
    # 创建网格用于绘制决策边界
    x_min, x_max = -0.5, 1.5
    y_min, y_max = -0.5, 1.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                         np.arange(y_min, y_max, 0.01))

    # 预测网格中每个点的输出
    Z = mlp.forward(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # 绘制决策边界填充图
    plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlGn)
    # 绘制XOR样本点（带黑色边框，更清晰）
    scatter = plt.scatter(X_xor[:, 0], X_xor[:, 1], c=y_xor.ravel(),
                          cmap=plt.cm.RdYlGn, edgecolors='black', s=100)
    plt.xlabel("特征1")
    plt.ylabel("特征2")
    plt.title("MLP解决XOR问题（决策边界）")
    plt.legend(*scatter.legend_elements(), title="标签")

    # 调整布局并显示图形
    plt.tight_layout()
    plt.show()

    # 5. 打印XOR问题的预测结果（验证MLP的效果）
    print("\n===== XOR问题预测结果 =====")
    y_pred = mlp.forward(X_xor)
    for xi, yi, pred in zip(X_xor, y_xor, y_pred):
        # 四舍五入后得到最终分类结果
        pred_rounded = round(pred[0])
        print(f"输入: {xi}, 真实值: {yi[0]}, 预测值: {pred[0]:.4f} (四舍五入: {pred_rounded})")

11.6 作为普适近似的 MLP

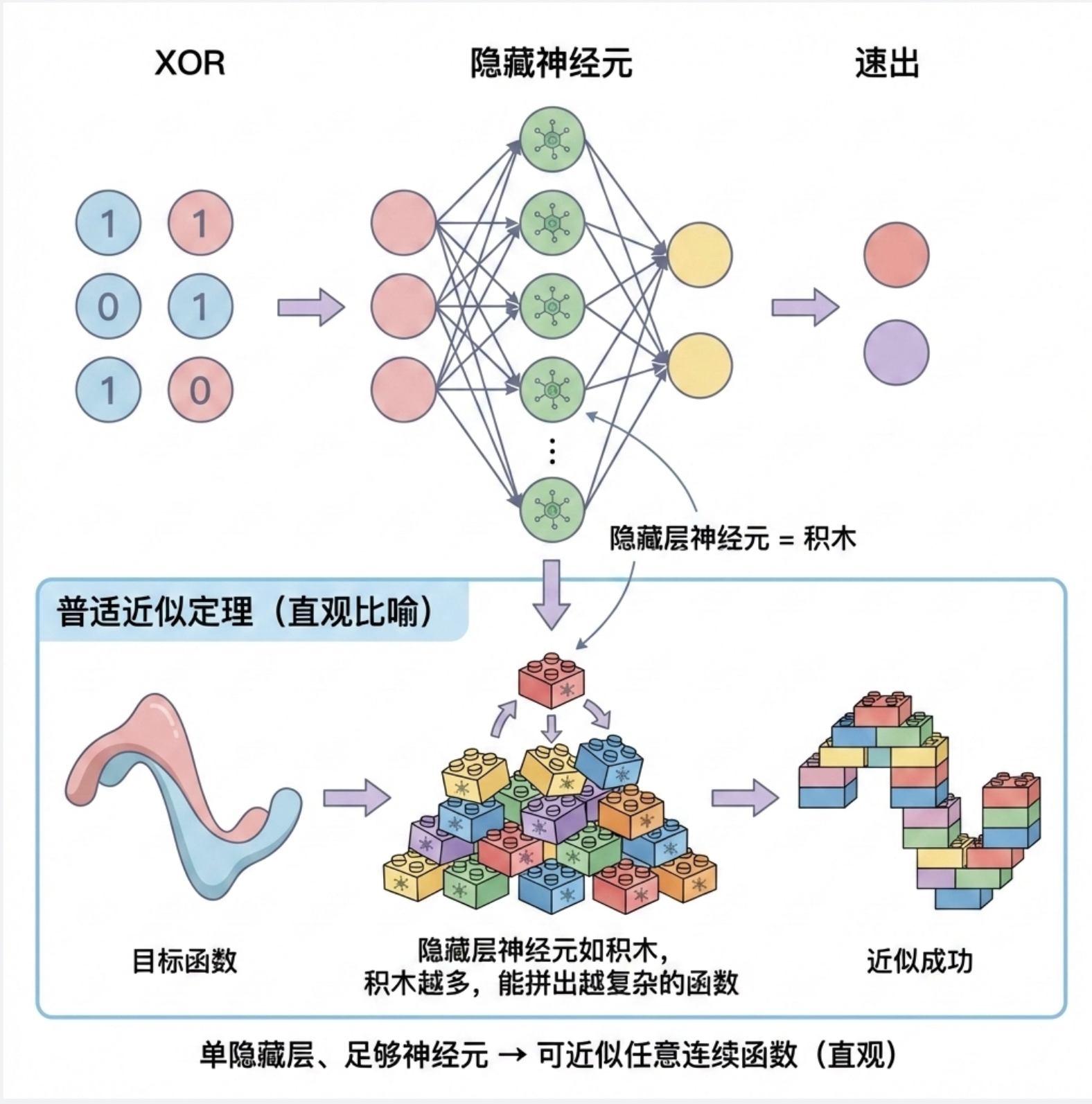
MLP 有一个强大的特性：普适近似定理。简单来说：

只要隐藏层有足够多的神经元，单隐藏层的 MLP 可以近似任何连续函数（不管多复杂）！

这就像用乐高积木拼东西：只要积木足够多，你可以拼出任何形状。MLP 的隐藏层神经元就是 "积木"，越多越能拟合复杂的函数。

代码实现：MLP 拟合非线性函数（可视化对比）

python 复制代码 
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色


# ==================== 多层感知器（MLP）类 ====================
class MLP:
    """多层感知器（1个隐藏层），用于拟合非线性函数"""

    def __init__(self, input_dim, hidden_dim, output_dim):
        """
        初始化MLP权重和偏置
        input_dim: 输入维度（特征数）
        hidden_dim: 隐藏层神经元数量
        output_dim: 输出维度（回归目标数）
        """
        # 输入层→隐藏层 权重（小随机数初始化）和偏置（全0）
        self.W1 = np.random.randn(input_dim, hidden_dim) * 0.01  # 缩放权重避免梯度消失
        self.b1 = np.zeros((1, hidden_dim))

        # 隐藏层→输出层 权重和偏置
        self.W2 = np.random.randn(hidden_dim, output_dim) * 0.01
        self.b2 = np.zeros((1, output_dim))

    def sigmoid(self, x):
        """sigmoid激活函数：引入非线性"""
        return 1 / (1 + np.exp(-x))

    def sigmoid_derivative(self, x):
        """sigmoid导数：用于反向传播计算梯度"""
        return x * (1 - x)

    def forward(self, X):
        """前向传播：从输入层到输出层的完整计算"""
        # 输入层→隐藏层：线性变换 + 激活
        self.z1 = np.dot(X, self.W1) + self.b1  # 线性输出
        self.a1 = self.sigmoid(self.z1)  # 隐藏层激活输出

        # 隐藏层→输出层：线性变换 + 激活
        self.z2 = np.dot(self.a1, self.W2) + self.b2  # 线性输出
        self.a2 = self.sigmoid(self.z2)  # 输出层激活输出

        # 缩放输出到sin(x)的范围（-1~1），提升拟合效果
        self.a2 = self.a2 * 2 - 1
        return self.a2

    def backward(self, X, y, y_pred, learning_rate):
        """反向传播：计算梯度并更新权重/偏置"""
        m = X.shape[0]  # 样本数量，用于梯度归一化

        # 1. 计算输出层误差和梯度（注意输出缩放后的误差调整）
        delta2 = (y_pred - y) * self.sigmoid_derivative((self.a2 + 1) / 2)  # 还原sigmoid输入计算导数
        dW2 = np.dot(self.a1.T, delta2) / m  # W2的梯度
        db2 = np.sum(delta2, axis=0, keepdims=True) / m  # b2的梯度

        # 2. 计算隐藏层误差和梯度（反向传递）
        delta1 = np.dot(delta2, self.W2.T) * self.sigmoid_derivative(self.a1)  # 隐藏层误差项
        dW1 = np.dot(X.T, delta1) / m  # W1的梯度
        db1 = np.sum(delta1, axis=0, keepdims=True) / m  # b1的梯度

        # 3. 更新权重和偏置（梯度下降）
        self.W1 -= learning_rate * dW1
        self.b1 -= learning_rate * db1
        self.W2 -= learning_rate * dW2
        self.b2 -= learning_rate * db2

    def train(self, X, y, epochs=10000, learning_rate=0.1):
        """
        训练MLP
        X: 输入数据 (样本数, 特征数)
        y: 标签 (样本数, 输出维度)
        epochs: 训练轮数
        learning_rate: 学习率（梯度下降步长）
        """
        loss_history = []  # 记录每轮损失，用于可视化

        for epoch in range(epochs):
            # 前向传播得到预测值
            y_pred = self.forward(X)
            # 计算均方误差（回归损失）
            loss = np.mean((y_pred - y) ** 2)
            loss_history.append(loss)
            # 反向传播更新参数
            self.backward(X, y, y_pred, learning_rate)

            # 每5000轮打印一次训练进度
            if (epoch + 1) % 5000 == 0:
                print(f"Epoch {epoch + 1}, 损失: {loss:.6f}")

        return loss_history


# ==================== 非线性数据生成函数 ====================
def generate_nonlinear_data(n_samples=100):
    """生成sin(x) + 高斯噪声的非线性回归数据"""
    # 固定随机种子，保证结果可复现
    np.random.seed(42)
    # 生成0~2π范围内的均匀采样点，reshape为2维数组（匹配MLP输入格式）
    X = np.linspace(0, 2 * np.pi, n_samples).reshape(-1, 1)
    # 生成sin(x) + 少量噪声，增加拟合难度
    y = np.sin(X) + 0.1 * np.random.randn(n_samples, 1)
    return X, y


# ==================== 测试代码：MLP拟合sin(x)非线性函数 ====================
if __name__ == "__main__":
    # 1. 生成非线性数据（sin(x) + 噪声）
    X, y = generate_nonlinear_data(n_samples=100)
    print("===== 生成sin(x)非线性数据完成 =====")

    # 2. 创建不同规模的MLP模型（对比隐藏层神经元数量的影响）
    mlp_small = MLP(input_dim=1, hidden_dim=5, output_dim=1)  # 小规模：5个隐藏神经元
    mlp_large = MLP(input_dim=1, hidden_dim=50, output_dim=1)  # 大规模：50个隐藏神经元

    # 3. 训练两个MLP模型
    print("\n===== 开始训练小规模MLP（5个隐藏神经元） =====")
    loss_small = mlp_small.train(X, y, epochs=50000, learning_rate=0.1)

    print("\n===== 开始训练大规模MLP（50个隐藏神经元） =====")
    loss_large = mlp_large.train(X, y, epochs=50000, learning_rate=0.1)

    # 4. 用训练好的模型预测
    y_pred_small = mlp_small.forward(X)
    y_pred_large = mlp_large.forward(X)

    # 5. 可视化对比结果
    plt.figure(figsize=(12, 8))

    # 子图1：训练损失对比（展示不同规模MLP的收敛效果）
    plt.subplot(2, 1, 1)
    plt.plot(loss_small, 'b-', label='5个隐藏神经元', alpha=0.7, linewidth=1.5)
    plt.plot(loss_large, 'r-', label='50个隐藏神经元', alpha=0.7, linewidth=1.5)
    plt.xlabel("训练轮数")
    plt.ylabel("均方误差")
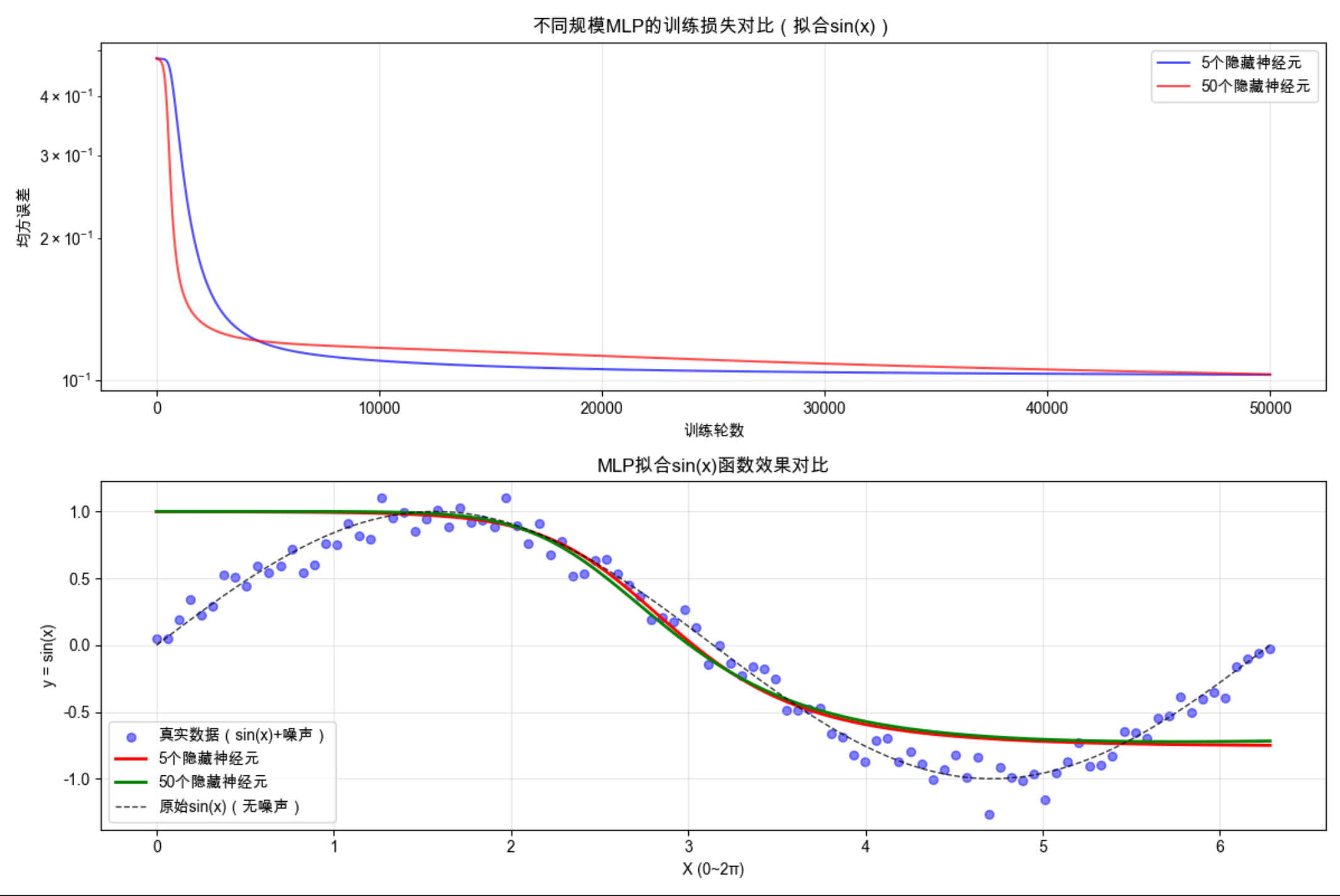
    plt.title("不同规模MLP的训练损失对比（拟合sin(x)）")
    plt.legend(loc='upper right')
    plt.grid(True, alpha=0.3)
    plt.yscale('log')  # 对数刻度，更清晰展示损失差异

    # 子图2：拟合效果对比（展示不同规模MLP的拟合精度）
    plt.subplot(2, 1, 2)
    # 绘制真实数据点
    plt.scatter(X, y, c='blue', alpha=0.5, label='真实数据（sin(x)+噪声）', s=30)
    # 绘制小规模MLP拟合曲线
    plt.plot(X, y_pred_small, 'r-', linewidth=2, label='5个隐藏神经元')
    # 绘制大规模MLP拟合曲线
    plt.plot(X, y_pred_large, 'g-', linewidth=2, label='50个隐藏神经元')
    # 绘制原始sin(x)曲线（无噪声）
    plt.plot(X, np.sin(X), 'k--', linewidth=1, label='原始sin(x)（无噪声）', alpha=0.8)
    plt.xlabel("X (0~2π)")
    plt.ylabel("y = sin(x)")
    plt.title("MLP拟合sin(x)函数效果对比")
    plt.legend(loc='lower left')
    plt.grid(True, alpha=0.3)

    # 调整布局并显示图形
    plt.tight_layout()
    plt.show()

    # 6. 计算并打印拟合误差（量化对比效果）
    mse_small = np.mean((y_pred_small - y) ** 2)
    mse_large = np.mean((y_pred_large - y) ** 2)
    print("\n===== 拟合效果量化对比 =====")
    print(f"小规模MLP（5个神经元）均方误差: {mse_small:.6f}")
    print(f"大规模MLP（50个神经元）均方误差: {mse_large:.6f}")
    print(f"误差提升比例: {((mse_small - mse_large) / mse_small * 100):.2f}%")

11.7 向后传播算法

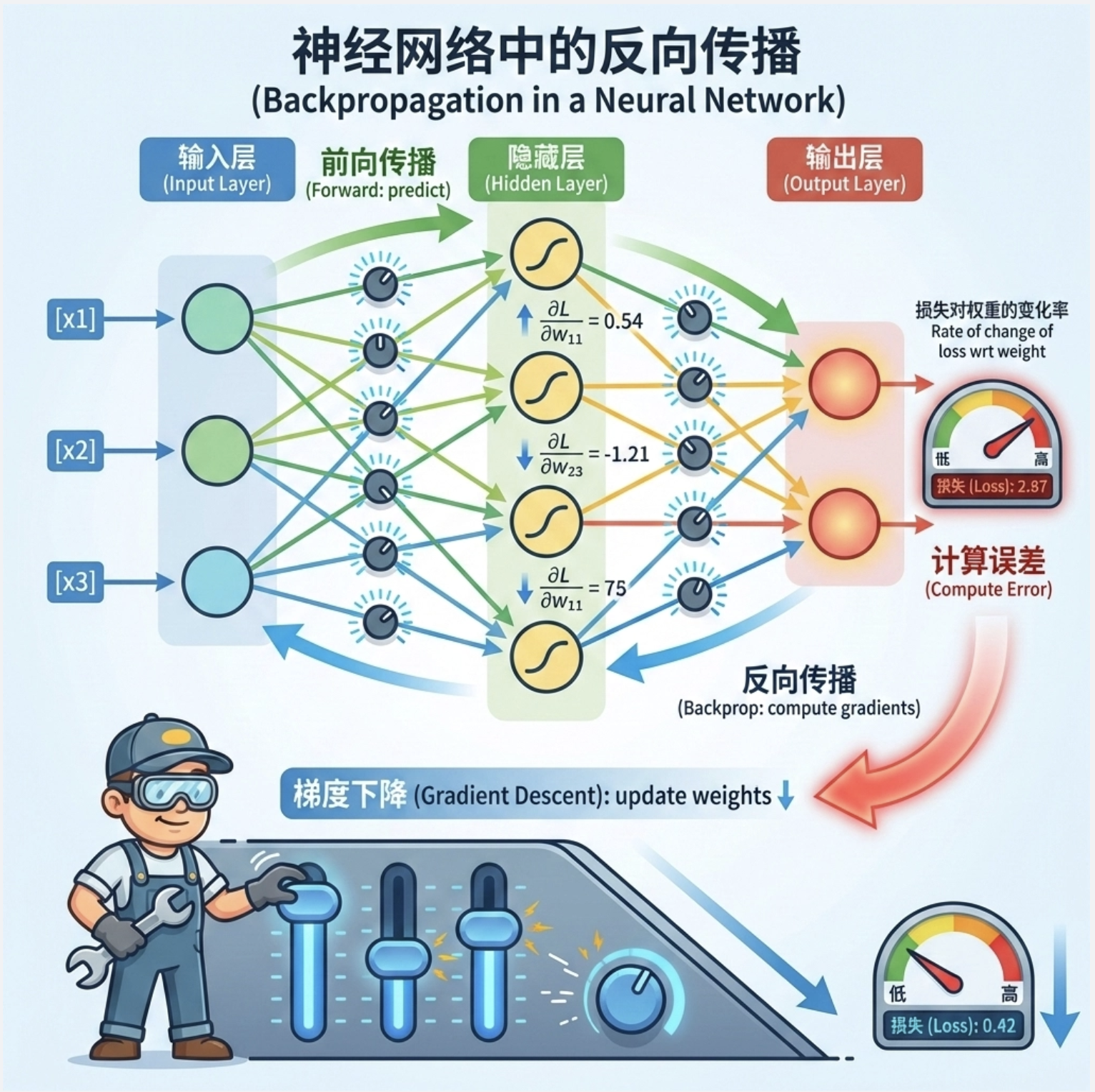
反向传播（Backpropagation）是训练 MLP 的核心算法，就像 "从结果倒推原因"：

  1. 前向传播：计算预测值，得到损失
  2. 反向传播：从输出层到输入层，逐层计算每个权重的梯度（损失对权重的变化率）
  3. 梯度下降：沿着梯度反方向更新权重，减小损失

11.7.1 非线性回归

前面的 sin (x) 拟合就是典型的非线性回归任务，MLP 通过反向传播学习函数规律。

11.7.2 两类判别式

二分类是 MLP 最常见的应用之一（如：判断邮件是否为垃圾邮件），输出层用 sigmoid 函数，输出 0-1 之间的概率值。

11.7.3 多类判别式

多分类任务（如：手写数字识别），输出层用 softmax 函数，输出每个类别的概率（总和为 1）。

11.7.4 多个隐藏层

增加隐藏层可以提升 MLP 的表达能力（深度学习的基础），但也更容易过拟合。

11.8 训练过程

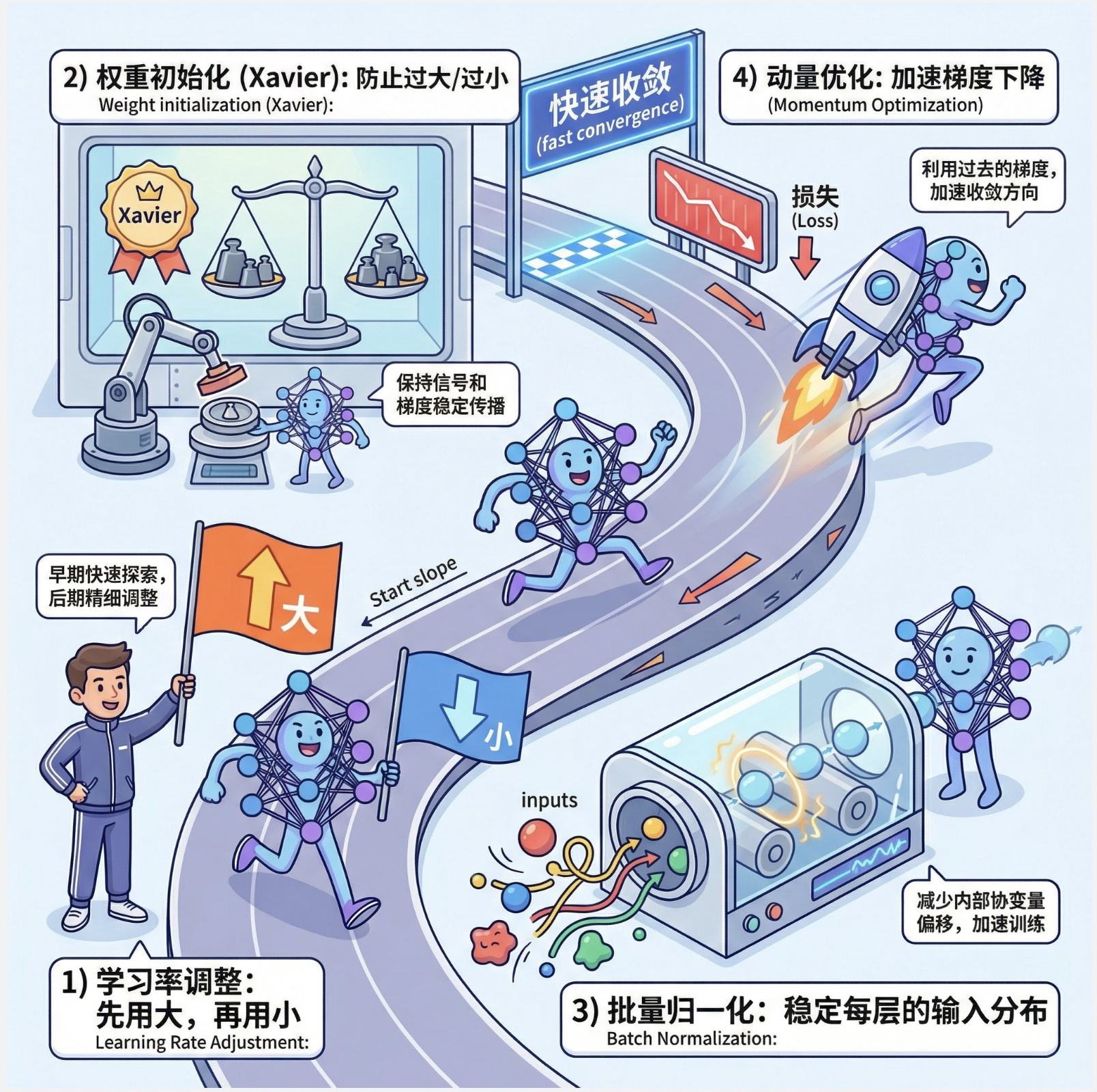
11.8.1 改善收敛性

训练 MLP 时，收敛慢是常见问题，可以通过这些方法改善：

  1. 学习率调整 ：先用大学习率，后用小学习率
  2. 权重初始化：避免权重过大 / 过小（如 Xavier 初始化）
  3. 批量归一化：让每层输入分布更稳定
  4. 动量优化：加速梯度下降

11.8.2 过分训练（过拟合）

过拟合就是 "学太死"------ 模型在训练数据上表现极好，但在新数据上表现差。

解决方法：

  • 早停法：训练过程中监控验证集损失，变差时停止
  • 正则化：给损失函数加惩罚项，限制权重大小
  • 数据增强：增加训练数据多样性
  • Dropout：训练时随机关闭部分神经元

11.8.3 构造网络

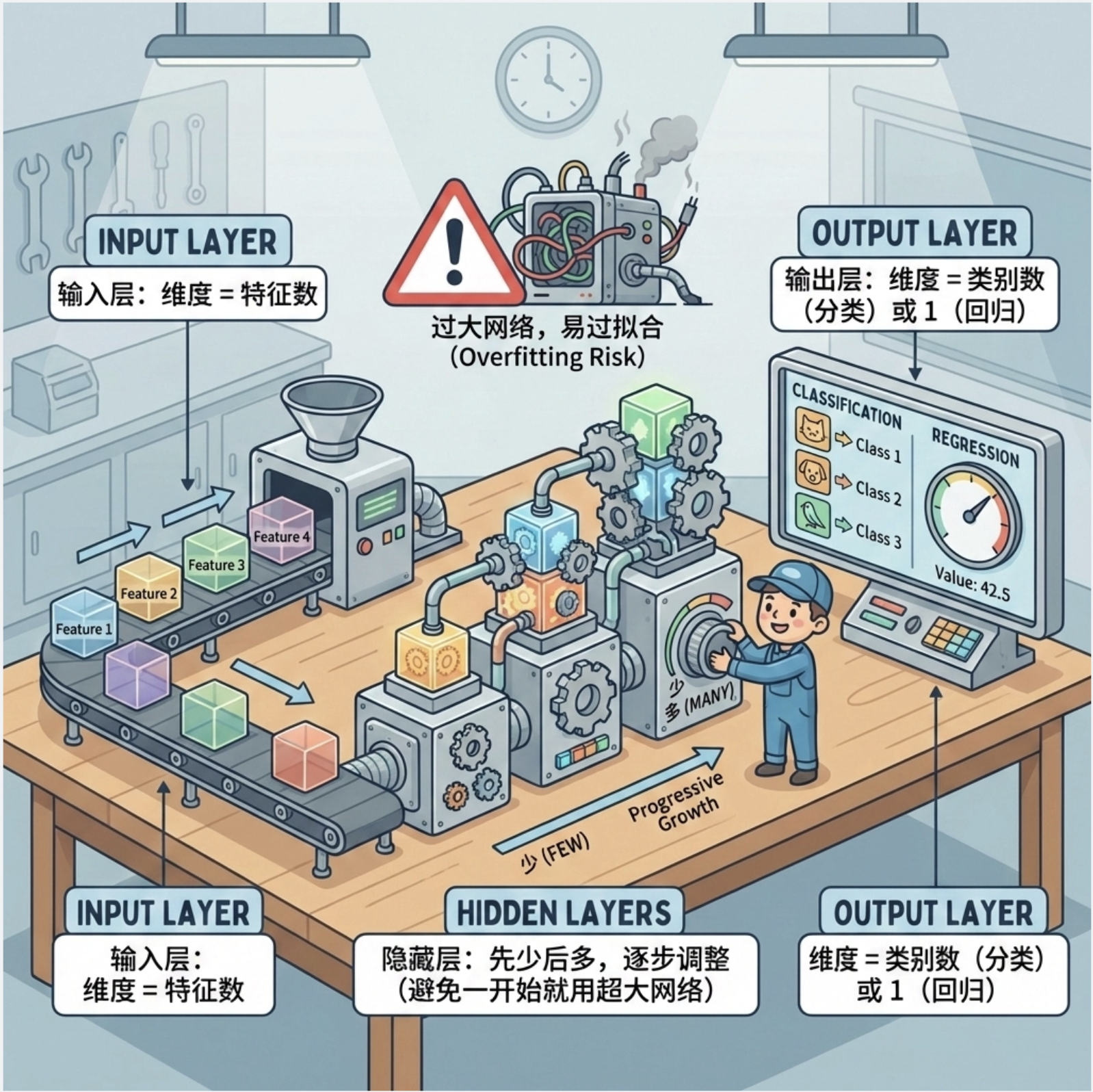
MLP 网络结构设计原则：

  • 输入层：维度 = 特征数
  • 输出层：维度 = 类别数（分类）或 1（回归）
  • 隐藏层：先少后多，逐步调整（避免一开始就用超大网络）

11.8.4 线索

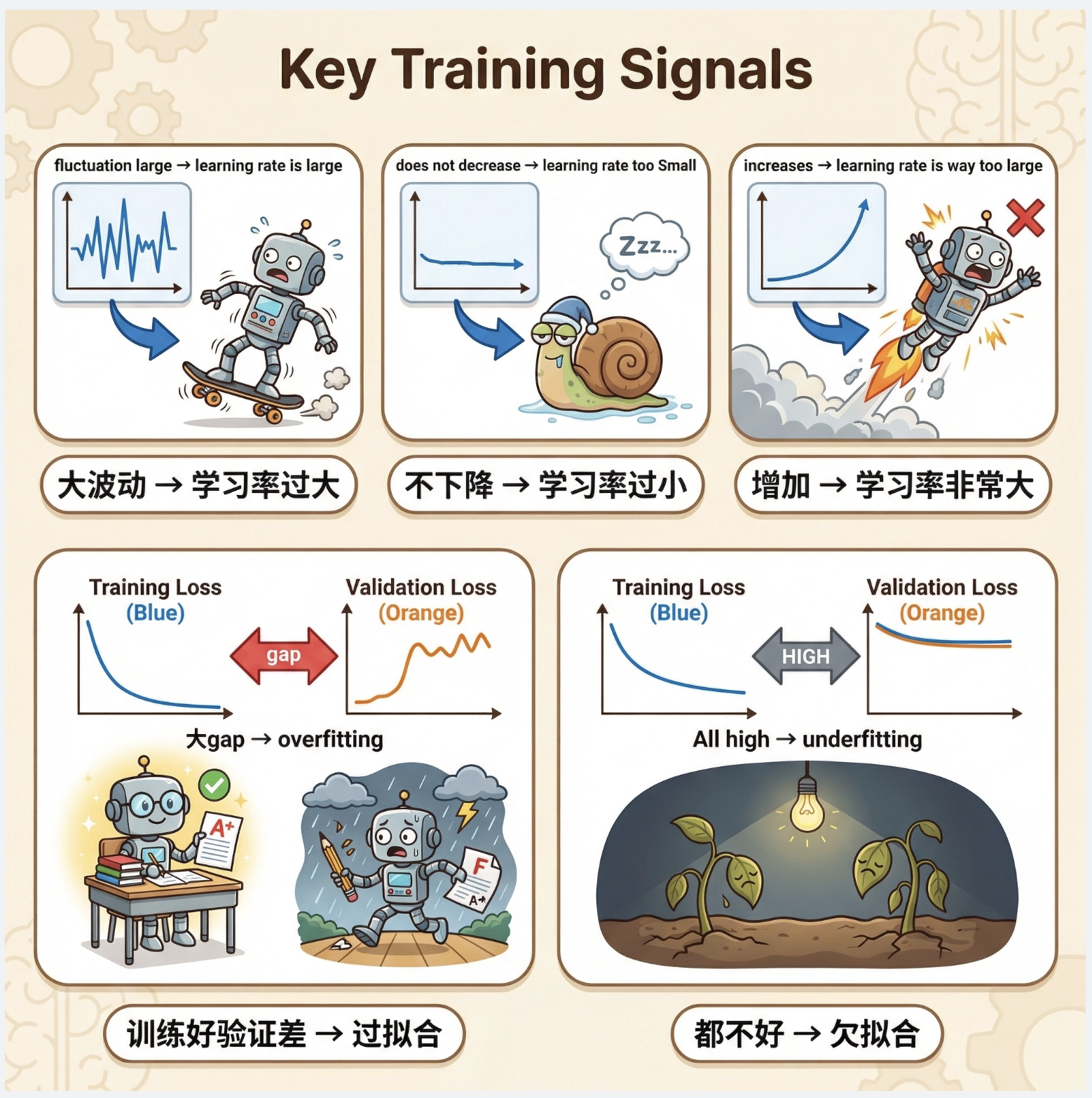
训练时的重要线索：

  • 损失曲线：持续下降→正常；波动大→学习率太大；不下降→学习率太小
  • 训练 / 验证损失：差距大→过拟合；都高→欠拟合

11.9 调整网络规模

网络规模（神经元数、层数）的调整策略：

  1. 从小规模开始，逐步增大
  2. 监控训练 / 验证损失：都高→增大网络；训练低 / 验证高→减小网络或加正则化
  3. 避免 "过度设计"：够用就好

11.10 学习的贝叶斯观点

从贝叶斯角度看，MLP 的学习过程就是：

  • 先验：对权重的初始假设（如：权重服从正态分布）
  • 似然：模型对数据的拟合程度
  • 后验：学习后的权重分布（结合先验和数据）

贝叶斯方法可以量化模型的不确定性，提升鲁棒性。

11.11 维度归约

维度归约（降维）是 MLP 的重要预处理步骤：

  • 减少特征数量，加速训练
  • 去除噪声和冗余信息
  • 常用方法：PCA、t-SNE、自编码器（MLP 的一种）

代码实现：MLP 自编码器降维

python 复制代码 
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt

# ==================== Mac系统Matplotlib中文显示配置 ====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']  # Mac原生支持的中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 强制指定中文字体
plt.rcParams['axes.facecolor'] = 'white'  # 设置画布背景色


# ==================== 基础MLP类（自编码器的父类） ====================
class MLP:
    """多层感知器基础类（作为自编码器的父类）"""

    def __init__(self, input_dim, hidden_dim, output_dim):
        # 初始化权重（小随机数）和偏置（全0）
        self.W1 = np.random.randn(input_dim, hidden_dim) * 0.01
        self.b1 = np.zeros((1, hidden_dim))
        self.W2 = np.random.randn(hidden_dim, output_dim) * 0.01
        self.b2 = np.zeros((1, output_dim))

    def sigmoid(self, x):
        """sigmoid激活函数：压缩值到0-1之间，适合自编码器"""
        return 1 / (1 + np.exp(-x))

    def sigmoid_derivative(self, x):
        """sigmoid导数：用于反向传播"""
        return x * (1 - x)

    def forward(self, X):
        """前向传播（自编码器完整重构过程）"""
        # 编码：输入→隐藏
        self.z1 = np.dot(X, self.W1) + self.b1
        self.a1 = self.sigmoid(self.z1)

        # 解码：隐藏→输出
        self.z2 = np.dot(self.a1, self.W2) + self.b2
        self.a2 = self.sigmoid(self.z2)

        return self.a2

    def backward(self, X, y, y_pred, learning_rate):
        """反向传播：计算梯度并更新权重"""
        m = X.shape[0]  # 样本数

        # 输出层误差和梯度
        delta2 = (y_pred - y) * self.sigmoid_derivative(self.a2)
        dW2 = np.dot(self.a1.T, delta2) / m
        db2 = np.sum(delta2, axis=0, keepdims=True) / m

        # 隐藏层误差和梯度
        delta1 = np.dot(delta2, self.W2.T) * self.sigmoid_derivative(self.a1)
        dW1 = np.dot(X.T, delta1) / m
        db1 = np.sum(delta1, axis=0, keepdims=True) / m

        # 更新权重和偏置
        self.W1 -= learning_rate * dW1
        self.b1 -= learning_rate * db1
        self.W2 -= learning_rate * dW2
        self.b2 -= learning_rate * db2

    def train(self, X, y, epochs=10000, learning_rate=0.1):
        """训练自编码器（重构输入）"""
        loss_history = []

        for epoch in range(epochs):
            # 前向传播得到重构结果
            y_pred = self.forward(X)
            # 计算重构损失（均方误差）
            loss = np.mean((y_pred - y) ** 2)
            loss_history.append(loss)

            # 反向传播更新参数
            self.backward(X, y, y_pred, learning_rate)

            # 每1000轮打印进度
            if (epoch + 1) % 1000 == 0:
                print(f"Epoch {epoch + 1}, 重构损失: {loss:.6f}")

        return loss_history


# ==================== 自编码器类（继承MLP） ====================
class Autoencoder(MLP):
    """自编码器（专门用于降维的MLP）"""

    def __init__(self, input_dim, hidden_dim):
        """
        初始化自编码器
        input_dim: 输入维度（高维数据维度）
        hidden_dim: 隐藏层维度（降维后的维度）
        """
        # 调用父类初始化（输出维度=输入维度，实现重构）
        super().__init__(input_dim, hidden_dim, input_dim)

    def encode(self, X):
        """编码：高维→低维（降维核心方法）"""
        z1 = np.dot(X, self.W1) + self.b1
        a1 = self.sigmoid(z1)
        return a1

    def decode(self, X):
        """解码：低维→高维（重构）"""
        z2 = np.dot(X, self.W2) + self.b2
        a2 = self.sigmoid(z2)
        return a2


# ==================== 测试代码：自编码器降维 ====================
if __name__ == "__main__":
    # 1. 生成模拟高维数据（10维，100个样本）
    np.random.seed(42)  # 固定随机种子，结果可复现
    X_high = np.random.randn(100, 10)  # 10维原始数据
    # 数据归一化到0-1区间（适合sigmoid激活）
    X_high = (X_high - X_high.min()) / (X_high.max() - X_high.min())

    print("===== 生成10维模拟数据完成 =====")

    # 2. 创建自编码器（10维→2维→10维）
    autoencoder = Autoencoder(input_dim=10, hidden_dim=2)

    # 3. 训练自编码器（目标是重构输入数据）
    print("\n===== 开始训练自编码器 =====")
    loss_history = autoencoder.train(X_high, X_high, epochs=10000, learning_rate=0.5)

    # 4. 对高维数据编码降维（10维→2维）
    X_low = autoencoder.encode(X_high)
    print("\n===== 完成10维数据→2维降维 =====")

    # 5. 可视化结果
    plt.figure(figsize=(10, 4))

    # 子图1：训练损失曲线（展示重构效果收敛过程）
    plt.subplot(1, 2, 1)
    plt.plot(loss_history, 'purple', linewidth=2)
    plt.xlabel("训练轮数")
    plt.ylabel("重构损失（均方误差）")
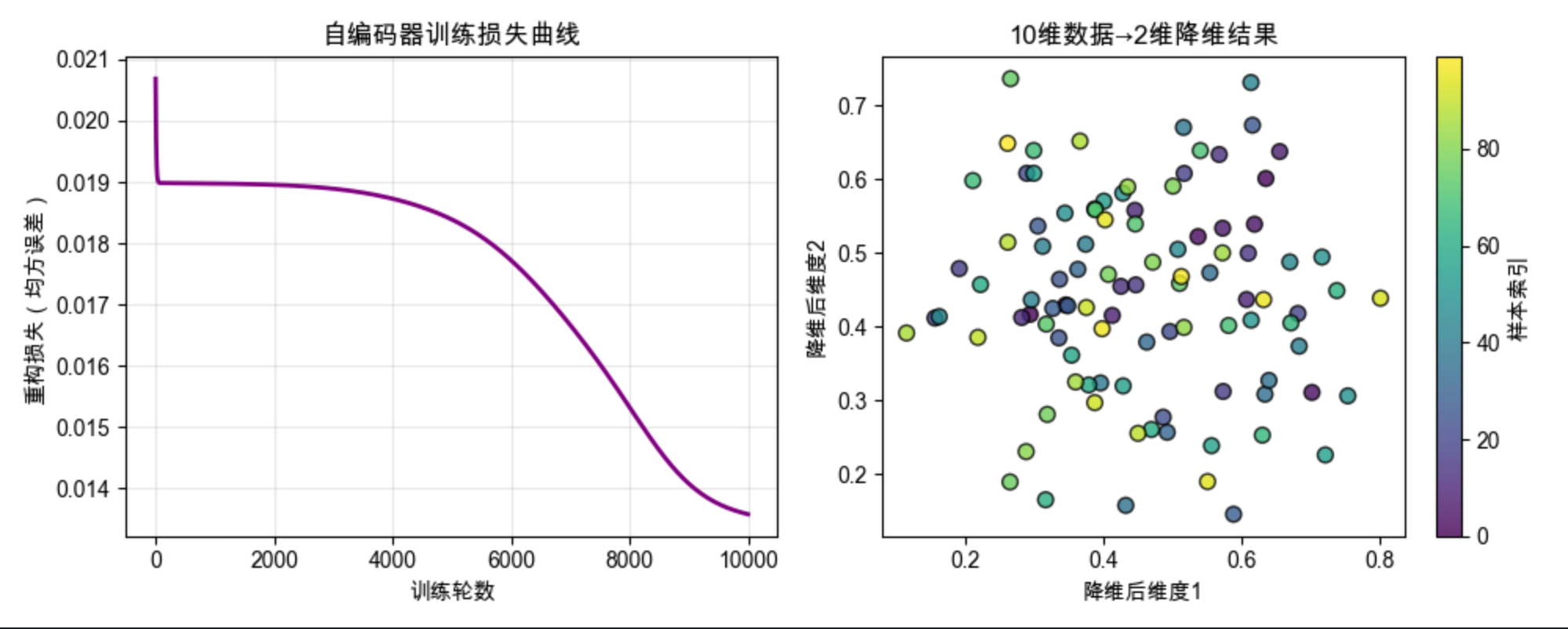
    plt.title("自编码器训练损失曲线")
    plt.grid(True, alpha=0.3)

    # 子图2：降维结果可视化（2维散点图）
    plt.subplot(1, 2, 2)
    scatter = plt.scatter(
        X_low[:, 0], X_low[:, 1],
        c=np.arange(100),  # 用样本索引着色
        cmap='viridis',  # 配色方案
        s=50,  # 点大小
        edgecolors='black',  # 黑色边框，更清晰
        alpha=0.8  # 透明度
    )
    plt.xlabel("降维后维度1")
    plt.ylabel("降维后维度2")
    plt.title("10维数据→2维降维结果")
    # 添加颜色条（标注样本索引）
    cbar = plt.colorbar(scatter, label="样本索引")

    # 调整布局并显示
    plt.tight_layout()
    plt.show()

    # 6. 量化评估降维效果（计算重构误差）
    X_recon = autoencoder.forward(X_high)  # 重构高维数据
    recon_error = np.mean((X_recon - X_high) ** 2)
    print(f"\n===== 降维效果评估 =====")
    print(f"平均重构误差: {recon_error:.6f}")
    print(f"降维维度：10维 → 2维（压缩比5:1）")

11.12 学习时间

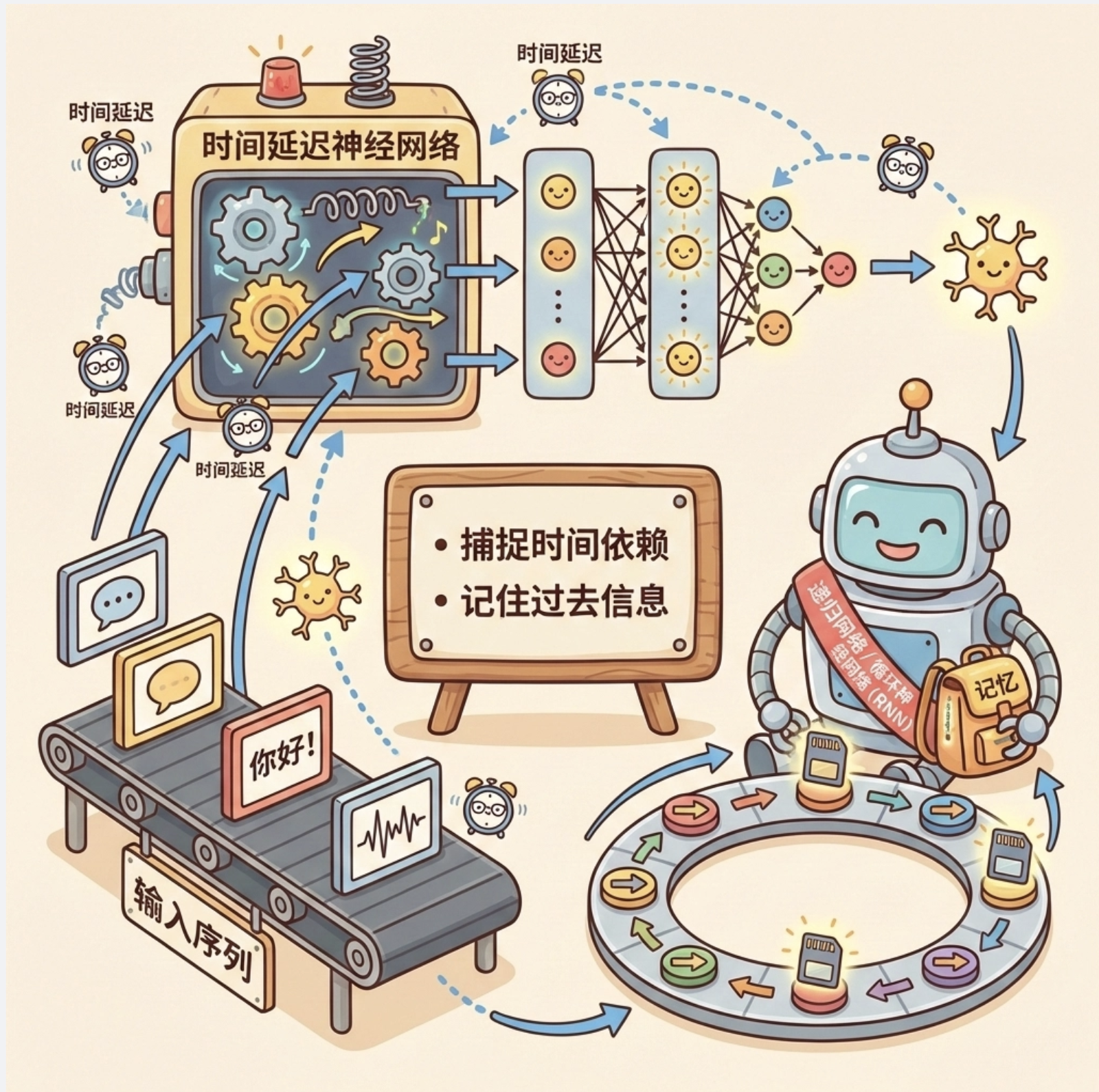
11.12.1 时间延迟神经网络

处理时序数据（如语音、文本），在输入中加入时间延迟，捕捉时间依赖。

11.12.2 递归网络

循环神经网络（RNN）是处理时序数据的专用网络，神经元可以**"记住" 过去的信息**。

11.13 深度学习

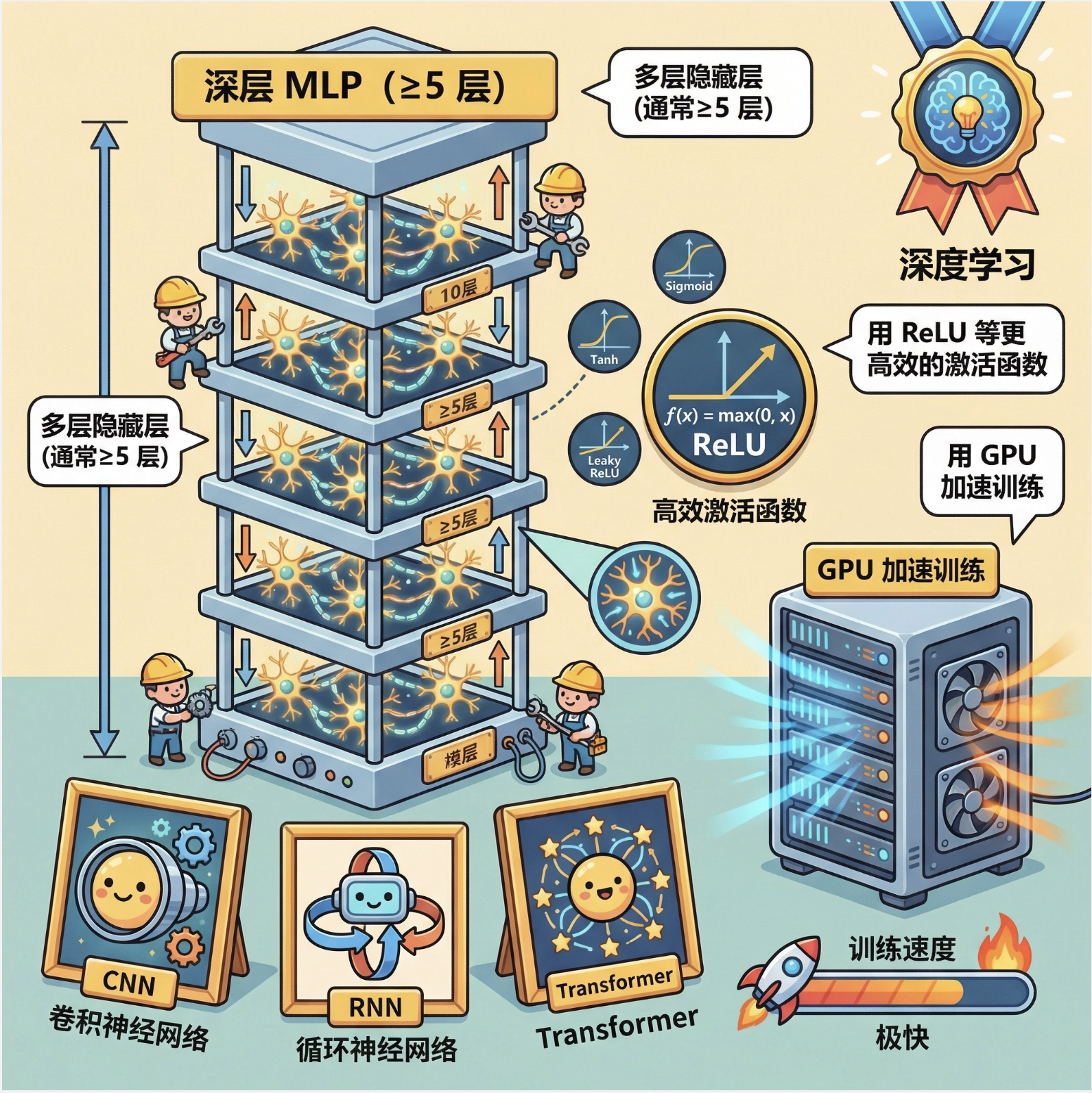
深度学习就是 "深层的 MLP"：

  • 多层隐藏层（通常≥5 层）
  • 用 ReLU 等更高效的激活函数
  • 用 GPU 加速训练
  • 代表模型：CNN、RNN、Transformer

11.14 注释

本文所有代码均基于 NumPy 和 Matplotlib 实现，未使用高级框架（如 TensorFlow/PyTorch），目的是让大家理解 MLP 的底层原理。实际应用中，建议使用成熟框架提升效率。

11.15 习题

  1. 修改感知器代码，尝试学习 OR 函数和 XOR 函数，观察结果差异。
  2. 调整 MLP 的隐藏层神经元数，看看对 XOR 问题拟合效果的影响。
  3. 给 MLP 加入 L2 正则化，解决过拟合问题。
  4. 用 MLP 实现手写数字识别（MNIST 数据集）。

11.16 参考文献

  1. 《机器学习导论》（Ethem Alpaydin 著）
  2. 《神经网络与深度学习》（邱锡鹏 著）
  3. Bishop, C. M. (2006). Pattern Recognition and Machine Learning.

总结

1.核心概念 ：单个感知器只能处理线性可分问题，多层感知器（MLP）通过堆叠感知器 + 非线性激活函数，可处理非线性问题，且满足普适近似定理。

2.关键算法 ：反向传播是 MLP 的核心训练算法，通过 "前向计算损失，反向计算梯度，梯度下降更新权重" 完成学习。

3.实践要点 ：训练 MLP 时需关注收敛性和过拟合问题，可通过调整学习率、正则化、早停法等优化，网络规模应 "够用就好"，避免过度设计。

希望本文能帮助你真正理解多层感知器！所有代码均可直接运行，建议动手调试参数，感受不同设置对结果的影响。如有问题，欢迎在评论区交流～

相关推荐
九.九14 小时前
ops-transformer：AI 处理器上的高性能 Transformer 算子库
人工智能·深度学习·transformer
春日见14 小时前
拉取与合并：如何让个人分支既包含你昨天的修改，也包含 develop 最新更新
大数据·人工智能·深度学习·elasticsearch·搜索引擎
恋猫de小郭14 小时前
AI 在提高你工作效率的同时，也一直在增加你的疲惫和焦虑
前端·人工智能·ai编程
寻寻觅觅☆14 小时前
东华OJ-基础题-106-大整数相加（C++）
开发语言·c++·算法
YJlio15 小时前
1.7 通过 Sysinternals Live 在线运行工具：不下载也能用的“云端工具箱”
c语言·网络·python·数码相机·ios·django·iphone
deephub15 小时前
Agent Lightning：微软开源的框架无关 Agent 训练方案，LangChain/AutoGen 都能用
人工智能·microsoft·langchain·大语言模型·agent·强化学习
偷吃的耗子15 小时前
【CNN算法理解】：三、AlexNet 训练模块(附代码)
深度学习·算法·cnn
l1t15 小时前
在wsl的python 3.14.3容器中使用databend包
开发语言·数据库·python·databend
大模型RAG和Agent技术实践15 小时前
从零构建本地AI合同审查系统：架构设计与流式交互实战（完整源代码）
人工智能·交互·智能合同审核
老邋遢15 小时前
第三章-AI知识扫盲看这一篇就够了
人工智能
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03243 行 microGPT：把“训练 + 推理”拆到骨头里04Zsh/Bash Conda设置延迟启动，启动速度优化05openclaw配置教程（linux+局域网ollama）06openclaw 配置飞书 报错 应用未建立长连接07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南08UV安装并设置国内源09MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法10冰达ROS机器人快速使用指南