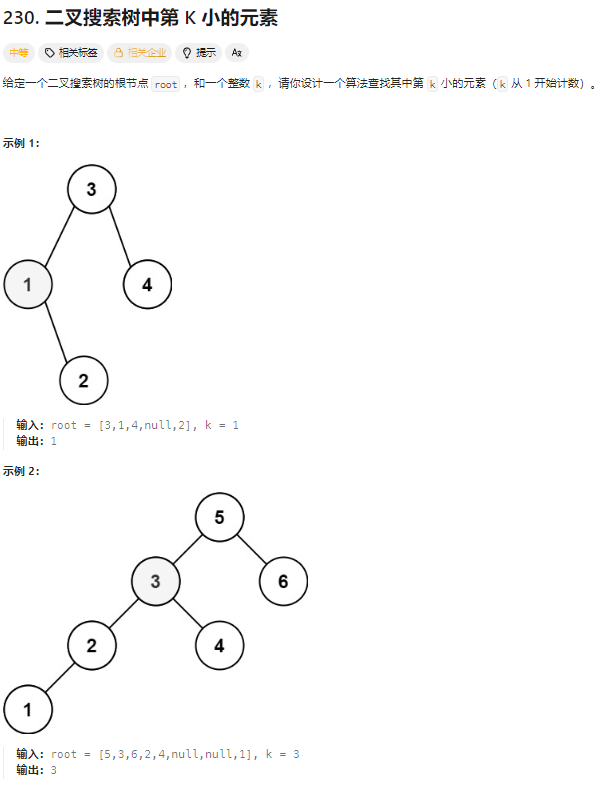
leetcode hot100 230. 二叉搜索树中第 K 小的元素 medium

二叉搜索树的中序遍历为递增序列。
本题可被转化为求中序遍历的第 k 个节点。

递归在"往回走 "的过程中，才真正开始了"数数 "的工作

递归是"深入 "，回溯才是"点名"

二叉搜索树中，最小的元素在最左边的深处。

dfs(node.left) 不是在数数，而是在找路。一直在往左钻，直到钻不动为止（遇到 None）。
当左边到底了：递归开始"回溯"（返回）。
回到父节点时：就是中序遍历中"左-中-右"的"中"。这时候，当前节点就是此时剩余数字里最小的那一个

示例：

python 复制代码

	   4          <-- 第一层 (根节点)
     /   \
    2     6       <-- 第二层
   / \   / \
  1   3 5   7     <-- 第三层 (叶子节点)

想象一个小球从根节点 4 出发：

深入最左：球必须先滚到最左边的 1。

回弹点名：碰到 1，点名（k=5→4k=5 \rightarrow 4k=5→4）。

回弹到 2，点名（k=4→3k=4 \rightarrow 3k=4→3）。

滚向 2 的右边碰到 3，点名（k=3→2k=3 \rightarrow 2k=3→2）。

大回弹到 4，点名（k=2→1k=2 \rightarrow 1k=2→1）。

滚向 4 的右子树，先钻到该子树的最左边，碰到 5，点名（k=1→0k=1 \rightarrow 0k=1→0）找到了！

python 复制代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        self.k = k # 把 k 存成实例变量，方便子函数修改
        self.res = 0 

        def dfs(node):
            if not node or k == 0:
                return    # 中断、结束

            dfs(node.left)  # 左子树递归，先检查左子树

            self.k -= 1       # 回到根节点，继续K-1，并判断根节点是不是第k个
            if self.k == 0:
                self.res = node.val
                return 

            dfs(node.right)  # 右子树递归，检查右子树

        dfs(root)
        return self.res

时间复杂度：O(n)，其中 n 是二叉树的节点个数。

空间复杂度：O(h)，其中 h 是二叉树的高度。递归需要 O(h) 的栈空间。最坏情况下，二叉树退化成一条链，递归需要 O(n) 的栈空间。