参考b站徐小湛老师视频做的线性代数学习笔记,仅供学习使用
第一节 二阶与三阶行列式
一、二元线性方程组与二阶行列式
行列式的概念是从解线性方程组的问题中引入的。
解二元线性方程组 { a 11 x 1 + a 12 x 2 = b 1 a 21 x 1 + a 22 x 2 = b 2 \begin{cases}a_{11}x_{1}+a_{12}x_{2}=b_{1}\\ a_{21}x_{1}+a_{22}x_{2}=b_{2}\end{cases} {a11x1+a12x2=b1a21x1+a22x2=b2,
为了方便记忆解的形式与变量系数的关系,引入行列式记号来表示两个乘积的差:
∣ a 11 a 12 a 21 a 22 ∣ = a 11 a 22 − a 12 a 21 \begin{vmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{vmatrix}=a_{11} a_{22}-a_{12}a_{21} a11a21a12a22 =a11a22−a12a21
这是由4个元素构成的二阶行列式。
它的计算规则是:主对角线上的两个数 a 11 a_{11} a11 和 a 22 a_{22} a22 的乘积,减去次对角线上的两个数 a 12 a_{12} a12 和 a 21 a_{21} a21 的乘积。
例如, ∣ 2 − 1 3 7 ∣ = 2 × 7 − ( − 1 ) × 3 = 17 \begin{vmatrix}2 & -1 \\ 3 & 7\end{vmatrix}=2 \times 7-(-1) \times 3=17 23−17 =2×7−(−1)×3=17。
命题(二元线性方程组的克拉默法则):
设二元线性方程组 { a 11 x 1 + a 12 x 2 = b 1 a 21 x 1 + a 22 x 2 = b 2 \begin{cases}a_{11} x_{1}+a_{12} x_{2}=b_{1}\\ a_{21} x_{1}+a_{22} x_{2}=b_{2}\end{cases} {a11x1+a12x2=b1a21x1+a22x2=b2 的系数行列式 D = ∣ a 11 a 12 a 21 a 22 ∣ ≠ 0 D=\begin{vmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{vmatrix}\neq 0 D= a11a21a12a22 =0,
则方程组有唯一解: x 1 = D 1 D = ∣ b 1 a 12 b 2 a 22 ∣ ∣ a 11 a 12 a 21 a 22 ∣ , x 2 = D 2 D = ∣ a 11 b 1 a 21 b 2 ∣ ∣ a 11 a 12 a 21 a 22 ∣ x_{1}=\frac{D_{1}}{D}=\frac{\begin{vmatrix}b_{1} & a_{12}\\ b_{2} & a_{22}\end{vmatrix}}{\begin{vmatrix}a_{11} & a_{12}\\ a_{21} & a_{22}\end{vmatrix}}, x_{2}=\frac{D_{2}}{D}=\frac{\begin{vmatrix}a_{11} & b_{1}\\ a_{21} & b_{2}\end{vmatrix}}{\begin{vmatrix}a_{11} & a_{12}\\ a_{21} & a_{22}\end{vmatrix}} x1=DD1= a11a21a12a22 b1b2a12a22 ,x2=DD2= a11a21a12a22 a11a21b1b2 。
二、三元线性方程组与三阶行列式
三阶行列式的概念与三元线性方程组的解的表达式有关。
解三元线性方程组
{ a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 = b 3 \begin{cases}a_{11} x_{1}+a_{12} x_{2}+a_{13} x_{3}=b_{1}\\ a_{21} x_{1}+a_{22} x_{2}+a_{23} x_{3}=b_{2}\\ a_{31} x_{1}+a_{32} x_{2}+a_{33} x_{3}=b_{3}\end{cases} ⎩ ⎨ ⎧a11x1+a12x2+a13x3=b1a21x1+a22x2+a23x3=b2a31x1+a32x2+a33x3=b3

同二元方程的解一样为了便于记忆,我们引入三阶行列式来表示这6项乘积的代数和:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 11 a 23 a 32 − a 12 a 21 a 33 − a 13 a 22 a 31 \left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31} a11a21a31a12a22a32a13a23a33 =a11a22a33+a12a23a31+a13a21a32−a11a23a32−a12a21a33−a13a22a31
这9个元素构成一个3行3列的三阶行列式。
元素 a i j a_{ij} aij 位于行列式的第i行,第j列(i和j分别是该元素的行标和列标)。
行列式的展开式是6项的代数和,其中每一项都是不同行,不同列的三个数的乘积,其中3项带正号,3项带负号。
可用以下图形来示意各项乘积的符号取法(对角线法则)。
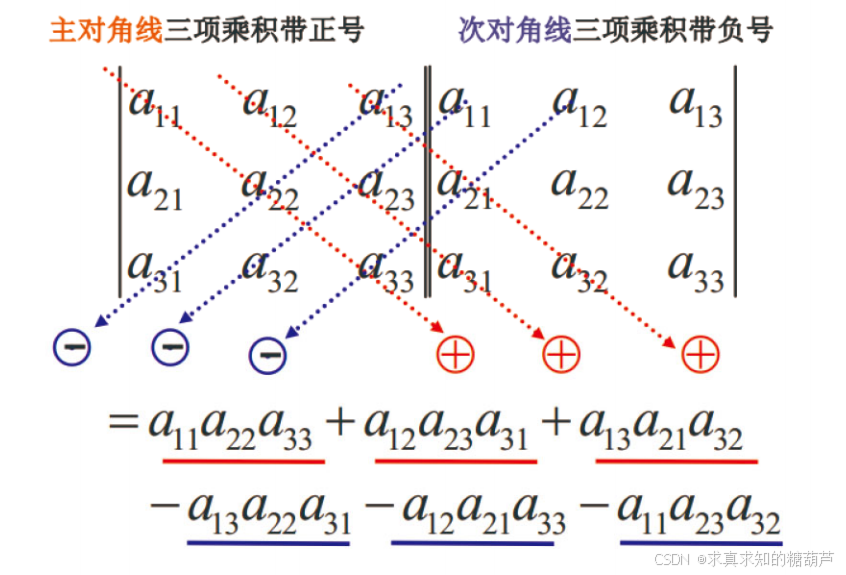
- 主对角线三项乘积带正号
- 次对角线三项乘积带负号
= a 11 a 22 a 33 ‾ + a 12 a 23 a 31 ‾ + a 13 a 21 a 32 ‾ − a 13 a 22 a 31 ‾ − a 12 a 21 a 33 ‾ − a 11 a 23 a 32 ‾ \begin{array}{l} =\underline{a_{11} a_{22} a_{33}}+\underline{a_{12} a_{23} a_{31}}+\underline{a_{13} a_{21} a_{32}} \\ -\underline{a_{13} a_{22} a_{31}}-\underline{a_{12} a_{21} a_{33}}-\underline{a_{11} a_{23} a_{32}} \end{array} =a11a22a33+a12a23a31+a13a21a32−a13a22a31−a12a21a33−a11a23a32
Rule of Sarrus 沙路法则:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31 − a 12 a 21 a 33 − a 11 a 23 a 32 \left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-a_{13} a_{22} a_{31}-a_{12} a_{21} a_{33}-a_{11} a_{23} a_{32} a11a21a31a12a22a32a13a23a33 =a11a22a33+a12a23a31+a13a21a32−a13a22a31−a12a21a33−a11a23a32
三、三元线性方程组的克拉默法则
命题(三元线性方程组的克拉默法则)系数行列式的值不为零,方程组有唯一解,并且给出显式解公式:
设三元线性方程组
{ a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 = b 3 \begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}=b_{1}\\ a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}=b_{2}\\ a_{31}x_{1}+a_{32}x_{2}+a_{33}x_{3}=b_{3}\end{cases} ⎩ ⎨ ⎧a11x1+a12x2+a13x3=b1a21x1+a22x2+a23x3=b2a31x1+a32x2+a33x3=b3
系数行列式 D = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ ≠ 0 D=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{vmatrix}\neq 0 D= a11a21a31a12a22a32a13a23a33 =0,
则方程组有唯一解:
x 1 = D 1 D = ∣ b 1 a 12 a 13 b 2 a 22 a 23 b 3 a 32 a 33 ∣ ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ , x 2 = D 2 D = ∣ a 11 b 1 a 13 a 21 b 2 a 23 a 31 b 3 a 33 ∣ ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ , x 3 = D 3 D = ∣ a 11 a 12 b 1 a 21 a 22 b 2 a 31 a 32 b 3 ∣ ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ x_{1}=\frac{D_{1}}{D}=\frac{\begin{vmatrix}b_{1}&a_{12}&a_{13}\\ b_{2}&a_{22}&a_{23}\\ b_{3}&a_{32}&a_{33}\end{vmatrix}}{\begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{vmatrix}},x_{2}=\frac{D_{2}}{D}=\frac{\begin{vmatrix}a_{11}&b_{1}&a_{13}\\ a_{21}&b_{2}&a_{23}\\ a_{31}&b_{3}&a_{33}\end{vmatrix}}{\begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{vmatrix}},x_{3}=\frac{D_{3}}{D}=\frac{\begin{vmatrix}a_{11}&a_{12}&b_{1}\\ a_{21}&a_{22}&b_{2}\\ a_{31}&a_{32}&b_{3}\end{vmatrix}}{\begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{vmatrix}} x1=DD1= a11a21a31a12a22a32a13a23a33 b1b2b3a12a22a32a13a23a33 ,x2=DD2= a11a21a31a12a22a32a13a23a33 a11a21a31b1b2b3a13a23a33 ,x3=DD3= a11a21a31a12a22a32a13a23a33 a11a21a31a12a22a32b1b2b3
其中 D i D_{i} Di 是将系数行列式D的第i列用方程组右端的常数 b 1 , b 2 b_{1},b_{2} b1,b2 和 b 3 b_{3} b3 取代后的三阶行列式(i=1,2,3)。
例验证等式: ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 ∣ a 22 a 23 a 32 a 33 ∣ − a 12 ∣ a 21 a 23 a 31 a 33 ∣ + a 13 ∣ a 21 a 22 a 31 a 32 ∣ \begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{vmatrix}=a_{11}\begin{vmatrix}a_{22}&a_{23}\\ a_{32}&a_{33}\end{vmatrix}-a_{12}\begin{vmatrix}a_{21}&a_{23}\\ a_{31}&a_{33}\end{vmatrix}+a_{13}\begin{vmatrix}a_{21}&a_{22}\\ a_{31}&a_{32}\end{vmatrix} a11a21a31a12a22a32a13a23a33 =a11 a22a32a23a33 −a12 a21a31a23a33 +a13 a21a31a22a32 。
解:
a 11 ∣ a 22 a 23 a 32 a 33 ∣ − a 12 ∣ a 21 a 23 a 31 a 33 ∣ + a 13 ∣ a 21 a 22 a 31 a 32 ∣ = a 11 ( a 22 a 33 − a 23 a 32 ) − a 12 ( a 21 a 33 − a 23 a 31 ) + a 13 ( a 21 a 32 − a 22 a 31 ) = a 11 a 22 a 33 − a 11 a 23 a 32 − a 12 a 21 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31 = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 11 a 23 a 32 − a 12 a 21 a 33 − a 13 a 22 a 31 = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ . a_{11}\begin{vmatrix}a_{22}&a_{23}\\ a_{32}&a_{33}\end{vmatrix}-a_{12}\begin{vmatrix}a_{21}&a_{23}\\ a_{31}&a_{33}\end{vmatrix}+a_{13}\begin{vmatrix}a_{21}&a_{22}\\ a_{31}&a_{32}\end{vmatrix}=a_{11}(a_{22}a_{33}-a_{23}a_{32})-a_{12}(a_{21}a_{33}-a_{23}a_{31})+a_{13}(a_{21}a_{32}-a_{22}a_{31})=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{vmatrix}. a11 a22a32a23a33 −a12 a21a31a23a33 +a13 a21a31a22a32 =a11(a22a33−a23a32)−a12(a21a33−a23a31)+a13(a21a32−a22a31)=a11a22a33−a11a23a32−a12a21a33+a12a23a31+a13a21a32−a13a22a31=a11a22a33+a12a23a31+a13a21a32−a11a23a32−a12a21a33−a13a22a31= a11a21a31a12a22a32a13a23a33 .
注:以上结论是三阶行列式按第一行展开的结果,这是化高阶行列式为低阶行列式的方法(详见第一章第五节)。
四、三阶行列式在空间解析几何中的应用 (这部分内容需要空间解析几何知识)
在直角坐标系中,
两个向量 a = a 1 i + a 2 j + a 3 k = ( a 1 , a 2 , a 3 ) a=a_{1}i+a_{2}j+a_{3}k=(a_{1},a_{2},a_{3}) a=a1i+a2j+a3k=(a1,a2,a3) 和 b = b 1 i + b 2 j + b 3 k = ( b 1 , b 2 , b 3 ) b=b_{1}i+b_{2}j+b_{3}k=(b_{1},b_{2},b_{3}) b=b1i+b2j+b3k=(b1,b2,b3) 的向量积为
a × b = ∣ i j k a 1 a 2 a 3 b 1 b 2 b 3 ∣ = 按第一行展开 ∣ a 2 a 3 b 2 b 3 ∣ i − ∣ a 1 a 3 b 1 b 3 ∣ j + ∣ a 1 a 2 b 1 b 2 ∣ k . a\times b=\begin{vmatrix}i&j&k\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\end{vmatrix}\stackrel{\text{按第一行展开}}{=}\begin{vmatrix}a_{2}&a_{3}\\ b_{2}&b_{3}\end{vmatrix}i-\begin{vmatrix}a_{1}&a_{3}\\ b_{1}&b_{3}\end{vmatrix}j+\begin{vmatrix}a_{1}&a_{2}\\ b_{1}&b_{2}\end{vmatrix}k. a×b= ia1b1ja2b2ka3b3 =按第一行展开 a2b2a3b3 i− a1b1a3b3 j+ a1b1a2b2 k.
或者
a × b = ∣ i j k a 1 a 2 a 3 b 1 b 2 b 3 ∣ = ∣ a 2 a 3 b 2 b 3 ∣ i + ∣ a 3 a 1 b 3 b 1 ∣ j + ∣ a 1 a 2 b 1 b 2 ∣ k = ( ∣ a 2 a 3 b 2 b 3 ∣ , ∣ a 3 a 1 b 3 b 1 ∣ , ∣ a 1 a 2 b 1 b 2 ∣ ) a\times b=\begin{vmatrix}i&j&k\\ a_{1}&a_{2}&a_{3}\\ b_{1}&b_{2}&b_{3}\end{vmatrix}=\begin{vmatrix}a_{2}&a_{3}\\ b_{2}&b_{3}\end{vmatrix}i+\begin{vmatrix}a_{3}&a_{1}\\ b_{3}&b_{1}\end{vmatrix}j+\begin{vmatrix}a_{1}&a_{2}\\ b_{1}&b_{2}\end{vmatrix}k=(\begin{vmatrix}a_{2}&a_{3}\\ b_{2}&b_{3}\end{vmatrix},\begin{vmatrix}a_{3}&a_{1}\\ b_{3}&b_{1}\end{vmatrix},\begin{vmatrix}a_{1}&a_{2}\\ b_{1}&b_{2}\end{vmatrix}) a×b= ia1b1ja2b2ka3b3 = a2b2a3b3 i+ a3b3a1b1 j+ a1b1a2b2 k=( a2b2a3b3 , a3b3a1b1 , a1b1a2b2 )
三个向量 a = ( a 1 , a 2 , a 3 ) a=(a_{1},a_{2},a_{3}) a=(a1,a2,a3), b = ( b 1 , b 2 , b 3 ) b=(b_{1},b_{2},b_{3}) b=(b1,b2,b3) 和 c = ( c 1 , c 2 , c 3 ) c=(c_{1},c_{2},c_{3}) c=(c1,c2,c3) 的混合积(绝对值代表以三个向量构成的平行六面体的体积)(记为 [ a b c ] [abc] [abc])为
a b c \] = a ⋅ ( b × c ) \[abc\]=a\\cdot(b\\times c) \[abc\]=a⋅(b×c) = ( a 1 , a 2 , a 3 ) ⋅ ( ∣ b 2 b 3 c 2 c 3 ∣ , ∣ b 3 b 1 c 3 c 1 ∣ , ∣ b 1 b 2 c 1 c 2 ∣ ) T =(a_{1},a_{2},a_{3})\\cdot(\\begin{vmatrix}b_{2}\&b_{3}\\\\ c_{2}\&c_{3}\\end{vmatrix},\\begin{vmatrix}b_{3}\&b_{1}\\\\ c_{3}\&c_{1}\\end{vmatrix},\\begin{vmatrix}b_{1}\&b_{2}\\\\ c_{1}\&c_{2}\\end{vmatrix})\^T =(a1,a2,a3)⋅( b2c2b3c3 , b3c3b1c1 , b1c1b2c2 )T = a 1 ∣ b 2 b 3 c 2 c 3 ∣ + a 2 ∣ b 3 b 1 c 3 c 1 ∣ + a 3 ∣ b 1 b 2 c 1 c 2 ∣ = ∣ a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ∣ =a_{1}\\begin{vmatrix}b_{2}\&b_{3}\\\\ c_{2}\&c_{3}\\end{vmatrix}+a_{2}\\begin{vmatrix}b_{3}\&b_{1}\\\\ c_{3}\&c_{1}\\end{vmatrix}+a_{3}\\begin{vmatrix}b_{1}\&b_{2}\\\\ c_{1}\&c_{2}\\end{vmatrix}=\\begin{vmatrix}a_{1}\&a_{2}\&a_{3}\\\\ b_{1}\&b_{2}\&b_{3}\\\\ c_{1}\&c_{2}\&c_{3}\\end{vmatrix} =a1 b2c2b3c3 +a2 b3c3b1c1 +a3 b1c1b2c2 = a1b1c1a2b2c2a3b3c3