FA :formulas and algorithm, FF :fusion and filtering
扩展卡尔曼滤波器(EKF)全解析:原理、非线性处理细节与实战代码
你希望深入了解扩展卡尔曼滤波器(EKF),特别是其非线性处理的核心细节,并获取可运行的示例代码。我会从基础原理入手,重点拆解非线性处理的关键步骤,最后提供完整的实战代码(以无人机姿态估计为例),让你既能理解理论又能落地实践。
一、EKF 核心概念:卡尔曼滤波的非线性扩展
1. 为什么需要 EKF?
标准卡尔曼滤波器(KF)仅适用于线性系统(状态方程和观测方程均为线性),但现实中绝大多数系统是非线性的(如无人机运动、机器人定位、传感器观测模型)。EKF 通过一阶泰勒展开将非线性系统近似为线性系统,从而让卡尔曼滤波的框架依然可用。
2. EKF 的核心假设
系统的非线性函数可微(保证泰勒展开可行);
系统噪声和观测噪声均为零均值高斯白噪声(KF 的核心假设,EKF 继承);
泰勒展开仅保留一阶项(忽略高阶项),这是 EKF 的近似误差来源。3. EKF 的系统模型定义
首先明确非线性系统的标准形式:
状态方程(过程模型)
xk=f(xk−1,uk−1)+wk−1x_k=f(x_{k-1},u_{k-1})+w_{k-1}xk=f(xk−1,uk−1)+wk−1
- xkx_kxk:k 时刻的系统状态(如无人机的位置、速度、姿态);
- f(⋅)f(⋅)f(⋅):非线性状态转移函数(核心非线性项);
- uk−1u_{k−1}uk−1:k-1 时刻的控制输入(如无人机的电机转速);
- wk−1w_{k−1}wk−1:过程噪声(高斯分布,协方差为QQQ)。
观测方程(测量模型)
zk=h(xk)+vkz_k=h(x_k)+v_kzk=h(xk)+vk
- zkz_kzk:k 时刻的观测值(如 GPS、IMU 的测量数据);
- h(⋅)h(⋅)h(⋅):非线性观测函数(核心非线性项);
- vkv_kvk:观测噪声(高斯分布,协方差为R)。
二、EKF 的核心步骤:非线性处理的关键细节
EKF 的核心是对非线性函数f(⋅)f(⋅)f(⋅)和h(⋅)h(⋅)h(⋅)做一阶线性化,步骤分为「预测」和「更新」两大阶段,其中非线性处理集中在这两个阶段的线性化步骤。
阶段 1:预测(Predict)------ 状态和协方差的先验估计
步骤 1.1:先验状态估计(非线性)
直接使用非线性状态转移函数预测状态,无近似:
x^k−=f(x^kk−1+,uk−1)\hat{x}{k}^{-}=f(\hat{x}{kk-1}^{+},u_{k-1})x^k−=f(x^kk−1+,uk−1)
- x^k−\hat{x}_{k}^{-}x^k−:kkk 时刻的先验状态估计(未融合观测的预测值);
- x^k−1+\hat{x}_{k−1}^{+}x^k−1+:k−1k-1k−1 时刻的后验状态估计(融合观测后的最优值)。
步骤 1.2:状态转移矩阵(雅可比矩阵)计算(核心线性化)
对非线性状态转移函数f(⋅)f(⋅)f(⋅)在x^k−1+\hat{x}_{k−1}^{+}x^k−1+处做一阶泰勒展开,忽略高阶项,得到状态转移雅可比矩阵 FkF_kFk:
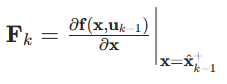
- 雅可比矩阵Fk的维度:n×n(n 为状态维度);
- 物理意义:将非线性的状态转移近似为线性的 "状态转移矩阵",这是 EKF 处理非线性的核心;
- 计算细节:对f(⋅)的每个输出维度,分别对每个状态变量求偏导,组成矩阵。
步骤 1.3:先验协方差估计(线性近似)
利用雅可比矩阵FkF_kFk近似计算状态协方差的先验值:
Pk−=FkPk−1+FkT+QP_{k}^{-}=F_kP_{k-1}^{+}F_{k}^{T}+QPk−=FkPk−1+FkT+Q
- Pk−P_{k}^{-}Pk−:k 时刻的先验协方差矩阵;
- Pk−1+P_{k−1}^{+}Pk−1+:k-1 时刻的后验协方差矩阵;
- QQQ:过程噪声协方差矩阵。
阶段 2:更新(Update)------ 融合观测的后验估计
步骤 2.1:观测矩阵(雅可比矩阵)计算(核心线性化)
对非线性观测函数h(⋅)h(⋅)h(⋅)在x^k−\hat{x}_{k}^{-}x^k−处做一阶泰勒展开,得到观测雅可比矩阵 HkH_kHk:
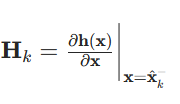
- 雅可比矩阵HkH_kHk的维度:m×n(m 为观测维度,n 为状态维度);
- 计算细节:对h(⋅)h(⋅)h(⋅)的每个输出维度,分别对每个状态变量求偏导,组成矩阵。
步骤 2.2:卡尔曼增益计算(线性)
Kk=Pk−HkT(HkPk−HkT+R)−1K_k=P_{k}^{-}H_{k}^{T}(H_kP_{k}^{-}H_{k}^{T}+R)^{-1}Kk=Pk−HkT(HkPk−HkT+R)−1
- KkK_kKk:卡尔曼增益(权衡预测值和观测值的权重);
- RRR:观测噪声协方差矩阵。
步骤 2.3:后验状态估计(融合观测)
x^k+=x^k−Kk(zk−h(x^k−))\hat{x}{k}^{+}=\hat{x}{k}^{-}K_k(z_k-h(\hat{x}_{k}^{-}))x^k+=x^k−Kk(zk−h(x^k−))
- zk−h(x^k−)z_{k}^{-}h(\hat{x}_{k}^{-})zk−h(x^k−):观测残差(实际观测与预测观测的差值);
- 注意:这里的预测观测依然用非线性函数h(⋅) 计算,仅雅可比矩阵用于线性近似。
步骤 2.4:后验协方差更新(线性)
Pk+=(I−KkHk)Pk−P_{k}^{+}=(I−K_kH_k)P_{k}^{-}Pk+=(I−KkHk)Pk−
- III:单位矩阵;
- Pk+P_{k}^{+}Pk+:k 时刻的后验协方差矩阵(最优协方差)。
非线性处理的关键细节总结
表格
核心操作 位置 数学方法 误差来源
状态转移线性化 预测阶段 对f(⋅)求雅可比矩阵Fk 忽略泰勒展开的高阶项
观测线性化 更新阶段 对h(⋅)求雅可比矩阵Hk 忽略泰勒展开的高阶项
状态预测 预测阶段 直接使用非线性f(⋅) 无(仅协方差用线性近似)
观测残差计算 更新阶段 直接使用非线性h(⋅) 无(仅卡尔曼增益用线性近似)
三、EKF 实战示例:无人机 2D 位置 - 速度估计
场景说明
状态x=[x,vx,y,vy]T:x 位置、x 方向速度、y 位置、y 方向速度(4 维);
控制输入u=[ax,ay]T:x 和 y 方向的加速度(2 维);
状态转移函数(非线性):假设加速度受速度非线性影响(如空气阻力);
观测函数(非线性):GPS 观测的是距离原点的极坐标(r,θ),需转换为笛卡尔坐标(非线性);
过程噪声Q:加速度噪声;
观测噪声R:GPS 极坐标观测噪声。完整示例代码
bash
import numpy as np
import matplotlib.pyplot as plt
class ExtendedKalmanFilter:
def __init__(self, x0, P0, Q, R):
"""
初始化扩展卡尔曼滤波器
:param x0: 初始状态 [x, vx, y, vy]
:param P0: 初始协方差矩阵 (4x4)
:param Q: 过程噪声协方差矩阵 (4x4)
:param R: 观测噪声协方差矩阵 (2x2)
"""
self.x = x0 # 状态估计 [x, vx, y, vy]
self.P = P0 # 协方差矩阵
self.Q = Q # 过程噪声协方差
self.R = R # 观测噪声协方差
self.n = len(x0) # 状态维度
self.m = R.shape[0] # 观测维度
def f(self, x, u, dt):
"""
非线性状态转移函数:x_k = f(x_{k-1}, u)
状态方程:考虑空气阻力的匀加速运动(非线性)
x = x_prev + vx_prev*dt + 0.5*ax*dt² * exp(-0.1*|vx_prev|)
vx = vx_prev + ax*dt * exp(-0.1*|vx_prev|)
y和vy同理
:param x: 前一时刻状态 [x, vx, y, vy]
:param u: 控制输入 [ax, ay] (加速度)
:param dt: 时间步长
:return: 预测状态
"""
x_prev, vx_prev, y_prev, vy_prev = x
ax, ay = u
# 非线性项:空气阻力(速度越大,加速度效果越弱)
drag_x = np.exp(-0.1 * abs(vx_prev))
drag_y = np.exp(-0.1 * abs(vy_prev))
# 状态转移
x_new = x_prev + vx_prev * dt + 0.5 * ax * dt**2 * drag_x
vx_new = vx_prev + ax * dt * drag_x
y_new = y_prev + vy_prev * dt + 0.5 * ay * dt**2 * drag_y
vy_new = vy_prev + ay * dt * drag_y
return np.array([x_new, vx_new, y_new, vy_new])
def F_jacobian(self, x, u, dt):
"""
状态转移函数的雅可比矩阵 F = ∂f/∂x
:param x: 状态 [x, vx, y, vy]
:param u: 控制输入 [ax, ay]
:param dt: 时间步长
:return: 雅可比矩阵 F (4x4)
"""
x_prev, vx_prev, y_prev, vy_prev = x
ax, ay = u
# 计算非线性项的偏导数
drag_x = np.exp(-0.1 * abs(vx_prev))
d_drag_x = -0.1 * np.sign(vx_prev) * drag_x # d(drag_x)/d(vx_prev)
drag_y = np.exp(-0.1 * abs(vy_prev))
d_drag_y = -0.1 * np.sign(vy_prev) * drag_y # d(drag_y)/d(vy_prev)
# 构建雅可比矩阵
F = np.eye(4)
# ∂x_new/∂x_prev = 1
F[0, 1] = dt + 0.5 * ax * dt**2 * d_drag_x # ∂x_new/∂vx_prev
# ∂x_new/∂y_prev = 0, ∂x_new/∂vy_prev = 0
# ∂vx_new/∂x_prev = 0
F[1, 1] = 1 + ax * dt * d_drag_x # ∂vx_new/∂vx_prev
# ∂vx_new/∂y_prev = 0, ∂vx_new/∂vy_prev = 0
# ∂y_new/∂x_prev = 0, ∂y_new/∂vx_prev = 0
F[2, 3] = dt + 0.5 * ay * dt**2 * d_drag_y # ∂y_new/∂vy_prev
# ∂y_new/∂y_prev = 1
# ∂vy_new/∂x_prev = 0, ∂vy_new/∂vx_prev = 0
F[3, 3] = 1 + ay * dt * d_drag_y # ∂vy_new/∂vy_prev
# ∂vy_new/∂y_prev = 0
return F
def h(self, x):
"""
非线性观测函数:z = h(x)
观测为极坐标 (r, θ):r = √(x² + y²), θ = arctan2(y, x)
:param x: 状态 [x, vx, y, vy]
:return: 观测预测 [r, θ]
"""
x_pos, _, y_pos, _ = x
r = np.sqrt(x_pos**2 + y_pos**2) # 距离原点的距离
theta = np.arctan2(y_pos, x_pos) # 角度
return np.array([r, theta])
def H_jacobian(self, x):
"""
观测函数的雅可比矩阵 H = ∂h/∂x
:param x: 状态 [x, vx, y, vy]
:return: 雅可比矩阵 H (2x4)
"""
x_pos, _, y_pos, _ = x
r = np.sqrt(x_pos**2 + y_pos**2)
# 避免除零
if r < 1e-6:
r = 1e-6
# 构建雅可比矩阵
H = np.zeros((self.m, self.n))
# ∂r/∂x = x/r, ∂r/∂vx = 0, ∂r/∂y = y/r, ∂r/∂vy = 0
H[0, 0] = x_pos / r
H[0, 2] = y_pos / r
# ∂θ/∂x = -y/(x²+y²), ∂θ/∂vx = 0, ∂θ/∂y = x/(x²+y²), ∂θ/∂vy = 0
H[1, 0] = -y_pos / (x_pos**2 + y_pos**2)
H[1, 2] = x_pos / (x_pos**2 + y_pos**2)
return H
def predict(self, u, dt):
"""
EKF预测阶段:计算先验状态和协方差
:param u: 控制输入 [ax, ay]
:param dt: 时间步长
"""
# 步骤1:先验状态估计(非线性)
self.x = self.f(self.x, u, dt)
# 步骤2:计算状态转移雅可比矩阵
F = self.F_jacobian(self.x, u, dt)
# 步骤3:先验协方差估计(线性近似)
self.P = F @ self.P @ F.T + self.Q
def update(self, z):
"""
EKF更新阶段:融合观测值,计算后验状态和协方差
:param z: 观测值 [r, θ] (极坐标)
"""
# 步骤1:计算观测雅可比矩阵
H = self.H_jacobian(self.x)
# 步骤2:计算卡尔曼增益
S = H @ self.P @ H.T + self.R # 残差协方差
K = self.P @ H.T @ np.linalg.inv(S) # 卡尔曼增益
# 步骤3:计算观测残差(非线性观测函数)
z_hat = self.h(self.x) # 预测观测值
residual = z - z_hat
# 角度残差归一化到[-π, π](避免θ=359°和θ=1°的残差为358°)
residual[1] = np.arctan2(np.sin(residual[1]), np.cos(residual[1]))
# 步骤4:后验状态估计
self.x = self.x + K @ residual
# 步骤5:后验协方差更新
self.P = (np.eye(self.n) - K @ H) @ self.P
# -------------------------- 仿真与测试 --------------------------
def generate_true_state_and_measurement(total_time, dt, u_func, Q_noise, R_noise):
"""
生成真实状态和带噪声的观测值
:param total_time: 总仿真时间
:param dt: 时间步长
:param u_func: 控制输入函数 (t) -> [ax, ay]
:param Q_noise: 过程噪声标准差
:param R_noise: 观测噪声标准差
:return: true_states, measurements, time_steps
"""
# 初始真实状态
x_true = np.array([0.0, 1.0, 0.0, 1.0]) # [x, vx, y, vy]
true_states = [x_true.copy()]
measurements = []
time_steps = np.arange(0, total_time, dt)
for t in time_steps[1:]:
# 控制输入
u = u_func(t)
# 真实状态转移(加过程噪声)
f = ExtendedKalmanFilter(x_true, None, None, None).f
x_true = f(x_true, u, dt)
x_true += np.random.normal(0, Q_noise, size=4)
# 生成观测值(极坐标,加观测噪声)
h = ExtendedKalmanFilter(x_true, None, None, None).h
z = h(x_true)
z += np.random.normal(0, R_noise, size=2)
true_states.append(x_true.copy())
measurements.append(z)
# 补充第一个时刻的观测
z0 = ExtendedKalmanFilter(true_states[0], None, None, None).h(true_states[0])
z0 += np.random.normal(0, R_noise, size=2)
measurements.insert(0, z0)
return np.array(true_states), np.array(measurements), time_steps
# 1. 仿真参数设置
total_time = 20.0 # 总仿真时间
dt = 0.1 # 时间步长
Q_std = 0.05 # 过程噪声标准差
R_std = 0.1 # 观测噪声标准差
# 过程噪声协方差矩阵(状态维度4x4)
Q = np.diag([Q_std**2, Q_std**2, Q_std**2, Q_std**2])
# 观测噪声协方差矩阵(观测维度2x2)
R = np.diag([R_std**2, R_std**2])
# 初始状态估计和协方差
x0 = np.array([0.0, 0.0, 0.0, 0.0]) # 初始估计(故意设置误差)
P0 = np.diag([1.0, 1.0, 1.0, 1.0]) # 初始协方差
# 控制输入函数:正弦变化的加速度
def u_func(t):
ax = 0.2 * np.sin(0.1 * t) # x方向加速度
ay = 0.2 * np.cos(0.1 * t) # y方向加速度
return np.array([ax, ay])
# 2. 生成真实数据和观测数据
true_states, measurements, time_steps = generate_true_state_and_measurement(
total_time, dt, u_func, Q_std, R_std
)
# 3. 运行EKF
ekf = ExtendedKalmanFilter(x0, P0, Q, R)
ekf_states = [x0.copy()]
for i in range(1, len(time_steps)):
# 控制输入
u = u_func(time_steps[i])
# EKF预测
ekf.predict(u, dt)
# EKF更新
ekf.update(measurements[i])
# 保存状态估计
ekf_states.append(ekf.x.copy())
ekf_states = np.array(ekf_states)
# 4. 结果可视化
plt.figure(figsize=(12, 8))
# 子图1:x位置对比
plt.subplot(2, 2, 1)
plt.plot(time_steps, true_states[:, 0], 'b-', label='True x')
plt.plot(time_steps, ekf_states[:, 0], 'r--', label='EKF Estimated x')
plt.xlabel('Time (s)')
plt.ylabel('X Position (m)')
plt.title('X Position Comparison')
plt.legend()
plt.grid(True)
# 子图2:y位置对比
plt.subplot(2, 2, 2)
plt.plot(time_steps, true_states[:, 2], 'b-', label='True y')
plt.plot(time_steps, ekf_states[:, 2], 'r--', label='EKF Estimated y')
plt.xlabel('Time (s)')
plt.ylabel('Y Position (m)')
plt.title('Y Position Comparison')
plt.legend()
plt.grid(True)
# 子图3:x速度对比
plt.subplot(2, 2, 3)
plt.plot(time_steps, true_states[:, 1], 'b-', label='True vx')
plt.plot(time_steps, ekf_states[:, 1], 'r--', label='EKF Estimated vx')
plt.xlabel('Time (s)')
plt.ylabel('X Velocity (m/s)')
plt.title('X Velocity Comparison')
plt.legend()
plt.grid(True)
# 子图4:y速度对比
plt.subplot(2, 2, 4)
plt.plot(time_steps, true_states[:, 3], 'b-', label='True vy')
plt.plot(time_steps, ekf_states[:, 3], 'r--', label='EKF Estimated vy')
plt.xlabel('Time (s)')
plt.ylabel('Y Velocity (m/s)')
plt.title('Y Velocity Comparison')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
# 5. 计算均方误差(MSE)
mse_x = np.mean((true_states[:, 0] - ekf_states[:, 0])**2)
mse_y = np.mean((true_states[:, 2] - ekf_states[:, 2])**2)
mse_vx = np.mean((true_states[:, 1] - ekf_states[:, 1])**2)
mse_vy = np.mean((true_states[:, 3] - ekf_states[:, 3])**2)
print(f"===== EKF 估计精度 =====")
print(f"X位置均方误差: {mse_x:.4f} m²")
print(f"Y位置均方误差: {mse_y:.4f} m²")
print(f"X速度均方误差: {mse_vx:.4f} (m/s)²")
print(f"Y速度均方误差: {mse_vy:.4f} (m/s)²")四、代码关键细节解析
-
非线性函数设计
状态转移函数f():引入空气阻力的非线性项exp(-0.1*|vx_prev|),模拟真实世界中速度越大、加速度效果越弱的物理规律;
观测函数h():将笛卡尔坐标转换为极坐标(x2+y2
、arctan2(y,x)),典型的非线性观测模型。
-
雅可比矩阵计算(核心非线性处理)
状态转移雅可比F_jacobian():对状态转移函数的每个输出维度求偏导,重点处理非线性项exp(-0.1*|vx_prev|)的偏导数;
观测雅可比H_jacobian():对极坐标转换函数求偏导,需注意除零保护和角度的周期性。
-
仿真与验证
生成带噪声的真实状态和观测值,模拟实际传感器的噪声特性;
初始状态估计故意设置误差,验证 EKF 的收敛性;
计算均方误差(MSE),量化 EKF 的估计精度。
五、EKF 的优缺点与适用场景
优点
保留卡尔曼滤波的最优估计特性,计算量小(仅一阶泰勒展开);
实现简单,是处理非线性系统的基础方法;
适用于 "弱非线性" 系统(非线性程度低,泰勒展开近似误差小)。缺点
仅一阶近似,强非线性系统误差大;
雅可比矩阵计算复杂,需手动求导(易出错);
对噪声的高斯假设敏感,非高斯噪声下性能下降。适用场景
无人机 / 机器人的姿态、位置估计;
车辆导航(GPS+IMU 融合);
目标跟踪(如雷达跟踪机动目标);
弱非线性的工业过程控制。六、总结
EKF 核心:通过一阶泰勒展开 + 雅可比矩阵将非线性系统近似为线性系统,复用卡尔曼滤波的框架;
非线性处理关键:
状态转移和观测函数保持非线性,仅协方差和卡尔曼增益计算使用线性化的雅可比矩阵;
雅可比矩阵的手动推导是 EKF 实现的核心难点,需注意非线性项的偏导数计算;
实战要点:
合理设置过程噪声Q和观测噪声R(影响估计精度);
对周期性观测(如角度)需做残差归一化;
雅可比矩阵需做数值稳定性处理(如除零保护)。