高等数学第一章第三节函数的极限学习笔记（自用）

参考b站徐小湛老师视频的学习https://space.bilibili.com/34568010?spm_id_from=333.788.upinfo.head.click
第三节函数的极限

极限是微积分中的一种基本运算和方法。

微积分中的很多重要概念都要用极限来定义

(如函数的连续性、导数、定积分、重积分、曲线积分、曲面积分以及无穷级数的收敛性等等)。

很多重要的计算方法都要涉及极限运算。

函数极限的定义

1. 自变量趋于有限值时函数的极限 lim⁡x→x0f(x)\lim_{x\rightarrow x_0} f(x)limx→x0f(x)

定义

不管函数在一个点处是否有定义,我们都可以讨论函数在该点的极限。

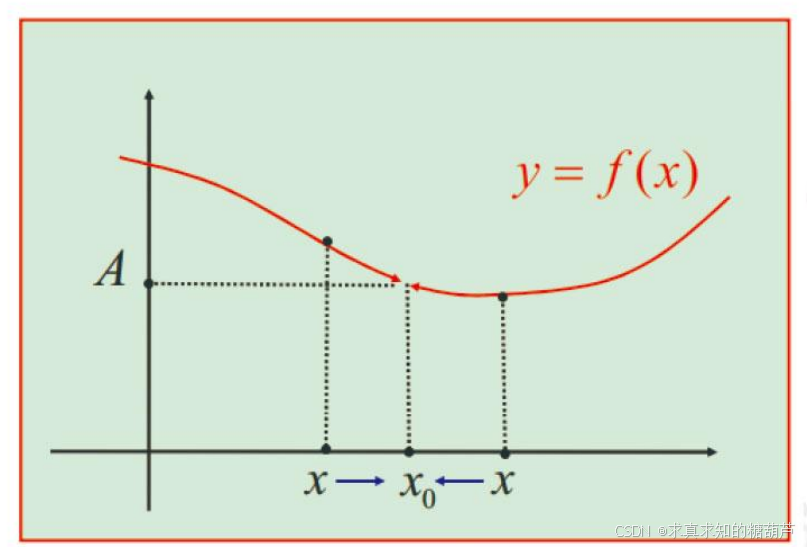
极限 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 的直观的定义

设函数 f(x)f(x)f(x) 在 x=x0x=x_0x=x0 的某个去心邻域内有定义。

若 x→x0(x≠x0)x\rightarrow x_0 (x\neq x_0)x→x0(x=x0) 时,有 f(x)→Af(x)\rightarrow Af(x)→A ( AAA 是实数),

则称函数 f(x)f(x)f(x) 在 x=x0x=x_0x=x0 处有极限 AAA,记作 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 或 f(x)→A(x→x0)f(x)\rightarrow A (x\rightarrow x_0)f(x)→A(x→x0)。

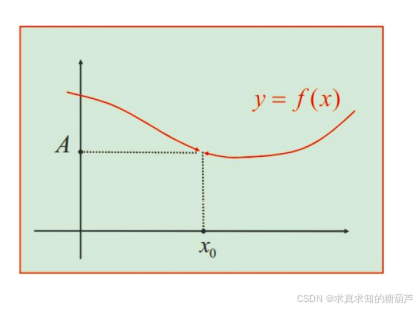
极限 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 的示意图

下面给出极限 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 的严格定义。

定义 1 设函数 f(x)f(x)f(x) 在 x=x0x=x_0x=x0 的某个去心邻域内有定义。

如果存在常数 AAA,对 ∀ε>0\forall\varepsilon>0∀ε>0 (无论它多么小),总存在数 δ>0\delta>0δ>0,
使得当自变量 xxx 满足不等式 0<∣x−x0∣<δ0<|x-x_0|<\delta0<∣x−x0∣<δ 时,
对应的函数值 f(x)f(x)f(x) 都满足不等式 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε,

则称当 x→x0x\rightarrow x_0x→x0 时,函数 f(x)f(x)f(x) 以 AAA 为极限,

记作 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 或 f(x)→A(x→x0)f(x)\rightarrow A (x\rightarrow x_0)f(x)→A(x→x0)。

以上定义叫做极限 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 的 ε−δ\varepsilon-\deltaε−δ 定义。

问:这个极限是否存在 以及极限值是多少 是否与函数 f(x)f(x)f(x) 在 x0x_0x0 处的函数值 f(x0)f(x_0)f(x0) 有关?答:无关。

因为定义中没有涉及到 f(x0)f(x_0)f(x0)。

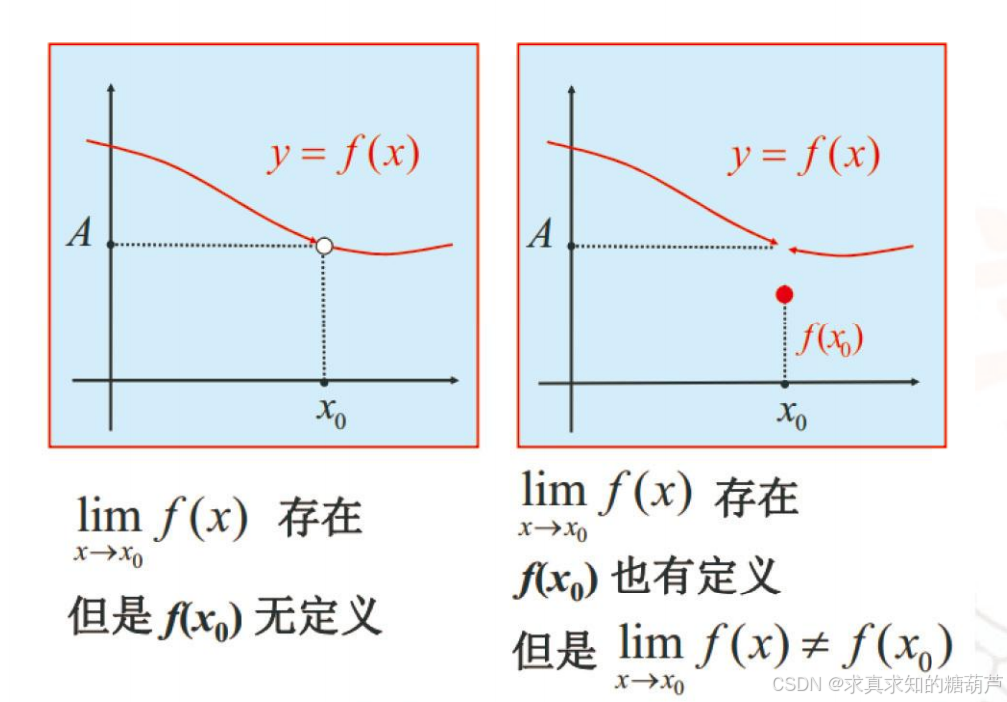
几何解释

lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 的几何解释

根据定义, lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 当且仅当 ∀ε>0,∃δ>0\forall\varepsilon>0,\exists\delta>0∀ε>0,∃δ>0,使得当 0<∣x−x0∣<δ0<|x-x_0|<\delta0<∣x−x0∣<δ 时,

就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε。

即 ∀ε>0,∃δ>0,∀x∈(x0−δ,x0)∪(x0,x0+δ)⇒A−ε<f(x)<A+ε\forall\varepsilon>0,\exists\delta>0,\forall x\in(x_0-\delta, x_0)\cup(x_0, x_0+\delta)\Rightarrow A-\varepsilon<f(x)<A+\varepsilon∀ε>0,∃δ>0,∀x∈(x0−δ,x0)∪(x0,x0+δ)⇒A−ε<f(x)<A+ε。

由此得到 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 的几何解释。

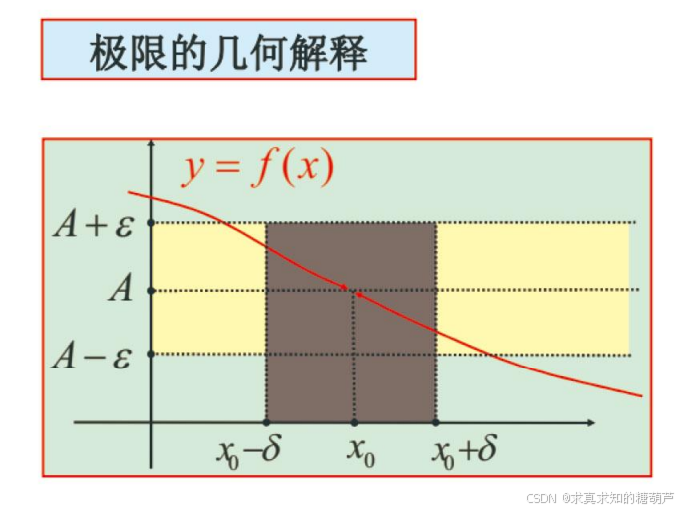
问:(1)在极限的 ε−δ\varepsilon-\deltaε−δ 定义中,是先有 ε\varepsilonε,还是先有 δ\deltaδ?为什么?
δ\deltaδ 取决于 ε\varepsilonε。
一般, ε\varepsilonε 越小, δ\deltaδ 也越小。
(2)由 ε\varepsilonε 所确定的 δ\deltaδ 是否唯一? 不唯一

以上极限严格定义是德国数学家魏尔斯特拉斯给出的。

魏尔斯特拉斯被誉为"现代分析之父"。

局部有界性

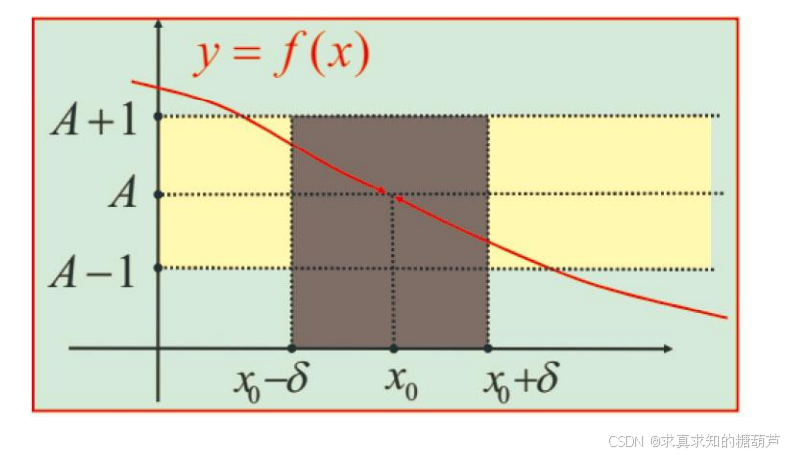
函数的局部有界性设 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A。

取 ε=1\varepsilon=1ε=1,则存在 δ>0\delta>0δ>0,

使得 ∀x∈(x0−δ,x0)∪(x0,x0+δ)⇒A−1<f(x)<A+1\forall x\in(x_0-\delta, x_0)\cup(x_0, x_0+\delta)\Rightarrow A-1<f(x)<A+1∀x∈(x0−δ,x0)∪(x0,x0+δ)⇒A−1<f(x)<A+1 (下图)。

这表明 f(x)f(x)f(x) 在集合 (x0−δ,x0)∪(x0,x0+δ)(x_0-\delta, x_0)\cup(x_0, x_0+\delta)(x0−δ,x0)∪(x0,x0+δ) (即 x0x_0x0 的一个去心邻域)内有界

(见极限的性质(定理 2,32页)。

定理2 (函数极限的局部有界性)

若极限 lim⁡x→x0f(x)\lim_{x\rightarrow x_0} f(x)limx→x0f(x) 存在,则函数 f(x)f(x)f(x) 在 x0x_0x0 的某个去心邻域内有界。

定义证明

用定义证明极限 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 的方法 (ε−δ(\varepsilon-\delta(ε−δ 法)(《高等数学学习手册》《高等数学学习手册》《高等数学学习手册》 31页 )))

对于任意给定的 ε>0\varepsilon>0ε>0,从 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε 分析出 ∣x−x0∣<φ(ε)|x-x_0|<\varphi(\varepsilon)∣x−x0∣<φ(ε),然后令 δ=φ(ε)\delta=\varphi(\varepsilon)δ=φ(ε)。

则当 0<∣x−x0∣<δ0<|x-x_0|<\delta0<∣x−x0∣<δ 时,就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε。

所以 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A。

有的极限的证明需要一些技巧，比如"适当放大法"。

重要的基本极限

几个重要的基本极限(证明见教材或高数视频)

lim⁡x→x0C=C\lim_{x\rightarrow x_0} C=Climx→x0C=C,其中 CCC 是常数。
lim⁡x→x0x=x0\lim_{x\rightarrow x_0} x=x_0limx→x0x=x0。
lim⁡x→x0x=x0(x0>0)\lim_{x\rightarrow x_0}\sqrt{x}=\sqrt{x_0} (x_0>0)limx→x0x =x0 (x0>0)。

单侧极限

极限 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 是双侧极限,即 xxx 从 x0x_0x0 的两侧趋于 x0x_0x0 时,函数 f(x)f(x)f(x) 以 AAA 为极限。

有时我们需要限制 xxx 从一侧趋于 x0x_0x0。

此时的极限就是单侧极限。

左极限 当 xxx 从左侧趋于 x0x_0x0 时(记 x→x0−x\rightarrow x_0^{-}x→x0−), f(x)→Af(x)\rightarrow Af(x)→A,则称 AAA 为函数 f(x)f(x)f(x) 的左极限,

记作 lim⁡x→x0−f(x)=A\lim_{x\rightarrow x_0^{-}} f(x)=Alimx→x0−f(x)=A 或 f(x0−)=Af(x_0^{-})=Af(x0−)=A (也可记作 f(x0−0)=Af(x_0-0)=Af(x0−0)=A)。

右极限 当 xxx 从右侧趋于 x0x_0x0 时(记 x→x0+x\rightarrow x_0^{+}x→x0+), f(x)→Af(x)\rightarrow Af(x)→A,则称 AAA 为函数 f(x)f(x)f(x) 的右极限,记作 lim⁡x→x0+f(x)=A\lim_{x\rightarrow x_{0}^{+}} f(x)=Alimx→x0+f(x)=A 或 f(x0+)=Af(x_{0}^{+})=Af(x0+)=A (也可记作 f(x0+0)=Af(x_{0}+0)=Af(x0+0)=A)。

左极限和右极限统称单侧极限。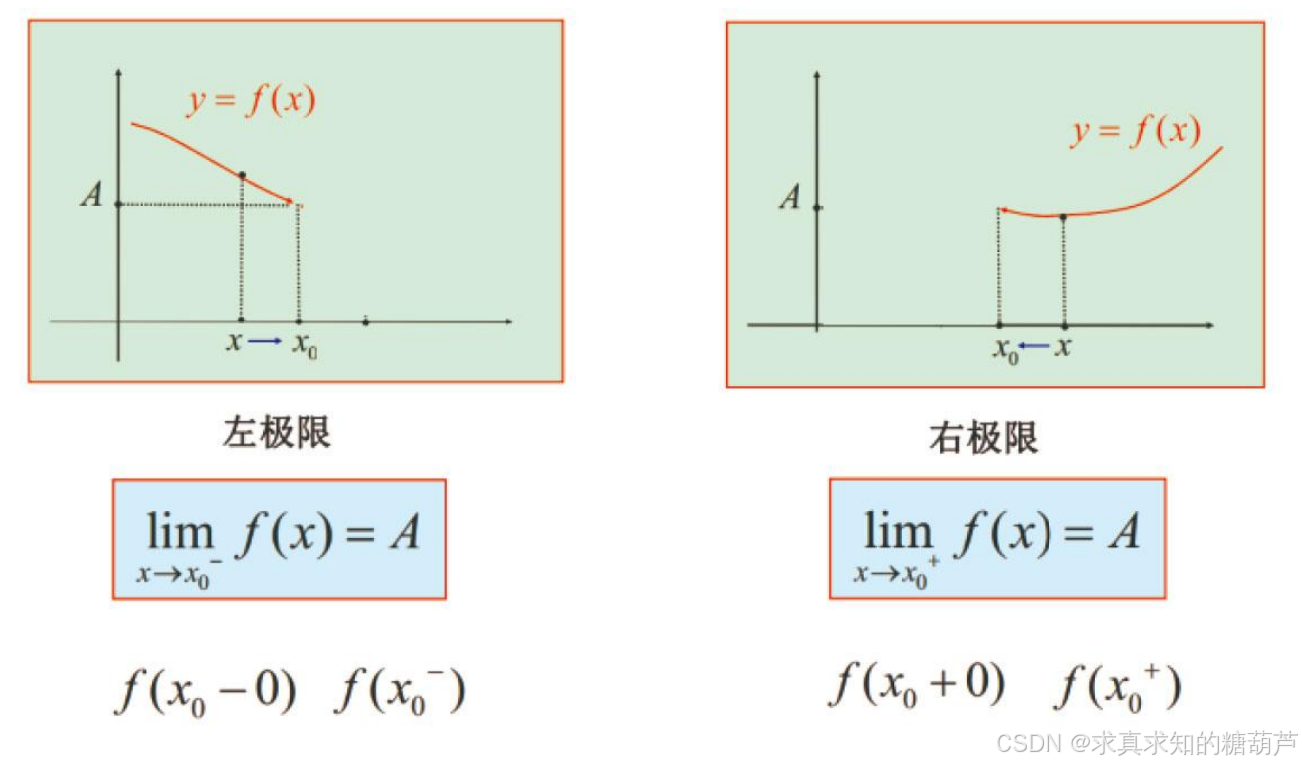

单侧极限的 ε−δ\varepsilon-\deltaε−δ 定义

lim⁡x→x0−f(x)=A\lim_{x\rightarrow x_0^{-}} f(x)=Alimx→x0−f(x)=A 当且仅当 ∀ε>0,∃δ>0\forall\varepsilon>0,\exists\delta>0∀ε>0,∃δ>0,使得当 x0−δ<x<x0x_0-\delta<x<x_0x0−δ<x<x0 时,就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε。

lim⁡x→x0+f(x)=A\lim_{x\rightarrow x_0^{+}} f(x)=Alimx→x0+f(x)=A 当且仅当 ∀ε>0,∃δ>0\forall\varepsilon>0,\exists\delta>0∀ε>0,∃δ>0,使得当 x0<x<x0+δx_0<x<x_0+\deltax0<x<x0+δ 时,就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε。

单侧极限与极限的关系

由 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A 的定义 (∀ε>0,∃δ>0(\forall\varepsilon>0,\exists\delta>0(∀ε>0,∃δ>0,使得当 0<∣x−x0∣<δ0<|x-x_0|<\delta0<∣x−x0∣<δ 时,就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε )))

可知:若 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A,则 lim⁡x→x0−f(x)=A\lim_{x\rightarrow x_0^{-}} f(x)=Alimx→x0−f(x)=A 且 lim⁡x→x0+f(x)=A\lim_{x\rightarrow x_0^{+}} f(x)=Alimx→x0+f(x)=A
(双侧极限存在,则单侧极限也存在,且相等。)

(因为 x0−δ<x<x0x_0-\delta<x<x_0x0−δ<x<x0 或 x0<x<x0+δ⇒0<∣x−x0∣<δx_0<x<x_0+\delta\Rightarrow 0<|x-x_0|<\deltax0<x<x0+δ⇒0<∣x−x0∣<δ )。

反之, lim⁡x→x0−f(x)=A\lim_{x\rightarrow x_0^{-}} f(x)=Alimx→x0−f(x)=A (或lim⁡x→x0+f(x)=A\text{或}\lim_{x\rightarrow x_0^{+}} f(x)=A或limx→x0+f(x)=A) 不能得出 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A。
(单侧极限存在,不能保证双侧极限也存在。)

(例如,左极限 lim⁡x→x0−f(x)=A\lim_{x\rightarrow x_0^{-}} f(x)=Alimx→x0−f(x)=A 不能确定 x0x_0x0 的右侧的情况)。

但是,如果 lim⁡x→x0−f(x)=A\lim_{x\rightarrow x_0^{-}} f(x)=Alimx→x0−f(x)=A 并且 lim⁡x→x0+f(x)=A\lim_{x\rightarrow x_0^{+}} f(x)=Alimx→x0+f(x)=A,则可以证明 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A。

命题

极限 lim⁡x→x0f(x)\lim_{x\rightarrow x_0} f(x)limx→x0f(x) 存在的充分必要条件是左极限 lim⁡x→x0−f(x)\lim_{x\rightarrow x_0^{-}} f(x)limx→x0−f(x) 和右极限 lim⁡x→x0+f(x)\lim_{x\rightarrow x_0^{+}} f(x)limx→x0+f(x) 存在且相等。

即 lim⁡x→x0f(x)=A⇔lim⁡x→x0−f(x)=A=lim⁡x→x0+f(x)\lim_{x\rightarrow x_0} f(x)=A\Leftrightarrow\lim_{x\rightarrow x_0^{-}} f(x)=A=\lim_{x\rightarrow x_0^{+}} f(x)limx→x0f(x)=A⇔limx→x0−f(x)=A=limx→x0+f(x)

(同济七版习题 1-3,11题,高数视频有证明)

推论如果 lim⁡x→x0−f(x)≠lim⁡x→x0+f(x)\lim_{x\rightarrow x_0^{-}} f(x)\neq\lim_{x\rightarrow x_0^{+}} f(x)limx→x0−f(x)=limx→x0+f(x) 或至少有一个不存在,则极限 lim⁡x→x0f(x)\lim_{x\rightarrow x_0} f(x)limx→x0f(x) 不存在。

左、右极限不相等的情况常出现在分段函数的分界点处 (下图)。

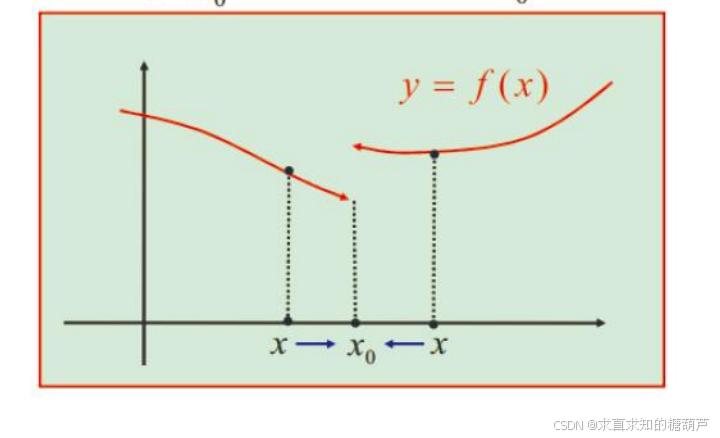
所以单侧极限常用来讨论分段函数在分界点处的极限。

单侧极限也常用来讨论函数在其定义区间端点的极限:

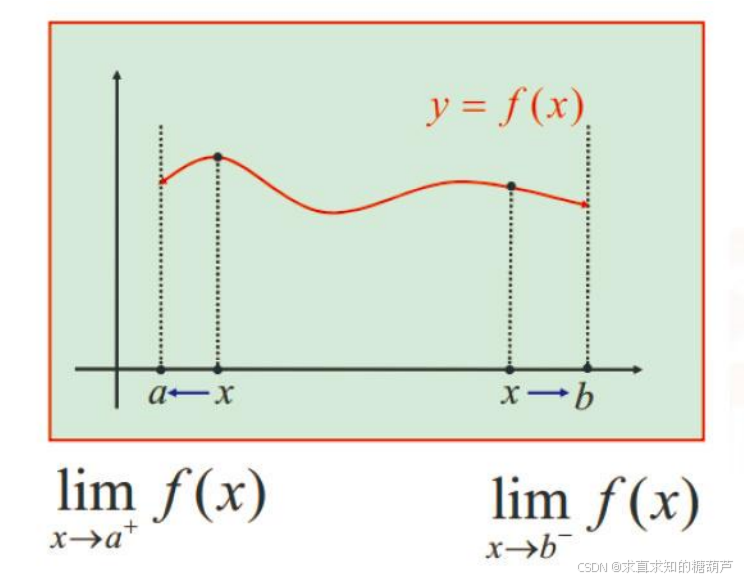
区间左端点只能讨论右极限,右端点只能讨论左极限(上图)。

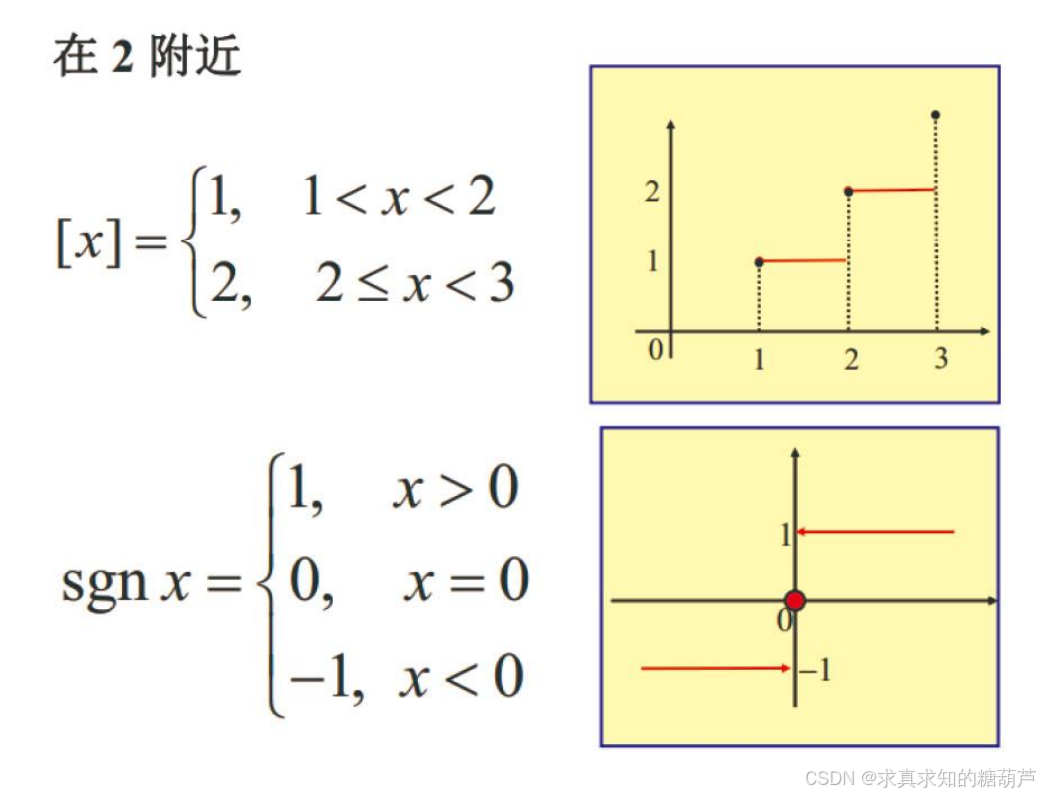
注:取整函数在整数点 kkk 处的极限都不存在。

取整函数sgn函数例

2. 自变量趋于无穷大时函数的极限 lim⁡x→∞f(x)\lim_{x\rightarrow\infty} f(x)limx→∞f(x)

定义

先看一个例子,然后给出极限的定义。

用记号 x→∞x\rightarrow\inftyx→∞ 表示 xxx 趋于无穷大(即 ∣x∣|x|∣x∣ 无限增大)。

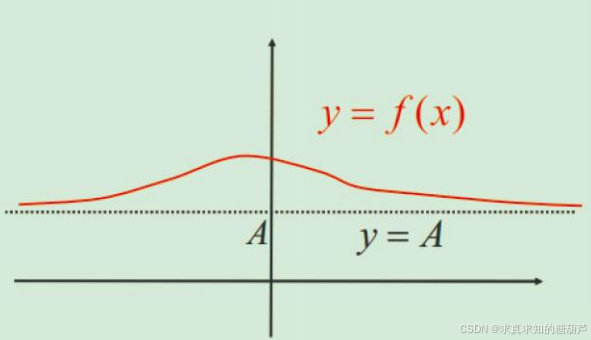
极限 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 的直观的定义

设函数 f(x)f(x)f(x) 在某个集合 {x∣∣x∣>M}(M>0)\{x\mid |x|>M\}(M>0){x∣∣x∣>M}(M>0) 上有定义。

若 x→∞x\rightarrow\inftyx→∞ 时,有 f(x)→Af(x)\rightarrow Af(x)→A ( AAA 是实数),则称函数 f(x)f(x)f(x) 当 x→∞x\rightarrow\inftyx→∞ 时有极限 AAA,

记作 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 或 f(x)→A(x→∞)f(x)\rightarrow A(x\rightarrow\infty)f(x)→A(x→∞)。

同样,以上极限定义是不严格的。

我们需要严格定义这种极限。

下面给出极限 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 的严格定义。

定义 2 设函数 f(x)f(x)f(x) 在某个集合 {x∣∣x∣>M}(M>0)\{x\mid |x|>M\}(M>0){x∣∣x∣>M}(M>0) 上有定义。

如果存在常数 AAA,对 ∀ε>0\forall\varepsilon>0∀ε>0 (无论它多么小),总存在数 X>0X>0X>0,

使得当自变量 xxx 满足不等式 ∣x∣>X|x|>X∣x∣>X 时,

对应的函数值 f(x)f(x)f(x) 都满足不等式 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε,

则称当 x→∞x\rightarrow\inftyx→∞ 时,函数 f(x)f(x)f(x) 以 AAA 为极限,

记作 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 或 f(x)→A(x→∞)f(x)\rightarrow A(x\rightarrow\infty)f(x)→A(x→∞)。

以上定义叫做极限 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 的 ε−X\varepsilon-Xε−X 定义。

几何解释

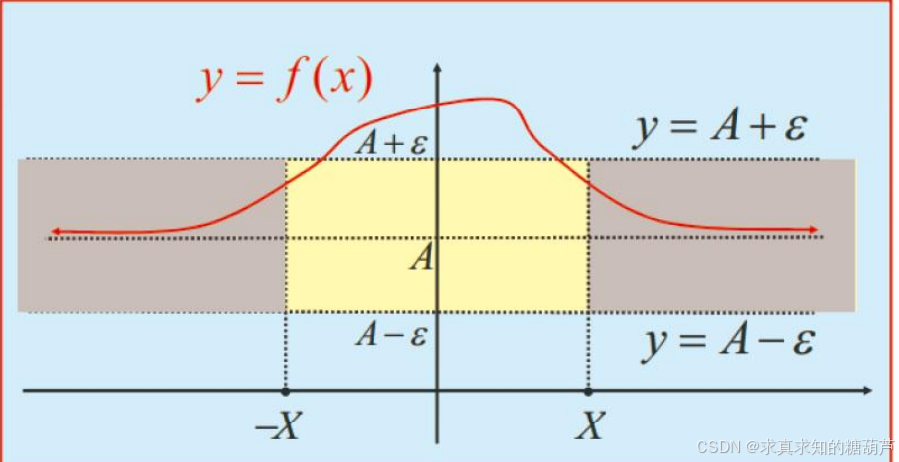
lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 的几何解释

根据定义, lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 当且仅当 ∀ε>0,∃X>0\forall\varepsilon>0,\exists X>0∀ε>0,∃X>0,

使得当 ∣x∣>X|x|>X∣x∣>X 时,就有, ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε,

即 ∀ε>0,∃δ>0,∀x∈(−∞,−X)∪(X,+∞)⇒A−ε<f(x)<A+ε\forall\varepsilon>0,\exists\delta>0,\forall x\in(-\infty,-X)\cup(X,+\infty)\Rightarrow A-\varepsilon<f(x)<A+\varepsilon∀ε>0,∃δ>0,∀x∈(−∞,−X)∪(X,+∞)⇒A−ε<f(x)<A+ε。

由此得到 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 的几何解释。

水平渐近线

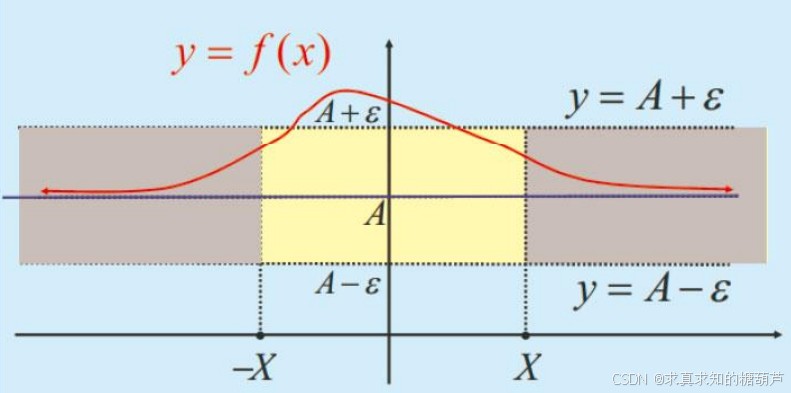
lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 表明,随着 ∣x∣|x|∣x∣ 的增加,

函数曲线 y=f(x)y=f(x)y=f(x) 与水平直线 y=Ay=Ay=A 的垂直距离将趋于 0。

水平直线 y=Ay=Ay=A 称为曲线 y=f(x)y=f(x)y=f(x) 的水平渐近线。

若 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A

则水平直线 y=Ay=Ay=A 为曲线 y=f(x)y=f(x)y=f(x) 的一条水平渐近线。

局部有界性

函数的局部有界性设 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A。

取 ε=1\varepsilon=1ε=1,则存在 X>0X>0X>0,

使得 ∀x∈(−∞,−X)∪(X,+∞)→A−1<f(x)<A+1\forall x\in(-\infty,-X)\cup(X,+\infty)\rightarrow A-1<f(x)<A+1∀x∈(−∞,−X)∪(X,+∞)→A−1<f(x)<A+1。

这表明 f(x)f(x)f(x) 在集合 (−∞,−X)∪(X,+∞)(-\infty,-X)\cup(X,+\infty)(−∞,−X)∪(X,+∞) 上有界(同济七版习题 1-3,12题)。

命题 (函数极限的局部有界性)若极限 lim⁡x→∞f(x)\lim_{x\rightarrow\infty} f(x)limx→∞f(x) 存在,

则函数 f(x)f(x)f(x) 在某个集合 {x∣∣x∣>X}\{x\mid |x|>X\}{x∣∣x∣>X} 内有界。

用定义证明极限 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 的方法 (ε−δ(\varepsilon-\delta(ε−δ 法)(《高等数学学习手册》《高等数学学习手册》《高等数学学习手册》 34页)

对于任意给定的 ε>0\varepsilon>0ε>0,从 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε 分析出 ∣x∣>φ(ε)|x|>\varphi(\varepsilon)∣x∣>φ(ε),然后令 X=φ(ε)X=\varphi(\varepsilon)X=φ(ε)。

则当 ∣x∣>X|x|>X∣x∣>X 时,就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε。

所以 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A。

单向极限

极限 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 是双向极限,

即 xxx 从正、负两个方向趋于无穷大时,函数 f(x)f(x)f(x) 以 AAA 为极限。

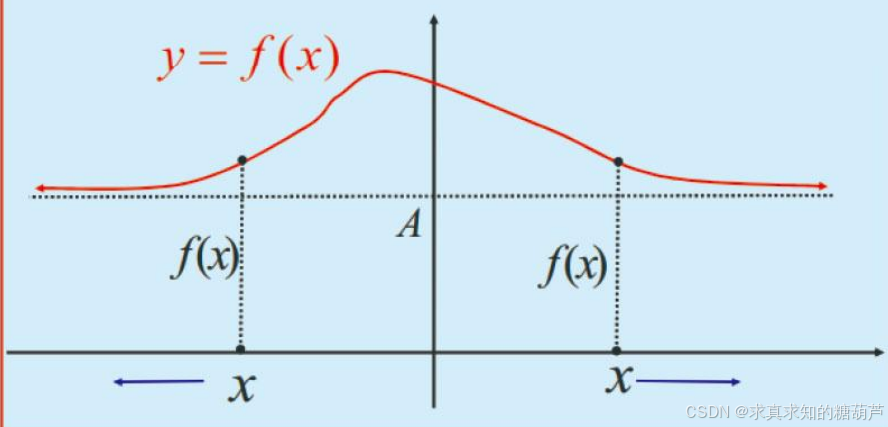
有时我们需要限制 xxx 向一个方向趋于无穷大。

此时的极限就是单向极限。

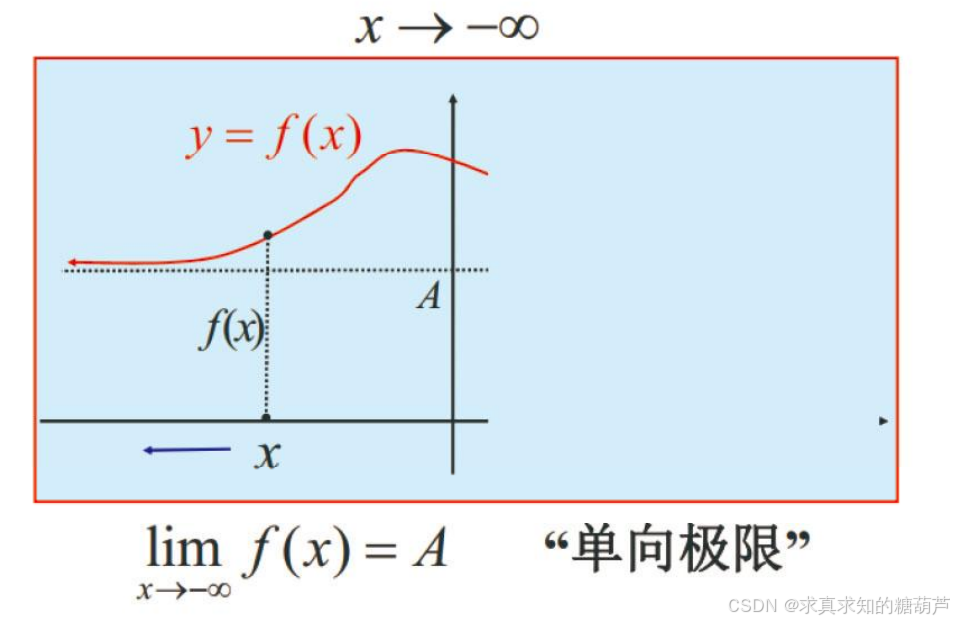
用 lim⁡x→−∞f(x)=A\lim_{x\rightarrow-\infty} f(x)=Alimx→−∞f(x)=A 表示当 xxx 向左趋于无穷大(即 xxx 趋于负无穷大,记 x→−∞x\rightarrow-\inftyx→−∞)时, f(x)→Af(x)\rightarrow Af(x)→A。

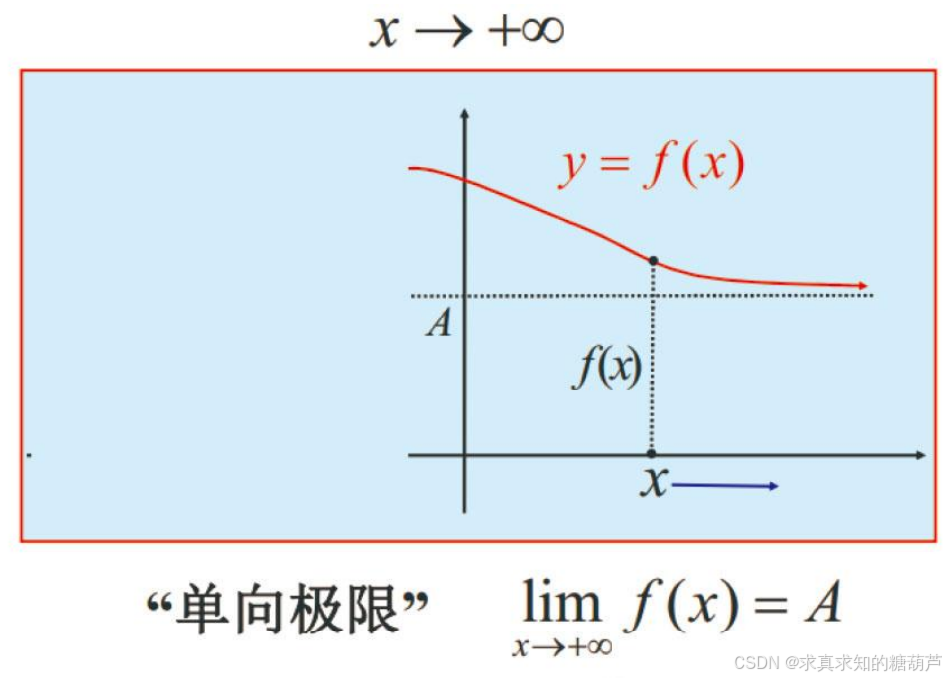
用 lim⁡x→+∞f(x)=A\lim_{x\rightarrow+\infty} f(x)=Alimx→+∞f(x)=A 表示当 xxx 向右趋于无穷大(即 xxx 趋于正无穷大,记 x→+∞x\rightarrow+\inftyx→+∞)时, f(x)→Af(x)\rightarrow Af(x)→A。

单向极限的 ε−X\varepsilon-Xε−X 定义

lim⁡x→−∞f(x)=A\lim_{x\rightarrow-\infty} f(x)=Alimx→−∞f(x)=A 当且仅当 ∀ε>0,∃X>0\forall\varepsilon>0,\exists X>0∀ε>0,∃X>0,使得当 x<−Xx<-Xx<−X 时,就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε。

lim⁡x→+∞f(x)=A\lim_{x\rightarrow+\infty} f(x)=Alimx→+∞f(x)=A 当且仅当 ∀ε>0,∃X>0\forall\varepsilon>0,\exists X>0∀ε>0,∃X>0,使得当 x>Xx>Xx>X 时,就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε。

单向极限与极限的关系

由 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A 的定义 (∀ε>0,∃X>0(\forall\varepsilon>0,\exists X>0(∀ε>0,∃X>0,使得当 ∣x∣>X|x|>X∣x∣>X 时,就有 ∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε ))) 可知:若 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A,则 lim⁡x→−∞f(x)=A\lim_{x\rightarrow-\infty} f(x)=Alimx→−∞f(x)=A 且 lim⁡x→+∞f(x)=A\lim_{x\rightarrow+\infty} f(x)=Alimx→+∞f(x)=A

(双向极限存在,则单向极限也存在,且相等。)

(因为 x<−Xx<-Xx<−X 或 x>X⇒∣x∣>Xx>X\Rightarrow|x|>Xx>X⇒∣x∣>X )。

反之, lim⁡x→−∞f(x)=A\lim_{x\rightarrow-\infty} f(x)=Alimx→−∞f(x)=A (或 lim⁡x→+∞f(x)=A\lim_{x\rightarrow+\infty} f(x)=Alimx→+∞f(x)=A) 不能得出 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A。

(单向极限存在，不能保证双向极限也存在)

(例如,左极限 lim⁡x→−∞f(x)=A\lim_{x\rightarrow-\infty} f(x)=Alimx→−∞f(x)=A 不能确定 000 的右侧的情况)。

但是,如果 lim⁡x→−∞f(x)=A\lim_{x\rightarrow-\infty} f(x)=Alimx→−∞f(x)=A 并且 lim⁡x→+∞f(x)=A\lim_{x\rightarrow+\infty} f(x)=Alimx→+∞f(x)=A,则可以证明 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A。

命题极限 lim⁡x→∞f(x)\lim_{x\rightarrow\infty} f(x)limx→∞f(x) 存在的充分必要条件是左极限 lim⁡x→−∞f(x)\lim_{x\rightarrow-\infty} f(x)limx→−∞f(x) 和右极限 lim⁡x→+∞f(x)\lim_{x\rightarrow+\infty} f(x)limx→+∞f(x) 存在且相等。

即 lim⁡x→∞f(x)=A⇔lim⁡x→−∞f(x)=A=lim⁡x→+∞f(x)\lim_{x\rightarrow\infty} f(x)=A\Leftrightarrow\lim_{x\rightarrow-\infty} f(x)=A=\lim_{x\rightarrow+\infty} f(x)limx→∞f(x)=A⇔limx→−∞f(x)=A=limx→+∞f(x)

(同济七版习题1-3,10题。证明见高数视频)

推论如果 lim⁡x→−∞f(x)≠lim⁡x→+∞f(x)\lim_{x\rightarrow-\infty} f(x)\neq\lim_{x\rightarrow+\infty} f(x)limx→−∞f(x)=limx→+∞f(x) 或至少有一个不存在,
则极限 lim⁡x→∞f(x)\lim_{x\rightarrow\infty} f(x)limx→∞f(x) 不存在。

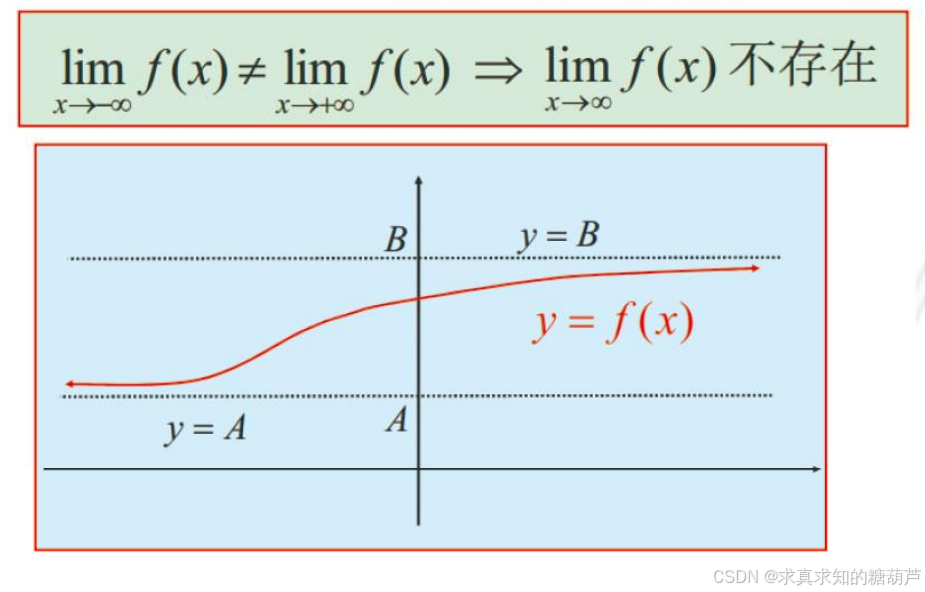
例如,对 y=arctan⁡xy=\arctan xy=arctanx,有 lim⁡x→−∞arctan⁡x=−π2,lim⁡x→+∞arctan⁡x=π2\lim_{x\rightarrow-\infty}\arctan x=-\frac{\pi}{2},\lim_{x\rightarrow+\infty}\arctan x=\frac{\pi}{2}limx→−∞arctanx=−2π,limx→+∞arctanx=2π。

因为 lim⁡x→−∞arctan⁡x≠lim⁡x→+∞arctan⁡x\lim_{x\rightarrow-\infty}\arctan x\neq\lim_{x\rightarrow+\infty}\arctan xlimx→−∞arctanx=limx→+∞arctanx,所以极限 lim⁡x→∞arctan⁡x\lim_{x\rightarrow\infty}\arctan xlimx→∞arctanx 不存在。

例求极限 lim⁡x→+∞sgnx\lim_{x\rightarrow+\infty} \text{sgn} xlimx→+∞sgnx, lim⁡x→−∞sgnx\lim_{x\rightarrow-\infty} \text{sgn} xlimx→−∞sgnx 和 lim⁡x→∞sgnx\lim_{x\rightarrow\infty} \text{sgn} xlimx→∞sgnx,其中 sgnx\text{sgn} xsgnx 是符号函数。

解
sgnx={1,x>00,x=0−1,x<0 \text{sgn} x= \begin{cases} 1, & x>0 \\ 0, & x=0 \\ -1, & x<0 \end{cases} sgnx=⎩ ⎨ ⎧1,0,−1,x>0x=0x<0

lim⁡x→−∞sgnx=lim⁡x→−∞(−1)=−1,lim⁡x→+∞sgnx=lim⁡x→+∞1=1. \lim_{x\rightarrow-\infty}\text{sgn} x=\lim_{x\rightarrow-\infty}(-1)=-1,\quad\lim_{x\rightarrow+\infty}\text{sgn} x=\lim_{x\rightarrow+\infty} 1=1. x→−∞limsgnx=x→−∞lim(−1)=−1,x→+∞limsgnx=x→+∞lim1=1.

因为 lim⁡x→−∞sgnx≠lim⁡x→+∞sgnx\lim_{x\rightarrow-\infty}\text{sgn} x\neq\lim_{x\rightarrow+\infty}\text{sgn} xlimx→−∞sgnx=limx→+∞sgnx,所以 lim⁡x→∞sgnx\lim_{x\rightarrow\infty}\text{sgn} xlimx→∞sgnx 不存在。

更多单向极限存在但双向极限不存在的例子(见《高等数学学习手册》第 35页):

函数极限的性质

就自变量的变化趋势而言,函数极限有六种:
lim⁡x→x0f(x),lim⁡x→x0−f(x),lim⁡x→x0+f(x)\lim_{x\rightarrow x_0} f(x),\lim_{x\rightarrow x_0^{-}} f(x),\lim_{x\rightarrow x_0^{+}} f(x)limx→x0f(x),limx→x0−f(x),limx→x0+f(x) 和 lim⁡x→∞f(x),lim⁡x→−∞f(x),lim⁡x→+∞f(x)\lim_{x\rightarrow\infty} f(x),\lim_{x\rightarrow-\infty} f(x),\lim_{x\rightarrow+\infty} f(x)limx→∞f(x),limx→−∞f(x),limx→+∞f(x)

以后用 lim⁡f(x)\lim f(x)limf(x) 表示这六种极限过程的某一种。

下面介绍函数极限的性质。

定理 1 (函数极限的唯一性)如果极限 lim⁡f(x)\lim f(x)limf(x) 存在,则极限是唯一的。

极限 lim⁡x→x0f(x)\lim_{x\rightarrow x_0} f(x)limx→x0f(x) 唯一性的证明见高数视频。

定理 2 (函数极限的局部有界性)

(1)如果 lim⁡x→x0f(x)=A\lim_{x\rightarrow x_0} f(x)=Alimx→x0f(x)=A,那么存在正数 MMM 和 δ\deltaδ,使得 ∣f(x)∣≤M(0<∣x−x0∣<δ)|f(x)|\leq M (0<|x-x_0|<\delta)∣f(x)∣≤M(0<∣x−x0∣<δ)。

即函数 f(x)f(x)f(x) 在 x0x_0x0 的某个去心邻域内有界。(前面已经证明)

(2)如果 lim⁡x→∞f(x)=A\lim_{x\rightarrow\infty} f(x)=Alimx→∞f(x)=A,那么存在正数 MMM 和 XXX,使得 ∣f(x)∣≤M(∣x∣>X)|f(x)|\leq M (|x|>X)∣f(x)∣≤M(∣x∣>X)。

即函数 f(x)f(x)f(x) 在某个集合 {x∣∣x∣>X}\{x\mid |x|>X\}{x∣∣x∣>X} 内有界。

定理3 (函数极限的局部保号性)

(1)若极限 lim⁡x→x0f(x)>0\lim_{x\rightarrow x_0} f(x)>0limx→x0f(x)>0,则函数 f(x)f(x)f(x) 在 x0x_0x0 的某个去心邻域内是正的。

(2)若极限 lim⁡x→x0f(x)<0\lim_{x\rightarrow x_0} f(x)<0limx→x0f(x)<0,则函数 f(x)f(x)f(x) 在 x0x_0x0 的某个去心邻域内是负的。

即,以正数为极限的函数在 x0x_0x0 附近是正的,以负数为极限的函数在 x0x_0x0 附近是负的。

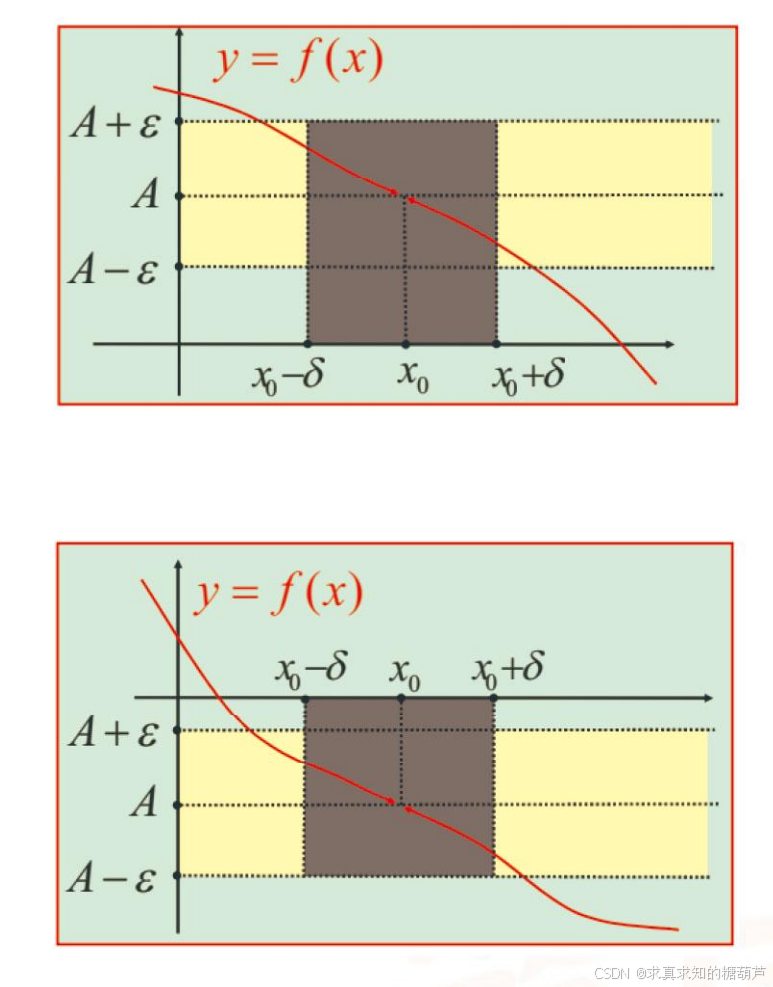
推论若 lim⁡x→x0f(x)>lim⁡x→x0g(x)\lim_{x\rightarrow x_0} f(x)>\lim_{x\rightarrow x_0} g(x)limx→x0f(x)>limx→x0g(x),则在 x0x_0x0 的某个去心邻域内,有 f(x)>g(x)f(x)>g(x)f(x)>g(x)。

(极限较大的函数,局部较大。)

证令 F(x)=f(x)−g(x)F(x)=f(x)-g(x)F(x)=f(x)−g(x),

则 lim⁡x→x0F(x)=lim⁡x→x0[f(x)−g(x)]=lim⁡x→x0f(x)−lim⁡x→x0g(x)>0\lim_{x\rightarrow x_0} F(x)=\lim_{x\rightarrow x_0}[f(x)-g(x)]=\lim_{x\rightarrow x_0} f(x)-\lim_{x\rightarrow x_0} g(x)>0limx→x0F(x)=limx→x0[f(x)−g(x)]=limx→x0f(x)−limx→x0g(x)>0,

由定理 3(1),在 x0x_0x0 的某个去心邻域内, F(x)=f(x)−g(x)>0F(x)=f(x)-g(x)>0F(x)=f(x)−g(x)>0,结论成立。

定理3'

(1)若极限 lim⁡x→x0f(x)=A>0\lim_{x\rightarrow x_0} f(x)=A>0limx→x0f(x)=A>0,则在 x0x_0x0 的某个去心邻域内 f(x)>A2f(x)>\frac{A}{2}f(x)>2A。

(2)若极限 lim⁡x→x0f(x)=A<0\lim_{x\rightarrow x_0} f(x)=A<0limx→x0f(x)=A<0,则在 x0x_0x0 的某个去心邻域内 f(x)<A2f(x)<\frac{A}{2}f(x)<2A。

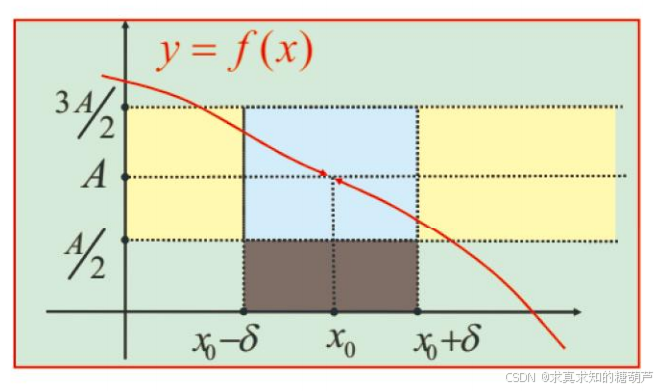
推论 1 反过来用

(1)如果在 x0x_0x0 的某个去心邻域内, f(x)≥0f(x)\geq 0f(x)≥0,则 lim⁡x→x0f(x)≥0\lim_{x\rightarrow x_0} f(x)\geq 0limx→x0f(x)≥0。(假定极限存在)

(非负函数的极限一定非负，非正函数的极限一定非正。)

注意:正函数的极限不一定是正的，可以为零。

例如,正函数 y=x2(x≠0)y=x^2(x\neq 0)y=x2(x=0) 的极限 lim⁡x→0x2=0\lim_{x\rightarrow 0} x^2=0limx→0x2=0。

(2)如果在 x0x_0x0 的某个去心邻域内, f(x)≤0f(x)\leq 0f(x)≤0,则 lim⁡x→x0f(x)≤0\lim_{x\rightarrow x_0} f(x)\leq 0limx→x0f(x)≤0。

推论 2 若 f(x)≥g(x)f(x)\geq g(x)f(x)≥g(x),则 lim⁡f(x)≥lim⁡g(x)\lim f(x)\geq\lim g(x)limf(x)≥limg(x) (假定极限存在)(大函数的极限较大。)

证令 F(x)=f(x)−g(x)F(x)=f(x)-g(x)F(x)=f(x)−g(x),再利用推论 1即得。

详证见教材第41页,定理5.

例设 lim⁡x→0f(x)sin⁡x=−1\lim_{x\rightarrow 0}\frac{f(x)}{\sin x}=-1limx→0sinxf(x)=−1,则()

(A)f(x)f(x)f(x)在x=0x=0x=0的某个去心邻域内为正;

(B) f(x)f(x)f(x) 在 x=0x=0x=0 的某个去心邻域内为负;
(C)(C)(C) f(x)f(x)f(x) 在 x=0x=0x=0 的某个左半邻域内为正,在 x=0x=0x=0 的某个右半邻域内为负;

(D) f(x)f(x)f(x) 在 x=0x=0x=0 的某个左半邻域内为负,在 x=0x=0x=0 的某个右半邻域内为正。

解 lim⁡x→0f(x)sin⁡x=−1<0\lim_{x\rightarrow 0}\frac{f(x)}{\sin x}=-1<0limx→0sinxf(x)=−1<0,由函数极限的局部保号性,在 x=0x=0x=0 的某个去心邻域 UUU 内 f(x)sin⁡x<0\frac{f(x)}{\sin x}<0sinxf(x)<0。

即在 UUU 内分子与分母异号。

因为 sin⁡x\sin xsinx 在 x=0x=0x=0 的两侧附近左负右正(下图),所以 f(x)f(x)f(x) 在 x=0x=0x=0 的两侧附近左正右负。选(C)(C)(C)。