MATLAB路径规划仿真 轨迹规划,船舶轨迹跟踪控制,数学模型基于两轮差速的小车模型,用PID环节对航向角进行控制,迫使小车走向目标,或用PID环节对航向角和距离进行控制,迫使小车走向目标 LQR 算法 可自行小车起点坐标
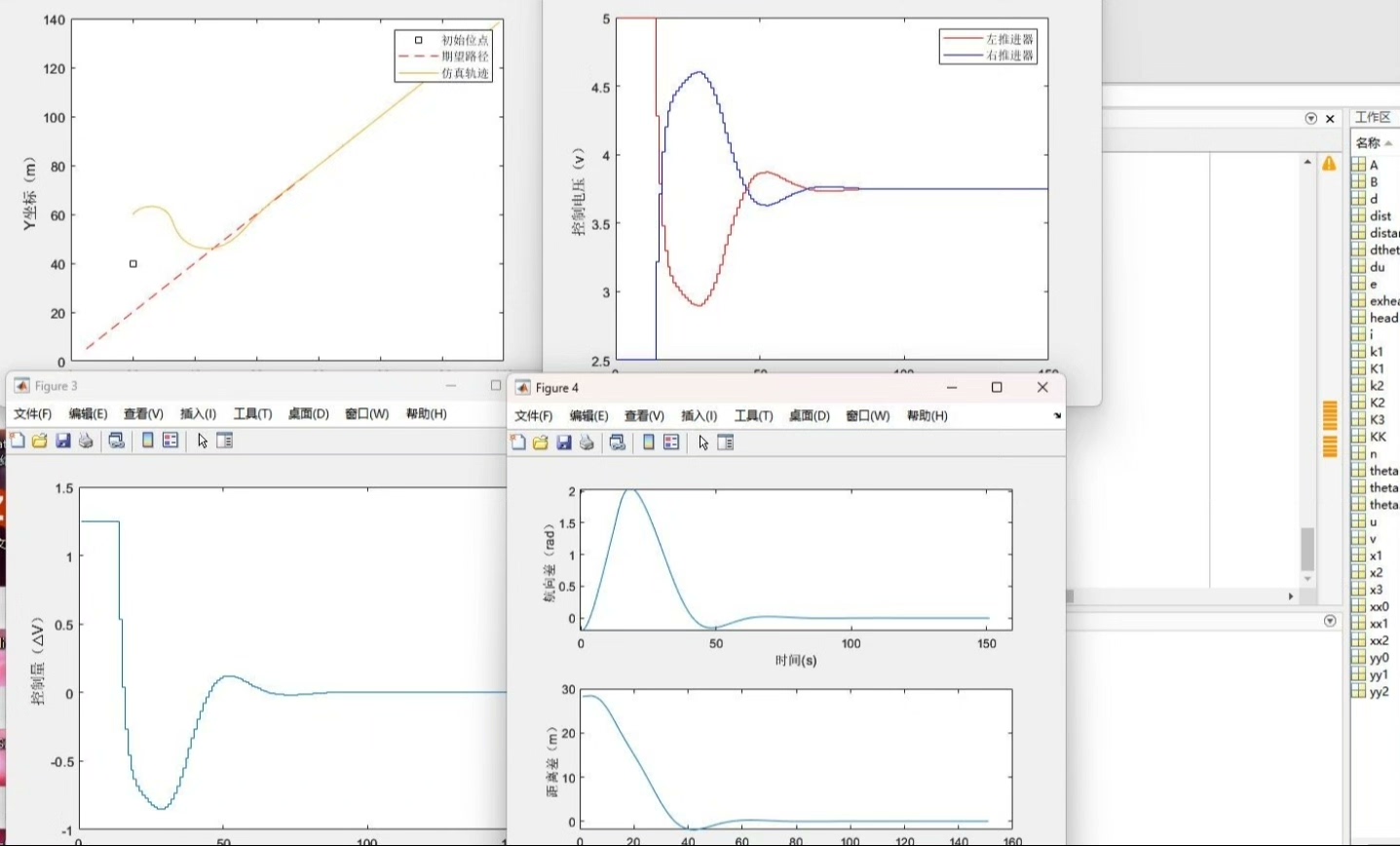
最近在研究路径规划和轨迹跟踪控制,借助 MATLAB 做了不少有意思的仿真实验。今天就来和大家分享一下,我是如何利用两轮差速的小车模型,通过 PID 环节和 LQR 算法让小车走向目标的。
两轮差速小车模型
在开始仿真之前,我们得先有一个合适的数学模型。这里我采用的是两轮差速的小车模型。简单来说,两轮差速小车通过控制左右轮的转速差来实现转向和前进。假设小车的状态向量包含位置 (x, y) 和航向角 \\theta,那么小车的运动学方程可以表示为:
matlab
% 两轮差速小车运动学方程
function dx = diff_drive_kinematics(x, u, L)
% x 是状态向量 [x; y; theta]
% u 是控制输入 [v; omega],v 是线速度,omega 是角速度
% L 是两轮之间的轴距
dx = [cos(x(3))*u(1);
sin(x(3))*u(1);
u(2)];
end代码分析
这个函数接收三个参数:状态向量 x、控制输入 u 和轴距 L。通过三角函数计算出小车在 x 和 y 方向上的速度分量,再加上航向角的变化率,就得到了状态向量的导数 dx。这个导数描述了小车状态随时间的变化情况。
PID 控制环节
有了小车模型,接下来就是要让小车朝着目标点前进。这里我们可以使用 PID 控制环节来对航向角或者航向角和距离进行控制。
仅对航向角进行控制
matlab
% PID 控制航向角
function u = pid_heading_control(x, goal, Kp, Ki, Kd)
% x 是当前状态 [x; y; theta]
% goal 是目标点 [x_goal; y_goal]
% Kp, Ki, Kd 是 PID 控制器的参数
error_theta = atan2(goal(2) - x(2), goal(1) - x(1)) - x(3);
% 误差范围限制在 [-pi, pi]
error_theta = atan2(sin(error_theta), cos(error_theta));
persistent integral_error_theta
if isempty(integral_error_theta)
integral_error_theta = 0;
end
derivative_error_theta = error_theta - (x(3) - x(3_prev));
% 计算控制输入
u(1) = 1; % 固定线速度
u(2) = Kp*error_theta + Ki*integral_error_theta + Kd*derivative_error_theta;
integral_error_theta = integral_error_theta + error_theta;
x(3_prev) = x(3);
return
end代码分析
这个函数实现了一个简单的 PID 控制器,用于控制小车的航向角。首先计算当前位置与目标点之间的夹角,然后与当前航向角作差得到误差。通过积分和微分环节,结合比例系数,计算出角速度控制输入。线速度这里固定为 1,实际应用中可以根据情况调整。
对航向角和距离进行控制
matlab
% PID 控制航向角和距离
function u = pid_distance_heading_control(x, goal, Kp_d, Ki_d, Kd_d, Kp_theta, Ki_theta, Kd_theta)
% x 是当前状态 [x; y; theta]
% goal 是目标点 [x_goal; y_goal]
% Kp_d, Ki_d, Kd_d 是距离控制的 PID 参数
% Kp_theta, Ki_theta, Kd_theta 是航向角控制的 PID 参数
% 计算距离误差
error_d = norm(goal - x(1:2));
% 计算航向角误差
error_theta = atan2(goal(2) - x(2), goal(1) - x(1)) - x(3);
error_theta = atan2(sin(error_theta), cos(error_theta));
persistent integral_error_d
if isempty(integral_error_d)
integral_error_d = 0;
end
derivative_error_d = error_d - (norm(x(1:2) - x(1:2_prev)));
persistent integral_error_theta
if isempty(integral_error_theta)
integral_error_theta = 0;
end
derivative_error_theta = error_theta - (x(3) - x(3_prev));
% 计算控制输入
u(1) = Kp_d*error_d + Ki_d*integral_error_d + Kd_d*derivative_error_d;
u(2) = Kp_theta*error_theta + Ki_theta*integral_error_theta + Kd_theta*derivative_error_theta;
integral_error_d = integral_error_d + error_d;
integral_error_theta = integral_error_theta + error_theta;
x(1:2_prev) = x(1:2);
x(3_prev) = x(3);
return
end代码分析
这个函数在前面的基础上,增加了对距离的控制。通过计算当前位置与目标点之间的距离误差,同样使用 PID 控制器计算线速度控制输入。这样可以让小车在接近目标点时自动调整速度,提高控制效果。
LQR 算法
除了 PID 控制,我们还可以使用 LQR 算法来进行轨迹跟踪控制。LQR 算法可以根据系统的状态和目标状态,计算出最优的控制输入。
matlab
% LQR 控制器
function u = lqr_controller(x, goal, A, B, Q, R)
% x 是当前状态 [x; y; theta]
% goal 是目标状态 [x_goal; y_goal; theta_goal]
% A, B 是系统的状态空间矩阵
% Q, R 是 LQR 控制器的权重矩阵
error = x - goal;
K = lqr(A, B, Q, R);
u = -K*error;
return
end代码分析
这个函数实现了一个简单的 LQR 控制器。首先计算当前状态与目标状态之间的误差,然后使用 lqr 函数计算出最优控制增益矩阵 K。最后根据误差和增益矩阵计算出控制输入。
仿真实验
现在我们可以把这些部分组合起来,进行仿真实验了。假设小车的起点坐标为 [0; 0; 0],目标点坐标为 [10; 10]。
matlab
% 仿真参数
dt = 0.1; % 时间步长
T = 20; % 仿真时间
t = 0:dt:T;
N = length(t);
% 小车初始状态
x0 = [0; 0; 0];
x = zeros(3, N);
x(:, 1) = x0;
% 目标点
goal = [10; 10];
% PID 参数
Kp = 1;
Ki = 0.1;
Kd = 0.01;
% 轴距
L = 0.5;
% 仿真循环
for i = 1:N-1
% 计算控制输入
u = pid_heading_control(x(:, i), goal, Kp, Ki, Kd);
% 更新小车状态
dx = diff_drive_kinematics(x(:, i), u, L);
x(:, i+1) = x(:, i) + dx*dt;
end
% 绘制轨迹
figure;
plot(x(1, :), x(2, :), 'b-', 'LineWidth', 2);
hold on;
plot(goal(1), goal(2), 'ro', 'MarkerSize', 10);
xlabel('X');
ylabel('Y');
title('小车轨迹');
grid on;代码分析
这个仿真代码首先设置了仿真参数,包括时间步长、仿真时间等。然后初始化小车的状态和目标点。在仿真循环中,不断计算控制输入,更新小车的状态。最后绘制小车的轨迹。
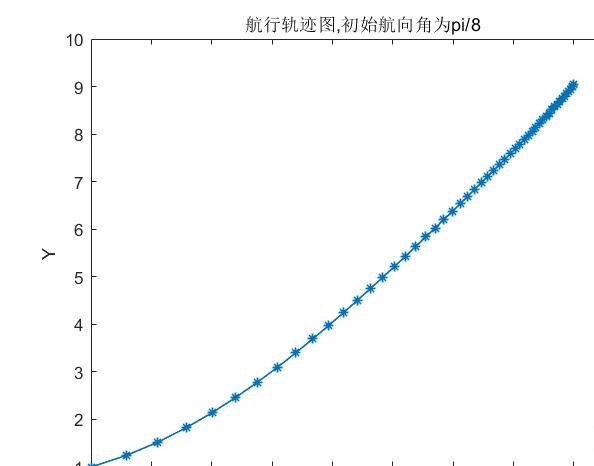
MATLAB路径规划仿真 轨迹规划,船舶轨迹跟踪控制,数学模型基于两轮差速的小车模型,用PID环节对航向角进行控制,迫使小车走向目标,或用PID环节对航向角和距离进行控制,迫使小车走向目标 LQR 算法 可自行小车起点坐标
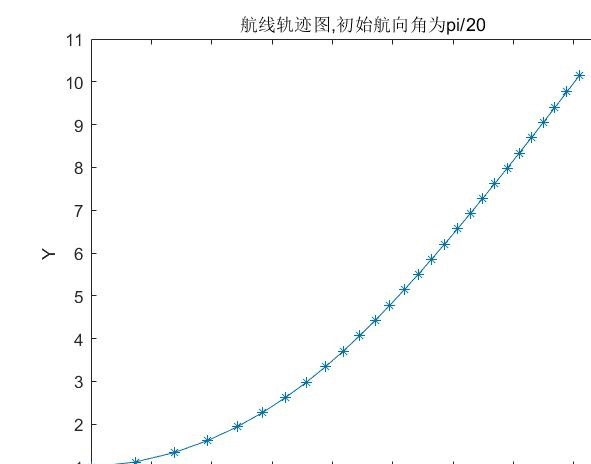
通过这些代码和算法,我们可以实现两轮差速小车的路径规划和轨迹跟踪控制。PID 控制和 LQR 算法各有优缺点,在实际应用中可以根据具体情况选择合适的方法。希望这篇文章能对大家有所帮助!
以上就是我这次的分享,后续还会继续探索更多有趣的路径规划和控制算法,欢迎大家一起交流讨论!