算法刷题--二叉树（一）

文章目录

- [1、144 二叉树的前序遍历（递归版）](#1、144 二叉树的前序遍历（递归版）)
- - 思路推演：逻辑是怎么流动的？
- [2、94 二叉树的中序遍历（递归版）](#2、94 二叉树的中序遍历（递归版）)
- [3、145 二叉树的后序遍历（递归版）](#3、145 二叉树的后序遍历（递归版）)
- [4、144 二叉树的前序遍历（迭代版）](#4、144 二叉树的前序遍历（迭代版）)
- - [1. 观察切入点：手动维护"待办清单"](#1. 观察切入点：手动维护“待办清单”)
  - [2. 核心原理：右孩子先入栈](#2. 核心原理：右孩子先入栈)
  - [3. C 语言实现代码](#3. C 语言实现代码)
  - [4. 逻辑推演：为什么顺序不会乱？](#4. 逻辑推演：为什么顺序不会乱？)
  - [5. 避坑指南](#5. 避坑指南)
  - [🚀 进阶思考](#🚀 进阶思考)
  - [1. 核心原理：为什么要用 `**`（二级指针）？](#1. 核心原理：为什么要用 **（二级指针）？)
  - [2. 内存布局拆解](#2. 内存布局拆解)
  - [3. 避坑指南：它在迭代中是怎么干活的？](#3. 避坑指南：它在迭代中是怎么干活的？)
  - - **这里有一个面试常问的坑：**
  - 总结
- [5、94 二叉树的中序遍历（迭代版）](#5、94 二叉树的中序遍历（迭代版）)
- - [1. 观察切入点：处理时机的滞后性](#1. 观察切入点：处理时机的滞后性)
  - [2. 核心原理：先推入，后弹出](#2. 核心原理：先推入，后弹出)
  - [3. C 语言代码实现](#3. C 语言代码实现)
  - [4. 思路推演：逻辑是怎么"丝滑"起来的？](#4. 思路推演：逻辑是怎么“丝滑”起来的？)
  - [5. 避坑指南：中序迭代的"精髓"](#5. 避坑指南：中序迭代的“精髓”)
  - [📊 三大遍历迭代法对比总结](#📊 三大遍历迭代法对比总结)
- [6、145 二叉树的后序遍历（迭代版）](#6、145 二叉树的后序遍历（迭代版）)
- [7、102 二叉树的层序遍历](#7、102 二叉树的层序遍历)
- - [1. 核心模型：队列 (Queue)](#1. 核心模型：队列 (Queue))
  - [2. 关键技巧：固定窗口大小 (Batch Processing)](#2. 关键技巧：固定窗口大小 (Batch Processing))
  - [3. C 语言实现的难点：内存管理](#3. C 语言实现的难点：内存管理)
  - [4. 思路推演：BFS 模板](#4. 思路推演：BFS 模板)
  - 内存结构深度详解
  - 为什么这个解法很快？
  - 提交前的最后检查
- [8、107 二叉树的层序遍历②](#8、107 二叉树的层序遍历②)
- [9、199 二叉树的右视图](#9、199 二叉树的右视图)
- [10、637 二叉树的层平均值](#10、637 二叉树的层平均值)
- [11、429 N叉树的层序遍历](#11、429 N叉树的层序遍历)
- - [1. 核心区别：观察节点结构](#1. 核心区别：观察节点结构)
  - [2. 解题思路：从二叉树平移到 N 叉树](#2. 解题思路：从二叉树平移到 N 叉树)
  - - 逻辑对比：
  - [3. C 语言代码实现的关键点](#3. C 语言代码实现的关键点)
  - [4. 总结](#4. 总结)
- [12、515 在每个树行中找最大值](#12、515 在每个树行中找最大值)
- [13、116 填充每个节点的下一个右侧节点指针](#13、116 填充每个节点的下一个右侧节点指针)
- - [1. 思路解析：利用"上帝视角"的横向连接](#1. 思路解析：利用“上帝视角”的横向连接)
  - - 核心逻辑分为两种连接情况：
  - [2. 完整代码实现 (C 语言)](#2. 完整代码实现 (C 语言))
  - [3. 逻辑推演：为什么不需要队列？](#3. 逻辑推演：为什么不需要队列？)
  - [4. 复杂度对比](#4. 复杂度对比)
  - [5. 避坑指南](#5. 避坑指南)
- [14、117 填充每个节点的下一个右侧节点指针](#14、117 填充每个节点的下一个右侧节点指针)
- [15、104 二叉树的最大深度](#15、104 二叉树的最大深度)
- - [1. 递归思路：自底向上的"高度汇报"](#1. 递归思路：自底向上的“高度汇报”)
  - [2. 迭代思路：层序遍历计数（BFS）](#2. 迭代思路：层序遍历计数（BFS）)
  - [3. C 语言代码实现](#3. C 语言代码实现)
  - [4. 复杂度分析](#4. 复杂度分析)
  - [💡 深度思考：深度 (Depth) vs 高度 (Height)](#💡 深度思考：深度 (Depth) vs 高度 (Height))
  - 总结
- [16、111 二叉树的最小深度](#16、111 二叉树的最小深度)
- - [1. 核心陷阱：什么是"最小深度"？](#1. 核心陷阱：什么是“最小深度”？)
  - [2. 思路一：递归法（DFS）](#2. 思路一：递归法（DFS）)
  - [3. 思路二：层序遍历（BFS）------ 推荐方案](#3. 思路二：层序遍历（BFS）—— 推荐方案)
  - [4. BFS 迭代法实现逻辑](#4. BFS 迭代法实现逻辑)
  - [💡 总结对比](#💡 总结对比)
- [17、226 翻转二叉树](#17、226 翻转二叉树)
- - [1. 递归思路：自顶向下的"镜像反转"](#1. 递归思路：自顶向下的“镜像反转”)
  - [2. 迭代思路：层序遍历（BFS）](#2. 迭代思路：层序遍历（BFS）)
  - [3. C 语言代码实现](#3. C 语言代码实现)
  - [4. 深度解析：为什么这能行？](#4. 深度解析：为什么这能行？)
  - [5. 复杂度分析](#5. 复杂度分析)
  - [💡 总结建议](#💡 总结建议)

1、144 二叉树的前序遍历（递归版）

题目：

代码：

递归三要素：

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 void preorder(struct TreeNode* root,int* res,int* returnSize){
    if(root == NULL){
        return;
    }
    res[(*returnSize)++] = root->val;
    preorder(root->left,res,returnSize);
    preorder(root->right,res,returnSize);
 }
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    int* res = (int*)malloc(sizeof(int)*100);
    *returnSize = 0;
    preorder(root,res,returnSize);
    return res;
}

前序遍历的逻辑顺序非常直观，即：根节点 -> 左子树 -> 右子树。

思路推演：逻辑是怎么流动的？

假设有一棵树：[1, 2, 3]（1是根，2是左，3是右）。

调用 preorder(1)

res[0] = 1，returnSize 变为 1。
去左边：调用 preorder(2)。

调用 preorder(2)：

res[1] = 2，returnSize 变为 2。
再去 2 的左边（NULL），返回；去 2 的右边（NULL），返回。

回到 preorder(1)：

左边执行完了，去右边：调用 preorder(3)。

调用 preorder(3)：

res[2] = 3，returnSize 变为 3。
左右皆 NULL，返回。

结束：得到 res = [1, 2, 3]。

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

2、94 二叉树的中序遍历（递归版）

题目：

代码：

如果把前序递归弄懂了其实中序和后序就是res[(*returnSize)++] = root->val;这行代码换了个位置而已。

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 void inorder(struct TreeNode* root,int* res,int* returnSize){
    if(root == NULL){
        return;
    }
    inorder(root->left,res,returnSize);
    res[(*returnSize)++] = root->val;
    inorder(root->right,res,returnSize);
 }
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    int* res = (int*)malloc(sizeof(int)*100);
    *returnSize = 0;
    inorder(root,res,returnSize);
    return res;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

3、145 二叉树的后序遍历（递归版）

题目：

代码：

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 void postorder(struct TreeNode* root,int* res,int* returnSize){
    if(root == NULL){
        return;
    }
    postorder(root->left,res,returnSize);
    postorder(root->right,res,returnSize);
    res[(*returnSize)++] = root->val;
 }
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    int* res = (int*)malloc(sizeof(int)*100);
    *returnSize = 0;
    postorder(root,res,returnSize);
    return res;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

4、144 二叉树的前序遍历（迭代版）

题目：

代码：

1. 观察切入点：手动维护"待办清单"

递归的逻辑：系统自动帮我们记住了"处理完左边，还要回来处理右边"。
迭代的矛盾：当我们向下访问左子树时，如果不把右子树"存起来"，我们就再也找不回它了。
工具选择 ：我们需要一个栈（Stack） 。栈的特性是"后进先出"，这完美契合了：后看到的右子树，要在处理完左边后，先被拿出来处理。

2. 核心原理：右孩子先入栈

前序遍历是 根 -> 左 -> 右 。

当我们把根节点弹出并处理后，为了让左孩子 先被处理，根据栈的特性，我们必须先让右孩子入栈，再让左孩子入栈。这样，左孩子就会位于栈顶，下次循环优先弹出。

3. C 语言实现代码

在 C 语言中，我们需要手动模拟一个简单的栈。

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 * int val;
 * struct TreeNode *left;
 * struct TreeNode *right;
 * };
 */

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    if (root == NULL) return NULL;

    // 1. 初始化结果数组和辅助栈
    int* res = (int*)malloc(sizeof(int) * 100); // 节点数不超过100
    struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 100);
    int top = 0;

    // 2. 根节点入栈
    stack[top++] = root;

    // 3. 开始迭代推演
    while (top > 0) {
        // 弹出栈顶元素
        struct TreeNode* node = stack[--top];
        
        // 访问当前节点（根）
        res[(*returnSize)++] = node->val;

        // 关键：先压入右孩子，再压入左孩子
        // 这样弹出的顺序就是：左 -> 右
        if (node->right != NULL) {
            stack[top++] = node->right;
        }
        if (node->left != NULL) {
            stack[top++] = node->left;
        }
    }

    free(stack); // 释放辅助栈空间
    return res;
}

4. 逻辑推演：为什么顺序不会乱？

假设树结构为：1 是根，2 是左，3 是右。

初始状态 ：栈 [1]。
第一次循环 ：弹出 1，存入结果。

把 1 的右孩子 3 压入，栈 [3]。
把 1 的左孩子 2 压入，栈 [3, 2]。

第二次循环 ：弹出栈顶 2（左孩子），存入结果。

2 没有子节点，不压栈。栈剩下 [3]。

第三次循环 ：弹出栈顶 3（右孩子），存入结果。
结束：结果数组 [1, 2, 3]。

5. 避坑指南

空树处理 ：迭代法必须先判断 if (root == NULL)，否则在压栈时会出错。
入栈顺序：这是最容易写反的地方。记住**"先进后出"**，想先访问左，就必须后压左。
栈的大小：在 C 语言中，栈的深度最坏情况下等于树的高度（退化成链表时为 n）。

🚀 进阶思考

迭代法的真正威力在于：它能让我们在中途停下来 。比如我们要找二叉树中第一个值大于 10 的节点，迭代法找到就可以立刻跳出循环，而递归法需要多层 return 嵌套。

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 100);详解这段话

这句话是 C 语言中处理二叉树迭代 最核心的基础，它实际上是在手动搭建一个"存放指针的货架"。

我们可以通过你的思维模型，从三个维度拆解这句"套娃式"的代码：

1. 核心原理：为什么要用 `**`（二级指针）？

观察点：栈里存的是什么？
我们要存的是二叉树的节点。
在 C 语言中，一个节点是用 struct TreeNode* 表示的。
推演过程：
如果你要存一个整数，你需要 int* 来指向一块内存。
如果你要存一堆整数，你需要 int** 或 int array[]。
同理，我们要存一堆节点指针 ，所以我们需要一个指向"节点指针"的指针，即 struct TreeNode**。

形象化理解：

struct TreeNode 是书本的内容。

struct TreeNode* 是书的索引（指针）。

struct TreeNode** 是索引目录（栈）。

2. 内存布局拆解

我们将这行代码从右向左"切开"来看：

sizeof(struct TreeNode*)：

计算的是一个指针的大小（在 64 位系统下通常是 8 字节）。
注意：这里不是计算节点本身的大小，因为栈里只存地址。

* 100：

在堆区开辟连续的空间，足以容纳 100 个地址。

(struct TreeNode**)：

强制类型转换 。malloc 返回的是无意义的 void*，我们要告诉编译器："请把这块地皮看作是一个专门存放 TreeNode 指针的数组。"

struct TreeNode** stack：

定义一个名叫 stack 的变量，它指向这个数组的开头。

3. 避坑指南：它在迭代中是怎么干活的？

在你的迭代代码中，stack 的用法如下：

压栈 (stack[top++] = root)：
实际上是把 root 这个地址，填进了 stack 数组的第 top 个格子。
出栈 (node = stack[--top])：
从 stack 数组里把地址取出来，赋给临时变量 node。

这里有一个面试常问的坑：

问：为什么不直接定义 struct TreeNode stack[100]？
答：

如果定义 struct TreeNode stack[100]，栈里存的是整个节点的内容。
压栈时会发生大量的数据拷贝（把整个结构体复制一遍），效率极低。
而使用 struct TreeNode* 数组，压栈时只拷贝一个 8 字节的地址，这才是工业级的标准写法。

总结

这行代码本质上是：在内存中申请了一块连续的空间，专门用来当作"暂存二叉树节点地址"的保险箱。

5、94 二叉树的中序遍历（迭代版）

题目：

代码：

中序遍历（Inorder Traversal）的顺序是 左 -> 根 -> 右。

在迭代法中，它的逻辑和前序遍历大不相同。前序遍历是"边走边打印"，而中序遍历必须**"一路向左钻到底，憋着不发，等撞了南墙（NULL）再回过头来收割"**。

1. 观察切入点：处理时机的滞后性

核心矛盾：当你遇到根节点时，你不能立刻处理它，因为它的左子树里所有的值都比它小，必须先处理左边。
解决方案 ：我们需要一个指针 curr 带着我们冲锋，再用一个栈作为我们的"回生药"，把经过的每一个根节点都存起来，方便以后"回头"。

2. 核心原理：先推入，后弹出

向左冲锋 ：只要 curr 不为空，就把它压入栈，然后走向 curr->left。
触底反弹 ：当 curr 为空时，说明左边到头了。此时从栈中弹出的那个节点，就是当前最左的节点（根）。
收割并右转 ：打印这个节点，然后把 curr 指向它的右孩子，重复上述过程。

3. C 语言代码实现

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 * int val;
 * struct TreeNode *left;
 * struct TreeNode *right;
 * };
 */

int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    if (root == NULL) return NULL;

    int* res = (int*)malloc(sizeof(int) * 100); // 假设节点数上限
    struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 100);
    int top = 0;

    struct TreeNode* curr = root;

    // 核心逻辑：curr 不为空或者栈不为空，循环就不能停
    while (curr != NULL || top > 0) {
        // 步骤 A：一路向左钻到底，路过的全部进栈
        while (curr != NULL) {
            stack[top++] = curr;
            curr = curr->left;
        }

        // 步骤 B：走到头了，从栈里弹出一个（这是目前最左的根）
        curr = stack[--top];
        res[(*returnSize)++] = curr->val; // 收割！

        // 步骤 C：转向右子树
        // 如果右子树为空，下一轮循环会直接进入步骤 B，继续弹出上层的根
        curr = curr->right;
    }

    free(stack);
    return res;
}

4. 思路推演：逻辑是怎么"丝滑"起来的？

假设树为：1 是根，2 是左孩子，3 是右孩子。

初始：curr = 1，栈为空。
钻左边：

1 进栈，curr 变成 2。
2 进栈，curr 变成 NULL（2 的左边）。

反弹收割：

弹出 2，结果数组 [2]。
curr 变成 2 的右孩子，即 NULL。

继续收割：

因为 curr 为空但栈里有 1，弹出 1，结果数组 [2, 1]。
curr 变成 1 的右孩子，即 3。

处理右边：

3 进栈，然后再弹出 3，结果数组 [2, 1, 3]。

结束：栈空且 curr 为空，大功告成。

5. 避坑指南：中序迭代的"精髓"

循环条件 ：一定要写 curr != NULL || top > 0。
如果只写 top > 0，初始状态循环就进不去。
如果只写 curr != NULL，当你从左边回来准备处理根时，curr 正好是 NULL，循环会意外终止。
无需 prev 指针：
相比于后序遍历，中序遍历不需要 prev 标记。因为中序遍历在处理完根之后，直接就去右边了，不需要第二次回到根节点。

📊 三大遍历迭代法对比总结

遍历方式	栈的应用策略	关键点
前序 (根左右)	入栈即处理，先压右再压左	利用栈的 FILO 实现左先右后
中序 (左根右)	一路向左压栈，弹出才处理	必须"钻"到最左端再回头
后序 (左右根)	根右左 + 反转，或使用 `prev`	是迭代法中最难的一类

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

6、145 二叉树的后序遍历（迭代版）

题目：

代码：

前序弄懂的话，后序就是变了一下，先序遍历是中左右，后序遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后再反转result数组，输出的结果顺序就是左右中了~

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 void reverse(int* res,int returnSize){
    int left = 0;
    int right = returnSize-1;
    while(right > left){
        int tmp = res[right];
        res[right] = res[left];
        res[left] = tmp;
        left++;
        right--;
    }
 }

int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    if(root == NULL){
        return NULL;
    }
    int* res = (int*)malloc(sizeof(int)*100);
    struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*)*100);
    int top = 0;
    stack[top++] = root;
    while(top > 0){
        struct TreeNode* node = stack[--top];
        res[(*returnSize)++] = node->val;
        if(node->left != NULL){
            stack[top++] = node->left;
        }
        if(node->right != NULL){
            stack[top++] = node->right;
        }
    }
    reverse(res,*returnSize);
    free(stack);
    return res;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

7、102 二叉树的层序遍历

题目：

代码：

如果说前序、中序、后序遍历是"纵向"的深度优先搜索 (DFS) ，那么层序遍历就是典型的"横向"广度优先搜索 (BFS)。

1. 核心模型：队列 (Queue)

层序遍历的本质是"先进先出"。

逻辑：当我们访问某一层的节点时，为了不丢失下一层的信息，我们需要把当前节点的子节点按顺序放入一个容器中。
工具：队列是最佳选择。
父亲出队时，它的左孩子和右孩子依次进队。
这样队列中排队的顺序自然就是从左到右、从上到下的。

2. 关键技巧：固定窗口大小 (Batch Processing)

BFS 本身会将树"拉平"，但题目要求按层输出（返回 [[1], [2,3], [4,5,6,7]]）。如何区分哪些节点属于同一层呢？

核心思路：在处理每一层之前，先数一数队列里有多少个元素。

开始处理新的一层。
记录当前队列长度 size = tail - head。这个 size 就是当前层的所有节点数。
只连续弹出 size 个节点。
这 size 个节点的孩子会进入队列，但它们排在后面，不会在这一轮被处理，而是留到下一轮。

3. C 语言实现的难点：内存管理

在 C 语言中，这道题的挑战在于处理复杂的返回类型：int** 和 int* returnColumnSizes。

int** result：这是一个指针数组，每个元素指向一个代表"层"的动态数组。
int* returnColumnSizes：这是一个一维数组，你需要告诉调用者每一层具体有多少个元素。
模拟队列 ：由于树节点总数有限（通常为 2000），我们可以直接开辟一个足够大的数组 struct TreeNode* queue[2000]，配合 head 和 tail 指针，避免手写链表队列。

4. 思路推演：BFS 模板

c 复制代码

// 1. 根节点入队
// 2. While (队列不为空) {
//      当前层的节点数 size = tail - head;
//      为这一层申请结果内存: malloc(sizeof(int) * size);
//
//      For (i = 0 到 size - 1) {
//          节点出队;
//          把值存入当前层的数组;
//          如果左孩子存在，左孩子入队;
//          如果右孩子存在，右孩子入队;
//      }
//
//      层数计数 returnSize++;
// }

C语言代码

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 * int val;
 * struct TreeNode *left;
 * struct TreeNode *right;
 * };
 */

/**
 * returnSize: 返回的层数（纵向长度）
 * returnColumnSizes: 返回每一层有多少个节点（横向长度数组）
 */
int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes) {
    *returnSize = 0;
    if (root == NULL) return NULL;

    // 1. 初始化：预分配最大可能的层数空间
    int** result = (int**)malloc(sizeof(int*) * 2000);
    *returnColumnSizes = (int*)malloc(sizeof(int) * 2000);

    // 2. 模拟队列：存放节点指针
    struct TreeNode* queue[2000];
    int head = 0, tail = 0;

    // 根节点入队
    queue[tail++] = root;

    // 3. 开始 BFS
    while (head < tail) {
        // 当前层的节点个数
        int size = tail - head;
        // 记录当前层的列数
        (*returnColumnSizes)[*returnSize] = size;
        // 为当前层分配存放 int 值的空间
        result[*returnSize] = (int*)malloc(sizeof(int) * size);

        for (int i = 0; i < size; i++) {
            // 出队
            struct TreeNode* curr = queue[head++];
            result[*returnSize][i] = curr->val;

            // 将下一层节点入队
            if (curr->left)  queue[tail++] = curr->left;
            if (curr->right) queue[tail++] = curr->right;
        }

        // 处理完一层，层数自增
        (*returnSize)++;
    }

    return result;
}

C 语言处理这道题最坑的地方就在于多级指针的内存分配 。很多同学逻辑写对了，但因为没处理好 returnColumnSizes 的解引用导致报错。

内存结构深度详解

为了让你彻底明白 int** 和 *returnColumnSizes 到底在干什么，请参考下图：

result (二级指针) ：它指向一个数组，数组里存的是 int* 指针。每个指针指向堆区的一行数据。
*returnColumnSizes ：这其实是一个一维数组。由于函数参数是 int**，意味着你要修改外部那个指针的指向。所以代码里写成 *returnColumnSizes = malloc(...)，然后用 (*returnColumnSizes)[i] 来访问。

避坑指南 ：千万不要写成 *returnColumnSizes[i]，因为 [] 优先级高，这会被解释为先取下标再解引用，导致内存访问错误。

为什么这个解法很快？

数组模拟队列 ：避免了频繁调用 malloc 创建链表节点的开销。
一次性分配指针空间：虽然预留 2000 个位置看起来有点浪费，但在算法竞赛中，这种"空间换时间"且规避复杂内存管理的做法非常稳健。
**线性时间复杂度 **：每个节点只进出队列一次，且没有冗余的遍历。

提交前的最后检查

空树处理 ：if (root == NULL) 必须返回 NULL 且 *returnSize = 0。
层数统计 ：*returnSize 是通过 (*returnSize)++ 逐层累加的，确保了它反映的是树的深度。

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

8、107 二叉树的层序遍历②

题目：

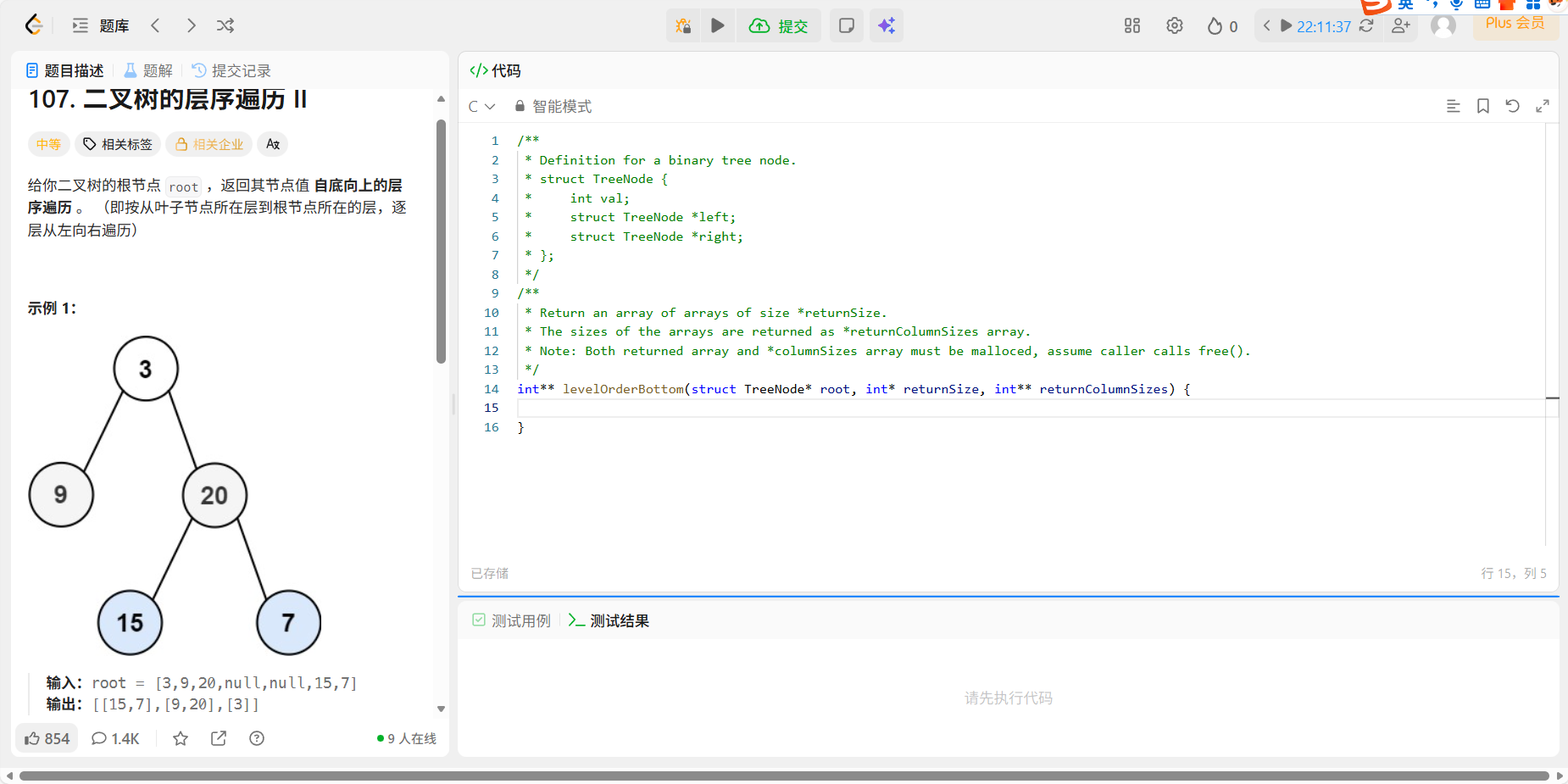
代码：
先正常层序遍历，最后统一翻转指针。

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** levelOrderBottom(struct TreeNode* root, int* returnSize, int** returnColumnSizes) {
    *returnSize = 0;
    if(root == NULL){
        return NULL;
    }
    int** result = (int**)malloc(sizeof(int*)*2000);
    *returnColumnSizes = (int*)malloc(sizeof(int)*2000);
    struct TreeNode* queue[2000];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        (*returnColumnSizes)[*returnSize] = size;
        result[*returnSize] = (int*)malloc(sizeof(int)*size);
        for(int i = 0;i < size;i++){
            struct TreeNode* curr = queue[head++];
            result[*returnSize][i] = curr->val;
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
        (*returnSize)++;
    }
    int left = 0;
    int right = (*returnSize)-1;
    while(left < right){
        int* temp = result[left];
        result[left] = result[right];
        result[right] = temp;
        int tempSize = (*returnColumnSizes)[left];
        (*returnColumnSizes)[left] = (*returnColumnSizes)[right];
        (*returnColumnSizes)[right] = tempSize;
        right--;
        left++;
    }
    return result;
}

为什么必须交换 returnColumnSizes？

这是很多同学容易忽略的细节。

result 决定了每一层的数据在哪。
returnColumnSizes 告诉力扣系统每一层有多少个数。如果你只反转了 result 而没反转 returnColumnSizes，系统会用第一层的人数去读最后一层的数据，导致输出混乱甚至溢出。

将反转代码封装成函数：

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
 void reverse(int** result,int* returnSize,int** returnColumnSizes){
    int left = 0;
    int right = (*returnSize)-1;
    while(left < right){
        int* temp = result[left];
        result[left] = result[right];
        result[right] = temp;
        int tempSize = (*returnColumnSizes)[left];
        (*returnColumnSizes)[left] = (*returnColumnSizes)[right];
        (*returnColumnSizes)[right] = tempSize;
        right--;
        left++;
    }
 }
int** levelOrderBottom(struct TreeNode* root, int* returnSize, int** returnColumnSizes) {
    *returnSize = 0;
    if(root == NULL){
        return NULL;
    }
    int** result = (int**)malloc(sizeof(int*)*2000);
    *returnColumnSizes = (int*)malloc(sizeof(int)*2000);
    struct TreeNode* queue[2000];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        (*returnColumnSizes)[*returnSize] = size;
        result[*returnSize] = (int*)malloc(sizeof(int)*size);
        for(int i = 0;i < size;i++){
            struct TreeNode* curr = queue[head++];
            result[*returnSize][i] = curr->val;
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
        (*returnSize)++;
    }
    reverse(result,returnSize,returnColumnSizes);
    return result;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

9、199 二叉树的右视图

题目：

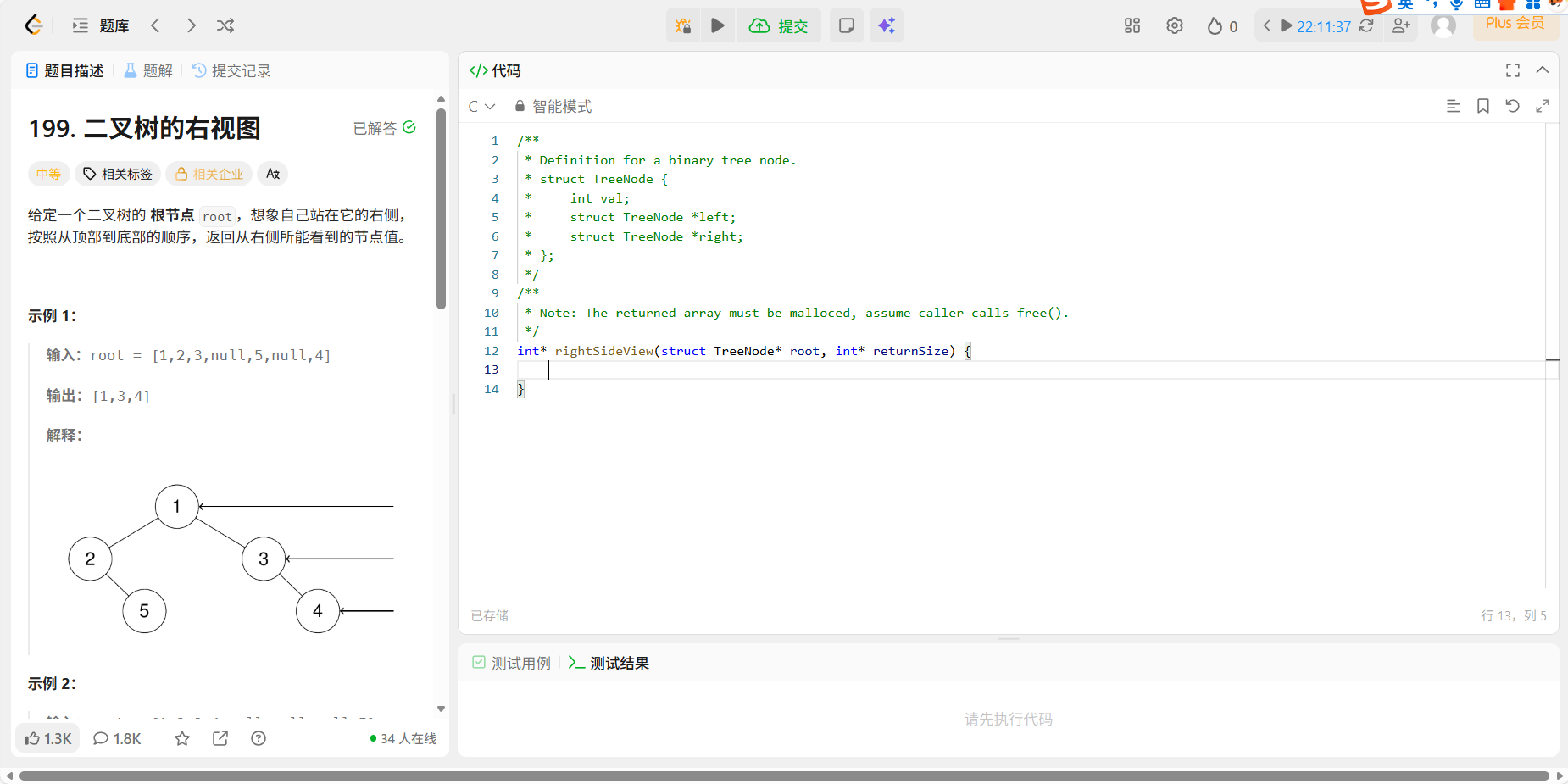
代码：

就是在层序遍历的时候，加一个判断当是该行的最后一个元素时，加入result数组即可。

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* rightSideView(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    if(root == NULL){
        return NULL;
    }
    int* result = (int*)malloc(sizeof(int)*101);
    struct TreeNode* queue[105];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    int count = 0;
    while(head < tail){
        int size = tail - head;
        for(int i= 0;i < size;i++){
            struct TreeNode* curr = queue[head++];
            if(i == size-1){
                result[count++] = curr->val;
            }
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
    }
    *returnSize = count;
    return result;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

如果是求二叉树的左视图

可以将上述判断条件改为 i == 0 是最直接的方法。

在 BFS（从左往右） 的遍历过程中：

每一层的 第一个 元素（i == 0）就是左视图。
每一层的 最后一个 元素（i == size - 1）就是右视图。

除了改 i == 0，还有另一种"骚操作"：

如果你依然想保留 i == size - 1 的判断，但又想得到左视图，你可以改变孩子入队的顺序：

右视图逻辑：先放左孩子，后放右孩子每一层最后出来的就是最右边的。
左视图逻辑 ：先放右孩子 ，后放左孩子 每一层最后出来的就是最左边的。

c 复制代码

// 这种入队顺序下，i == size - 1 拿到的就是左视图
if (curr->right) queue[tail++] = curr->right;
if (curr->left)  queue[tail++] = curr->left;

10、637 二叉树的层平均值

题目：

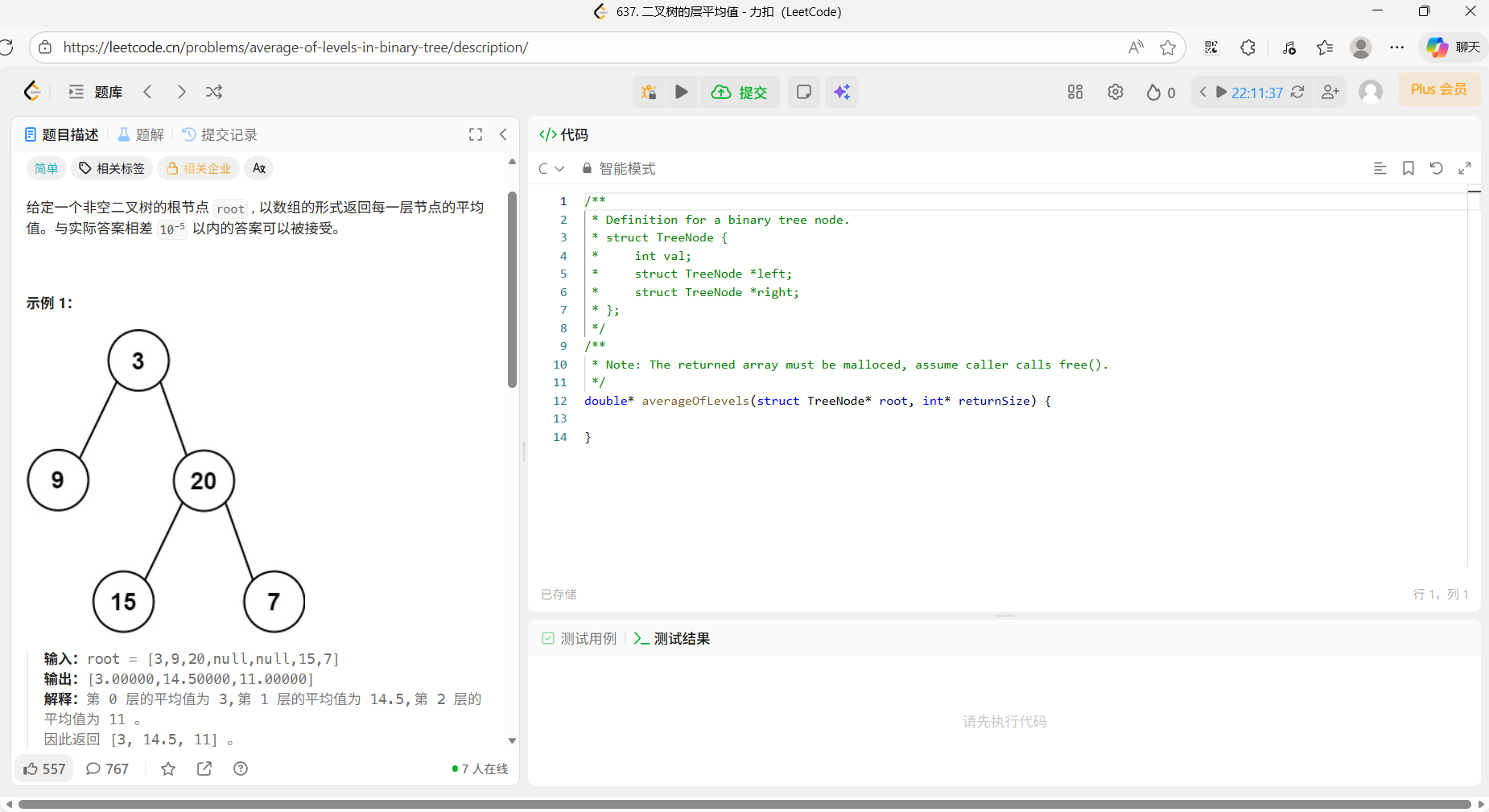
代码：

也是在层序遍历的基础上，计算每一层的和然后计算均值解决问题。

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
double* averageOfLevels(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    if(root == NULL){
        return NULL;
    }
    double* result = (double*)malloc(sizeof(double)*10000);
    struct TreeNode* queue[10000];
    int head = 0;
    int tail = 0;
    int count = 0;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        double sum = 0;
        for(int i = 0;i < size;i++){
            struct TreeNode* curr = queue[head++];
            sum += curr->val;
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            } 
        }
        result[count++] = sum/size;
    }
    *returnSize = count;
    return result;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

11、429 N叉树的层序遍历

题目：

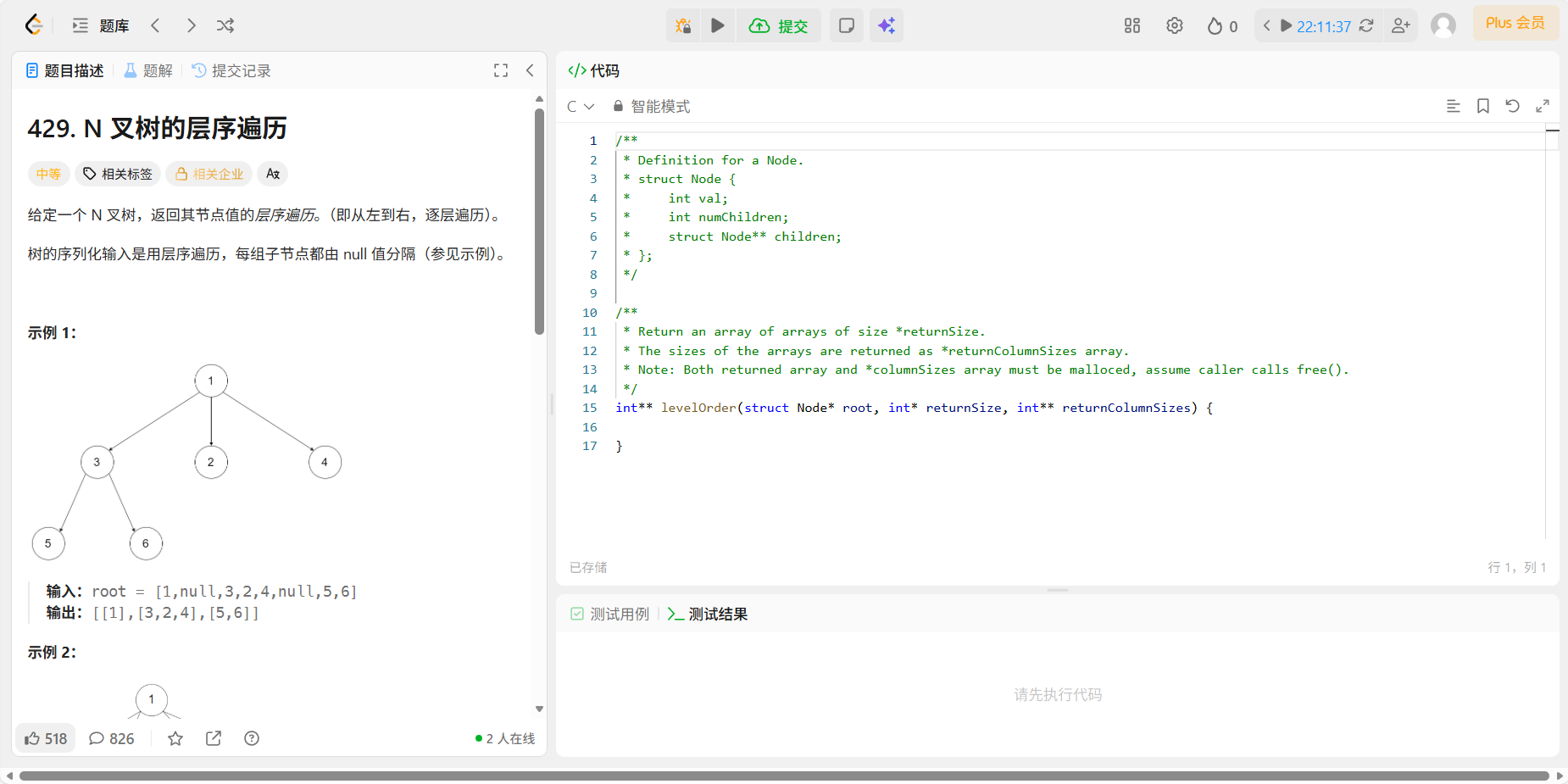
代码：

在力扣（LeetCode）第 429 题"N 叉树的层序遍历"中，判断它是几叉树并不需要你通过代码去"算"出来，而是通过数据结构的定义直接体现出来的。

1. 核心区别：观察节点结构

在二叉树中，节点结构通常只有 left 和 right。但在 N 叉树中，节点使用一个列表或数组来存储所有的子节点。

C 语言的结构体定义通常如下：

c 复制代码

struct Node {
    int val;
    int childrenSize;        // 重点：这个变量告诉了你当前节点有几个孩子
    struct Node** children;   // 重点：这是一个指向指针数组的指针，存放了所有孩子
};

如何判断？ ：通过 childrenSize。
每一个节点的 childrenSize 可能都不一样。有的节点可能有 3 个孩子，有的可能有 0 个（叶子节点）。
"N 叉树"的 N 是指最大限制 ，但在实际编程中，我们只需要遍历 0 到 childrenSize - 1 即可。

2. 解题思路：从二叉树平移到 N 叉树

解决这道题的思路和你之前做的 102 题（二叉树层序遍历）几乎一模一样，唯一的区别就在于"入队"的那一步。

逻辑对比：

二叉树：

c 复制代码

if (curr->left) queue[tail++] = curr->left;
if (curr->right) queue[tail++] = curr->right;

N 叉树：

c 复制代码

for (int j = 0; j < curr->childrenSize; j++) {
    queue[tail++] = curr->children[j];
}

3. C 语言代码实现的关键点

由于 N 叉树的层序遍历同样需要返回 int** 和 int* returnColumnSizes，你可以复用 102 题的模板：

c 复制代码

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     int numChildren;
 *     struct Node** children;
 * };
 */

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** levelOrder(struct Node* root, int* returnSize, int** returnColumnSizes) {
    *returnSize = 0;
    if(root == NULL){
        *returnColumnSizes = NULL;
        return NULL;
    }
    int** result = (int**)malloc(sizeof(int*)*10001);
    *returnColumnSizes = (int*)malloc(sizeof(int)*10001);

    struct Node* queue[20001];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        (*returnColumnSizes)[*returnSize] = size;
        result[*returnSize] = (int*)malloc(sizeof(int)*size);
        for(int i = 0;i < size;i++){
            struct Node* curr = queue[head++];
            result[*returnSize][i] = curr->val;
            for(int j = 0;j < curr->numChildren;j++){
                if(curr->children[j]){
                    queue[tail++] = curr->children[j];
                }
            }
        }
        (*returnSize)++;
    }
    return result;
}

4. 总结

不需要预先知道是几叉树 ：代码逻辑是通用的。只要按照 childrenSize 遍历 children 数组即可。
动态性：N 叉树的"N"是动态的。同一个树里，A 节点可以是 3 叉，B 节点可以是 2 叉。
空间预估 ：N 叉树通常比二叉树更"宽"，所以模拟队列的数组（queue）建议开得稍微大一些。

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

12、515 在每个树行中找最大值

题目：

代码：

依然是在层序遍历的基础上，在每一层初始化max为INT_MIN(int的最小值)，判断该节点是否为该层最大节点。

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* largestValues(struct TreeNode* root, int* returnSize) {
    *returnSize = 0;
    if(root == NULL){
        return NULL;
    }
    int* result = (int*)malloc(sizeof(int)*10000);
    struct TreeNode* queue[10000];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        int max = INT_MIN;
        for(int i = 0;i < size;i++){
            struct TreeNode* curr = queue[head++];
            if(curr->val > max){
                max = curr->val;
            }
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
        result[(*returnSize)++] = max;
    }
    return result;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

13、116 填充每个节点的下一个右侧节点指针

题目：

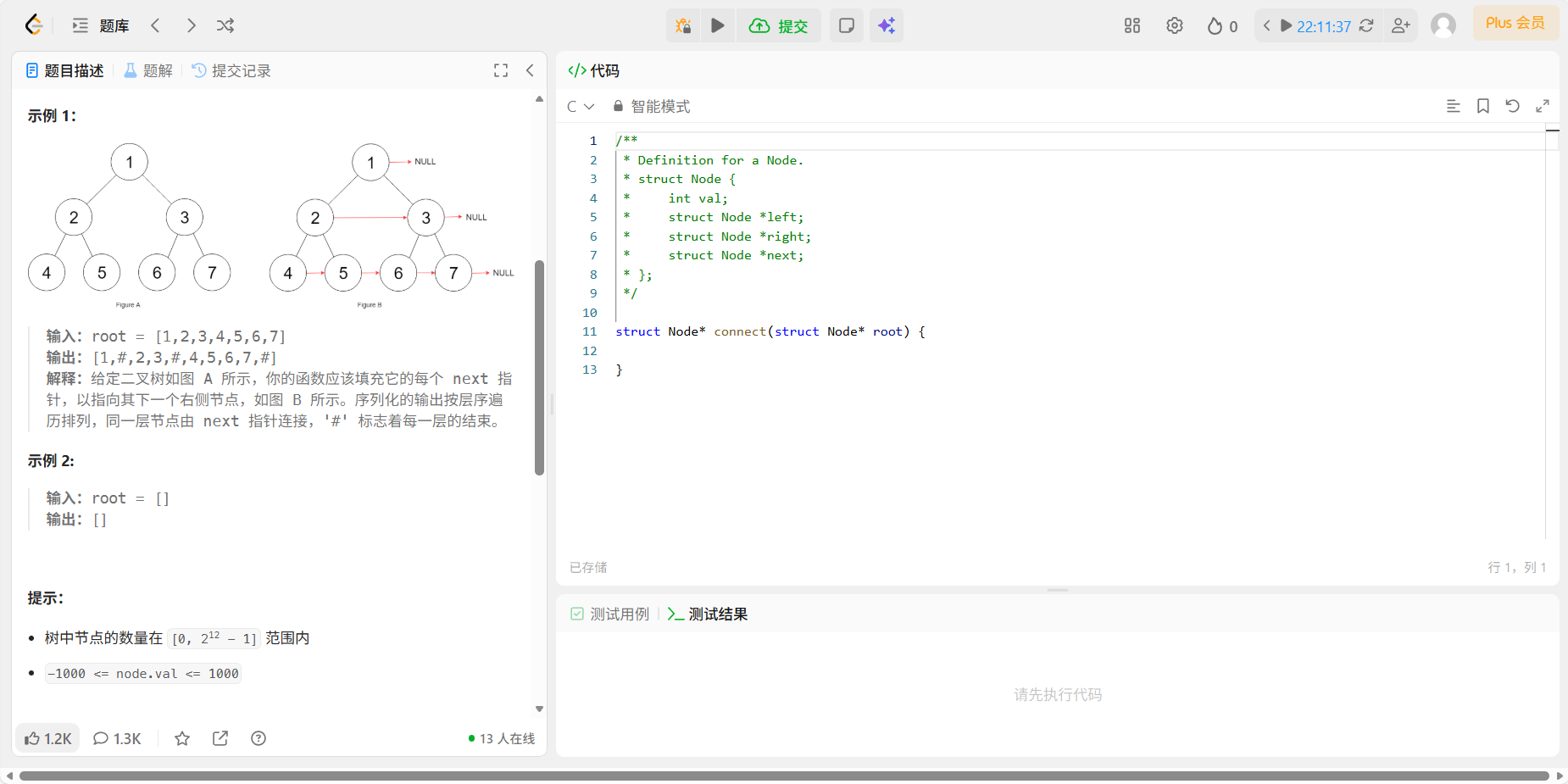
代码：

感觉就是层序遍历，然后将该层的每个节点的next指针指向后一个节点，最后每层的最后节点设置为NULL。

c 复制代码

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *left;
 *     struct Node *right;
 *     struct Node *next;
 * };
 */

struct Node* connect(struct Node* root) {
	if(root == NULL){
        return NULL;
    }
    struct Node* queue[5000];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        for(int i = 0;i < size;i++){
            struct Node* curr = queue[head++];
            if(i < size-1){
                struct Node* nextnode = queue[head];
                curr->next = nextnode;
            }
            else{
                curr->next = NULL;
            }
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
    }
    return root;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)
另解

力扣 116 题的"大神写法"核心在于：利用已经建立好的 next 指针，像拉链一样缝合下一层的节点。

这种方法不需要队列，因此空间复杂度能从 O ( N ) O(N) O(N) 降到 O ( 1 ) O(1) O(1)。

1. 思路解析：利用"上帝视角"的横向连接

在普通的层序遍历中，我们必须依赖队列来记住"下一层有哪些节点"。但在本题中，题目给出的是完美二叉树 ，且已经定义了 next 指针。

如果我们已经把第 i i i 层的所有节点通过 next 指针连成了一个单链表 ，那么在处理第 i i i 层时，我们就可以直接通过这一层的 next 关系，去把第 i + 1 i+1 i+1 层的所有孩子连起来。

核心逻辑分为两种连接情况：

同父连接（内部连接） ：
同一个父亲的左孩子指向右孩子。

公式：node->left->next = node->right

跨父连接（外部连接） ：
父亲的右孩子指向"父亲的邻居"的左孩子。

公式：node->right->next = node->next->left （前提是 node->next 存在）

2. 完整代码实现 (C 语言)

c 复制代码

/**
 * Definition for a Node.
 * struct Node {
 * int val;
 * struct Node *left;
 * struct Node *right;
 * struct Node *next;
 * };
 */

struct Node* connect(struct Node* root) {
    if (root == NULL) return NULL;

    // leftmost 记录每一层的第一个节点（最左节点）
    struct Node* leftmost = root;

    // 当还没到最后一层（叶子层）时，继续循环
    while (leftmost->left != NULL) {
        
        // head 指针负责横向遍历当前已连好的层
        struct Node* head = leftmost;

        while (head != NULL) {
            // 1. 同父连接：连接自己的左右孩子
            head->left->next = head->right;

            // 2. 跨父连接：如果当前节点右边还有邻居
            // 那么把自己的右孩子连到邻居的左孩子上
            if (head->next != NULL) {
                head->right->next = head->next->left;
            }

            // 指针横向移动到本层的下一个节点
            head = head->next;
        }

        // 本层处理完，下移到下一层的最左节点
        leftmost = leftmost->left;
    }

    return root;
}

3. 逻辑推演：为什么不需要队列？

假设我们正在处理第 2 层（节点 2 和 3 已经连好）：

初始化 ：leftmost 指向 2。
横向遍历开始 ：head 指向 2。

执行 2->left->next = 2->right（即 4 连向 5）。
因为 2->next 是 3，执行 2->right->next = 3->left（即 5 连向 6）。

横向移动 ：head 移动到 3。

执行 3->left->next = 3->right（即 6 连向 7）。
3->next 是 NULL，跨父连接跳过。

下移：leftmost 移动到 4，继续下一层循环。

4. 复杂度对比

维度	BFS 队列写法	O ( 1 ) O(1) O(1)指针写法
时间复杂度	O ( N ) O(N) O(N)	O ( N ) O(N) O(N)(每个节点访问一次)
空间复杂度	O ( N ) O(N) O(N)	O ( 1 ) O(1) O(1) (仅需两个指针)
适用范围	任意二叉树	仅限带 next 指针且结构较规律的树

5. 避坑指南

终止条件 ：while (leftmost->left != NULL)。因为我们在当前层连接下一层，所以当我们已经在最后一层（叶子层）时，不需要再往下了，否则访问 leftmost->left 会报错。
完美二叉树的特权 ：这种写法极度依赖"完美二叉树"的对称性。如果是普通的二叉树（力扣 117 题），这种写法需要加入更复杂的判断（因为 head->next 的孩子可能不存在）。

恭喜你！ 你现在已经掌握了从基础 BFS 到进阶指针操作的跨越。

14、117 填充每个节点的下一个右侧节点指针

题目：

代码：

这个就用不了大神代码，只能创建队列老老实实层序遍历队列了。

c 复制代码

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *left;
 *     struct Node *right;
 *     struct Node *next;
 * };
 */

struct Node* connect(struct Node* root) {
	if(root == NULL){
        return NULL;
    }
    struct Node* queue[6000];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        for(int i = 0;i < size;i++){
            struct Node* curr = queue[head++];
            if(i < size-1){
                curr->next = queue[head];
            }
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
    }
    return root;
}

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

15、104 二叉树的最大深度

题目：

代码：

力扣第 104 题 "二叉树的最大深度" (Maximum Depth of Binary Tree) 是理解递归思想的绝佳入门题。

解决这道题有两种主流思维：一种是**"自底向上"的递归（DFS），另一种是"按层计数"的迭代（BFS）**。

1. 递归思路：自底向上的"高度汇报"

这是最优雅、代码量最少的写法。

核心矛盾：整棵树的最大深度是多少？
拆解逻辑：

如果我是空节点，我的深度是 0。
如果我不是空节点，我的深度等于：左子树深度和右子树深度中的较大者，再加 1（加上我自己这一层）。

数学公式 ：
D e p t h ( r o o t ) = max ⁡ ( D e p t h ( r o o t → l e f t ) , D e p t h ( r o o t → r i g h t ) ) + 1 Depth(root) = \max(Depth(root \rightarrow left), Depth(root \rightarrow right)) + 1 Depth(root)=max(Depth(root→left),Depth(root→right))+1

2. 迭代思路：层序遍历计数（BFS）

如果你对之前的层序遍历（102题）已经很熟悉了，那么这道题对你来说就是"换汤不换药"。

核心逻辑：

使用队列进行层序遍历。
每完整处理完一层（即内循环结束），深度计数器 ans 就加 1。
当队列为空时，计数器就是最大深度。

适用场景：当你担心树的深度过大导致递归栈溢出时，BFS 是更稳健的选择。

3. C 语言代码实现

（递归版）

这是面试中最推荐的写法，只需三行逻辑：

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 * int val;
 * struct TreeNode *left;
 * struct TreeNode *right;
 * };
 */

int maxDepth(struct TreeNode* root) {
    // 1. 终止条件：空树深度为 0
    if (root == NULL) {
        return 0;
    }
    
    // 2. 递归获取左右子树的最大深度
    int leftHeight = maxDepth(root->left);
    int rightHeight = maxDepth(root->right);
    
    // 3. 返回较大者 + 1
    return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}

（迭代版）

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int maxDepth(struct TreeNode* root) {
    if(root == NULL){
        return 0;
    }
    struct TreeNode* queue[10000];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    int count = 0;
    while(head < tail){
        int size = tail - head;
        for(int i = 0;i < size;i++){
            struct TreeNode* curr = queue[head++];
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
        count++;
    }
    return count;
}

4. 复杂度分析

时间复杂度 ： O ( N ) O(N) O(N)。每个节点都必须且仅被访问一次。
空间复杂度：
最坏情况 ： O ( N ) O(N) O(N)（树退化成链表，递归栈深度为）。
最好情况 ： O ( log ⁡ N ) O(\log N) O(logN)（平衡二叉树，递归栈深度为树高）。

💡 深度思考：深度 (Depth) vs 高度 (Height)

虽然这道题求的是深度，但在递归实现中，我们实际上是在求高度。

深度：从根节点往下看（自顶向下）。
高度：从叶子节点往上看（自底向上）。
对于整棵树来说，根节点的高度 = 树的最大深度。

总结

如果你追求代码简洁和直观，用递归。
如果你追求在大数据量下的稳定性，用BFS 迭代。

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

16、111 二叉树的最小深度

题目：

代码：

力扣第 111 题 "二叉树的最小深度" (Minimum Depth of Binary Tree) 看起来和 104 题（最大深度）几乎一样，但它隐藏了一个极其容易翻车的陷阱。

1. 核心陷阱：什么是"最小深度"？

题目定义：最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

叶子节点的定义 ：左孩子和右孩子都为空的节点。

容易出错的点：

如果一个节点的左子树为空，右子树不为空（比如像一个 L 型的长条），你不能说它的最小深度是 1（即它自己）。你必须继续走到右子树的叶子节点才行。

2. 思路一：递归法（DFS）

我们需要对递归逻辑做精细化的分情况讨论：

节点为空 ：返回 0。
叶子节点（左右都空） ：返回 1。
单边为空：

如果左子树为空，最小深度是 右子树最小深度 + 1。
如果右子树为空，最小深度是 左子树最小深度 + 1。

左右都不为空 ：返回 左右子树深度的较小值 + 1。

C 语言代码片段：

c 复制代码

int minDepth(struct TreeNode* root) {
    if (root == NULL) return 0;
    
    // 如果左子树为空，必须去右子树找叶子
    if (root->left == NULL) return minDepth(root->right) + 1;
    // 如果右子树为空，必须去左子树找叶子
    if (root->right == NULL) return minDepth(root->left) + 1;
    
    // 左右都不为空，取较小者
    int leftMin = minDepth(root->left);
    int rightMin = minDepth(root->right);
    return (leftMin < rightMin ? leftMin : rightMin) + 1;
}

3. 思路二：层序遍历（BFS）------ 推荐方案

对于"找最短路径"这类问题，BFS 其实比 DFS 更高效。

原理：我们按层扫描。一旦遇到第一个叶子节点，它所在的层数就是我们要找的最小深度。
优势：
比如一棵树左边很浅，右边极深。DFS 会先钻到右边最深处再回来，而 BFS 扫描到左边浅处直接就返回结果了。
效率更高：不需要遍历完整棵树。

4. BFS 迭代法实现逻辑

使用队列进行层序遍历，初始 depth = 1。
大循环处理每一层。
内循环处理当前层节点时，检查：

如果是叶子节点 (curr->left == NULL && curr->right == NULL) ：直接返回当前 depth。

如果没有遇到叶子节点，将子节点入队。
处理完一层，depth++。

c语言代码

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int minDepth(struct TreeNode* root) {
    if(root == NULL){
        return 0;
    }
    struct TreeNode* queue[10000];
    int head = 0;
    int tail = 0;
    int depth = 1;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        for(int i = 0;i < size;i++){
            struct TreeNode* curr = queue[head++];
            if(curr->left == NULL && curr->right == NULL){
                return depth;
            }
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
        depth++;
    }
    return depth;
}

💡 总结对比

维度	最大深度 (104)	最小深度 (111)
递归逻辑	`max(left, right) + 1`	分情况处理（避开非叶子节点）
BFS 行为	必须跑完所有层	遇到首个叶子即停止
关键点	找最远的路径	找最近的叶子路径

这个"单边为空"的陷阱是面试官最爱考察的细节。

时间复杂度： O ( n ) O(n) O(n)

空间复杂度： O ( n ) O(n) O(n)

17、226 翻转二叉树

题目：

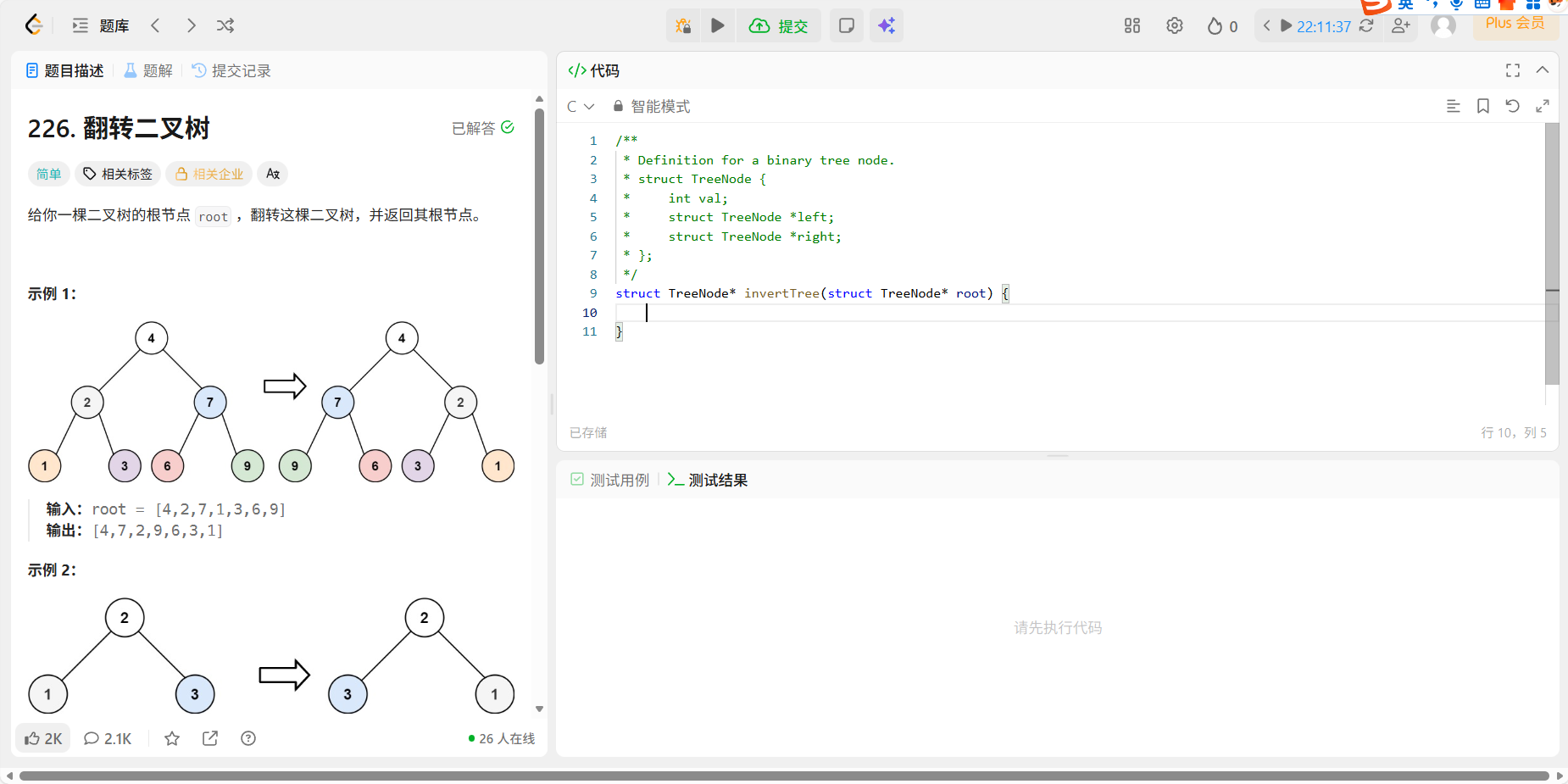
代码：

力扣第 226 题 "翻转二叉树" (Invert Binary Tree) 是一道极具传奇色彩的题目（Homebrew 的作者 Max Howell 曾因没在白板上写出这道题而被 Google 拒绝）。

但其实，它的核心逻辑非常简单：对于每一个节点，交换它的左孩子和右孩子。

1. 递归思路：自顶向下的"镜像反转"

这是最直观的写法。想象你面前有一面镜子，树的左边变成了右边，右边变成了左边。

核心步骤：

终止条件：如果节点为空，直接返回。
交换：将当前节点的 left 指针和 right 指针互换。
递归：对左子树进行翻转，对右子树进行翻转。

2. 迭代思路：层序遍历（BFS）

如果你不想用递归，完全可以用你最擅长的 BFS 模板 来搞定。

逻辑：

把根节点放入队列。
当队列不为空时，弹出一个节点 curr。
交换 curr->left 和 curr->right。
如果子节点不为空，把它们加入队列。
重复直到队列为空。

这种方法的本质：我们不管层级，只要见到一个节点，就把它那两个"胳膊"（左右孩子）换个位置。

3. C 语言代码实现

（递归版）

递归写法简洁得像一首诗：

c 复制代码

struct TreeNode* invertTree(struct TreeNode* root) {
    // 1. 基础情况：空树不需要翻转
    if (root == NULL) {
        return NULL;
    }

    // 2. 交换当前节点的左右子树指针
    struct TreeNode* temp = root->left;
    root->left = root->right;
    root->right = temp;

    // 3. 递归处理子节点
    invertTree(root->left);
    invertTree(root->right);

    return root;
}

（迭代版）

c 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* invertTree(struct TreeNode* root) {
    if (root == NULL) {
        return NULL;
    }
    struct TreeNode* queue[100];
    int head = 0;
    int tail = 0;
    queue[tail++] = root;
    while(head < tail){
        int size = tail - head;
        for(int i = 0;i < size;i++){
            struct TreeNode* curr = queue[head++];
            struct TreeNode* temp = curr->left;
            curr->left = curr->right;
            curr->right = temp;
            if(curr->left){
                queue[tail++] = curr->left;
            }
            if(curr->right){
                queue[tail++] = curr->right;
            }
        }
    }
    return root;
}

4. 深度解析：为什么这能行？

很多初学者会担心："我刚把左边换到右边，递归进去的时候顺序不就乱了吗？"

其实不会。因为二叉树是递归定义的结构。当你交换了根节点的左右指针后，原先整个左子树（作为一个整体）已经跑到了右边。接下来的递归只是在这些已经换过位置的"大块"内部进行细节调整。

5. 复杂度分析

时间复杂度 ： O ( N ) O(N) O(N)。每个节点都被访问并交换一次。
空间复杂度：
递归： O ( H ) O(H) O(H)， H是树的高度（系统栈消耗）。
迭代 (BFS) ： O ( W ) O(W) O(W)， W是树的最大宽度（队列消耗）。

💡 总结建议

这道题是二叉树"结构操作"的基础。掌握了它，你就掌握了处理二叉树指针变换的通用方法。

算法刷题--二叉树（一）

文章目录

1、144 二叉树的前序遍历（递归版）

思路推演：逻辑是怎么流动的？

2、94 二叉树的中序遍历（递归版）

3、145 二叉树的后序遍历（递归版）

4、144 二叉树的前序遍历（迭代版）

1. 观察切入点：手动维护"待办清单"

2. 核心原理：右孩子先入栈

3. C 语言实现代码

4. 逻辑推演：为什么顺序不会乱？

5. 避坑指南

🚀 进阶思考

1. 核心原理：为什么要用 **（二级指针）？

2. 内存布局拆解

3. 避坑指南：它在迭代中是怎么干活的？

这里有一个面试常问的坑：

总结

5、94 二叉树的中序遍历（迭代版）

1. 观察切入点：处理时机的滞后性

2. 核心原理：先推入，后弹出

3. C 语言代码实现

4. 思路推演：逻辑是怎么"丝滑"起来的？

5. 避坑指南：中序迭代的"精髓"

📊 三大遍历迭代法对比总结

6、145 二叉树的后序遍历（迭代版）

7、102 二叉树的层序遍历

1. 核心模型：队列 (Queue)

2. 关键技巧：固定窗口大小 (Batch Processing)

3. C 语言实现的难点：内存管理

4. 思路推演：BFS 模板

内存结构深度详解

为什么这个解法很快？

提交前的最后检查

8、107 二叉树的层序遍历②

9、199 二叉树的右视图

10、637 二叉树的层平均值

11、429 N叉树的层序遍历

1. 核心区别：观察节点结构

2. 解题思路：从二叉树平移到 N 叉树

逻辑对比：

3. C 语言代码实现的关键点

4. 总结

12、515 在每个树行中找最大值

13、116 填充每个节点的下一个右侧节点指针

1. 思路解析：利用"上帝视角"的横向连接

核心逻辑分为两种连接情况：

2. 完整代码实现 (C 语言)

3. 逻辑推演：为什么不需要队列？

4. 复杂度对比

5. 避坑指南

14、117 填充每个节点的下一个右侧节点指针

15、104 二叉树的最大深度

1. 递归思路：自底向上的"高度汇报"

2. 迭代思路：层序遍历计数（BFS）

3. C 语言代码实现

4. 复杂度分析

💡 深度思考：深度 (Depth) vs 高度 (Height)

总结

16、111 二叉树的最小深度

1. 核心陷阱：什么是"最小深度"？

2. 思路一：递归法（DFS）

3. 思路二：层序遍历（BFS）------ 推荐方案

4. BFS 迭代法实现逻辑

💡 总结对比

17、226 翻转二叉树

1. 递归思路：自顶向下的"镜像反转"

2. 迭代思路：层序遍历（BFS）

3. C 语言代码实现

4. 深度解析：为什么这能行？

5. 复杂度分析

💡 总结建议

1. 核心原理：为什么要用 `**`（二级指针）？