【leetcode】将二叉搜索树变平衡

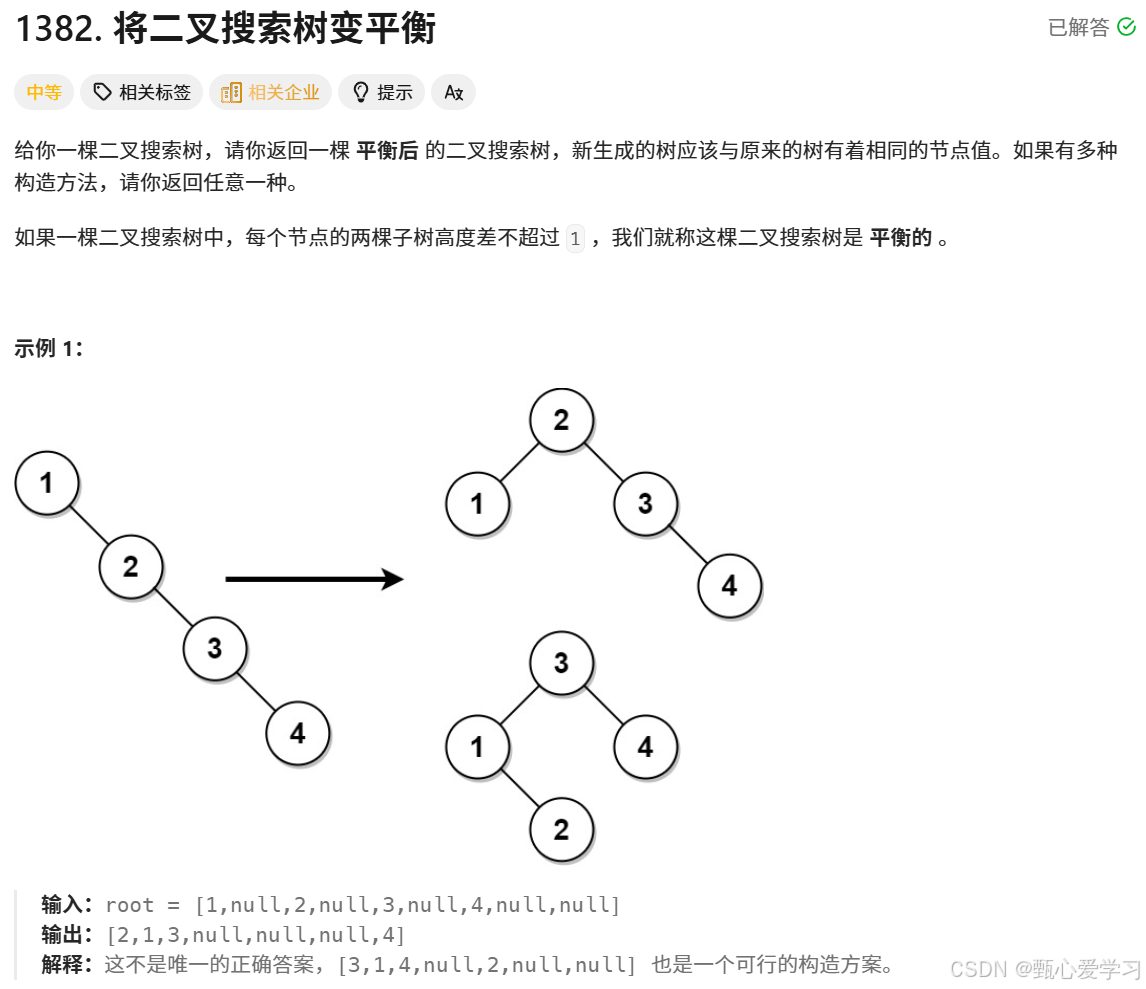
目前是二叉搜索树，二叉搜索树的性质是，左子树<根<右子树，如果想要保持好大小关系，用中序遍历存储，中序遍历，左子树->根->右子树

得到整个树的数值构成的列表，然后用二分法，递归求根，保证平衡

class Solution:
    def balanceBST(self, root: TreeNode) -> TreeNode:
        # 第一步：中序遍历，将树"压扁"成有序数组
        nums = []
        def inorder(node):
            if not node:
                return
            inorder(node.left)
            nums.append(node.val)
            inorder(node.right)
        
        inorder(root)
        
        # 第二步：分治法，将有序数组"提"成平衡树
        def build(left, right):
            # Base Case: 只有当区间不合法（左边跑到右边去了），才返回 None
            # 这比在调用前检查 left <= mid-1 要优雅得多
            if left > right:
                return None
            
            # 1. 找中间点（作为根）
            mid = (left + right) // 2 
            root = TreeNode(nums[mid])
            
            # 2. 递归构建左右子树
            # 这里的逻辑是：既然我是根，那我的左孩子就是左边那半段的根...
            root.left = build(left, mid - 1)
            root.right = build(mid + 1, right)
            
            return root
            
        # 这里的入口就是整个数组范围
        return build(0, len(nums) - 1)