leetcode 1382. 将二叉搜索树变平衡 中等

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法，请你返回任意一种。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

示例 1：

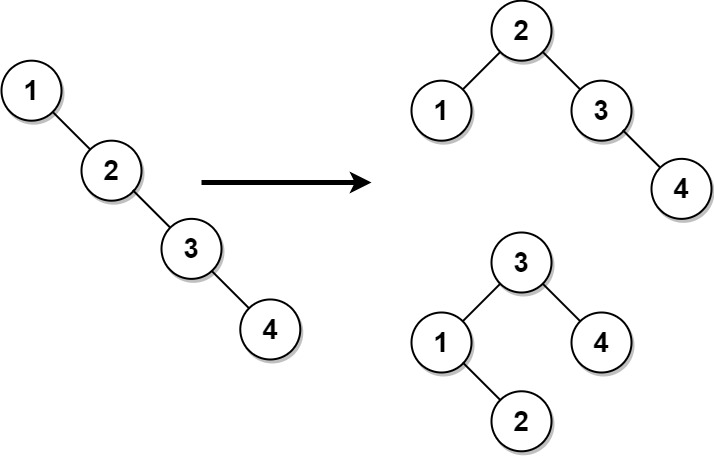
输入：root = [1,null,2,null,3,null,4,null,null]
输出：[2,1,3,null,null,null,4]
解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

示例 2：

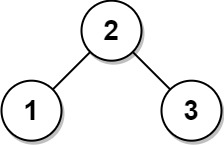
输入: root = [2,1,3]
输出: [2,1,3]

提示：

• 树节点的数目在 [1, 10^4] 范围内。
• 1 <= Node.val <= 10^5

分析：先对原来的二叉搜索树进行中序遍历，得到递增序列。之后令中点作为新平衡树的根，再递归地建立根的左、右子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void inorder(TreeNode* node,vector<int>&val)
    {
        if(node->left!=NULL)inorder(node->left,val);
        val.push_back(node->val);
        if(node->right!=NULL)inorder(node->right,val);
    }
    TreeNode* build(vector<int>&val,int l,int r)
    {
        if(l==r)return NULL;

        int mid=(l+r)/2;
        TreeNode *p=(TreeNode*)malloc(sizeof(TreeNode));
        p->val=val[mid];p->left=build(val,l,mid);p->right=build(val,mid+1,r);
        return p;
    }
    TreeNode* balanceBST(TreeNode* root) {
        vector<int>val;
        inorder(root,val);
        int n=val.size();

        TreeNode *root_new=build(val,0,n);
        return root_new;
    }
};