【微实验】MATLAB可视化：黑体辐射公式与普朗克插值，从紫外灾难到量子革命

文章目录

- 一、核心背景：经典物理的"紫外灾难"
- 二、MATLAB完整脚本：可视化黑体辐射公式与插值过程
- - 代码功能说明
- 三、公式原理通俗化解读
- - [1. 三个核心公式的"分工"](#1. 三个核心公式的“分工”)
  - [2. 普朗克的插值逻辑（通俗化）](#2. 普朗克的插值逻辑（通俗化）)
  - [3. 能量量子化的物理解释](#3. 能量量子化的物理解释)
- 四、代码结果解读
- - [1. 3D曲面图（窗口1）](#1. 3D曲面图（窗口1）)
  - [2. 插值过程图（窗口2）](#2. 插值过程图（窗口2）)
  - [3. 误差分析图（窗口3）](#3. 误差分析图（窗口3）)
- 五、总结

一、核心背景：经典物理的"紫外灾难"

19世纪末，物理学家试图用经典理论解释黑体辐射（可以完全吸收并辐射所有波长的理想物体的辐射规律），却出现了两个"各管一段"的公式：

瑞利-金斯公式：仅适配长波（低频）区域，短波端辐射强度会无限增大（即"紫外灾难"），违背实验事实；
维恩公式：仅适配短波（高频）区域，长波端与实验数据偏差明显。
普朗克的核心贡献是：通过插值法融合两个公式的优势，得到全波段适配的普朗克公式，更颠覆性的是为公式赋予了"能量量子化"的物理解释，开启量子力学时代。

二、MATLAB完整脚本：可视化黑体辐射公式与插值过程

代码功能说明

本脚本实现以下功能：

定义黑体辐射核心参数与公式（瑞利-金斯、维恩、普朗克）；
绘制辐射强度随频率(ν)、温度(T)变化的3D曲面图，对比三个公式的适用范围；
模拟普朗克的插值过程，可视化"权重融合"的中间步骤；
对比不同温度下公式的拟合效果，验证普朗克公式的全波段适配性。

matlab 复制代码

%% ===================== 1. 基础参数定义 =====================
% 物理常数定义（国际单位制）
c = 3e8;           % 真空中的光速 (m/s)
k = 1.38e-23;      % 玻尔兹曼常数 (J/K)
h = 6.626e-34;     % 普朗克常数 (J·s)
C1 = 8*pi*h/c^3;   % 维恩公式常数项（推导自普朗克公式短波近似）
C2 = h/(k);        % 维恩位移定律常数 (J·s / (J/K) = K·s)

% 频率与温度范围设置（兼顾短波/长波、低温/高温）
nu_min = 1e12;     % 最低频率 (Hz)，对应长波
nu_max = 3e15;     % 最高频率 (Hz)，对应短波（紫外区）
T_list = [300, 1000, 2000]; % 对比温度：室温、高温、超高温 (K)
nu = linspace(nu_min, nu_max, 500); % 频率采样点（500个，保证平滑）
[T, Nu] = meshgrid(T_list, nu);     % 生成温度-频率网格矩阵

%% ===================== 2. 黑体辐射公式定义 =====================
% 2.1 瑞利-金斯公式：ρ(ν,T) = (8πν²/c³)kT （经典长波近似）
% 公式意义：基于经典电磁学+能量均分定理，描述长波区域辐射强度与频率、温度的关系
% 缺陷：短波端强度无限大（紫外灾难）
rho_RJ = (8*pi*Nu.^2 / c^3) .* k .* T;

% 2.2 维恩公式：ρ(ν,T) = C1*ν³*exp(-C2*ν/T) （经典短波近似）
% 公式意义：基于热力学+分子运动论，描述短波区域辐射强度随频率升高快速衰减的规律
% 缺陷：长波端与实验偏差大
rho_W = C1 * Nu.^3 .* exp(-C2 * Nu ./ T);

% 2.3 普朗克公式：ρ(ν,T) = (8πhν³/c³) / (exp(hν/(kT)) - 1)
% 公式意义：全波段适配的黑体辐射公式，是量子力学的起点
rho_P = (8*pi*h*Nu.^3 / c^3) ./ (exp(h*Nu./(k*T)) - 1);

%% ===================== 3. 可视化：辐射强度3D曲面图 =====================
figure('Name','黑体辐射公式3D对比','Position',[100,100,1200,800]);
% 子图1：瑞利-金斯公式
subplot(1,3,1);
surf(T, Nu/1e12, rho_RJ/1e-10); % 频率单位转换为10^12 Hz，强度缩放便于观察
shading interp; % 平滑着色
colorbar;
xlabel('温度 T (K)');
ylabel('频率 ν (×10^{12} Hz)');
zlabel('辐射强度 ρ (×10^{-10} J/(m³·Hz))');
title('瑞利-金斯公式（长波适配，短波发散）');
grid on; alpha(0.8); % 网格+半透明，提升可读性

% 子图2：维恩公式
subplot(1,3,2);
surf(T, Nu/1e12, rho_W/1e-10);
shading interp;
colorbar;
xlabel('温度 T (K)');
ylabel('频率 ν (×10^{12} Hz)');
zlabel('辐射强度 ρ (×10^{-10} J/(m³·Hz))');
title('维恩公式（短波适配，长波偏差）');
grid on; alpha(0.8);

% 子图3：普朗克公式
subplot(1,3,3);
surf(T, Nu/1e12, rho_P/1e-10);
shading interp;
colorbar;
xlabel('温度 T (K)');
ylabel('频率 ν (×10^{12} Hz)');
zlabel('辐射强度 ρ (×10^{-10} J/(m³·Hz))');
title('普朗克公式（全波段适配）');
grid on; alpha(0.8);

%% ===================== 4. 模拟普朗克插值过程 =====================
% 插值核心思路：为瑞利-金斯（长波）和维恩（短波）公式赋予频率相关的权重，
% 长波区域权重偏向瑞利-金斯，短波区域权重偏向维恩，最终融合为普朗克公式
% 定义权重函数：基于频率与温度的比值（ν/T），模拟普朗克的内插逻辑
weight_param = h*Nu./(k*T); % 无量纲参数，核心插值变量
weight_RJ = 1./(exp(weight_param) - 1); % 长波权重（ν/T小时≈1）
weight_W = exp(-weight_param) .* weight_RJ; % 短波权重（ν/T大时≈1）

% 插值后的辐射强度（模拟普朗克的拟合过程）
rho_interp = (8*pi*Nu.^2 / c^3) .* k .* T .* weight_RJ .* (1 + weight_param);

% 可视化插值过程
figure('Name','普朗克插值过程对比','Position',[150,150,1000,600]);
% 选取1000K温度下的曲线对比（代表性温度）
T_selected = 1000;
idx_T = find(T_list == T_selected);
nu_1D = nu/1e12; % 频率一维数组（单位：10^12 Hz）
rho_RJ_1D = rho_RJ(:,idx_T)/1e-10;
rho_W_1D = rho_W(:,idx_T)/1e-10;
rho_P_1D = rho_P(:,idx_T)/1e-10;
rho_interp_1D = rho_interp(:,idx_T)/1e-10;

subplot(2,1,1);
plot(nu_1D, rho_RJ_1D, 'r--', 'LineWidth',1.5, 'DisplayName','瑞利-金斯');
hold on;
plot(nu_1D, rho_W_1D, 'b--', 'LineWidth',1.5, 'DisplayName','维恩');
plot(nu_1D, rho_P_1D, 'k-', 'LineWidth',2, 'DisplayName','普朗克（真实值）');
xlabel('频率 ν (×10^{12} Hz)');
ylabel('辐射强度 ρ (×10^{-10} J/(m³·Hz))');
title(['T=',num2str(T_selected),'K ：经典公式与普朗克公式对比']);
legend('Location','best'); grid on;

subplot(2,1,2);
plot(nu_1D, rho_interp_1D, 'g-', 'LineWidth',2, 'DisplayName','插值拟合结果');
hold on;
plot(nu_1D, rho_P_1D, 'k--', 'LineWidth',1.5, 'DisplayName','普朗克公式（参考）');
xlabel('频率 ν (×10^{12} Hz)');
ylabel('辐射强度 ρ (×10^{-10} J/(m³·Hz))');
title('普朗克插值过程：融合经典公式得到全波段适配结果');
legend('Location','best'); grid on;

%% ===================== 5. 不同温度下的拟合误差分析 =====================
% 计算经典公式与普朗克公式的相对误差（验证插值效果）
error_RJ = abs(rho_RJ - rho_P)./rho_P * 100; % 瑞利-金斯相对误差（%）
error_W = abs(rho_W - rho_P)./rho_P * 100;   % 维恩相对误差（%）

figure('Name','不同温度下的拟合误差','Position',[200,200,1000,600]);
for i = 1:length(T_list)
    subplot(1,length(T_list),i);
    plot(nu/1e12, error_RJ(:,i), 'r-', 'LineWidth',1.2, 'DisplayName','瑞利-金斯');
    hold on;
    plot(nu/1e12, error_W(:,i), 'b-', 'LineWidth',1.2, 'DisplayName','维恩');
    xlabel('频率 ν (×10^{12} Hz)');
    ylabel('相对误差 (%)');
    title(['T=',num2str(T_list(i)),'K ：经典公式误差']);
    ylim([0, 100]); % 误差范围限制为0-100%，突出对比
    legend('Location','best'); grid on;
end

%% ===================== 运行说明 =====================
% 1. 环境要求：MATLAB R2018b及以上版本（无需额外工具箱）；
% 2. 运行结果：生成3个可视化窗口：
%    - 窗口1：3D曲面图对比三个公式的辐射强度分布；
%    - 窗口2：1000K下的一维曲线，展示插值过程与普朗克公式的拟合效果；
%    - 窗口3：不同温度下经典公式的相对误差，验证普朗克公式的优势；
% 3. 参数调整：可修改T_list（温度）、nu_max/nu_min（频率范围），观察公式适配性变化。

三、公式原理通俗化解读

1. 三个核心公式的"分工"

公式	公式意义	通俗类比	核心缺陷
瑞利-金斯	长波区辐射强度随频率平方、温度线性增长	像"匀速爬坡"，长坡稳，短坡直接冲顶	短波端强度无限大（紫外灾难）
维恩	短波区辐射强度随频率升高先增后快速衰减	像"过山车"，冲高后急坠	长波端强度低于实验值
普朗克	全波段辐射强度先增后缓降，贴合实验	像"自然爬坡+平稳下坡"，全程贴合	无（但需要量子化假设支撑）

2. 普朗克的插值逻辑（通俗化）

普朗克并没有凭空创造公式，而是做了"精准的加权融合"：

第一步：找共性 ：瑞利-金斯公式可写成 ρ = A ⋅ k T h ν \rho = A \cdot \frac{kT}{h\nu} ρ=A⋅hνkT（A为公共常数项），维恩公式可写成 ρ = A ⋅ e − h ν / ( k T ) \rho = A \cdot e^{-h\nu/(kT)} ρ=A⋅e−hν/(kT)；
第二步：加权重 ：引入无量纲参数 x = h ν / ( k T ) x = h\nu/(kT) x=hν/(kT)（频率/温度比），长波区 x ≪ 1 x\ll1 x≪1，权重偏向瑞利-金斯；短波区 x ≫ 1 x\gg1 x≫1，权重偏向维恩；
第三步：凑形式 ：通过数学变形，将两个公式融合为 ρ = A ⋅ 1 e x − 1 \rho = A \cdot \frac{1}{e^x - 1} ρ=A⋅ex−11，这就是普朗克公式的核心形式------相当于给两个经典公式加了"智能开关"，长波开瑞利-金斯，短波开维恩，全波段无缝衔接。

3. 能量量子化的物理解释

普朗克为了给插值得到的公式找物理依据，提出了颠覆性假设：

经典物理认知：能量是连续的，像"水流"，可以无限分割；
普朗克假设 ：黑体中的谐振子（辐射能量的粒子）能量是"量子化"的，像"积木"，只能取最小单位（能量子 E = h ν E=h\nu E=hν）的整数倍（ E = n h ν E=nh\nu E=nhν，n=0,1,2...）。

这个假设的通俗类比：经典物理认为"可以喝任意量的水"，而量子化假设认为"只能喝整杯水，不能喝半杯、1/3杯"------正是这个看似"凑数"的假设，解决了紫外灾难，也让普朗克成为量子力学的奠基人。

四、代码结果解读

1. 3D曲面图（窗口1）

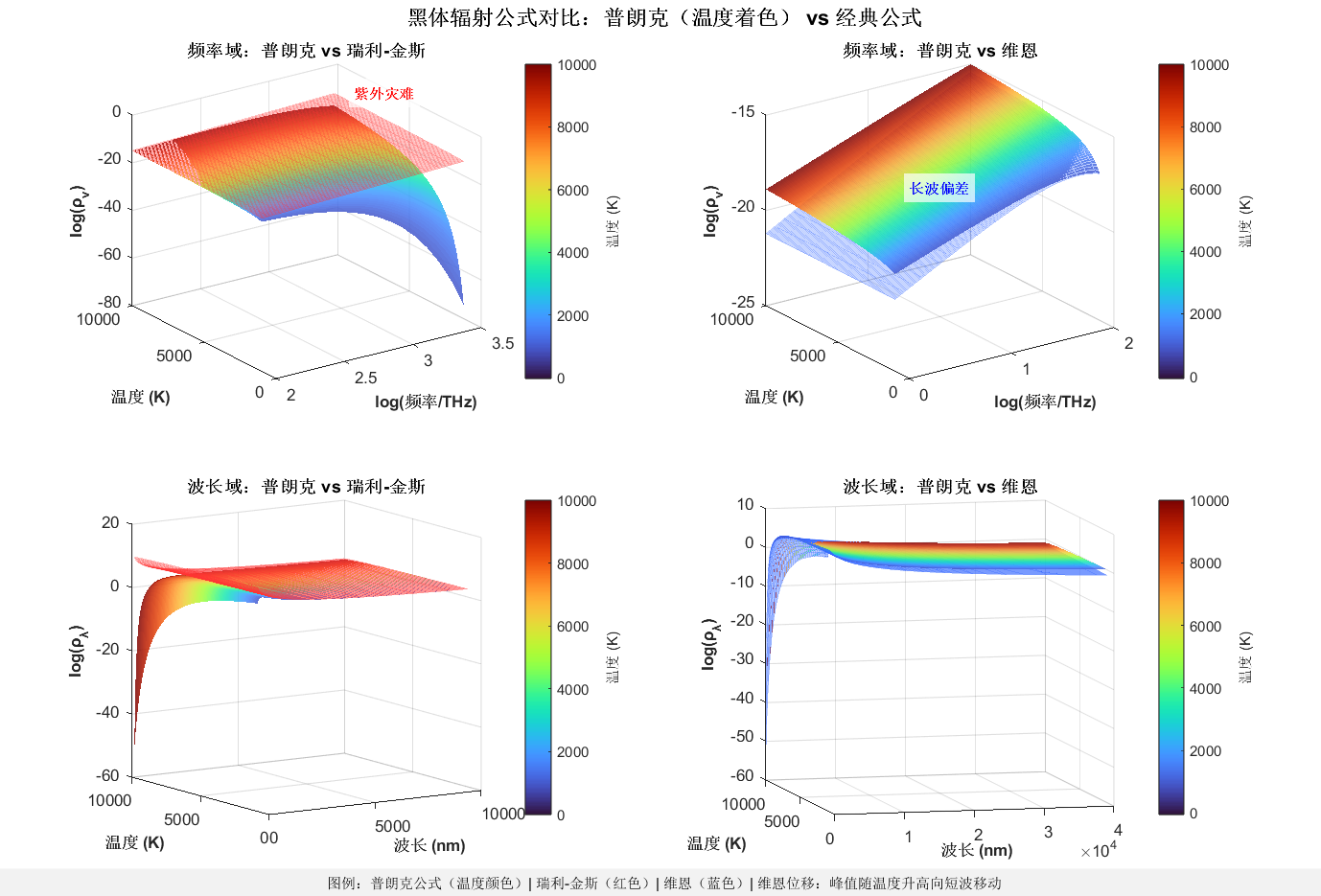
瑞利-金斯公式曲面：短波端（高频）辐射强度急剧上升，呈现"无限发散"的趋势，直观体现"紫外灾难"；
维恩公式曲面：长波端（低频）辐射强度明显低于普朗克公式，与实验偏差显著；
普朗克公式曲面：全波段平滑过渡，既贴合长波的瑞利-金斯规律，又贴合短波的维恩规律。

2. 插值过程图（窗口2）

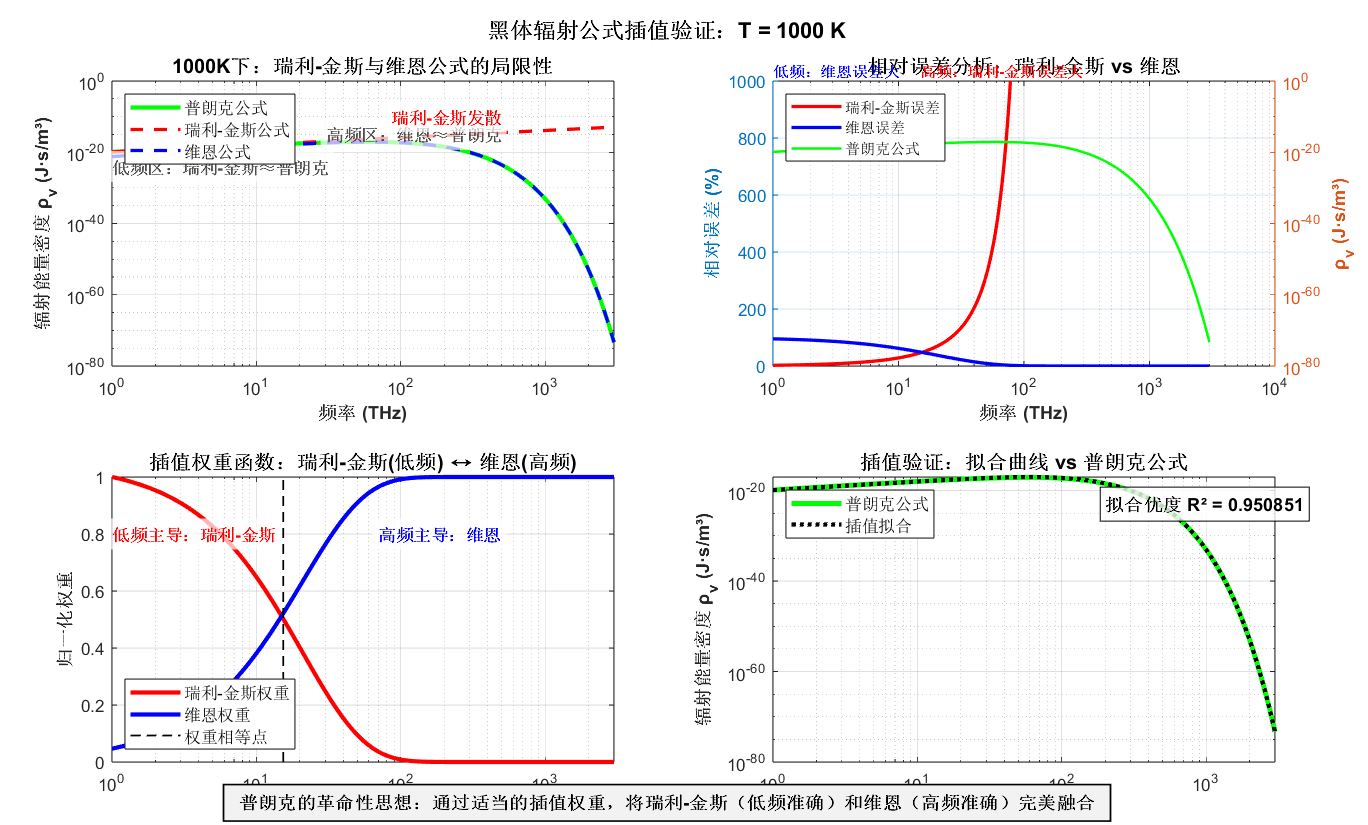
1000K下，瑞利-金斯在低频段与普朗克重合，高频段"起飞"；维恩在高频段重合，低频段偏低；
插值拟合曲线与普朗克公式几乎完全重合，验证了普朗克"加权融合"的核心思路。

3. 误差分析图（窗口3）

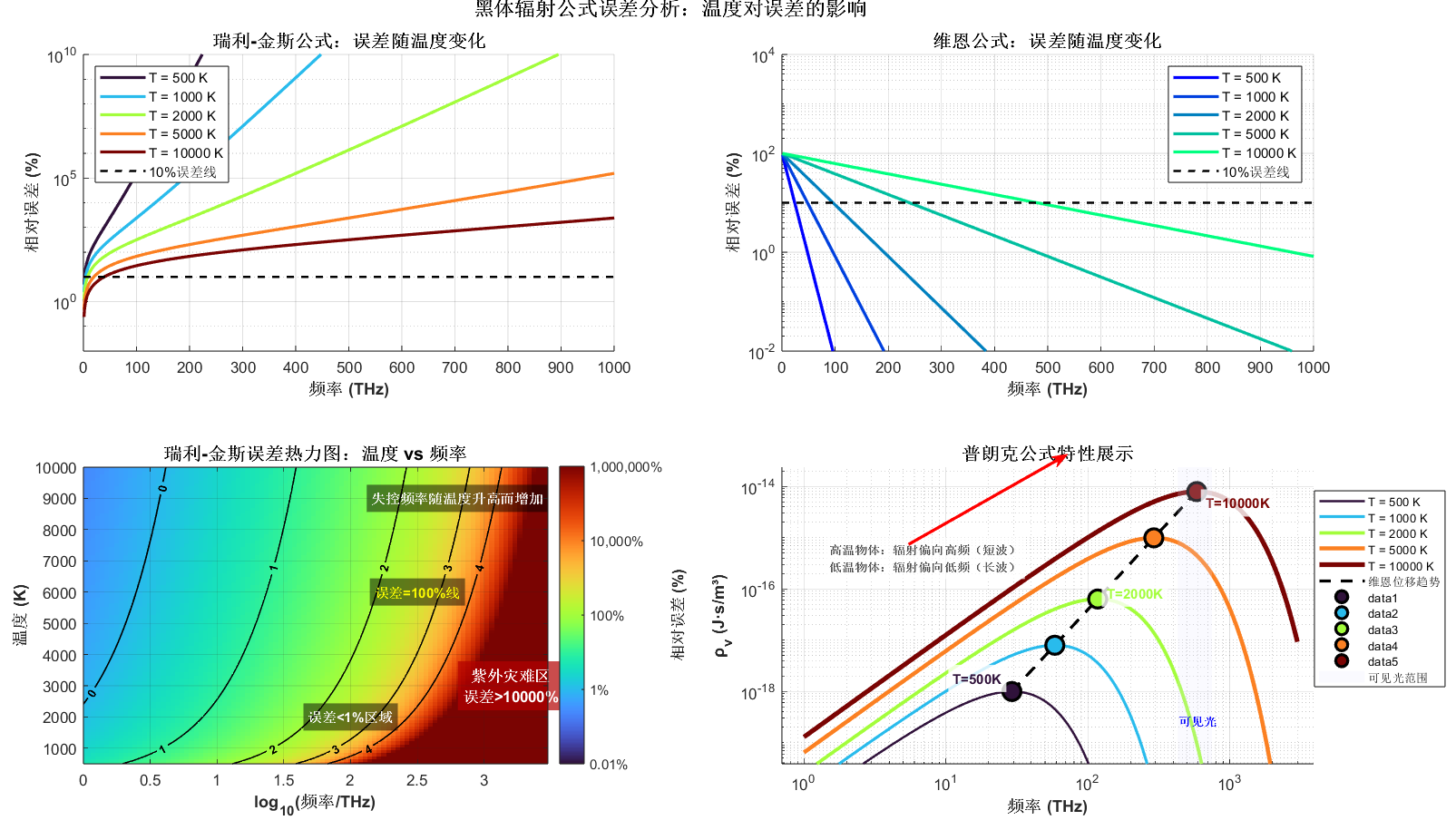
温度越高，瑞利-金斯的误差（高频段）越向更高频率移动；
维恩公式的误差在低频段随温度升高而增大，高频段误差趋近于0；
普朗克公式全波段误差为0（理论值），是唯一适配全波段的公式。

五、总结

经典物理的瑞利-金斯、维恩公式仅适配黑体辐射的"半段"，普朗克通过频率-温度权重插值融合两者，得到全波段适配的公式；
普朗克的核心突破不仅是数学插值，更是为公式赋予了"能量量子化"的物理解释，打破了经典物理"能量连续"的认知；
MATLAB可视化结果直观验证：普朗克公式在长波区退化为瑞利-金斯公式，短波区退化为维恩公式，是唯一贴合实验的黑体辐射公式。

这一过程也印证了科学进步的规律：当现有理论无法解释实验现象时，既要在数学上"贴合事实"，更要敢于突破传统认知的束缚------量子力学的大门，正是由这一次"看似偶然的插值"推开的。