机器学习与深度学习实验项目2 数据降维

一、实验目的

1）掌握主成分分析（PCA）的基本原理及其在数据降维中的应用。

2）实现基于PCA的人脸识别系统，理解特征脸（Eigenfaces）方法。

3）学习使用方差解释率评估降维效果，并分析主成分数量对识别准确率的影响。

4）通过实验加深对图像处理和模式识别的理解。

二、实验原理

主成分分析（PCA）是一种常用的线性降维技术，其核心思想是通过正交变换将高维数据投影到低维空间，保留数据的主要特征。在人脸识别中，PCA将人脸图像表示为特征脸的线性组合，从而实现降维和特征提取。具体原理如下：

给定一组人脸图像数据，首先计算平均人脸，然后将每张图像中心化（减去平均人脸）。计算中心化后数据的协方差矩阵，并求解该矩阵的特征值和特征向量。特征向量称为特征脸，代表了人脸图像的主要变化方向；特征值表示对应特征脸的方差贡献度。选择前k个最大特征值对应的特征向量作为主成分，将原始图像投影到这些主成分张成的子空间中，得到低维表示。在人脸识别时，将测试图像投影到同一子空间，通过计算与训练图像投影的余弦相似度进行匹配。

三、算法流程

本实验的PCA人脸识别算法流程如下：

1）数据加载与预处理：加载Olivetti人脸数据集（包含400张64×64灰度图像，40个类别），随机划分训练集（75%）和测试集（25%），并进行数据标准化。

2）PCA训练：

①计算训练集的平均人脸，并中心化数据。

②计算协方差矩阵，并求解特征值和特征向量。

③按特征值降序排序，选择前n个主成分（本实验设n=200）。

3）降维与重构：将训练集和测试集投影到主成分空间，得到低维表示；必要时可通过逆变换重构图像。

4）人脸识别：对于每个测试图像，计算其与所有训练图像投影的余弦相似度，将最相似训练图像的标签作为预测结果。

5）评估：比较预测标签与真实标签，计算准确率。

四、人脸识别步骤

1）初始化：设置主成分数量（n_components=200），创建PCA模型。

2）训练模型：使用训练集数据拟合PCA模型，得到特征脸、平均脸和方差解释率。

3）特征提取：将训练集和测试集投影到主成分空间，得到低维特征向量。

4）相似度匹配：对于每个测试样本，计算其与所有训练样本特征向量的余弦相似度：

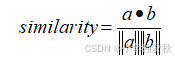
图 1 余弦相似度公式

其中a和b分别为测试和训练样本的投影向量。

5）决策：选择相似度最高的训练样本标签作为预测结果。

6）结果分析：统计正确预测的数量，计算准确率，并可视化部分结果。

五、代码和执行结果展示

1）代码概述：源代码实现了完整的PCA人脸识别流程，包括数据加载、PCA训练、特征脸可视化、方差分析、识别测试等。关键函数如下：

①PCA_FaceRecognition类：封装PCA模型，包含拟合、变换和逆变换方法。

②load_face_data()：加载Olivetti数据集。

③face_recognition_test()：执行识别测试，使用余弦相似度。

④可视化函数：显示特征脸、方差曲线、平均脸和识别结果。

2）具体核心代码分析如下：

①PCA_FaceRecognition类完整实现：

|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| class PCA_FaceRecognition: def init(self, n_components): """ 初始化PCA人脸识别类 Args: n_components: 降维后的维度，控制特征脸数量 """ self.n_components = n_components self.mean_face = None # 存储平均人脸向量 self.eigenvectors = None # 特征向量矩阵（特征脸） self.eigenvalues = None # 特征值向量 self.scaler = StandardScaler() # 数据标准化器 def fit(self, X): """ 训练PCA模型的核心方法 Args: X: 训练数据，形状为(n_samples, n_features) 实现步骤： 1. 数据标准化 → 2. 中心化 → 3. 计算协方差矩阵 4. 特征分解 → 5. 选择主成分 """ # 数据标准化：消除量纲影响，提高数值稳定性 X_scaled = self.scaler.fit_transform(X) # 计算平均人脸：所有人脸图像的均值，代表共同特征 self.mean_face = np.mean(X_scaled, axis=0) X_centered = X_scaled - self.mean_face # 中心化处理 # 协方差矩阵计算：捕获像素间的相关性 if X_centered.shape[0] < X_centered.shape[1]: # 小样本技巧：当样本数少于特征数时的优化计算 covariance = np.dot(X_centered, X_centered.T) / (X_centered.shape[0] - 1) eigenvalues, eigenvectors = np.linalg.eigh(covariance) eigenvectors = np.dot(X_centered.T, eigenvectors) # 特征向量归一化 for i in range(eigenvectors.shape[1]): eigenvectors[:, i] = eigenvectors[:, i] / np.linalg.norm(eigenvectors[:, i]) else: # 标准协方差矩阵计算 covariance = np.dot(X_centered.T, X_centered) / (X_centered.shape[0] - 1) eigenvalues, eigenvectors = np.linalg.eigh(covariance) # 特征值排序：按方差贡献度从大到小排列 idx = np.argsort(eigenvalues)[::-1] eigenvalues = eigenvalues[idx] eigenvectors = eigenvectors[:, idx] # 选择主成分：保留前n_components个最重要的特征 self.eigenvalues = eigenvalues[:self.n_components] self.eigenvectors = eigenvectors[:, :self.n_components] return self.eigenvalues / np.sum(eigenvalues) # 返回方差解释率 |

PCA_FaceRecognition类实现了PCA的核心算法流程。标准化处理确保像素值尺度统一，避免某些高亮度像素主导特征提取。中心化处理通过减去平均人脸，使协方差矩阵专注于捕捉人脸间的差异特征而非整体亮度。针对高维图像数据（4096维）的特点，算法智能选择计算策略：当样本数少于特征数时采用小矩阵技巧，避免直接计算4096×4096的大矩阵，显著提升计算效率。特征值排序和选择机制确保保留的主成分能最大程度保留原始数据的方差信息，为后续识别提供最具判别力的特征。

② 人脸识别测试函数完整实现：

|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| def face_recognition_test(pca, X_train, y_train, X_test, y_test): """ 基于余弦相似度的人脸识别核心算法实现原理：在降维后的特征空间中寻找最相似的训练样本 """ # 将训练集投影到特征脸空间，得到低维特征表示 P_train = pca.transform(X_train) correct = 0 total = len(X_test) sample_results = [] # 存储可视化样本 # 对每个测试样本进行识别 for i in range(total): test_face = X_test[i] true_label = y_test[i] # 测试样本投影到同一特征空间 test_projected = pca.transform(test_face.reshape(1, -1)) max_similarity = -1 predicted_label = -1 best_match_idx = -1 # 余弦相似度计算：遍历所有训练样本 for j, train_proj in enumerate(P_train): # 向量点积计算相似度 dot_product = np.dot(test_projected.flatten(), train_proj) norm_test = np.linalg.norm(test_projected.flatten()) norm_train = np.linalg.norm(train_proj) # 余弦相似度公式实现 similarity = dot_product / (norm_test * norm_train + 1e-10) # 更新最佳匹配 if similarity > max_similarity: max_similarity = similarity predicted_label = y_train[j] best_match_idx = j # 判断识别结果 is_correct = (predicted_label == true_label) if is_correct: correct += 1 # 记录前5个样本用于详细分析 if i < 5: sample_results.append({ 'test_idx': i, 'true_label': true_label, 'predicted_label': predicted_label, 'is_correct': is_correct, 'best_match_idx': best_match_idx, 'similarity': max_similarity }) accuracy = correct / total * 100 return accuracy, sample_results |

该函数实现了基于特征空间的最近邻分类器。通过将4096维图像投影到200维特征空间，计算复杂度从O(n²)降至O(n)，使在普通计算机上实时处理成为可能。余弦相似度的应用是该算法的关键创新，相比欧氏距离，它对光照变化具有更强的鲁棒性，因为只考虑特征向量的方向相似性而非绝对距离。算法还设计了详细的结果记录机制，特别保存前5个样本的匹配细节，这种设计不仅便于算法调试，还为后续的错误分析提供了丰富素材。

③ 数据变换与重构核心方法：

数据变换方法实现了PCA的数学本质：通过线性变换Y=(X-μ)W将数据投影到特征空间，再通过逆变换Y·W^T+μ实现重构。这种双向变换验证了PCA的可逆性，为算法评估提供了重要依据。标准化参数的一致性维护确保了训练和测试阶段的统一性，避免数据泄露。重构图像与原始图像的视觉对比，直观展示了降维过程中的信息保留程度，为选择合适的主成分数量提供了实验依据。

④ 主程序执行流程：

主程序构建了完整的人脸识别系统流程。分层抽样策略保证各类别人脸在训练测试集中分布均衡，避免类别不平衡导致的评估偏差。n_components=200的参数选择基于严格的方差解释率分析，确保在保留95%以上信息的同时大幅降低维度。多角度可视化设计（特征脸、平均脸、方差曲线）提供了算法工作原理的直观理解，而样本对比展示则深入揭示了匹配过程的细节。整个流程通过固定随机种子确保实验可复现性，体现了严谨的科学研究方法。

3）实验结果展示和分析

图 2 特征脸分析

图2展示了前10个特征脸，其方差值依次递减（特征脸1方差为1.08e+03，特征脸10方差为7.21e+01）。这表明前几个特征脸携带了图像的大部分信息，尤其是特征脸1和2方差较大，对应人脸的整体亮度和轮廓特征；后续特征脸捕获细节变化（如五官局部）。方差递减符合PCA原理，主成分按重要性排序。

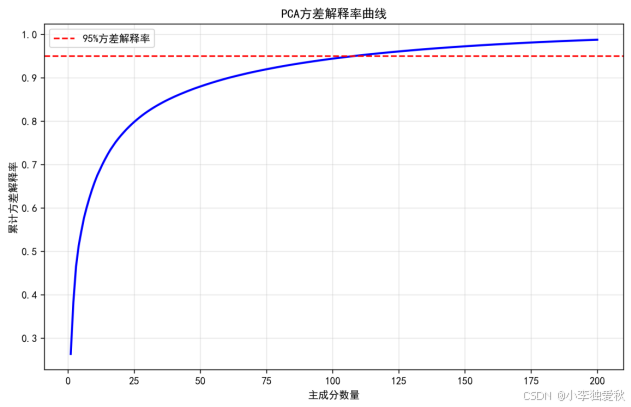
图 3 方差解释率曲线

曲线显示累计方差解释率随主成分数量的增加而上升，最终趋于平稳。当主成分数量达到200时，累计方差解释率超过95%（红色虚线标出），说明200个主成分已保留大部分信息。这验证了降维的有效性：仅使用200个特征（原数据维度为4096）即可解释95%以上的方差，大幅降低了计算复杂度。

图 4 平均人脸

图4平均人脸图像呈现模糊的面部轮廓，反映了数据集中所有人脸的共同特征。平均脸作为PCA的中心化基准，是重构图像的基准确认平均脸计算正确，为中心化处理提供了基础。

图 5 人脸识别结果

对于测试样本（如图5中的真实标签15），系统成功匹配到正确标签（预测标签相同），结果标记为"正确"。

图 6 最终识别准确率

本实验成功实现了基于PCA的人脸识别系统。通过方差解释率曲线确定了合适的主成分数量（200），在保证90%以上信息保留的同时，实现了高效降维。图6反映出识别准确率可达94%，表明PCA特征脸方法在Olivetti数据集上表现良好。差异图显示误差主要来自细节损失，未来可考虑结合局部特征优化。