(以下内容全部出自上述课程)
目录
- 树的存储结构
-
- [1. 树的逻辑结构](#1. 树的逻辑结构)
- [2. 树的存储结构](#2. 树的存储结构)
-
- [2.1 双亲表示法](#2.1 双亲表示法)
- [2.2 孩子表示法](#2.2 孩子表示法)
- [2.3 孩子兄弟表示法](#2.3 孩子兄弟表示法)
- [3. 小结](#3. 小结)
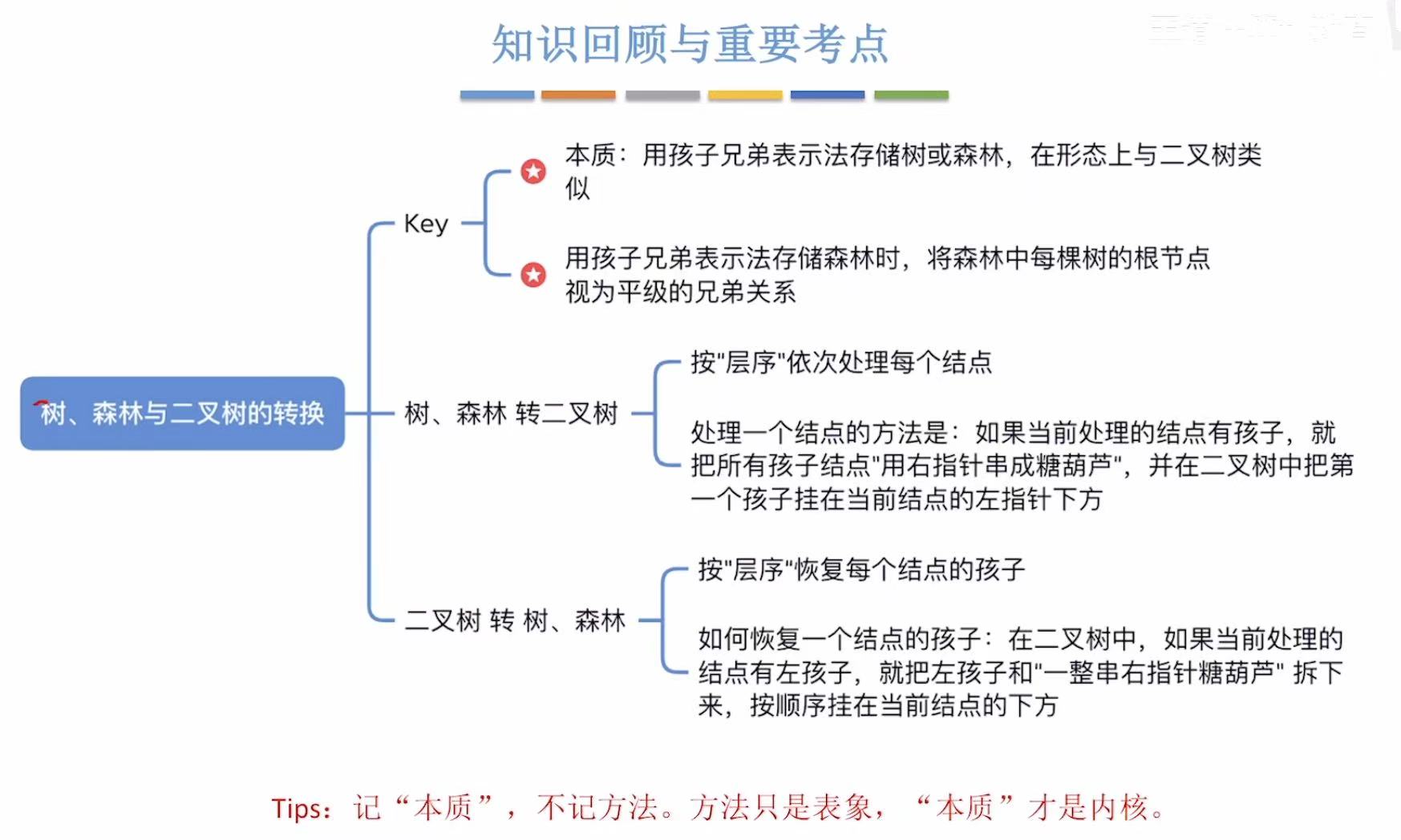
- 树、森林与二叉树的转换
-
- [1. 树-->二叉树](#1. 树-->二叉树)
- [2. 森林-->二叉树](#2. 森林-->二叉树)
- [3. 二叉树-->树](#3. 二叉树-->树)
- [4. 二叉树-->森林](#4. 二叉树-->森林)
- [5. 小结](#5. 小结)
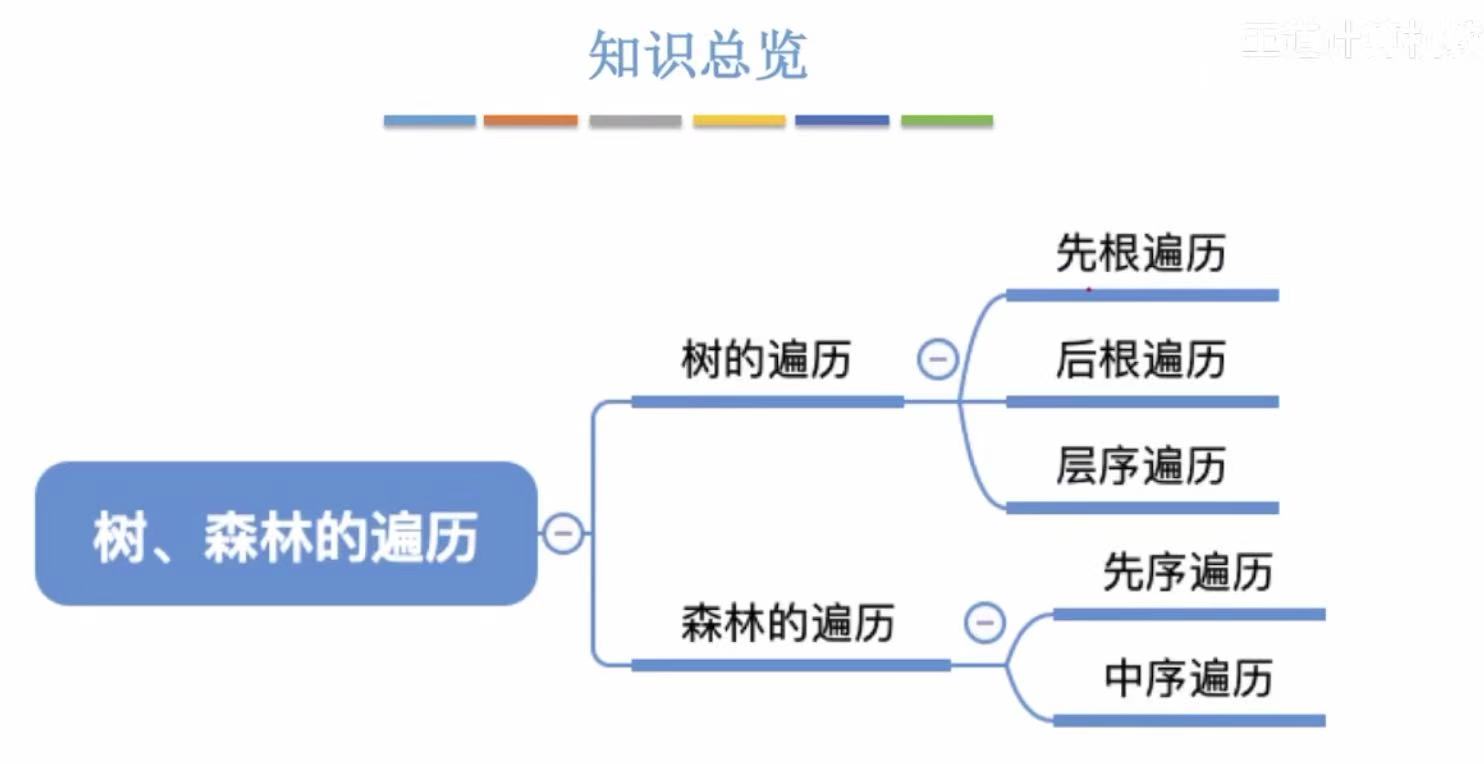
- 树、森林的遍历
-
- [1. 树的遍历](#1. 树的遍历)
-
- [1.1 先根遍历](#1.1 先根遍历)
- [1.2 后根遍历](#1.2 后根遍历)
- [1.3 层次遍历](#1.3 层次遍历)
- [2. 森林的遍历](#2. 森林的遍历)
-
- [2.1 先序遍历](#2.1 先序遍历)
- [2.2 中序遍历](#2.2 中序遍历)
- [3. 小结](#3. 小结)
- 哈夫曼树
-
- [1. 带权路径长度](#1. 带权路径长度)
- [2. 哈夫曼树](#2. 哈夫曼树)
-
- [2.1 定义](#2.1 定义)
- [2.2 构造](#2.2 构造)
- [3. 哈夫曼编码](#3. 哈夫曼编码)
- [4. 小结](#4. 小结)
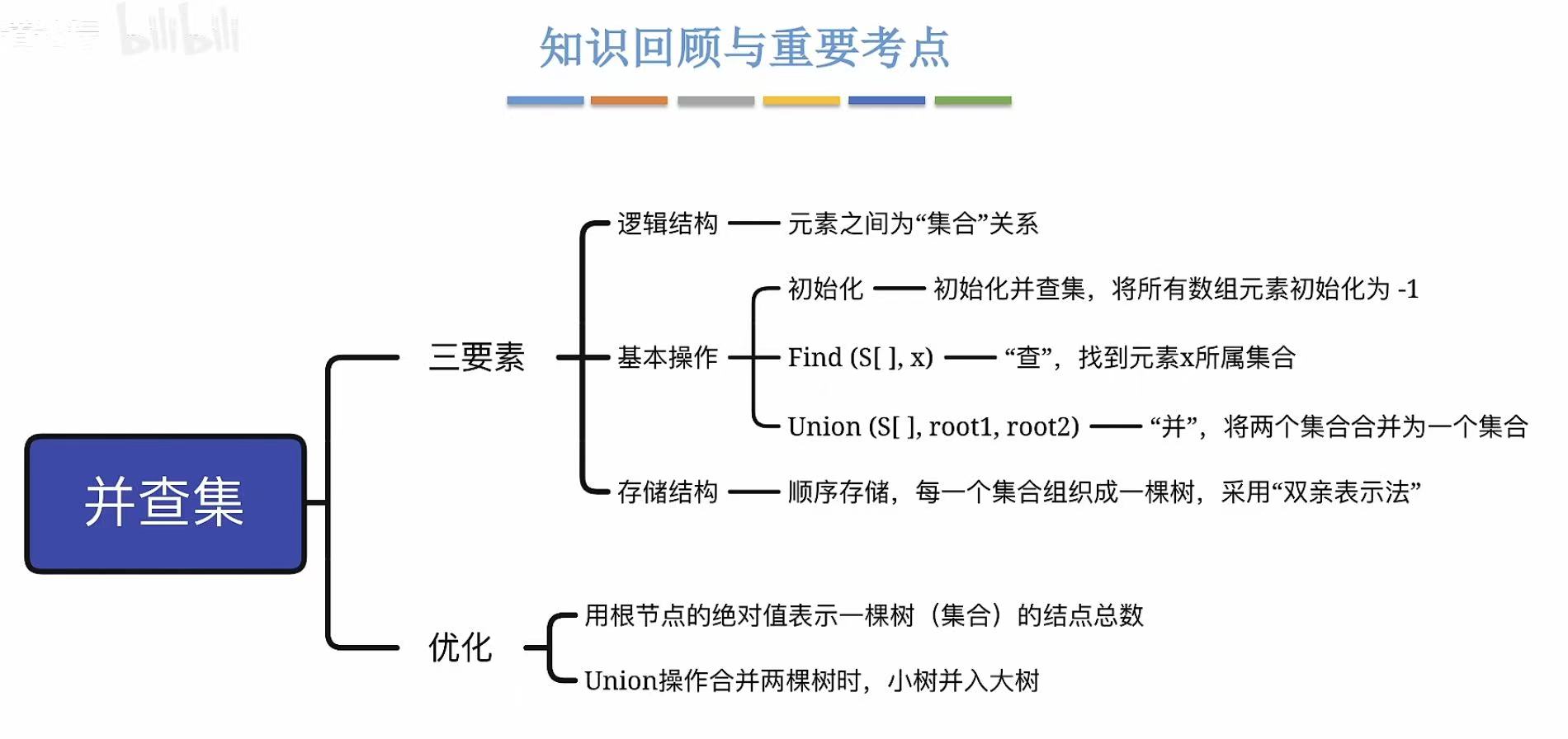
- 并查集
-
- [1. 如何表示集合关系?](#1. 如何表示集合关系?)
- [2. 并查集](#2. 并查集)
-
- [2.1 存储结构](#2.1 存储结构)
- [2.2 基本操作](#2.2 基本操作)
- [2.3 代码实现](#2.3 代码实现)
-
- [2.3.1 初始化](#2.3.1 初始化)
- [2.3.2 并、查](#2.3.2 并、查)
- [2.3.3 时间复杂度分析](#2.3.3 时间复杂度分析)
- [3. 优化](#3. 优化)
-
- [3.1 Union操作的优化](#3.1 Union操作的优化)
- [3.2 Find操作的优化](#3.2 Find操作的优化)
- [3.3 优化总结](#3.3 优化总结)
- [4. 小结](#4. 小结)
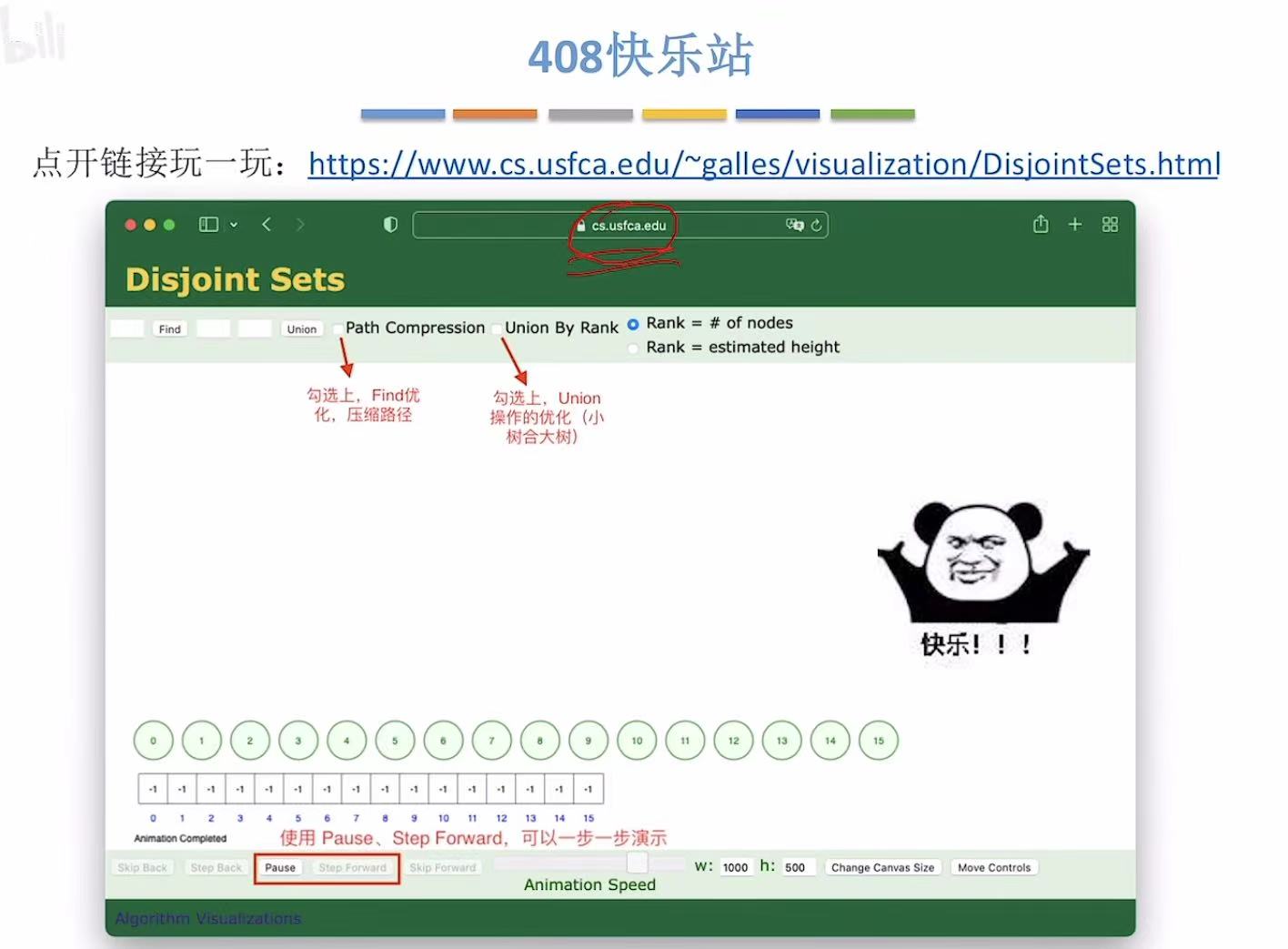
- [5. 拓展网站](#5. 拓展网站)
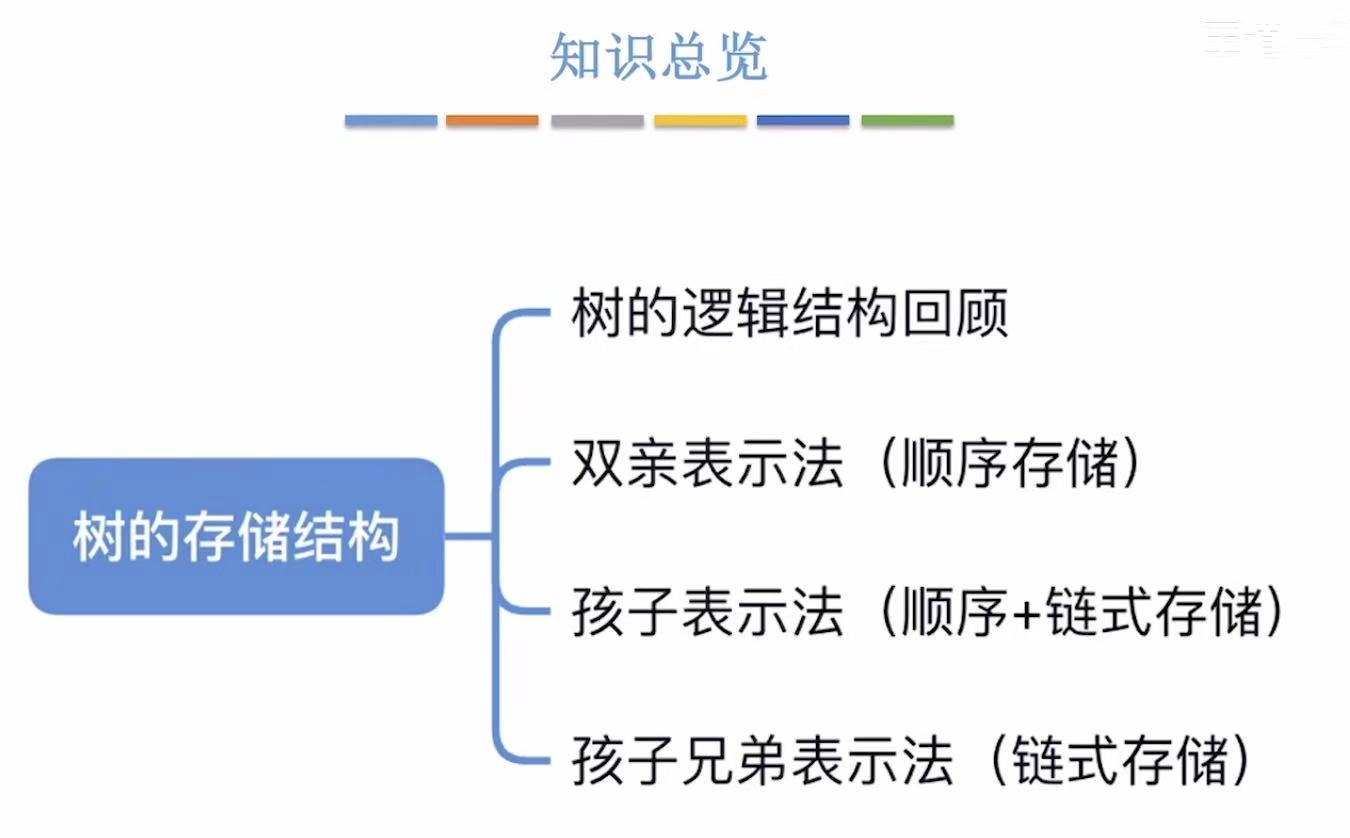
树的存储结构
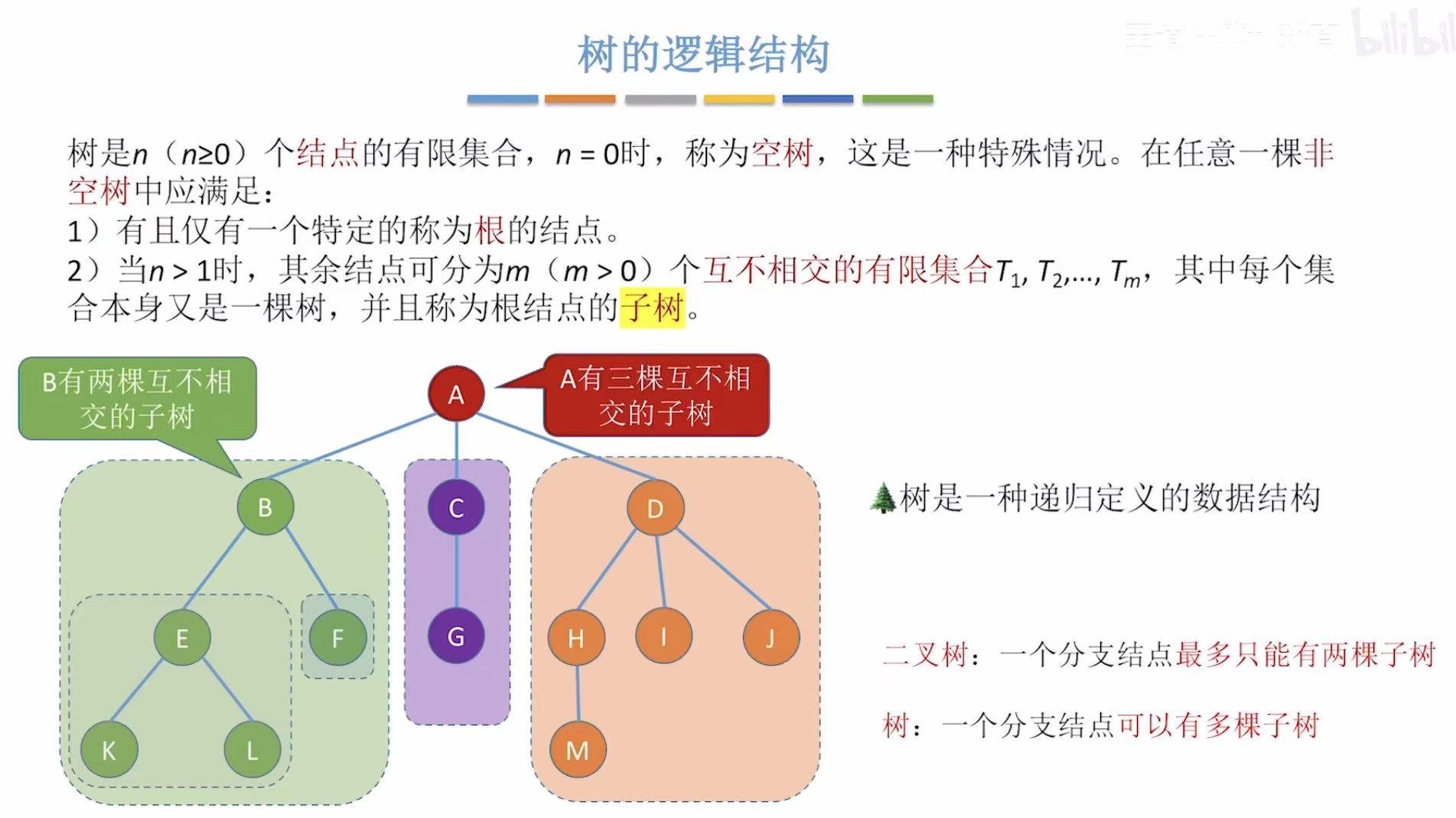
1. 树的逻辑结构
树的逻辑结构 :根+子树=超多或者0结点
具体可见:二叉树的存储结构
2. 树的存储结构
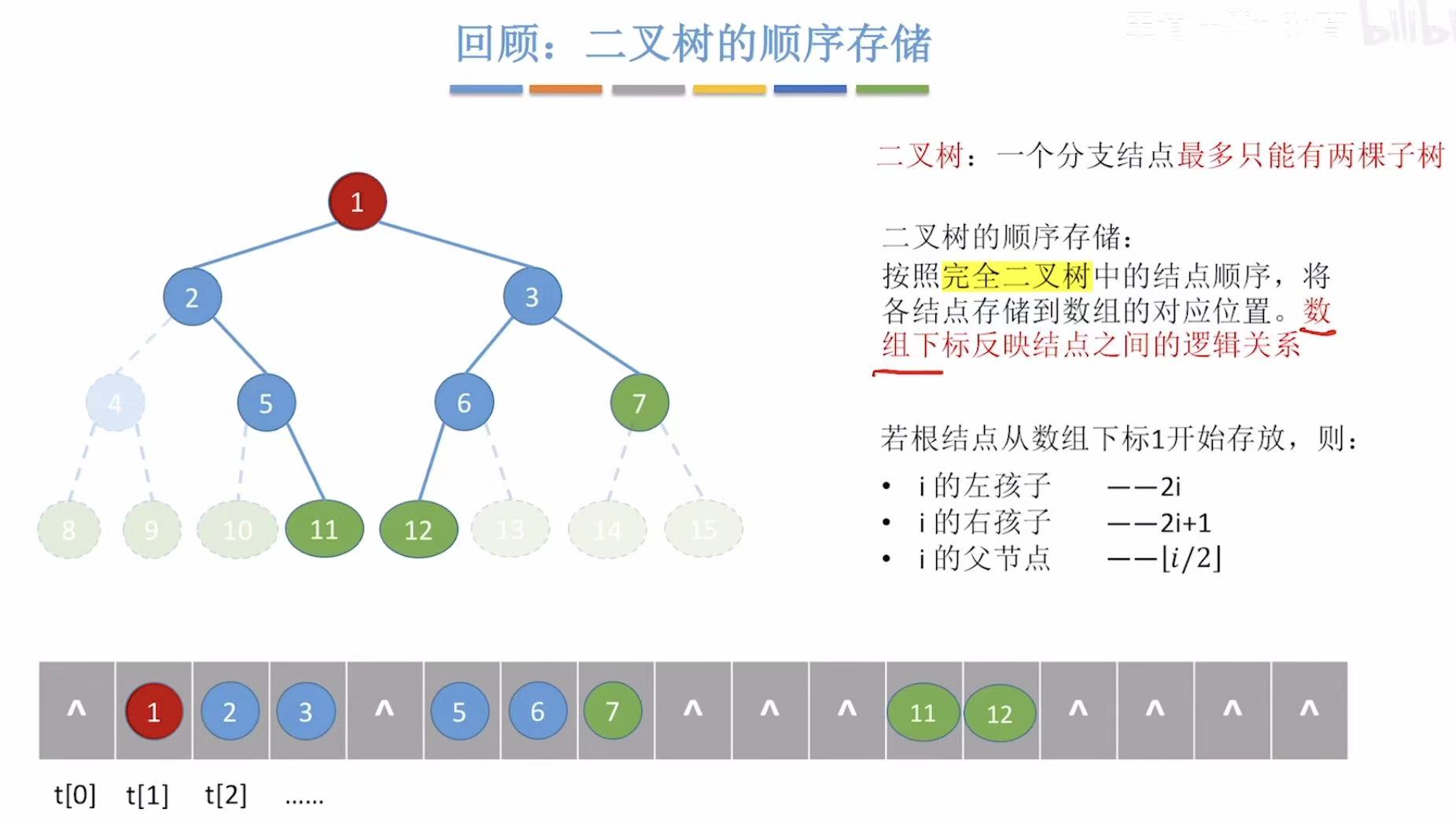
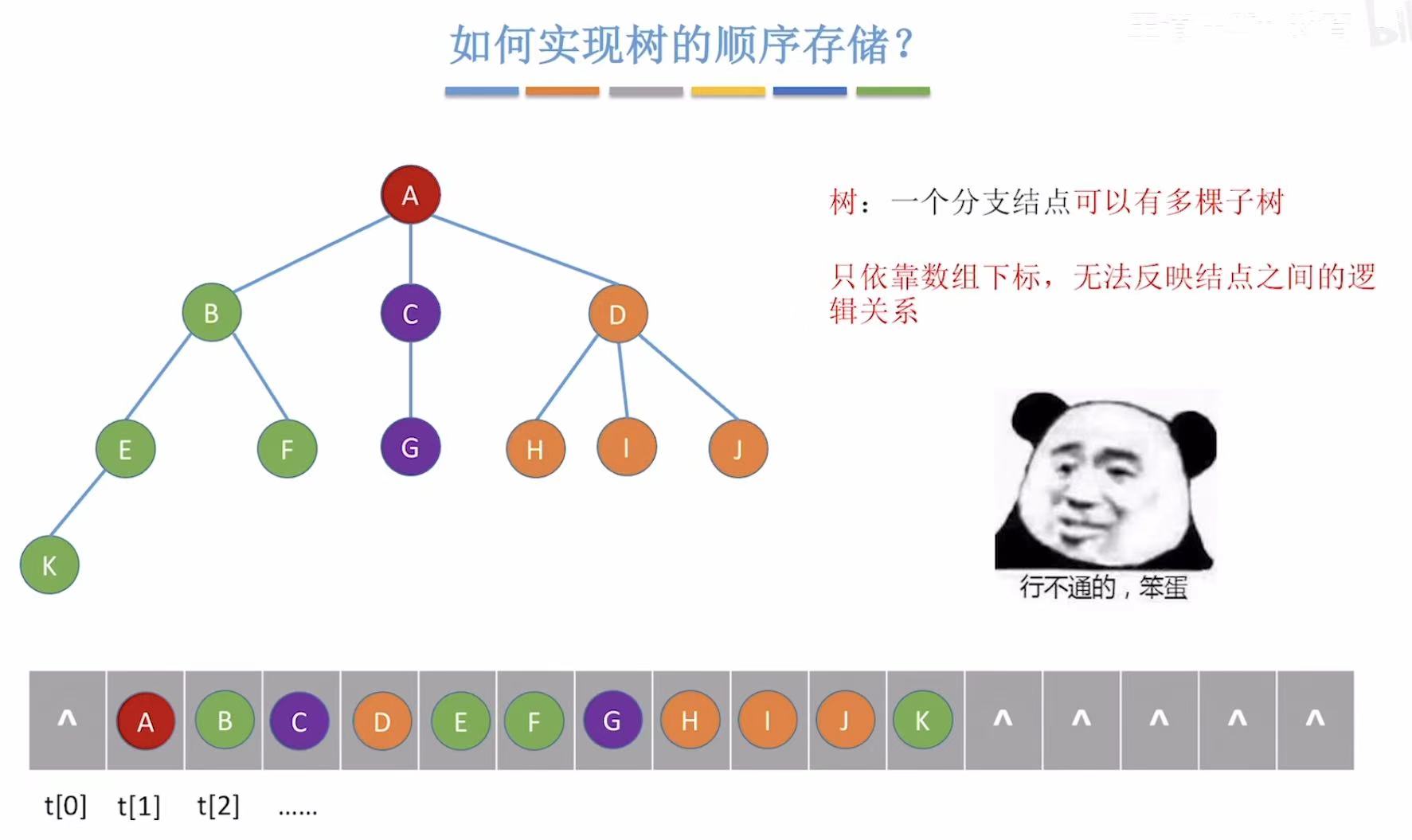
二叉树我们可以按满二叉树的固定编号来进行存储,但是单纯的树是没有满这个概念的,只依靠数组下标是无法反映结点之间的逻辑关系的。那么我们该如何实现树的顺序存储呢?
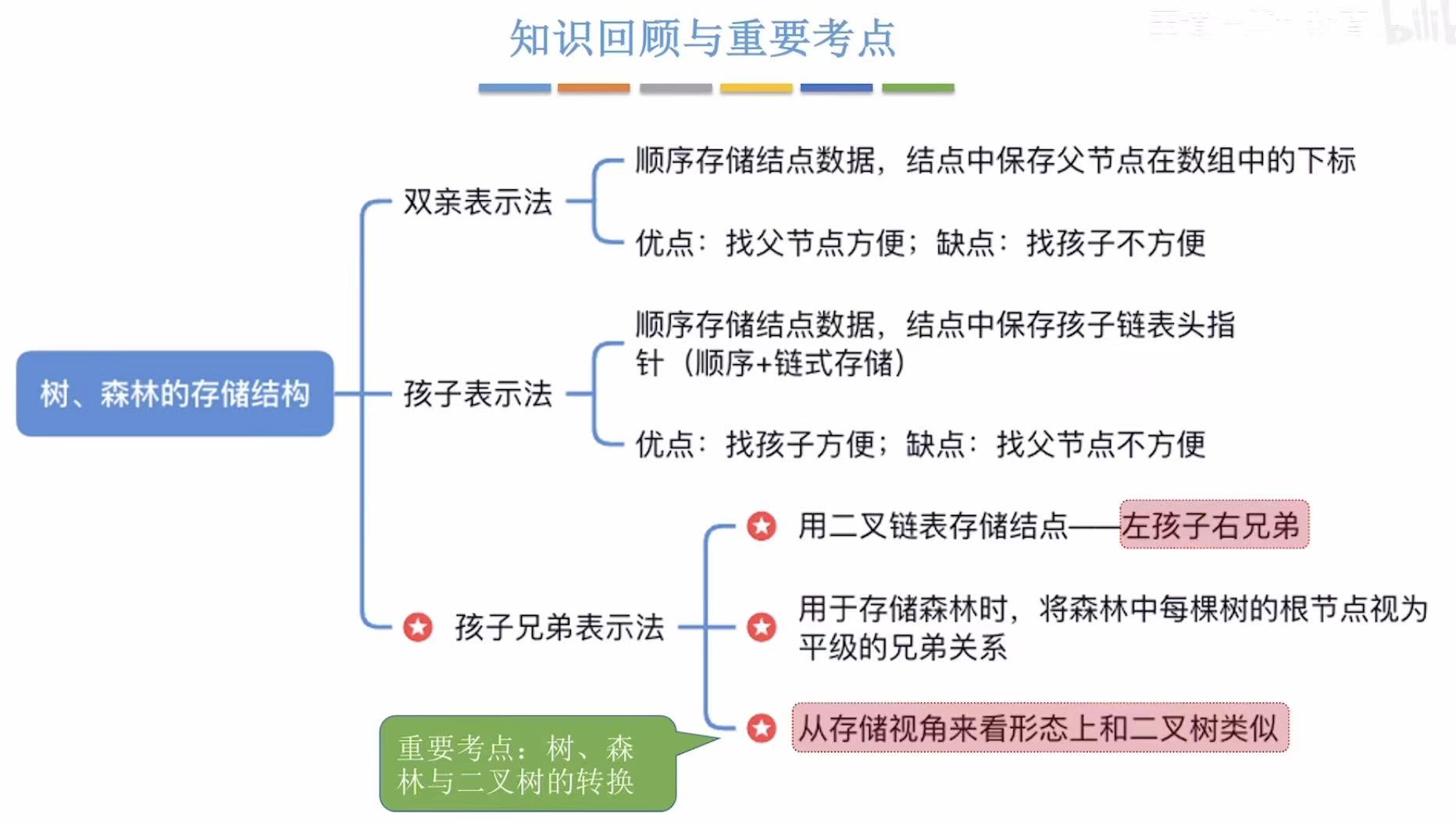
2.1 双亲表示法
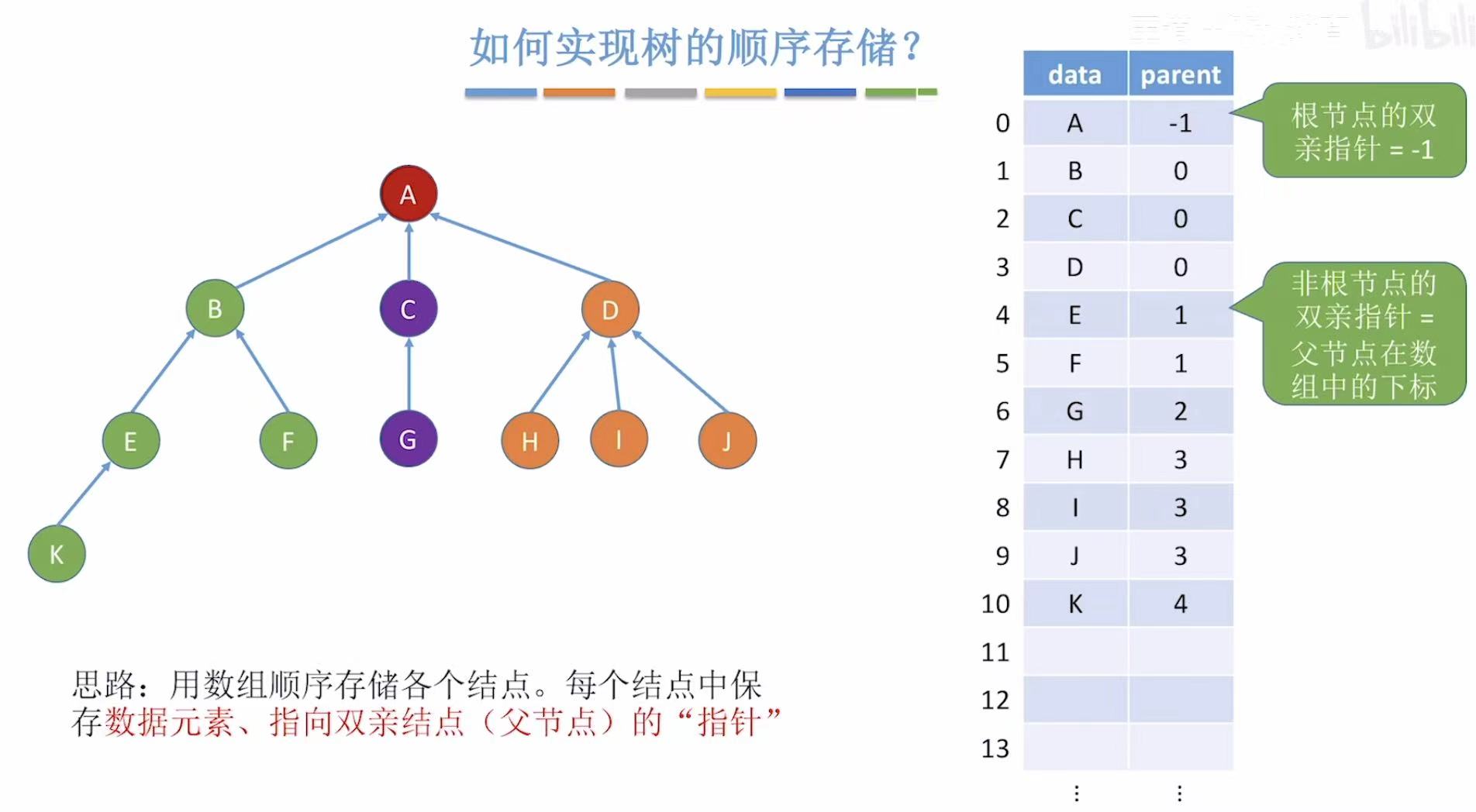
搞不定的东西,都可以用表来处理,因为只有两行,所以数组就可以轻松搞定。
- data:结点
- parent:当前结点的父节点(看图中箭头,比如B-->A,B的parent就是A的编号0)
- ps:因为数组中存的是自己的父节点,所以就叫做双亲表示法。
- PTNode:就是表中的一行,定义时需要定义表头(data&parent);
- PTree:就是整个表,也就是整个树,定义时需要定义行(所有数组)和列(数组个数)
java
#define MAX_TREE_SIZE 100 // 树中最多有 100 个结点
typedef struct {
ElemType data; // 数据域,存储结点值
int parent; // 双亲位置域:指向父结点的下标
} PTNode;
typedef struct {
PTNode nodes[MAX_TREE_SIZE]; // 存放所有结点的数组
int n; // 当前树中实际结点数(如 n=11)
} PTree;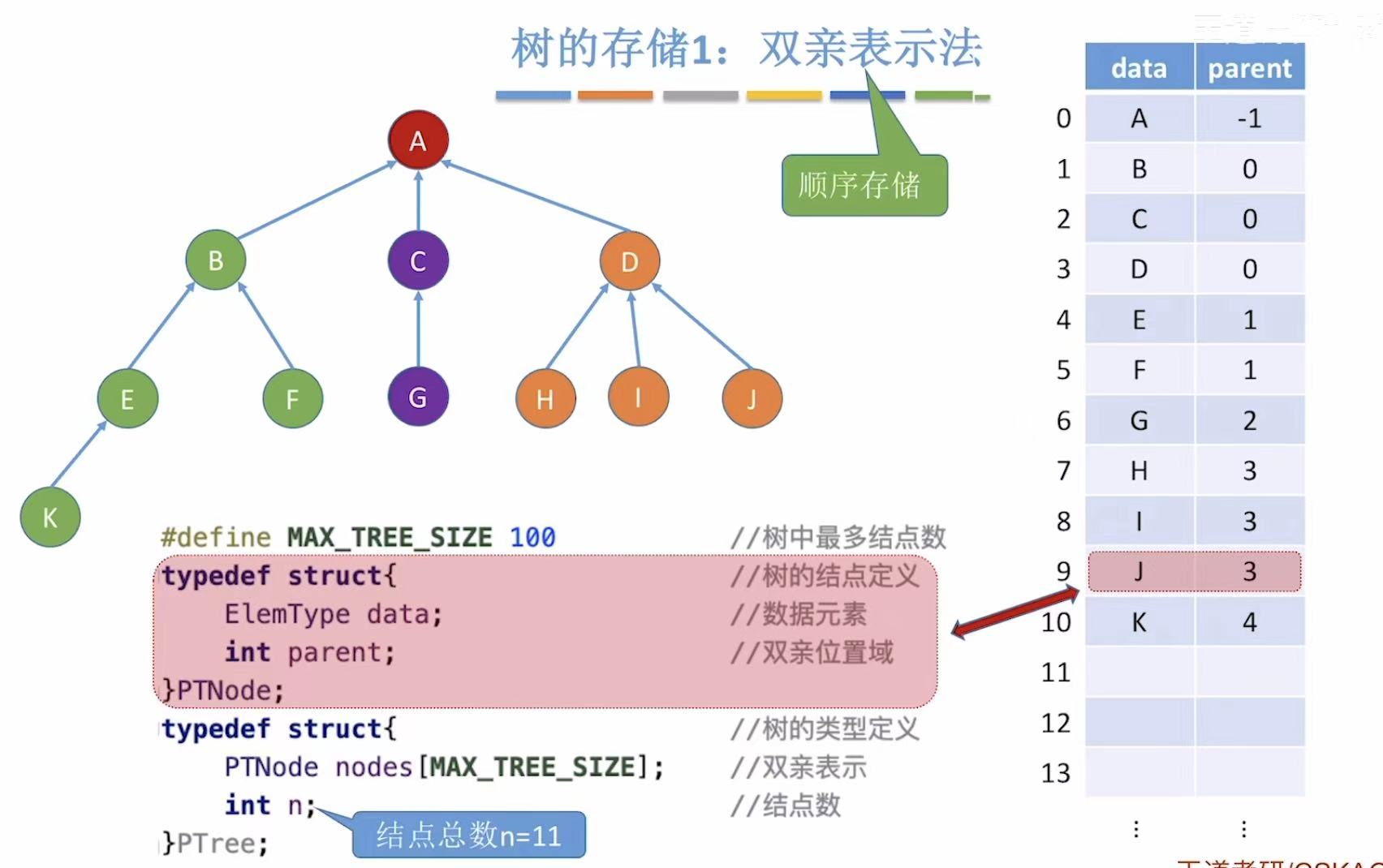
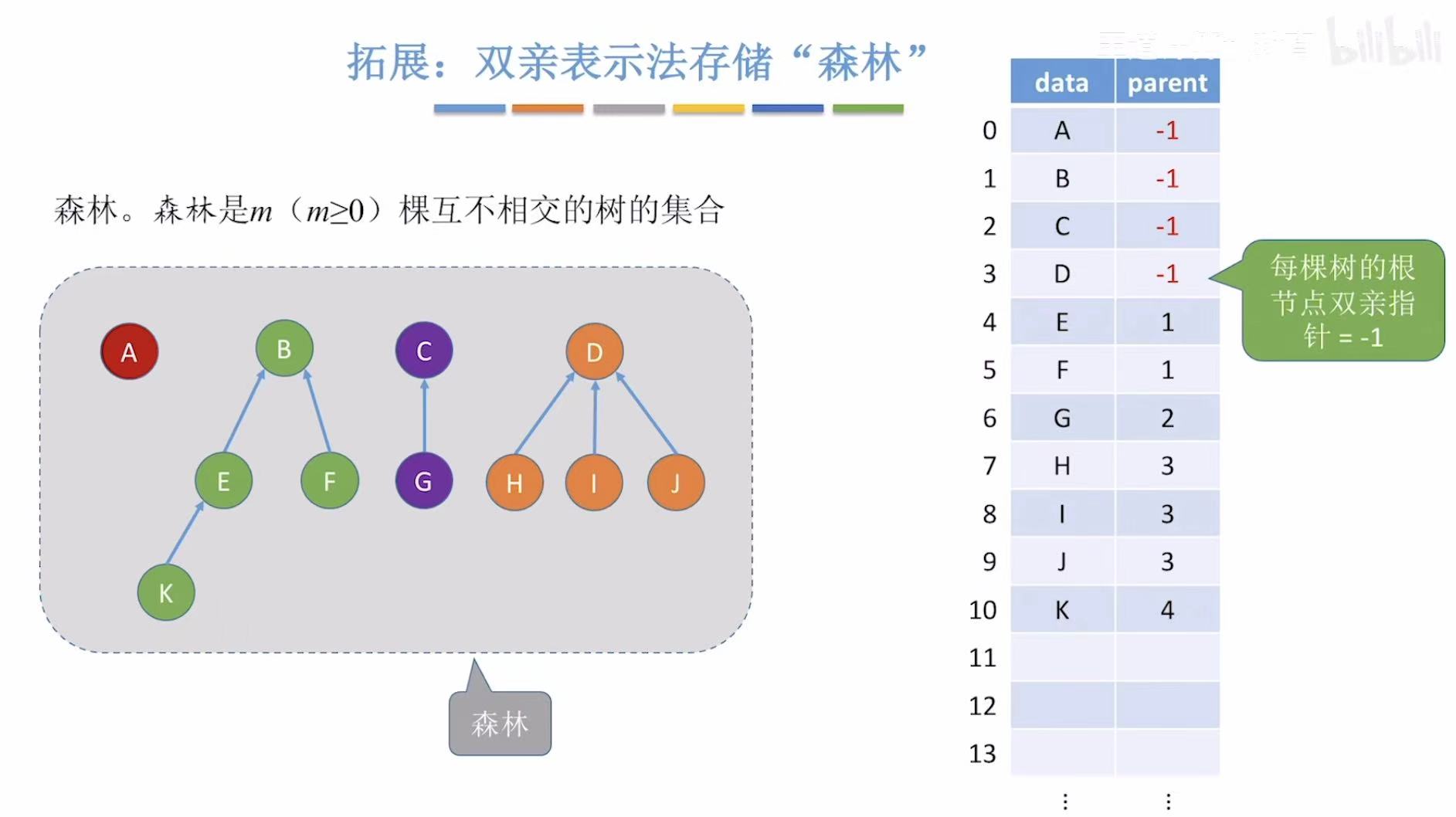
同理,也可以用来存储森林,每个树的根都指向-1,就代表自己是这个树的根了。
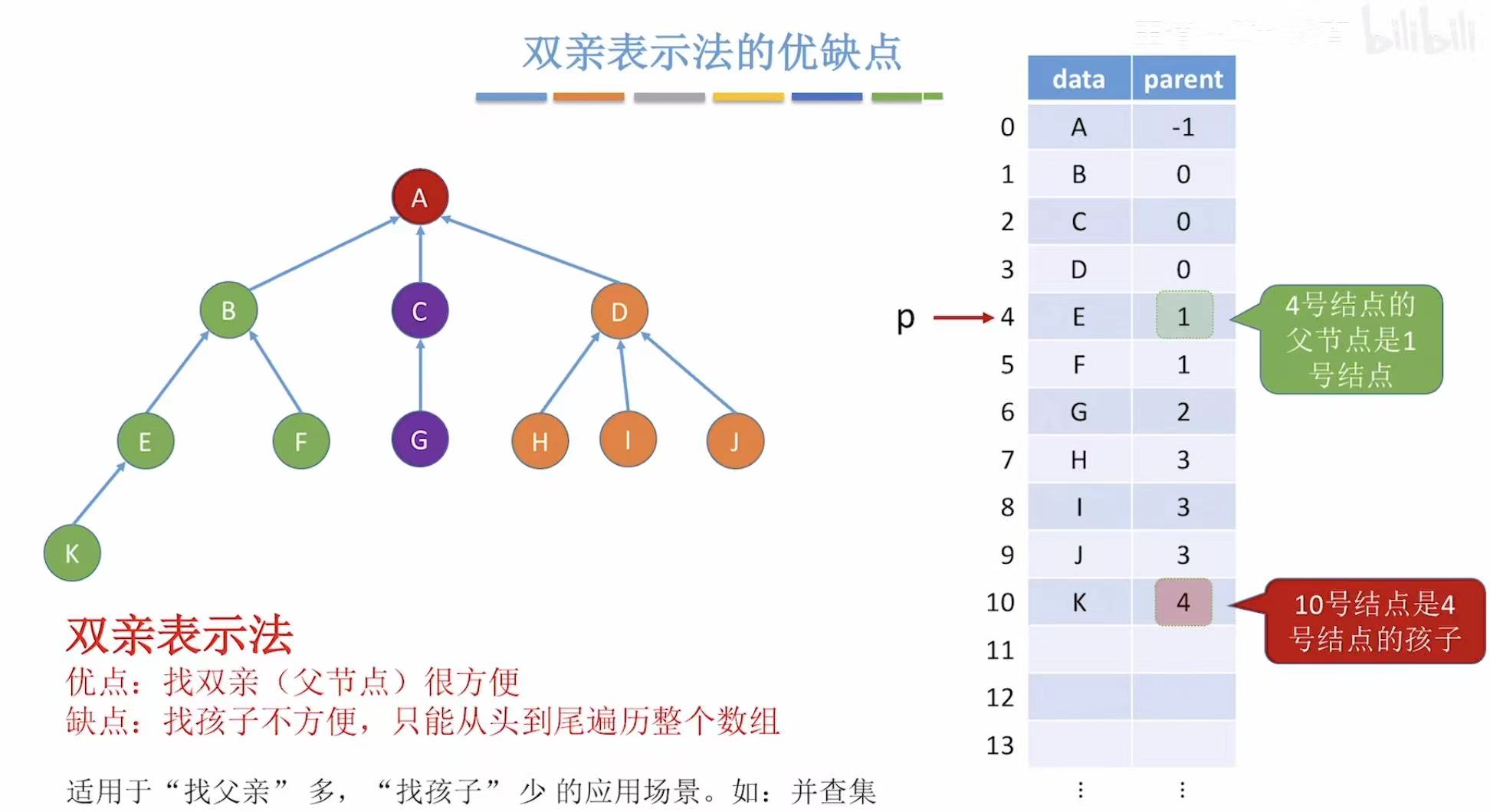
因为每个结点都是直接 存了自己的父节点的编号,所以找父节点就很方便 ;但如果想找自己的子节点该怎么办呢?
就只能从上到下依次遍历 一遍,找谁的父节点是自己的编号,才能知道谁是自己的孩子,这样看就很低效。
查找父节点容易,我们就要充分发挥这一功能,所以这种存储方式适用于找父亲多的场景,比如并查集。
- 固定寻找模式:该节点-->父节点
- 想找孩子也只能:该节点-->父节点-->循环遍历-->遍历到当前结点的父节点是自己想知道的-->刚遍历到的结点就是子节点
2.2 孩子表示法
为了弥补双亲表示法无法快速找到孩子的遗憾,所以又推出了孩子表示法:
- data:当前结点。
- firstChild :自己第一个孩子的结点。(孩子太多当然会用链表串成一串,老大、老二、老三...)
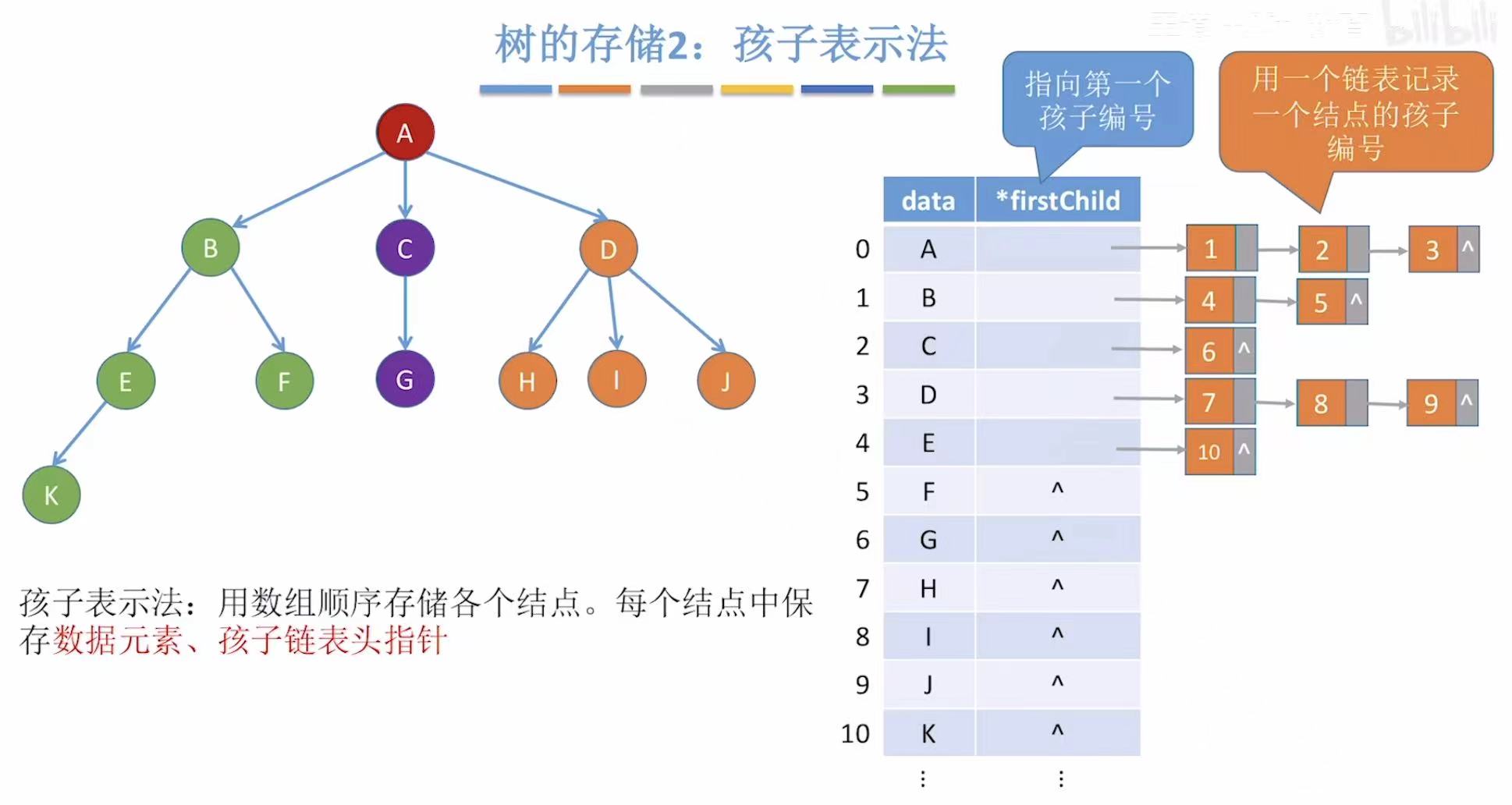
- CTNode:黄色方框的孩子,所以需要定义孩子的位置和下一个孩子(链表链接)。
- CTBox:红色方框的一行,所以需要定义data和*firstChild。
- CTree:整个表格/树,所以需要定义行(数组)和列(数组个数)。
- ps:双亲表示法可以通过 parent = -1 自动识别出根,无需额外变量;
而孩子表示法无法从结构中直接判断谁是根,必须显式记录根的位置(如 r)。
javatypedef
int child; // 孩子结点在数组中的下标
struct CTNode *next; // 指向下一个孩子(兄弟)
} CTNode;
typedef struct {
ElemType data;
CTNode *firstChild; // 指向第一个孩子的指针
} CTBox;
typedef struct {
CTBox nodes[MAX_TREE_SIZE]; // 所有结点存放在一个数组中
int n, r; // n: 结点总数;r: 根的位置(仅适用于单棵树)
} CTree;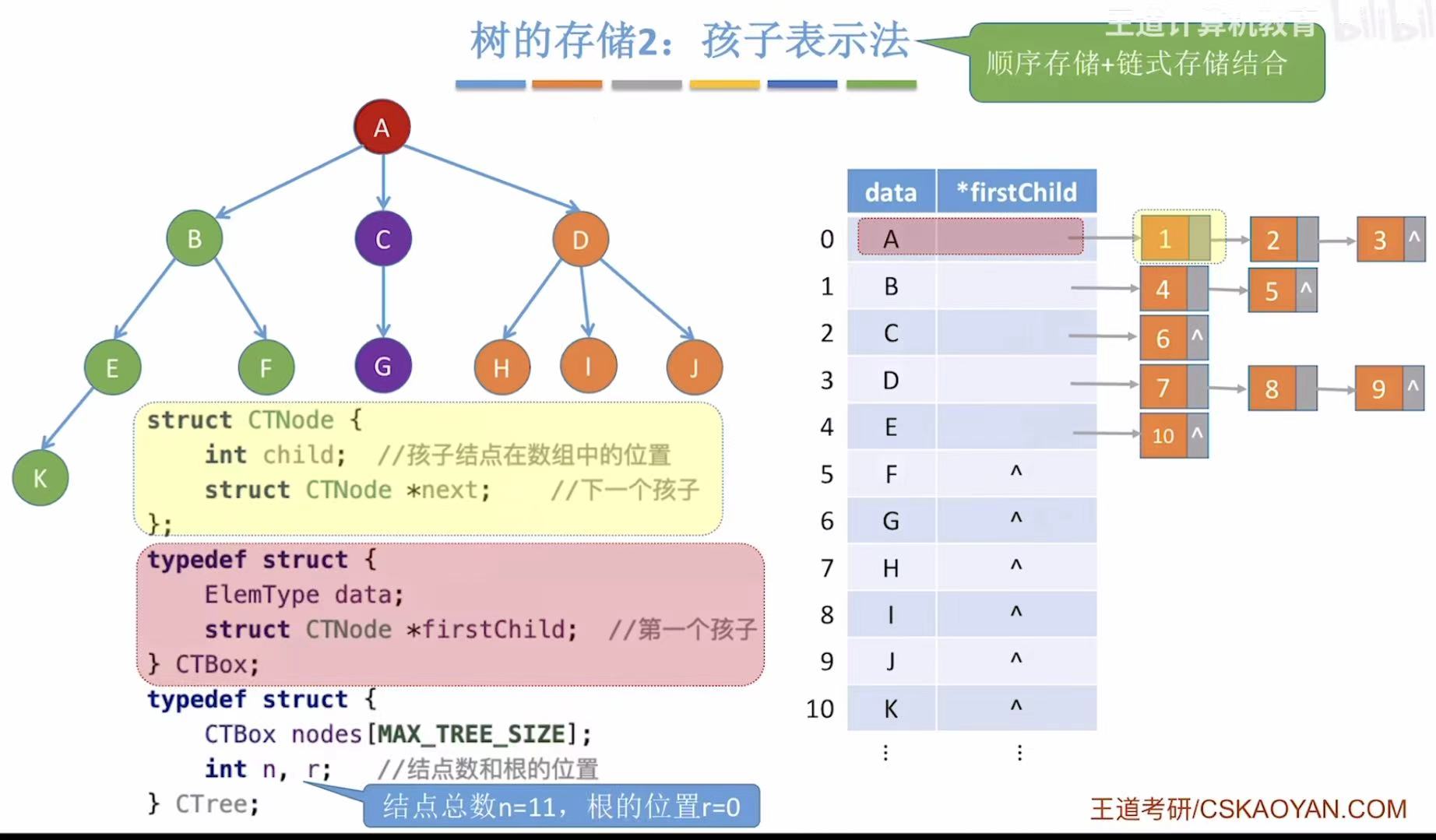
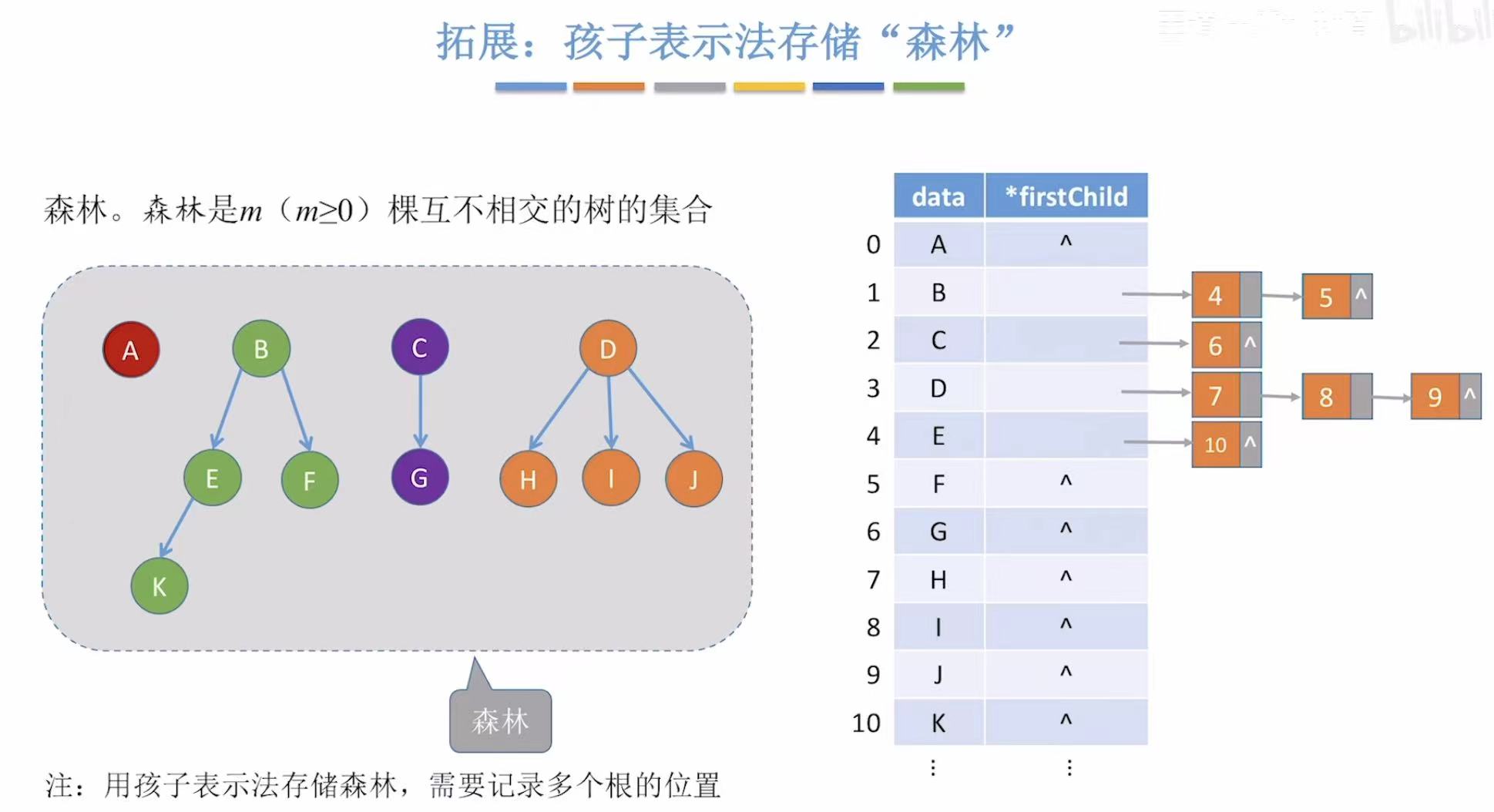
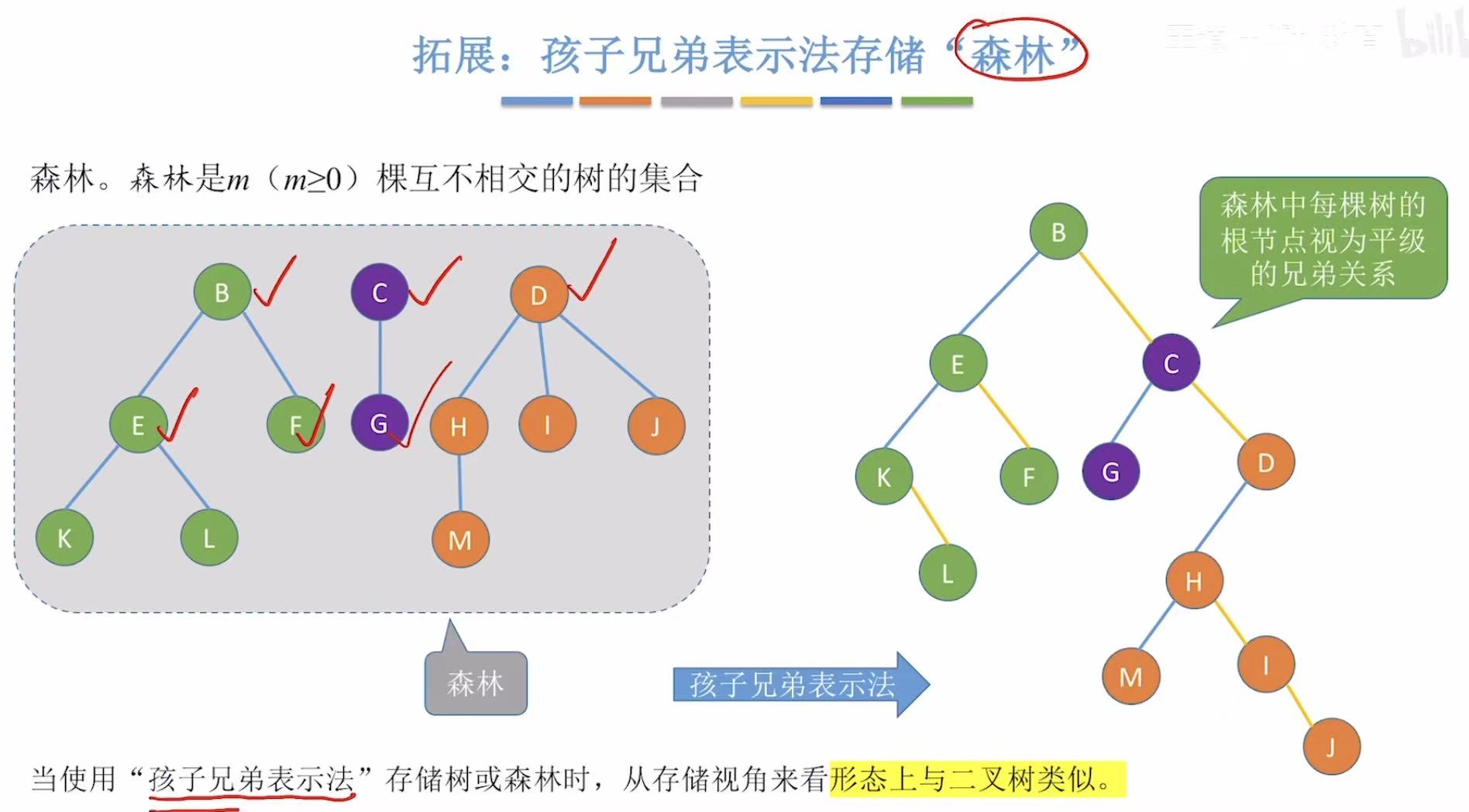
同理,可以存储森林,但是存树只需要知道一个根节点,森林有很多个根节点,所以就需要记录多个根的位置。
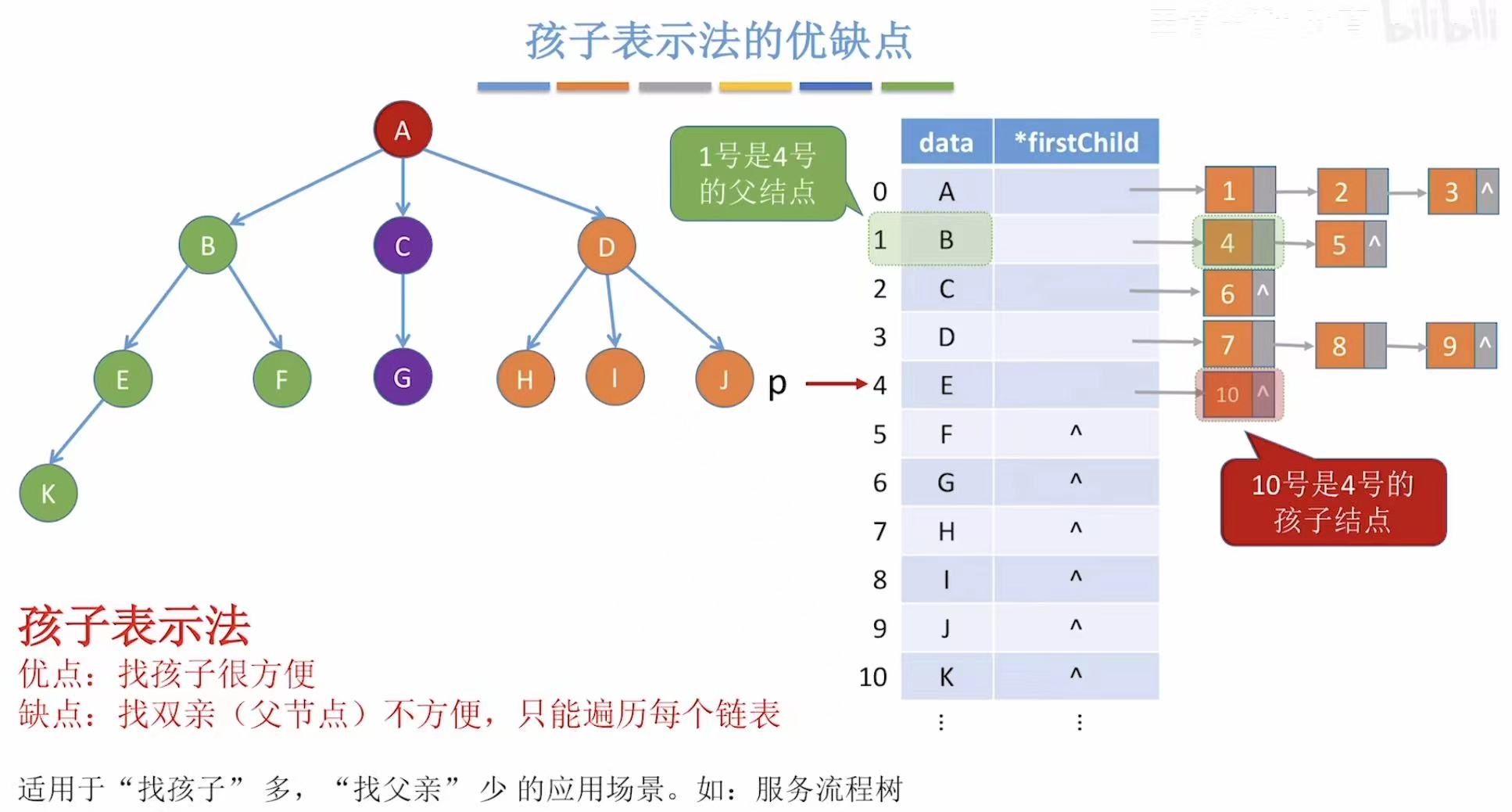
因为结点后面都直接 跟了自己的孩子,所以想找到自己的孩子轻而易举;
但是想找到自己的父节点,就又需要循环遍历看哪个结点后面的孩子结点是当前结点,所以又很低效。
- 固定寻找模式:父节点-->孩子结点
- 想找父亲也只能:父节点-->孩子结点-->这个父节点的孩子结点是当前结点-->当前结点的父节点是刚遍历到的这个结点
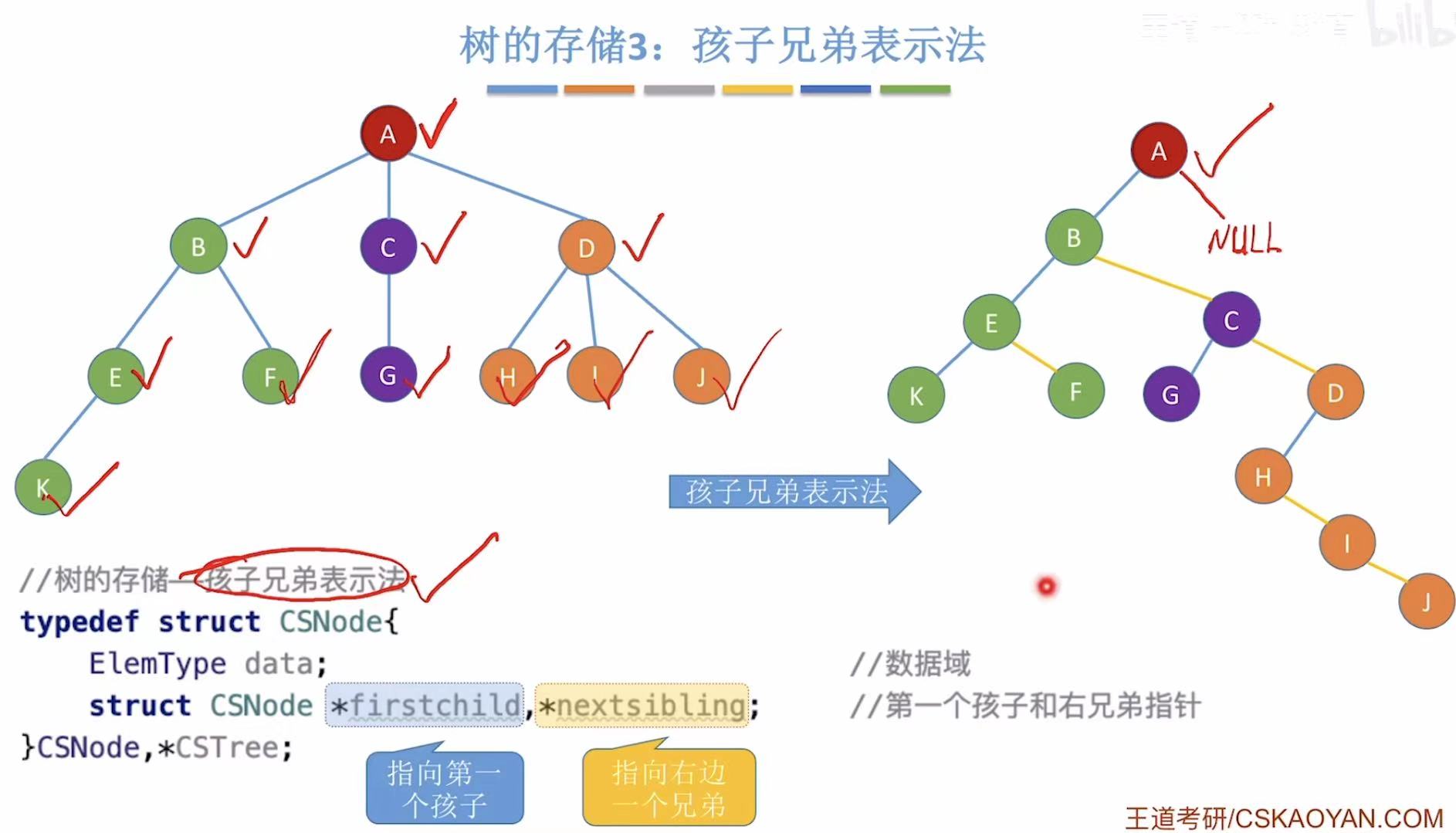
2.3 孩子兄弟表示法
完全的链式存储-->孩子兄弟表示法-->转化为二叉树的主要工具:
- CSNode:表示任意树,一个指向第一个孩子,一个指向右边第一个兄弟;
- BiTNode:表示二叉树,一个指向左孩子,一个指向右孩子;
java
// 二叉树的结点结构(链式存储)
typedef struct BiTNode {
ElemType data; // 数据域:存储结点的数据
struct BiTNode *lchild, *rchild; // 左孩子指针和右孩子指针
} BiTNode, *BiTree;
// 树的存储------孩子兄弟表示法(Child-Sibling Representation)
// 每个结点有两个指针:
// - firstchild:指向第一个孩子
// - nextsibling:指向右边的兄弟(同父的下一个结点)
typedef struct CSNode {
ElemType data; // 数据域:存储结点的数据
struct CSNode *firstchild; // 第一个孩子指针(指向左子树)
struct CSNode *nextsibling; // 右兄弟指针(指向右子树)
} CSNode, *CSTree;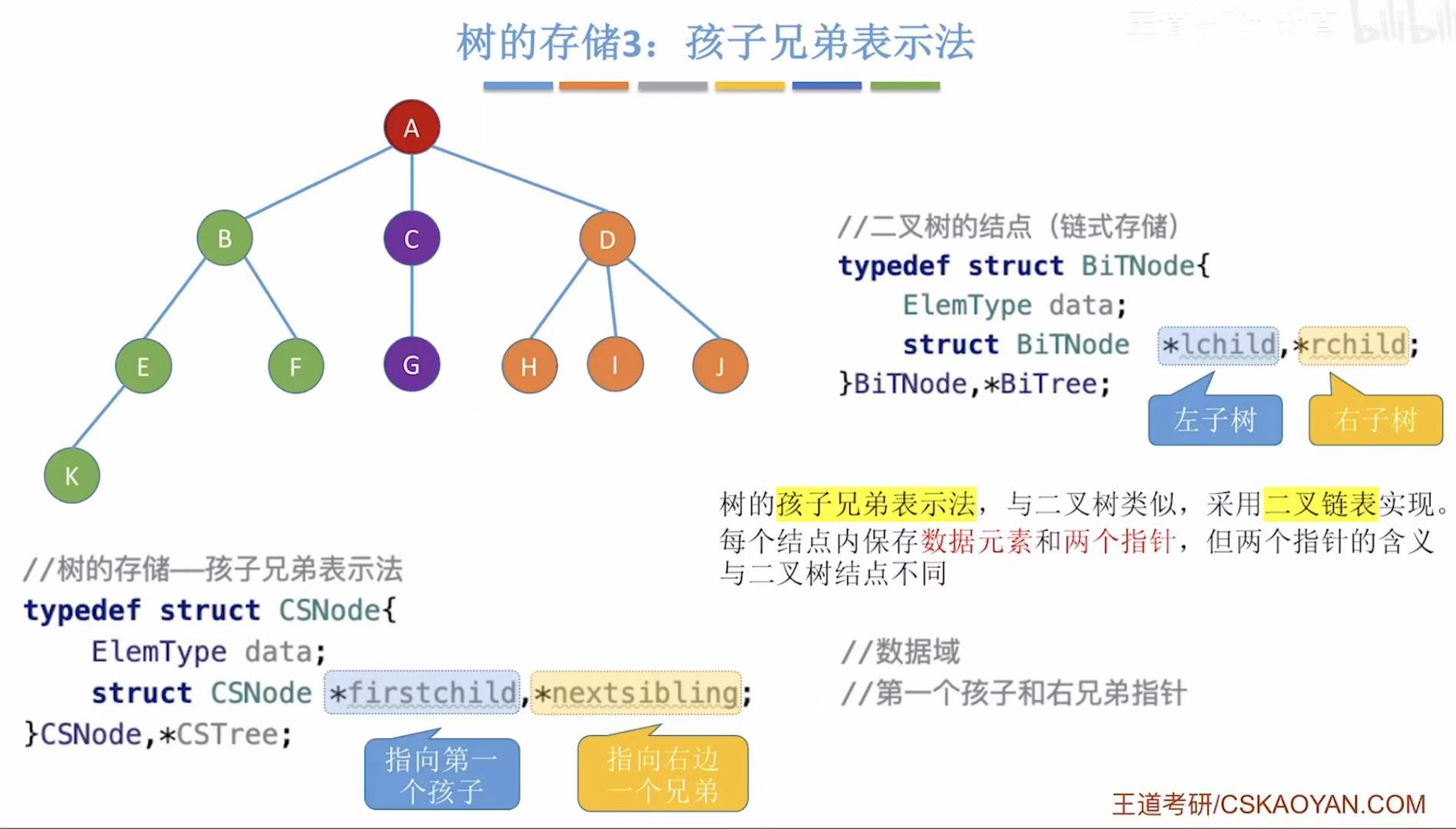
3. 小结
树、森林与二叉树的转换
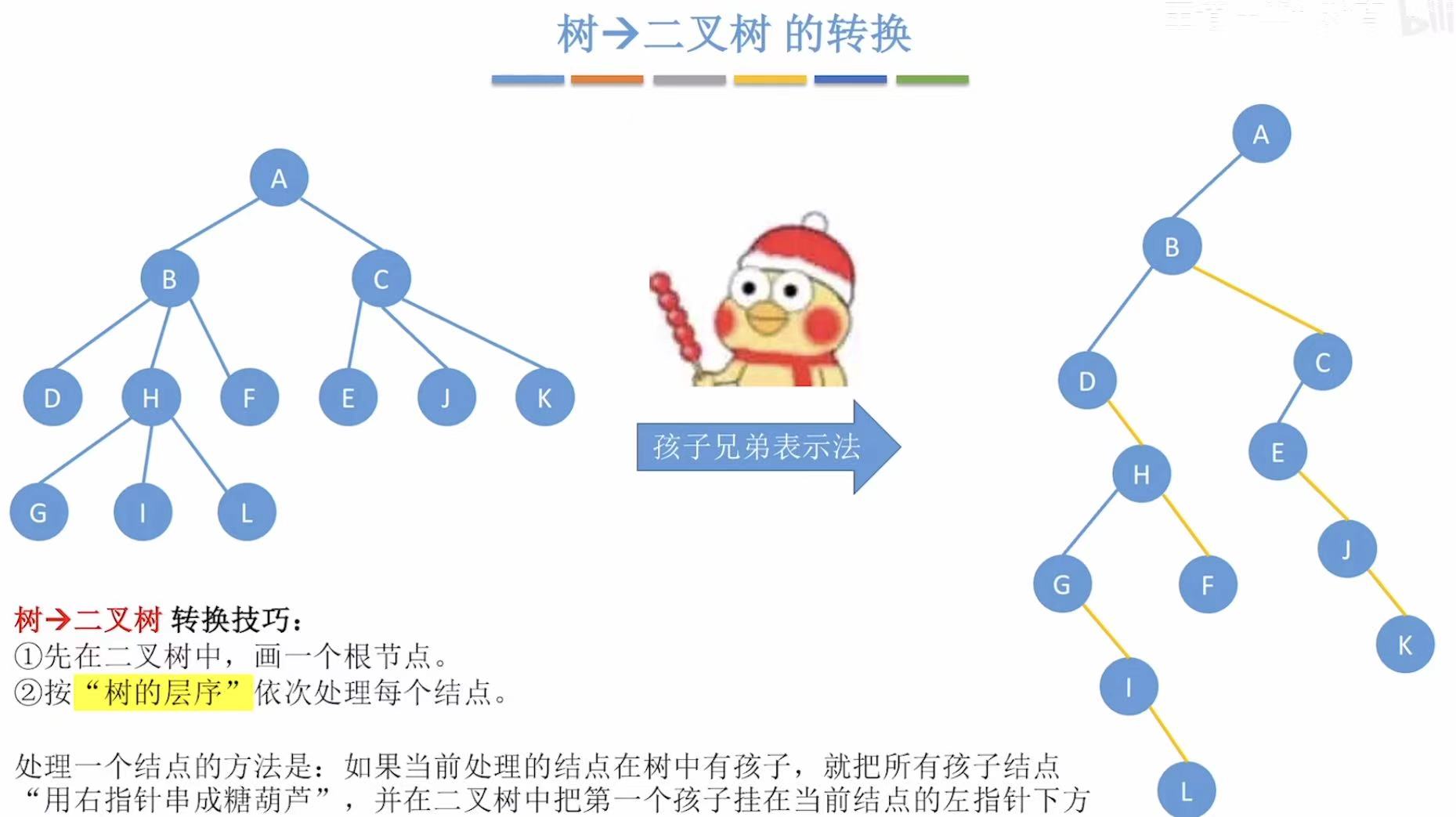
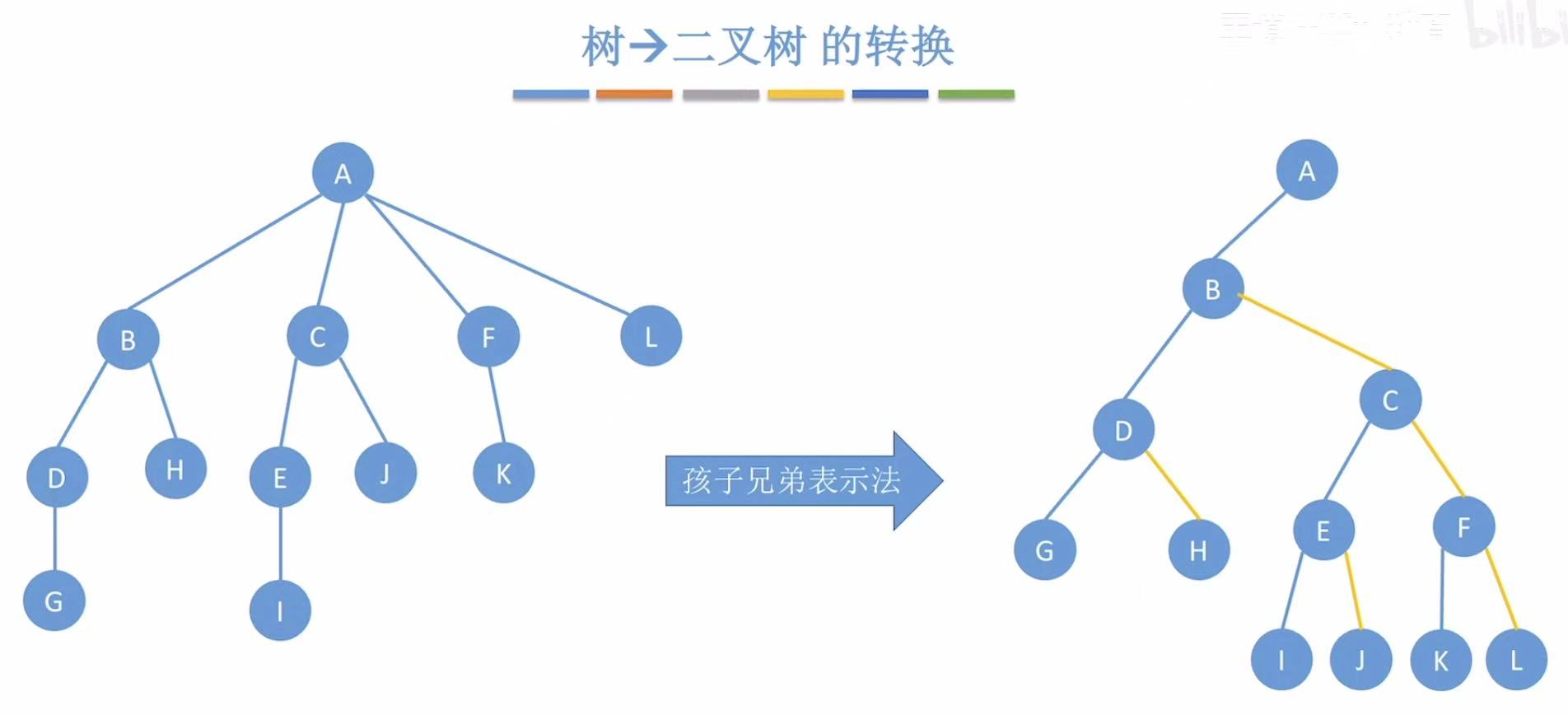
1. 树-->二叉树
按层来依次处理:
- A:A是根节点,直接放在最上面
- BC:按右下方向串成一串儿,连在A的左子树位置
- DHF:按右下方向串成一串儿,连在B的左子树位置;EJK:按右下方向串成一串儿,连在C的左子树位置
- GIL :按右下方向串成一串儿,连在H的左子树位置
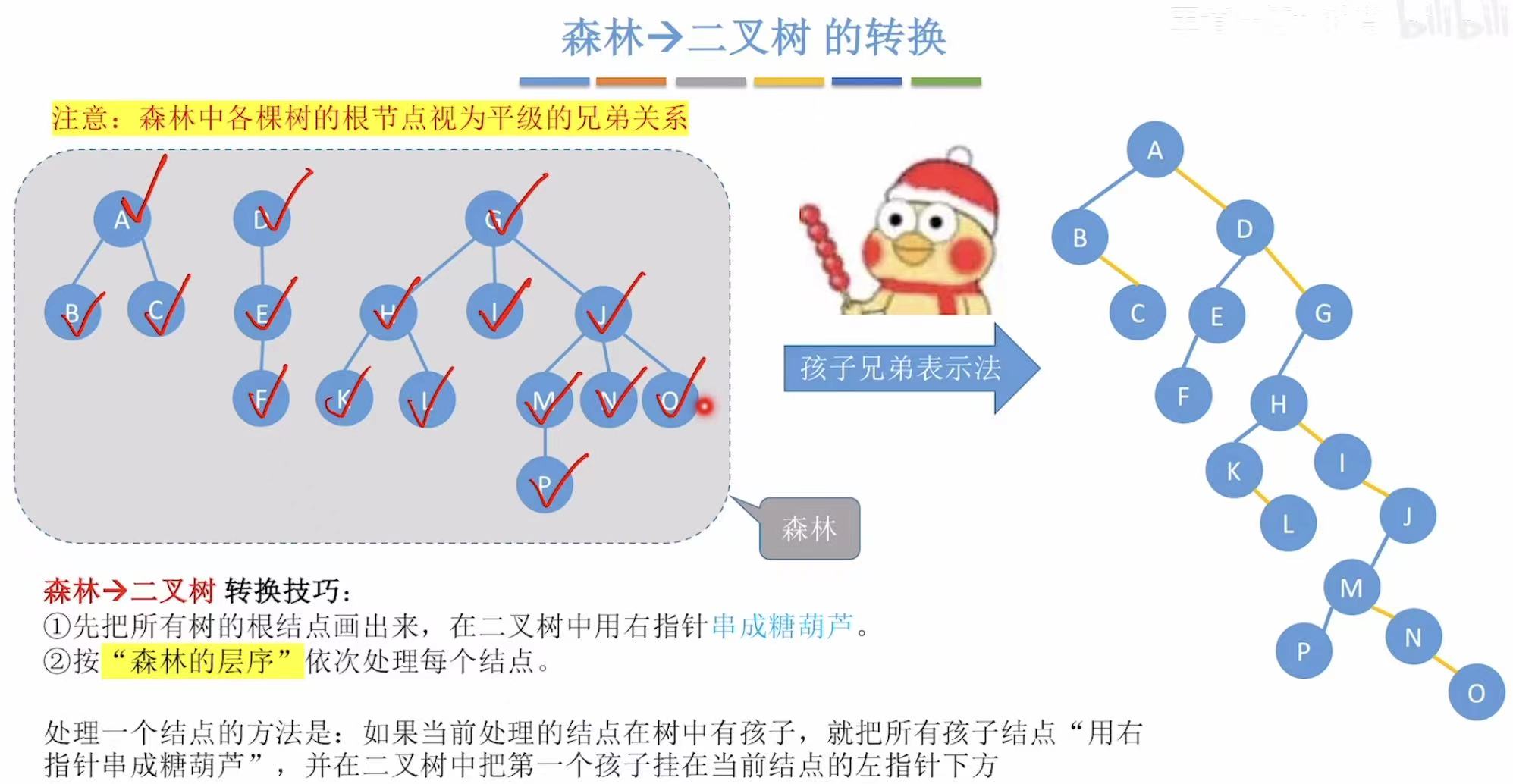
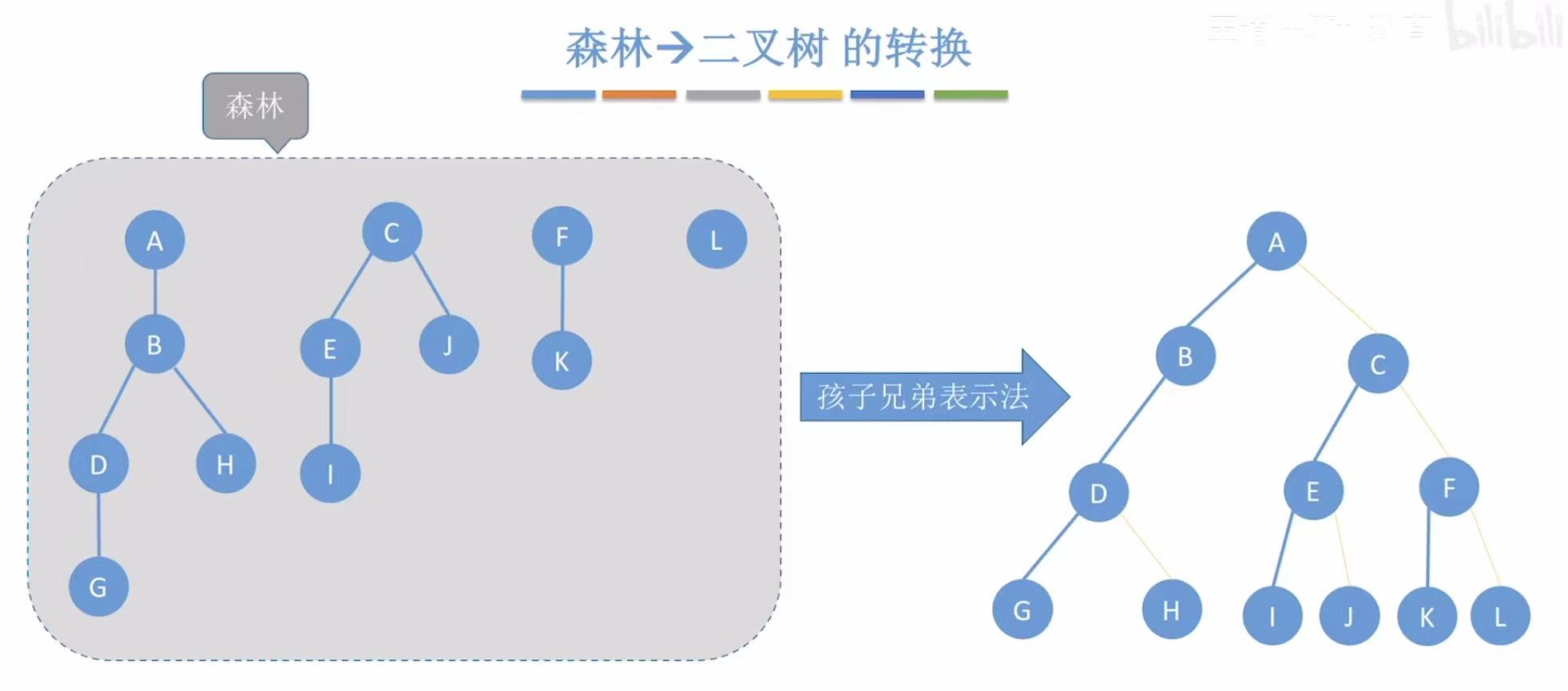
2. 森林-->二叉树
同样按层来依次处理:
- ADG:按右下方向串成一串儿,直接放在最高的位置
- BC:按右下方向串成一串儿,连在A的左子树位置;E:连在D的左子树位置;HIJ:按右下方向串成一串儿,连在G的左子树位置
- F :连在E的左子树位置;KL :按右下方向串成一串儿,连在H的左子树位置;
MNO:按右下方向串成一串儿,连在J的左子树位置 - P :连在M的左子树位置
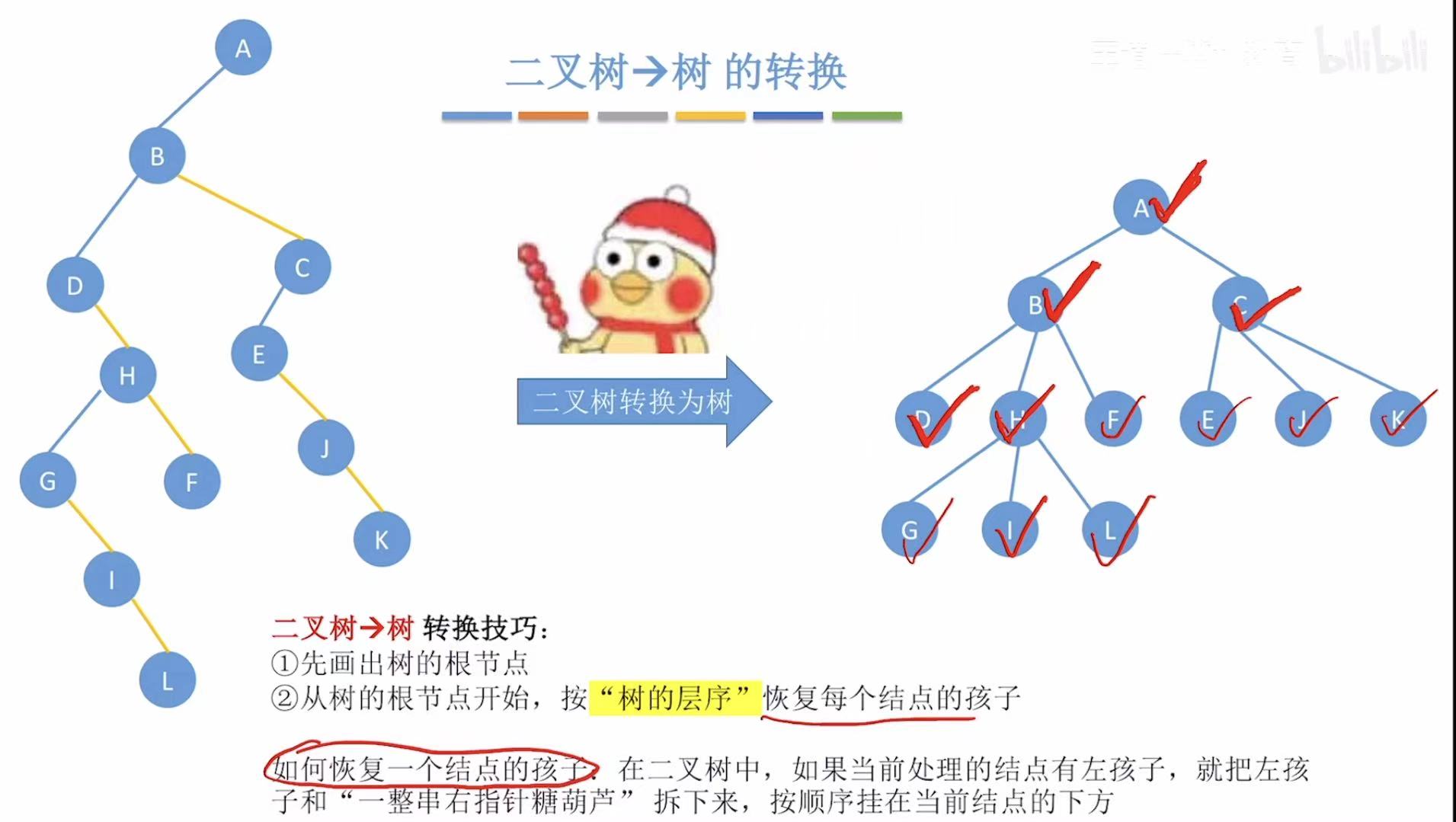
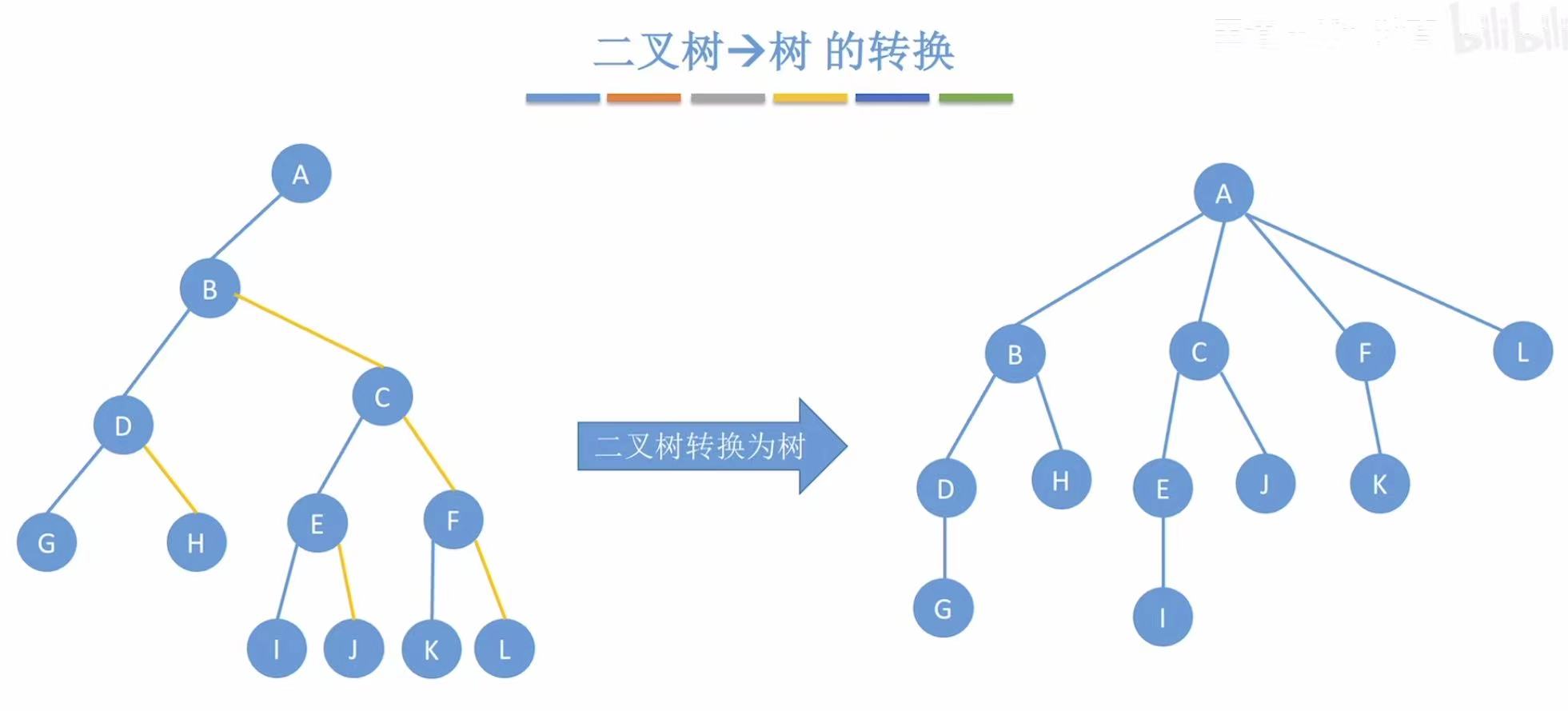
3. 二叉树-->树
一个串一个串地吃糖葫芦:
- A:根节点,直接放在最上面
- BC:去掉黄线,分别连到A的
- DHF :去掉黄线,分别连到B的下面;EJK:去掉黄线,分别连到C的下面
- GIL :去掉黄线,分别连到H的下面
4. 二叉树-->森林
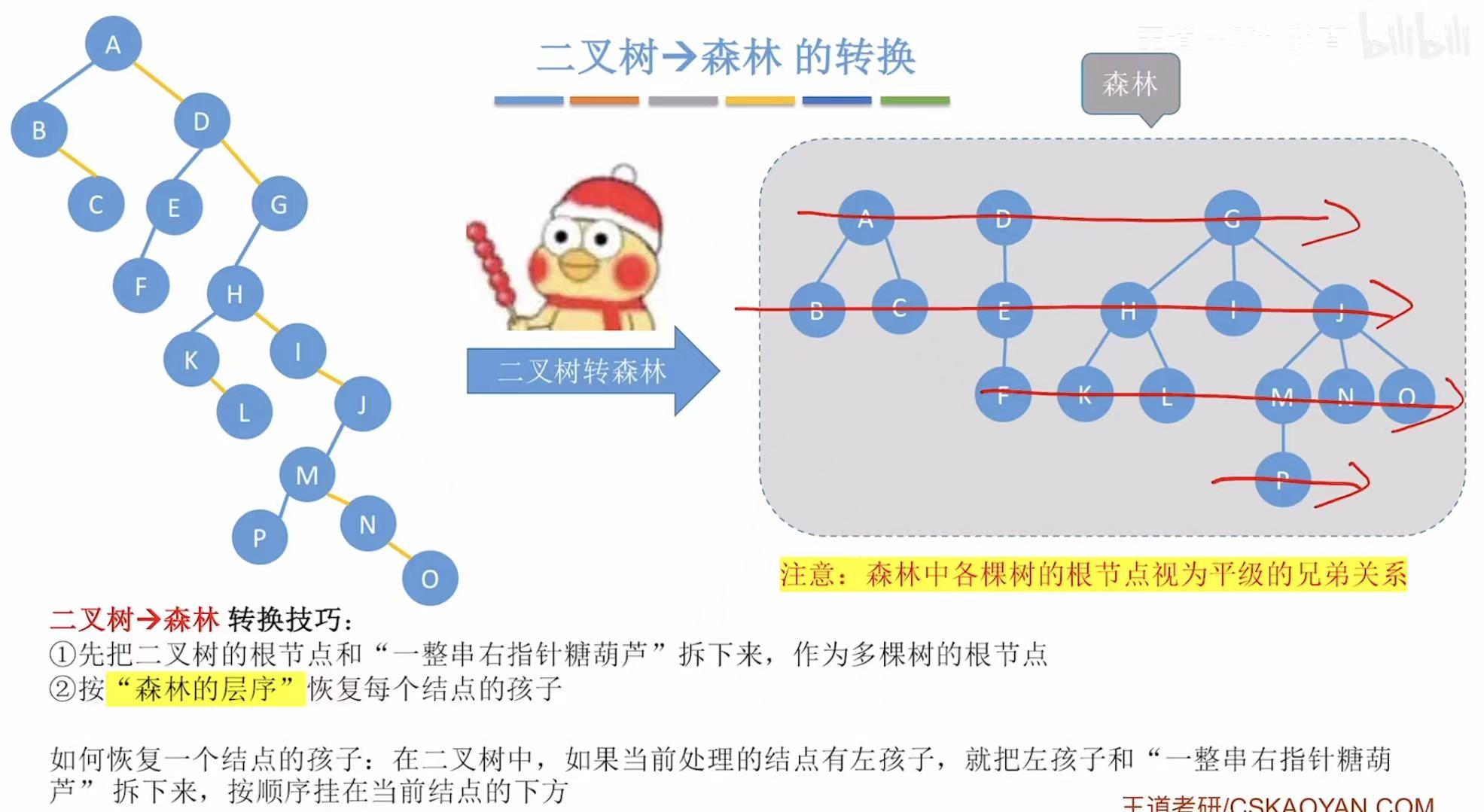
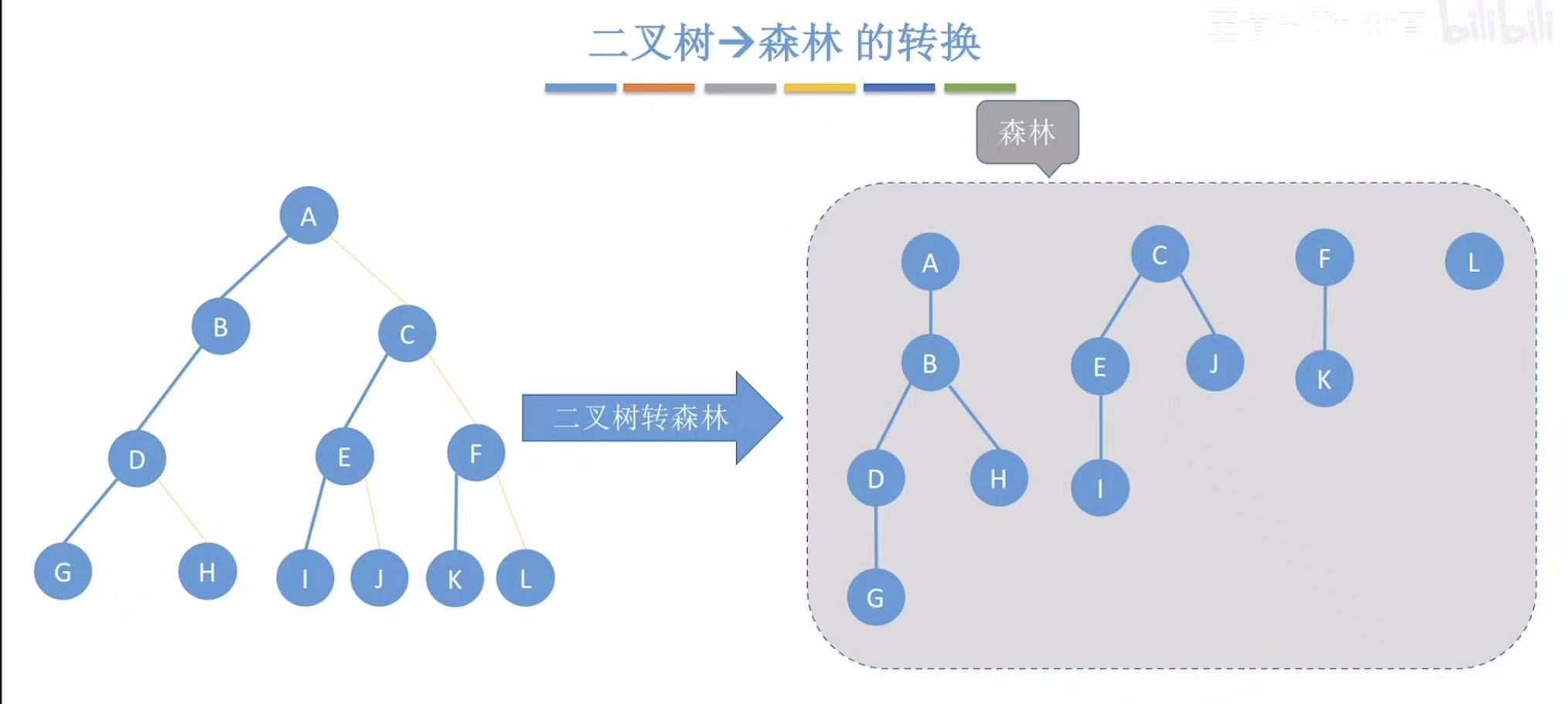
同理,也就是去掉黄线,复制蓝线:
- ADG:去掉黄线,分别放在最上面
- BC :去掉黄线,分别连到A的下面;E :无黄线,直接连在D的下面;HIJ:去掉黄线,分别连到G的下面;
- F :无黄线,直接连在E的下面;KL :去掉黄线,分别连到H的下面;MNO:去掉黄线,分别连到J的下面;
- P :无黄线,直接连在M的下面;
5. 小结
树、森林的遍历
1. 树的遍历
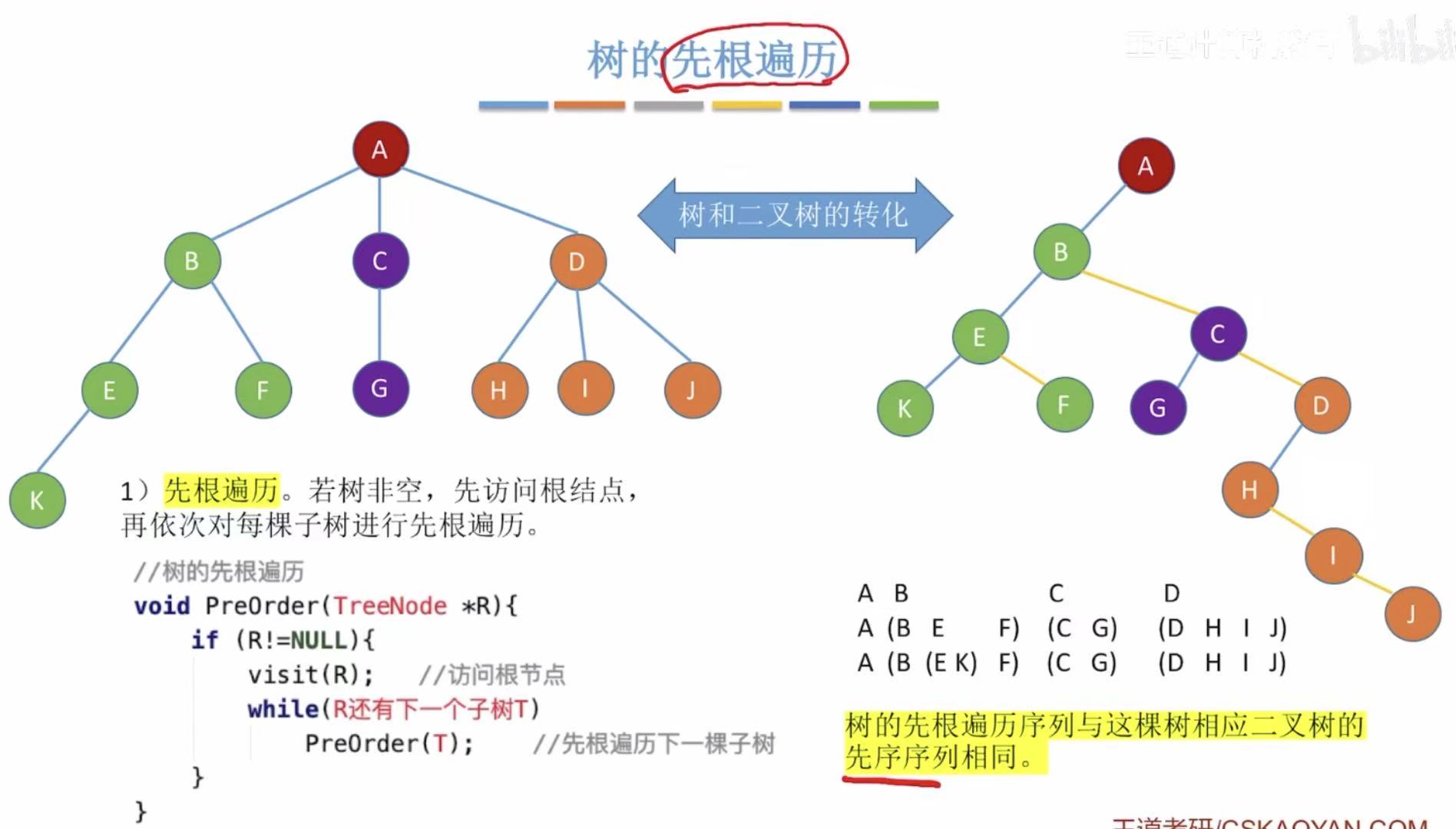
1.1 先根遍历
- 可以直接对这个树进行先根遍历
- 可以把这个树转化为二叉树,再进行先根遍历
java
// 树的先根遍历(递归实现)
void PreOrder(TreeNode *R) {
if (R != NULL) { // 如果当前结点 R 不为空
visit(R); // 访问当前根结点(处理数据)
while (R 还有下一个子树 T) { // 遍历所有子树(从第一个到最后一个)
PreOrder(T); // 递归对每个子树进行先根遍历
}
}
}
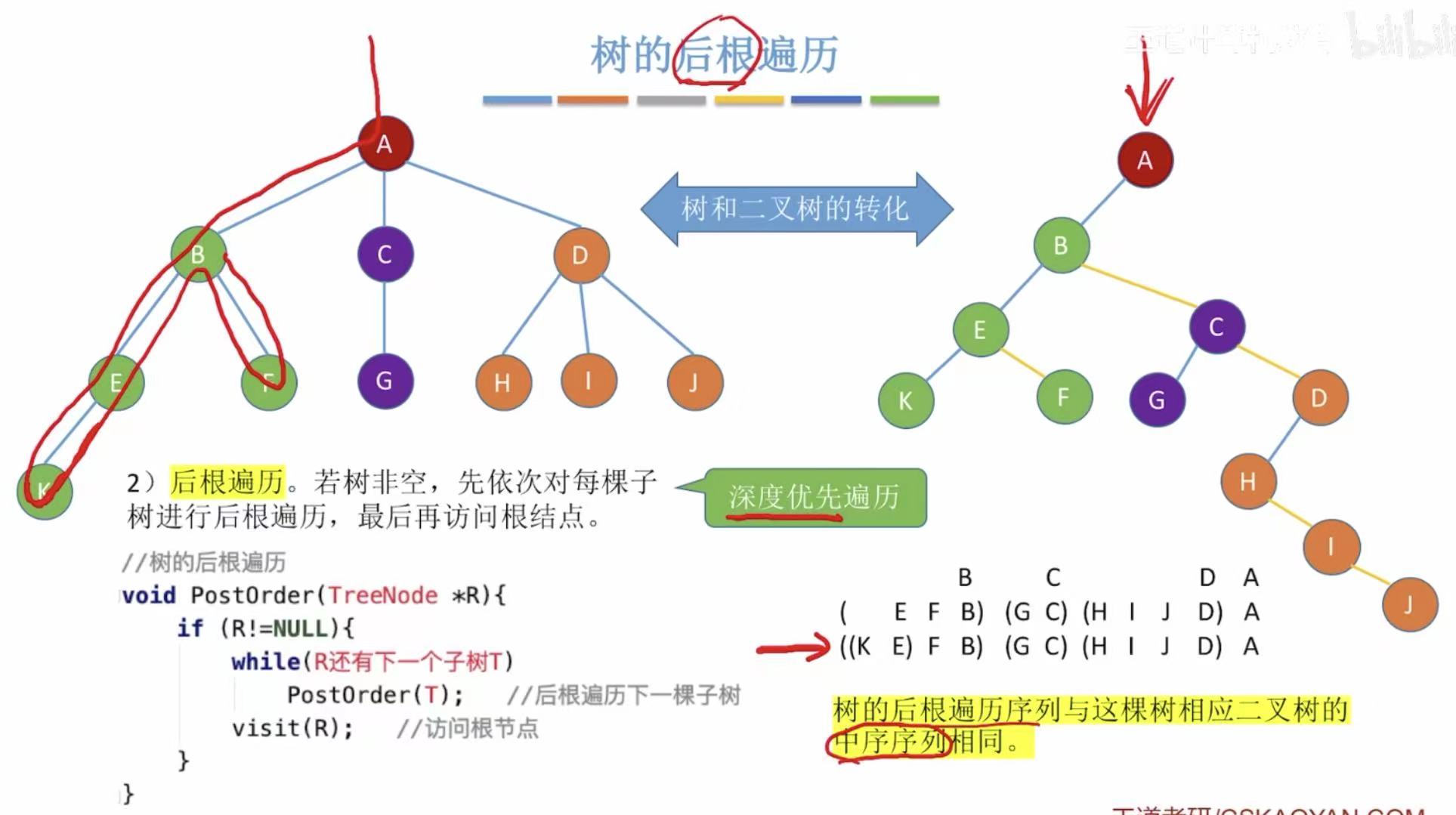
1.2 后根遍历
- 可以直接对这个树进行后根遍历
- 可以把这个树转化为二叉树,再进行后根遍历
- 也叫做深度优先遍历
java
// 树的后根遍历(递归实现)
void PostOrder(TreeNode *R) {
if (R != NULL) { // 如果当前结点 R 不为空
while (R 还有下一个子树 T) { // 遍历所有子树(从第一个到最后一个)
PostOrder(T); // 递归对每个子树进行后根遍历
}
visit(R); // 访问当前根结点(最后处理)
}
}
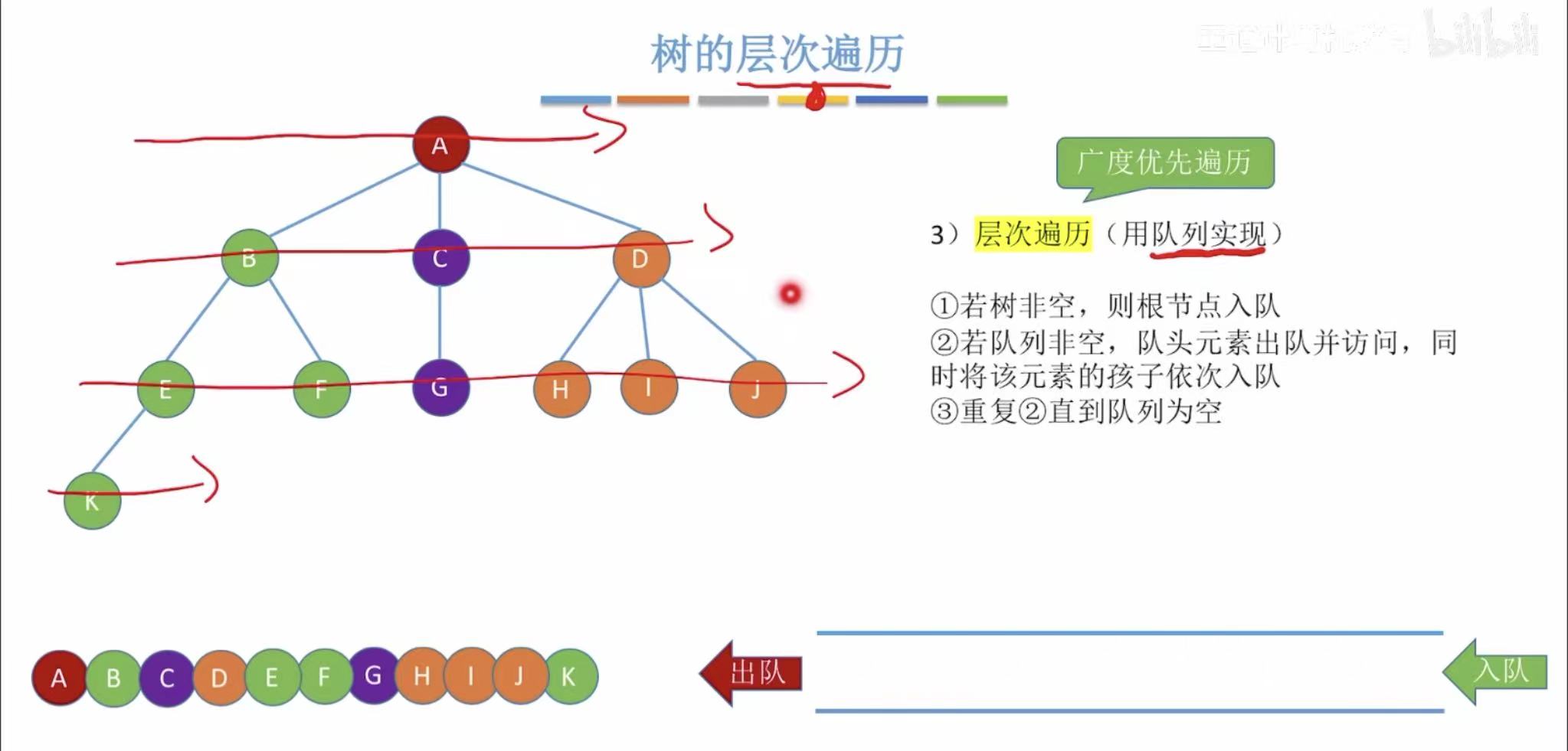
1.3 层次遍历
- 依旧一行一行入队出队
- 也叫做广度优先遍历
2. 森林的遍历
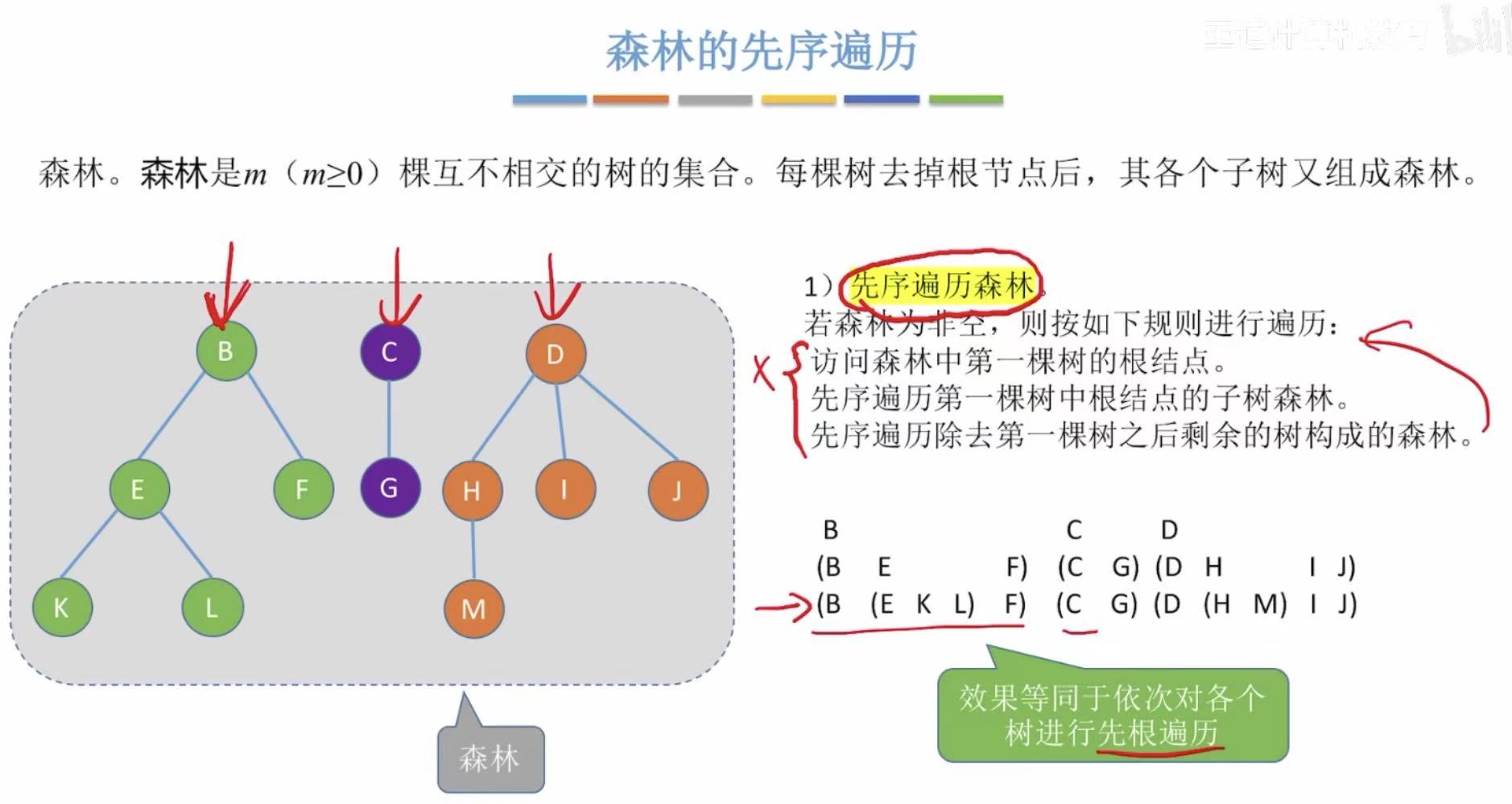
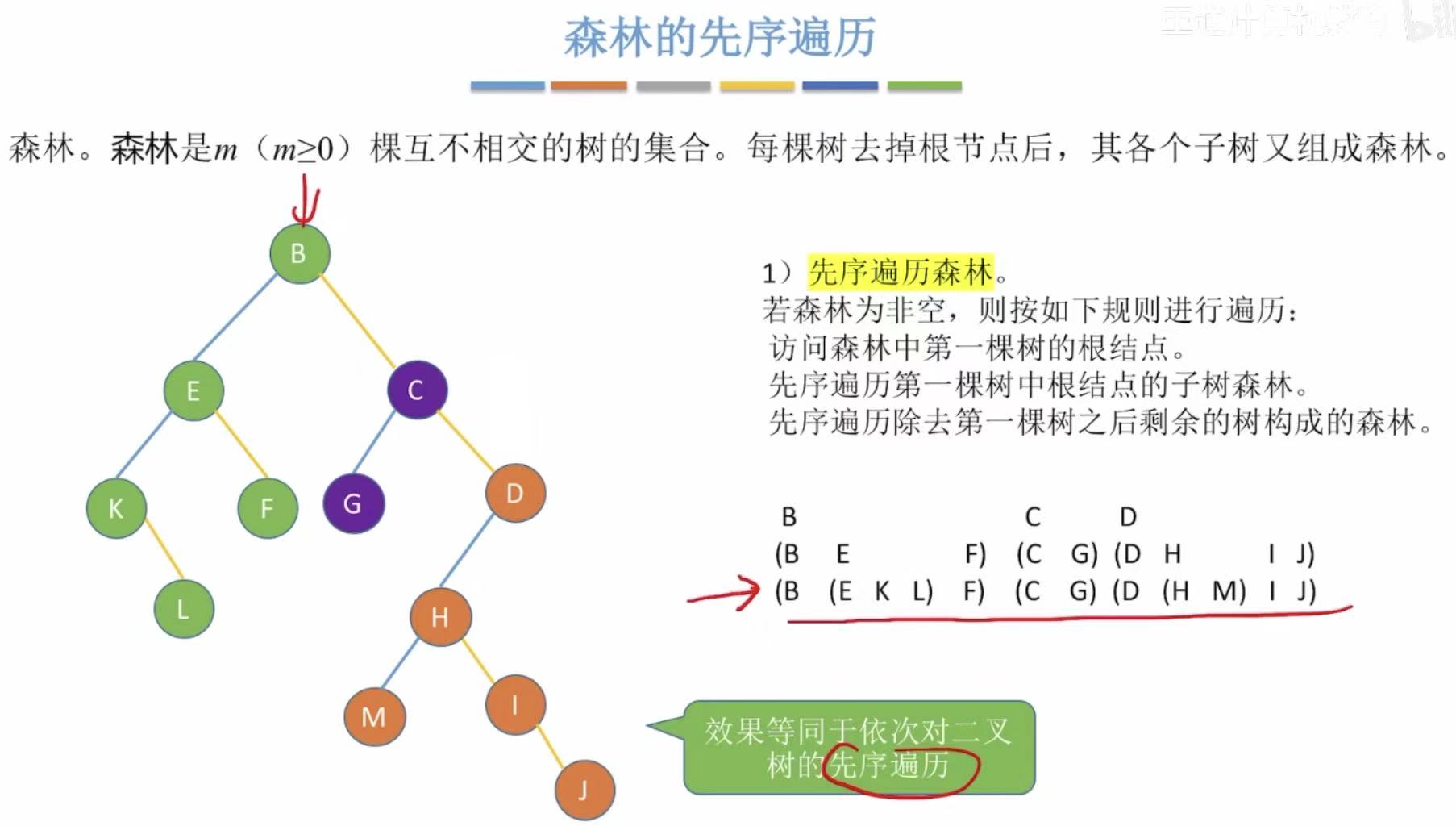
2.1 先序遍历
- 对每个树进行先根遍历
- 也可以把森林转化为二叉树,对二叉树进行先根遍历
2.2 中序遍历
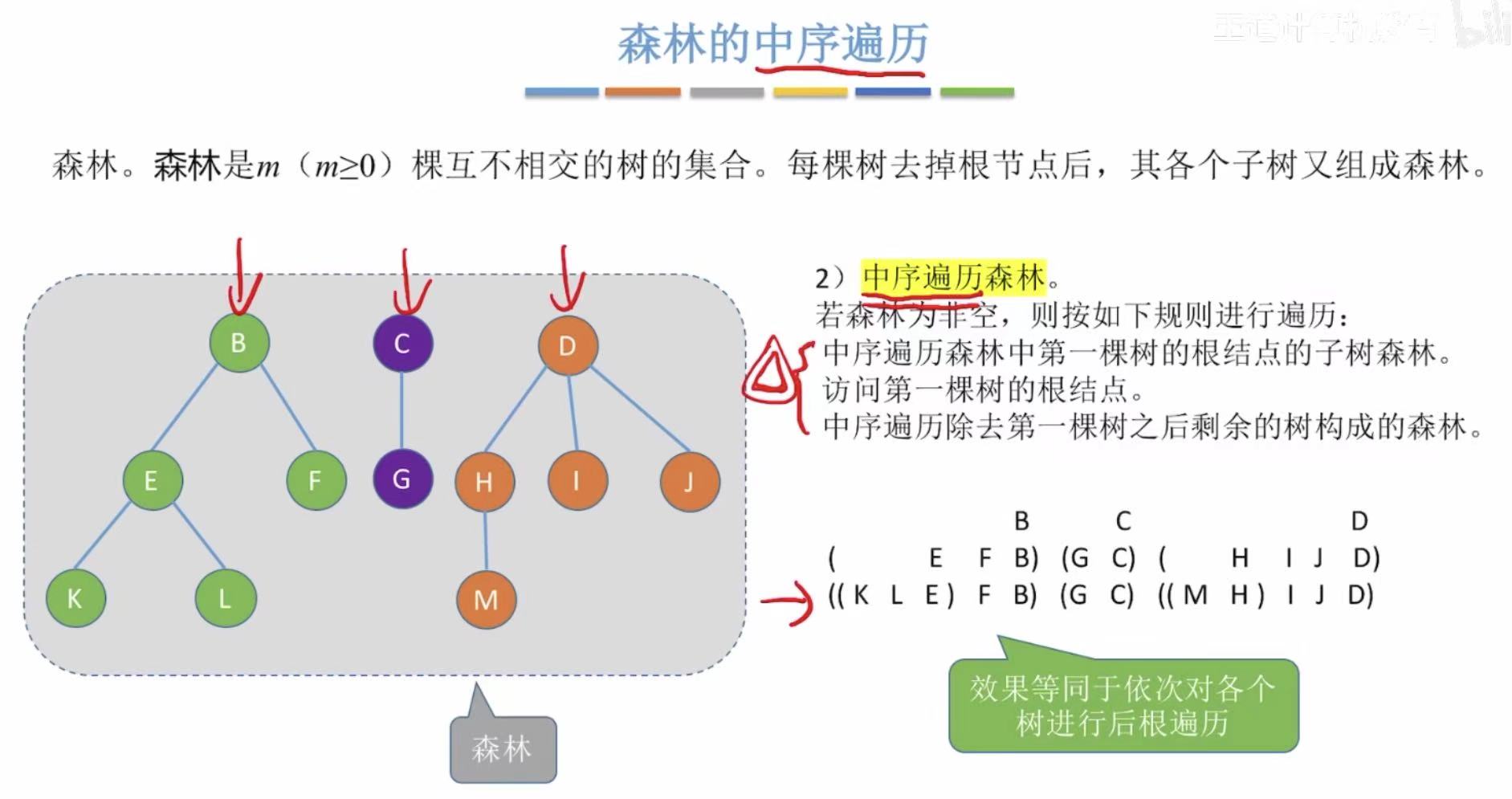
- 对每个树进行后根遍历
- 也可以把森林转化为二叉树,对二叉树进行中序遍历
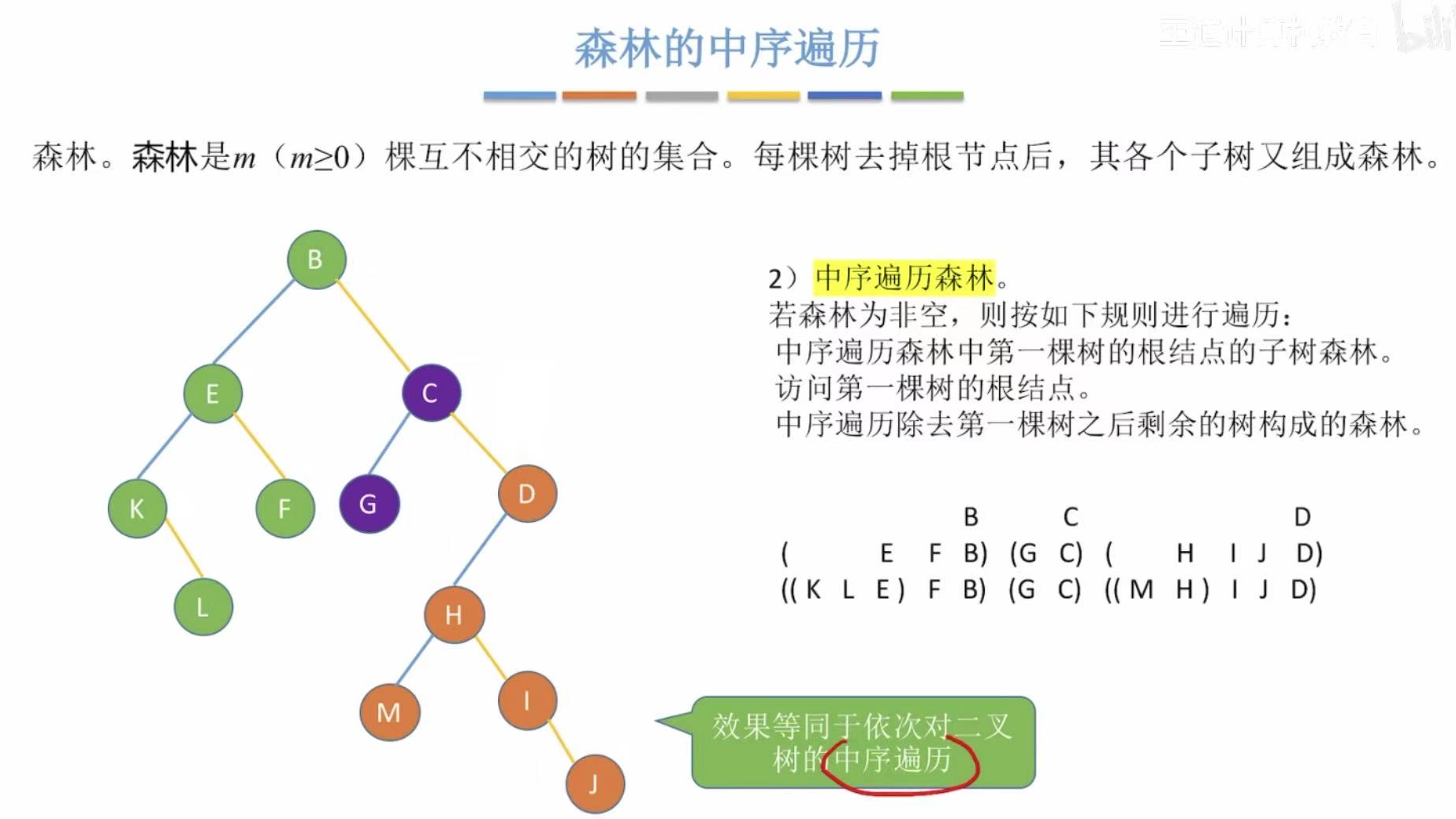
3. 小结
一行中的三个都是等价的,所以碰到这种题可以挑选一个自己最擅长的解决方法。
哈夫曼树
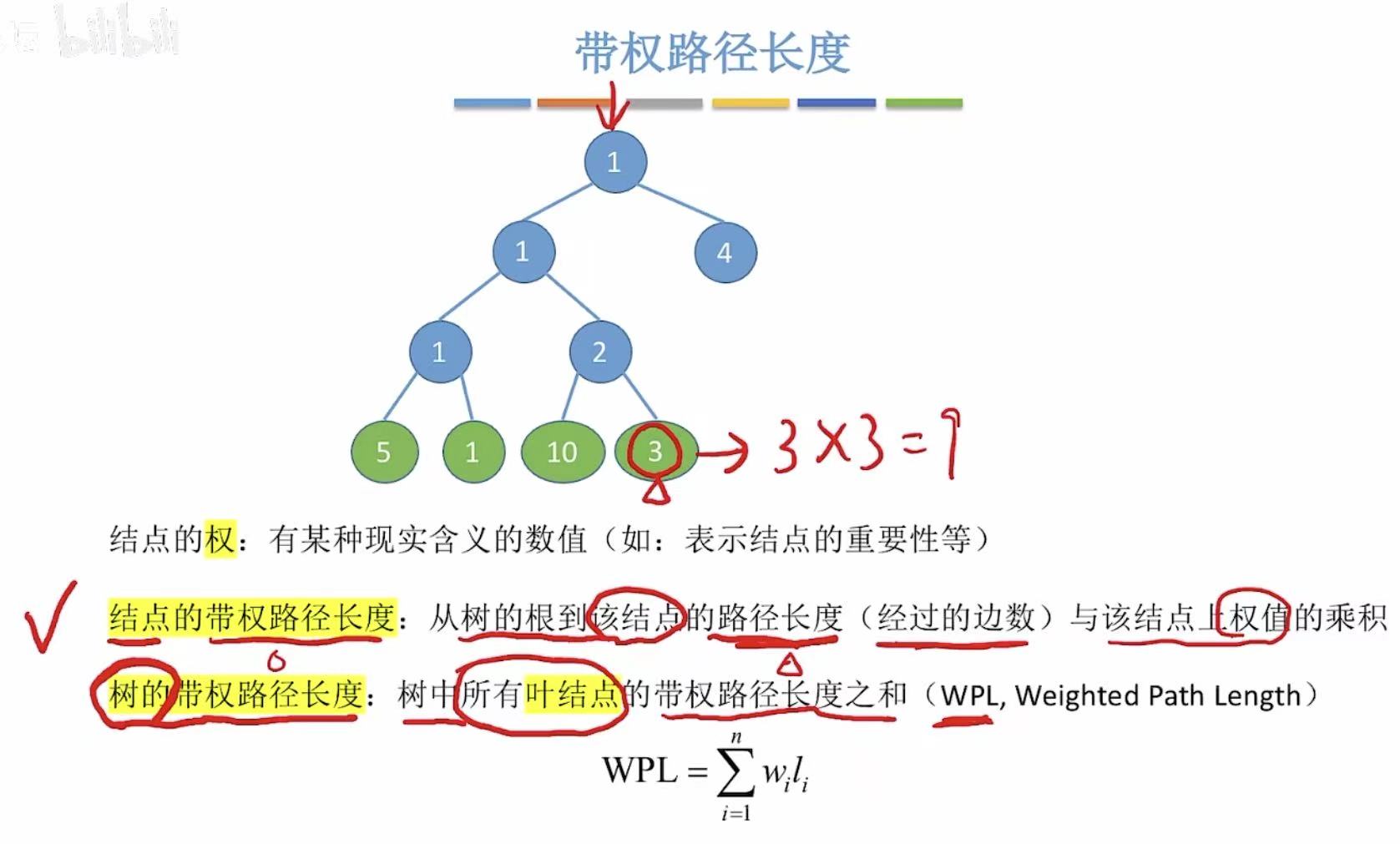
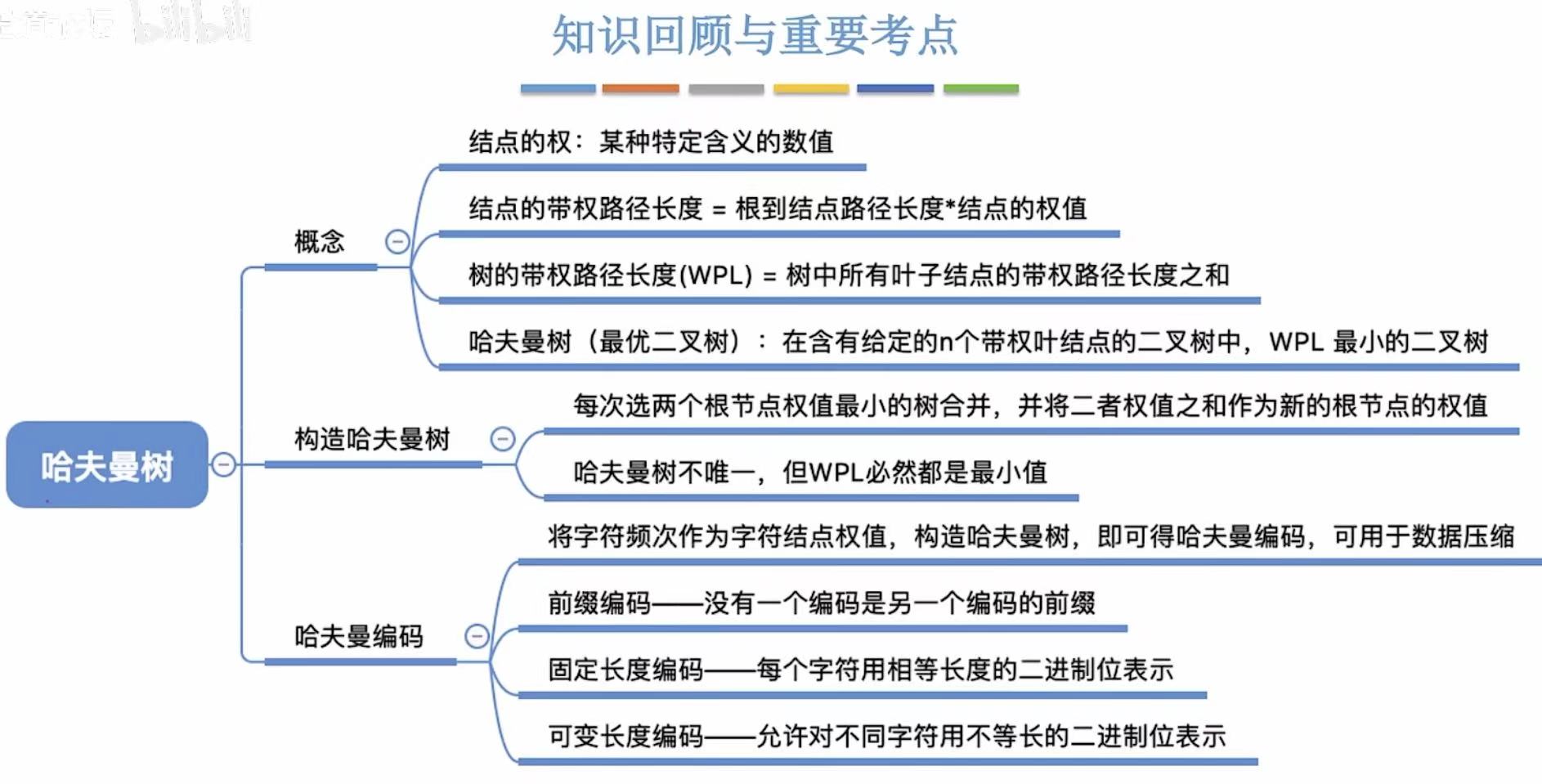
1. 带权路径长度
- 结点的权:可以理解为求这个结点帮自己办事需要花费的代价
- 结点的带权路径长度:可以理解为到这个结点需要花费的代价,3的带权路径长度就是3*3=9
- 树的带权路径长度 :所有叶子节点 的带权路径长度之和;注意是叶节点 !!!
2. 哈夫曼树
2.1 定义
哈夫曼树 :就是树的带权路径长度 最小的二叉树。
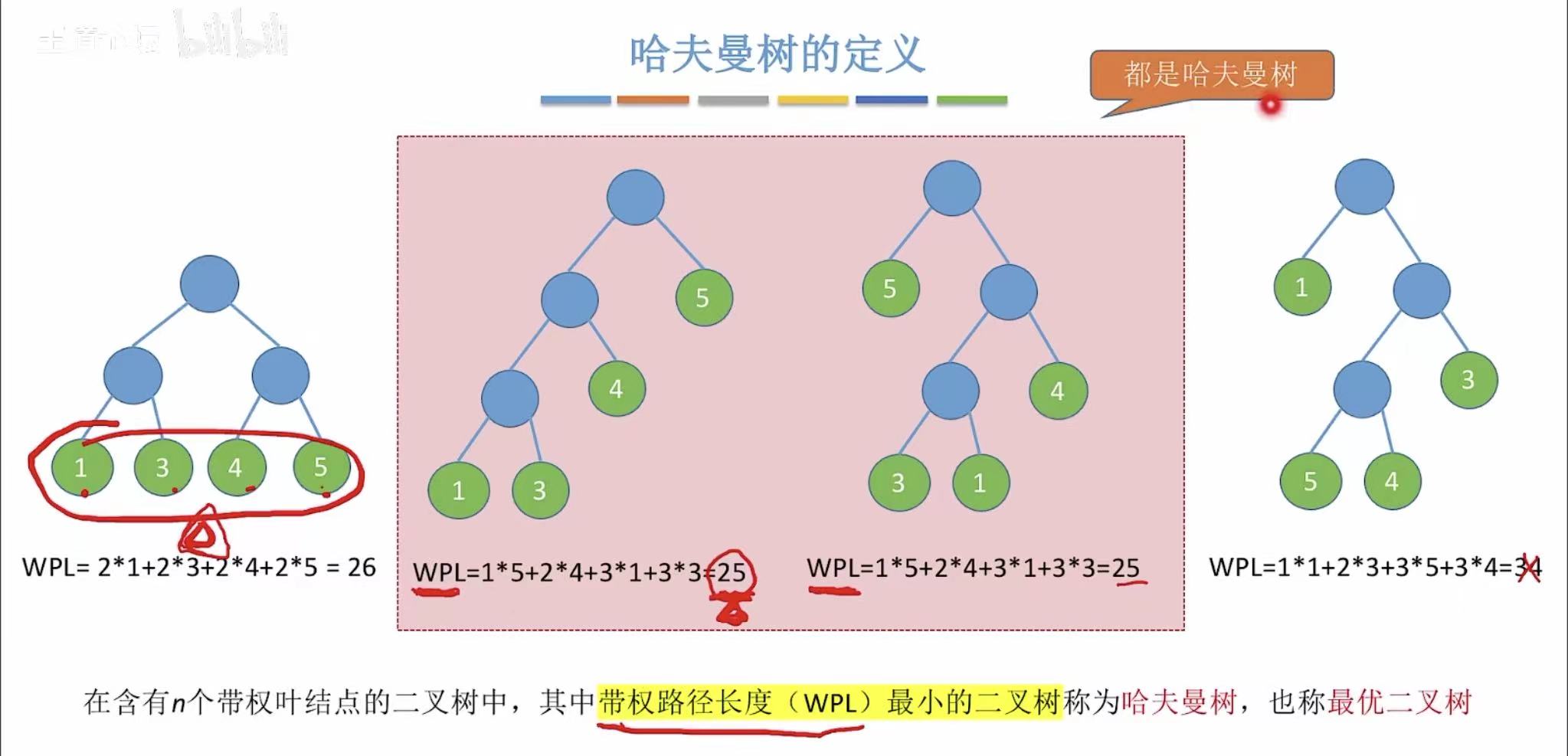
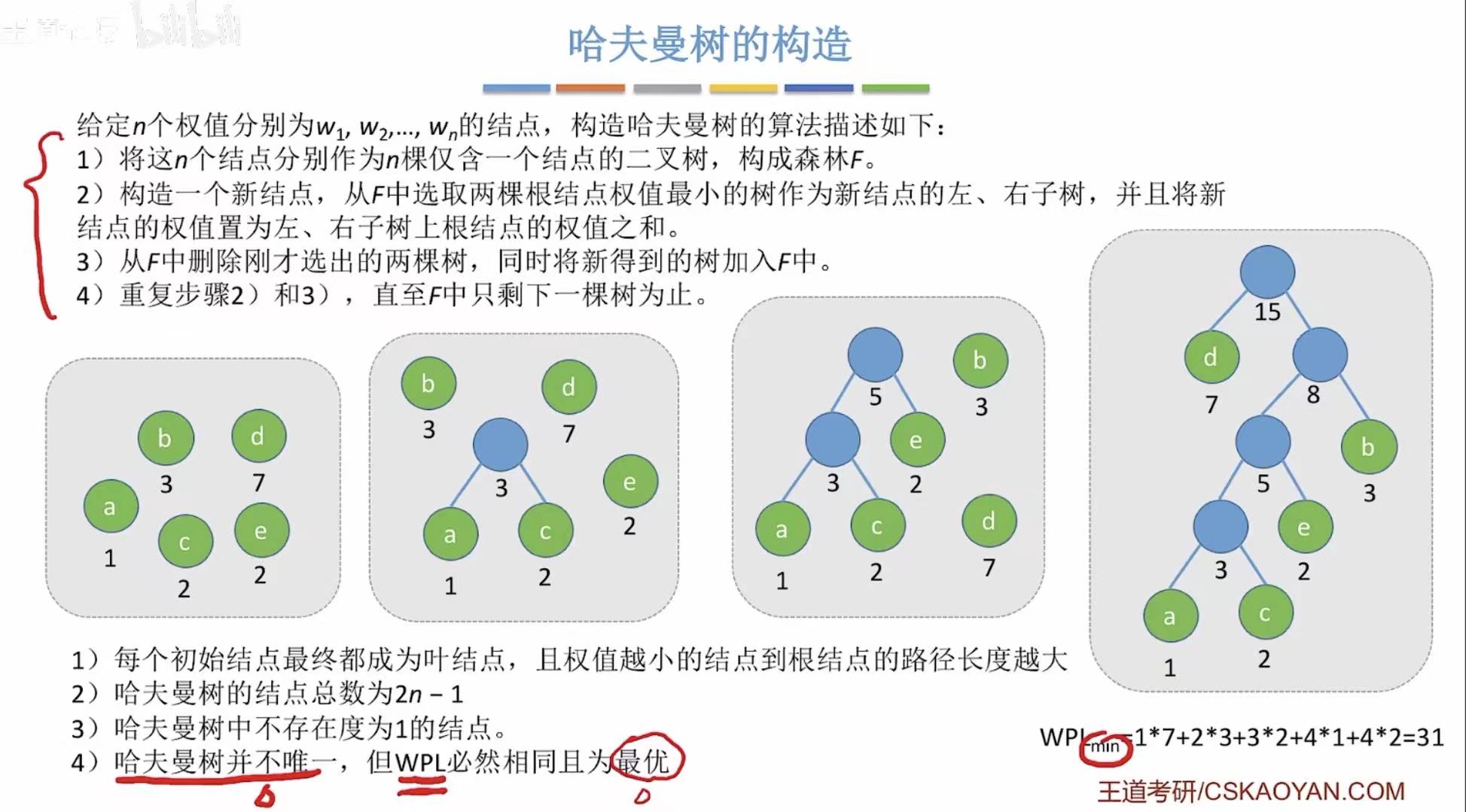
2.2 构造
两个最小的组成一个的循环:
- 1+2=3
- 2+3=5
- 3+5=8
- 7+8=15
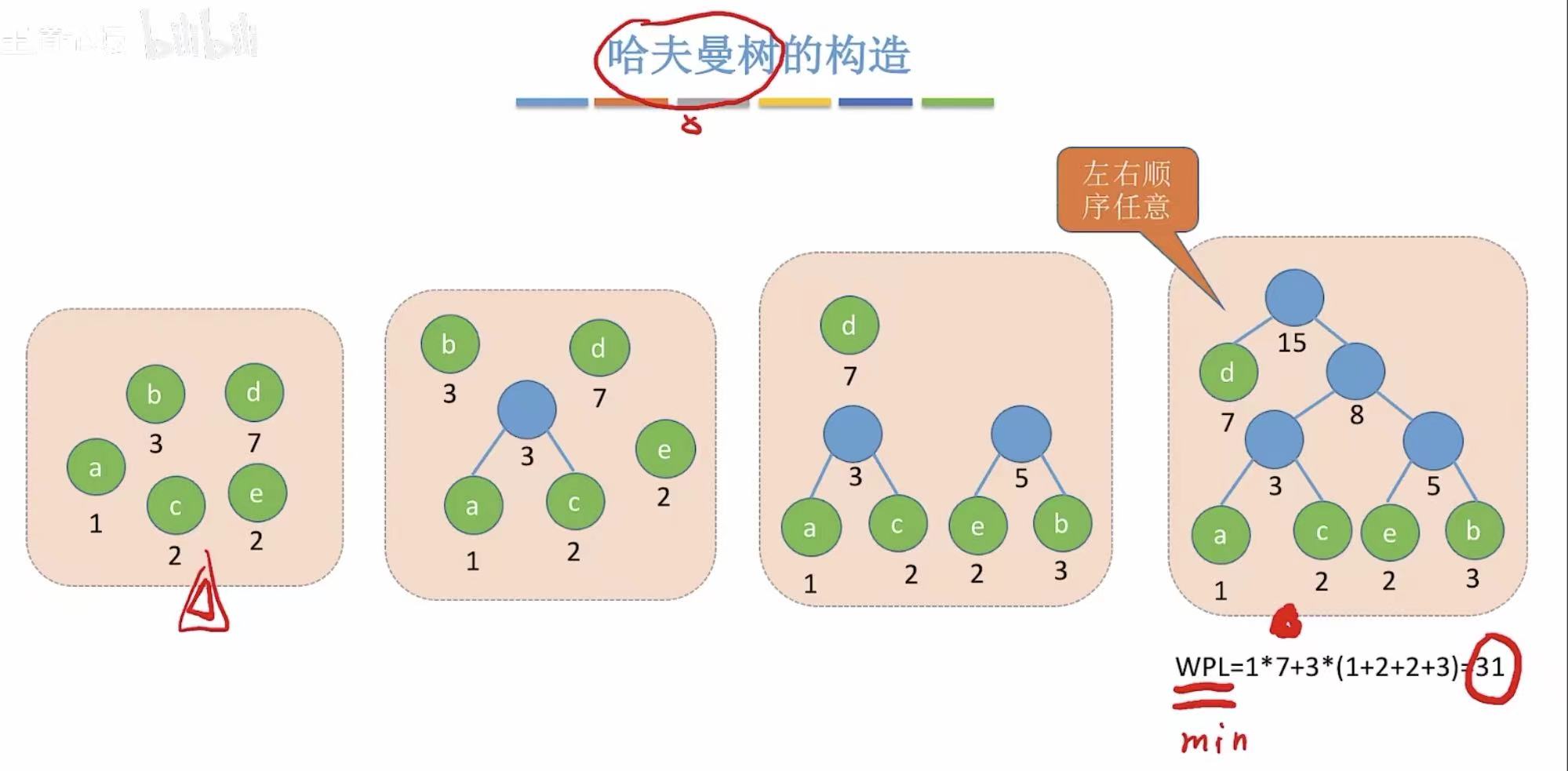
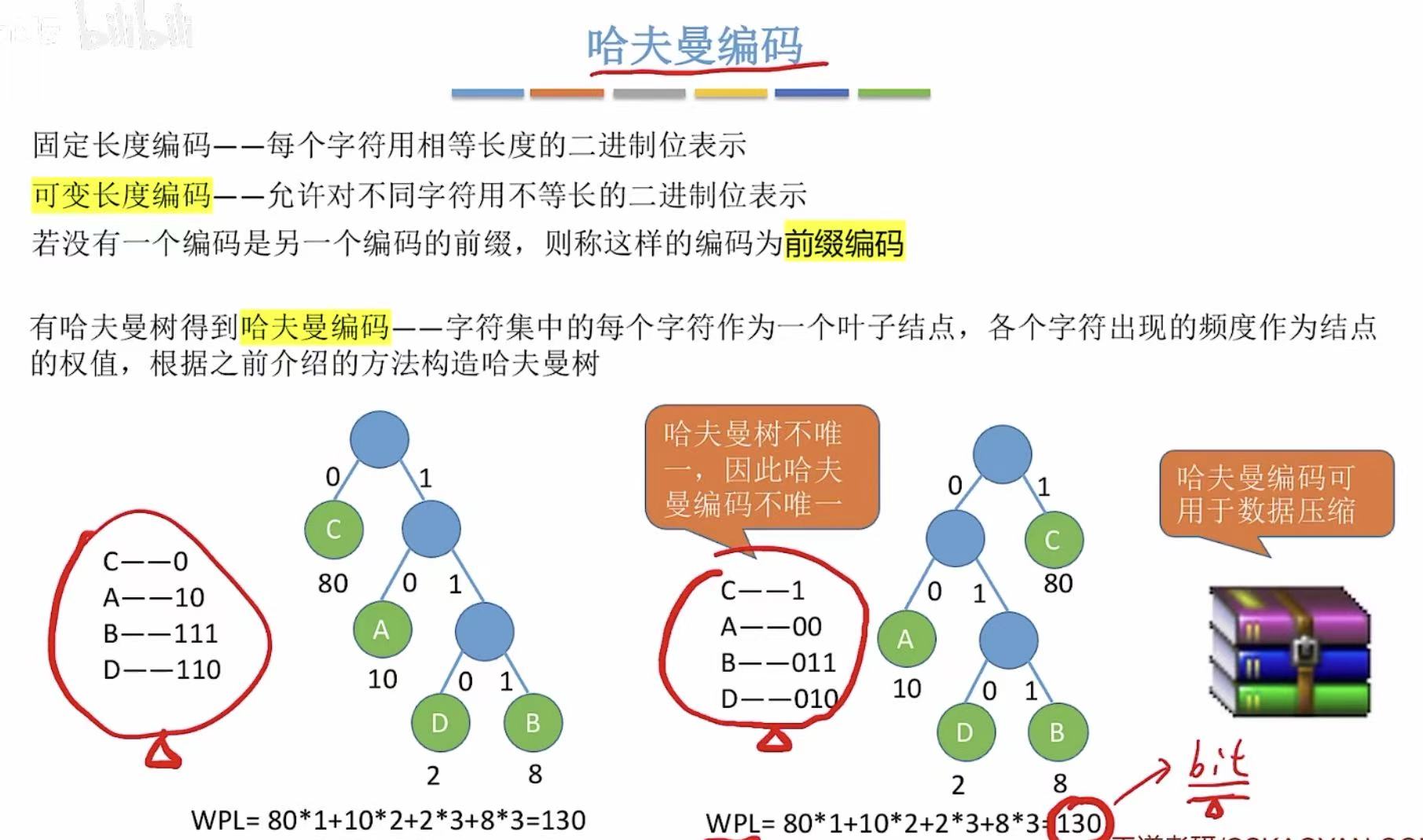
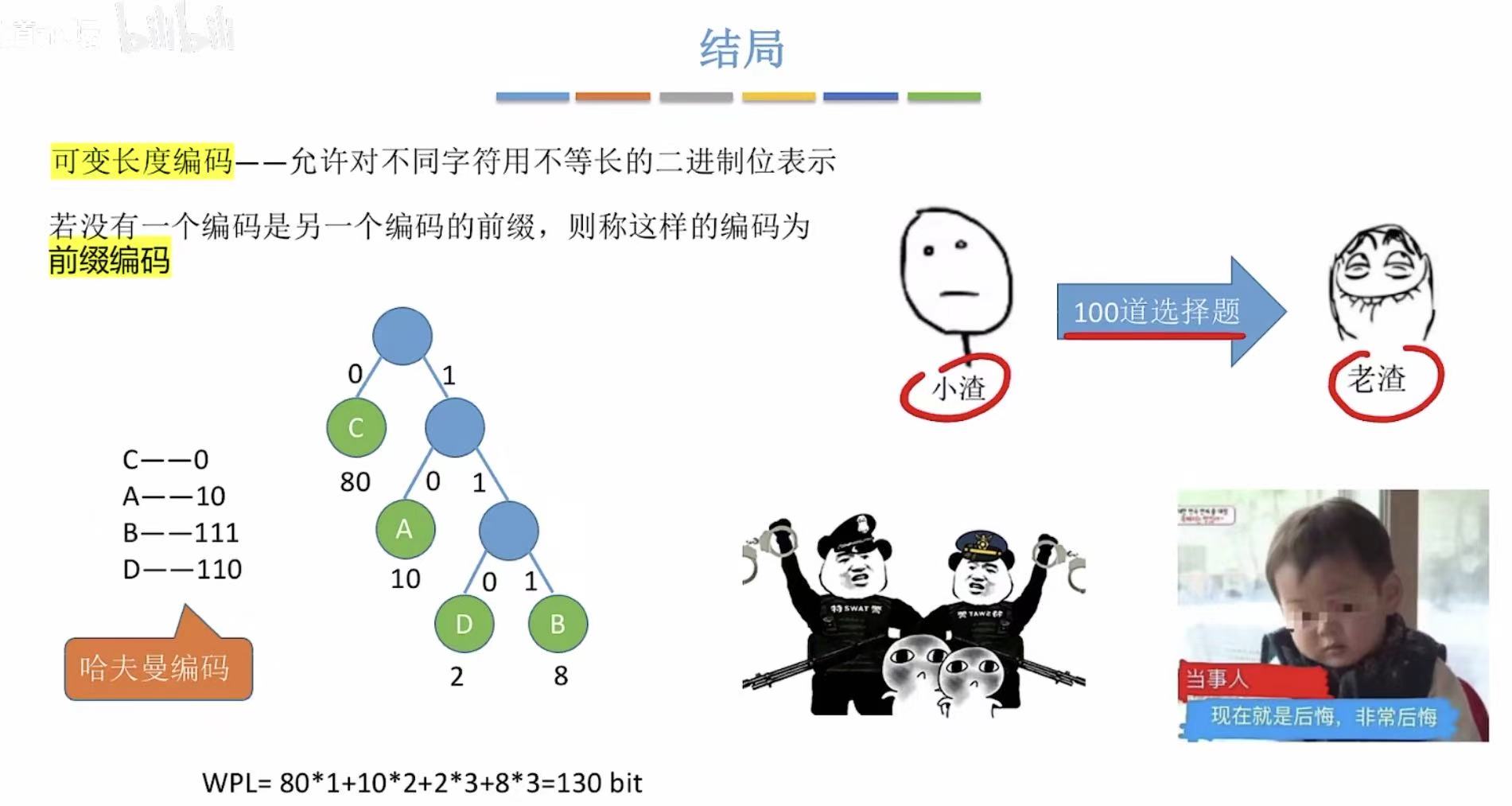
3. 哈夫曼编码
算是哈夫曼树的应用,想一想树的每个结点下边的两条边都变成0或1,就可以算出哈夫曼编码。

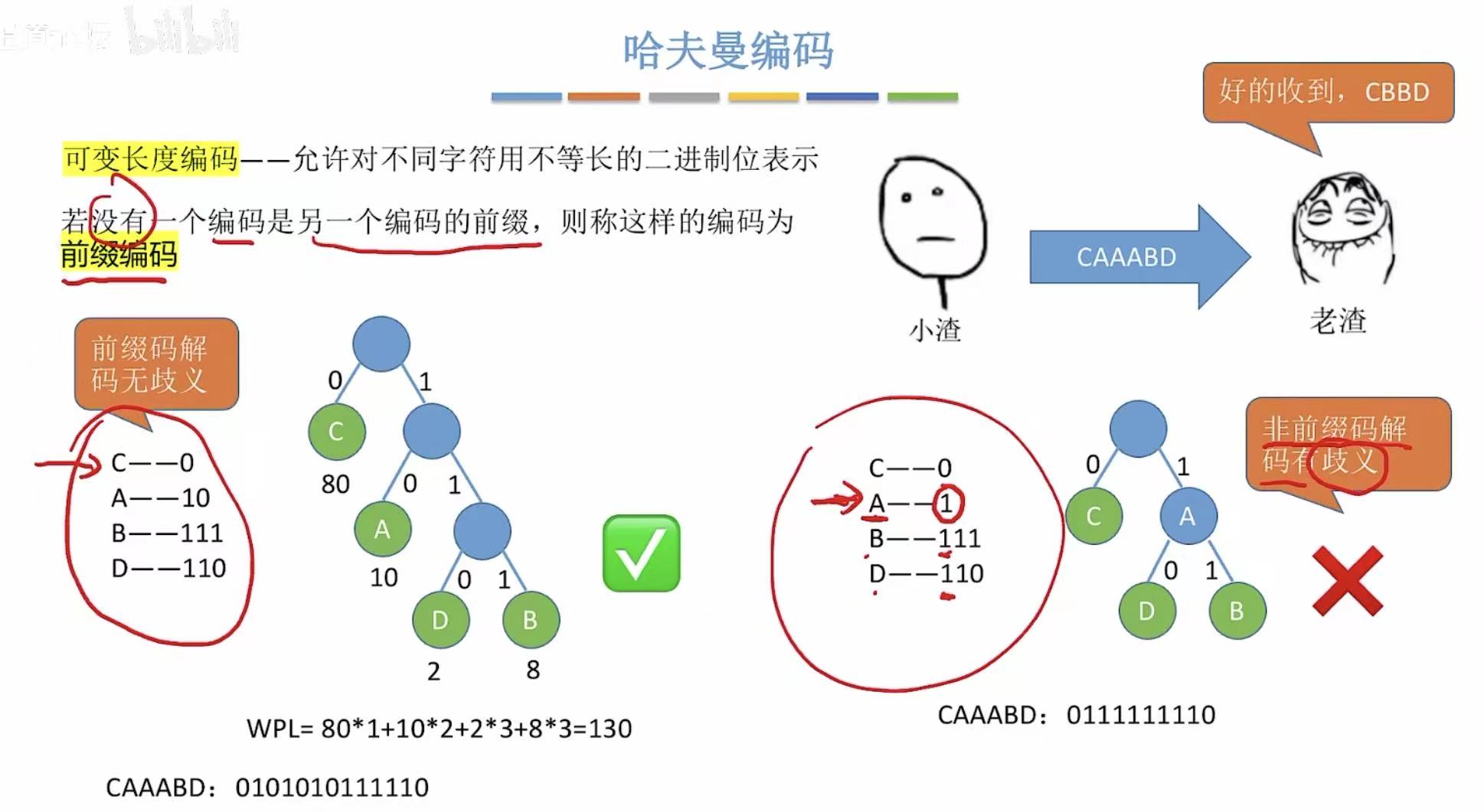
情景 :小渣和老渣有一天参加考试,小渣需要把100个选择题的答案通过咳嗽的不同方式(ke和ka)告诉老渣
假设 :100题中80题选C,10题选A,8题选B,2题选D
如果采用固定长度编码,也就是图中00、01、10、11的方式进行传递,小渣就需要连ke带ka咳嗽200次。
如果换一种方式呢?
用我们刚学过的哈夫曼树,将不同权重的答案当作结点,最后画出带权路径长度最小的树-->哈夫曼树
就能发现其实只需要咳嗽130次就可以了,而我们得到的不同的选项的编码:0、10、111、110,就是可变长度编码
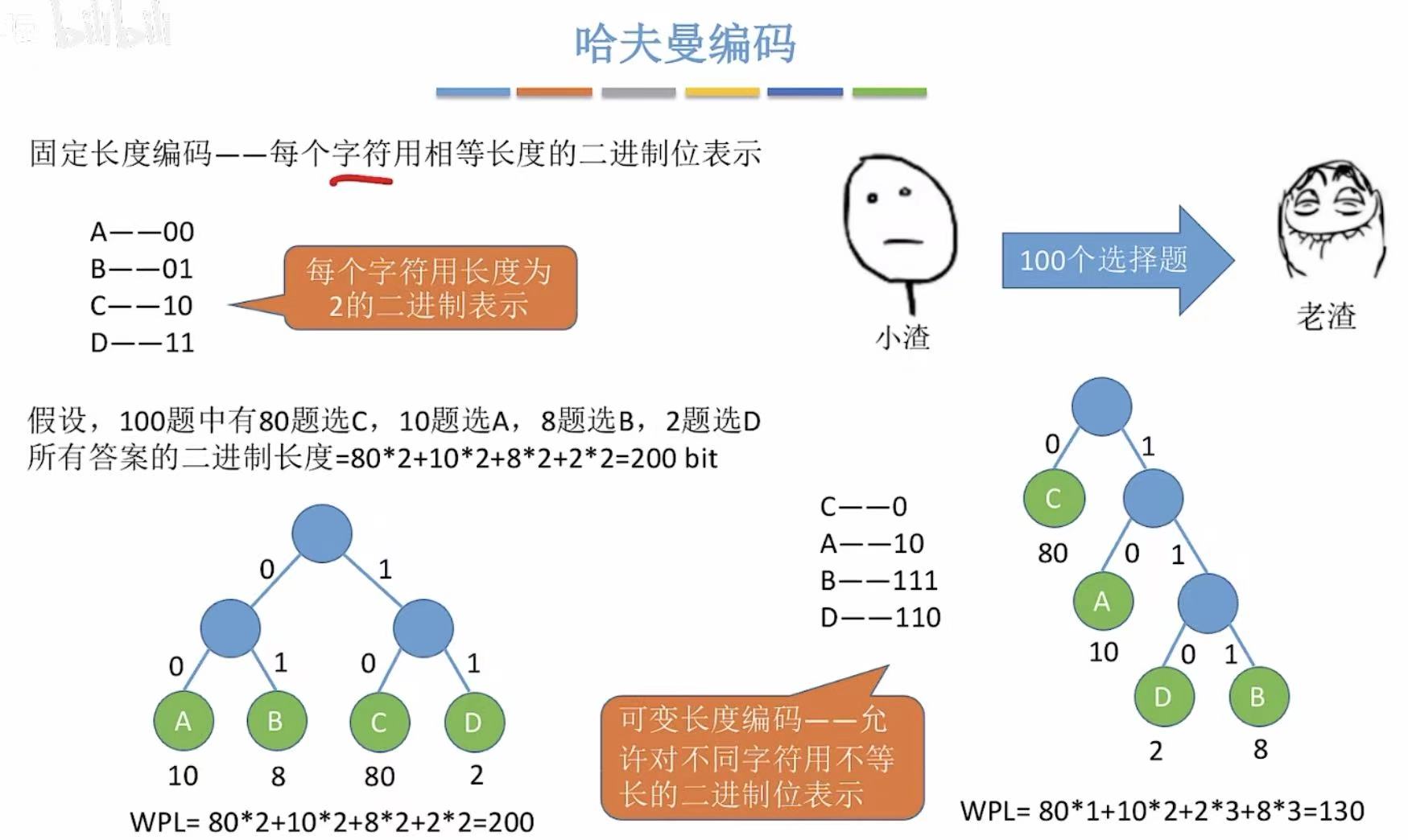
那么看着这个新的编码,我们又会出现疑问 :C-->0,那A-->1也不与它冲突,可以用1表示A么?
答案是:不可以,因为1是另外两个选项的编码的前缀。
比如小渣传给老渣110,那么老渣是该认为这是AAC还是单纯的D呢,所以有歧义 直接pass
所以这样不会产生歧义,没有一个编码是另一个编码的前缀-->的编码就是前缀编码 。
小总结:
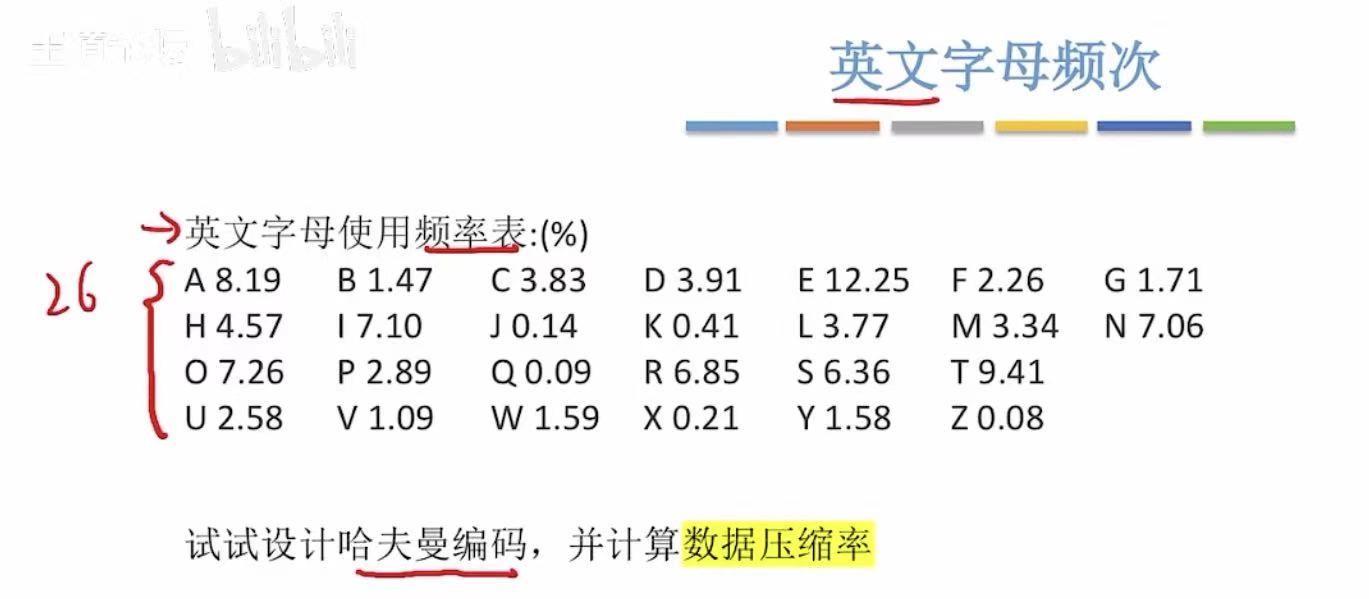
4. 小结
当然,最后小渣和老渣因为作弊都被抓了,所以千万不要效仿。
并查集
1. 如何表示集合关系?
补漏:集合
可以把集合 看成一个班中都独立的个体,也就是同学 。
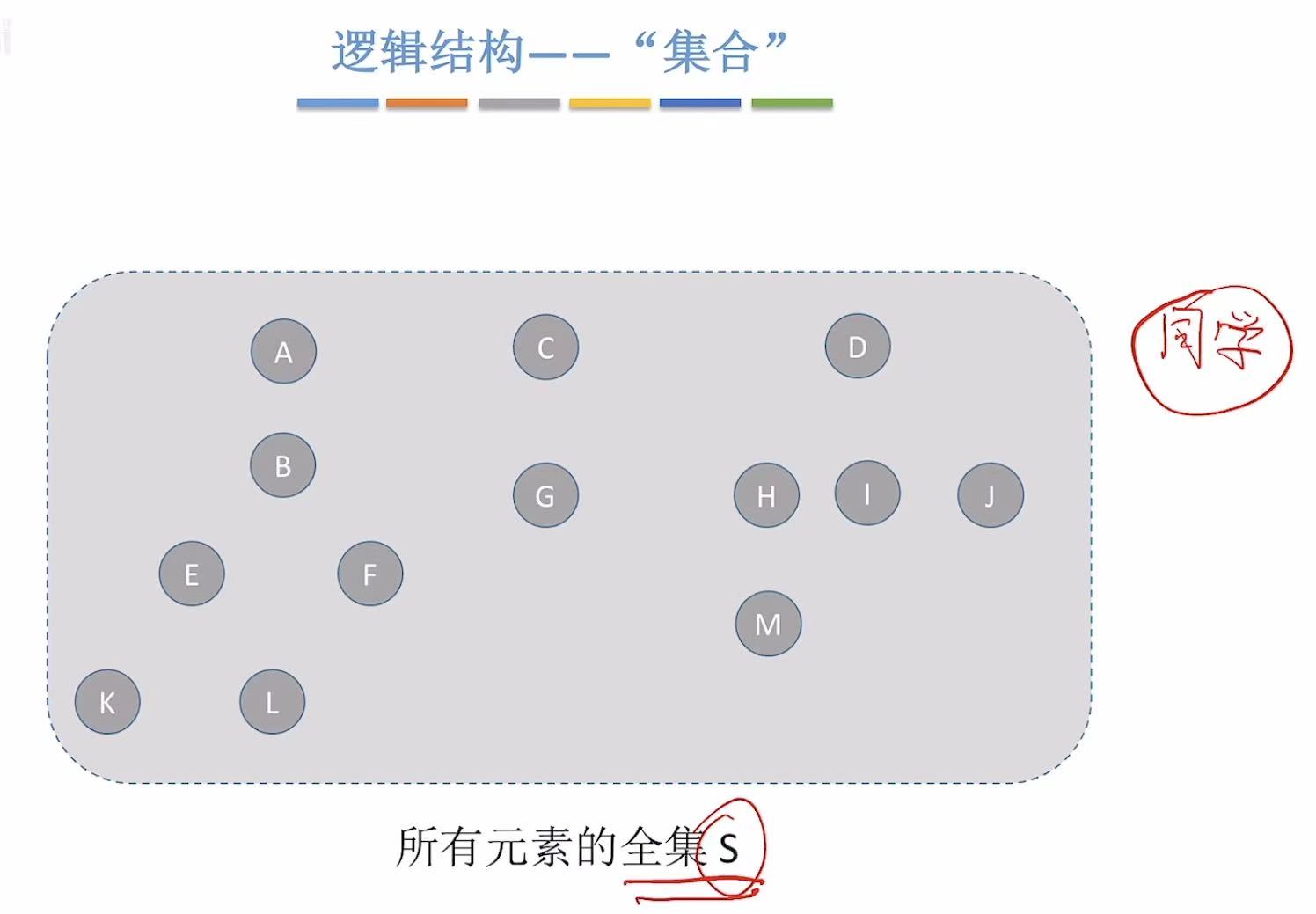
我们可以按照个人喜好把不同的同学划分成好几个组:
- 绿色:喜欢吃绿色葡萄的
- 紫色:喜欢吃紫色葡萄的
- 橙色:喜欢吃橙子的
通过这样的分组,我们很容易想起之前所学过的-->森林(个体树在一起就组成了森林)
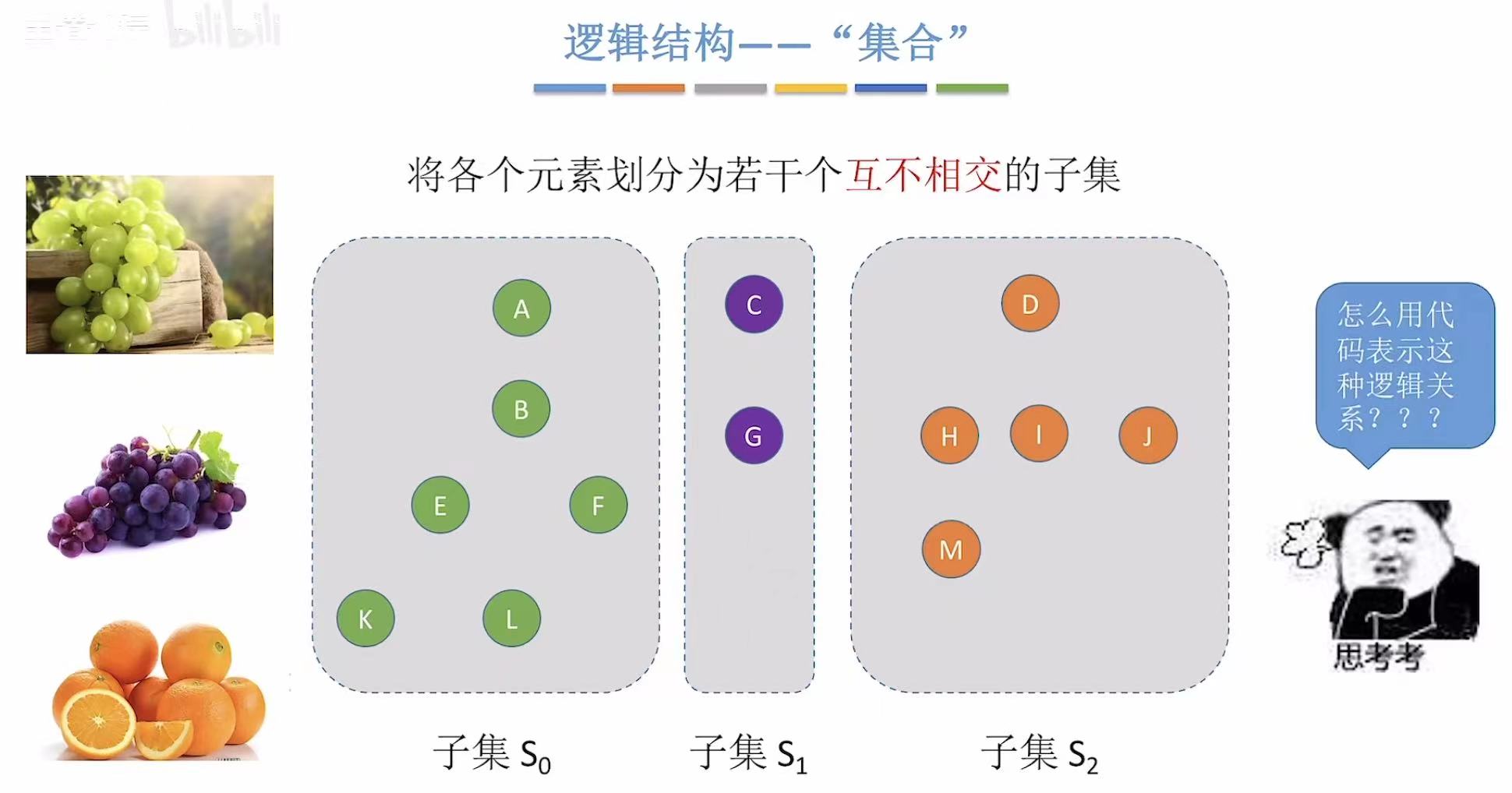
我们可以将同一个小组中的同学变为结点,将结点串成一个树,整个班就是一个森林。
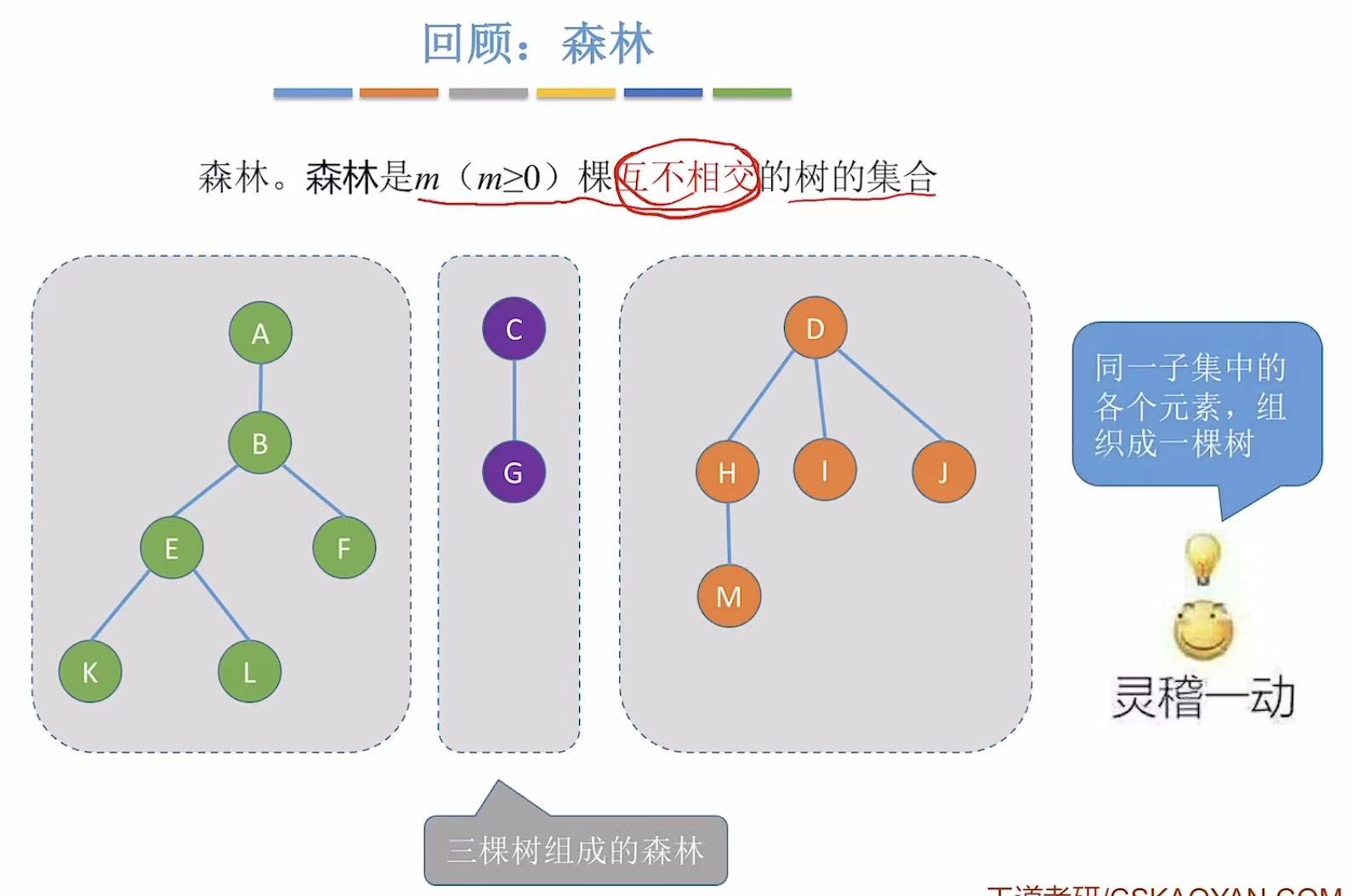
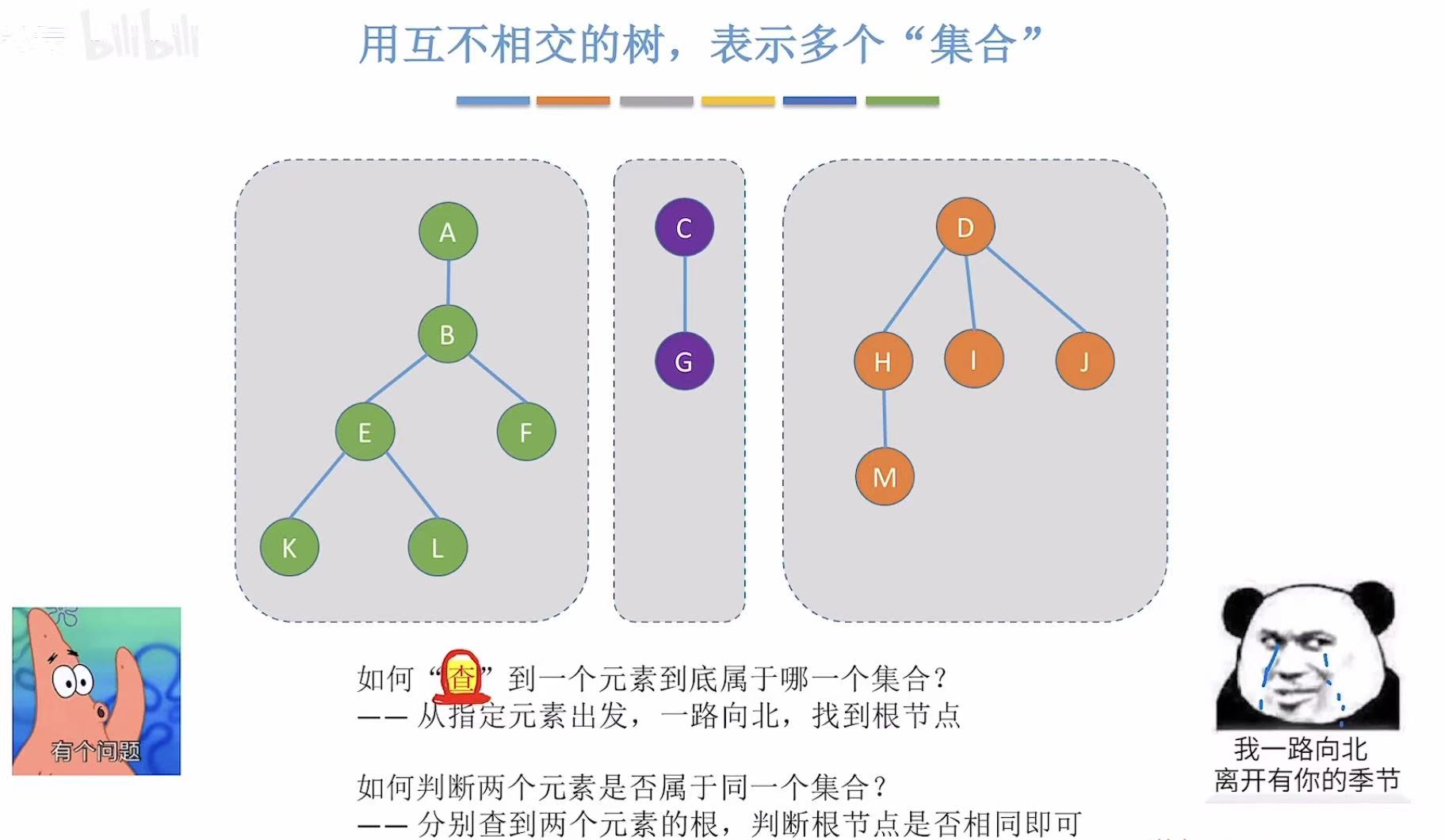
不同小组,我们可以把它们并 起来,就是一整个班级。
如果我们想知道这个同学和你自己属于一个小组么,就需要查 我们两个的根是不是同一个。
这就是并查集 。
如果想让两个树并在一起,我们就需要让一个树成为另外一个树的子树。
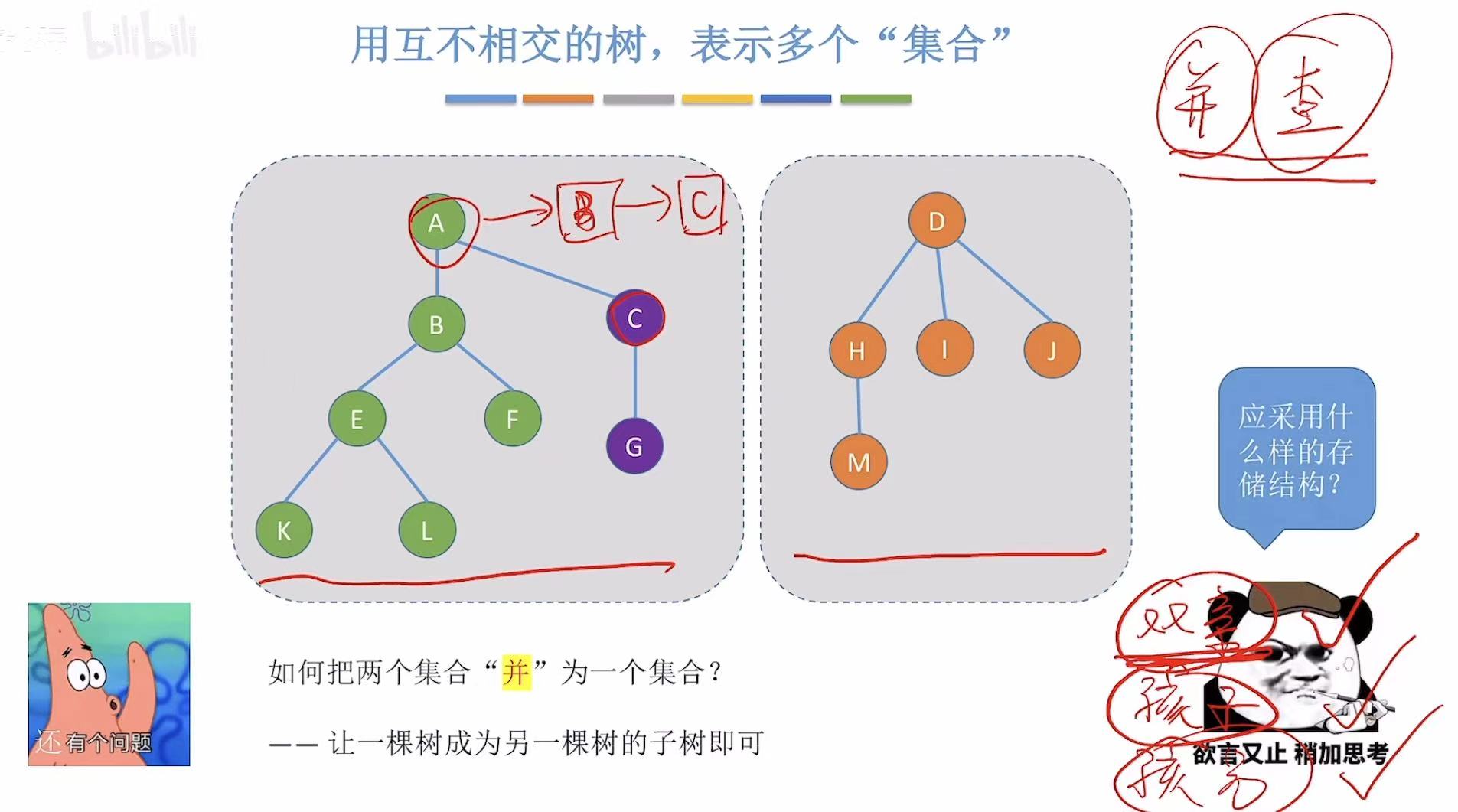
2. 并查集
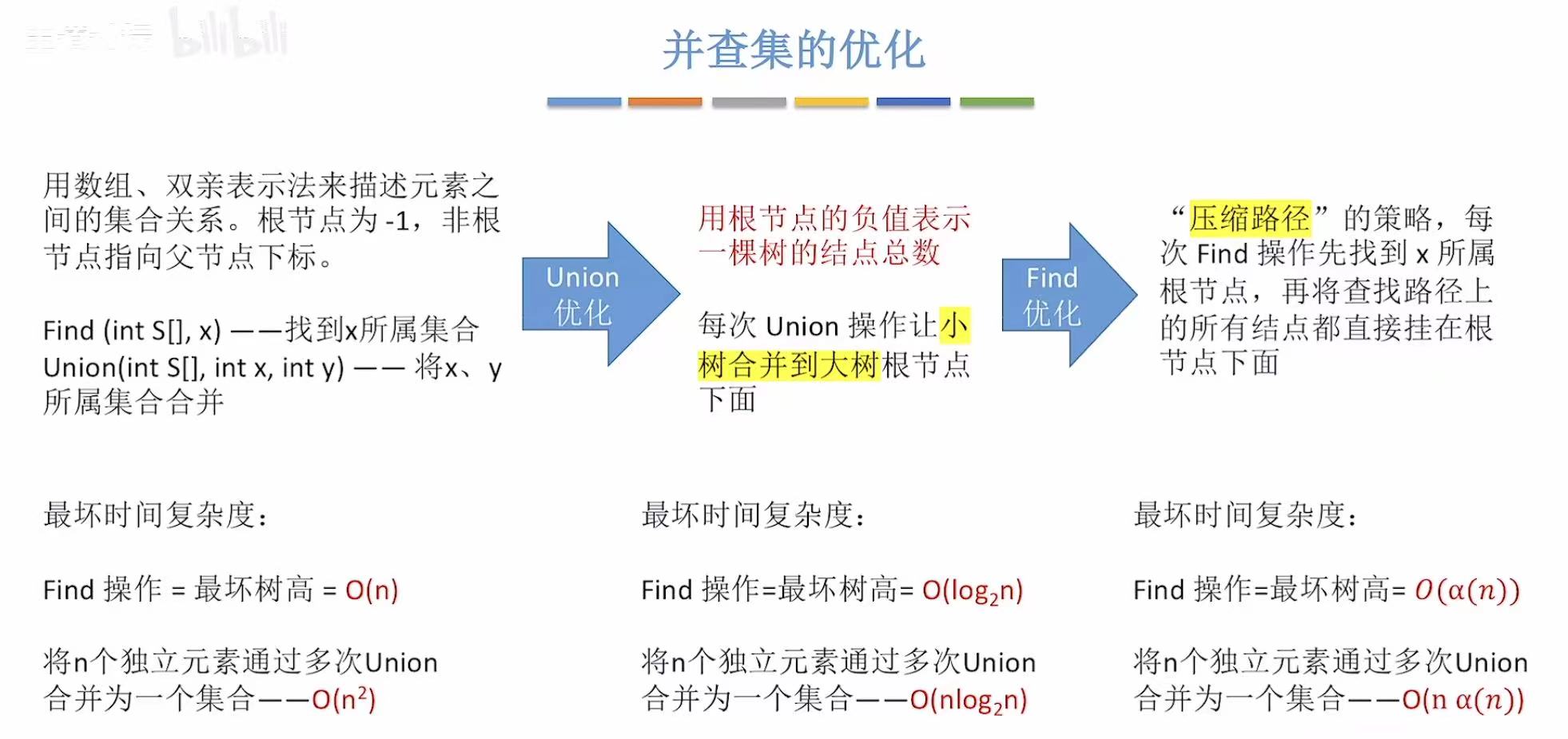
2.1 存储结构
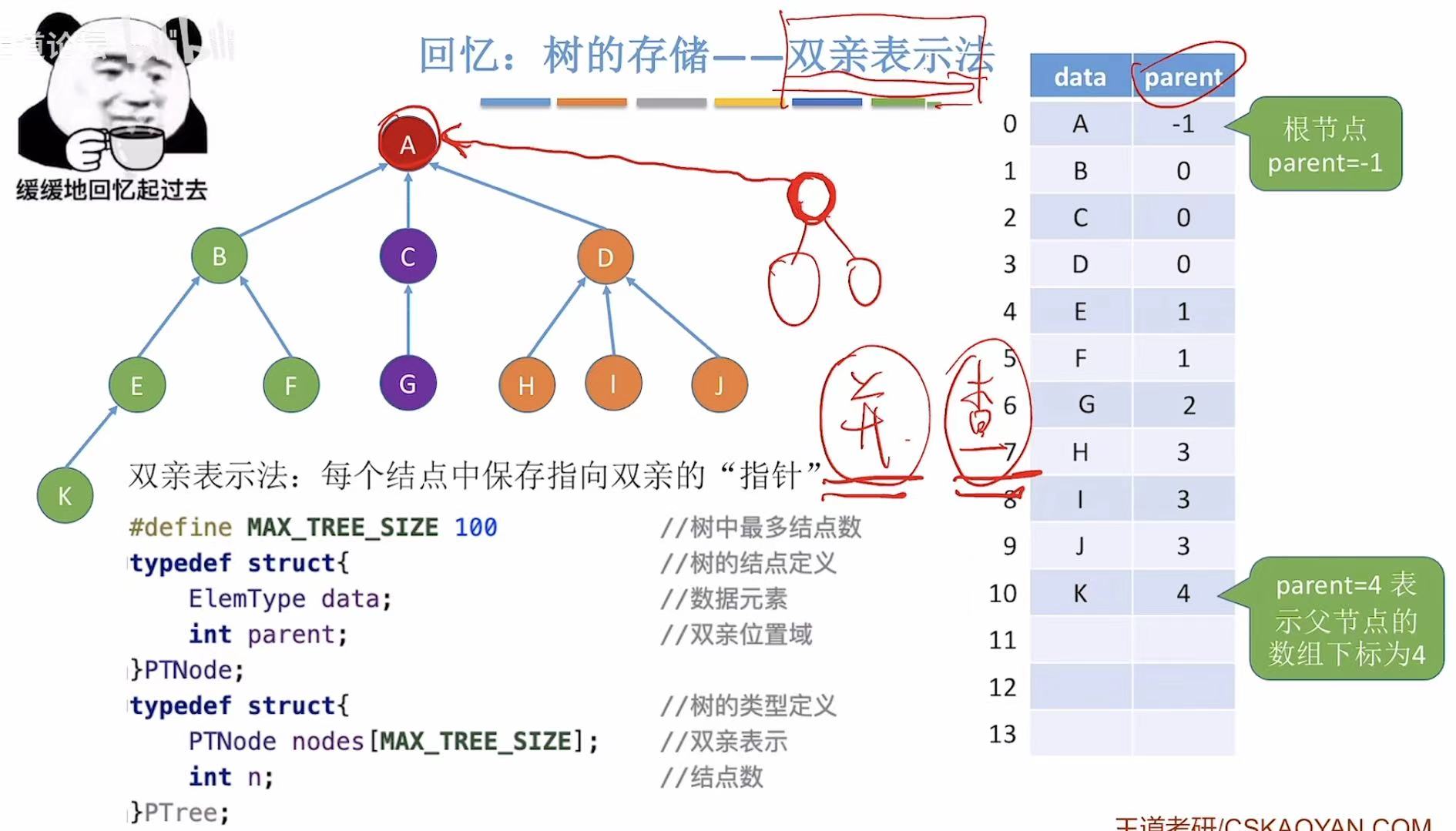
我们可以用双亲表示法来存储这个并查集(其实就是存储森林)。
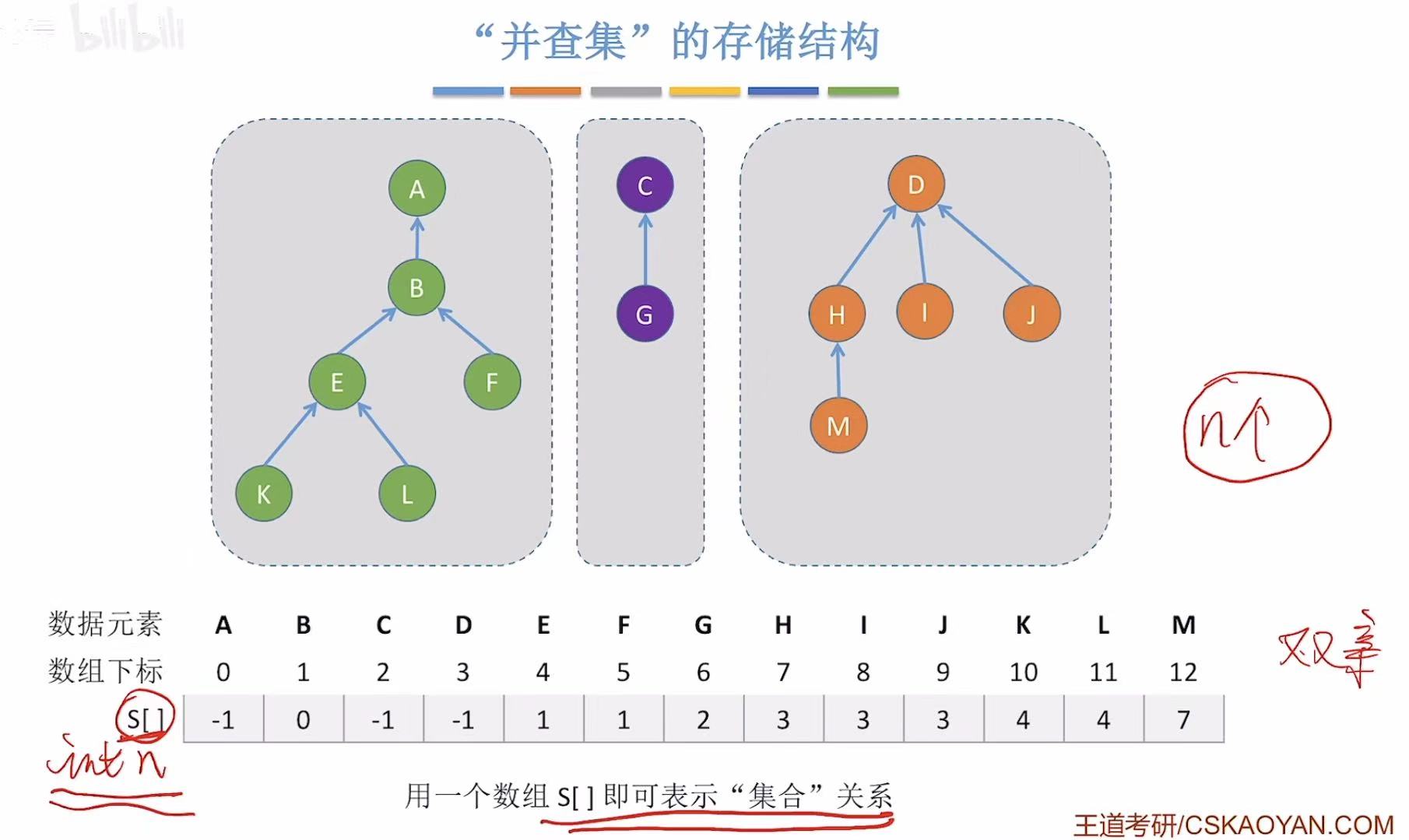
2.2 基本操作
顾名思义,并查集,只能并或者查。
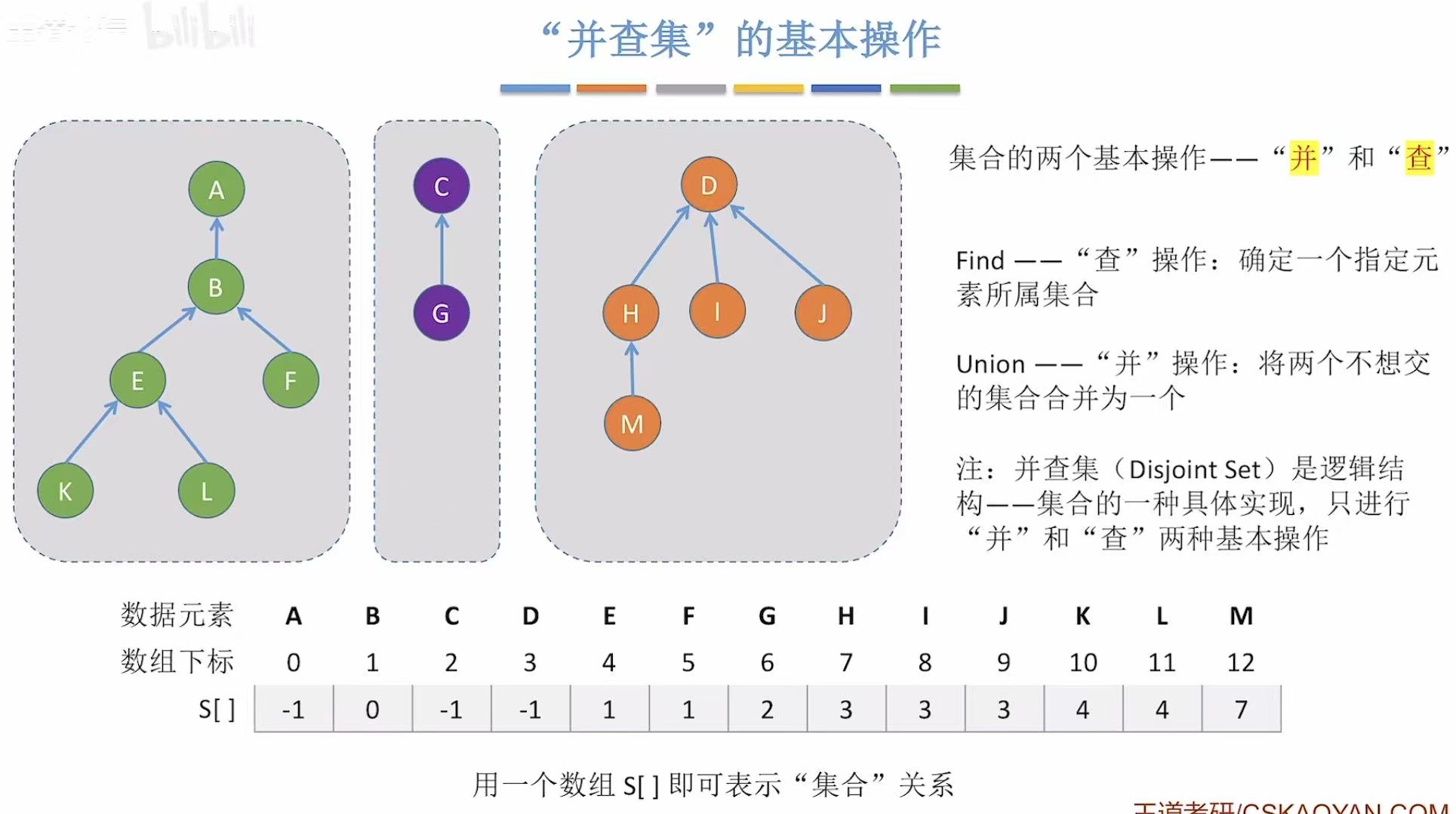
2.3 代码实现
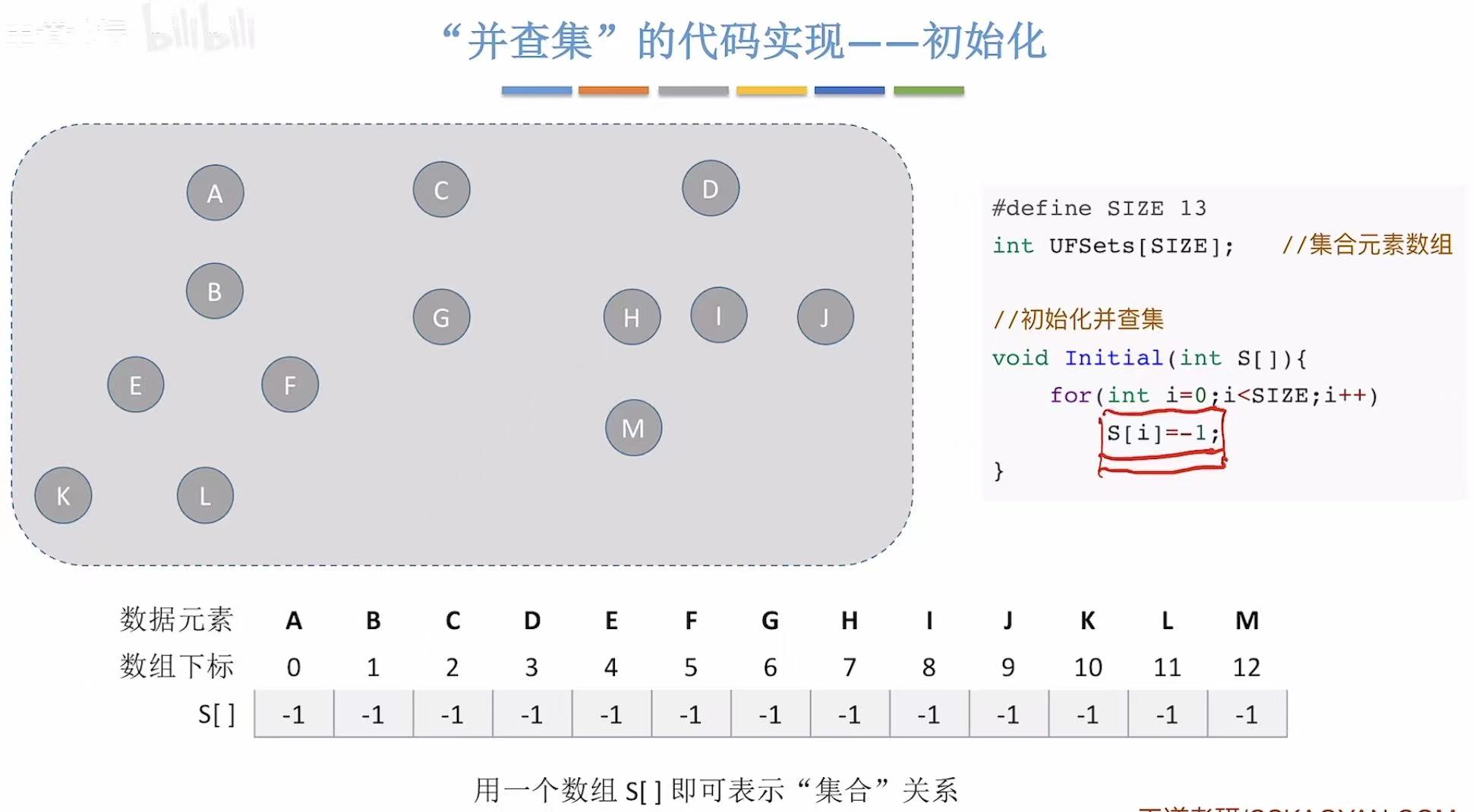
2.3.1 初始化
初始化 :相当于把每个结点都当成根节点,数组中都存储-1.
2.3.2 并、查
- 并:第二个树的根节点指向第一个树的根节点。比如C并入A,即将C数组中存储的-1改为A的数组下标0.
- 查 :就想上寻找当前结点所在树的根节点。
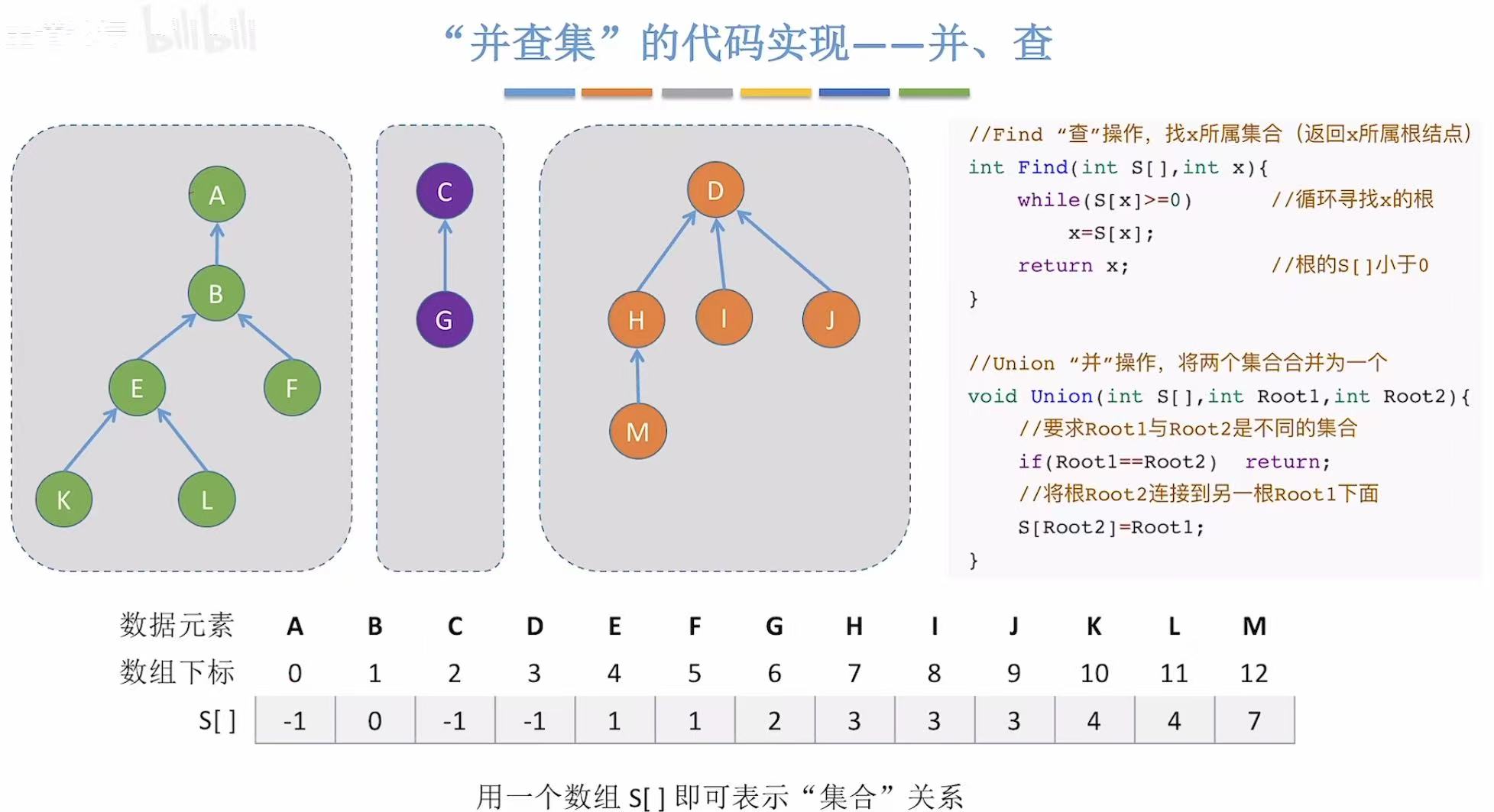
2.3.3 时间复杂度分析
最好 :结点就在根节点下方,一步直接找到
最坏 :结点离根节点最远,树有多高,结点就有多下
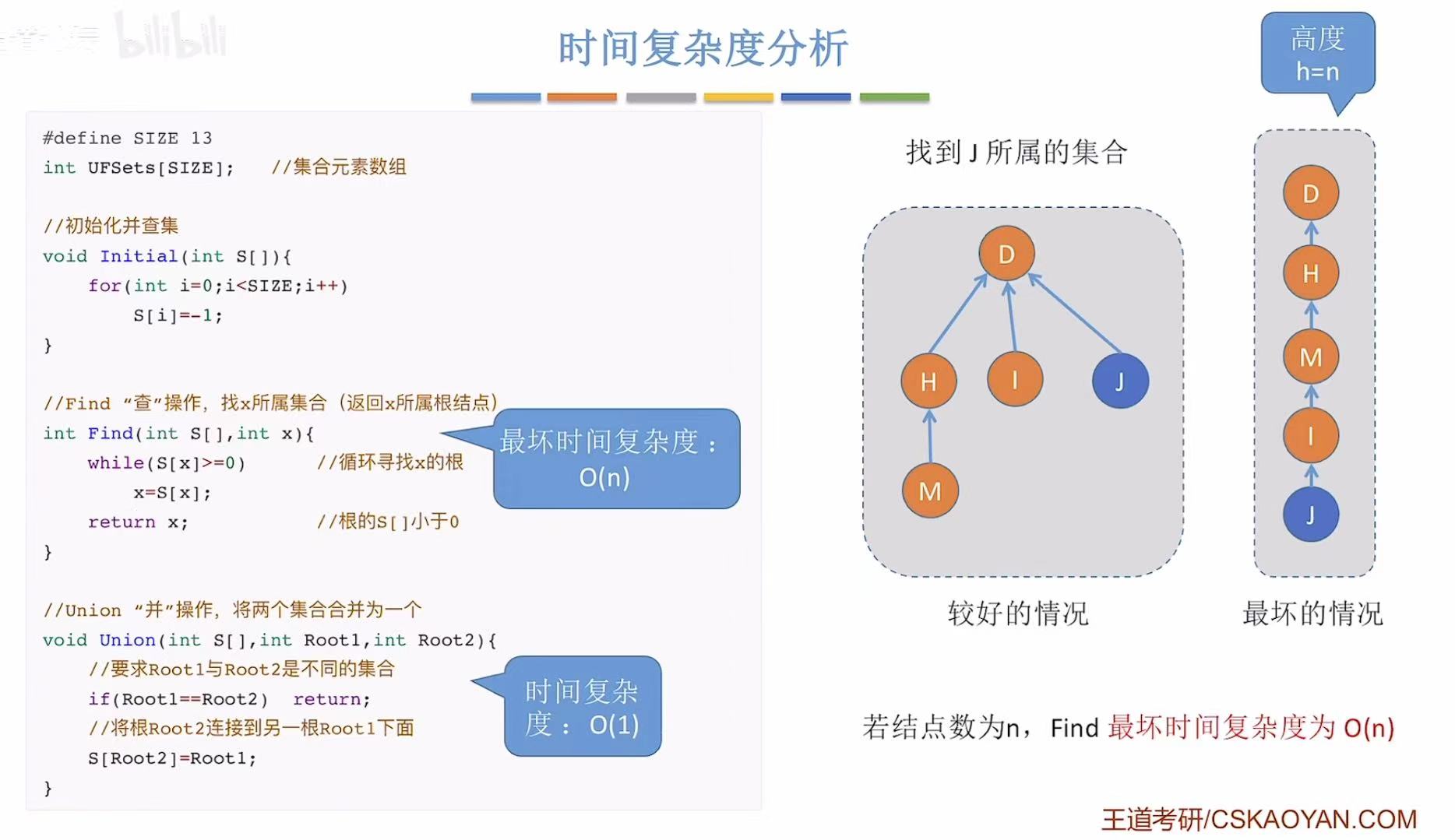
3. 优化
一共就俩操作,所以不是优化并操作,就是优化查操作。
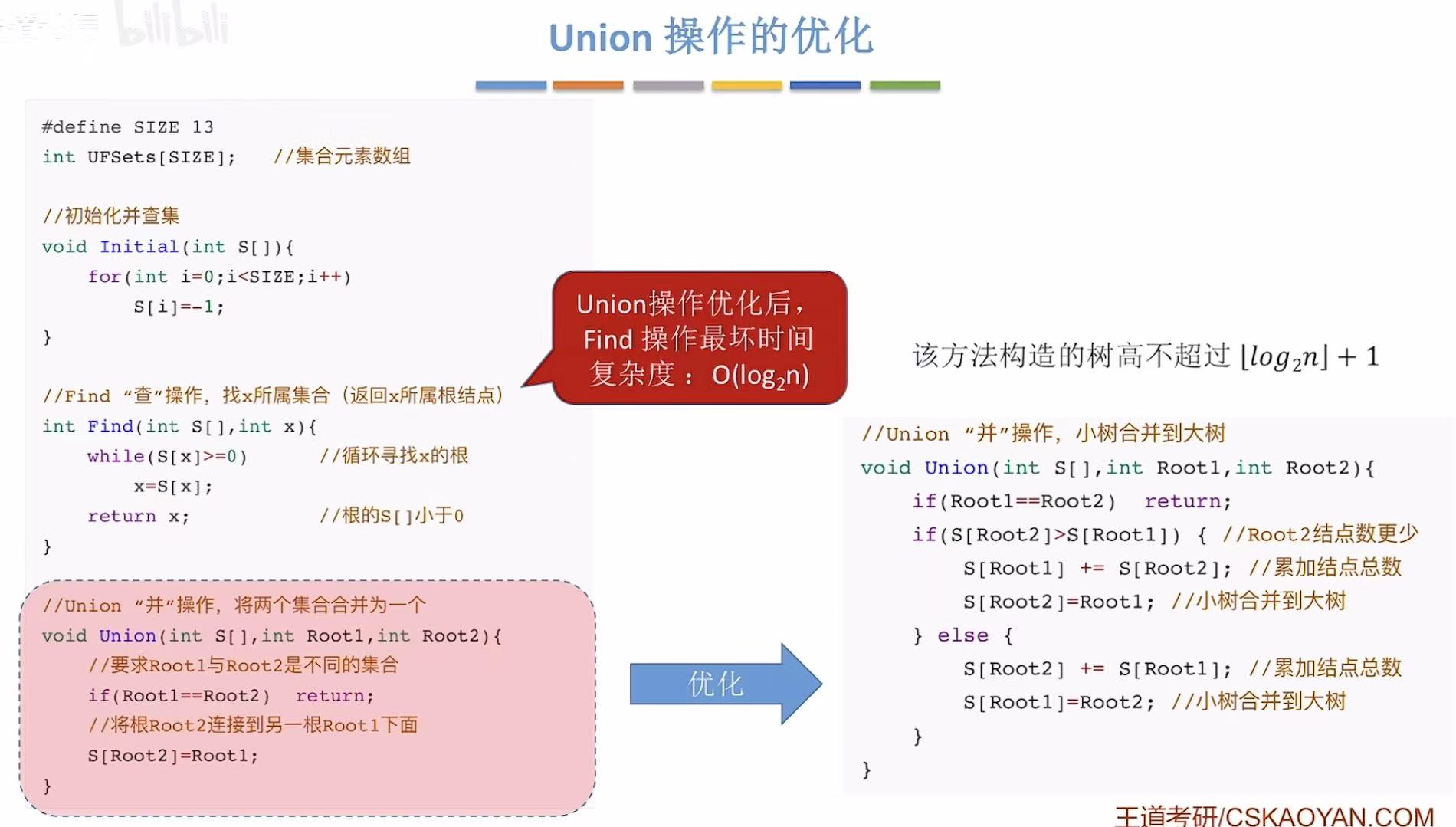
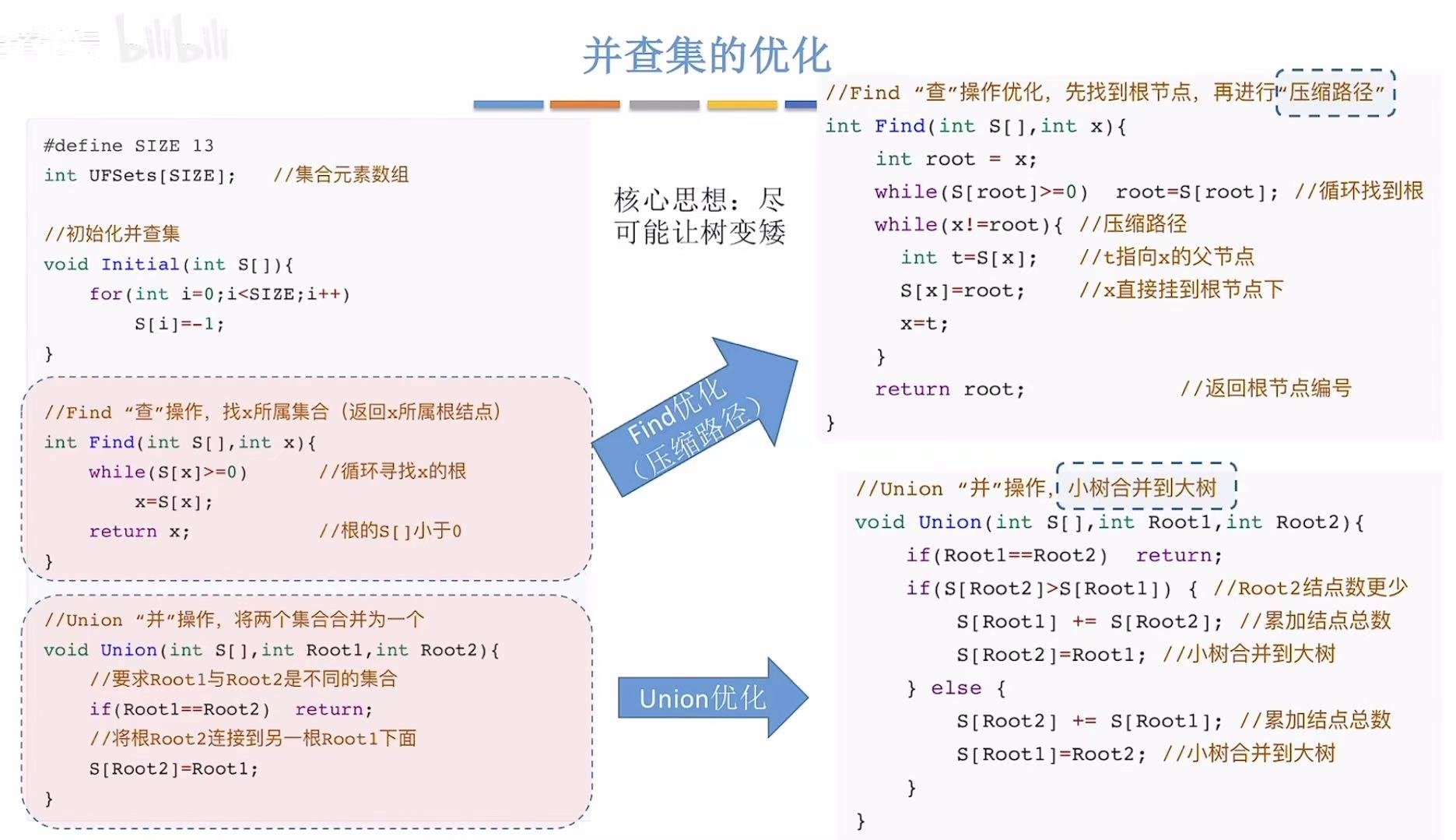
3.1 Union操作的优化
从时间复杂度看,最坏的情况是树有多高,结点有多下。
如果想优化最坏的情况,就必须禁止树再变高,所以在并的时候就可以矮树并入高树,这样就不会把原来的树增高。
怎么知道哪个是高树哪个是矮树呢,就可以把每个根节点在数组中存储的绝对值表示自己这棵树有多少个结点。
并之前:
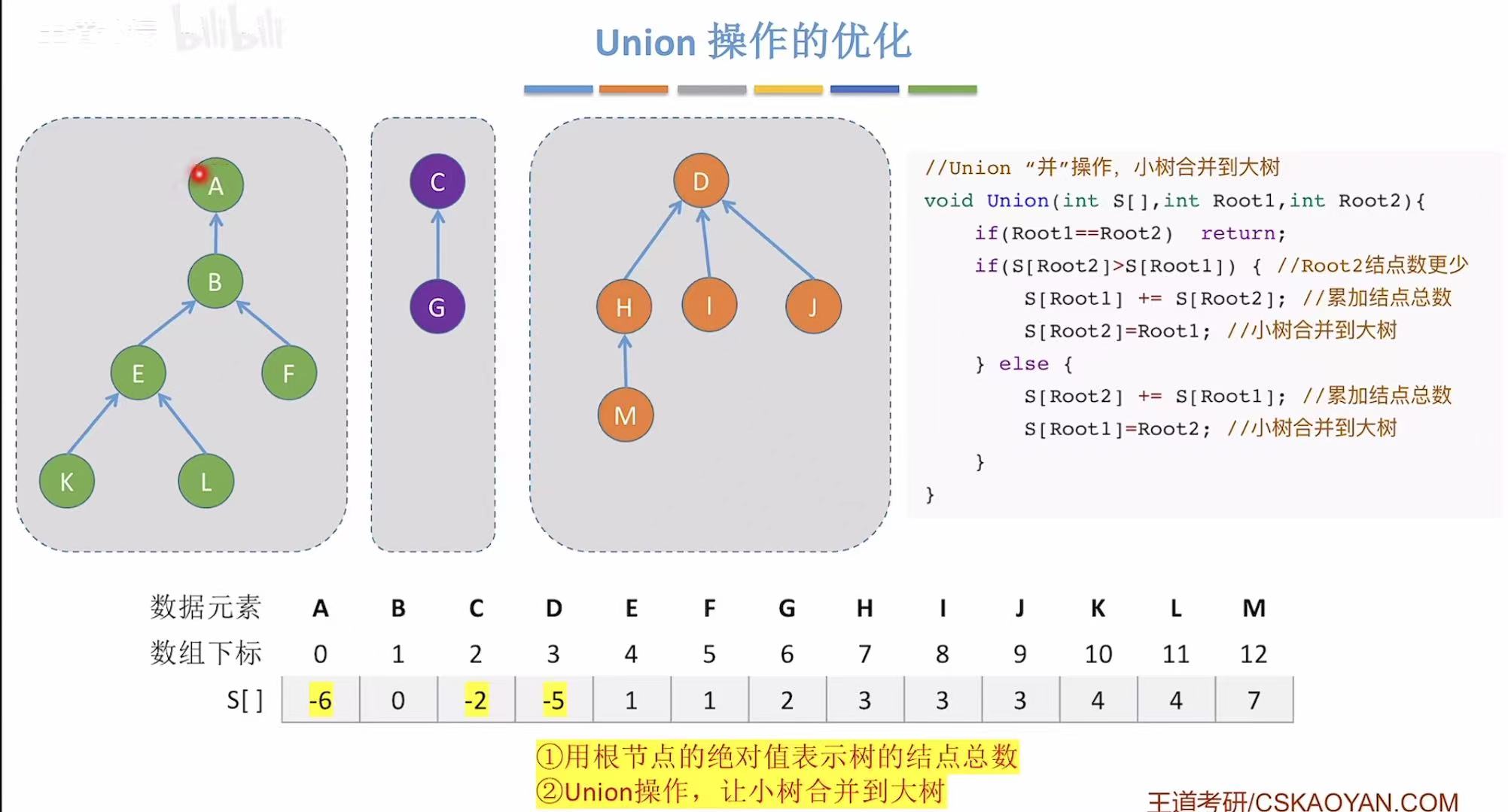
并一个:
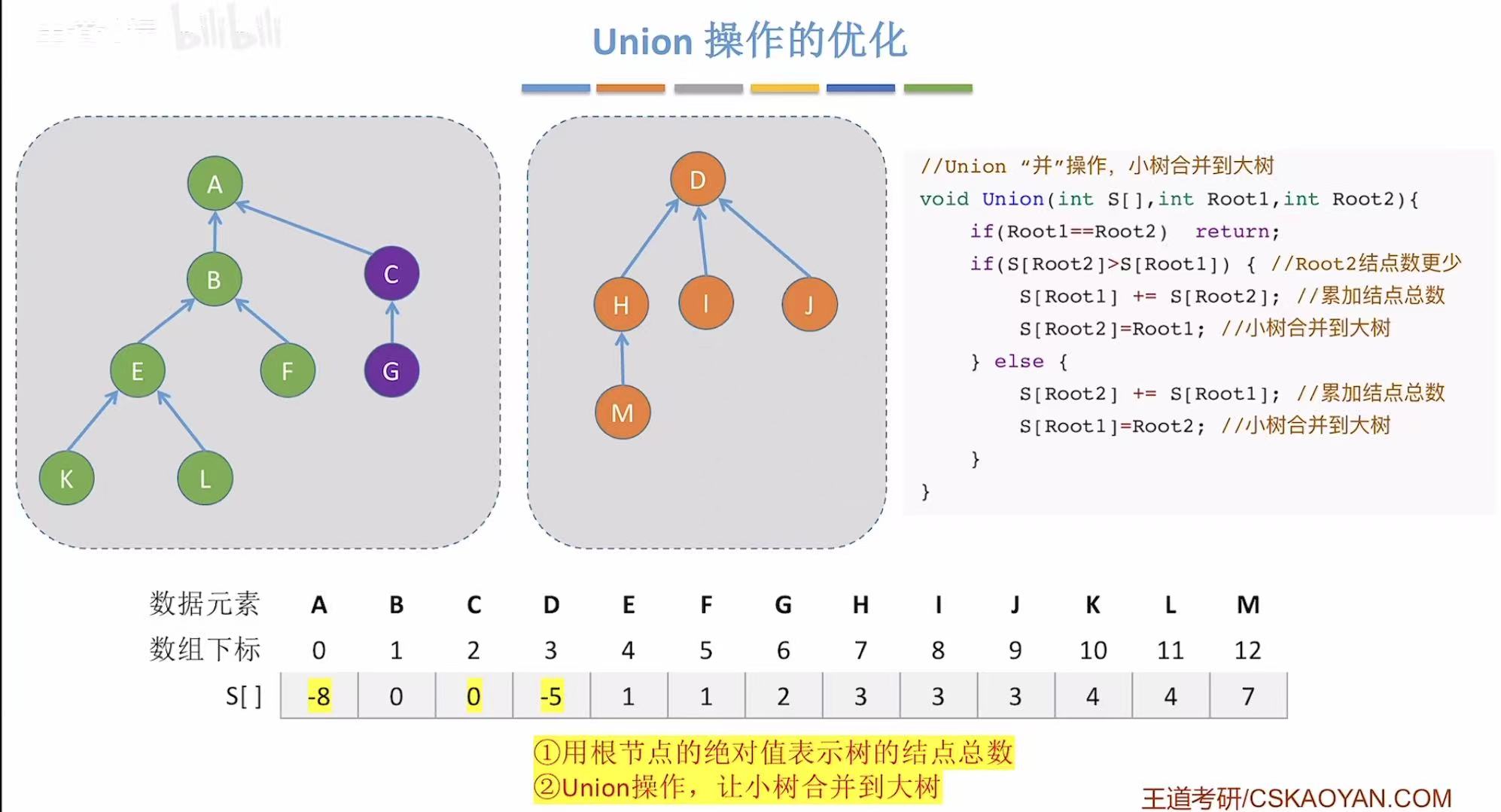
并两个:
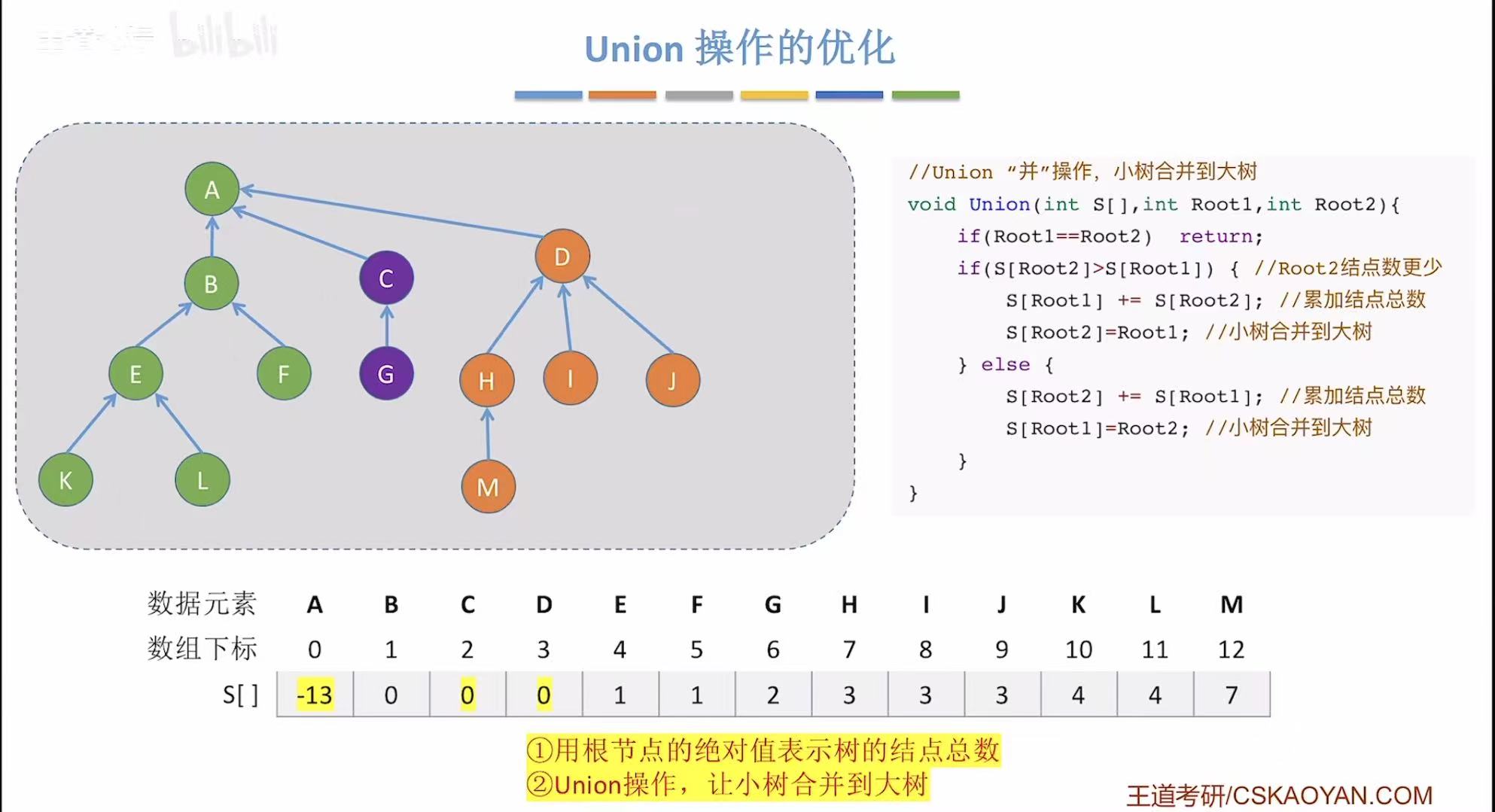
小总结:
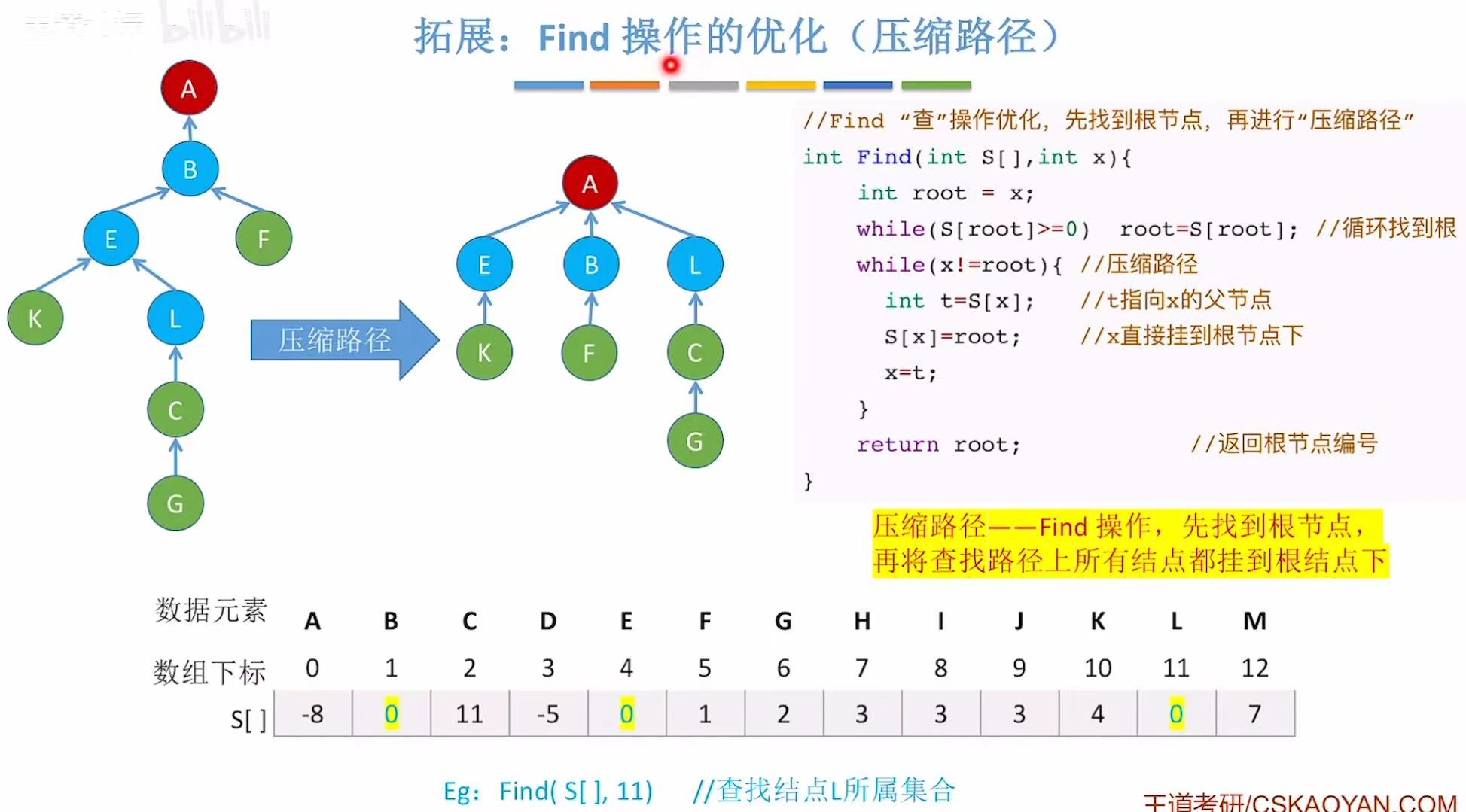
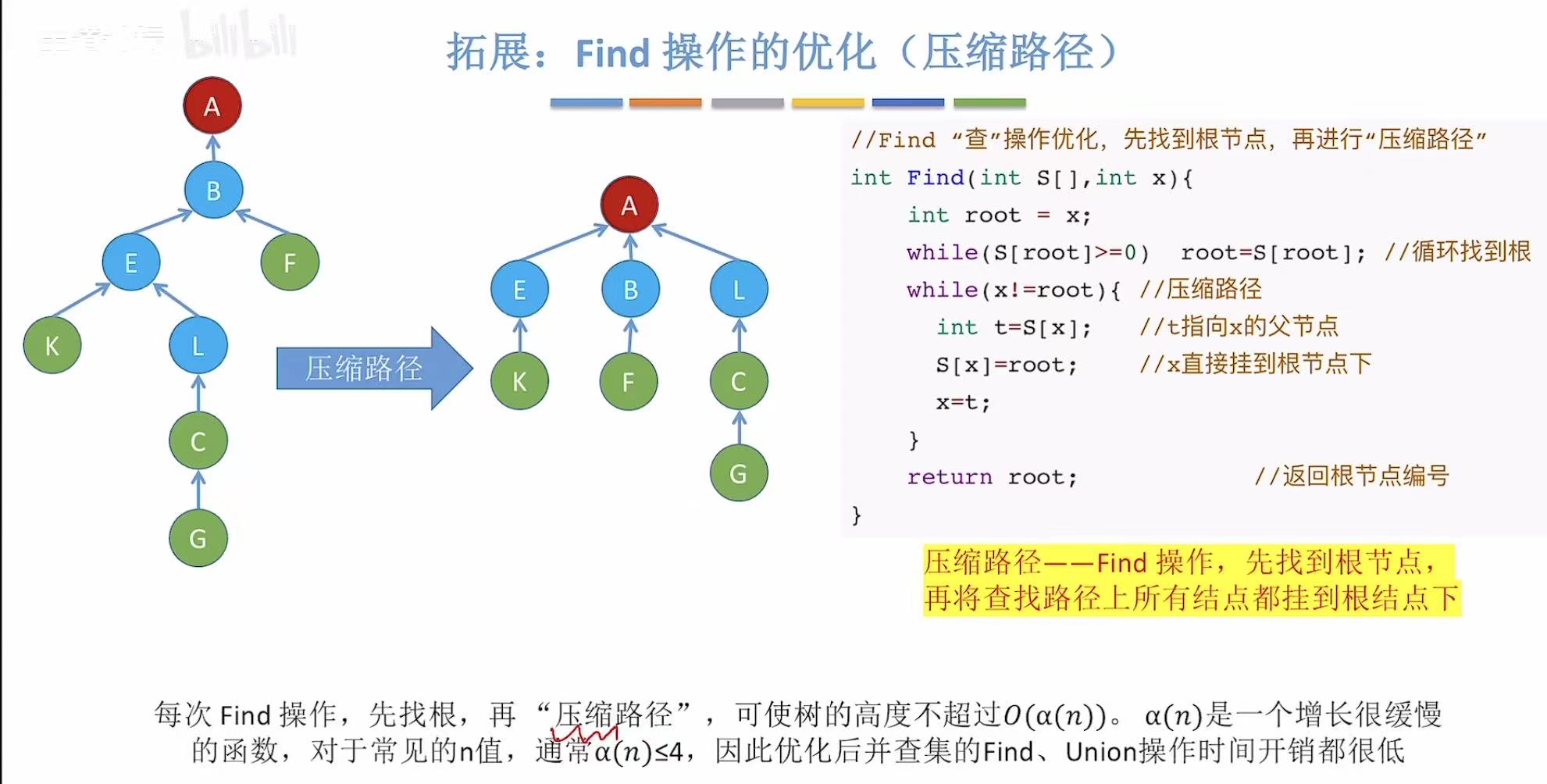
3.2 Find操作的优化
怎么优化查操作呢,可以将到达当前结点路径上的所有的结点都挂在根节点下方(一键直查)
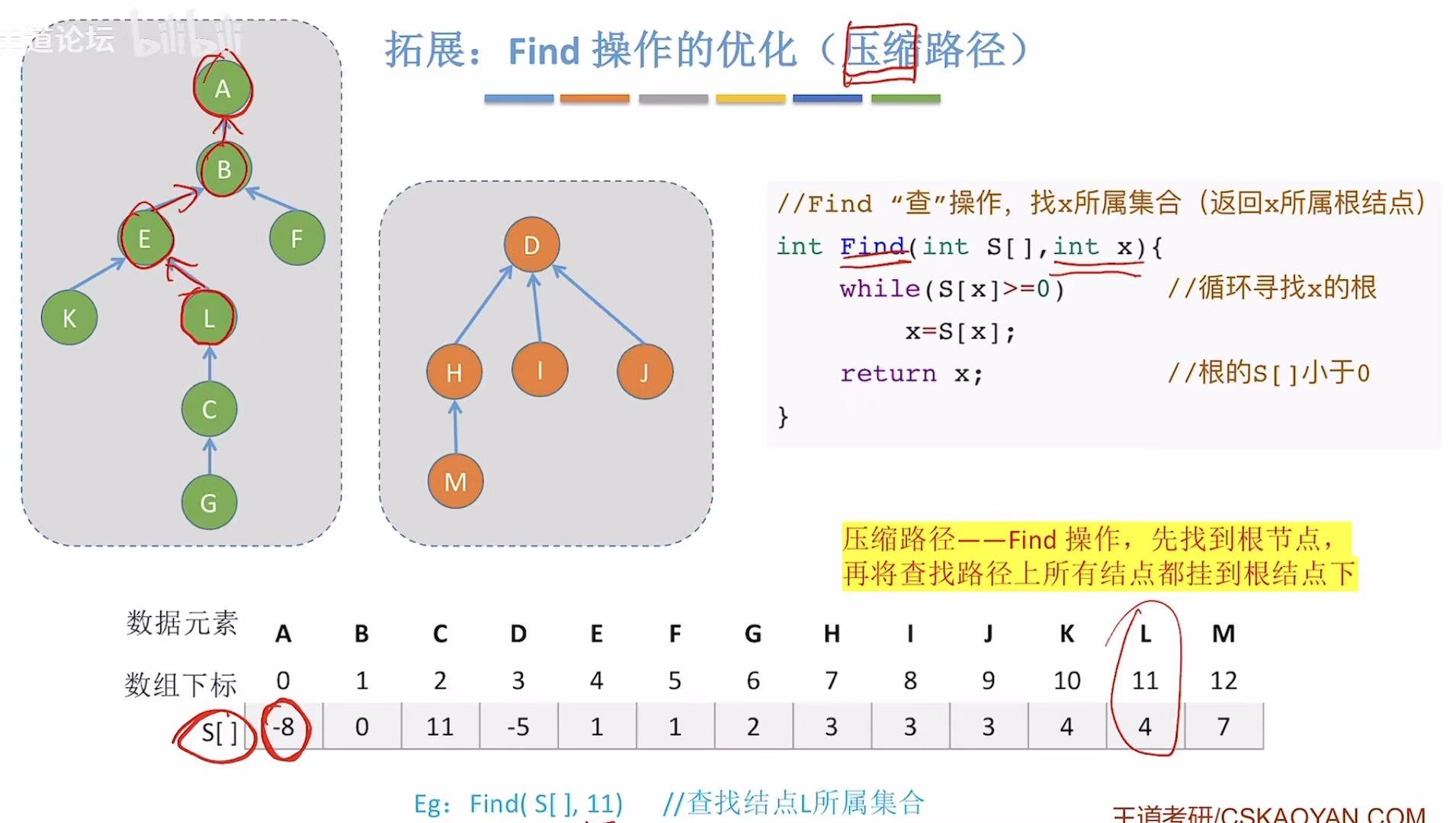
就比如我找L是哪个组的,往上经过EB,最后找到A,就给自己和EB直接挂在A下边儿。
其实思想也是把树变矮。
3.3 优化总结
4. 小结