目录
[一、什么是 Mat 类](#一、什么是 Mat 类)
[1.1 Mat的基本概念](#1.1 Mat的基本概念)
[1.2 Mat的类型](#1.2 Mat的类型)
[1.2.1 Mat 的模板化存储](#1.2.1 Mat 的模板化存储)
[1.2.2 OpenCV 规定的核心数据类型](#1.2.2 OpenCV 规定的核心数据类型)
[1.3 OpenCV Mat 类常用构造函数和访问方式](#1.3 OpenCV Mat 类常用构造函数和访问方式)
[1.3.1 Scalar 介绍](#1.3.1 Scalar 介绍)
一、什么是 Mat 类
1.1 Mat的基本概念
- OpenCV 里用于储存矩阵数据的类型
- 与
int、double等基础类型地位相同,是 OpenCV 中表示图像和矩阵的核心数据结构
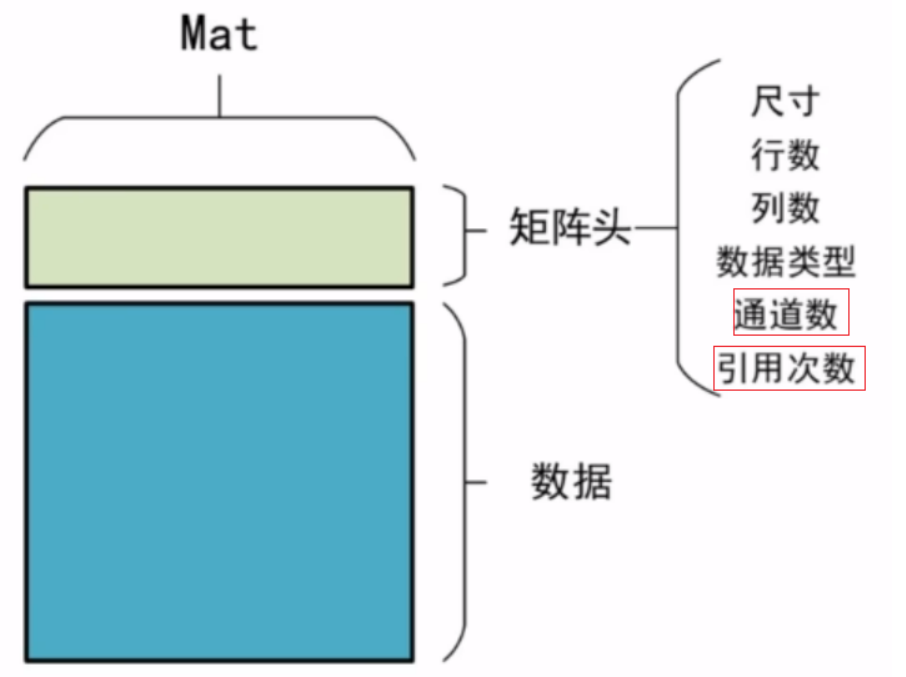
- 图像在 OpenCV 中本质上就是一个数值矩阵,每个像素对应矩阵中的一个元素。
- 灰度图像是单通道矩阵,每个元素是一个灰度值(如示例中的
133、63等);彩色图像则是多通道矩阵(如 BGR 三通道)。 - 图中红色框标注的是矩阵中一个具体的像素值,蓝色框则圈出了矩阵中的一个子区域。
1.2 Mat的类型
1.2.1 Mat 的模板化存储
cv::Mat 是一个模板化的矩阵容器,可以通过指定类型参数来存储不同的数据:
- 基础形式:
cv::Mat_<Tp>,其中Tp可自定义 - 常用特化:
cv::Mat_<double>cv::Mat_<float>cv::Mat_<uchar>/cv::Mat_<unsigned char>- 其他自定义类型
1.2.2 OpenCV 规定的核心数据类型
表格
| 数据类型 | 具体类型 | 取值范围 |
|---|---|---|
| CV_8U | 8 位无符号整数 | 0 --- 255 |
| CV_8S | 8 位有符号整数 | -128 --- 127 |
| CV_16U | 16 位无符号整数 | 0 --- 65535 |
| CV_16S | 16 位有符号整数 | -32768 --- 32767 |
| CV_32S | 32 位有符号整数 | -2147483648 --- 2147483647 |
| CV_32F | 32 位浮点数 | -FLT_MAX --- FLT_MAX,支持 INF、NAN |
| CV_64F | 64 位浮点数 | -DBL_MAX --- DBL_MAX,支持 INF、NAN |
1.3 OpenCV Mat 类常用构造函数和访问方式
1.3.1 Scalar 介绍
Scalar 是 OpenCV 中一个轻量级的数值容器类 ,本质是对 Vec4d(4 个双精度浮点型的向量)的封装,专门用来:
- 给
Mat矩阵 / 图像的像素做初始化赋值; - 表示颜色值(如 BGR 颜色)、坐标、权重等少量数值的组合;
- 作为函数参数传递多数值(比如
cv::addWeighted的权重参数)。
简单说,Scalar 就像一个 "万能小容器",可以装 1~4 个数值,默认是浮点型(double),适配 OpenCV 中大部分需要多值参数的场景。Scalar 最多支持 4 个参数(对应 4 个维度),参数数量不足时,未指定的维度会默认设为 0。
核心用途:初始化 Mat / 图像,Scalar 的参数数量和 Mat 的通道数匹配时,按顺序赋值;不匹配时,多余参数被忽略,不足则补 0。
cpp
include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main() {
// 1. 构造 Scalar(支持1~4个参数)
Scalar s1(255); // 1个参数:s1[0]=255, s1[1]=0, s1[2]=0, s1[3]=0
Scalar s2(0, 255, 0); // 3个参数:s2[0]=0, s2[1]=255, s2[2]=0, s2[3]=0
Scalar s3(10, 20, 30, 40); // 4个参数:s3[0]=10, s3[1]=20, s3[2]=30, s3[3]=40
// 2. 取值:通过 [] 索引访问(0~3)
cout << "s1[0] = " << s1[0] << ", s1[1] = " << s1[1] << endl; // 255, 0
cout << "s2[1] = " << s2[1] << ", s2[2] = " << s2[2] << endl; // 255, 0
cout << "s3[3] = " << s3[3] << endl; // 40
return 0;
}1.3.2常用构造函数
| 构造方式 | 代码示例 | 说明 |
|---|---|---|
| 空矩阵 | Mat mat; |
空矩阵,后续可通过 create() 或赋值填充数据 |
| 指定尺寸 + 类型 | Mat mat(3, 3, CV_8UC1); |
3 行 3 列、单通道 8 位无符号整型矩阵(灰度图基础)格式:CV_{位数}{类型}C{通道数}- 位数:8/16/32/64- 类型:U (无符号)/S (有符号)/F (浮点)- 通道数:1 (灰度)/2/3 (彩色)/4 |
| 指定尺寸 + 初始值 | Mat mat(5, 5, CV_8UC3, Scalar(4,5,6)); |
5 行 5 列 3 通道矩阵,所有像素初始化为 B=4、G=5、R=6 |
| 使用 Size 对象 | Mat mat(Size(4, 4), CV_8UC1); |
Size(宽, 高),等价于 4 列 4 行,更直观 |
| 直接赋值矩阵 | Mat mat = (Mat_<int>(1, 5) << 1, 2, 3, 4, 5); |
1 行 5 列整型矩阵,快速初始化固定值 |
| 对角矩阵 | Mat mat = Mat::diag(row_mat); |
由行矩阵生成对角矩阵(输入需为 1 行 N 列) |
| 深拷贝 | Mat mat2 = mat1.clone(); / mat1.copyTo(mat2); |
完全复制数据,修改 mat2 不影响 mat1 |
| 浅拷贝(ROI) | Mat roi = mat(Rect(x, y, width, height)); / Mat roi = mat(Range(y1,y2), Range(x1,x2)); |
仅创建新的矩阵头,修改 ROI 会同步修改原图 |
1.3.4Mat像素访问方式
Vec3b 是 OpenCV 库中定义的一个向量类型 ,专门用来表示3 个无符号字节(unsigned char) 的数据组合。
- 拆解命名:
Vec:Vector(向量)的缩写,代表这是一个固定长度的数组 / 向量;3:代表向量的长度是 3;b:代表数据类型是uchar(unsigned char,无符号字符型,范围 0~255)。
Vec2b:2 个无符号字节(比如灰度图的坐标 / 二维向量);Vec3f:3 个浮点型(比如表示 3D 坐标、颜色的浮点值);Vec4i:4 个整型(比如矩形的 x,y,width,height)。
| 访问方式 | 代码示例 | 适用场景 | 注意事项 |
|---|---|---|---|
at<>() 模板访问 |
单通道: uchar val = mat.at<uchar>(y, x); 3 通道: Vec3b val = mat.at<Vec3b>(y, x); uchar b = val[0], g = val[1], r = val[2]; |
零散像素读写、调试 | 顺序为 (行y, 列x),与日常 (x,y) 相反 |
| 指针访问 | uchar* row_ptr = mat.ptr<uchar>(y);``uchar val = row_ptr[x]; |
逐行遍历、批量处理 | 效率最高,适合循环处理整图 |
| 底层指针 + 步长 | *(mat.data + mat.step[0]*y + mat.step[1]*x + c) |
底层调试、特殊计算 | c 为通道索引,需理解 step 结构 |
| 迭代器 | MatIterator_<Vec3b> it = mat.begin<Vec3b>(); |
遍历所有像素 | 代码简洁,效率中等 |
- 坐标顺序 :
at(row, col)=at(y, x),切勿与图像坐标混淆,row对用y轴坐标值。 - 类型匹配:模板参数必须与矩阵实际类型一致,否则会导致未定义行为。
- 通道访问 :多通道读取后,通过
[]或.val[]访问各通道分量,OpenCV 默认通道顺序为 BGR。
1.3.5Mat的一些辅助函数
| 操作 | 代码示例 | 说明 |
|---|---|---|
| 获取尺寸 | int rows = mat.rows; int cols = mat.cols; Size sz = mat.size(); |
Size(宽, 高),即 (cols, rows) |
| 类型判断 | if (mat.type() == CV_8UC3) |
校验矩阵类型(如彩色 / 灰度) |
| 通道拆分 / 合并 | vector<Mat> channels; split(mat, channels); merge(channels, mat); |
对彩色图通道单独处理 |
| 释放数据 | mat.release(); |
释放矩阵数据,变为空矩阵 |
| 判断空矩阵 | if (mat.empty()) |
检查矩阵是否为空 |
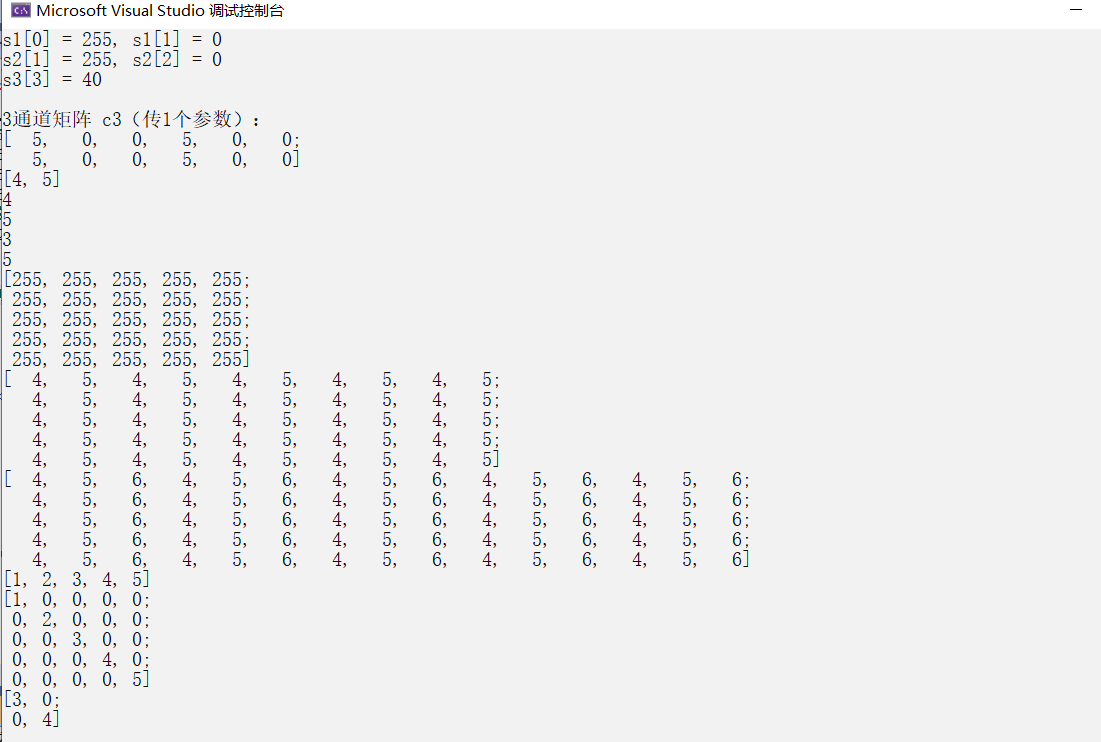
1.3.6测试举例
cpp
void testMatDefine()
{
// 1. 构造 Scalar(支持1~4个参数)
Scalar s1(255); // 1个参数:s1[0]=255, s1[1]=0, s1[2]=0, s1[3]=0
Scalar s2(0, 255, 0); // 3个参数:s2[0]=0, s2[1]=255, s2[2]=0, s2[3]=0
Scalar s3(10, 20, 30, 40); // 4个参数:s3[0]=10, s3[1]=20, s3[2]=30, s3[3]=40
// 2. 取值:通过 [] 索引访问(0~3)
cout << "s1[0] = " << s1[0] << ", s1[1] = " << s1[1] << endl; // 255, 0
cout << "s2[1] = " << s2[1] << ", s2[2] = " << s2[2] << endl; // 255, 0
cout << "s3[3] = " << s3[3] << endl; // 40
system("color F0");//背景变白
Mat a(3, 3, CV_8UC1);
Mat b(Size(4, 4), CV_8UC1);
Mat c0(5, 5, CV_8UC1, Scalar(255));//1通道
Mat c1(5, 5, CV_8UC2, Scalar(4, 5, 6));//2通道 第三个6会丢掉
Mat c2(5, 5, CV_8UC3, Scalar(4, 5, 6));//3通道
// 参数数 < 通道数(不足补0)
Mat c3(2, 2, CV_8UC3, Scalar(5));
cout << "\n3通道矩阵 c3(传1个参数):\n" << c3 << endl; // 每个像素是 (5,0,0)
//1行5列阵
Mat d = (cv::Mat_<int>(1, 5) << 1, 2, 3, 4, 5);
Mat e = Mat::diag(d);//对角阵需要行矩阵初始化
Mat f = Mat(e, Range(2, 4), Range(2, 4));
Vec2b vc1 = c1.at<Vec2b>(2, 3);//Vec2b Vec一维 2通道b是unsigned char Vec2i Vec3d
cout << vc1 << endl;
cout << (int)vc1[0] << endl;
cout << (int)vc1.val[1] << endl;
cout << (int)(d.at<int>(0, 2)) << endl;
cout << (int)(*(c2.data + c2.step[0] * 1 + c2.step[1] * 2 + 1)) << endl;
//(int)(*(c.data + c.step[0]*x + c.step[1]*y + z))
cout << c0 << endl;
cout << c1 << endl;
cout << c2 << endl;
cout << d << endl;
cout << e << endl;
cout << f << endl;
}
二、矩阵的运算
2.1矩阵运算方法
| 运算类型 | 操作 / 函数 | 语法示例 | 核心规则 / 注意事项 |
|---|---|---|---|
| 矩阵加减 | + / - |
Mat res = a + b; Mat res = a - b; |
1. a、b 必须尺寸、通道数、数据类型完全一致 2. 逐元素加减,结果维度与原矩阵一致 |
| 矩阵与标量加减 | + / - |
Mat res = a + 5; Mat res = a - 2.0; |
标量与矩阵每个元素逐元素运算 标量可以是整数 / 浮点数,矩阵类型会自动适配 |
| 矩阵标量乘 | * |
Mat res = 3 * a; Mat res = a * 2.5; |
标量与矩阵每个元素逐元素相乘 |
| 矩阵标量除 | / |
Mat res = a / 2; Mat res = a / 3.0; |
1. 标量建议用浮点数(如 2.0)避免整数除法截断 2. 逐元素相除 |
| 逐元素相乘 | mul() |
Mat res = a.mul(b); |
1. a、b 尺寸 / 类型 / 通道数必须一致 2. 对应位置元素相乘(≠ 线性代数矩阵乘法) |
| 线性代数矩阵乘法 | * / gemm() / mulTransposed() |
Mat res = a * b; gemm(a, b, 1, Mat(), 0, res); |
1. 要求:a 的列数 = b 的行数 2. a*b 仅适用于单通道矩阵 3. 多通道用 gemm 更稳定 |
| 矩阵除法 | divide() / / |
Mat res; divide(a, b, res); Mat res = a / b; |
1. divide() 是逐元素相除(推荐) 2. 避免除数为 0,建议先做非零判断 |
| 矩阵幂运算 | pow() |
Mat res; pow(a, 2, res); |
1. 对矩阵每个元素做幂运算(如 2 表示平方) 2. 支持浮点数幂(如 0.5 表示开方) |
| 矩阵绝对值 | abs() |
Mat res = abs(a); |
对矩阵每个元素取绝对值,适用于负数运算结果处理 |
| 矩阵点积 | dot() |
double res = a.dot(b); |
1. a、b 必须是单通道且尺寸相同 2. 返回所有元素相乘后求和的标量(线性代数点积) |
| 矩阵转置 | t() |
Mat res = a.t(); |
1. 单通道矩阵:行列互换 2. 多通道矩阵:每个通道独立转置 |
| 矩阵求逆 | inv() |
Mat res = a.inv(); |
1. 仅适用于方阵(行数 = 列数) 2. 要求矩阵可逆(行列式≠0),否则会报错 |
| 矩阵求和 | sum() |
Scalar res = sum(a); |
1. 单通道:返回 Scalar (总和,0, 0, 0) 2. 多通道:Scalar 每个值对应一个通道的总和 |
| 矩阵比较运算 | compare() / >/</== |
Mat res = (a > 10); compare(a, b, res, CMP_EQ); |
1. 逐元素比较,返回8 位单通道矩阵 2. 满足条件的元素值为 255,否则为 0 |
- 基础加减乘除(
+/-/*//)默认是逐元素运算,需保证矩阵维度 / 类型匹配; - 线性代数矩阵乘法优先用
a*b(单通道)或gemm()(多通道),注意行列数匹配规则; - 实用函数(
sum()/abs()/pow())是开发中高频操作,优先用 OpenCV 内置函数而非手动遍历,效率更高。
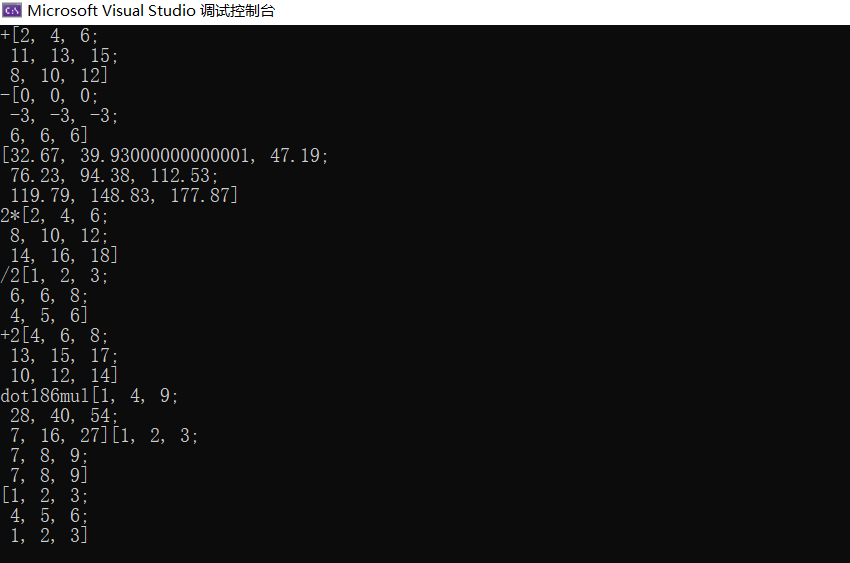
2.2矩阵运算举例
cpp
void testMatYunSuan()
{
Mat a = (Mat_<int>(3, 3)<< 1, 2, 3, 4, 5, 6, 7, 8, 9);
Mat b = (Mat_<int>(3, 3) << 1, 2, 3, 7, 8, 9, 1, 2, 3);
Mat a1 = (Mat_<double>(3, 3) << 1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7, 8.8, 9.9);
Mat b1 = (Mat_<double>(3, 3) << 1.1, 2.2, 3.3, 7.7, 8.8, 9.9,4.4, 5.5, 6.6 );
Mat c = a + b; cout <<"+"<< c << endl;
Mat d = a - b; cout <<"-"<< d << endl;
//Mat e = a * b; cout << a * b << endl; *只能是浮点
Mat e = a1 * b1; cout <<e << endl;
Mat f = 2 * a; cout <<"2*"<< f << endl;
Mat g = c / 2; cout << "/2"<<g << endl;
Mat h = c + 2 ; cout <<"+2"<<h << endl;
cout << "dot"<<a.dot(b);
cout << "mul"<<a.mul(b);
cout << cv::max(a, b) << endl;//每个元素取最大值
cout<<cv::min(a, b) << endl;
}