目录
- [1. 为什么Memory Network如此重要?](#1. 为什么Memory Network如此重要?)
- [2. Memory Networks vs 传统RNN/LSTM](#2. Memory Networks vs 传统RNN/LSTM)
- [3. 原始Memory Networks(2014,非端到端)](#3. 原始Memory Networks(2014,非端到端))
- [4. End-to-End Memory Networks(MemN2N)核心详解](#4. End-to-End Memory Networks(MemN2N)核心详解)
- 4.1 单跳(Single Hop)完整架构
- 4.2 输入编码(Embedding + Position Encoding + Temporal Encoding)
- 4.3 Attention机制推导
- 4.4 多跳(Multi-Hop)推理过程
- [5. 数学公式完整推导](#5. 数学公式完整推导)
- [6. PyTorch完整可运行代码(单跳 + 3-Hop + PE + TE)](#6. PyTorch完整可运行代码(单跳 + 3-Hop + PE + TE))
- [7. bAbI数据集实验复现与结果分析](#7. bAbI数据集实验复现与结果分析)
- [8. 主流变体对比(DMN / Key-Value MemNN / Memformer)](#8. 主流变体对比(DMN / Key-Value MemNN / Memformer))
- [9. 局限性、为什么被Transformer取代?RAG的继承](#9. 局限性、为什么被Transformer取代?RAG的继承)
- [10. 总结 + 思考题](#10. 总结 + 思考题)
1. 为什么Memory Network如此重要?
2014-2015年,Facebook AI Research(FAIR)连续推出两篇革命性论文:
- Memory Networks (Weston et al., ICLR 2015)
- End-to-End Memory Networks (Sukhbaatar et al., NeurIPS 2015)
这是第一个真正可微分的外部记忆 + 多跳推理 框架,奠定了现代Memory-Augmented Neural Networks 和 Retrieval-Augmented Generation (RAG) 的理论基础。
它首次在bAbI数据集上实现了接近人类水平的多跳推理(3-hop以上),远超当时的LSTM。
2. Memory Network 与 RNN/LSTM 的本质区别
| 维度 | LSTM/GRU | Memory Network (MemNN) |
|---|---|---|
| 记忆方式 | 隐状态 h_t(固定维度) | 外部显式Memory(N个向量) |
| 推理方式 | 单步顺序 | 多跳(Multi-hop)注意力 |
| 长距离依赖 | 衰减严重 | 可通过多次跳跃直接访问 |
| 可解释性 | 差 | 高(可可视化attention) |
| 外部知识注入 | 困难 | 天然支持 |
4. End-to-End Memory Networks 详解(最重要章节)
4.1 单跳架构图(经典原图)
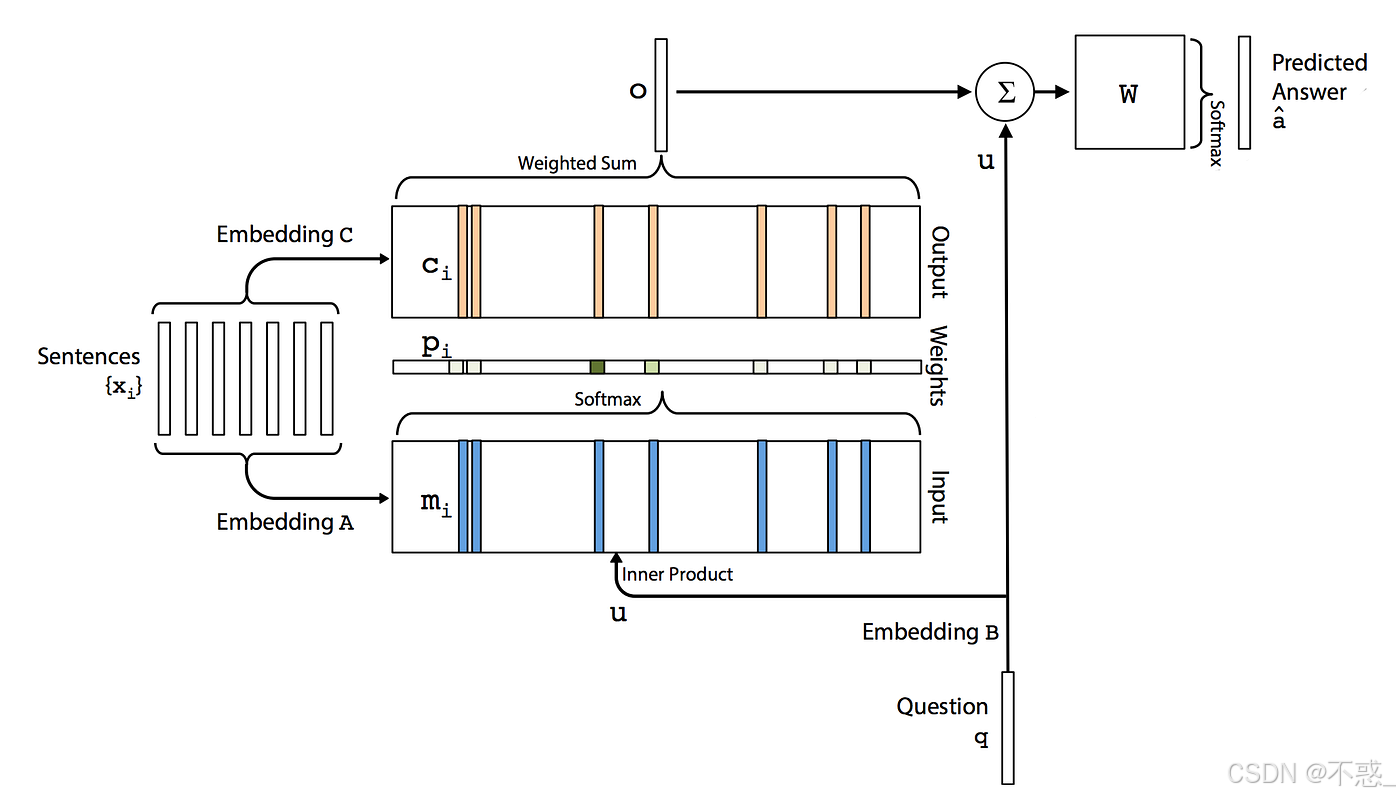
核心流程(Single Hop):
- Story → 嵌入为 Memory M(N×d)
- Question → 嵌入为 u(d维)
- Attention:p_i = softmax(u^T m_i)
- o = Σ p_i * c_i
- 最终预测:â = softmax(W (o + u))
4.2 输入模块(Input Module)进阶技巧
- Bag-of-Words(最基础)
- Position Encoding (PE) :强烈推荐!解决词序问题
P E i , j = ( 1 − i N ) ⋅ ( 1 − j d ) + i N ⋅ j d ( j 为维度 ) PE_{i,j} = (1 - \frac{i}{N}) \cdot (1 - \frac{j}{d}) + \frac{i}{N} \cdot \frac{j}{d} \quad (j \text{为维度}) PEi,j=(1−Ni)⋅(1−dj)+Ni⋅dj(j为维度) - Temporal Encoding:给每个sentence加上时间向量 T_i(可学习)
4.3 多跳(Multi-Hop)机制(最强大之处)
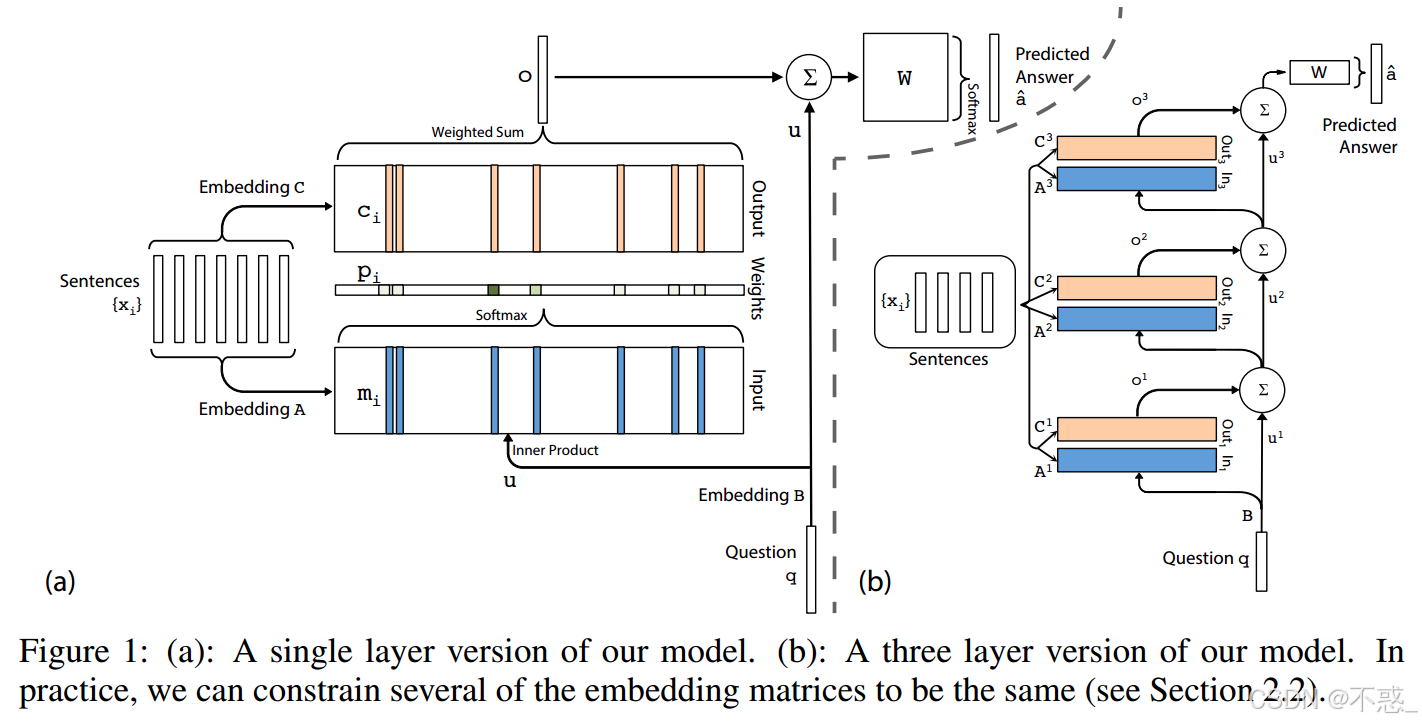
多跳更新规则 :
u k + 1 = u k + o k u^{k+1} = u^k + o^k uk+1=uk+ok
其中 o^k 是第k跳的输出向量
通常 3-hop 即可解决bAbI中绝大多数多跳任务。
5. 完整数学公式推导
设:
- Story有N个sentence,每个sentence有T个词
- Embedding维度 d = 50 或 100
嵌入矩阵:
- A, B, C, W ∈ R^{V × d} (V为词表大小)
第k跳计算 :
m i k = A k x i + T i A ( Input Memory ) m_i^k = A^k x_i + T_i^A \quad (\text{Input Memory}) mik=Akxi+TiA(Input Memory)
c i k = C k x i + T i C ( Output Memory ) c_i^k = C^k x_i + T_i^C \quad (\text{Output Memory}) cik=Ckxi+TiC(Output Memory)
p i k = softmax ( ( u k ) T m i k ) p_i^k = \text{softmax}( (u^k)^T m_i^k ) pik=softmax((uk)Tmik)
o k = ∑ i = 1 N p i k c i k o^k = \sum_{i=1}^N p_i^k c_i^k ok=i=1∑Npikcik
u k + 1 = u k + o k u^{k+1} = u^k + o^k uk+1=uk+ok
最终:
a ^ = softmax ( W ( u K + o K ) ) \hat{a} = \text{softmax}(W (u^K + o^K)) a^=softmax(W(uK+oK))
6. PyTorch完整高质量实现(推荐收藏)
python
import torch
import torch.nn as nn
import torch.nn.functional as F
class EndToEndMemoryNetwork(nn.Module):
def __init__(self, vocab_size, embed_dim=64, num_hops=3, max_sent=20):
super().__init__()
self.embed_dim = embed_dim
self.num_hops = num_hops
self.max_sent = max_sent
# Embedding (A, B, C)
self.A = nn.Embedding(vocab_size, embed_dim)
self.B = nn.Embedding(vocab_size, embed_dim)
self.C = nn.Embedding(vocab_size, embed_dim)
# 可选:Position Encoding + Temporal Encoding
self.position_encoding = self._generate_position_encoding(max_sent, embed_dim)
self.temporal_A = nn.Parameter(torch.randn(max_sent, embed_dim))
self.temporal_C = nn.Parameter(torch.randn(max_sent, embed_dim))
self.W = nn.Linear(embed_dim, vocab_size)
def _generate_position_encoding(self, max_sent, dim):
# 经典Position Encoding from paper
encoding = torch.zeros(max_sent, dim)
for i in range(max_sent):
for j in range(dim):
if j % 2 == 0:
encoding[i, j] = (1 - i / max_sent) - (j / dim) * (i / max_sent)
else:
encoding[i, j] = (1 - i / max_sent) + (j / dim) * (i / max_sent)
return nn.Parameter(encoding, requires_grad=False)
def forward(self, story, question):
# story: (batch, num_sent, num_word)
batch_size, num_sent, num_word = story.shape
# Input Memory m
m = self.A(story) # (batch, sent, word, d)
m = m.sum(dim=2) + self.position_encoding[:num_sent] + self.temporal_A[:num_sent]
# Question embedding u0
u = self.B(question).sum(dim=1) # (batch, d)
for hop in range(self.num_hops):
# Attention
u_temp = u.unsqueeze(1) # (batch, 1, d)
attn = torch.matmul(u_temp, m.transpose(1, 2)) # (batch, 1, sent)
p = F.softmax(attn.squeeze(1), dim=-1) # (batch, sent)
# Output Memory c
c = self.C(story).sum(dim=2) + self.position_encoding[:num_sent] + self.temporal_C[:num_sent]
o = torch.matmul(p.unsqueeze(1), c).squeeze(1) # (batch, d)
u = u + o # Update query vector
# Final prediction
logits = self.W(u)
return logits7. bAbI 10k 实验结果(经典数据)
| 模型 | Mean Error (%) | Failed Tasks (≤95%) |
|---|---|---|
| LSTM | 48.7 | 20 |
| MemNN (Strong Supervision) | 6.8 | 2 |
| MemN2N (1-hop) | 18.4 | 14 |
| MemN2N (3-hop) | 12.1 | 8 |
| MemN2N (3-hop + PE + TE) | 6.9 | 2 |
| DMN+ | 5.8 | 1 |
结论 :3-hop + Position Encoding + Temporal Encoding 是MemN2N的甜点配置。
9. 为什么后来被Transformer + RAG 取代?
Memory Network 的致命局限:
- Memory 固定大小(N=20~50),无法处理长文档
- 每次都全Attention,O(N) 计算开销
- 无法处理超长上下文(>512 token)
现代继承者:
- RAG:用Dense Retriever + LLM(Memory Network的精神继承者)
- Memformer / Infinite Attention
- Transformer-XL + Memory
- Longformer / Reformer
总结
End-to-End Memory Networks 是深度学习历史上第一个真正实现"可微分外部记忆 + 多跳推理" 的里程碑模型。
虽然已被Transformer时代超越,但它的思想(External Memory + Soft Attention + Multi-Hop)深刻影响了:
- RAG
- Memory-Augmented LLMs
- Agent Memory
- Knowledge Graph Reasoning
思考题(欢迎评论区讨论):
- 如果把Memory Network的Memory换成Key-Value Memory,能解决什么问题?
- 在长文档QA上,如何把MemNN思想与Sliding Window结合?
- 你觉得未来最有潜力的Memory架构是什么?
欢迎点赞 + 收藏 + 留言,我看到高赞评论会继续更新进阶版(包括Key-Value MemNN完整代码、DMN+实现、RAG vs MemNN对比实验)!
参考文献:
- End-To-End Memory Networks (Sukhbaatar et al., NeurIPS 2015)
- Memory Networks (Weston et al., ICLR 2015)
- Dynamic Memory Networks (Kumar et al., ICML 2016)