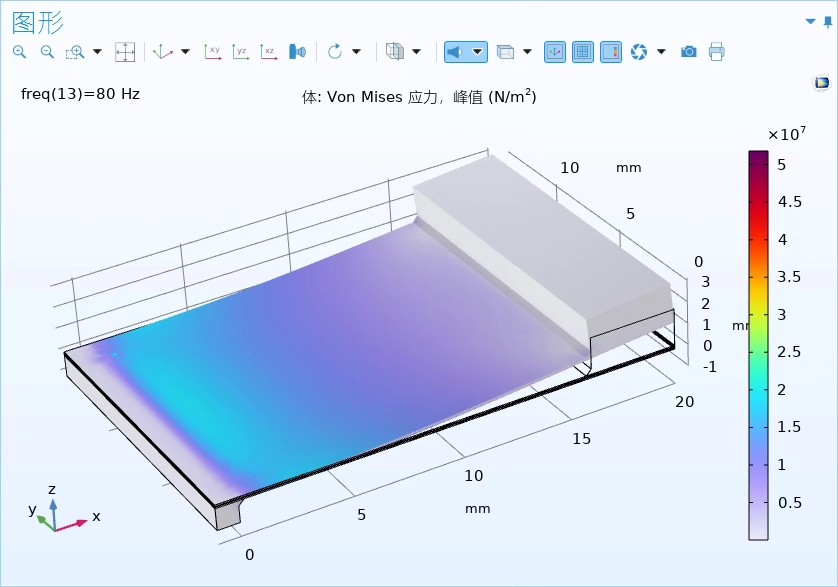
压电能量采集器三维模型：COMSOL 6.0案例探索

压电能量采集器-三维模型 COMSOL 6.0案例还原及此模型介绍如何分析一个简单的、基于悬臂梁的压电能量采集器，其中向能量采集器施加了一个正弦加速度，计算了随频率、载荷阻抗及加速度大小变化的输出功率。

最近研究压电能量采集器，用COMSOL 6.0做了相关案例还原，和大家分享下其中的乐趣与门道。

压电能量采集器基于压电材料的压电效应，简单说就是当压电材料受到机械应力时，会在材料两端产生电荷，从而实现机械能到电能的转换。在本次研究的基于悬臂梁的压电能量采集器里，悬臂梁的振动会让压电材料产生形变，进而输出电能。

在COMSOL 6.0中搭建这个三维模型，步骤不算少但逻辑清晰。首先定义材料属性，压电材料如PZT - 5H，其压电常数、弹性常数等参数得准确设置。这部分在COMSOL里可以通过材料库调用相关参数，也可以手动输入数据。

text 复制代码

// 假设这里通过手动输入部分关键压电常数
double d31 = -274e-12; // 单位：m/V，PZT - 5H的d31常数
double d33 = 593e-12; // 单位：m/V，PZT - 5H的d33常数

这里定义的d31和d33常数，分别对应压电材料在不同方向上的压电应变常数，在后续计算电场与应力应变关系时会用到。

接着设置几何结构，创建悬臂梁形状。可以通过COMSOL的几何建模工具，绘制出三维的悬臂梁。这里要注意尺寸比例准确，因为尺寸对悬臂梁的振动特性影响很大。

text 复制代码

// 假设悬臂梁长度L，宽度W，厚度T
double L = 0.05; // 单位：m
double W = 0.01; // 单位：m
double T = 0.001; // 单位：m

这些尺寸参数在后续有限元分析计算模态、振动响应等都起着关键作用。

向能量采集器施加一个正弦加速度，这是模拟实际应用中振动环境的关键。在COMSOL里，可以在"固体力学"模块中设置加速度载荷。

text 复制代码

// 定义正弦加速度函数
Function a(t) = A*sin(omega*t);
double A = 10; // 加速度幅值，单位：m/s^2
double omega = 2*pi*f; // 角频率，f为频率
double f = 50; // 频率，单位：Hz

这段代码定义了一个随时间变化的正弦加速度函数，通过调整幅值A和频率f，可以模拟不同强度和频率的振动激励。

边界条件方面，悬臂梁一端固定，模拟实际安装情况。在COMSOL里，直接在固定端设置"固定约束"即可，限制该端所有方向的位移。

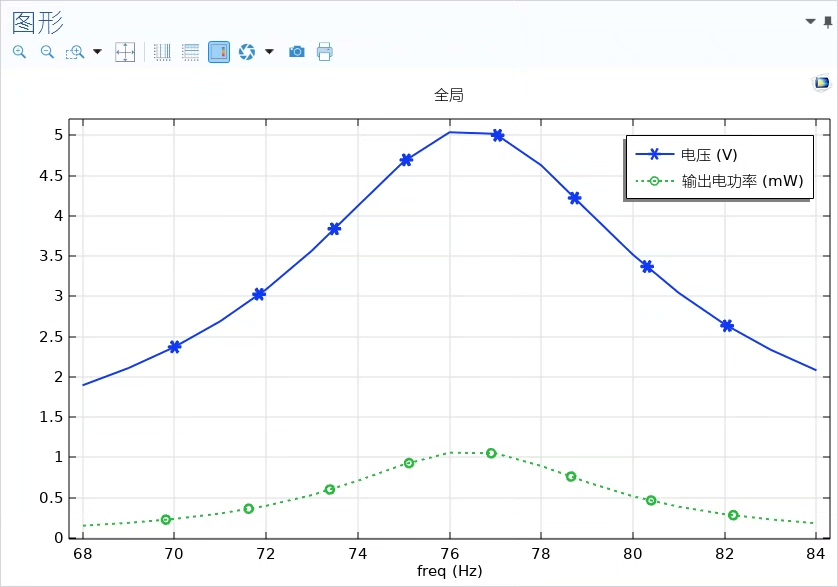
本次案例重点计算了随频率、载荷阻抗及加速度大小变化的输出功率。在COMSOL里，通过多物理场耦合，将固体力学模块与静电模块连接起来，利用压电效应的本构关系来计算输出电压，进而得到输出功率。

text 复制代码

// 计算输出功率的简化公式（假设已知输出电压V和载荷阻抗R）
double P = V*V/R;

这里通过简单的电学公式P = V² / R计算输出功率，实际在COMSOL中是通过复杂的数值计算得到准确的电压V值。通过改变频率、载荷阻抗及加速度大小这些参数，就能观察输出功率的变化情况，从而找到能量采集器的最优工作条件。

总的来说，通过COMSOL 6.0对压电能量采集器三维模型的模拟分析，能更深入理解其工作原理和性能特点，对实际应用中的设计优化有很大帮助。