题目
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 向左旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 下标 3 上向左旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
数据范围
1 <= nums.length <= 5000
-104 <= nums[i] <= 104
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104
测试用例
示例1
java
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4示例2
java
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1题解1
java
class Solution {
public int search(int[] nums, int target) {
int len = nums.length;
int l = 0;
int r = len - 1;
int mid = -1; // 用于记录旋转点(最大值)的索引
// 特殊情况处理:只有一个元素
if (len == 1) {
return nums[0] == target ? 0 : -1;
}
// --- 第一步:寻找旋转点(数组中的最大值) ---
// 目标是找到那个"断崖"点,即 nums[i] > nums[i+1] 的位置
while (l <= r) {
mid = (l + r) >> 1;
// 情况1:直接踩到了断崖边缘(mid 是最大值)
// 例如 [4, 5, 1, 2],mid 在 5,后面是 1
if ((mid + 1 < len) && (nums[mid] > nums[mid + 1])) {
break; // 找到了,mid 就是最大值索引,跳出循环
}
// 情况2:踩到了断崖的右侧(mid 是最小值,前一个就是最大值)
// 例如 [4, 5, 1, 2],mid 在 1,前面是 5
if ((mid - 1 >= 0) && (nums[mid - 1] > nums[mid])) {
mid = mid - 1; // 修正 mid 指向最大值
break; // 跳出循环
}
// 情况3:没有直接找到断崖,需要缩小范围
// 核心逻辑:判断 mid 在左半段(大数值段)还是右半段(小数值段)
if (nums[mid] >= nums[0]) {
// mid 的值大于等于起点,说明 mid 还在左半段上升区间
// 旋转点(最大值)肯定在 mid 的右边
l = mid + 1;
} else {
// mid 的值小于起点,说明 mid 已经掉落到右半段
// 旋转点(最大值)肯定在 mid 的左边
r = mid - 1;
}
}
// 循环结束后,mid 记录的是数组中最大值的索引(Pivot)
// 如果数组未旋转(如 [1, 2, 3]),mid 自然会停在最后一个元素
// --- 第二步:确定 target 所在的区间 ---
// 根据 target 和 数组起点 nums[0] 的关系,决定去 Pivot 的左边还是右边找
if (target >= nums[0]) {
// target 比起点大,说明 target 在左半段 [0, mid]
l = 0;
r = mid;
} else {
// target 比起点小,说明 target 在右半段 [mid+1, len-1]
l = mid + 1;
r = len - 1;
}
// --- 第三步:在选定的有序区间内进行标准二分查找 ---
while (l <= r) {
mid = (l + r) >> 1;
if (nums[mid] == target) {
break; // 找到了
}
if (nums[mid] > target) {
r = mid - 1;
}
if (nums[mid] < target) {
l = mid + 1;
}
}
// 返回结果:再次确认 mid 是否为目标值(处理找不到的情况)
return nums[mid] == target ? mid : -1;
}
}题解2(官解,时空同上,一次二分,多次判定)
java
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
// 1. 特殊情况处理:空数组直接返回 -1
if (n == 0) {
return -1;
}
// 2. 特殊情况处理:只有一个元素,直接比较返回
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
// 3. 定义二分查找的左右边界
int l = 0, r = n - 1;
// 4. 标准二分查找循环
while (l <= r) {
int mid = (l + r) / 2;
// 如果中间值就是要找的 target,直接返回索引
if (nums[mid] == target) {
return mid;
}
// --- 核心逻辑开始:判断哪一半是有序的 ---
// 比较 nums[0] 和 nums[mid]
// 如果 nums[0] <= nums[mid],说明 [0, mid] 这段是递增的(没有发生旋转断裂)
// 例如:[4, 5, 6, 7, 0, 1, 2],mid 在 7 的位置,左边 [4, 5, 6, 7] 是有序的
if (nums[0] <= nums[mid]) {
// 【左半边有序】的情况:
// 既然左边有序,我们就可以通过简单的比较,判断 target 是否在左边范围内
// 范围是:[nums[0], nums[mid])
if (nums[0] <= target && target < nums[mid]) {
// target 在左半边,收缩右边界
r = mid - 1;
} else {
// target 不在左半边,那它肯定在右半边(哪怕右半边是乱序的)
l = mid + 1;
}
} else {
// 【右半边有序】的情况:
// 如果 nums[0] > nums[mid],说明旋转点在左边,导致左边乱序,那么右边 [mid, n-1] 必然是有序的
// 例如:[7, 0, 1, 2, 4, 5, 6],mid 在 2 的位置,右边 [2, 4, 5, 6] 是有序的
// 既然右边有序,我们判断 target 是否在右边范围内
// 范围是:(nums[mid], nums[n-1]]
if (nums[mid] < target && target <= nums[n - 1]) {
// target 在右半边,收缩左边界
l = mid + 1;
} else {
// target 不在右半边,那它肯定在左半边
r = mid - 1;
}
}
}
// 循环结束也没找到,返回 -1
return -1;
}
}思路
这道题相比于前几道题,就稍微需要动一下脑筋了。
单从思路简单性来讲的话,博主的代码思路简单,就是先用二分找到"断崖",然后进行判断,找到target在断崖的哪一边,然后第二次二分存在target的那边即可。
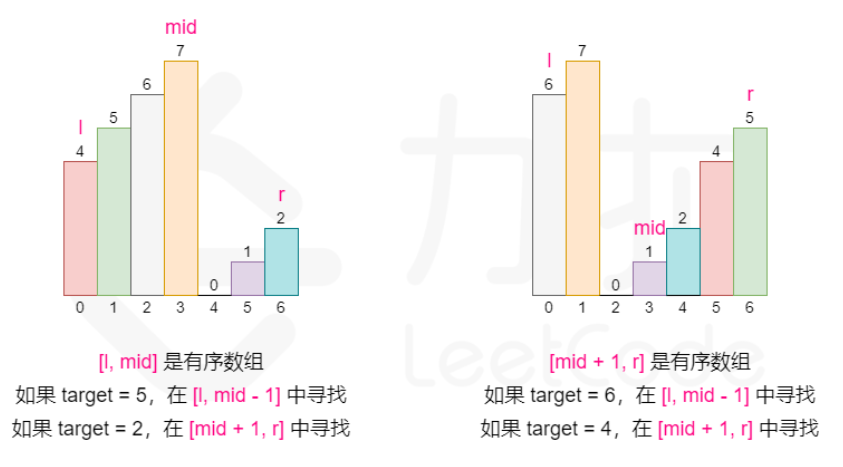
但是如果要论代码的可行性的话,还是官解更胜一筹,所有的逻辑都在二分钟处理,因为mid两边必然有有序数组,我们知道有序数组就能判定target是否在这一段,否则就在另一边。
两种方法的时空复杂度相同,根据个人习惯来把。