量子安全的Lamport One Time Signature 算法学习

学习Lamport原文链接

https://www.btcstudy.org/2025/08/25/quantum-safe-lamport-signatures/

专有名词解释和简写

原文	简写
One Time Signature	OTS

原理

前提条件

对于Lamport OTS 算法的原理，需要有一些明确的前提条件。

1. 假设Lamport 算法使用的加密算法是sha256（但实际上无论用什么hash算法都可以），后续提到的hash 即为这个算法
2. Lamport OTS 算法不考虑原文是否被加密，即对MSG的操作都是原文
3. 我们需要规定两个私钥集合A和集合B，两个集合中都含有长度为256位的256个随机数，如下图所示：

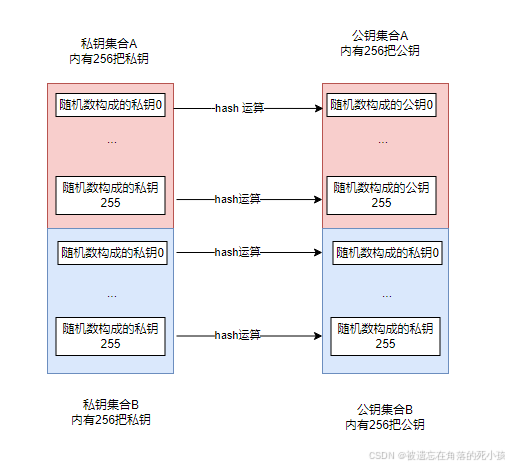
这两个集合中含有的随机数就是我们Lamport 算法的私钥，而公钥则是私钥通过hash 运算而来。因此两个私钥集合就会得到对应的两个公钥集合

工作原理

在刚才的前提条件中，我们已经讲解完了在Lamport 算法中密钥是如何生成的。简单来说只是生成了512个随机数，然后对他们做hash，就得到了我们的公钥，原本的随机数则是私钥

签名过程

先提出签名过程总体流程

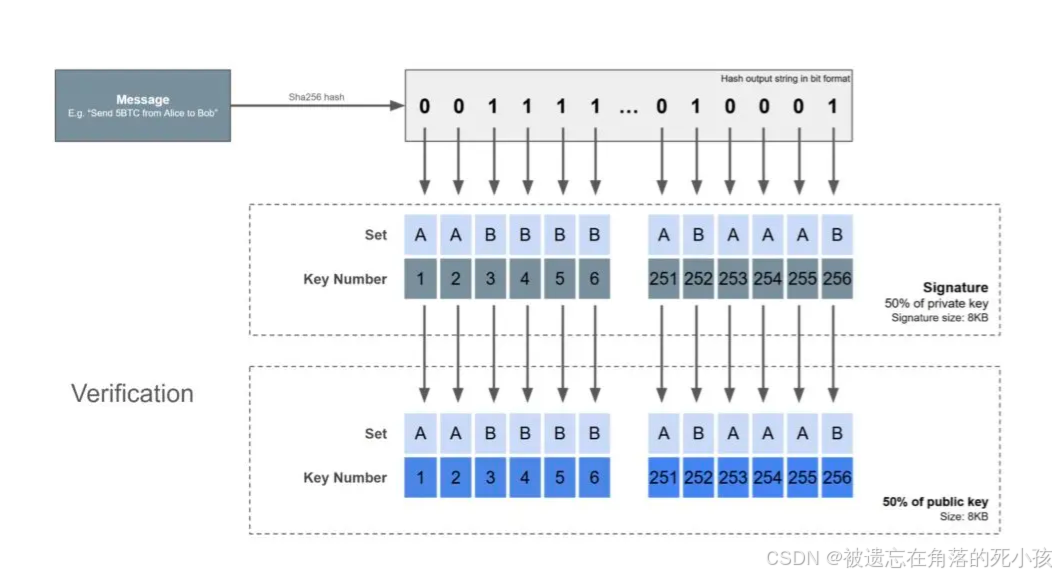
1. 将消息（msg message）进行一次hash 操作，这个操作记作h(m) ，得到输出 rslt ，rslt长度为256bit
2. 将hash 操作输出的结果rslt 视作一个0和1构成的比特流
3. 根据rslt 的比特流构成，（这里假设0对应私钥集合A，1对应私钥集合B）从两个私钥集合中取出对应序号的私钥来构成签名，每个私钥作为构成签名的一个数字（number） ，下面引用学习博客中的的一张图更直观的显示签名构建的过程
   

验签过程

1. 验签的时候，先对原本的消息M进行一次hash，得到结果table 。它的大小为256bit，结果与签名构建时的rslt相同
2. 再对签名S按照number进行划分，对每个number 做一次hash，这次操作为h(number) ，得到的结果的集合为rslt_set ，集合中的元素为h(number)
3. 这时，我们可以根据table中的bit来判断，每256bit 对应的是哪个一个集合的公钥。将rslt_set 中的元素与对应公钥集合里面的公钥对比，判断它们是否一致。如果一致，则继续往下检查，直到rslt_set中的所有元素都与公钥表中的公钥一致。

如果全都一致，则代表验签通过，否则验签失败

例如，table0（bit0） = 1，由于table = rslt_set，因此我们需要判断出rslt_set的一个元素要与公钥集合B中的第0个公钥要相同，不然的话，验签就失败了。

弊端

从原理中我们不难发现，由于签名的构造是根据私钥本身来拼凑而成的，每次验签过后，我们就会暴露出50%的私钥。等到下一次验签后，我们最多会暴露出一共75%的私钥。这样下去，我们没有暴露出的私钥就越来越少了