考研408--数据结构--day10--图的存储、基本操作和遍历

（以下内容全部出自上述课程）

图
- [1. 基本概念](#1. 基本概念)
- - [1.1 定义](#1.1 定义)
  - [1.2 应用](#1.2 应用)
  - [1.3 普通图](#1.3 普通图)
  - [1.4 顶点相关](#1.4 顶点相关)
  - [1.5 (强)连通分量](#1.5 (强)连通分量)
  - [1.6 生成树/森林](#1.6 生成树/森林)
  - [1.7 边的权](#1.7 边的权)
- [2. 特殊的图](#2. 特殊的图)
- [3. 小结](#3. 小结)
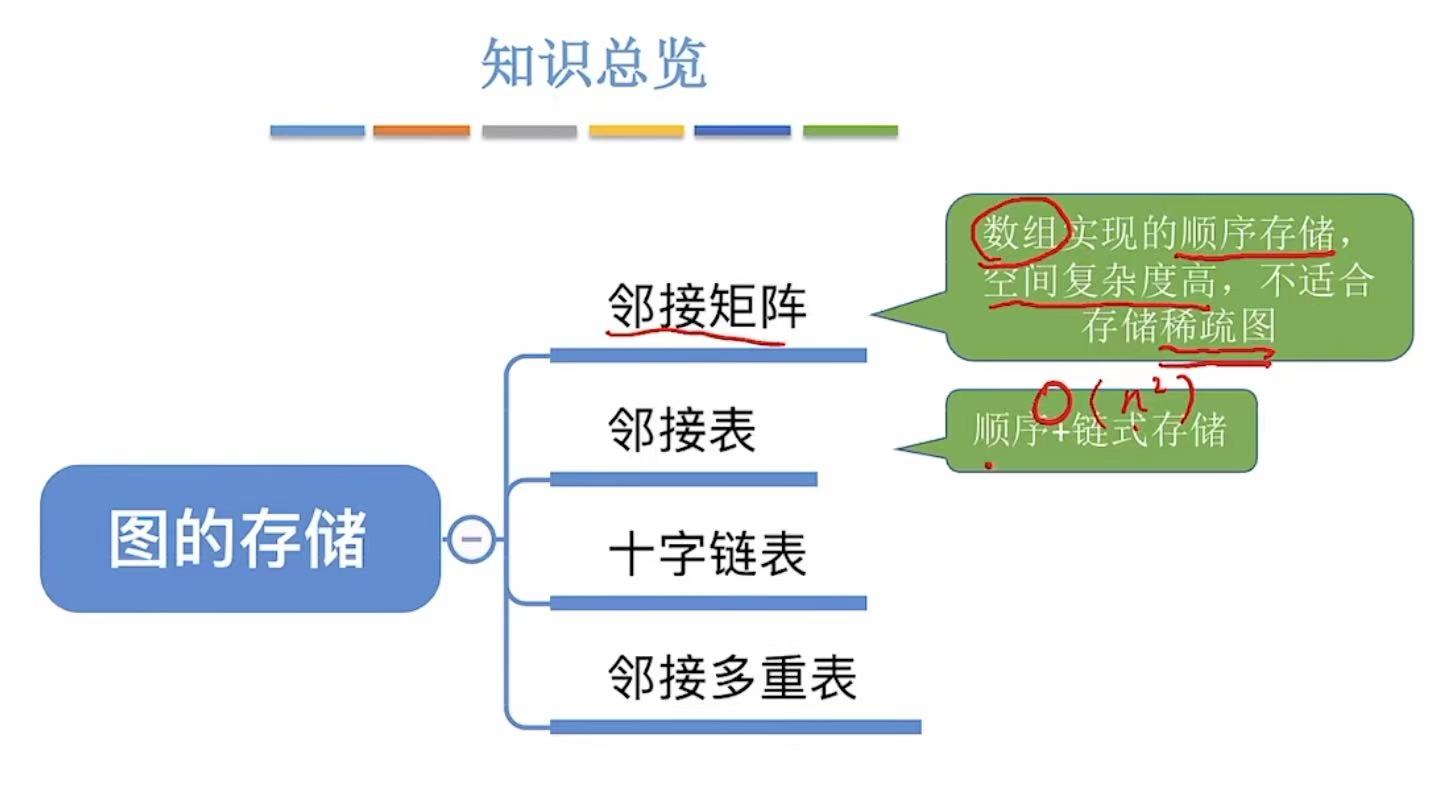
图的存储
- [1. 邻接矩阵](#1. 邻接矩阵)
- - [1.1 概念](#1.1 概念)
  - [1.2 带权图](#1.2 带权图)
  - [1.3 性能分析](#1.3 性能分析)
  - [1.4 性质](#1.4 性质)
  - [1.5 小结](#1.5 小结)
- [2. 邻接表](#2. 邻接表)
- - [2.1 概念](#2.1 概念)
  - [2.2 小结](#2.2 小结)
- [3. 十字链表法](#3. 十字链表法)
- [4. 邻接多重表](#4. 邻接多重表)
图的基本操作
- [1. Adjavent-->边存在](#1. Adjavent-->边存在)
- [2. Neighbors-->邻接边](#2. Neighbors-->邻接边)
- [3. InsertVertex-->插入点](#3. InsertVertex-->插入点)
- [4. DeleteVertex-->删除点](#4. DeleteVertex-->删除点)
- [5. RemoveEdge-->删除边](#5. RemoveEdge-->删除边)
- [6. FirstNeighbor-->第一个邻接点](#6. FirstNeighbor-->第一个邻接点)
- [7. NextNeighbor-->下一个邻接点](#7. NextNeighbor-->下一个邻接点)
- [8. 获取/设置权值](#8. 获取/设置权值)
图的遍历
- [1. 广度优先遍历（BFS）](#1. 广度优先遍历（BFS）)
- - [1.1 与树的广度优先遍历之间的联系](#1.1 与树的广度优先遍历之间的联系)
  - [1.2 代码实现](#1.2 代码实现)
  - [1.3 遍历序列](#1.3 遍历序列)
  - [1.4 最终实现](#1.4 最终实现)
  - [1.5 复杂度分析](#1.5 复杂度分析)
  - [1.6 广度优先生成树](#1.6 广度优先生成树)
  - [1.7 小结](#1.7 小结)
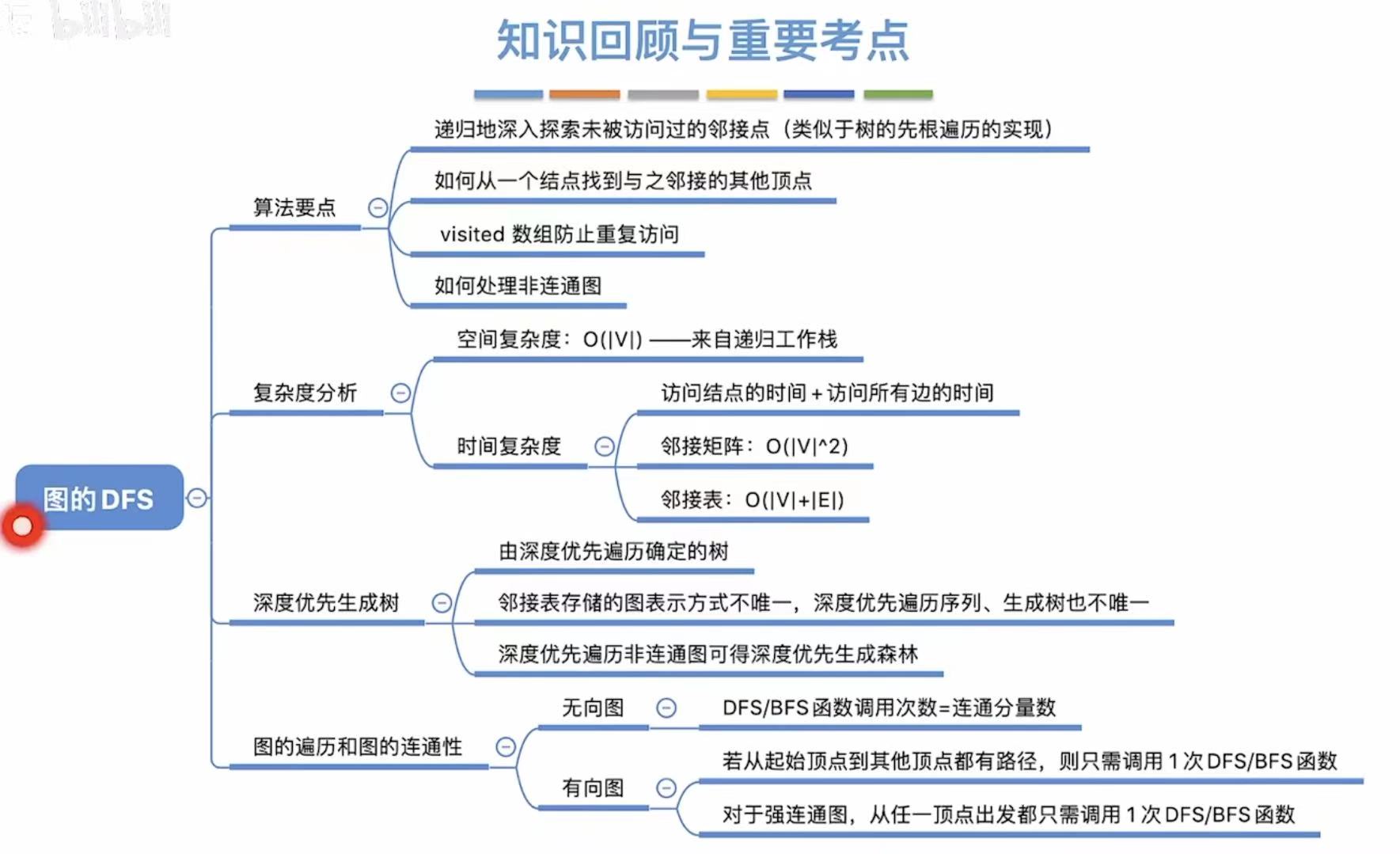
- [2. 深度优先遍历（DFS）](#2. 深度优先遍历（DFS）)
- - [2.1 概念](#2.1 概念)
  - [2.2 最终实现](#2.2 最终实现)
  - [2.3 复杂度分析](#2.3 复杂度分析)
  - [2.4 遍历序列](#2.4 遍历序列)
  - [2.5 深度优先生成树](#2.5 深度优先生成树)
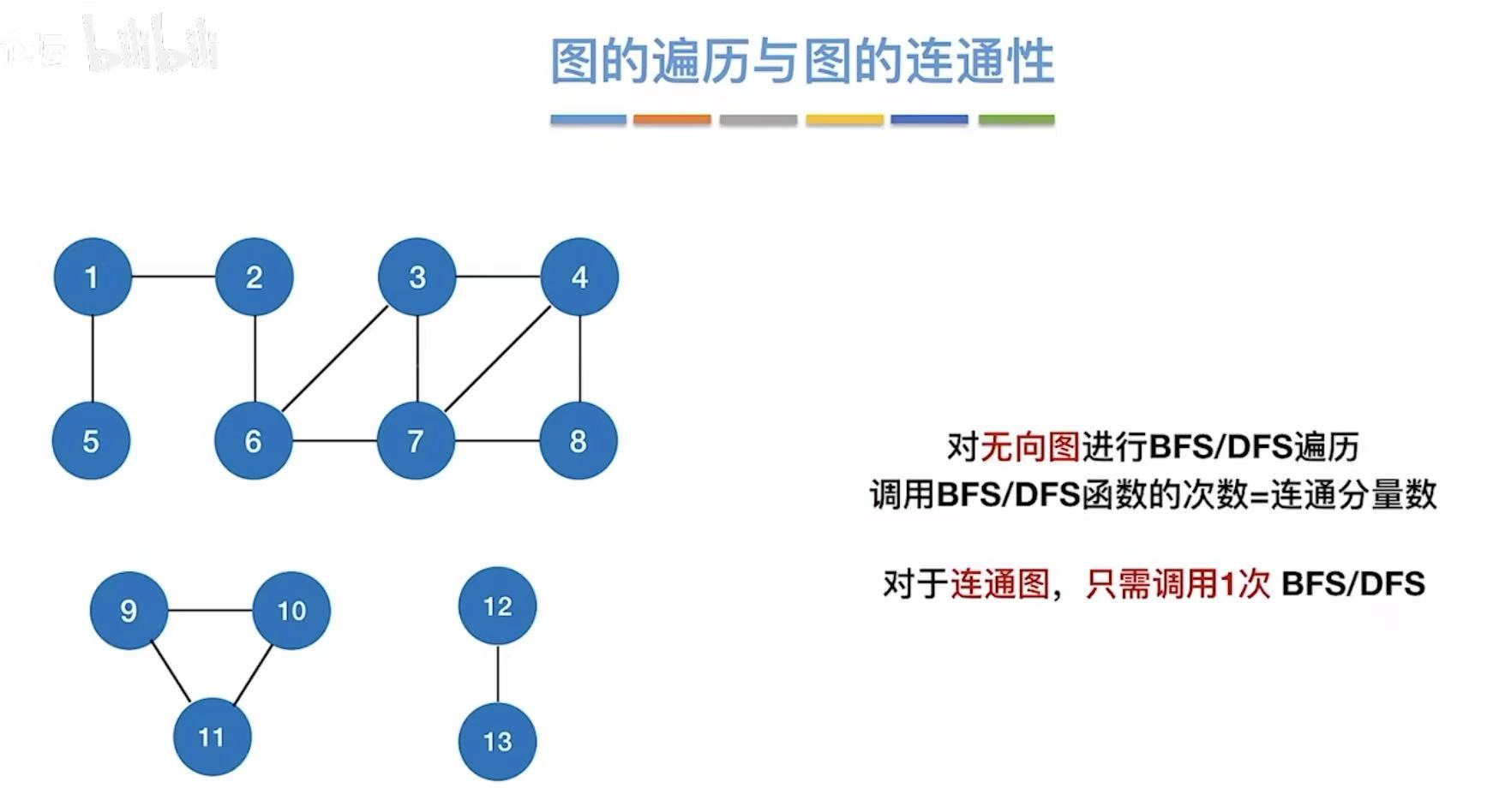
  - [2.6 图的遍历与图的连通性](#2.6 图的遍历与图的连通性)
  - [2.7 小结](#2.7 小结)

图

1. 基本概念

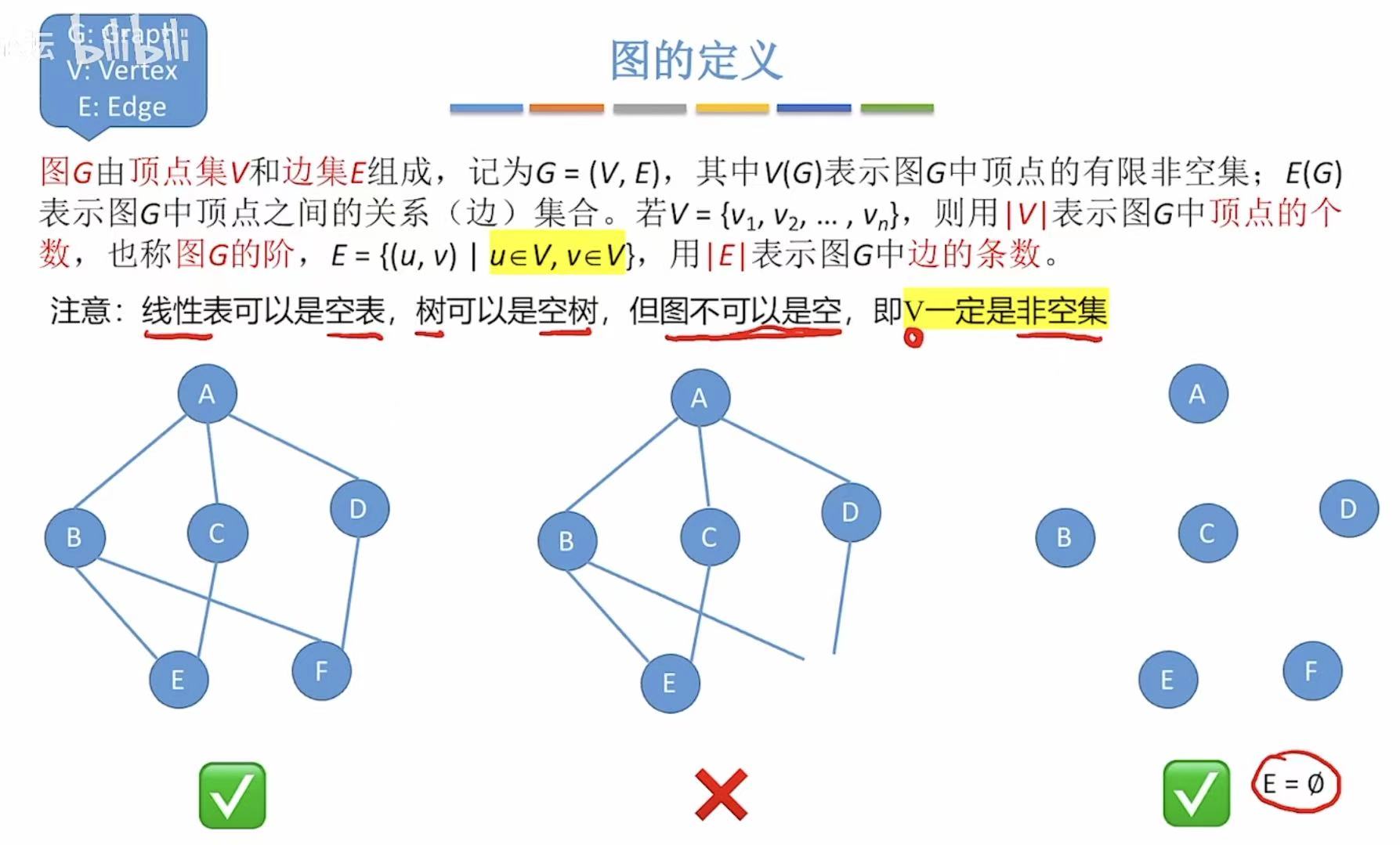
1.1 定义

图：G 顶点+边
顶点：V |V|-->顶点个数
边：E |E|-->边的个数
图可以没有边，但一定不能没有顶点。

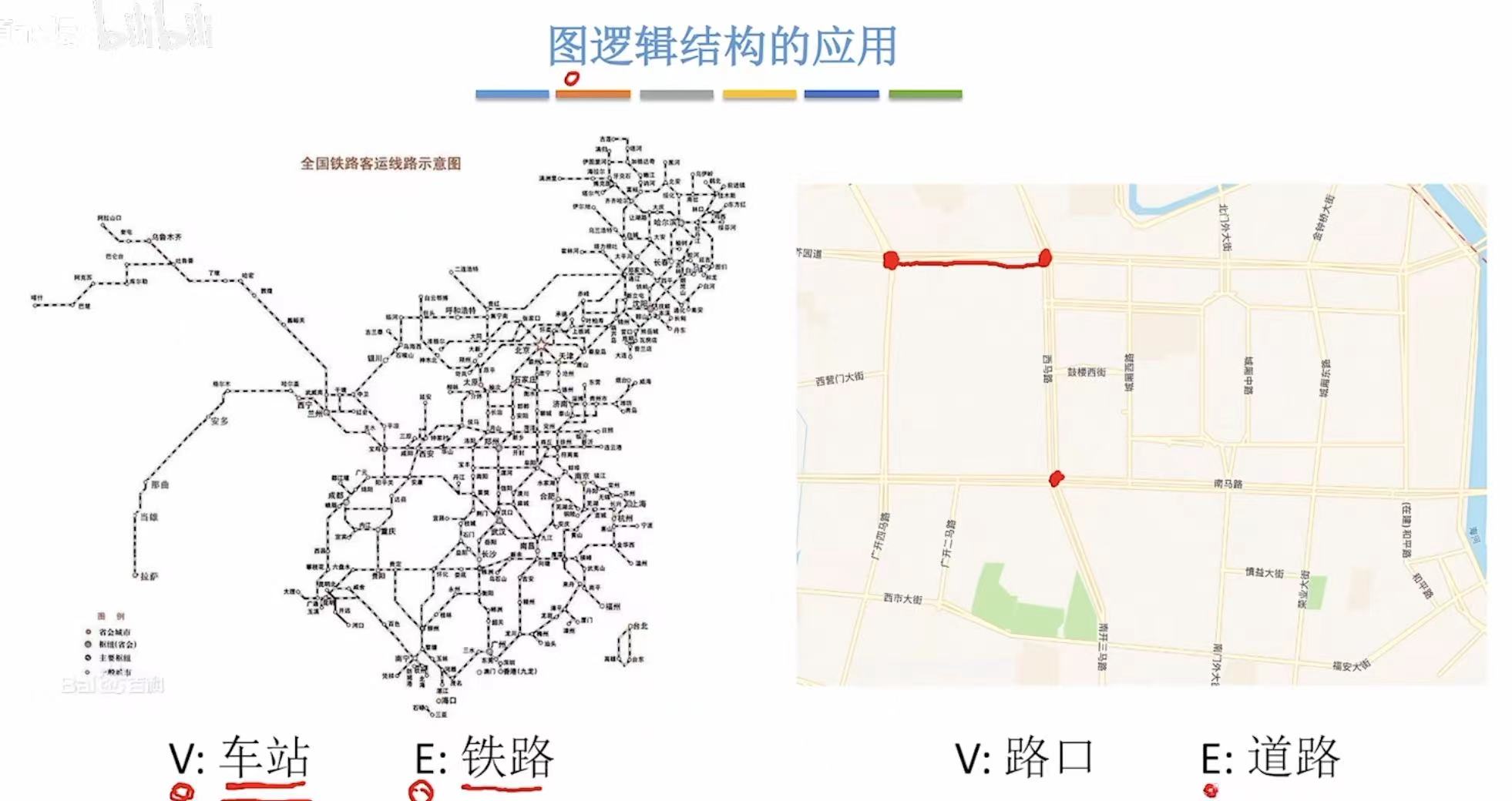
1.2 应用

图可以应用于各种线路，比如铁路和地图。
顶点相当于具体位置，边相当于道路路线。

图也可以用来表示各种关系，顶点相当于每个个体，边相当于每个人之间的关系。

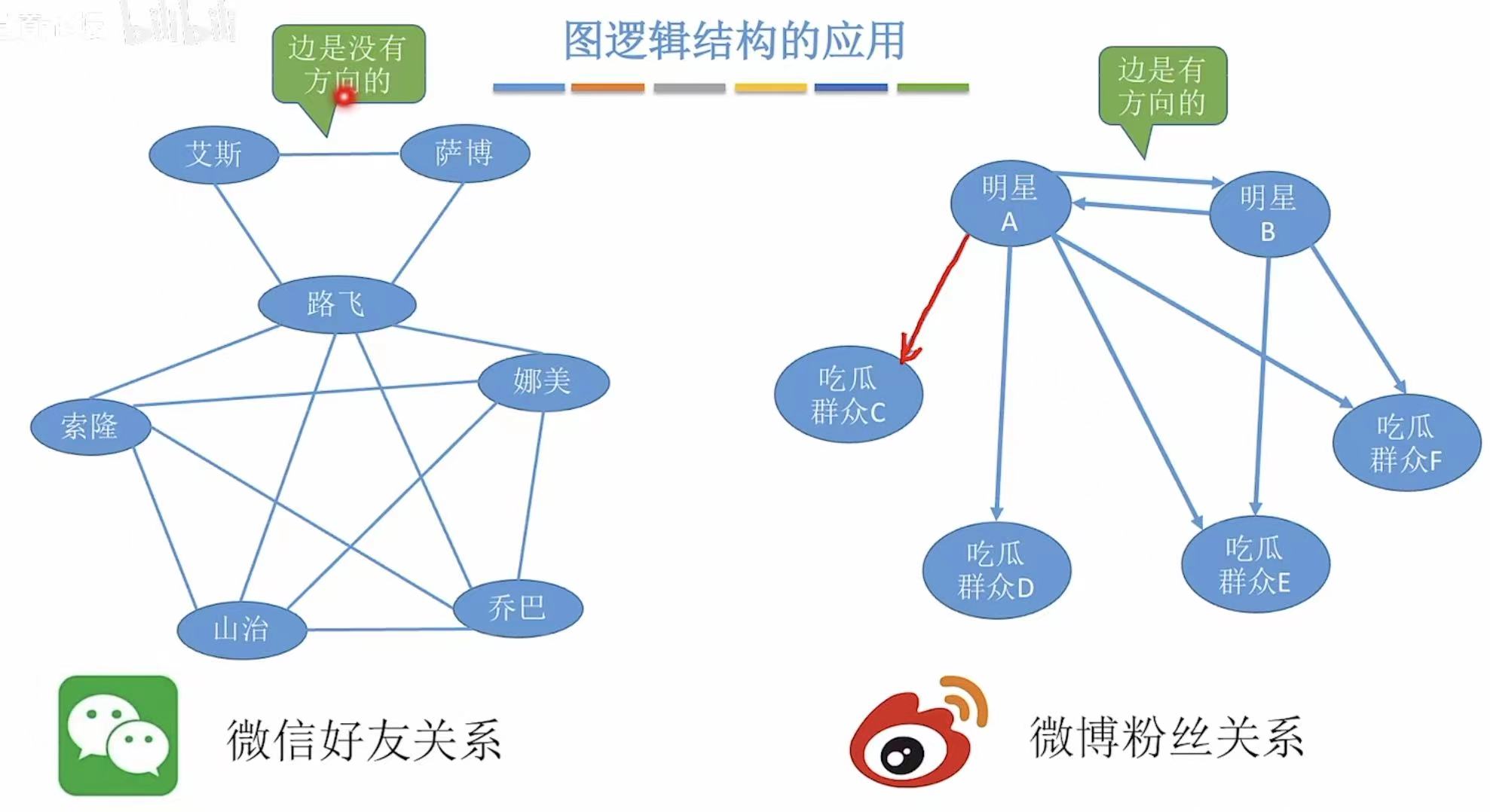
1.3 普通图

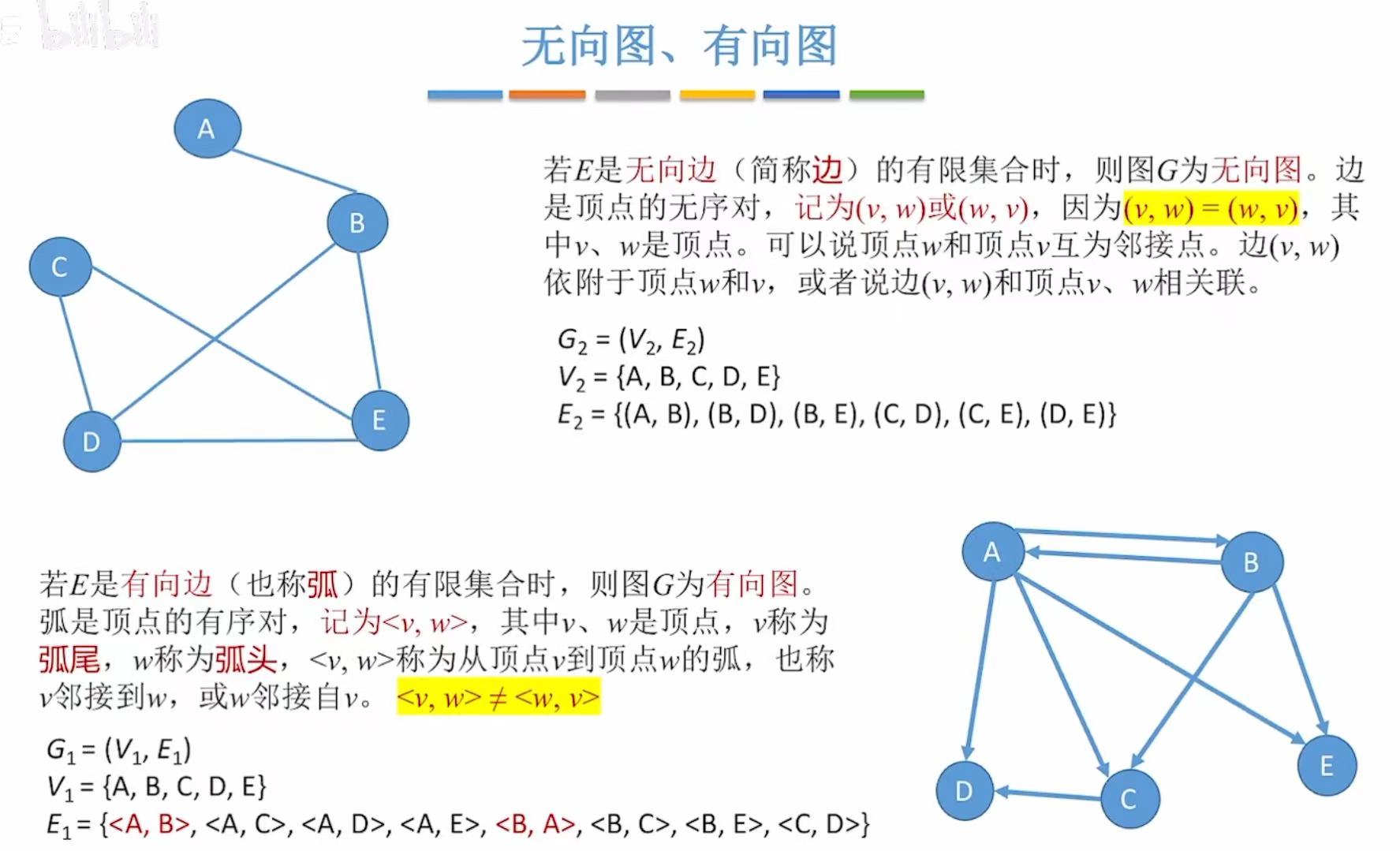
从上一个图，我们可以看出第一个图的边是没有箭头的，这就是无向图。
第二个图的边是有箭头的，这就是有向图 ，因为每个个体之间的指向是有区别的。
比如明星-->粉丝：明星的动态被关注自己的人看见，但是明星看不到粉丝的动态。
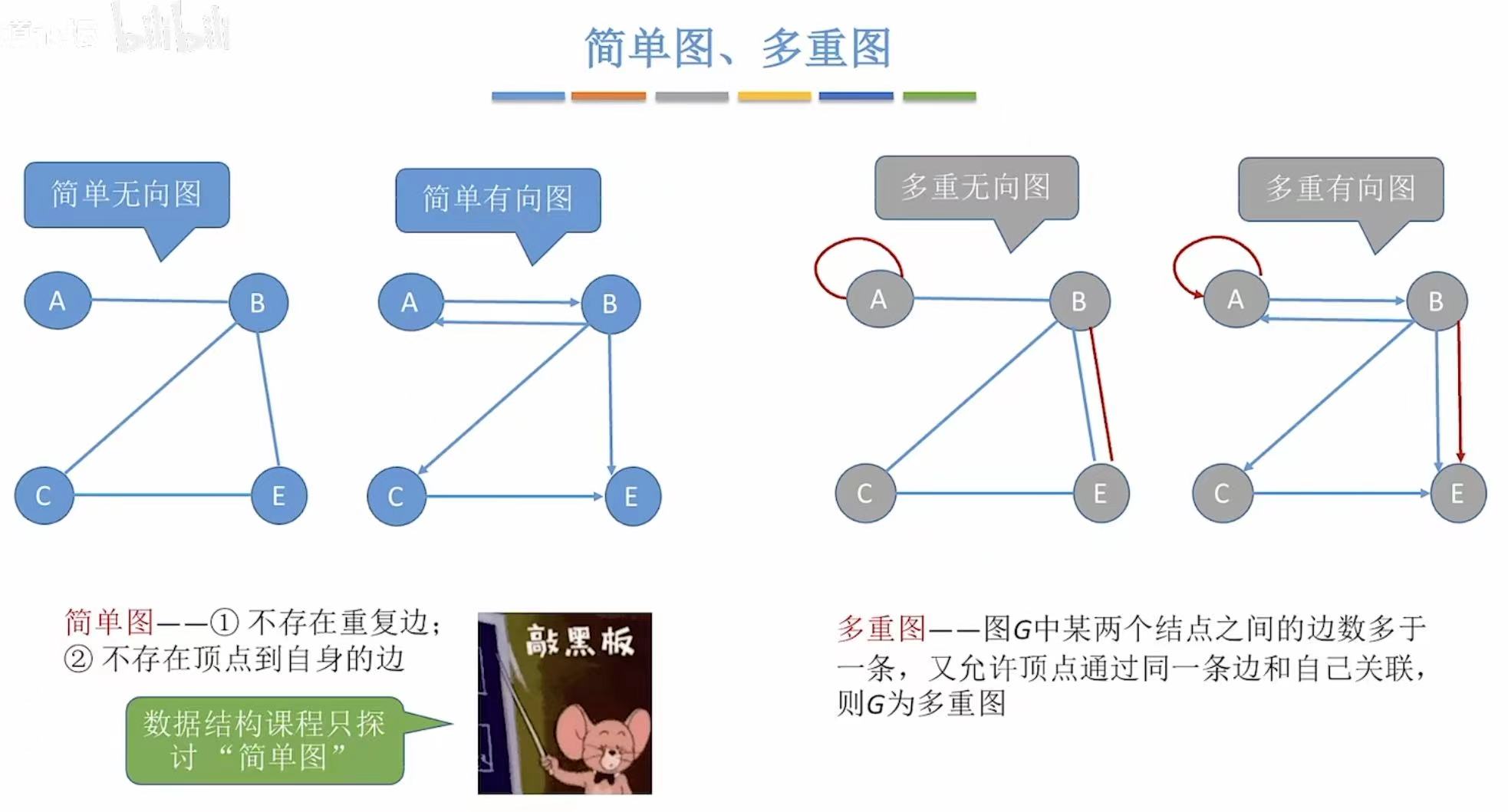
简单图：不存在重复边、不存在顶点到自身的边。
多重图：上面的都允许。
在数据结构中，我们只讨论简单图。

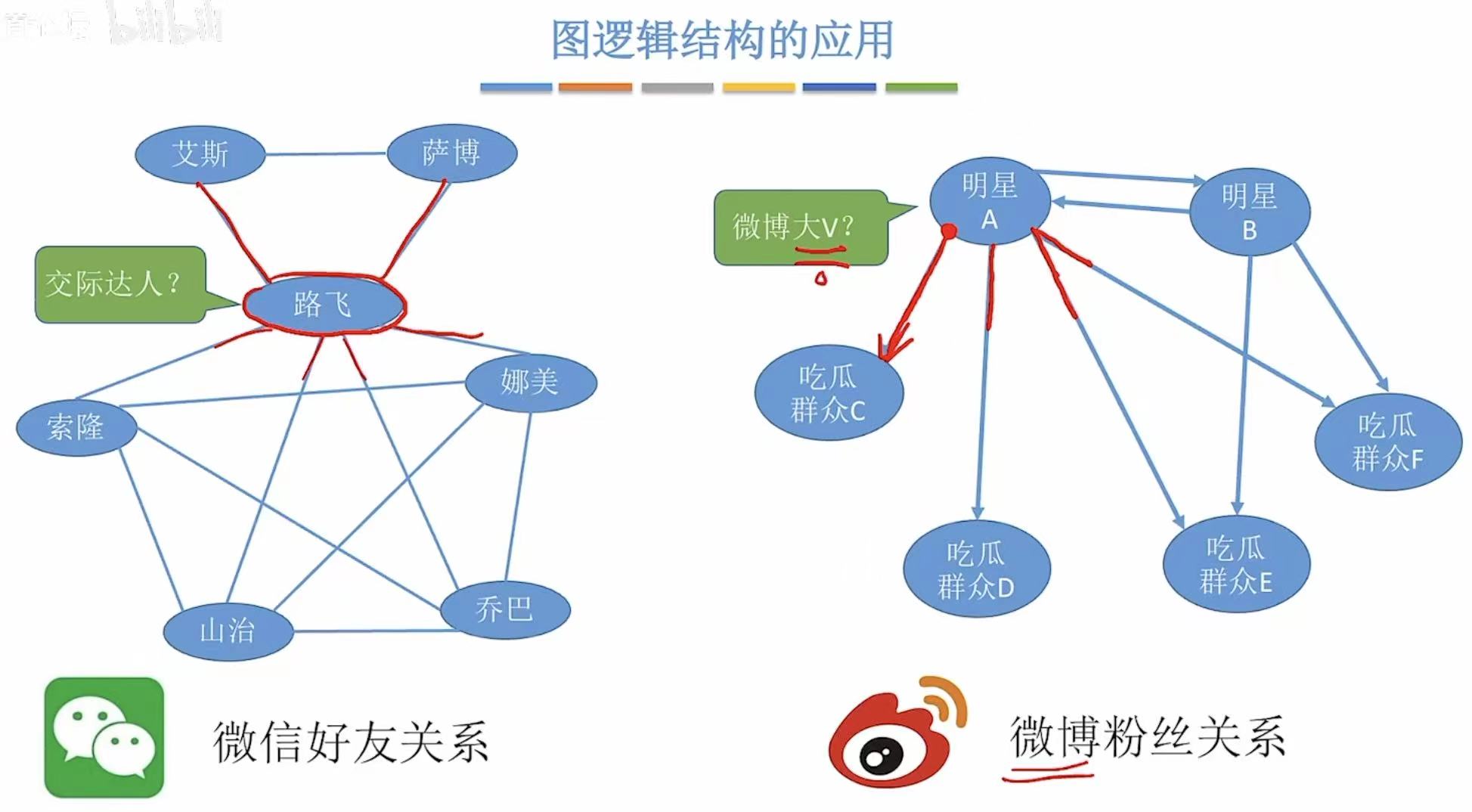
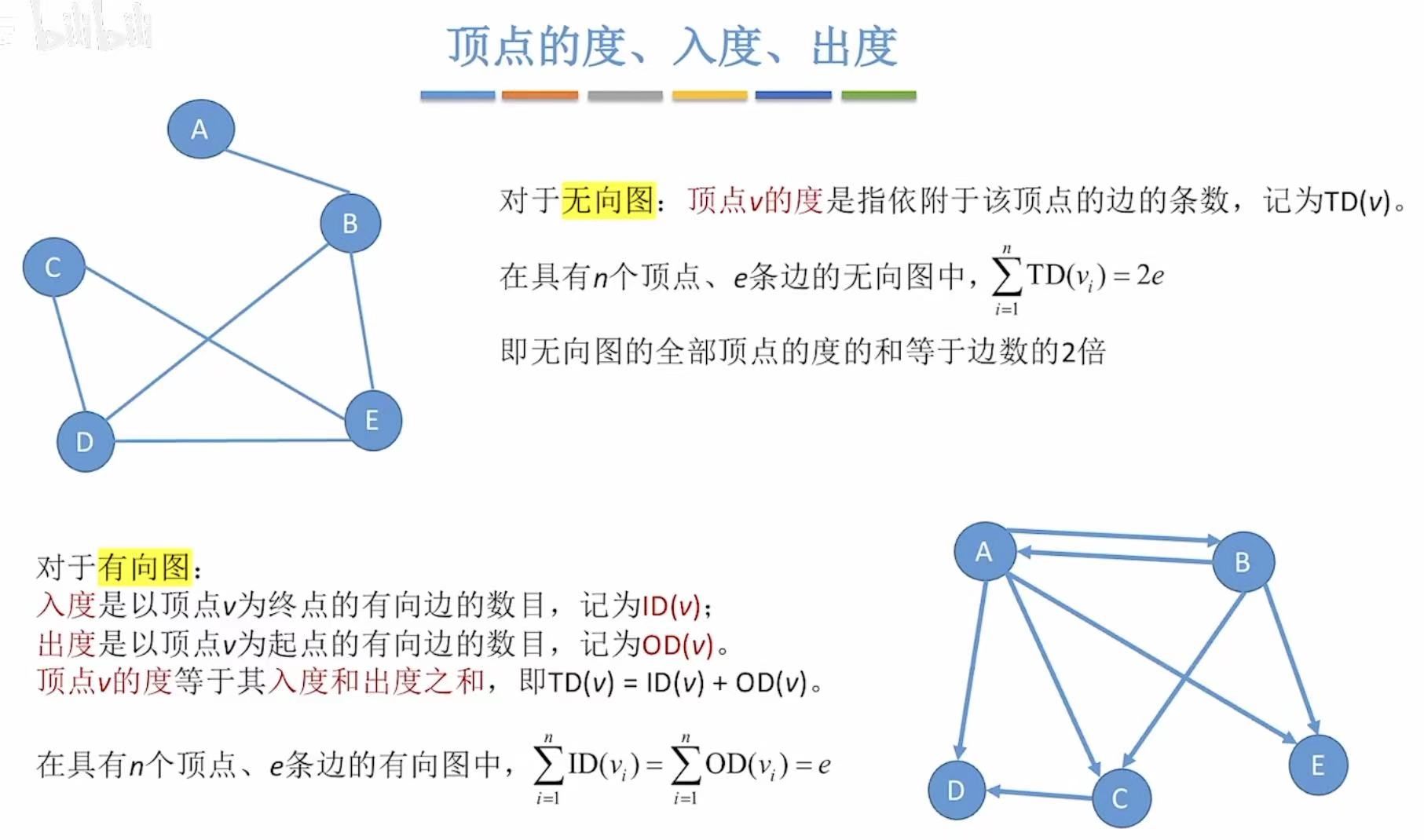
1.4 顶点相关

话说回来，那么我们应该怎样判断一个人是交际大人或者是微博大V呢？

我们就需要看这个人的顶点连接的边有的多少，这个边的条数 就叫做度。

无向图：顶点的度就是该顶点的边的条数。
有向图 ：因为是有方向的，所以又根据箭头和非箭头的两边分为入度和出度。
入度：被箭头指的点就是入度。
出度：没被箭头指的点就是出度。
顶点的度就是入度和出度的和。
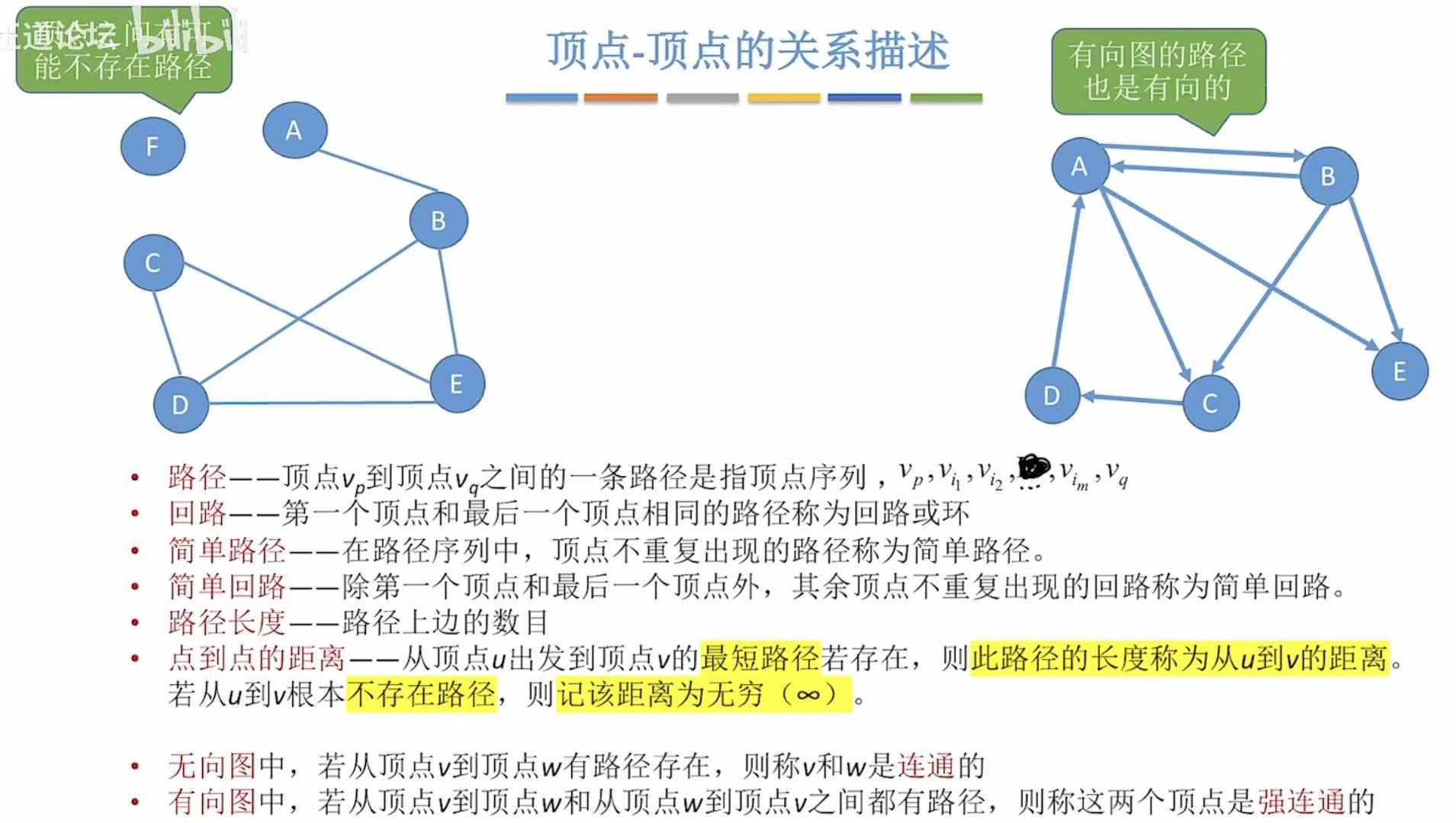
路径：比如C到E的路径-->CE、CDE、CDBE
回路：右图中的回路 ------ A ↔ B（来回）
上面举的几个例子都是简单路径/回路。
路径长度：CE的路径长度就是1.
点到点的距离：比如左图A到E的最短路径是ABE，那么点到点的距离就是2.
连通：A可以到B，就是连通。
强连通 ：A可以到B，B可以到A，就是强连通。
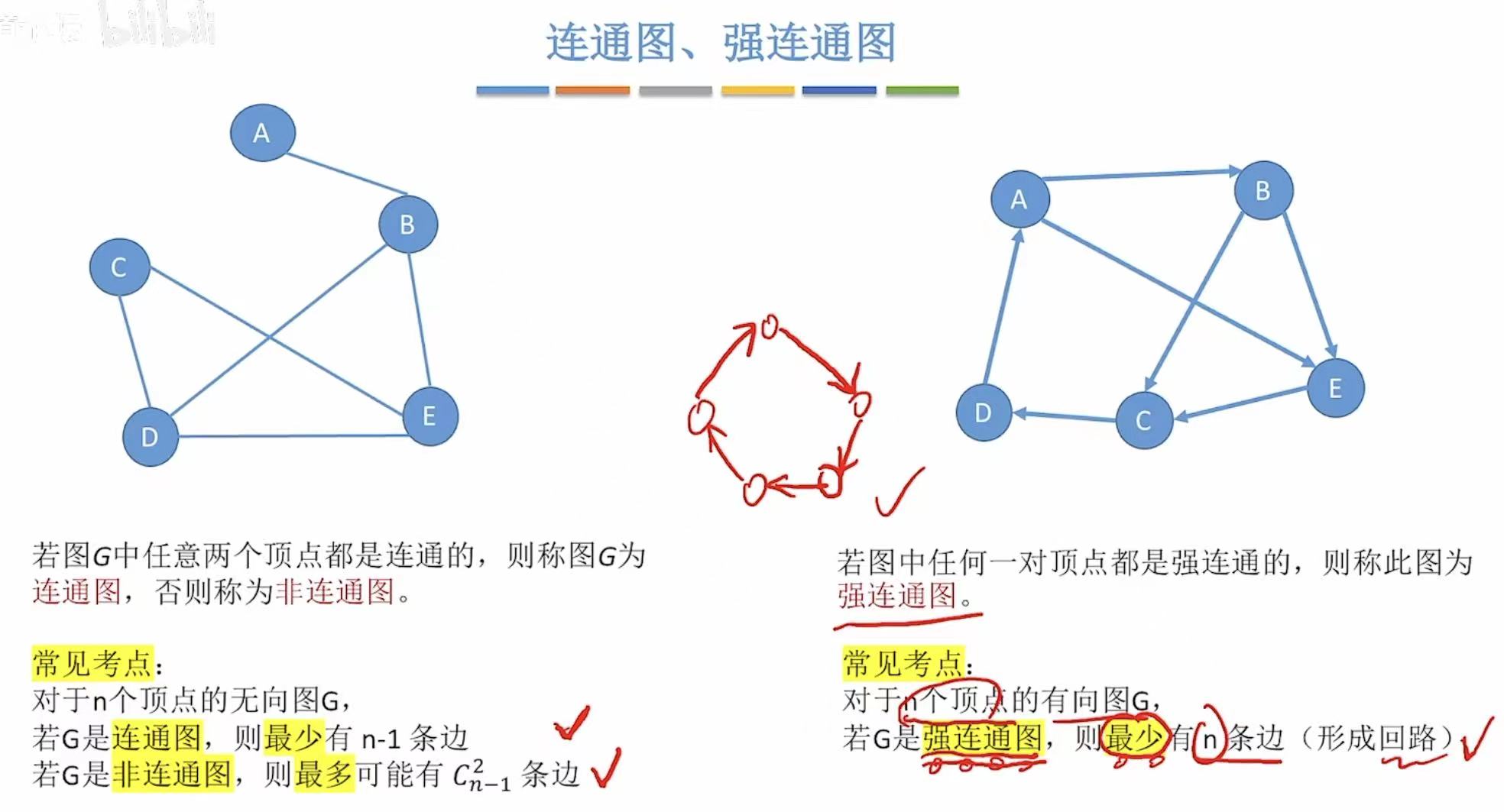
连通图：任意两点都能走得通。
强连通图 ：任意两点可以正向走得通，也可以反向走得通。

子图：从整体图上拆下来的图。老规矩，可以没边但是不能没顶点。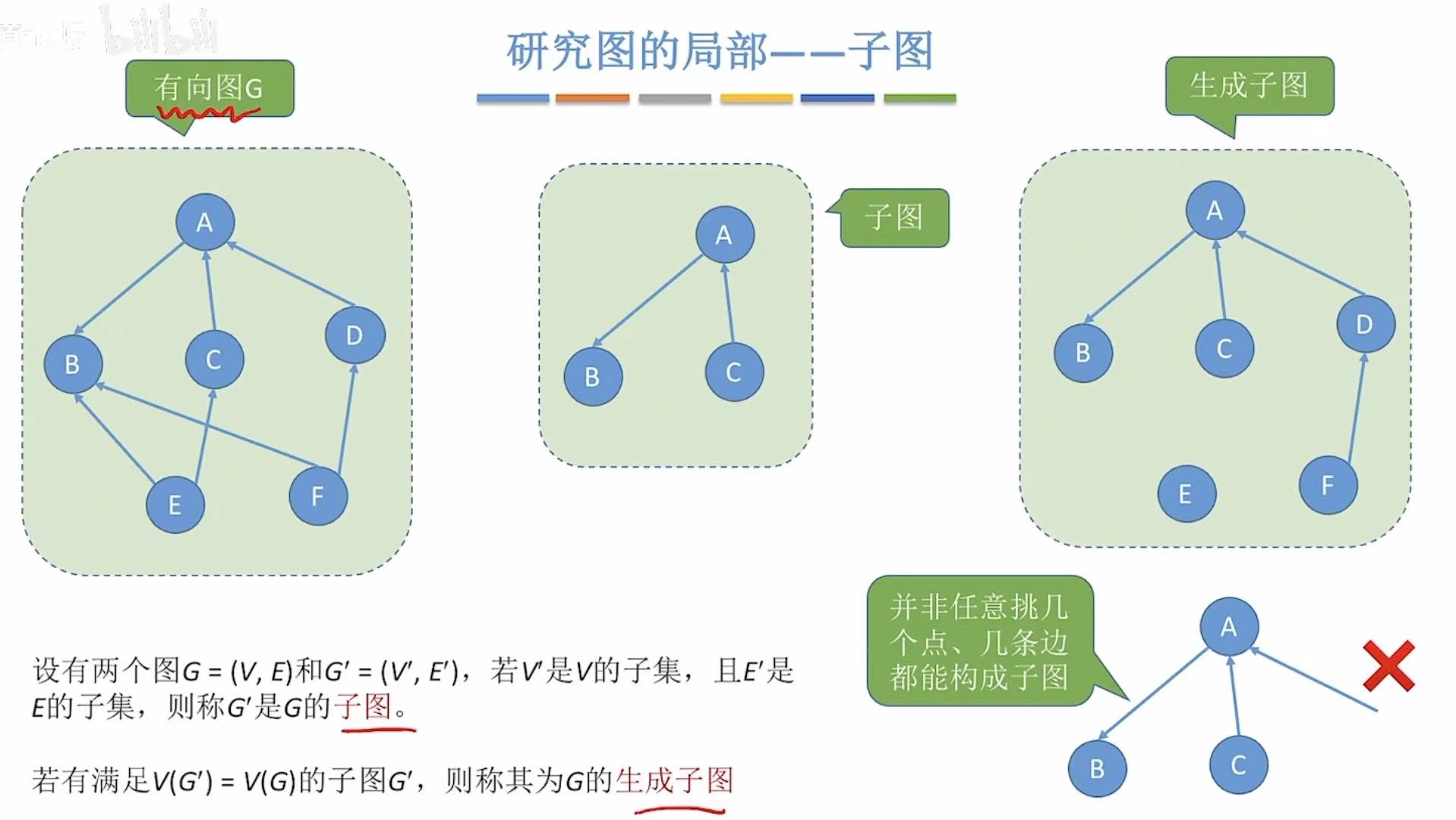

1.5 (强)连通分量

连通分量 ：几个内部全部连通的、但是外部相互之间不连通的个体。

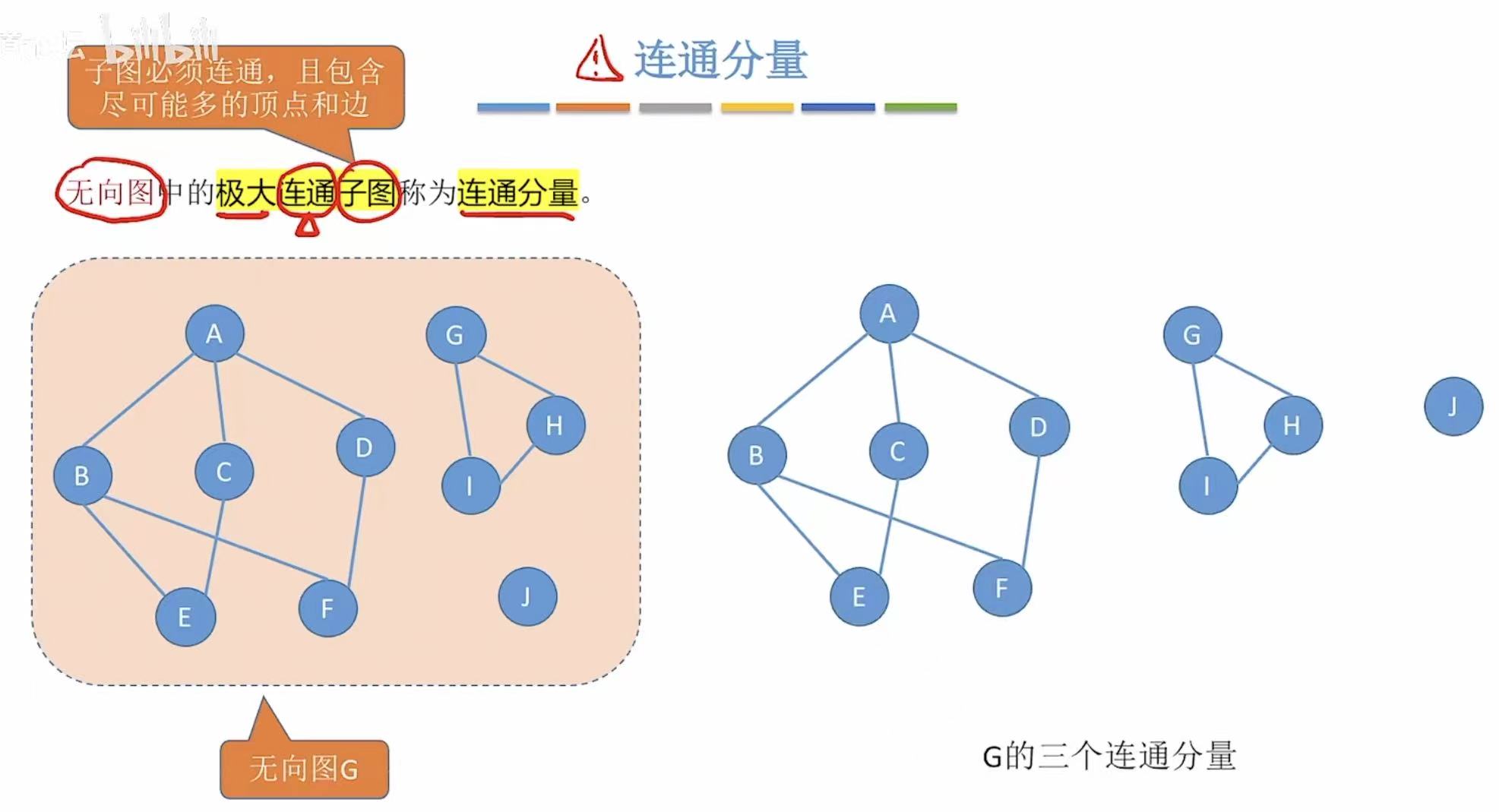
如图：

大陆之中的顶点相互之间全部连通，所以这是一个连通分量。
海南岛和台湾岛内部的顶点也是全部连通的，所以这是两个连通分量。
但是这三者之间不是相互连通的，所以这三个是独立的连通分量。

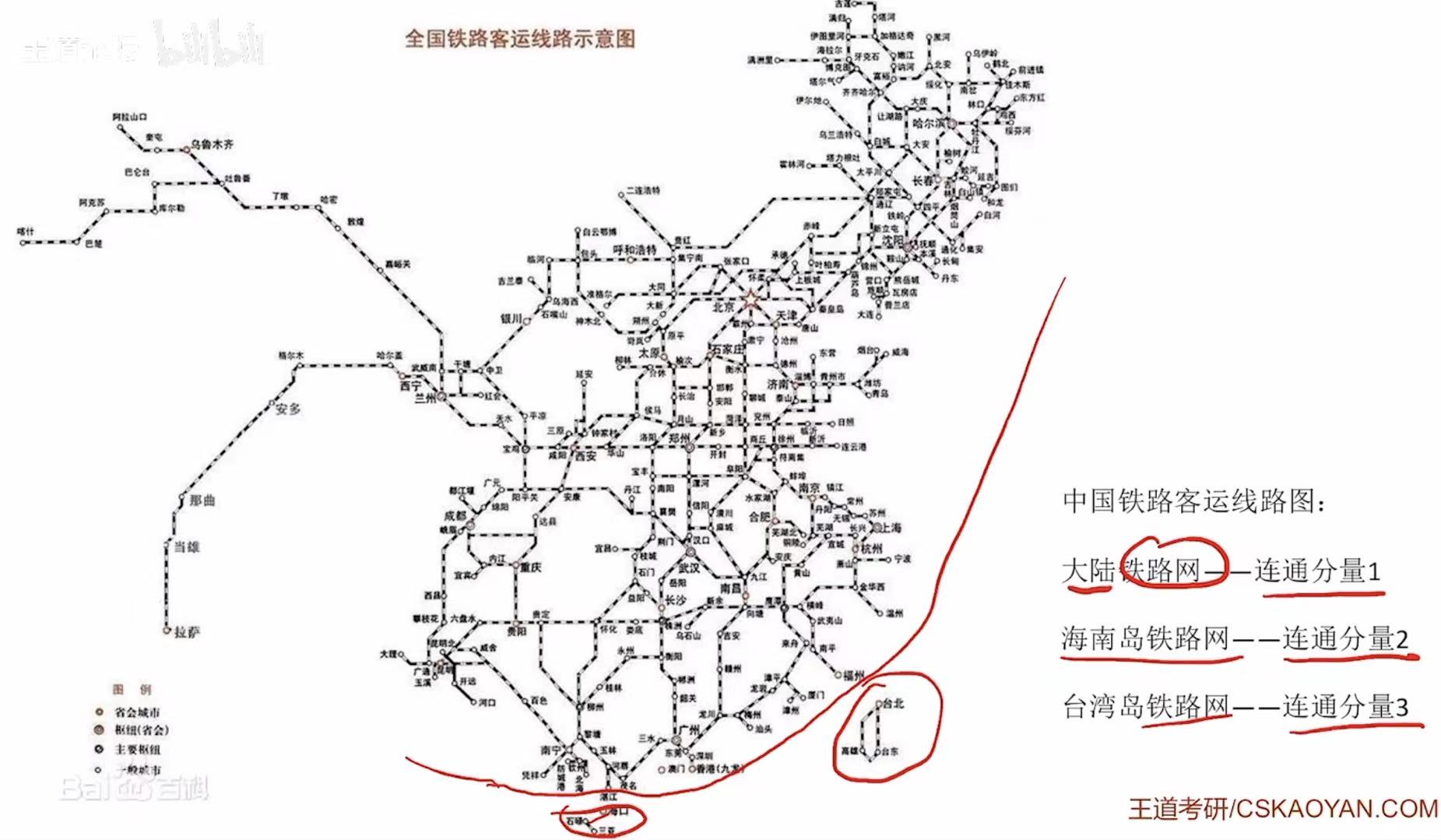
同理。（一坨一个分量）

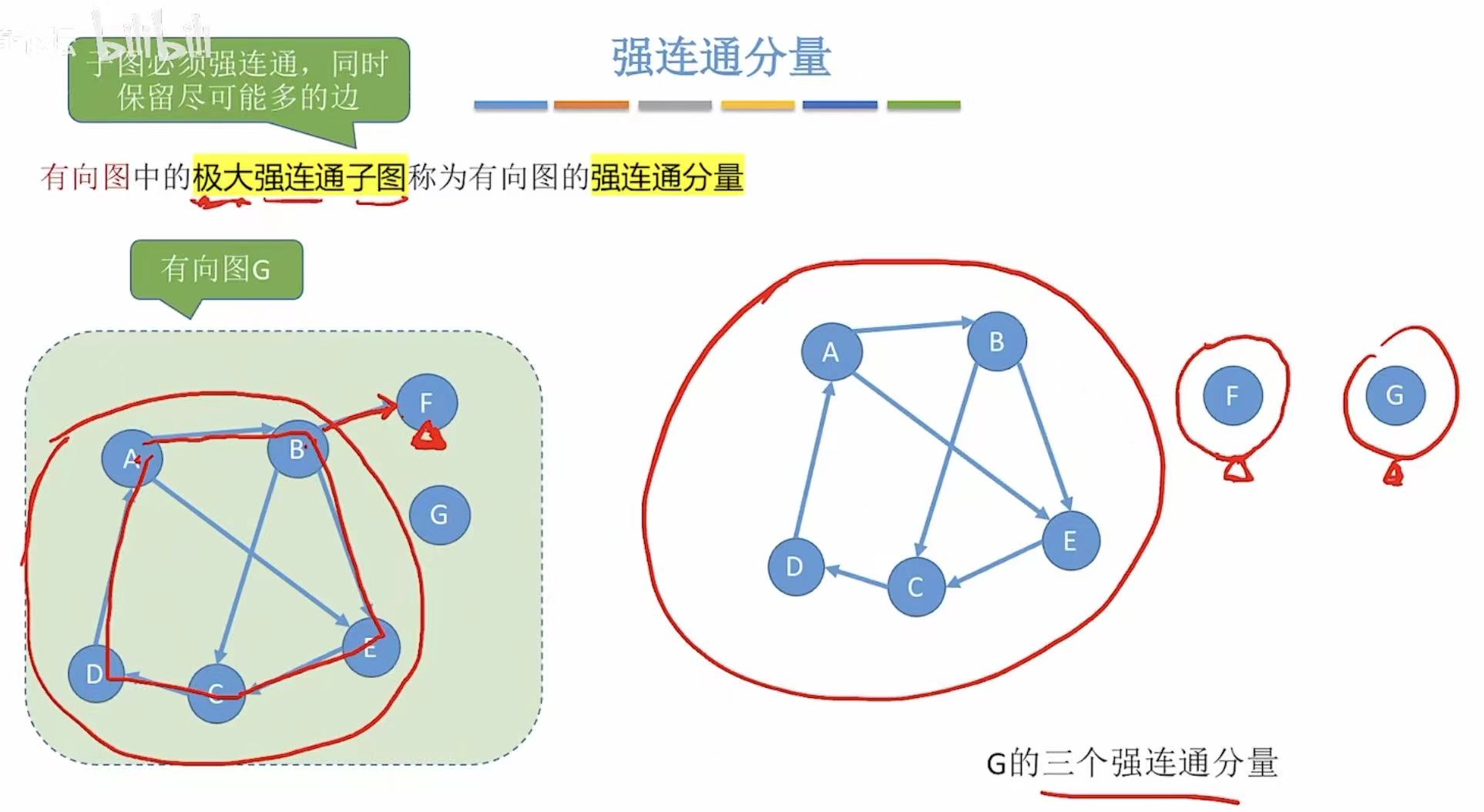
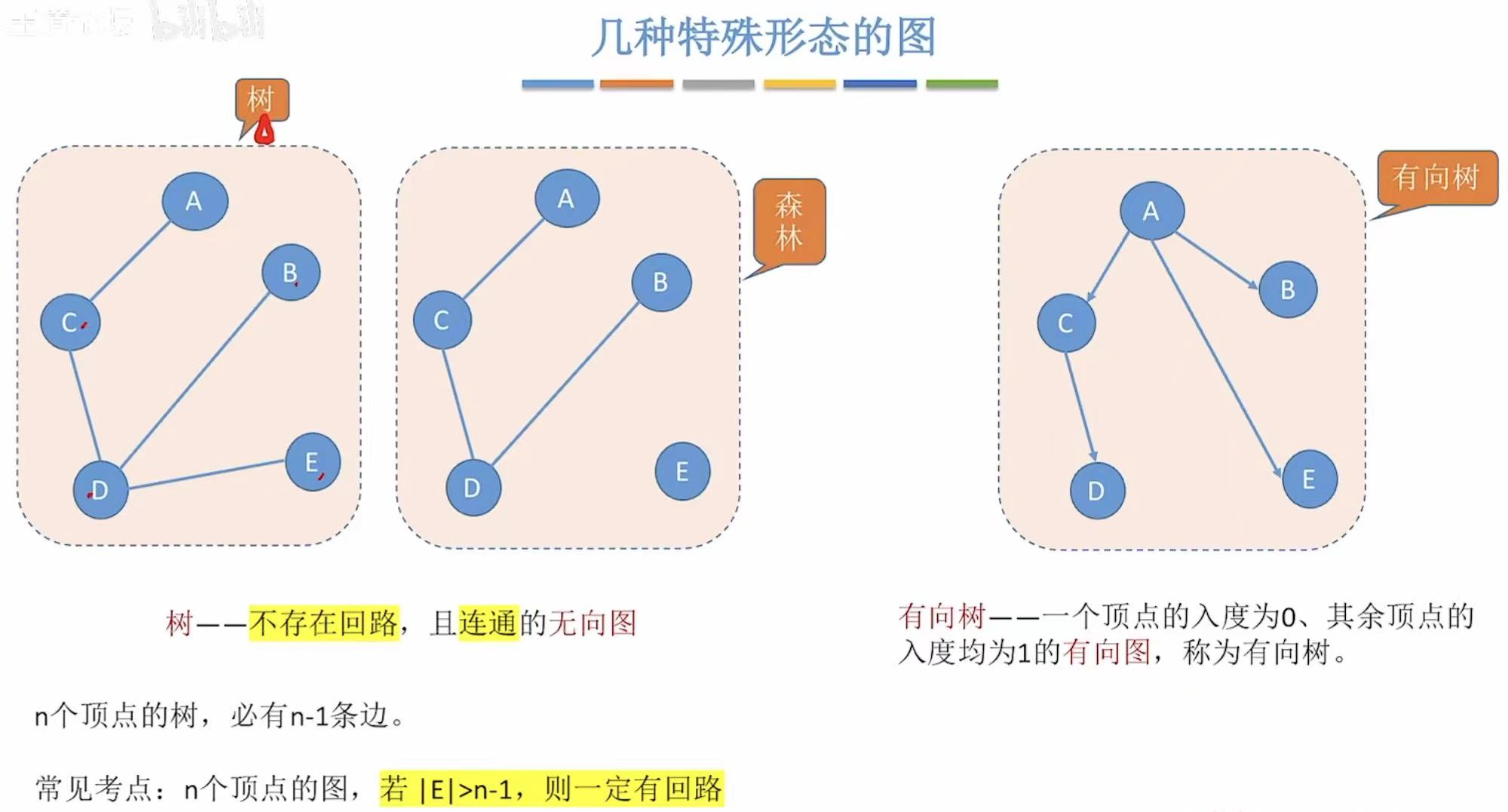
1.6 生成树/森林

边尽可能少+保持连通

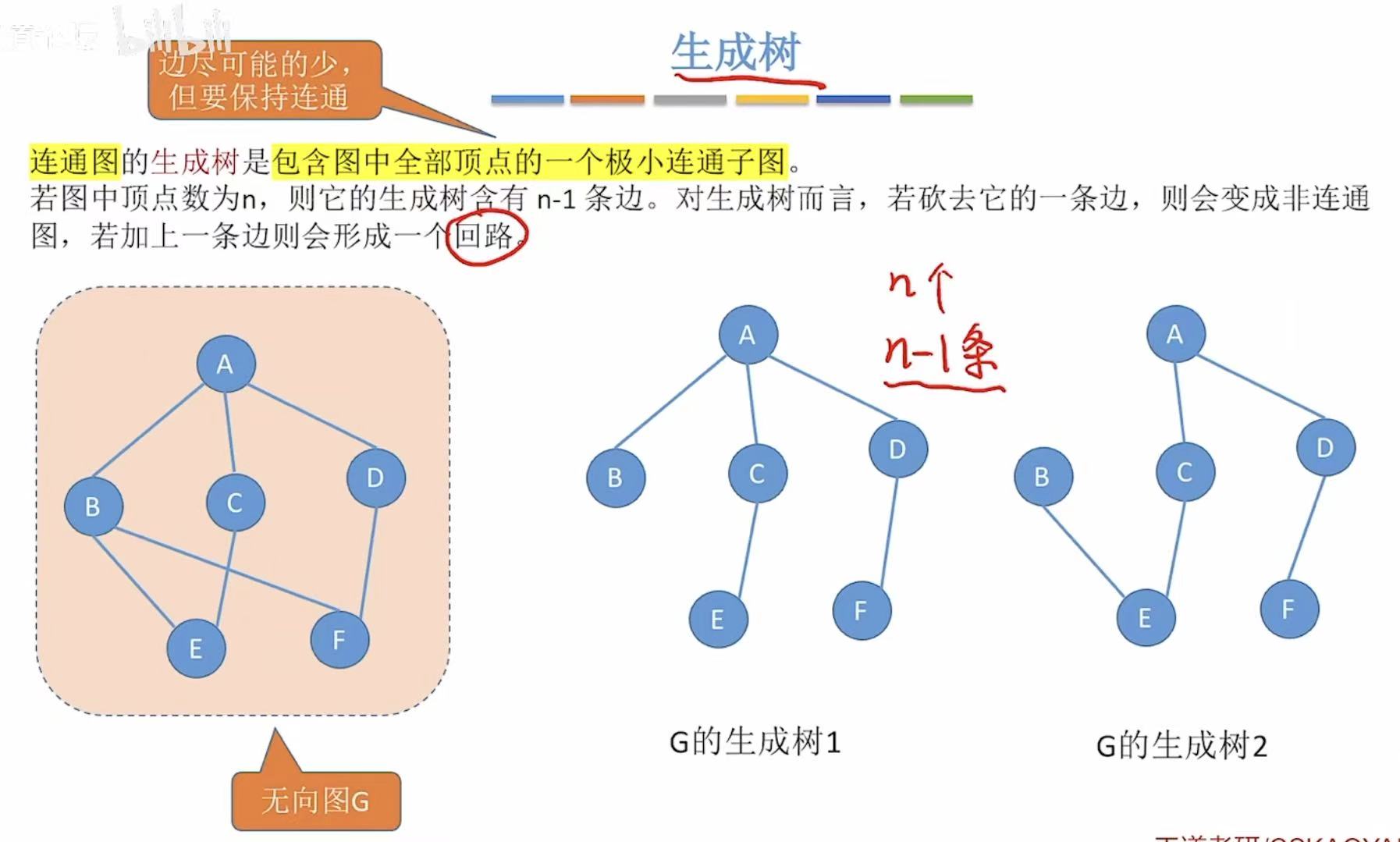
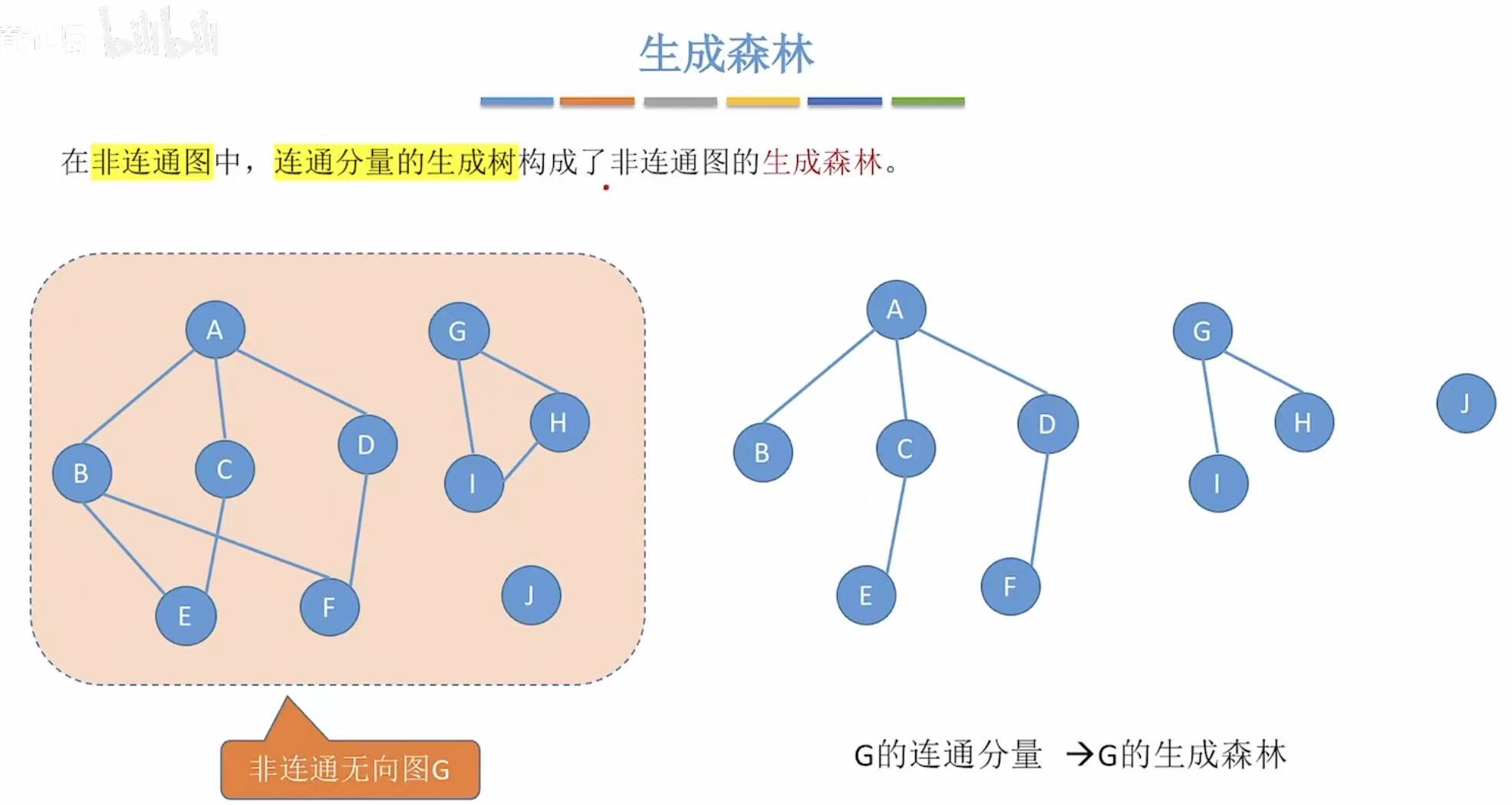
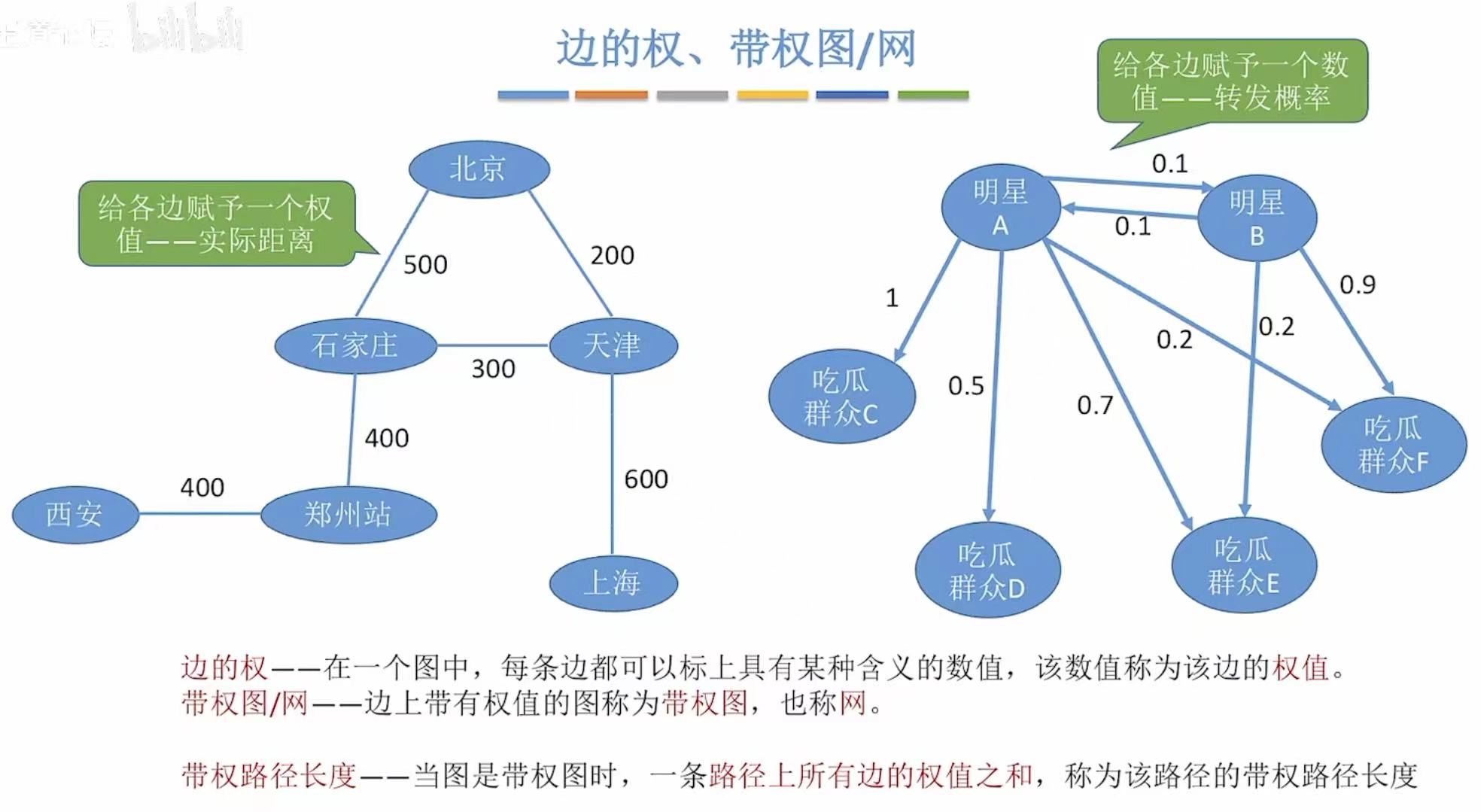
1.7 边的权

通过给每个边赋予一个权值，就可以代入具体的应用：比如修铁路看怎么修成本最低神马的。

有权值的图就叫做带权图 ，也叫网。

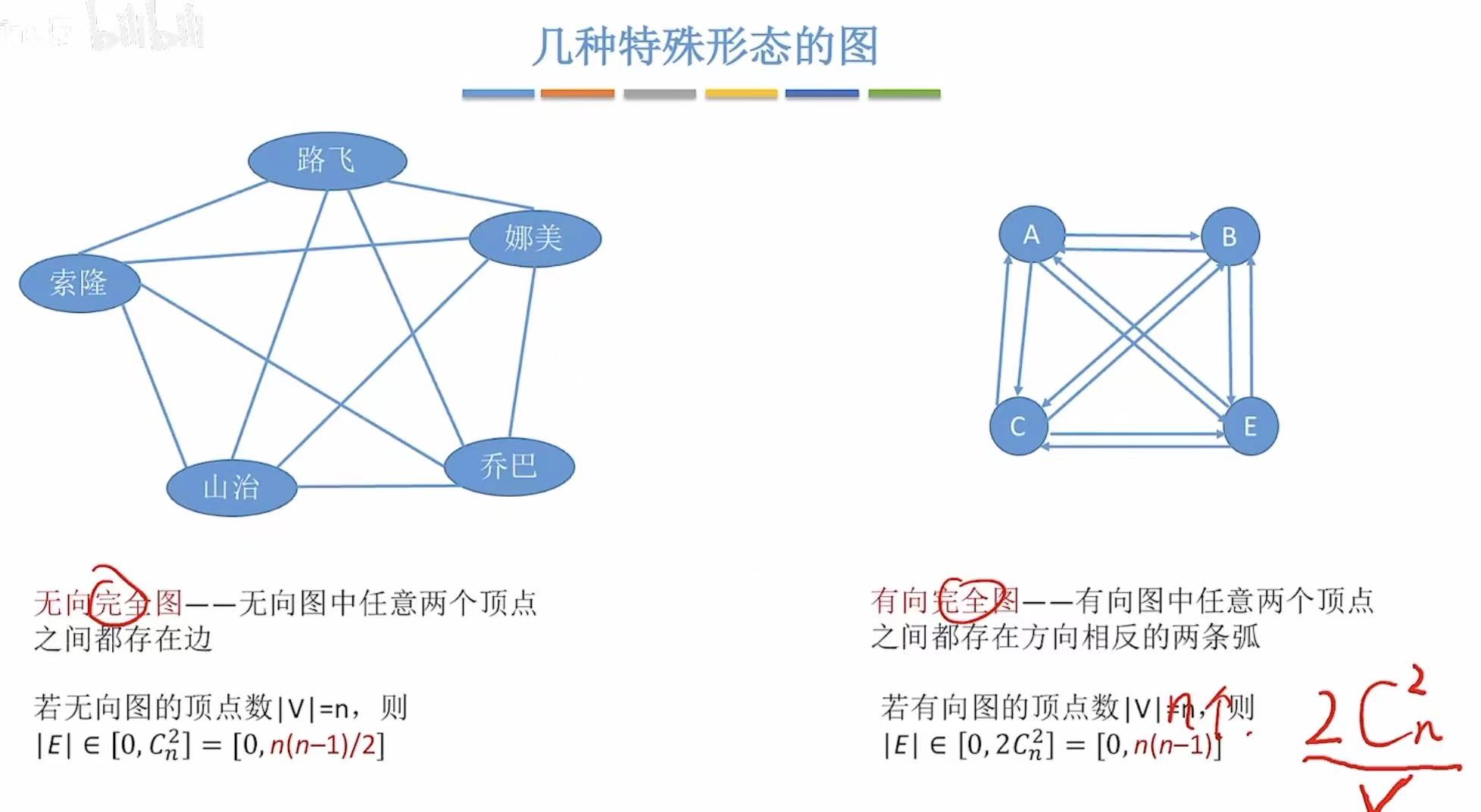
2. 特殊的图

无向完全图：重在完全，每个顶点之间都有一条直接的边。
有向完全图 ：同上，不过有箭头。
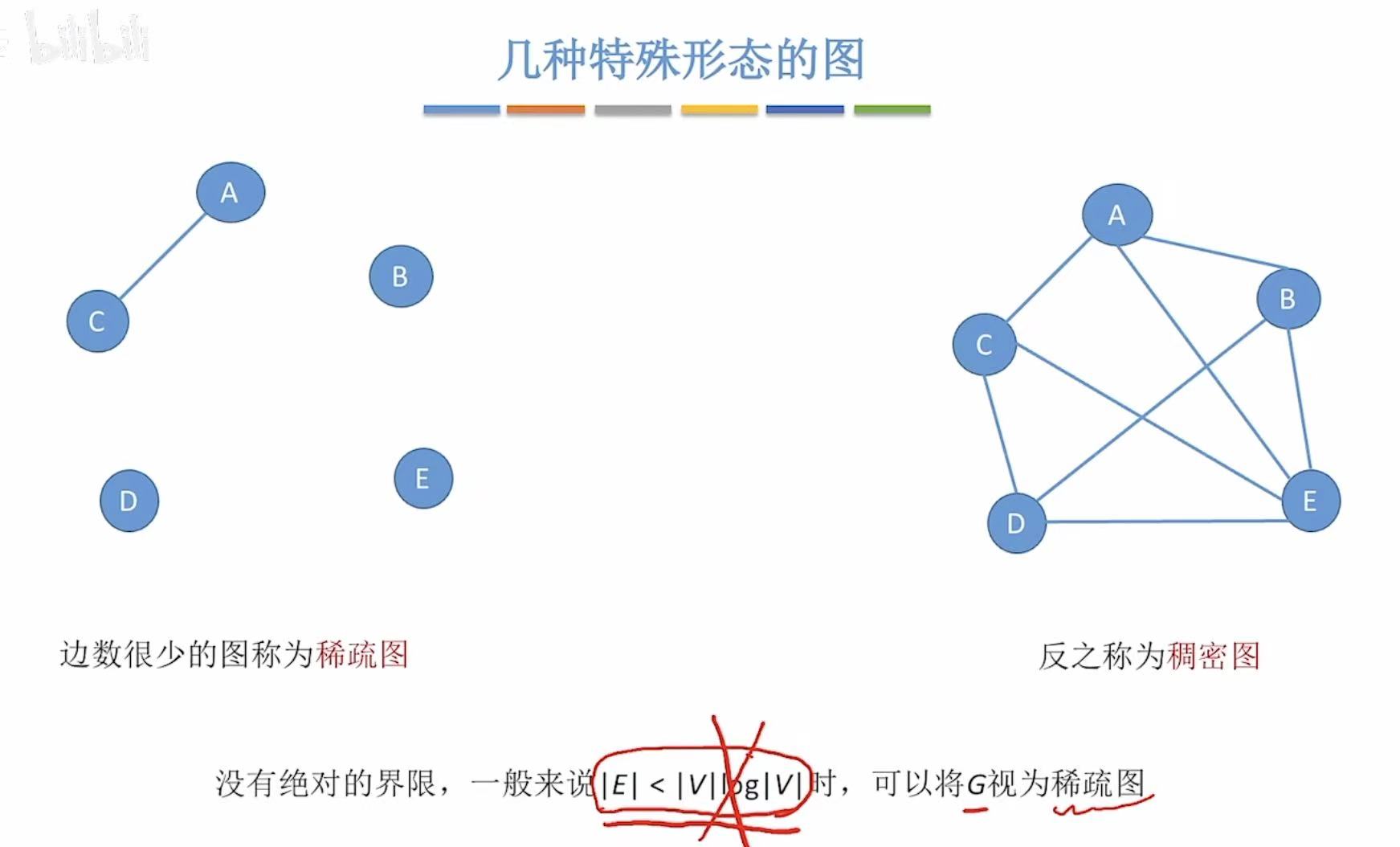
稀疏图：边数很少。
稠密图：和稀疏图相反。
了解就好。

特殊到和树/森林长得一模一样。

3. 小结

图的存储

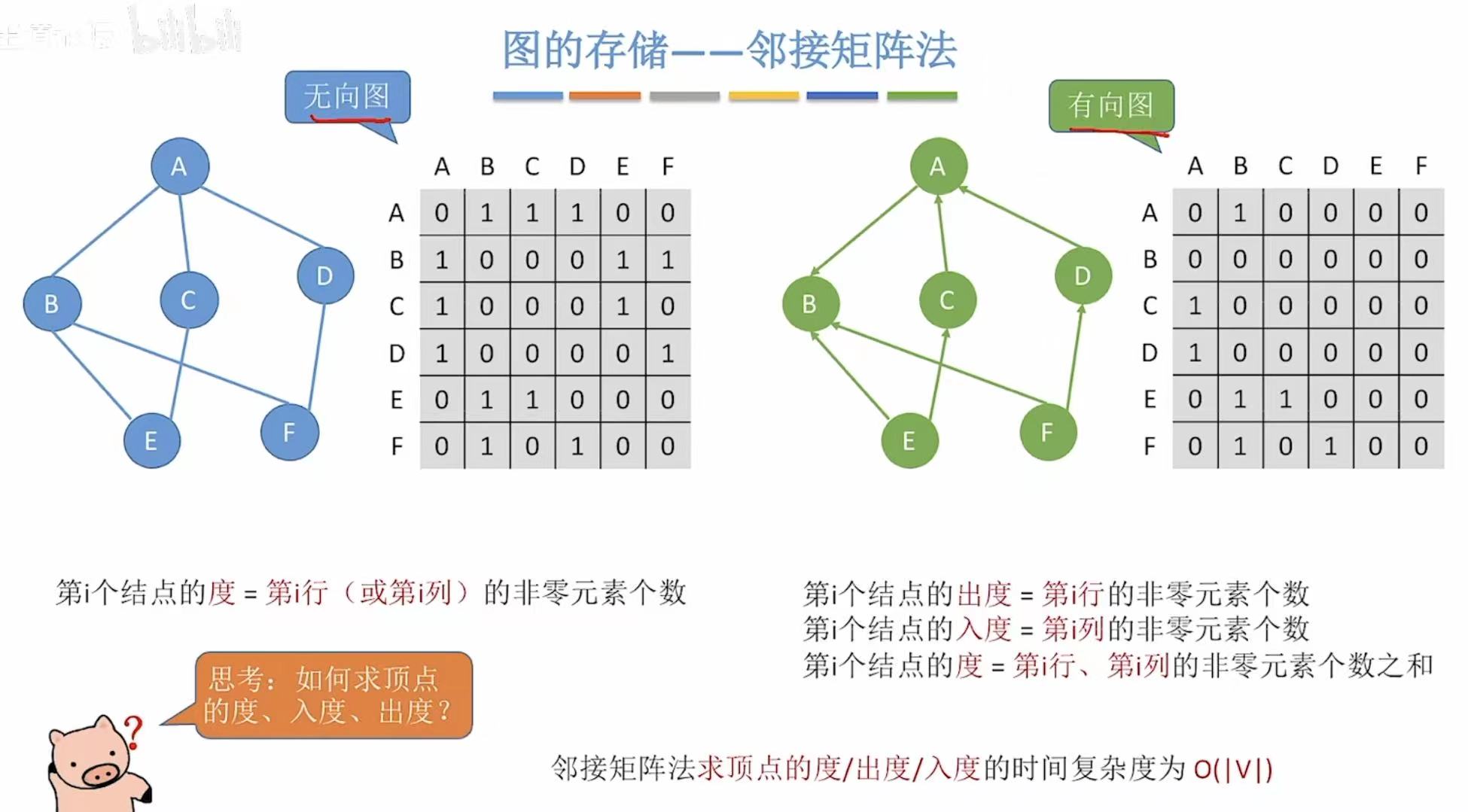
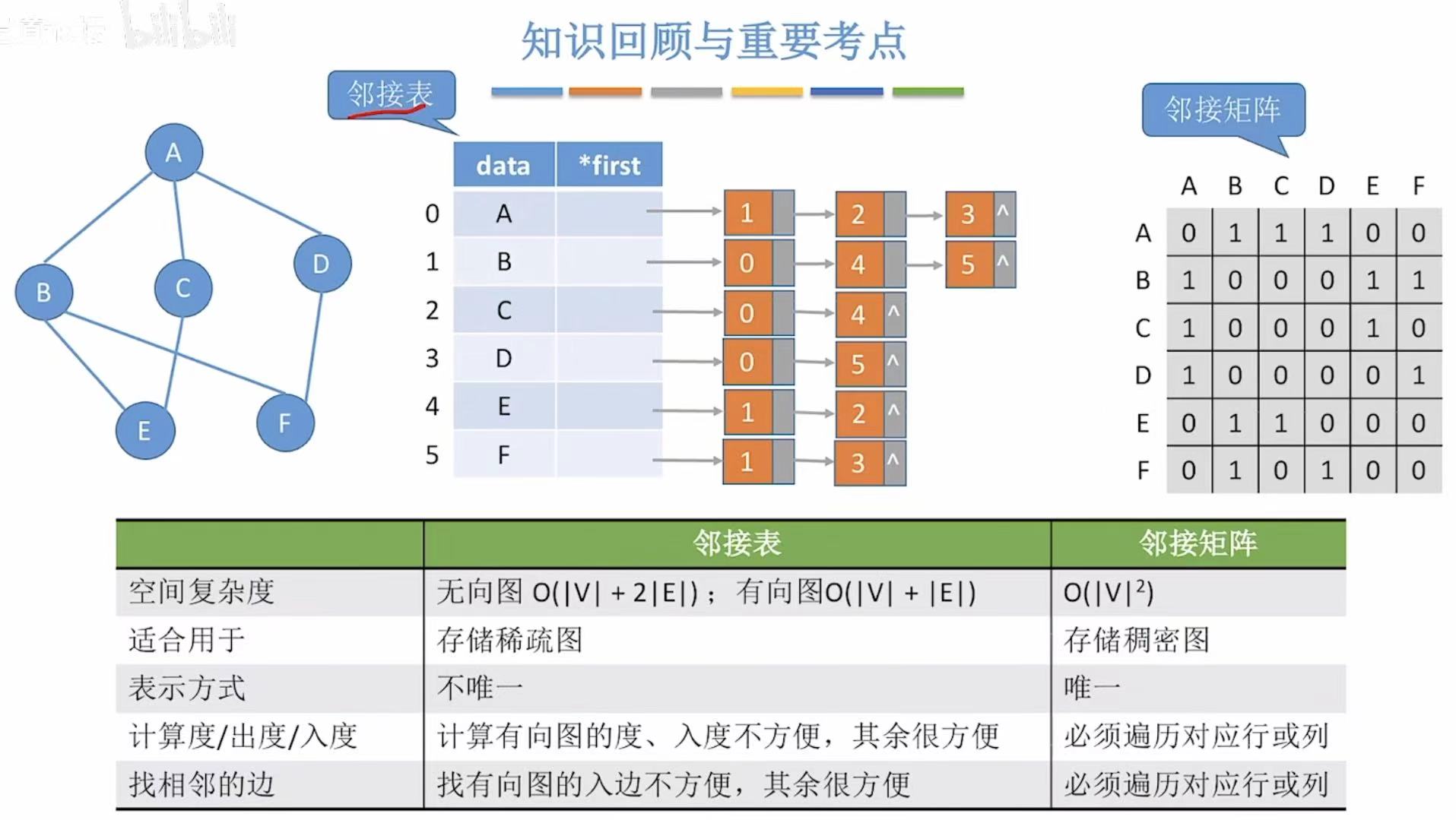
1. 邻接矩阵

1.1 概念

无向图：横纵轴表示含义相同，仅表示这两点之间有没有边，有1无0.
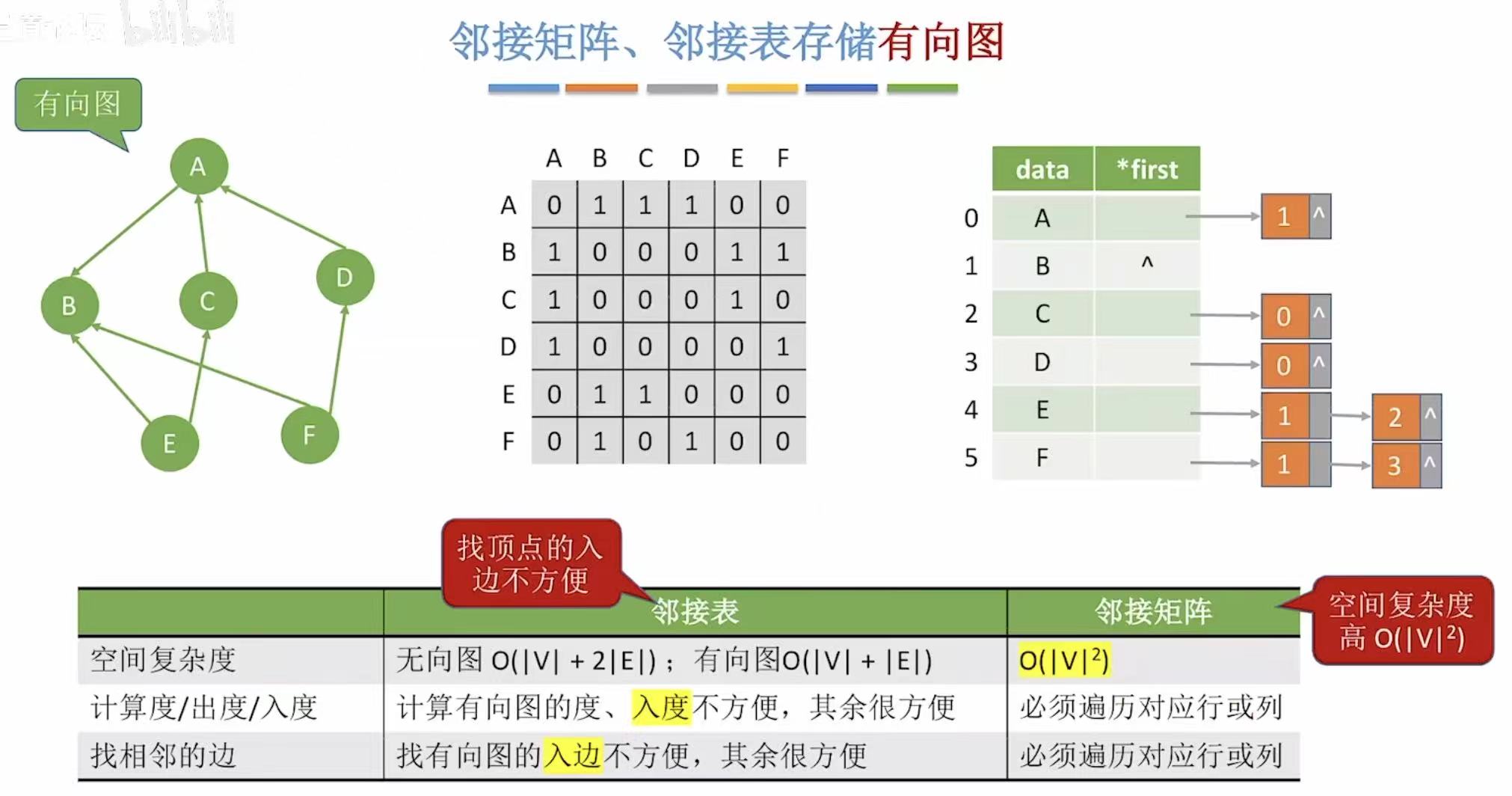
有向图：纵-->横，纵就是没箭头的那端，横就是有箭头的那段。

java 复制代码

#define MaxVertexNum 100            // 定义图中顶点数目的最大值（最多100个顶点）

// 定义图的结构体：MGGraph（Matrix Graph）
typedef struct {
    char Vex[MaxVertexNum];         // 顶点表：存储所有顶点的信息（如字符、数字等）
                                    // 这里用 char 类型，比如 'A', 'B', 'C' 等
                                    // 可以改为更复杂类型（如结构体）来存更多信息

    int Edge[MaxVertexNum][MaxVertexNum];  // 邻接矩阵：存储边的关系
                                           // Edge[i][j] 表示顶点 i 到顶点 j 是否有边
                                           // 无向图：Edge[i][j] == Edge[j][i]
                                           // 有向图：方向不同，值可能不同
                                           // 值为 0 表示无边，1 或权重表示有边

    int vexnum, arcnum;             // 图的当前实际顶点数和边数（弧数）
                                    // vexnum：当前有多少个顶点被使用
                                    // arcnum：当前有多少条边（或弧）
} MGGraph;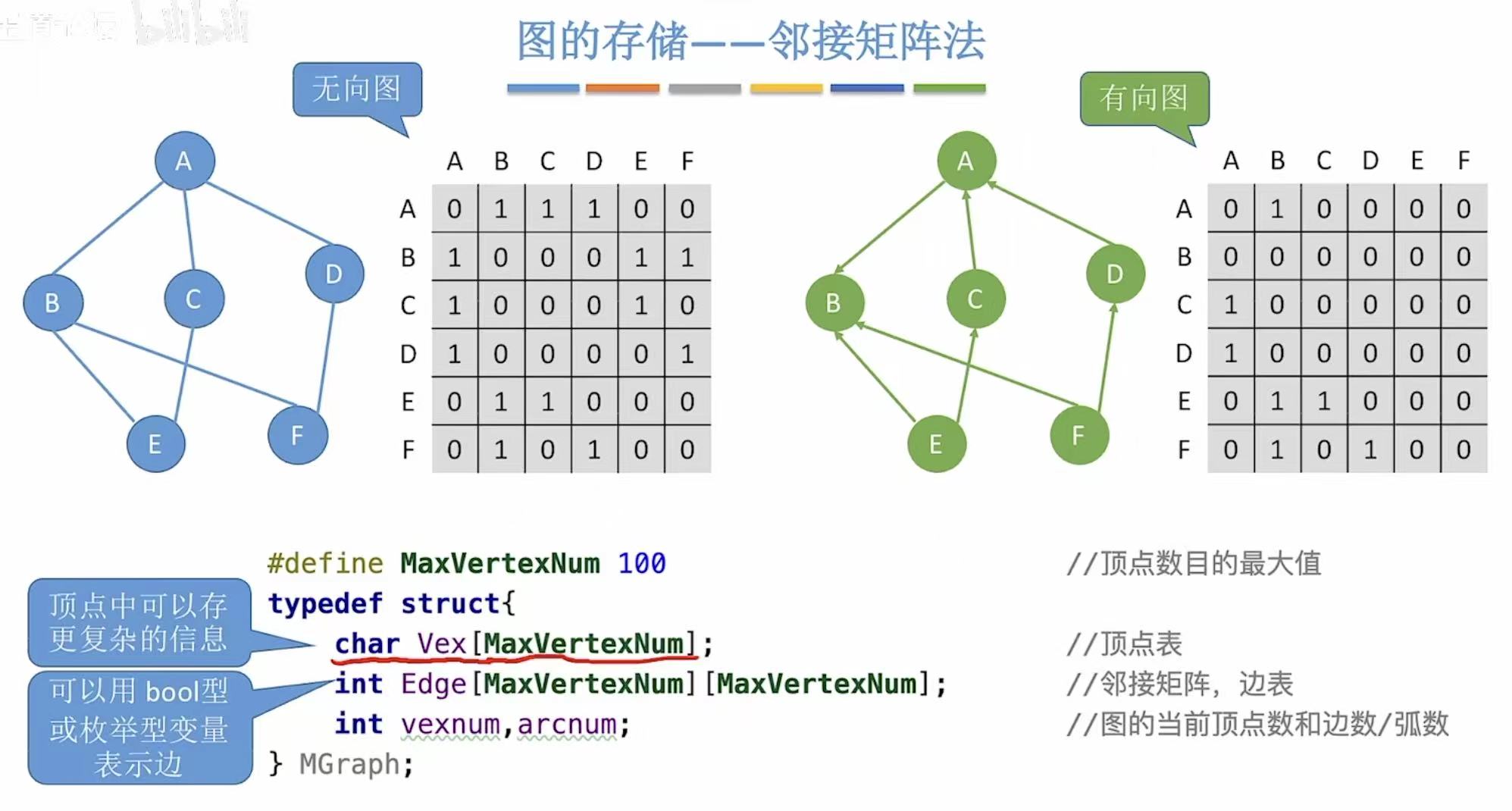

就是有边的标1，没有边的标0.

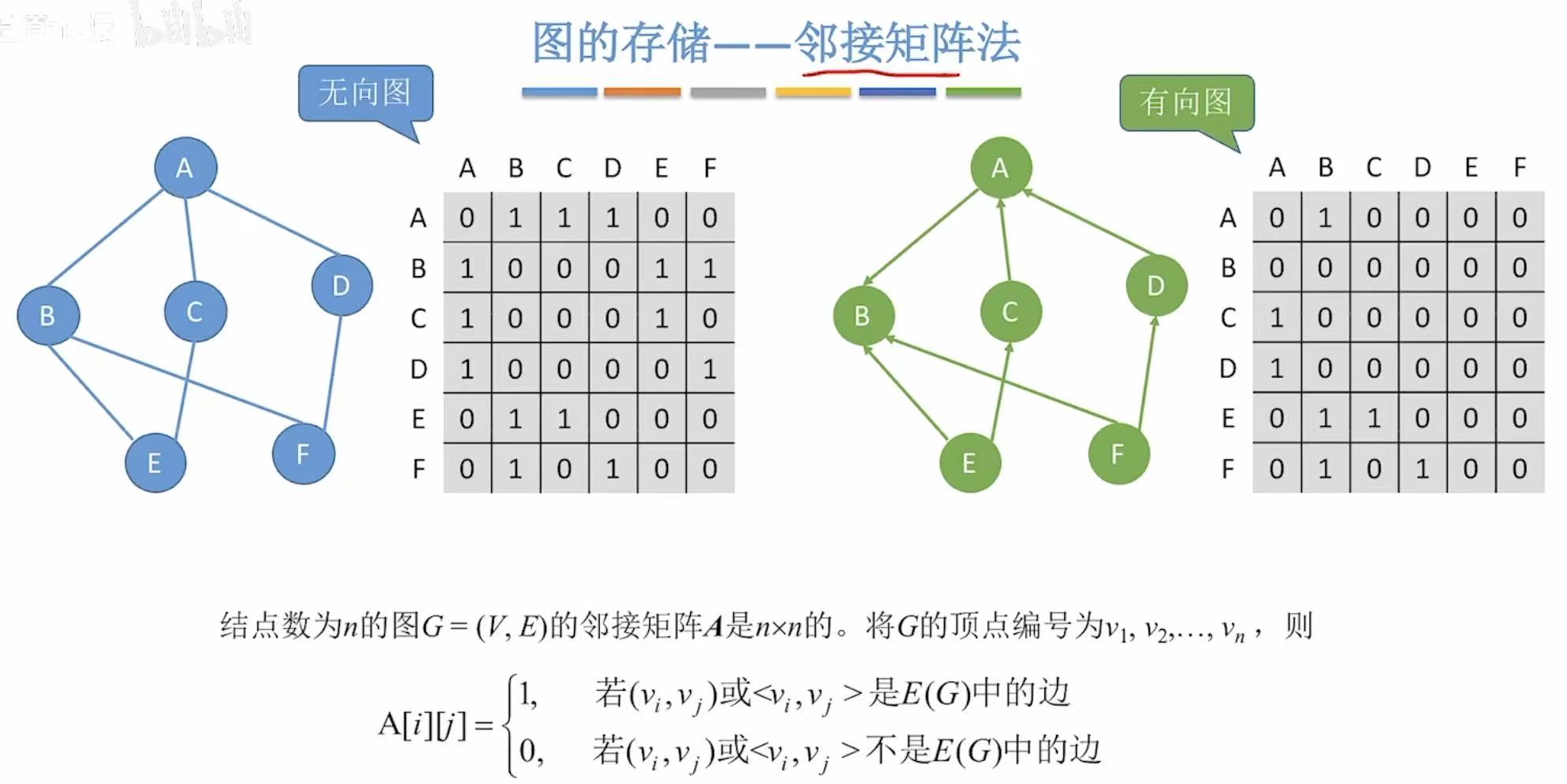
无向图：行或列的1的个数。
有向图 ：出度-->行；入度-->列；

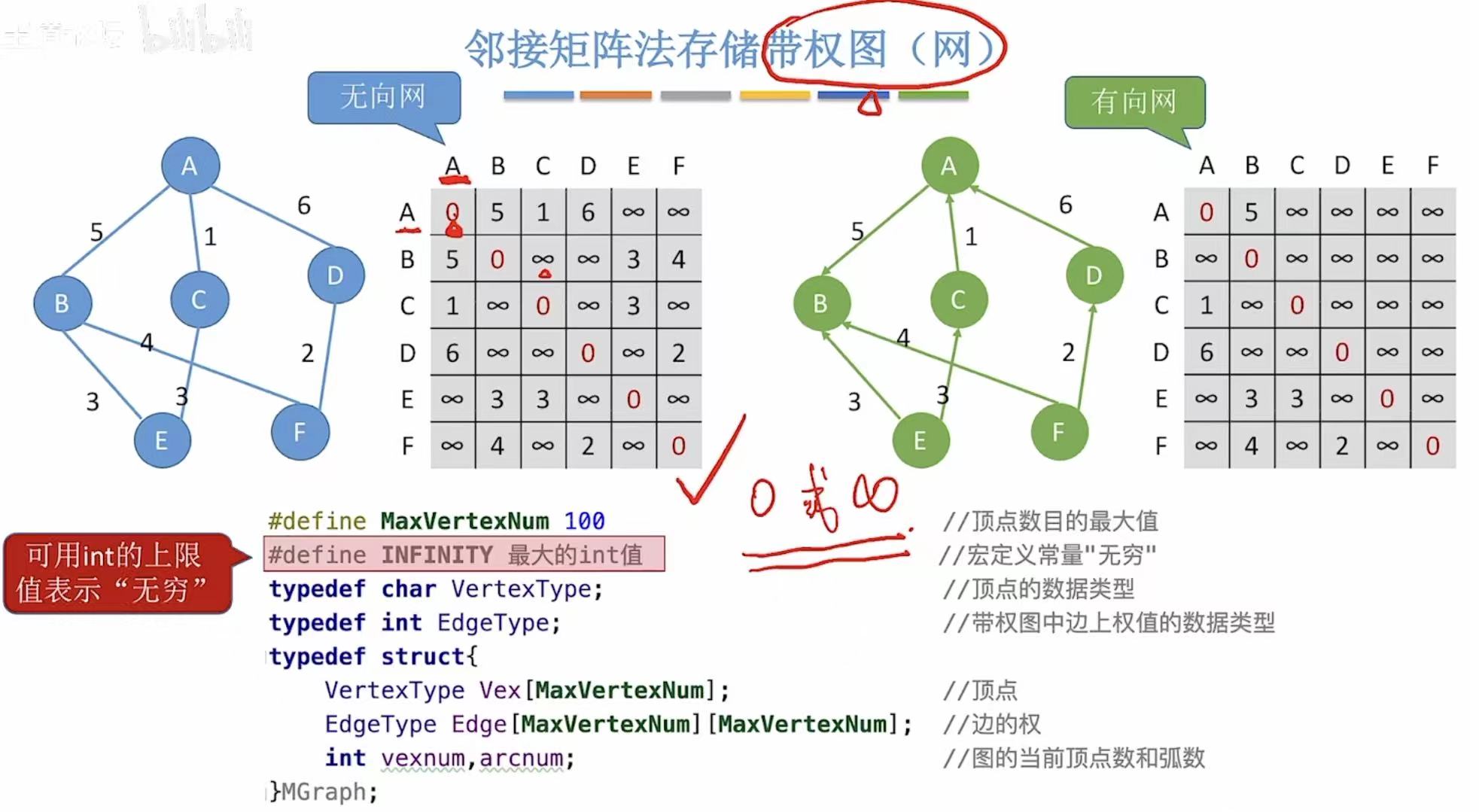
1.2 带权图

带权就可以将之前的0和1替换成∞和对应的权值。

java 复制代码

#define MaxVertexNum 100            // 定义图中顶点数目的最大值（最多100个顶点）

#define INFINITY INT_MAX            // 宏定义常量"无穷"：用 int 类型的最大值表示不可达
                                   // 在实际算法中（如 Dijkstra），若两点无路径，则设为 INF

typedef char VertexType;           // 定义顶点的数据类型：这里用 char 表示顶点（如 'A', 'B'）
                                  // 可以改为其他类型（如 int、string 或结构体）

typedef int EdgeType;              // 定义边的权值类型：这里用 int 表示边的权重（如距离、代价等）
                                  // 也可以是 float、double 等

typedef struct {
    VertexType Vex[MaxVertexNum];  // 顶点表：存储所有顶点的信息
                                   // 比如 Vex[0]='A', Vex[1]='B', ...
    
    EdgeType Edge[MaxVertexNum][MaxVertexNum];  // 邻接矩阵：存储边的权值
                                               // Edge[i][j] 表示从顶点 i 到顶点 j 的边权
                                               // 如果没有边，则设为 INFINITY（表示"无穷大"）
    
    int vexnum, arcnum;            // 图的当前实际顶点数和边数（弧数）
                                   // vexnum：实际使用的顶点数量
                                   // arcnum：实际存在的边的数量
} MGGraph;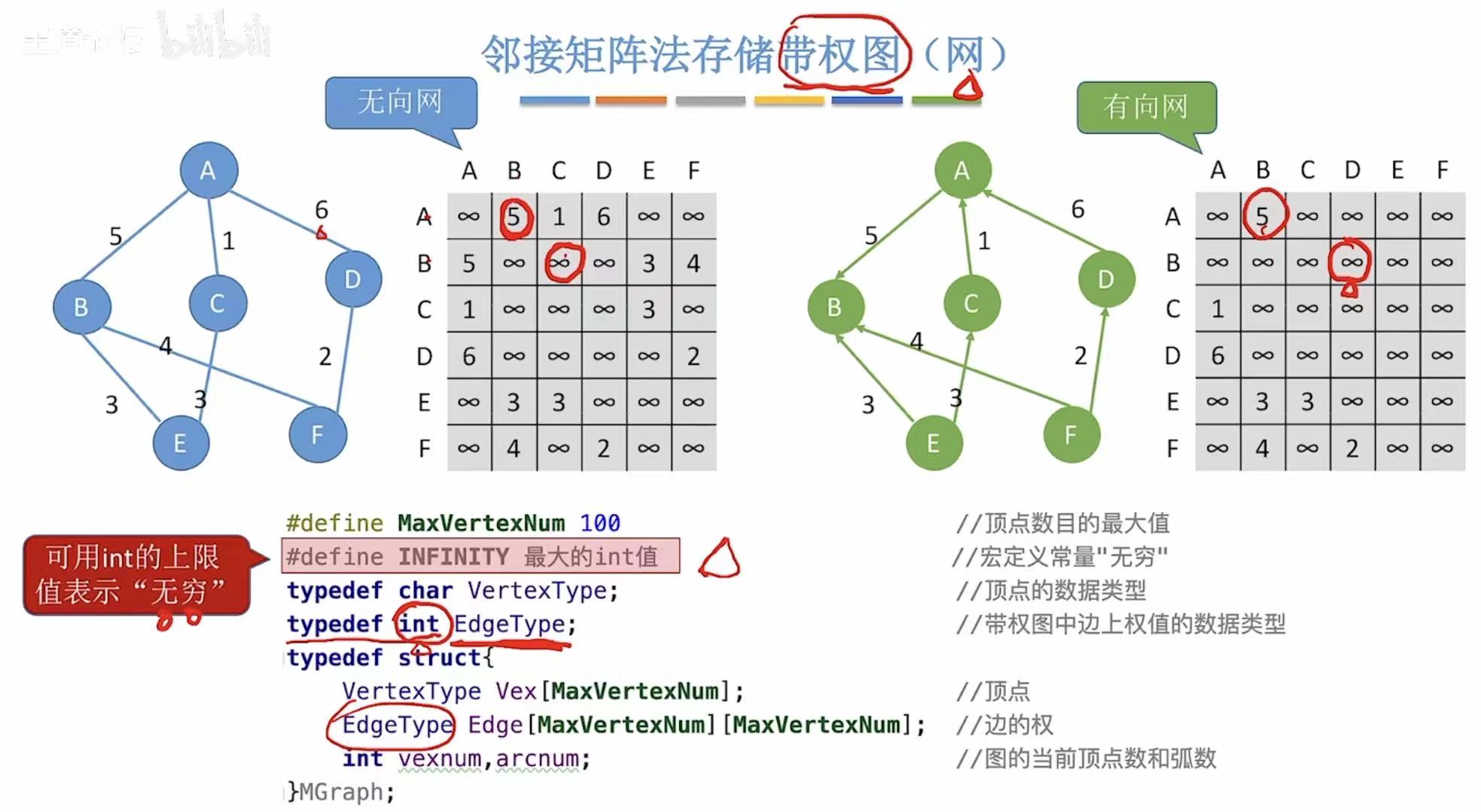

因为研究的是简单图，所以根本不可能出现自己指回自己的情况，所以也可以用0表示这种情况。

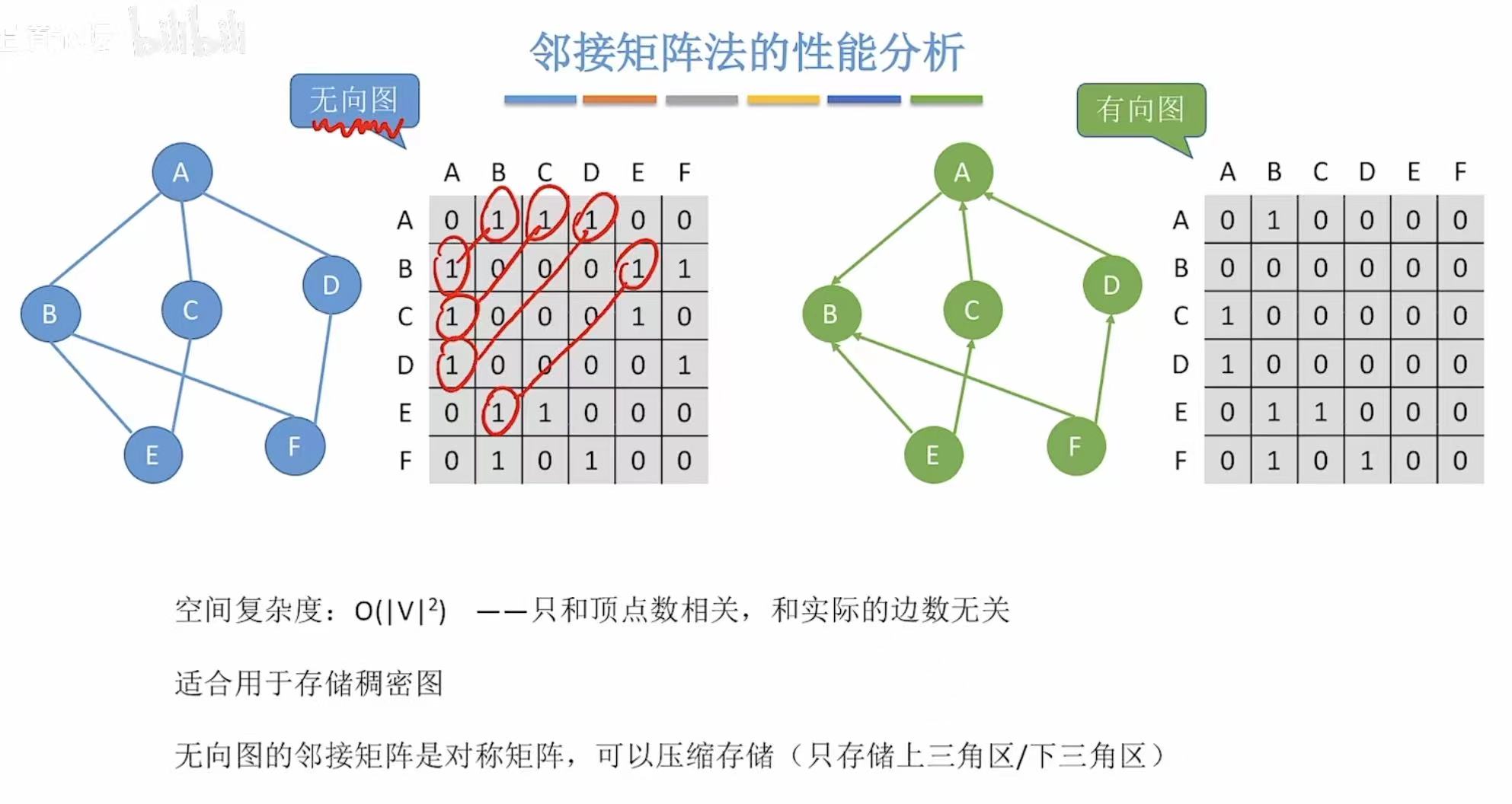
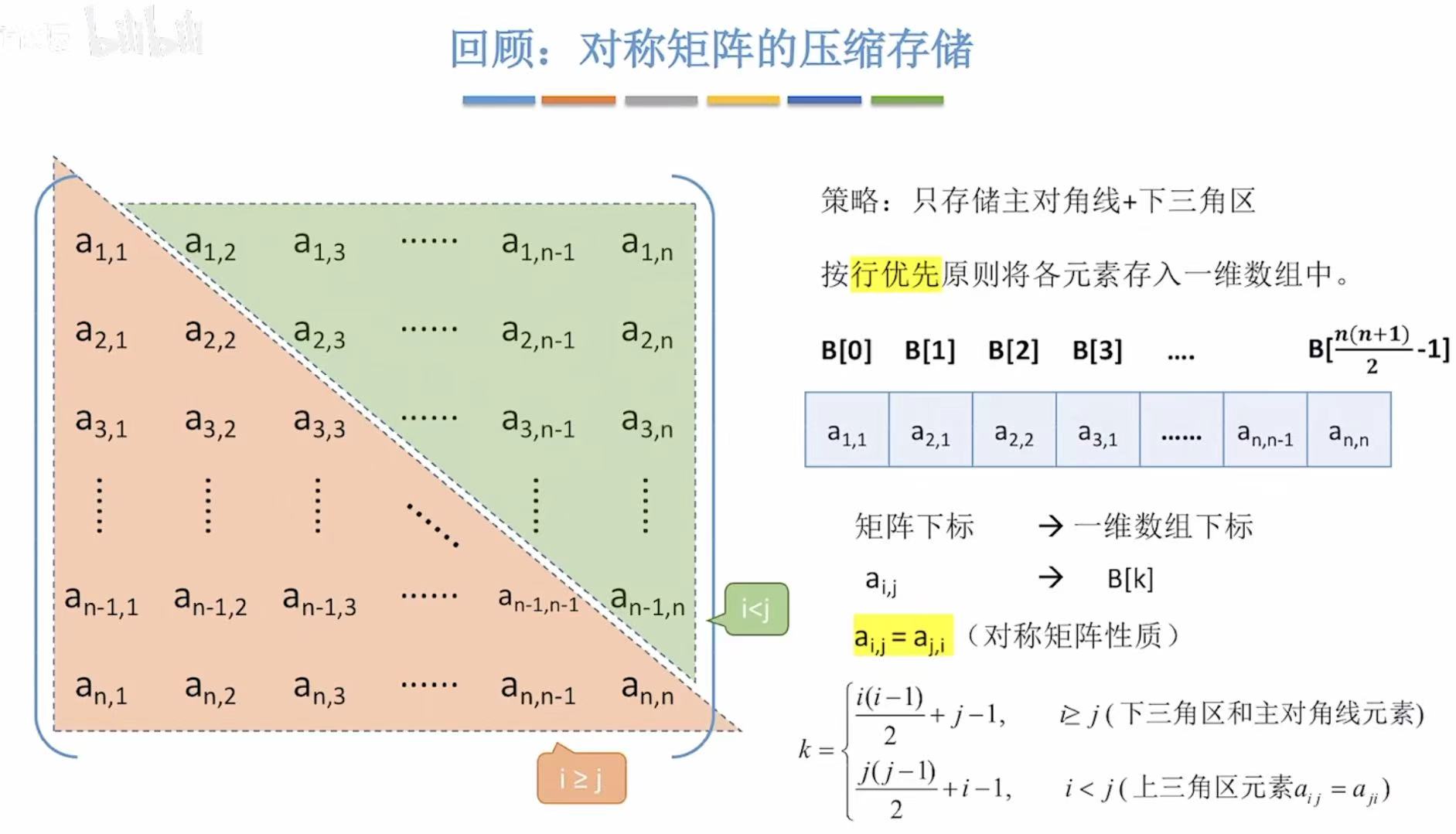
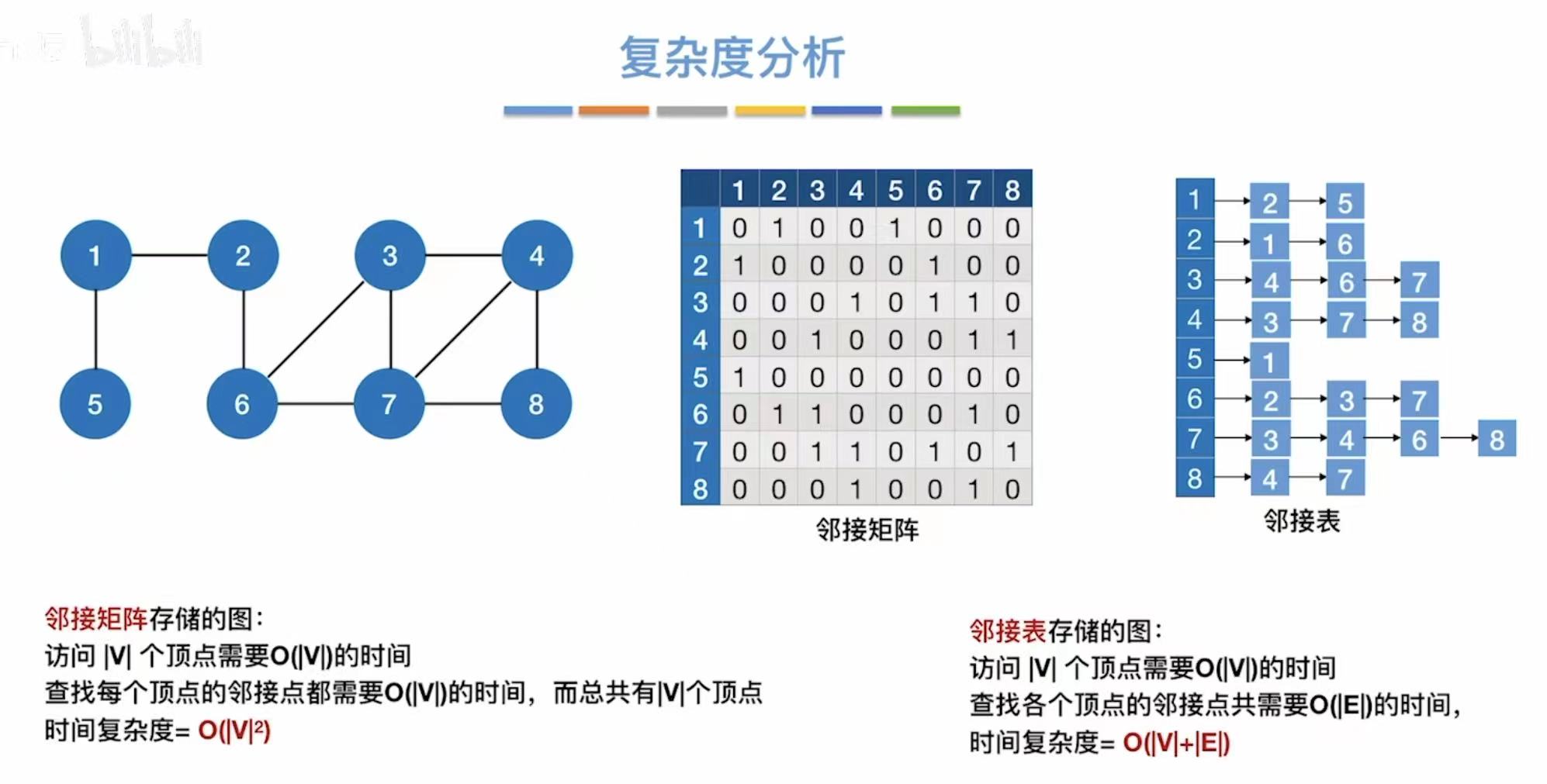
1.3 性能分析

因为邻接矩阵存的都是顶点，所以空间复杂度自然就和顶点相关。

|v²|：可以理解为这个邻接矩阵的大小。

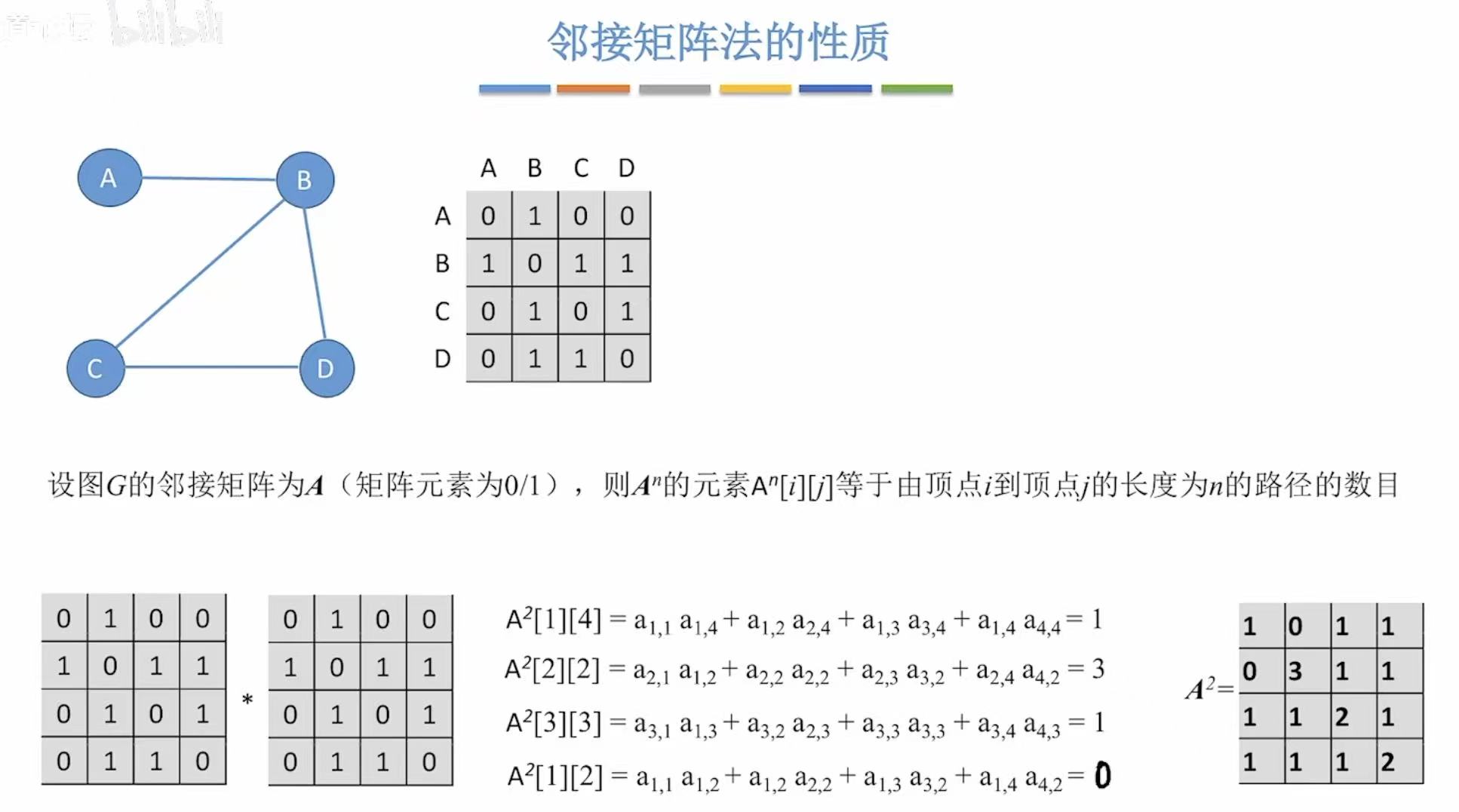
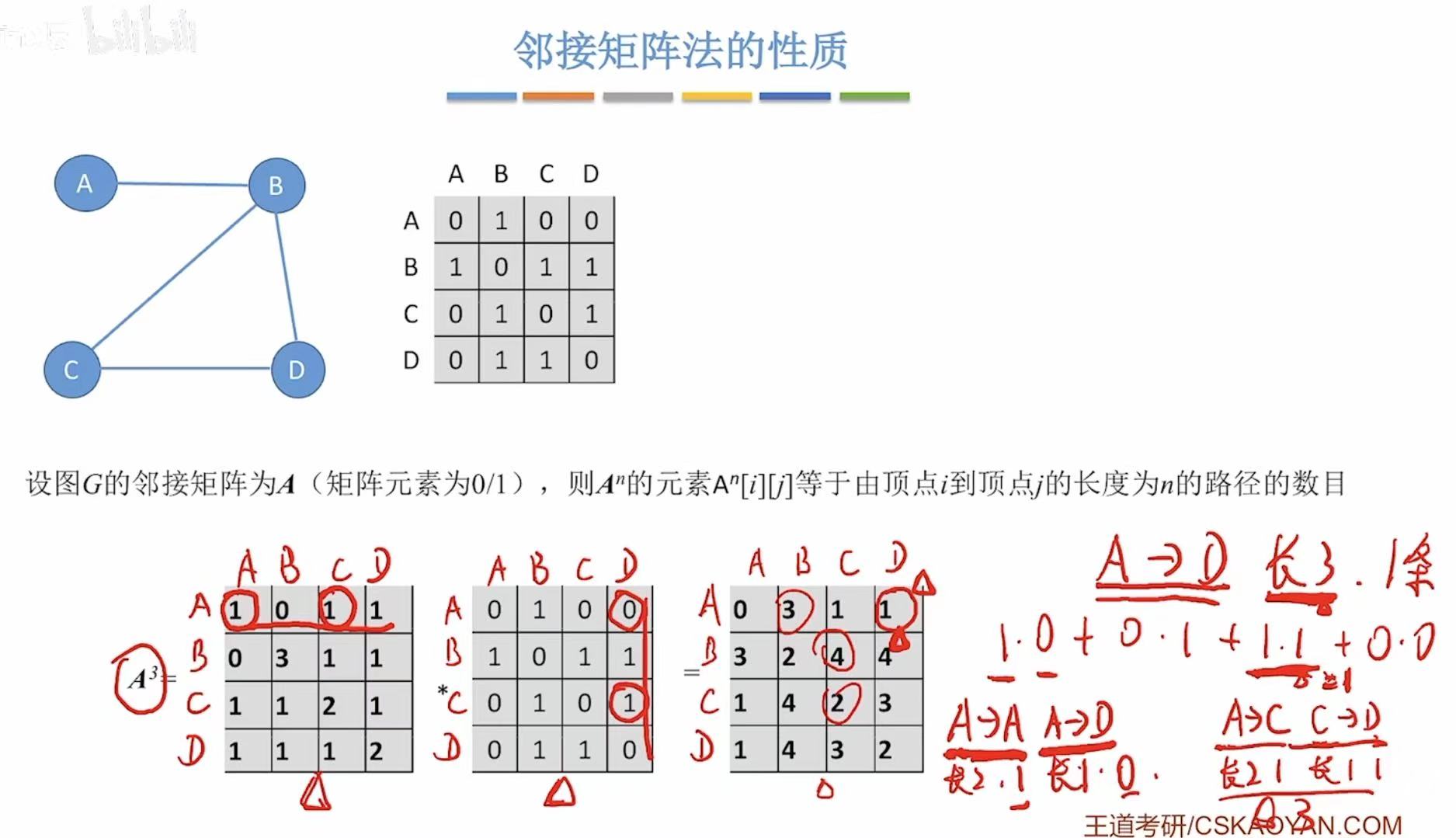
1.4 性质

A[i][j] = 1 表示有边从 i 到 j；

A[i][j] = 0 表示无边。

A²[1][4]（即从顶点 1 到顶点 4，长度为 2 的路径数）

k=1：1→1？没有（A[1][1]=0）
k=2：1→2（有），2→4（有） → 路径：1→2→4
k=3：1→3？没有（A[1][3]=0）
k=4：1→4？没有（A[1][4]=0）
只有一条路径：1→2→4 --> 所以 A²[1][4] = 1

1.5 小结

2. 邻接表

2.1 概念

java 复制代码

// 定义最大顶点数（常量）
#define MaxVertexNum 100            // 图中顶点数目的最大值

// 边（或弧）结点结构体：用于存储边的信息
typedef struct ArcNode {
    int adjvex;                     // 表示该边指向的顶点在数组中的下标（即邻接点）
                                    // 例如：A→B，则 adjvex = 1（B 的索引）

    struct ArcNode *next;           // 指向下一个边结点的指针（形成链表）
                                    // 实现同一顶点的所有邻接点按链表连接

    // InfoType info;               // 可选：存储边的权值或其他信息（如权重、距离等）
} ArcNode;

// 顶点结点结构体：用于存储顶点及其邻接表
typedef struct VNode {
    VertexType data;                // 存储顶点的数据（如字符 'A'、'B' 等）
                                    // 可以是 char、int 或更复杂类型

    ArcNode *first;                 // 指向该顶点第一条边（或弧）的指针
                                    // 即：该顶点的邻接表头指针
} VNode, AdjList[MaxVertexNum];     // VNode 是结点类型，AdjList 是顶点数组

// 图的整体结构体：ALGraph（Adjacency List Graph）
typedef struct {
    AdjList vertices;               // 顶点数组：存储所有顶点和它们的邻接表
                                    // vertices[i] 就是第 i 个顶点的 VNode 结构

    int vexnum, arcnum;             // 图的当前实际顶点数和边数（弧数）
                                    // vexnum：实际使用的顶点数量
                                    // arcnum：实际存在的边的数量
} ALGraph;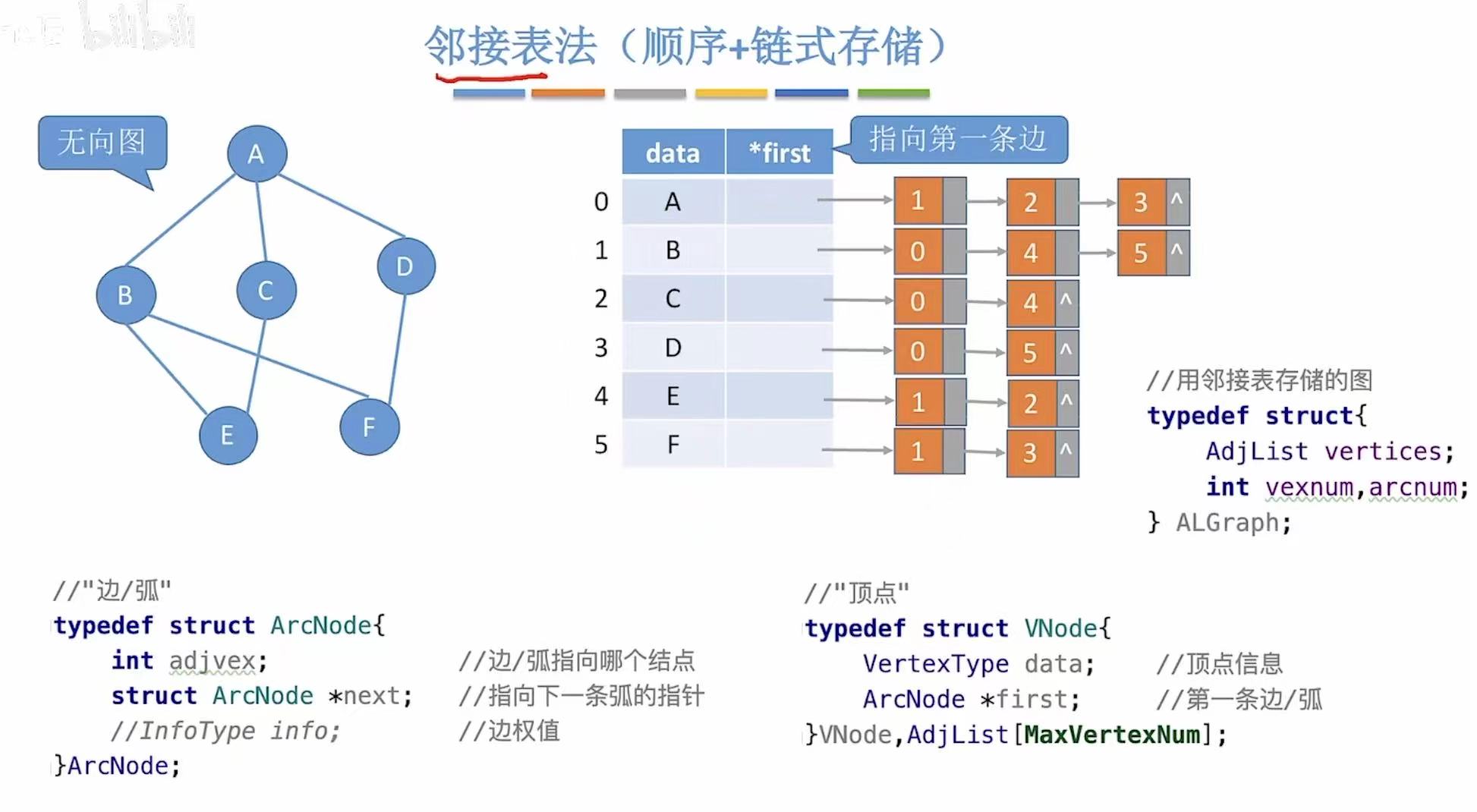

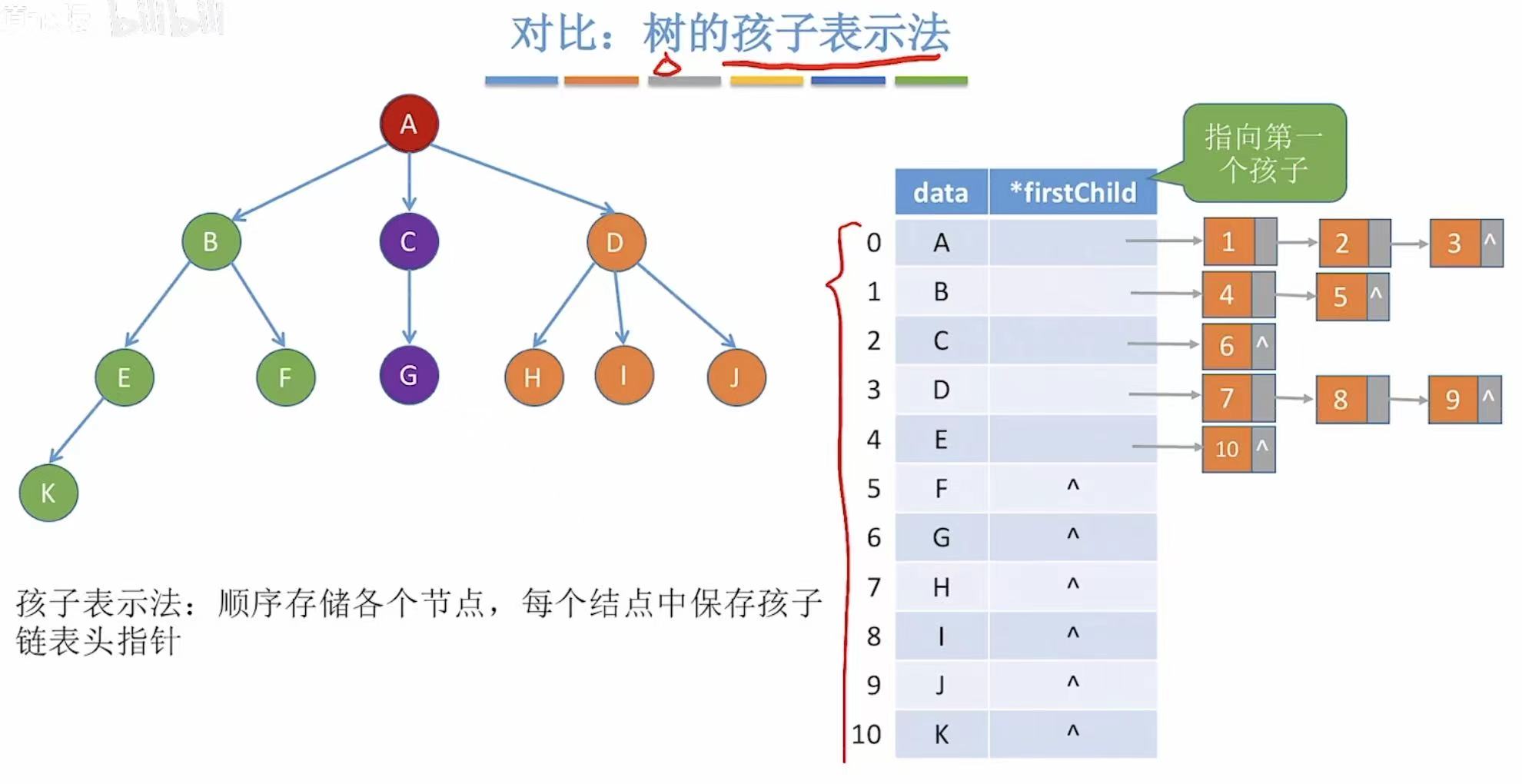
类比树的孩子表示法，具体可见：孩子表示法

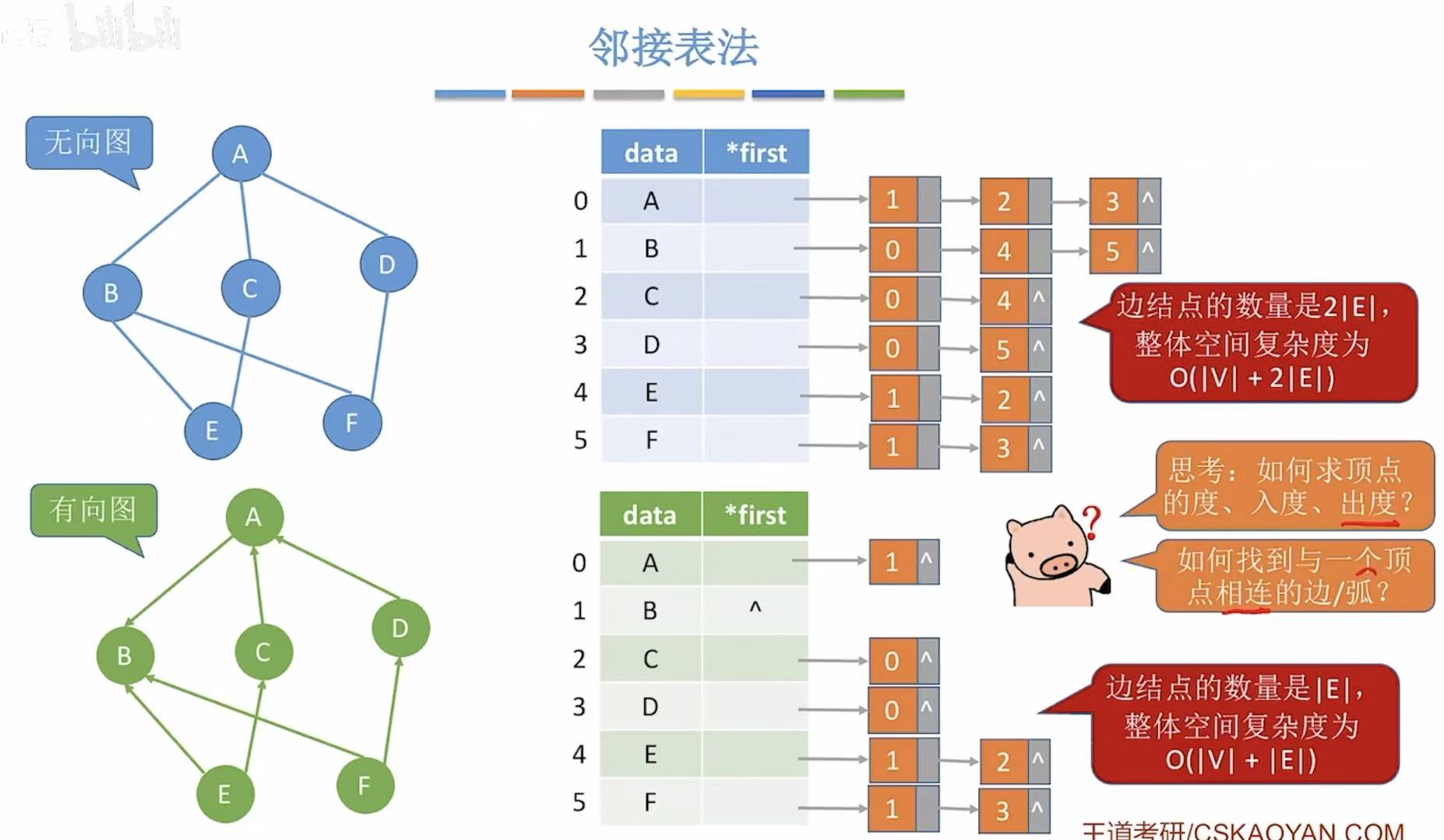
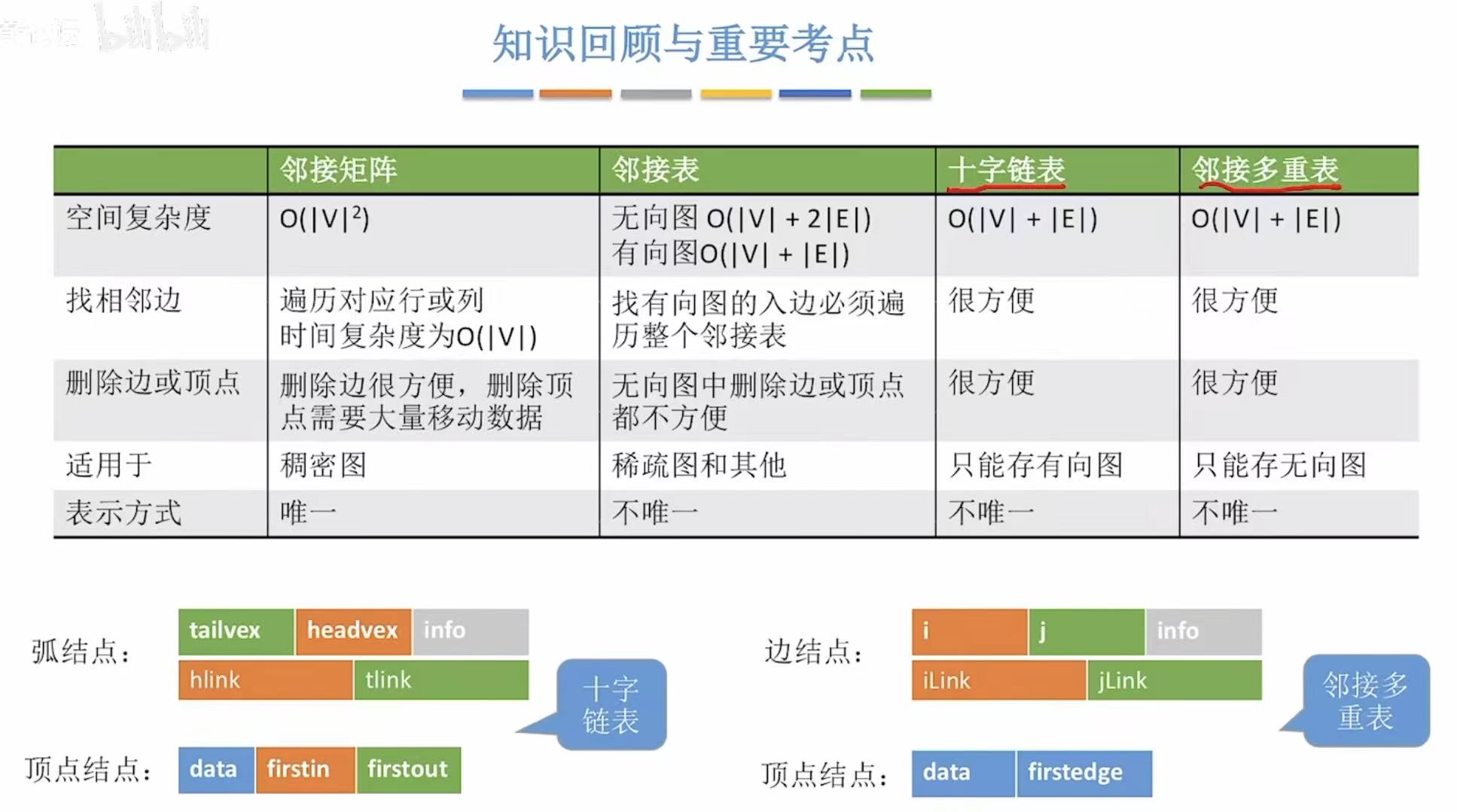
空间复杂度：

无向图：直接看这个表=顶点|V|+双倍的边2|E|
有向图 ：也是直接看表=顶点|V|+边|E|
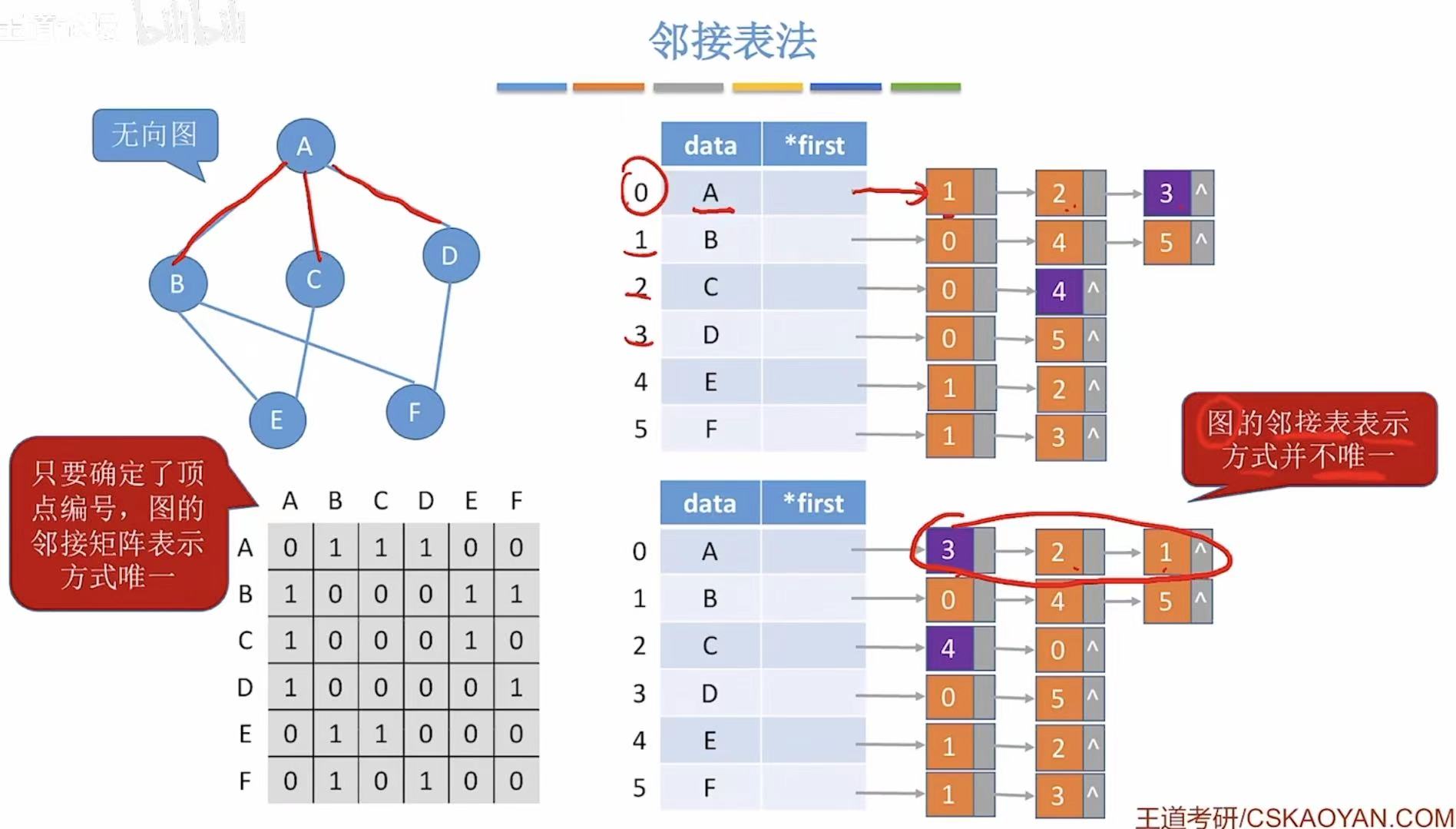
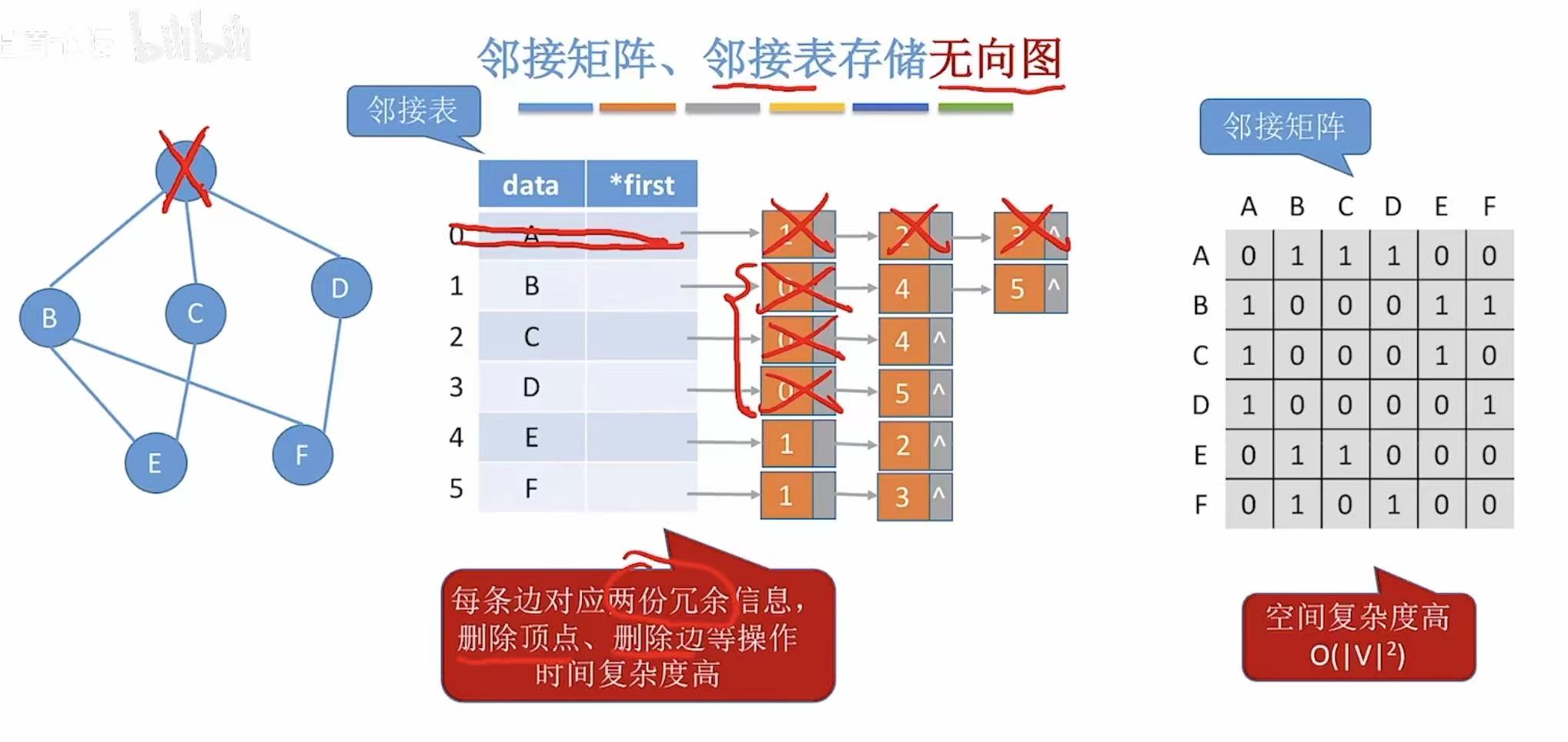
邻接矩阵：因为就0和1来表示，顶点都是按字母顺序排列的，所以表示方式唯一。
邻接表：因为后面用链表链接的序号可以随意排序，所以表示方式并不唯一。

2.2 小结

3. 十字链表法

前两种存储方式的缺点：

邻接表：和树的孩子表示法相同的缺点，都是data不好找。
邻接矩阵：因为直接是一个这么宽的表，太浪费空间了。

全新优化版-->十字链表法：
空间复杂度：ABCD-->顶点|V|+01、02...七个长方形对应七个边-->|E|
橙色：别人指向自己
绿色：自己指向别人

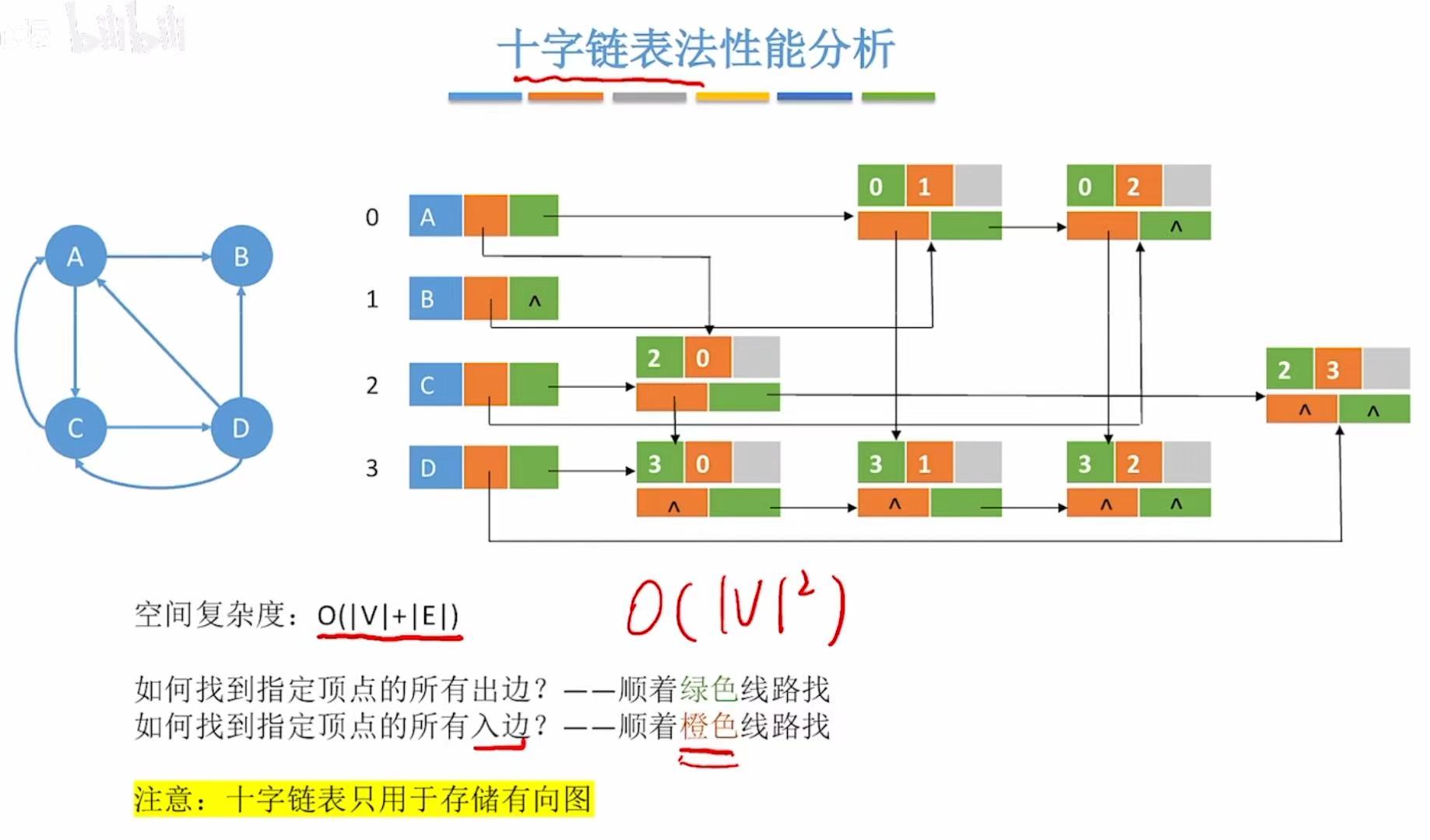
对比之前：

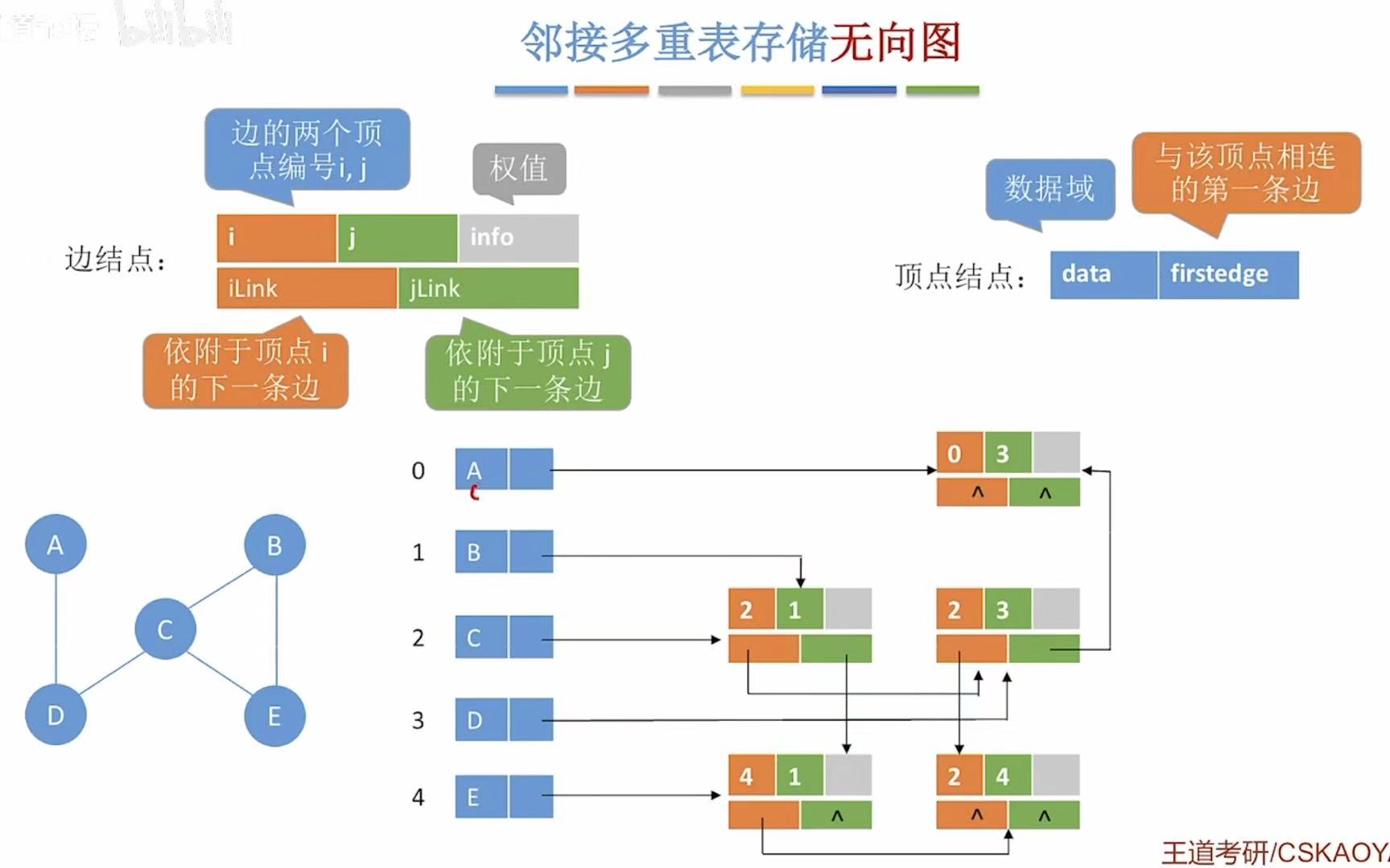
4. 邻接多重表

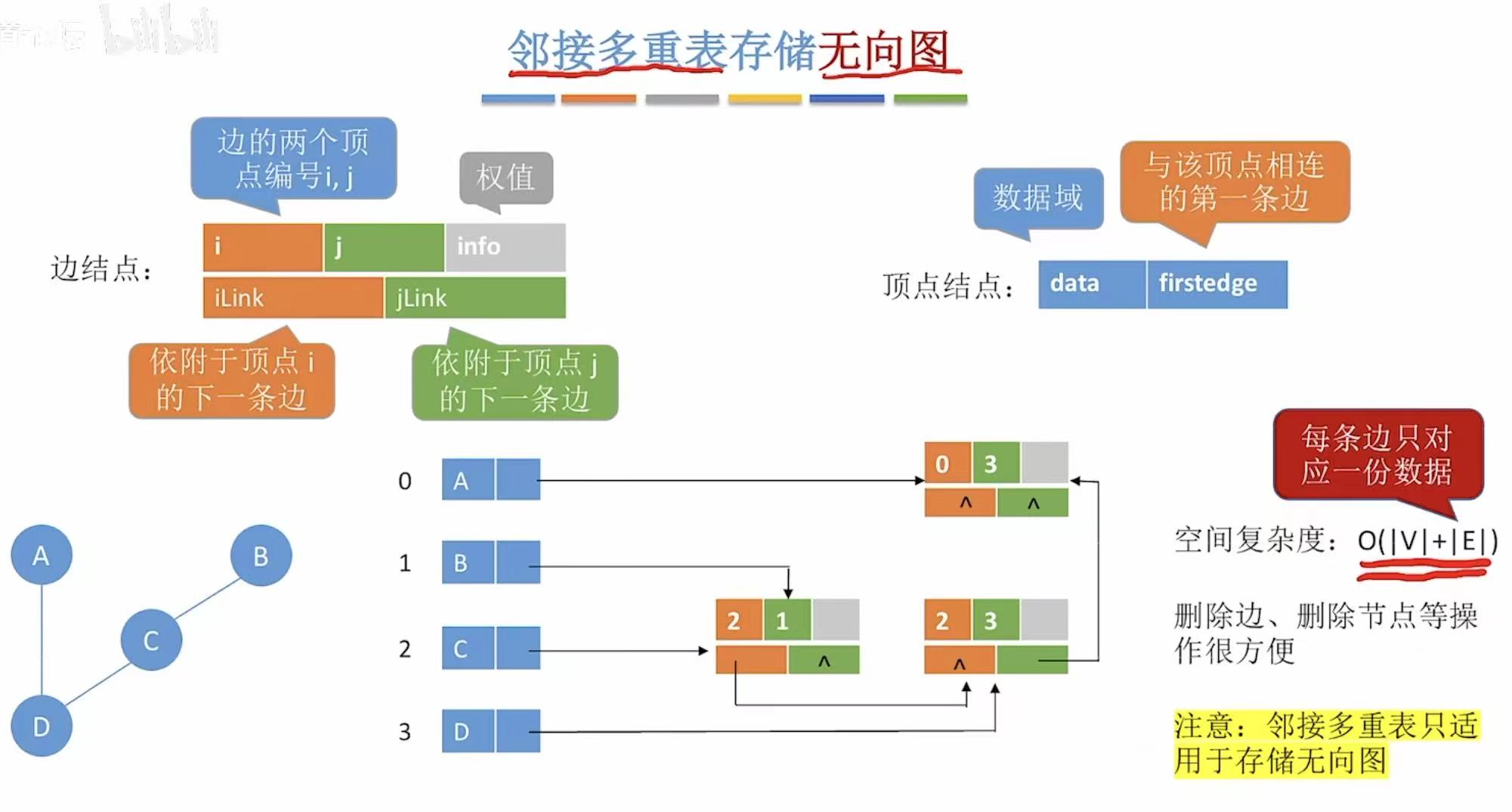
因为用来存无向图，所以顶点后面就不需要分橙or绿了。

空间复杂度：ABCD-->顶点|V|+三个边-->|E|

图的基本操作

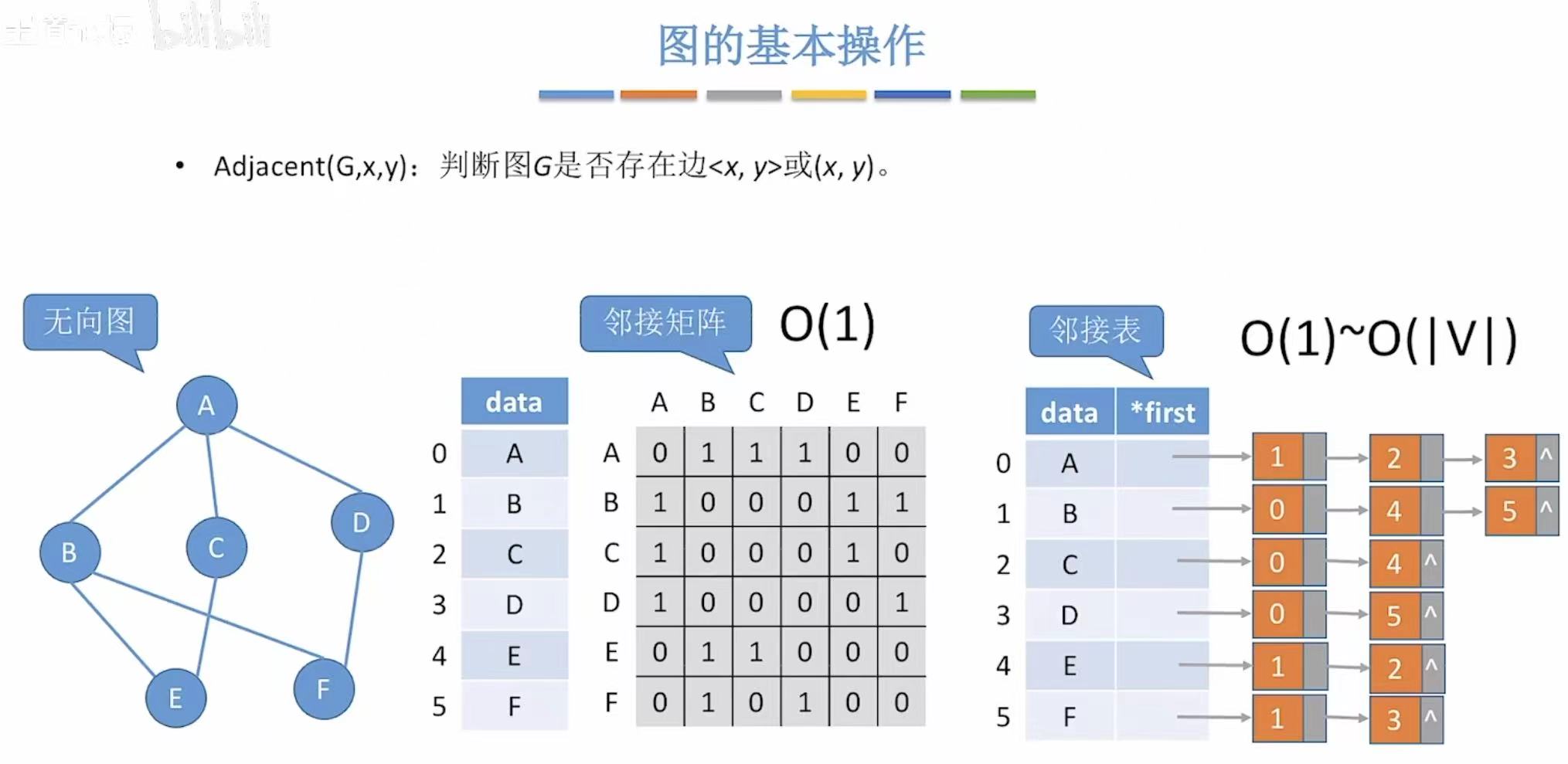
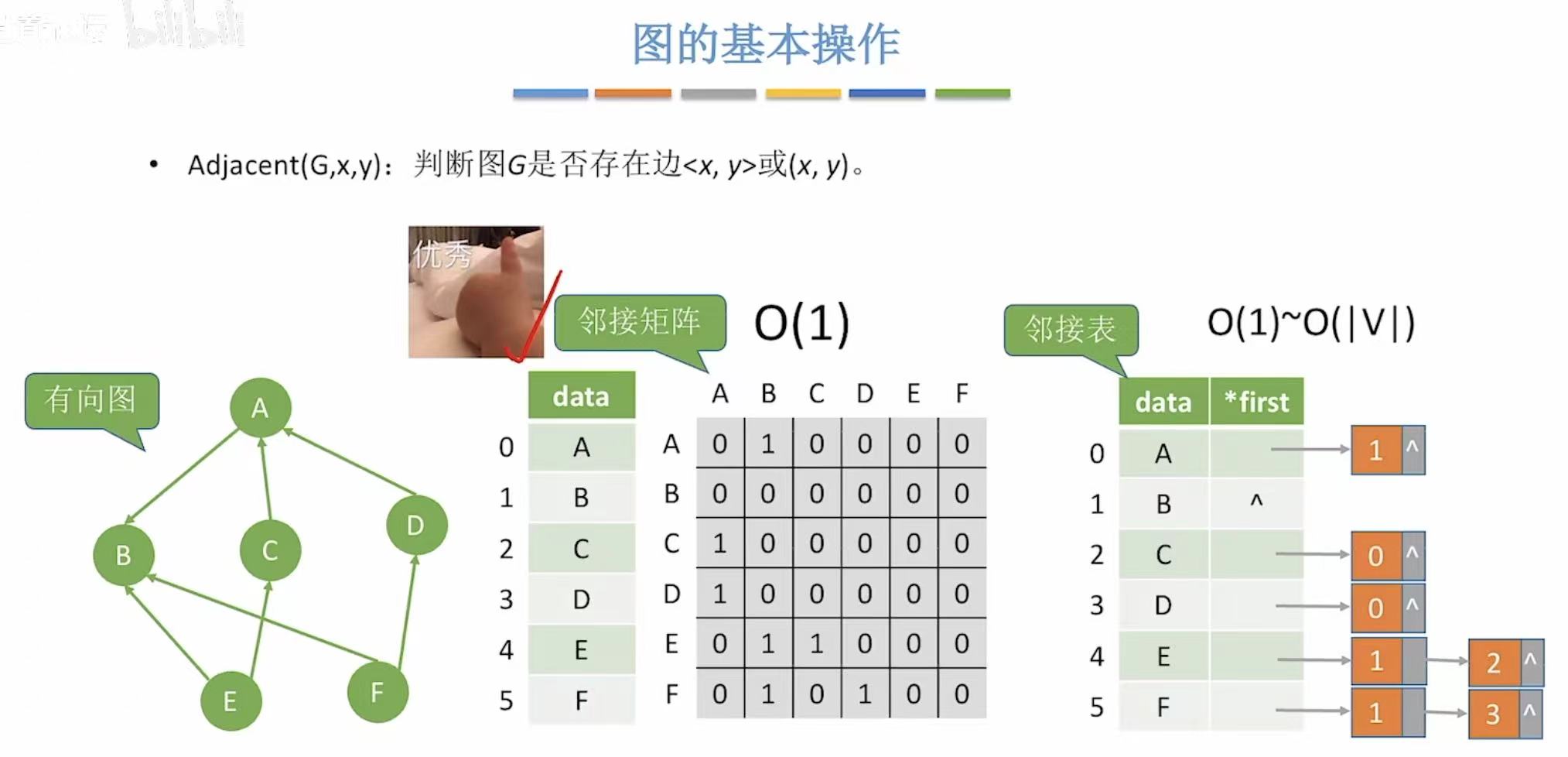
1. Adjavent-->边存在

邻接矩阵：看这个两个顶点相交的位置是1是0
邻接表：看其中一个顶点后面有没有连着另外一个顶点的编号

无向图：

有向图：

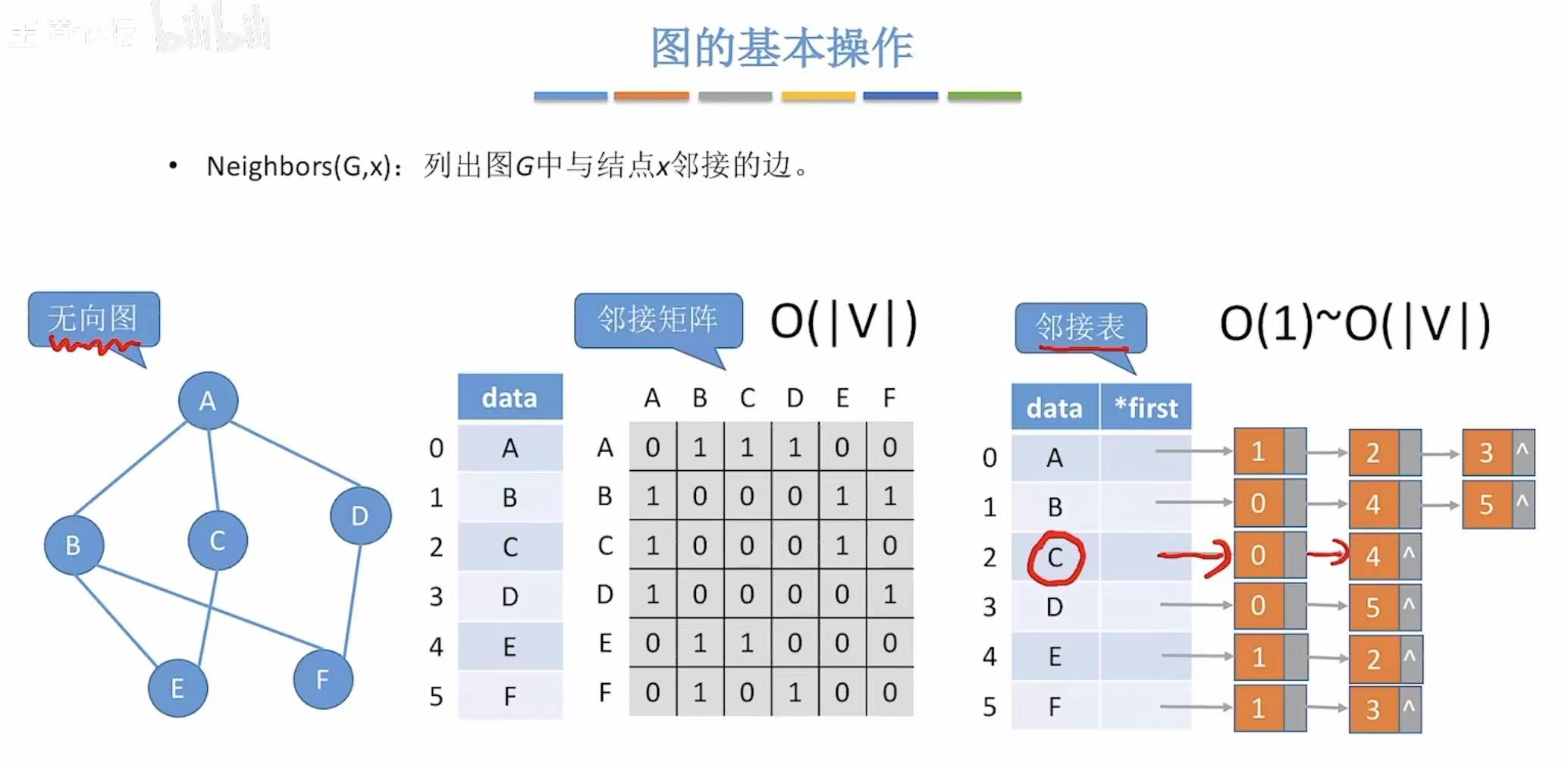
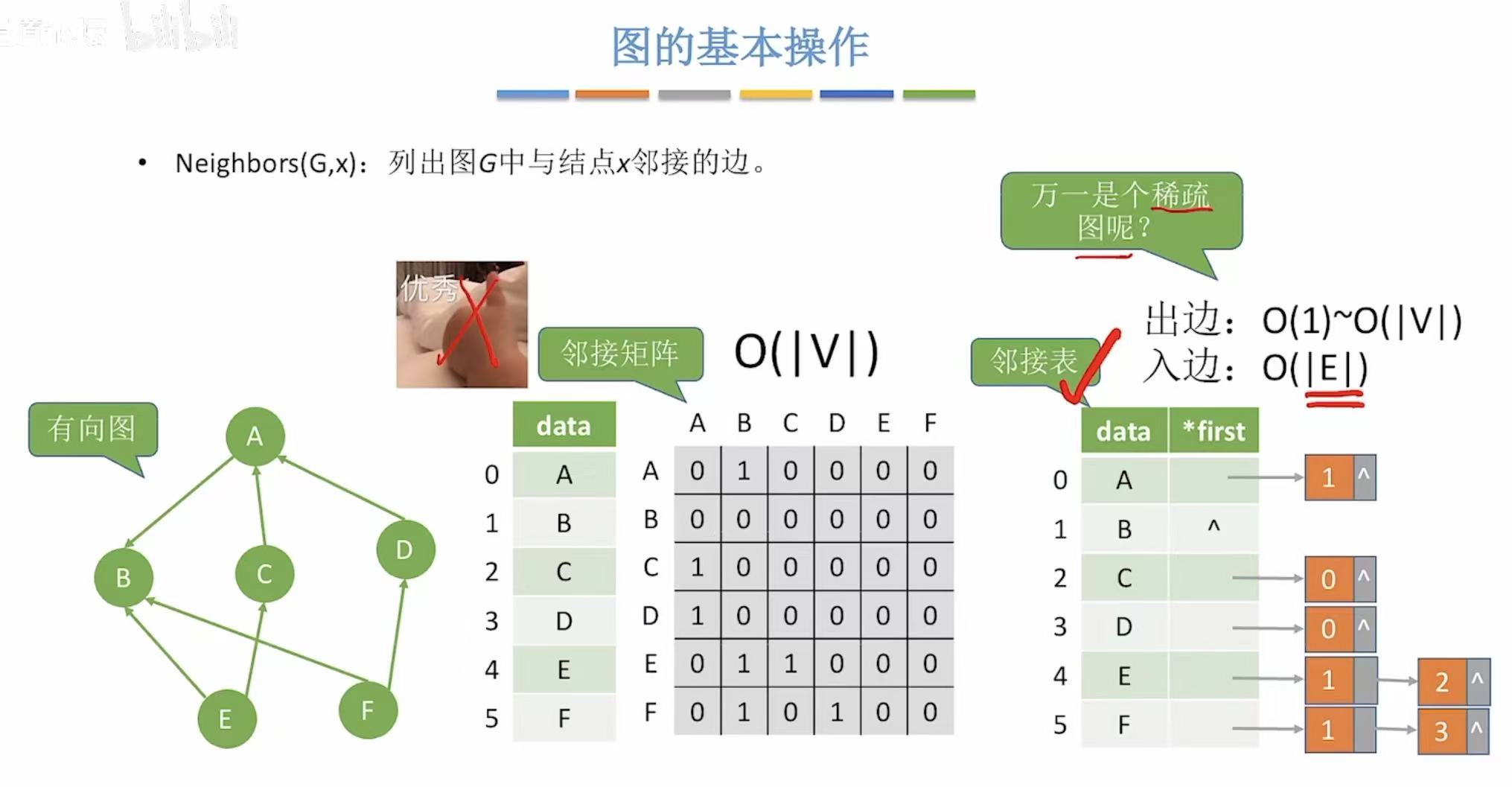
2. Neighbors-->邻接边

邻接矩阵：这个顶点在的这一行有几个1，都是和谁相交有1
邻接表：这个顶点后面都和谁相连

无向图：

有向图：

3. InsertVertex-->插入点

相当于往下初始化一个顶点。

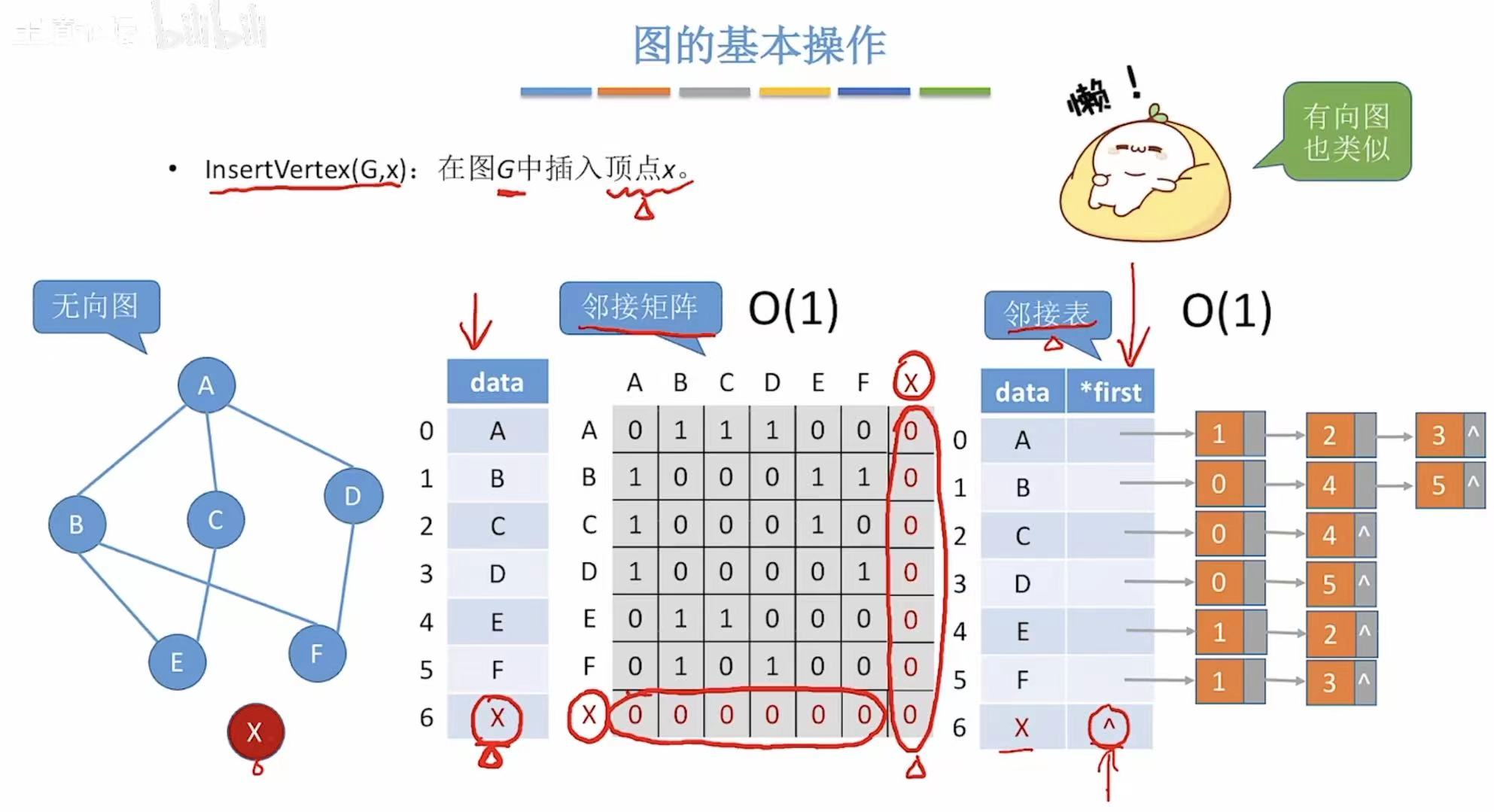
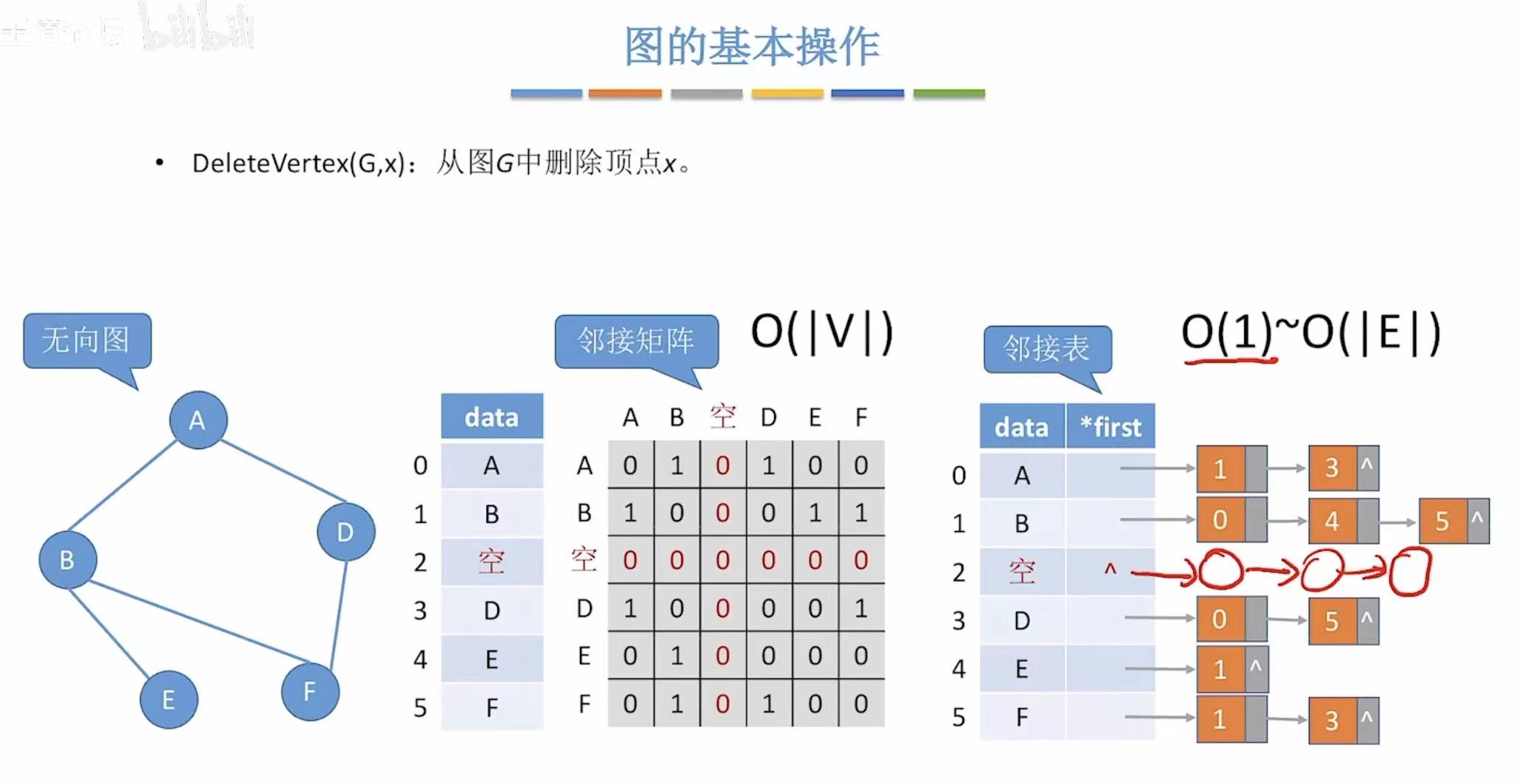
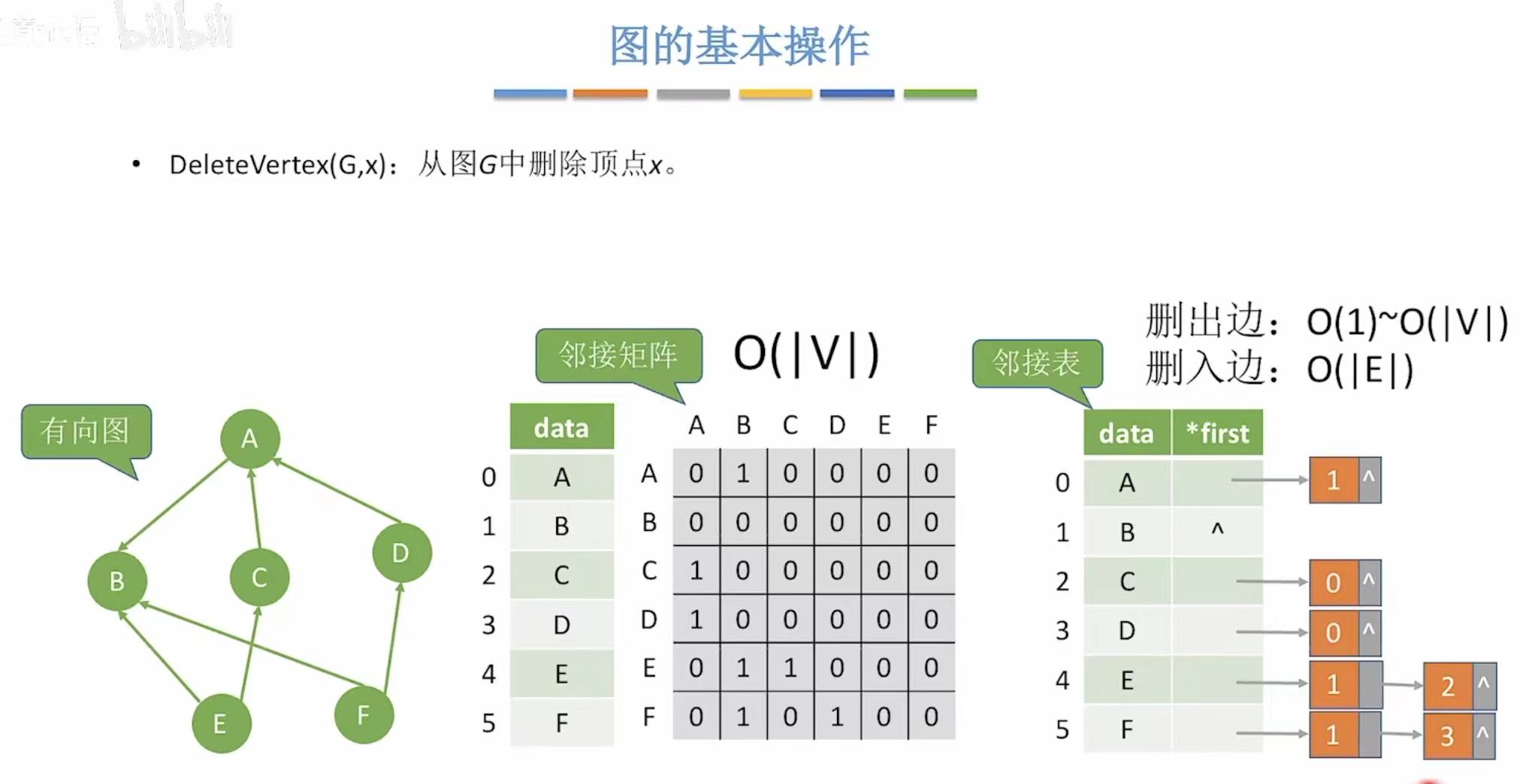
4. DeleteVertex-->删除点

就是从逻辑上（看起来是这样，但其实还存着，不过新数据可能会给它覆盖掉）把这个点删除。

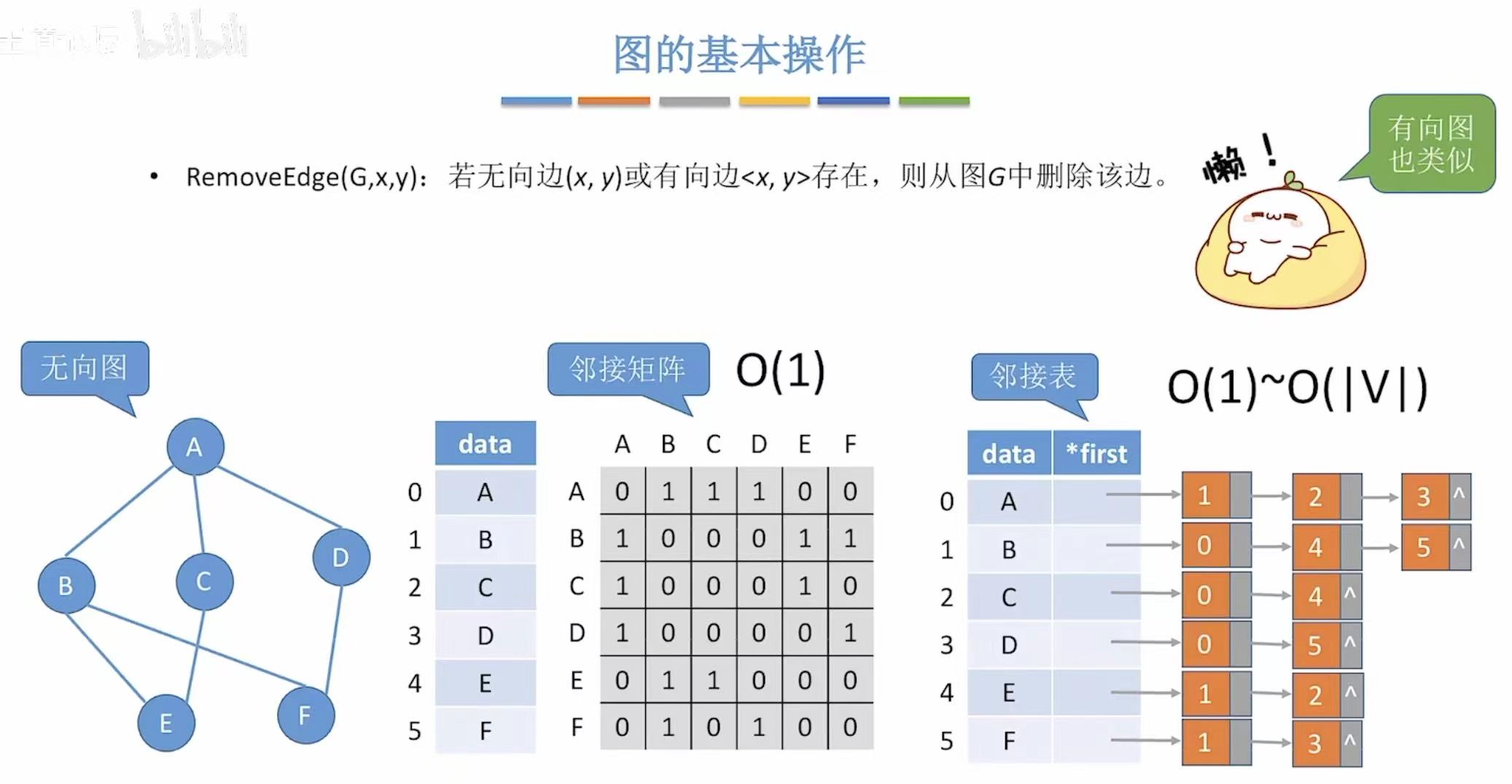
5. RemoveEdge-->删除边

邻接矩阵：相交的点置为0
邻接表：后面相连的直接砍掉

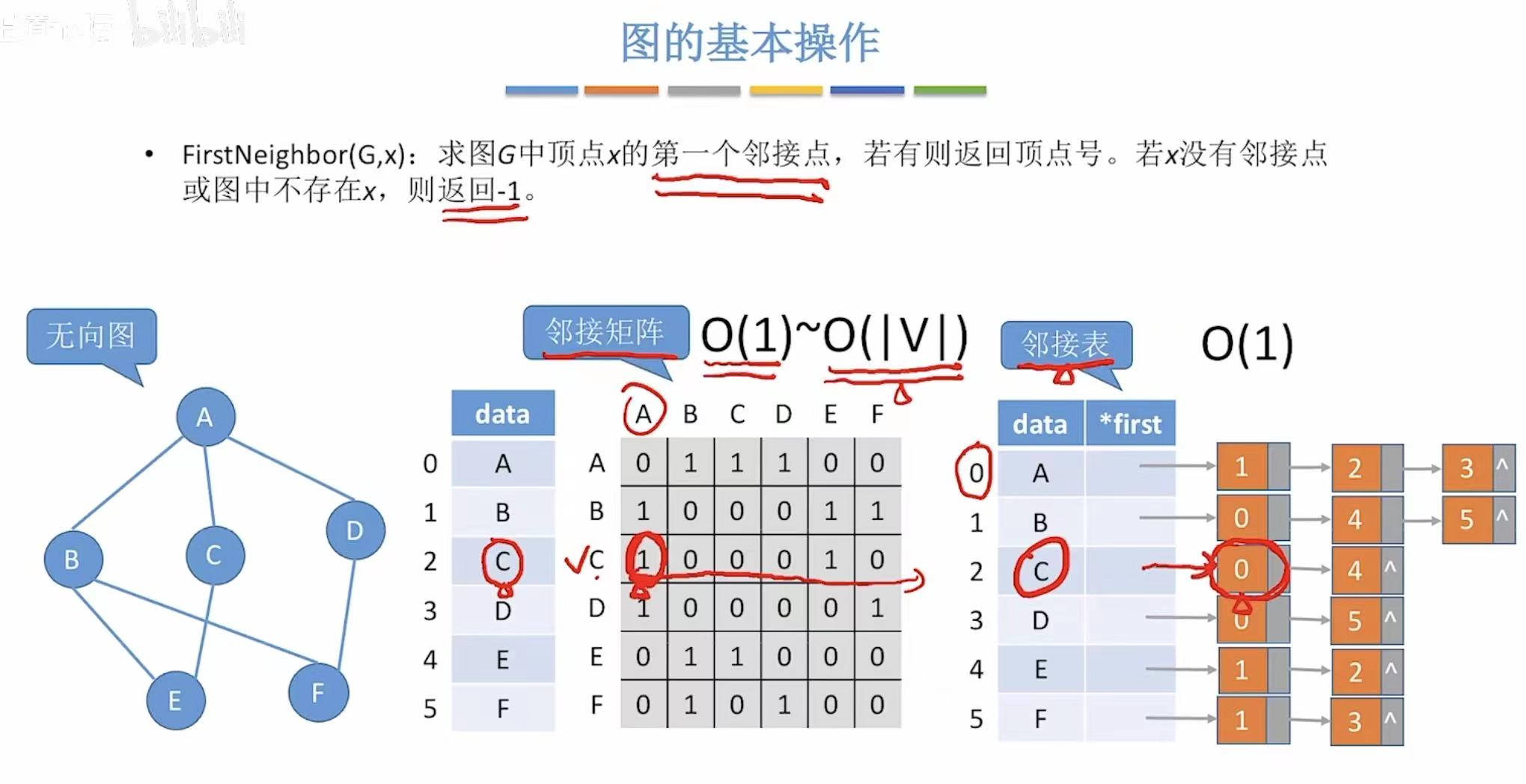
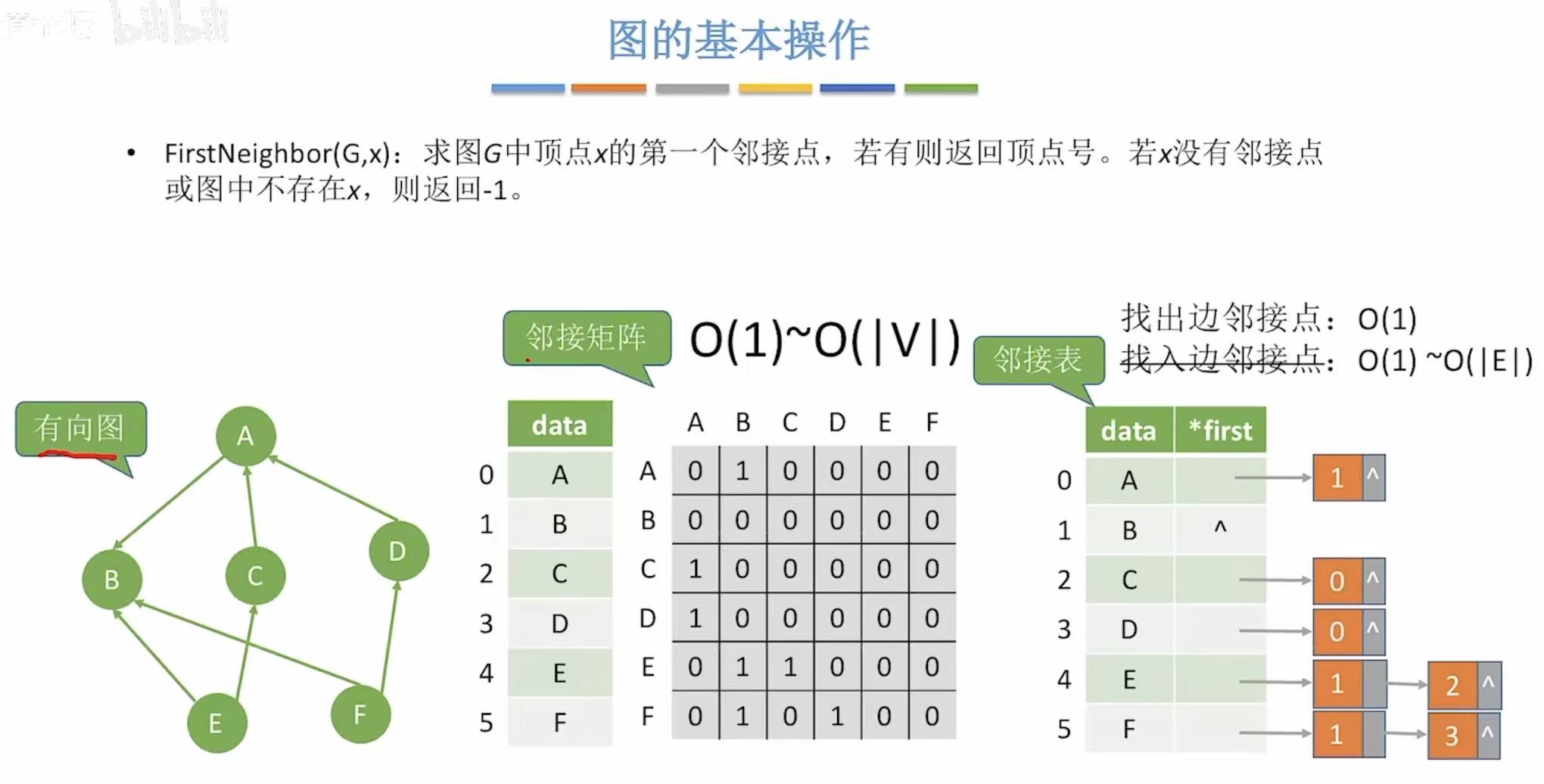
6. FirstNeighbor-->第一个邻接点

邻接矩阵：一行中从左往右看到的第一个1
邻接表：与表格直接相连的长方形

无向图：

有向图：

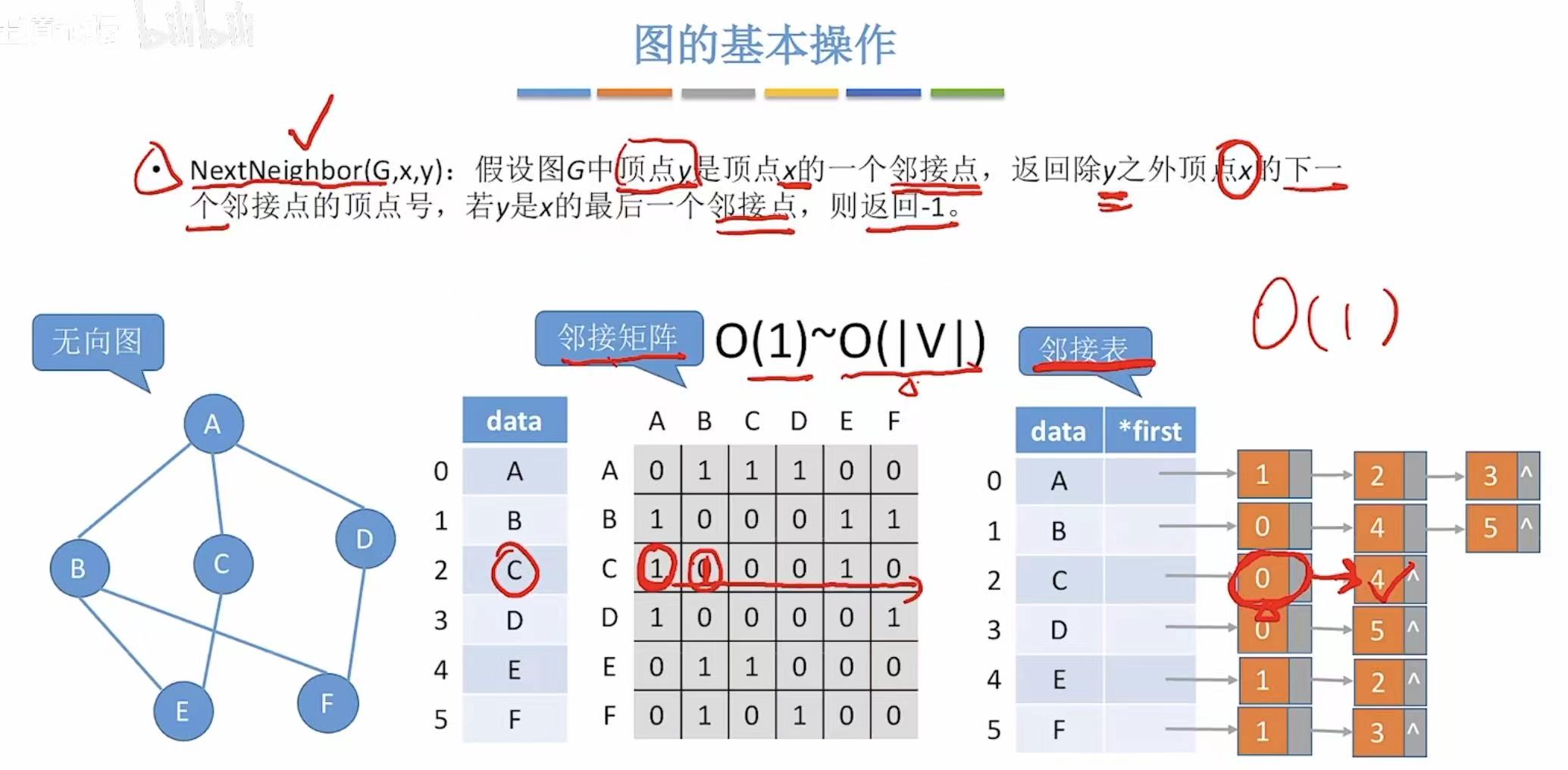
7. NextNeighbor-->下一个邻接点

邻接矩阵：

从列 y+1 开始，向右扫描第 x 行；
找到第一个 A[x][j] == 1 的列 j；
返回 j（即下一个邻接点）；
如果找不到，返回 -1（表示无更多邻接点）。
NextNeighbor(2, 1) → 从列2开始找，第一个1在列3 → 返回3

邻接表：

遍历顶点 x 的邻接链表；
找到 adjvex == y 的那个 ArcNode 节点；
返回该节点的 next->adjvex（如果 next 存在）；
否则返回 -1。

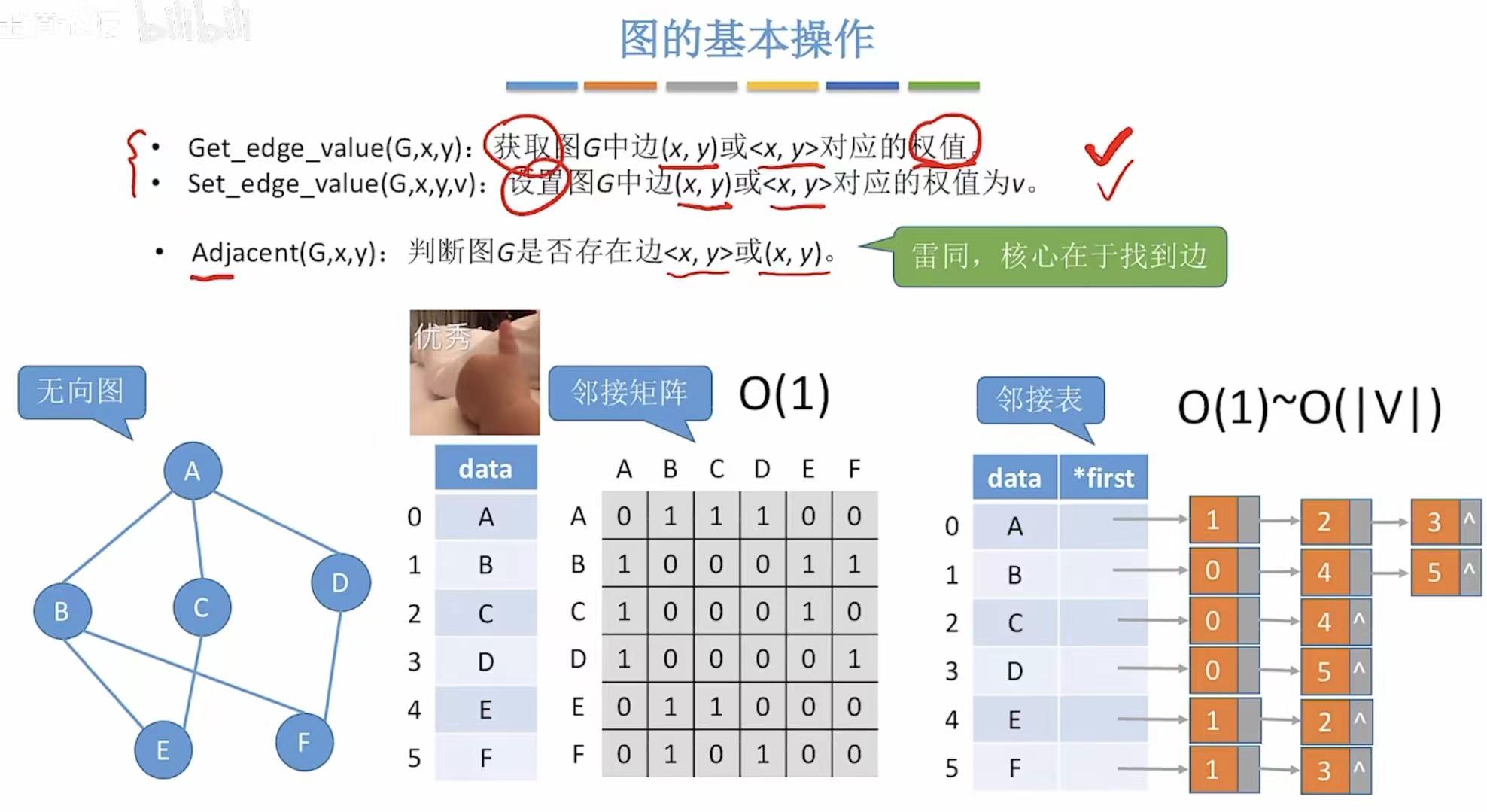
8. 获取/设置权值

图的遍历

1. 广度优先遍历（BFS）

广度优先遍历 ：就是一个顶点和谁相邻，就把相邻的点全部遍历到，再反复重复这个过程。

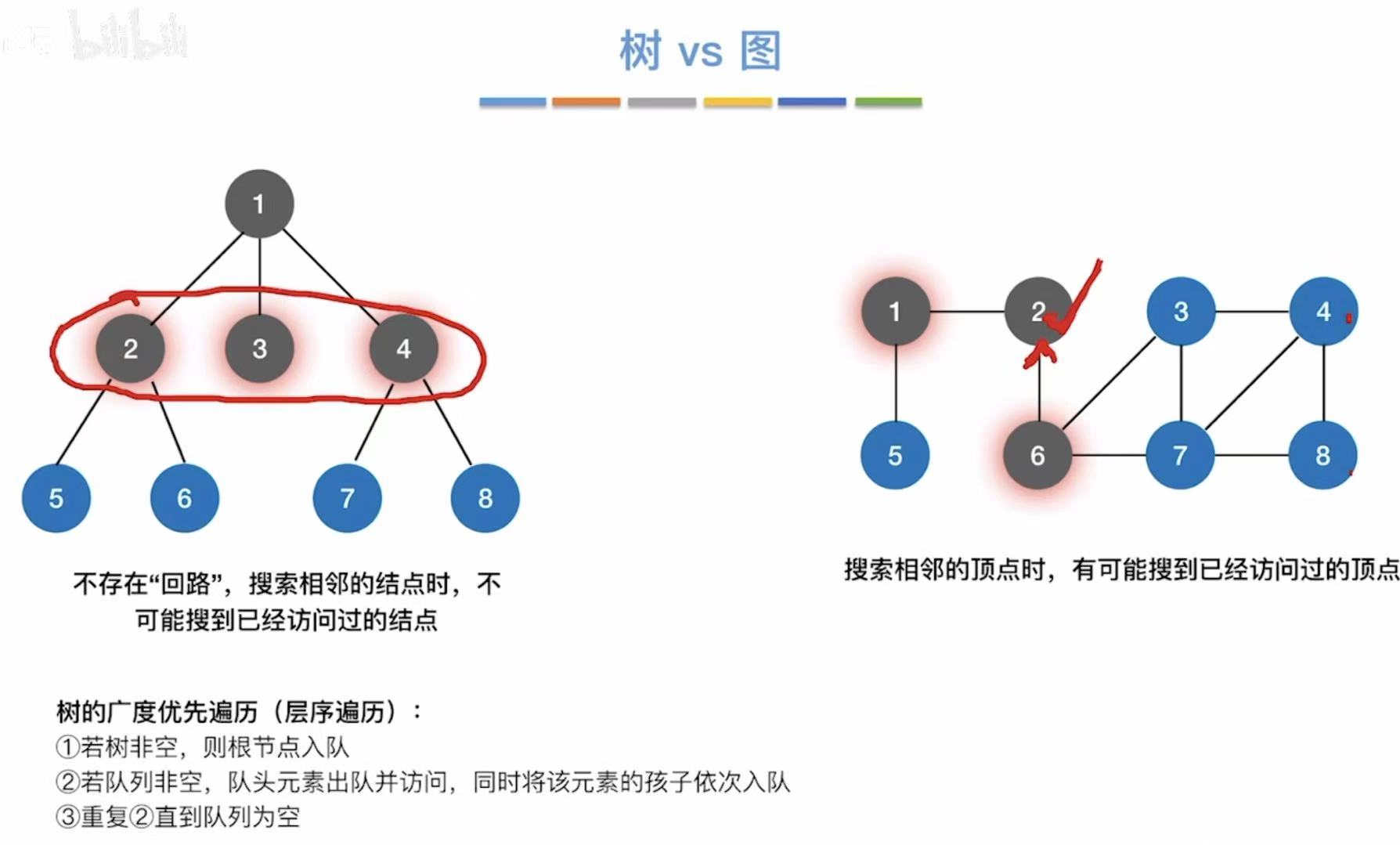
1.1 与树的广度优先遍历之间的联系

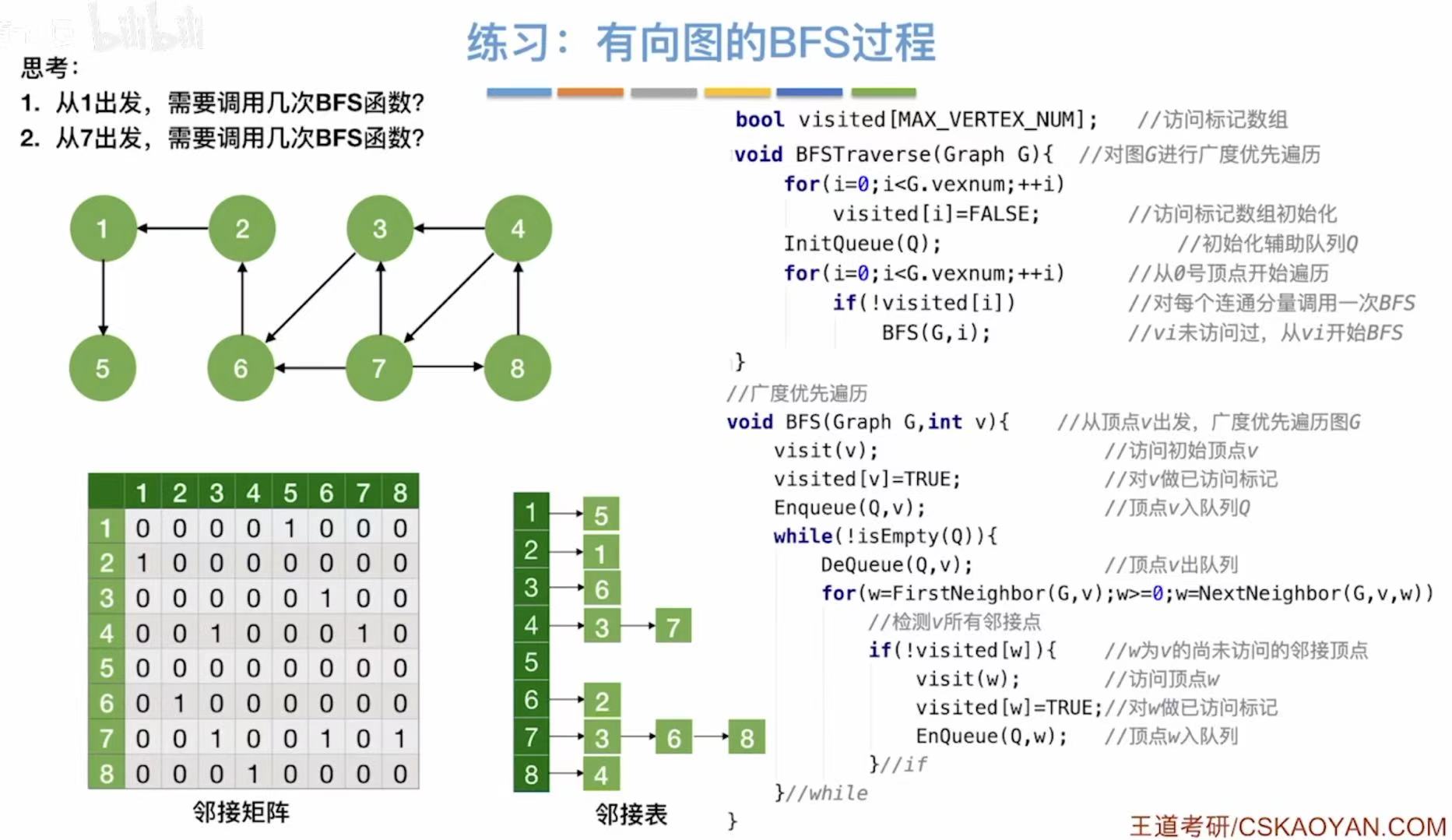
区别：遍历的过程中，树不可能有访问过的结点，而图可能会有访问过的顶点。

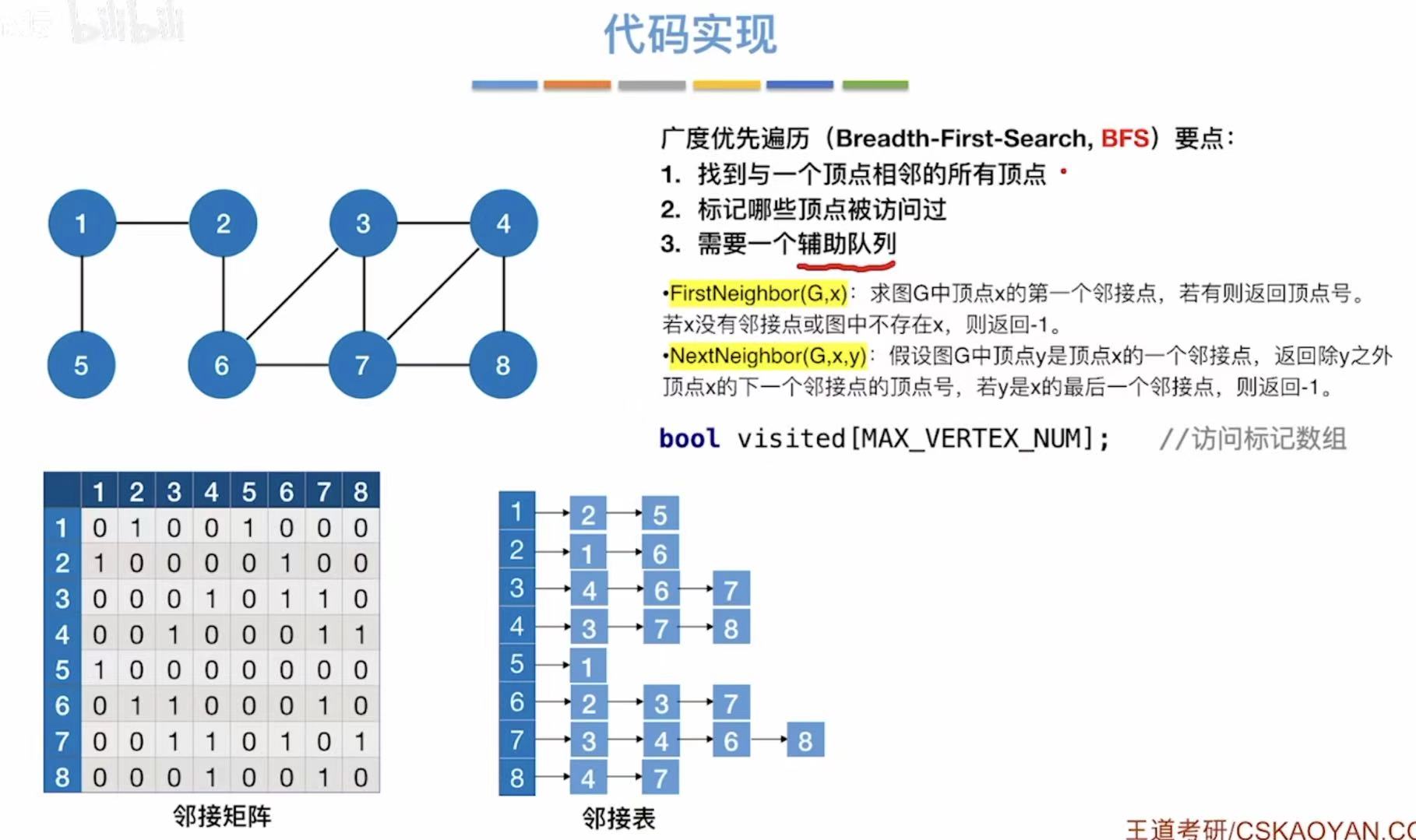
1.2 代码实现

比如挑2作为开始遍历的点
FirstNeighbor就可以以2为中心，找这个顶点的第一个邻接点-->1
NextNeighbor就可以在"2 的邻接点列表中"，找到紧跟在 1 后面的那个邻接点5。

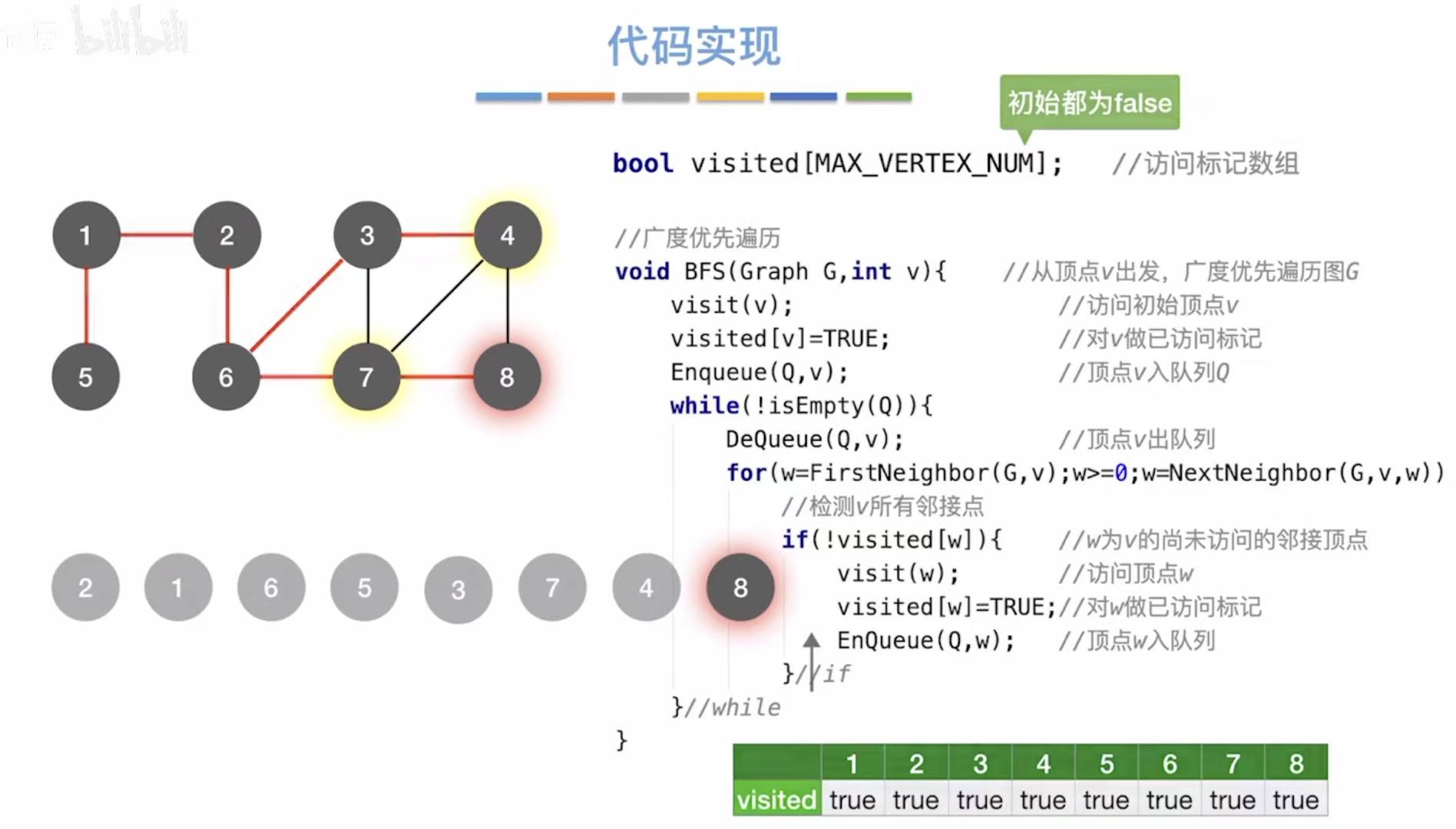
java 复制代码

// 访问标记数组：记录每个顶点是否已被访问过
// 初始时所有值都为 false（未访问）
bool visited[MAX_VERTEX_NUM];   // 访问标记数组

// 广度优先遍历函数
void BFS(Graph G, int v) {
    visit(v);                     // 访问起始顶点 v（如打印或处理数据）

    visited[v] = TRUE;            // 将顶点 v 标记为已访问

    Enqueue(Q, v);                // 将顶点 v 入队列 Q（准备开始遍历）

    while (!isEmpty(Q)) {         // 当队列不为空时，继续遍历
        DeQueue(Q, v);            // 从队列中取出一个顶点 v（先进先出）

        // 遍历当前顶点 v 的所有邻接点 w
        // 使用 FirstNeighbor 和 NextNeighbor 枚举所有邻接点
        for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
            if (!visited[w]) {    // 如果邻接点 w 还未被访问
                visit(w);         // 访问该邻接点 w
                visited[w] = TRUE;// 标记为已访问
                EnQueue(Q, w);    // 将 w 入队列，等待后续处理
            }
        }
    }
}

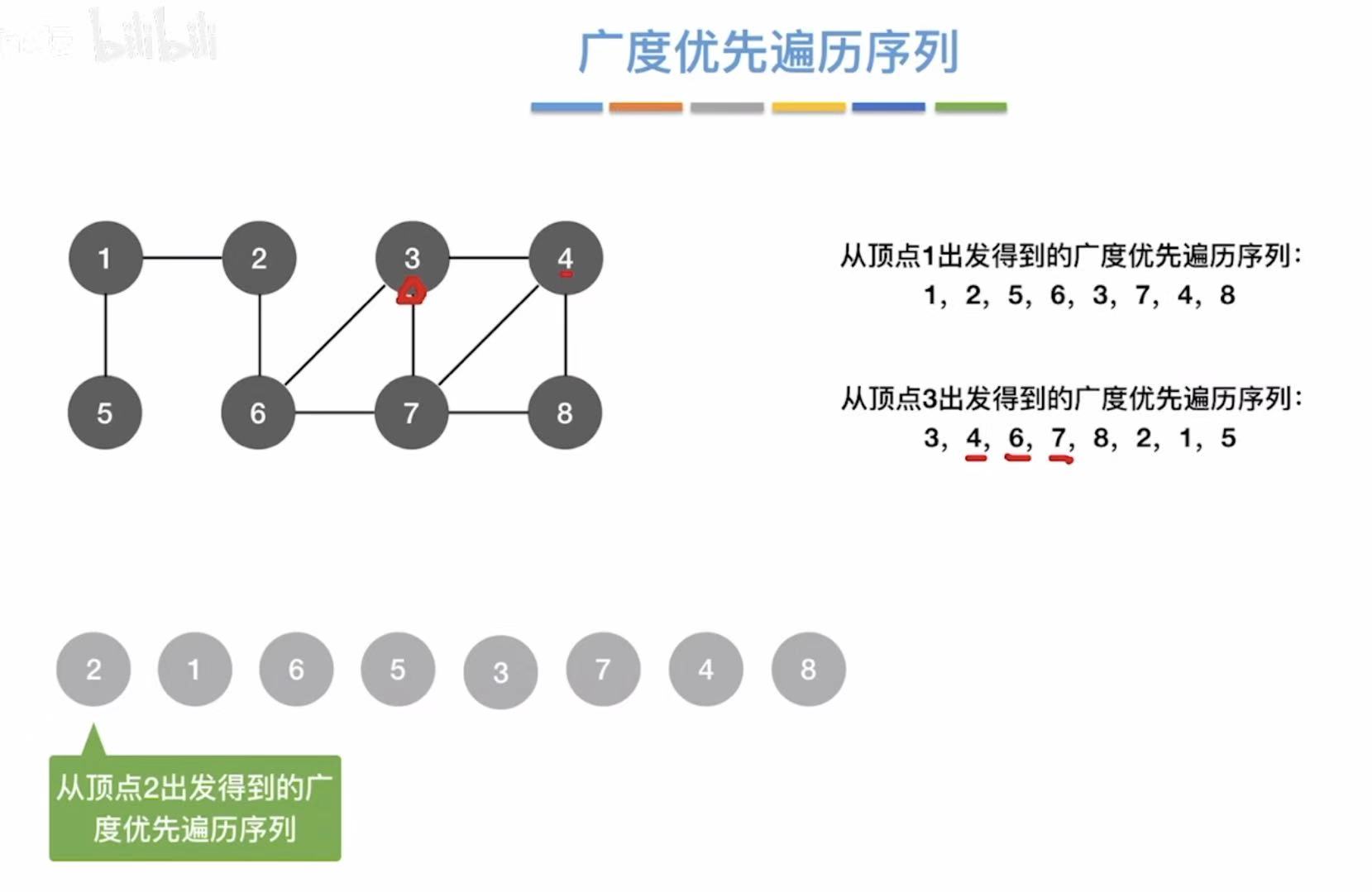
1.3 遍历序列

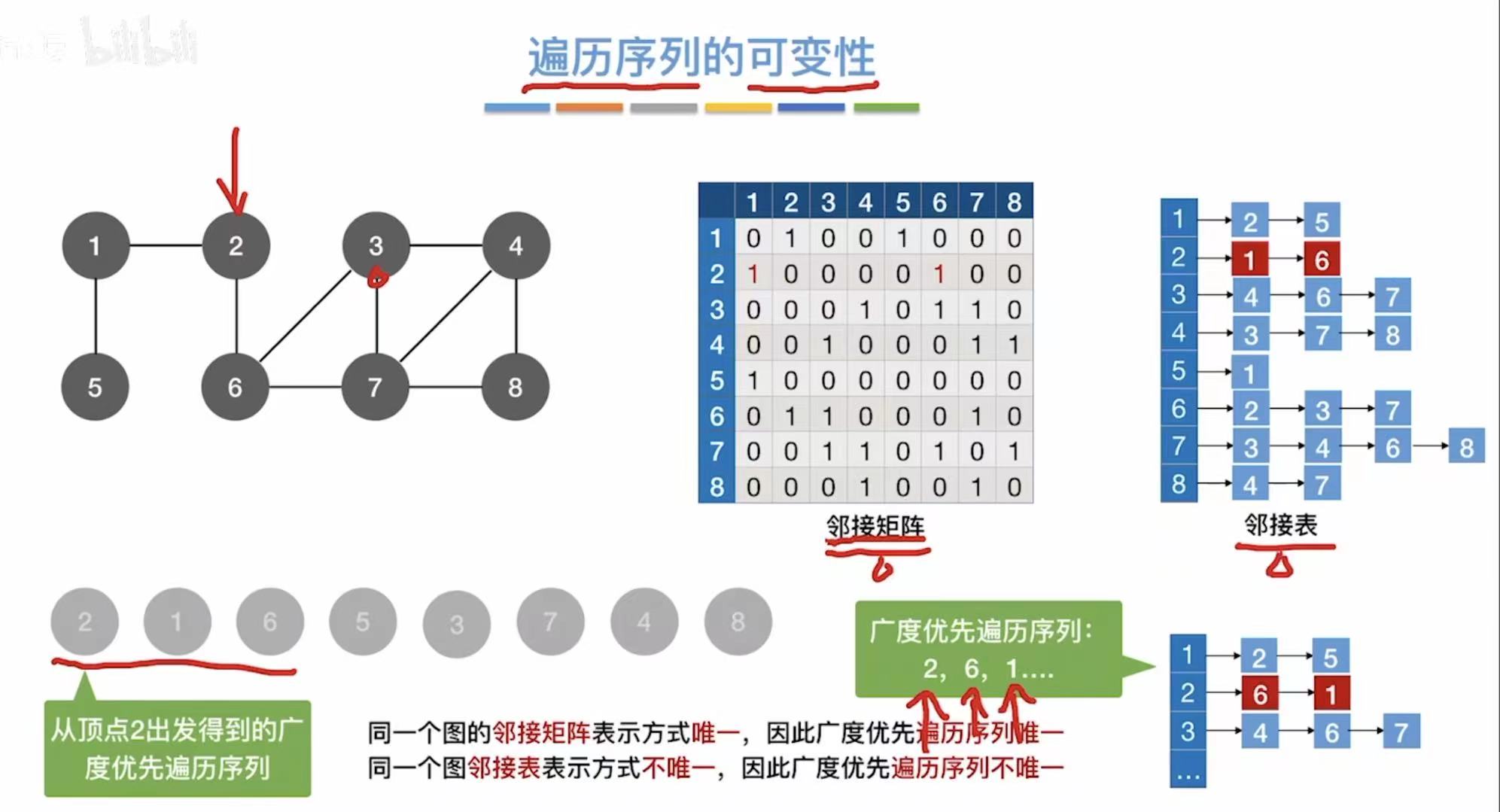
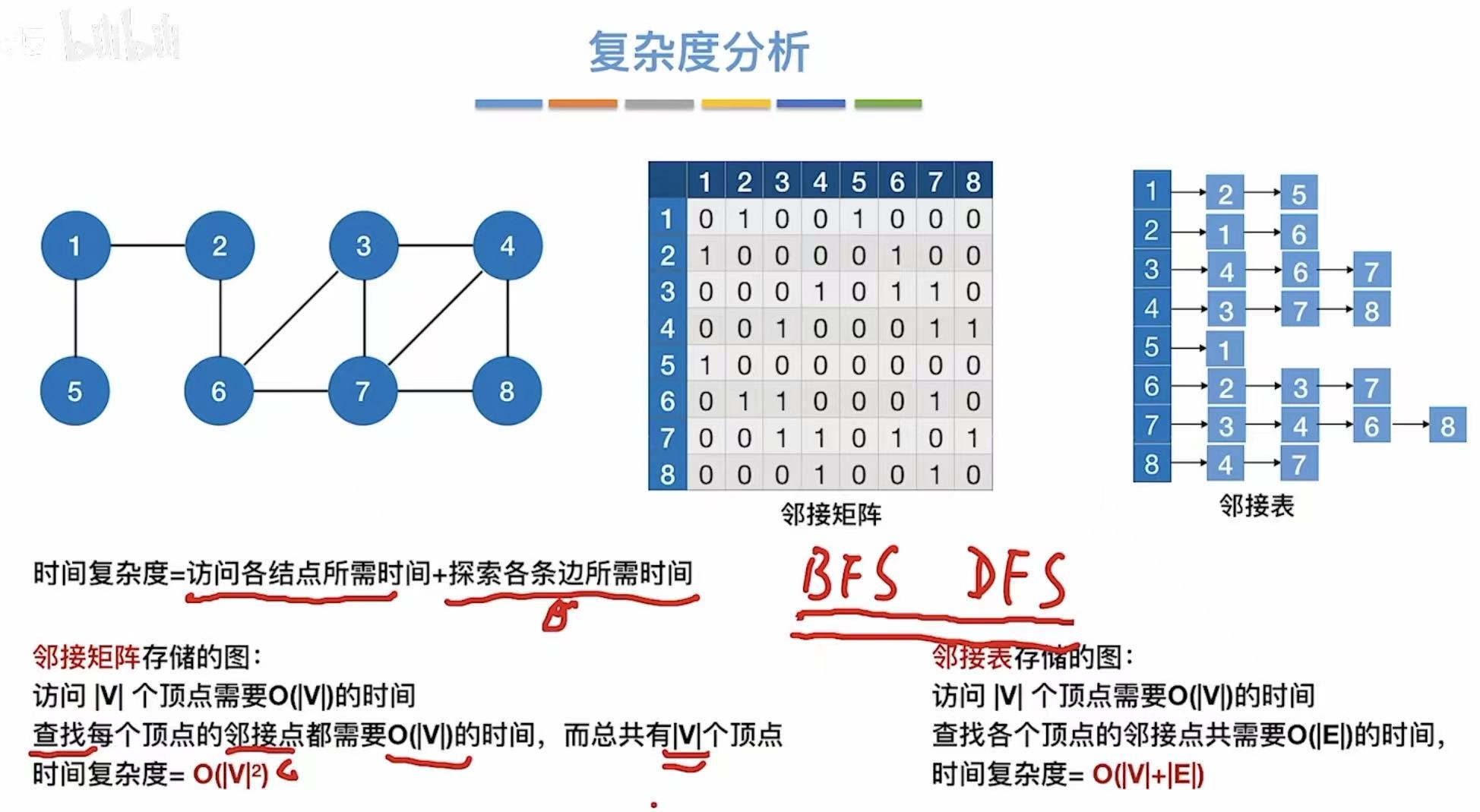
邻接矩阵：因为就0和1来表示，顶点都是按数字顺序排列的，所以表示方式唯一。
邻接表：因为后面用链表链接的序号可以随意排序，所以表示方式并不唯一。

1.4 最终实现

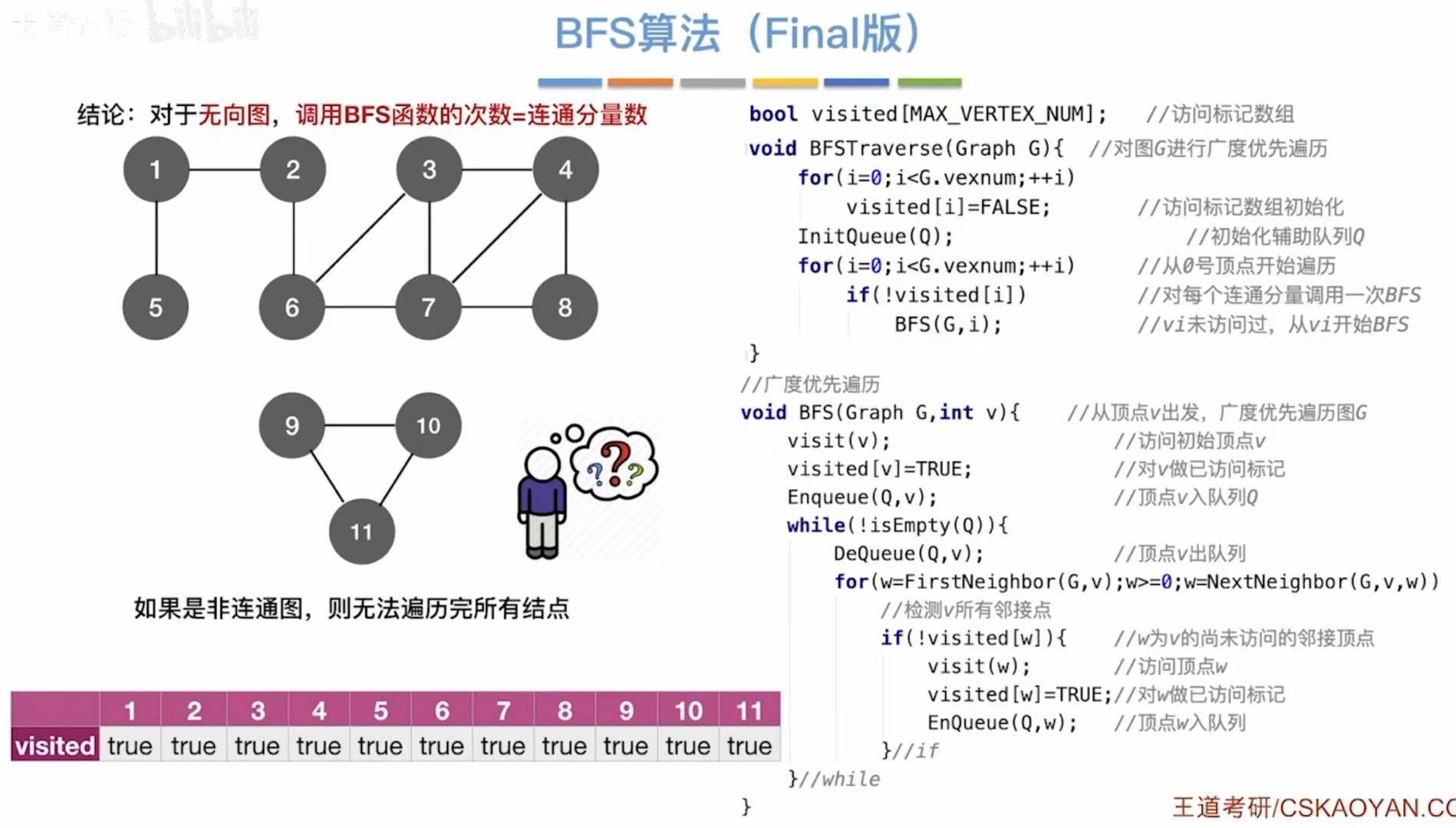
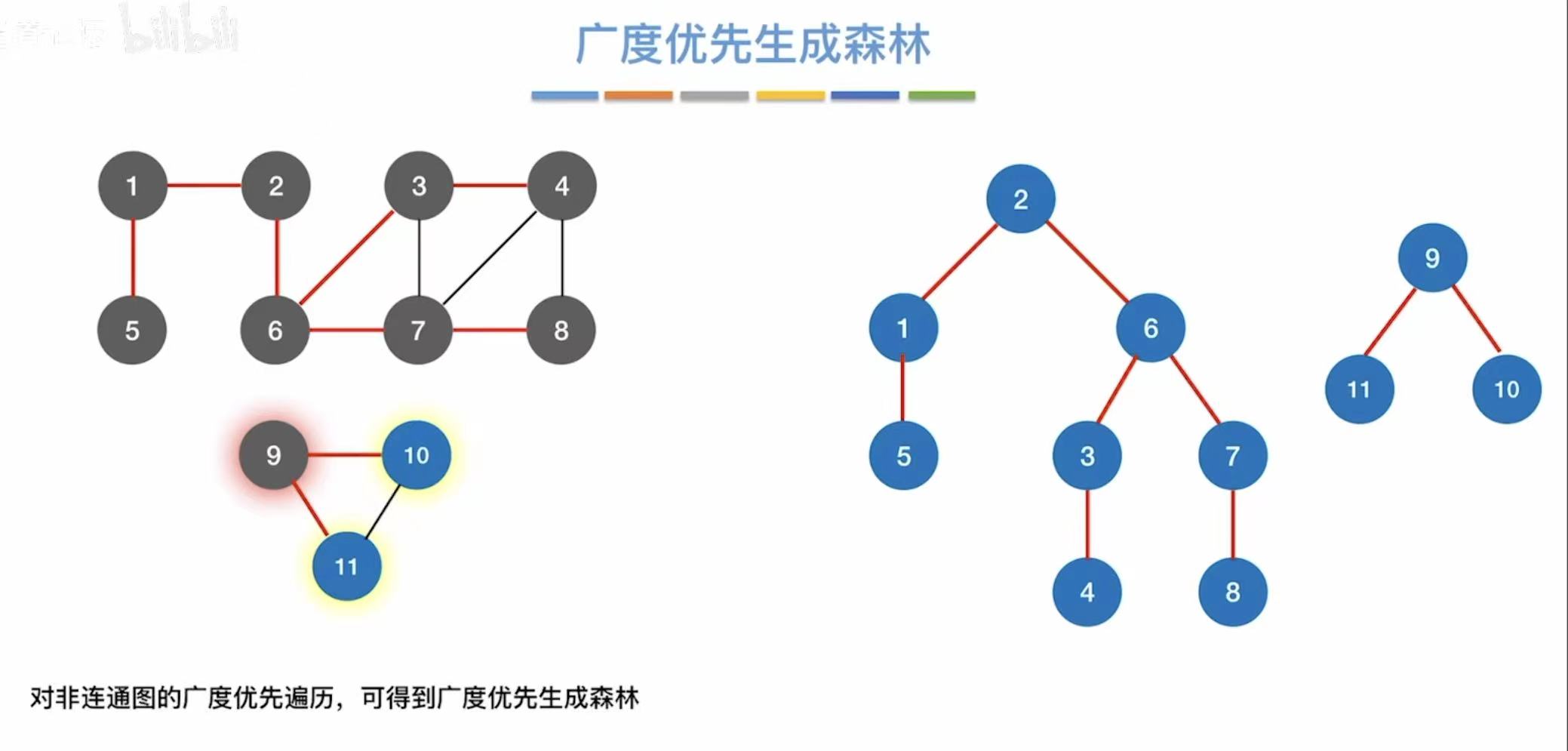
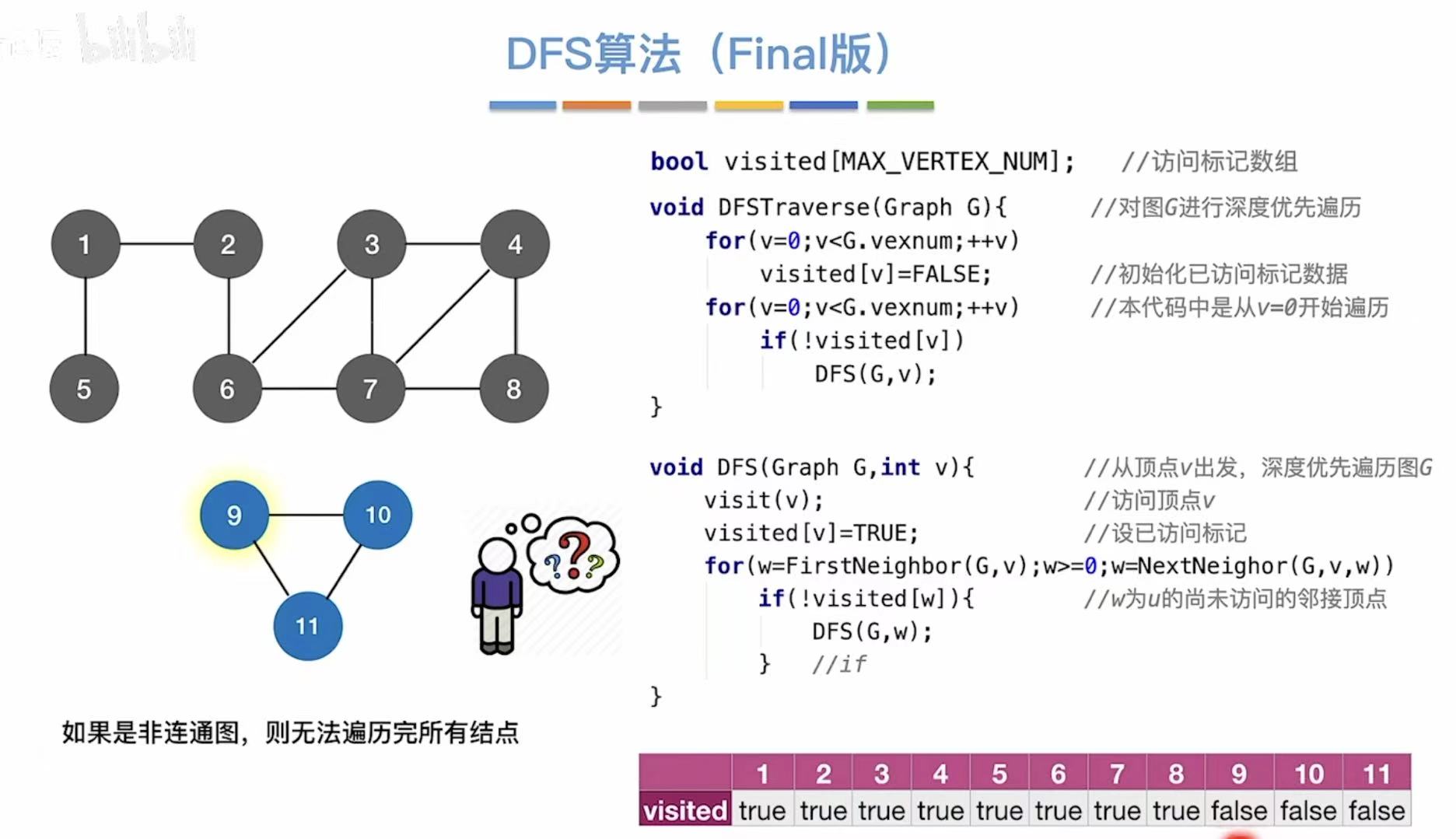
如果是非连通图，就没办法全部遍历到，所以我们就需要扩充我们的结点表，让没遍历到的结点进行遍历。

java 复制代码

// 访问标记数组：记录每个顶点是否已被访问过
// 初始时所有值都为 false（未访问）
bool visited[MAX_VERTEX_NUM];   // 访问标记数组

// 对图 G 进行广度优先遍历的主函数
void BFSTraverse(Graph G) {
    // 初始化访问标记数组：将所有顶点标记为"未访问"
    for (i = 0; i < G.vexnum; ++i) {
        visited[i] = FALSE;     // 所有顶点初始状态为未访问
    }

    // 初始化辅助队列 Q（用于 BFS 遍历）
    InitQueue(Q);                // 创建空队列

    // 遍历图中的每一个顶点（处理非连通图）
    for (i = 0; i < G.vexnum; ++i) {
        // 如果当前顶点 i 尚未被访问
        if (!visited[i]) {
            // 从该顶点出发，进行一次 BFS 遍历
            BFS(G, i);           // 调用 BFS 函数，遍历以 i 为起点的连通分量
        }
    }
}

// 广度优先遍历函数（从顶点 v 开始）
void BFS(Graph G, int v) {
    visit(v);                    // 访问起始顶点 v（如打印或处理数据）

    visited[v] = TRUE;           // 将顶点 v 标记为已访问

    Enqueue(Q, v);               // 将顶点 v 入队列 Q（准备开始遍历）

    while (!isEmpty(Q)) {        // 当队列不为空时，继续遍历
        DeQueue(Q, v);           // 从队列中取出一个顶点 v（先进先出）

        // 遍历当前顶点 v 的所有邻接点 w
        // 使用 FirstNeighbor 和 NextNeighbor 枚举所有邻接点
        for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
            // 如果邻接点 w 还未被访问
            if (!visited[w]) {
                visit(w);         // 访问该邻接点 w
                visited[w] = TRUE;// 标记为已访问
                EnQueue(Q, w);    // 将 w 入队列，等待后续处理
            }
        }
    }
}

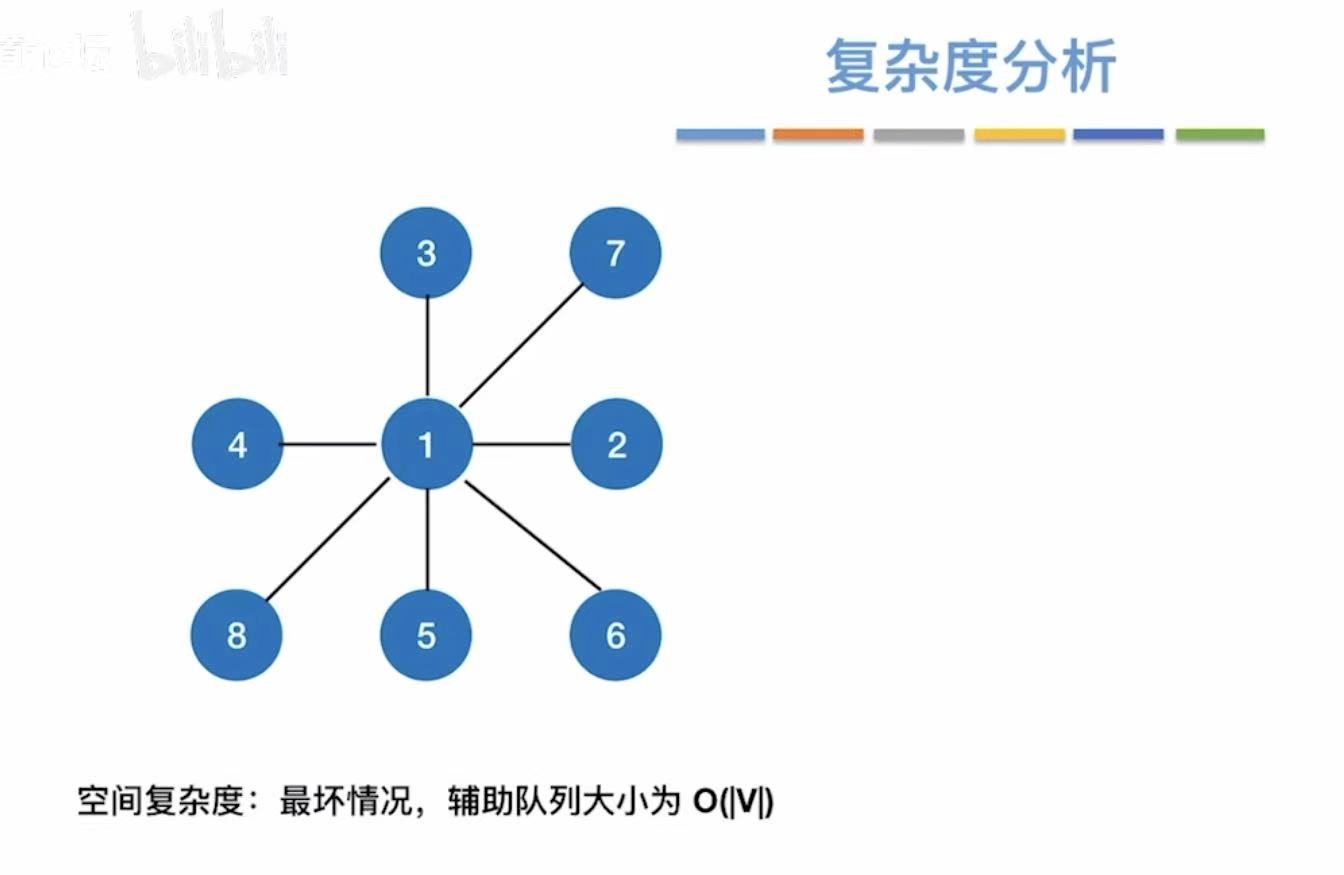
1.5 复杂度分析

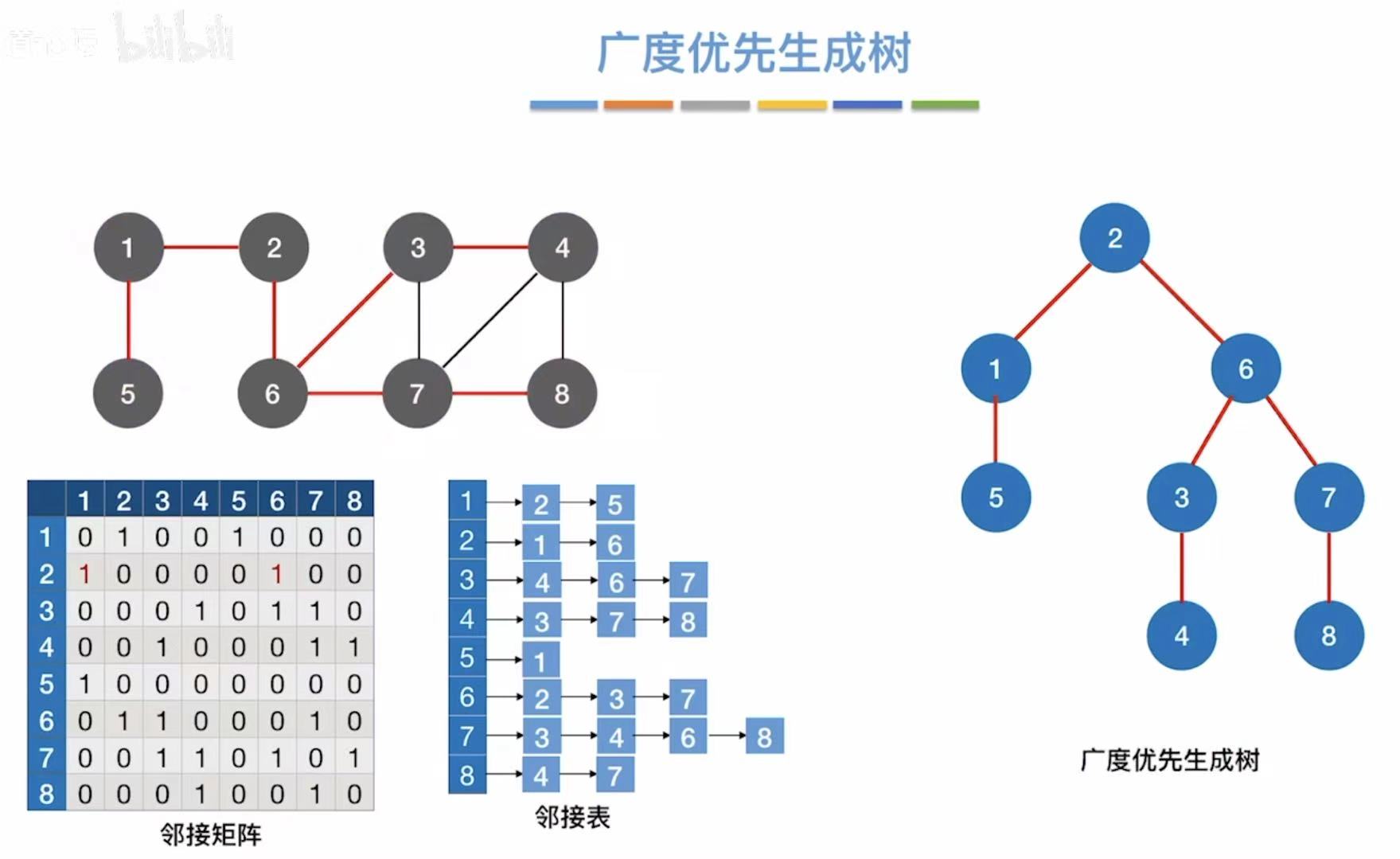
1.6 广度优先生成树

以2为起始点的生成树：

2-->1-->6-->5-->3-->7-->4-->8

2-->1-->6-->5-->7-->3-->4-->8

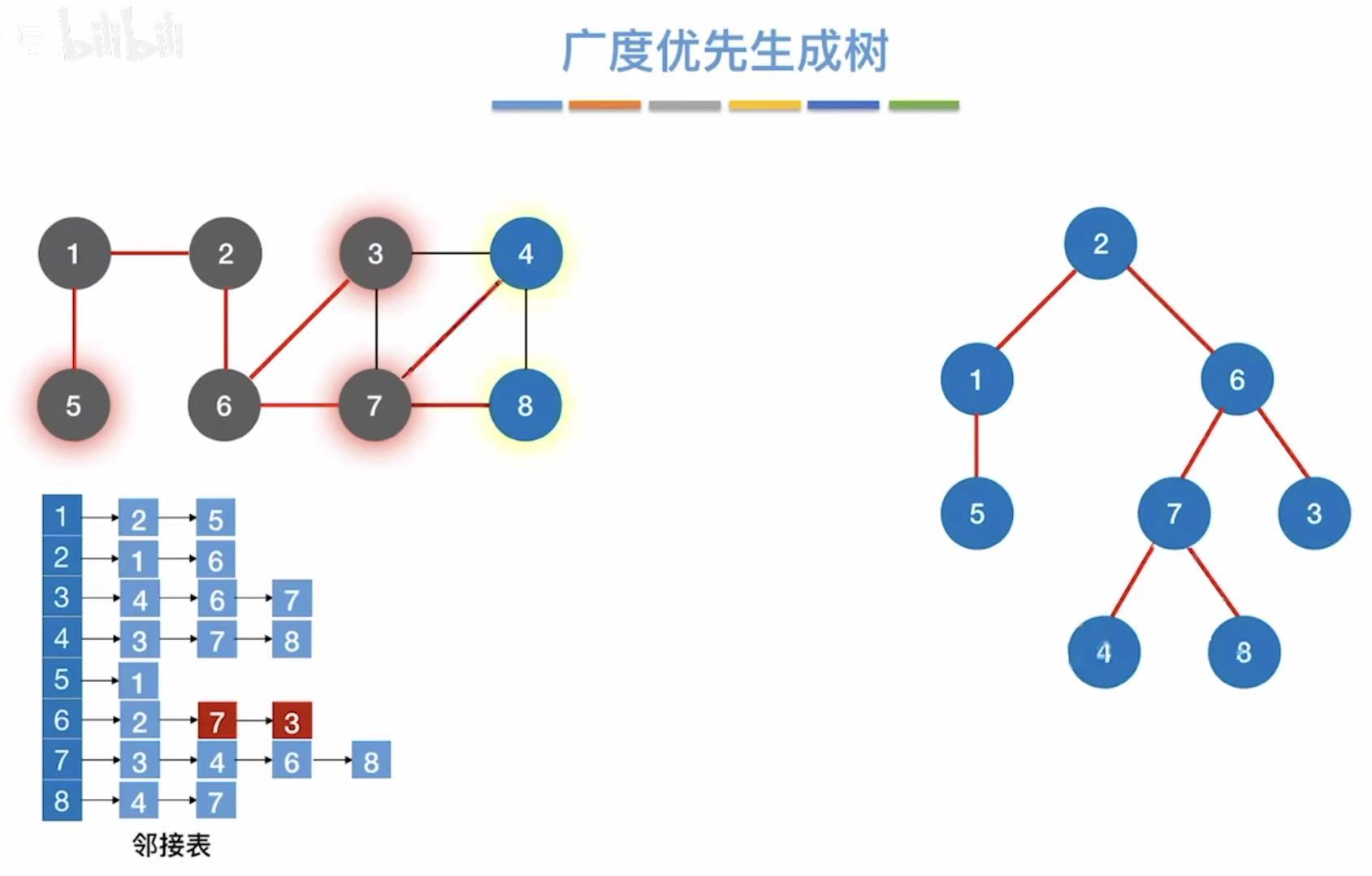
由此可见，访问顺序与路径的不同都会导致生成树的不同。

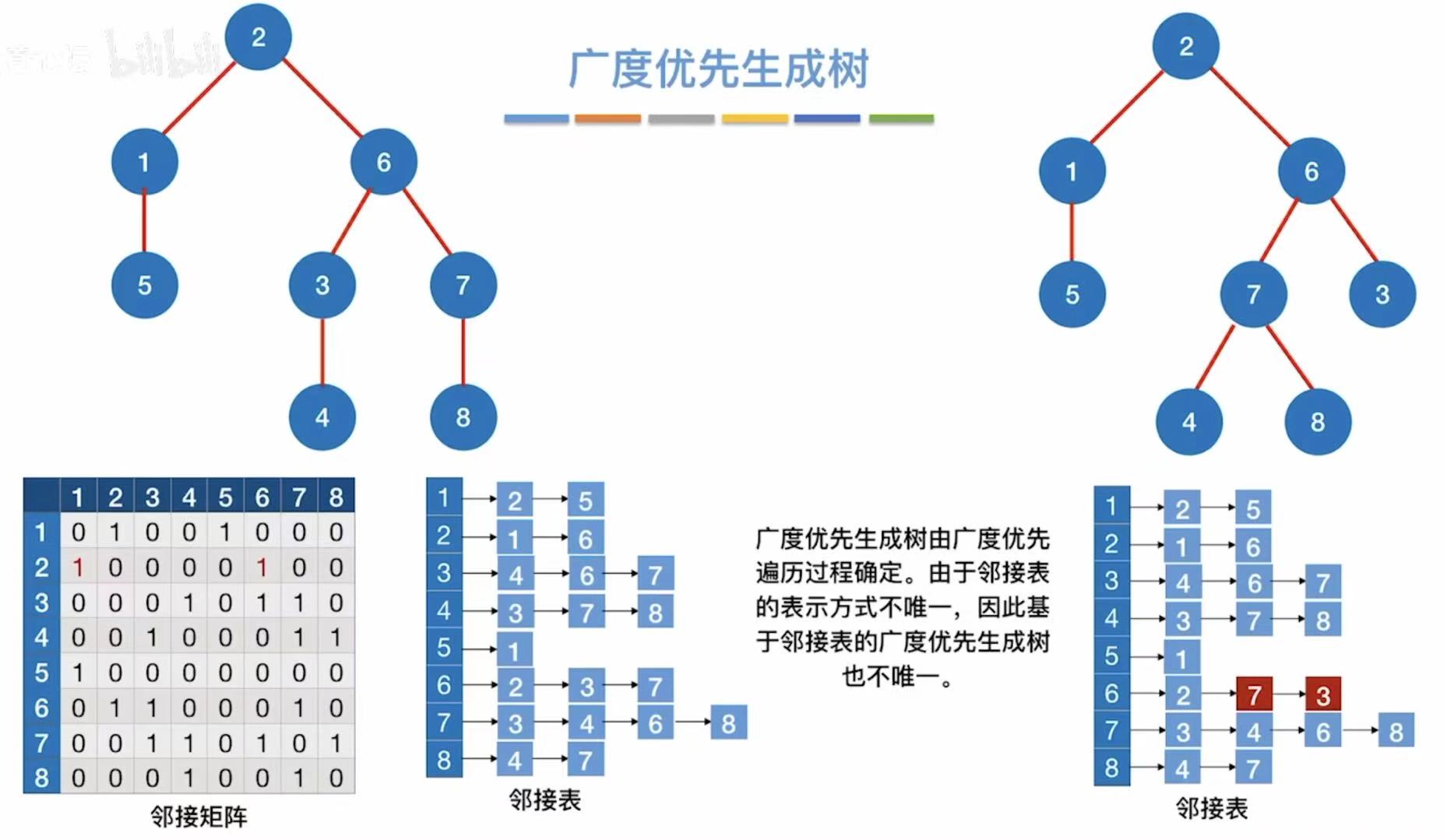
1.7 小结

2. 深度优先遍历（DFS）

2.1 概念

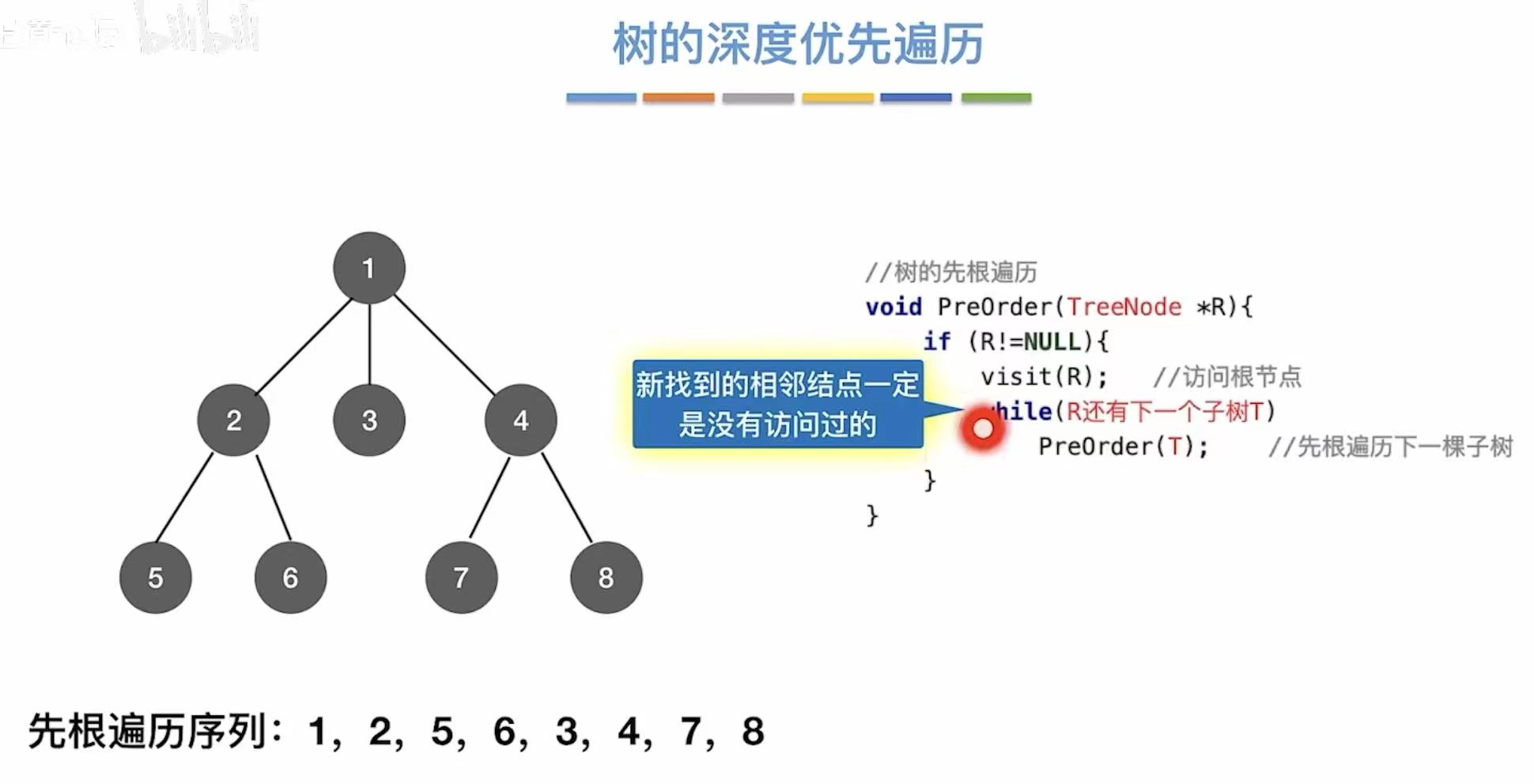
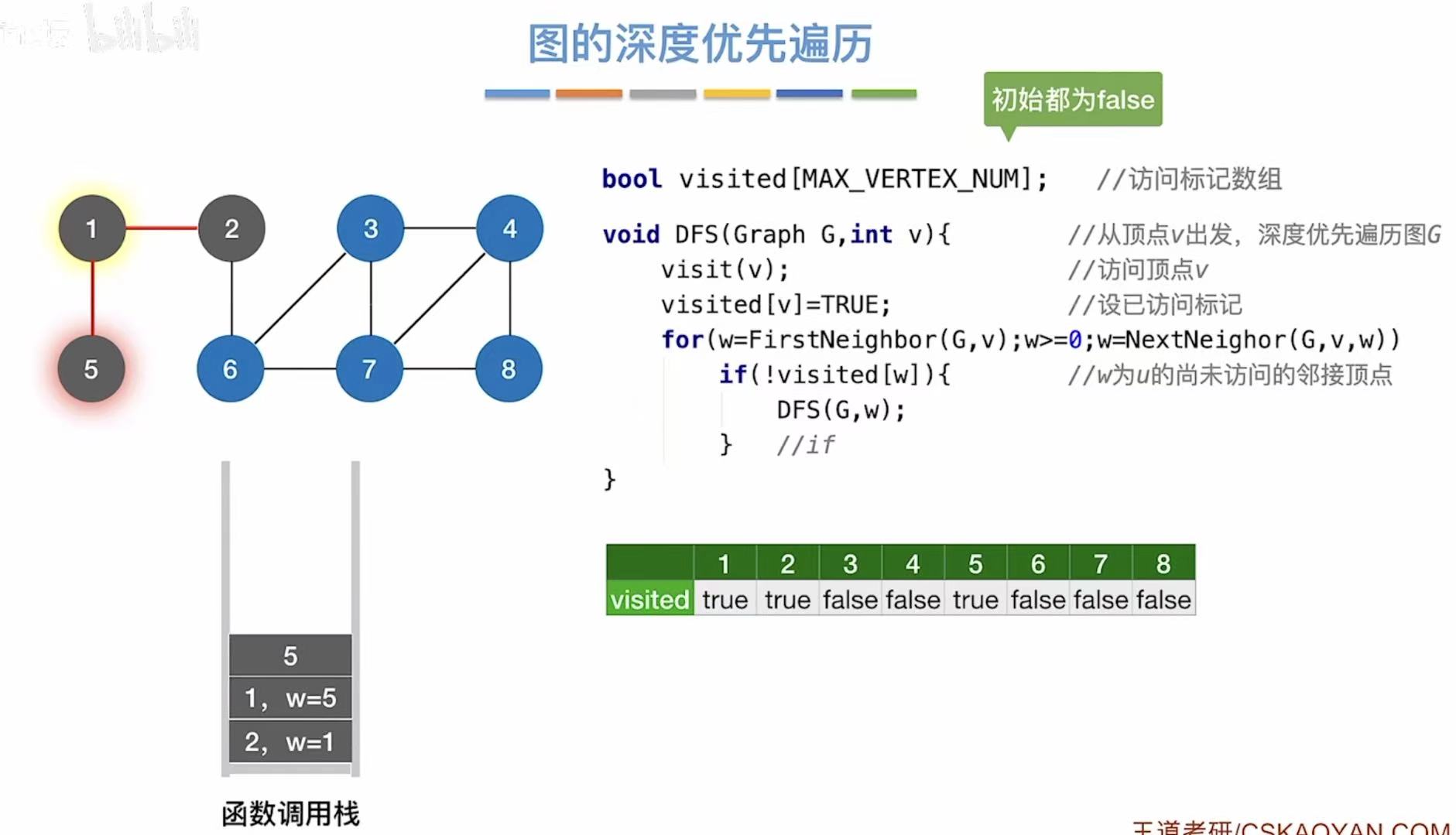
深度优先遍历：就是一个顶点和谁相邻，就先把一边的遍历到底，再遍历另外一边。

如图：先遍历2的左侧-->1-->5。

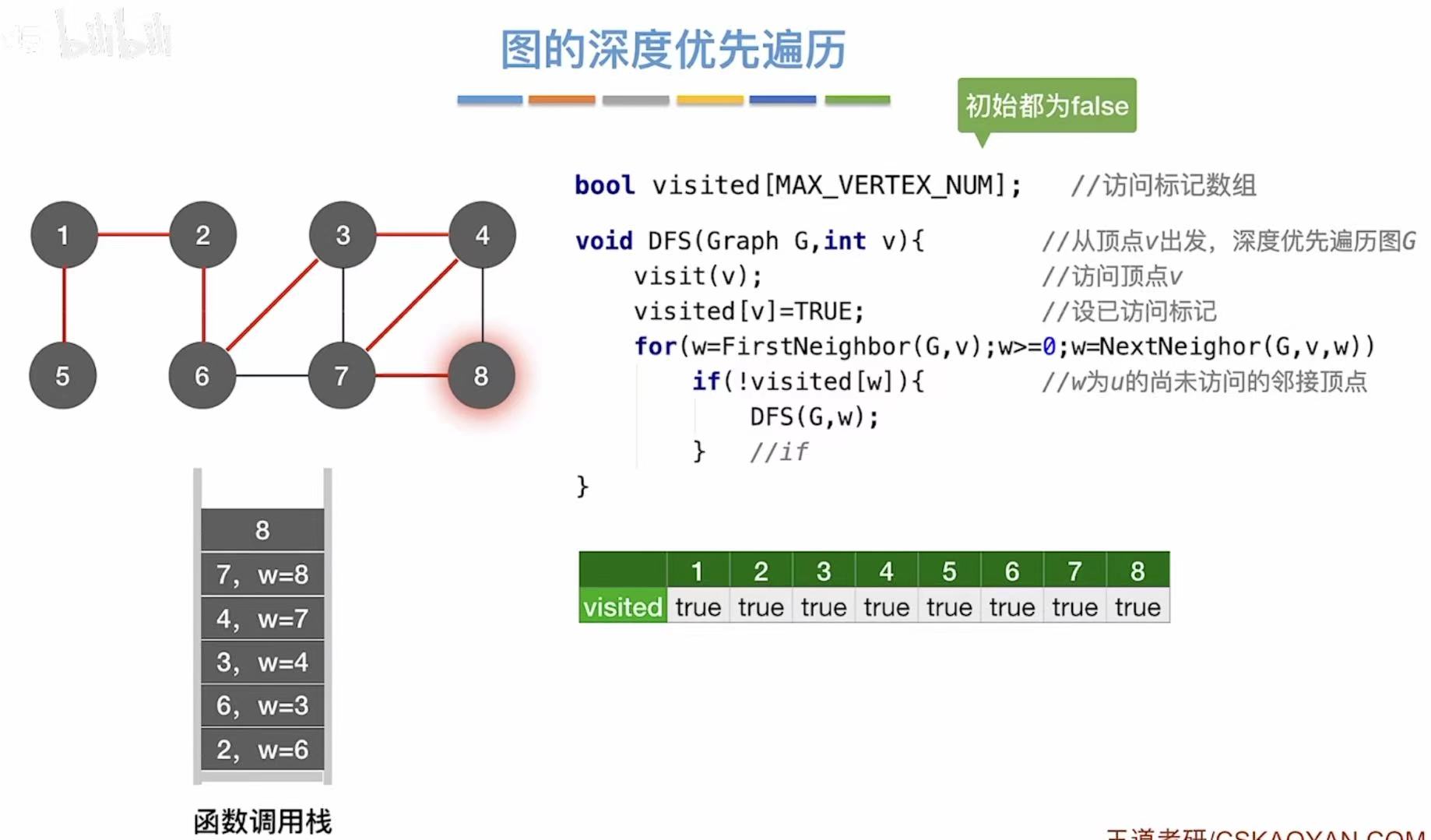
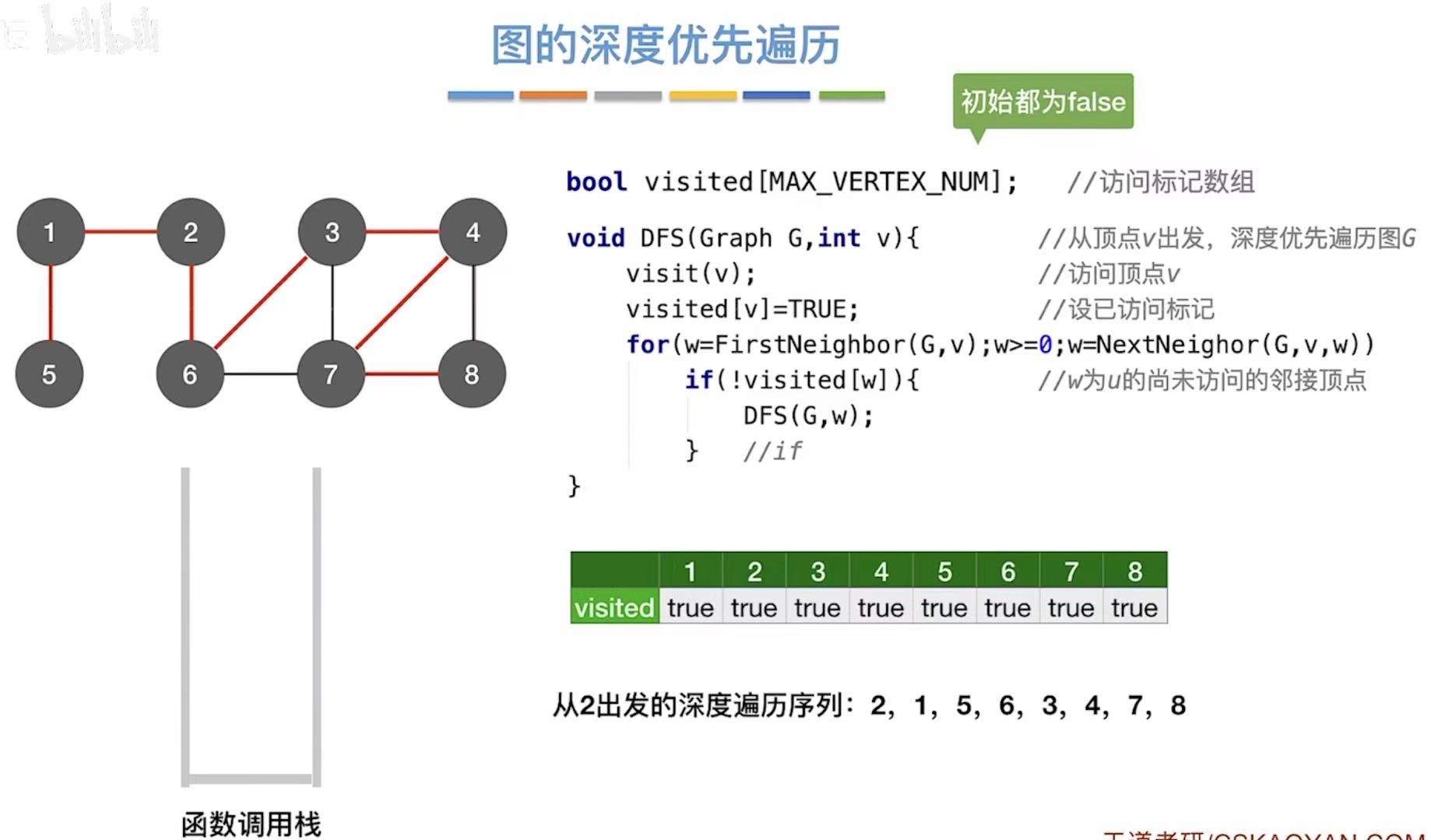
如图：再遍历另一边一直到底（8）.

java 复制代码

// 访问标记数组：记录每个顶点是否已被访问过
// 初始时所有值都为 false（未访问）
bool visited[MAX_VERTEX_NUM];   // 访问标记数组

// 深度优先遍历函数
void DFS(Graph G, int v) {
    visit(v);                     // 访问当前顶点 v（如打印或处理数据）

    visited[v] = TRUE;            // 将顶点 v 标记为已访问，防止重复访问

    // 遍历当前顶点 v 的所有邻接点 w
    // 使用 FirstNeighbor 和 NextNeighbor 枚举所有邻接点
    for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
        // 如果邻接点 w 还未被访问
        if (!visited[w]) {
            // 递归调用 DFS，从 w 开始继续深入遍历
            DFS(G, w);
        }
    }
}

2.2 最终实现

java 复制代码

// 访问标记数组：记录每个顶点是否已被访问过
// 初始时所有值都为 false（未访问）
bool visited[MAX_VERTEX_NUM];   // 访问标记数组

// 对图 G 进行深度优先遍历的主函数
void DFSTraverse(Graph G) {
    // 初始化访问标记数组：将所有顶点标记为"未访问"
    for (v = 0; v < G.vexnum; ++v) {
        visited[v] = FALSE;     // 所有顶点初始状态为未访问
    }

    // 遍历图中的每一个顶点（处理非连通图）
    for (v = 0; v < G.vexnum; ++v) {
        // 如果当前顶点 v 尚未被访问
        if (!visited[v]) {
            // 从该顶点出发，进行一次 DFS 遍历
            DFS(G, v);           // 调用 DFS 函数，遍历以 v 为起点的连通分量
        }
    }
}

// 深度优先遍历函数（从顶点 v 开始）
void DFS(Graph G, int v) {
    visit(v);                    // 访问当前顶点 v（如打印或处理数据）

    visited[v] = TRUE;           // 将顶点 v 标记为已访问，防止重复访问

    // 遍历当前顶点 v 的所有邻接点 w
    // 使用 FirstNeighbor 和 NextNeighbor 枚举所有邻接点
    for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)) {
        // 如果邻接点 w 还未被访问
        if (!visited[w]) {
            // 递归调用 DFS，从 w 开始继续深入遍历
            DFS(G, w);
        }
    }
}

2.3 复杂度分析

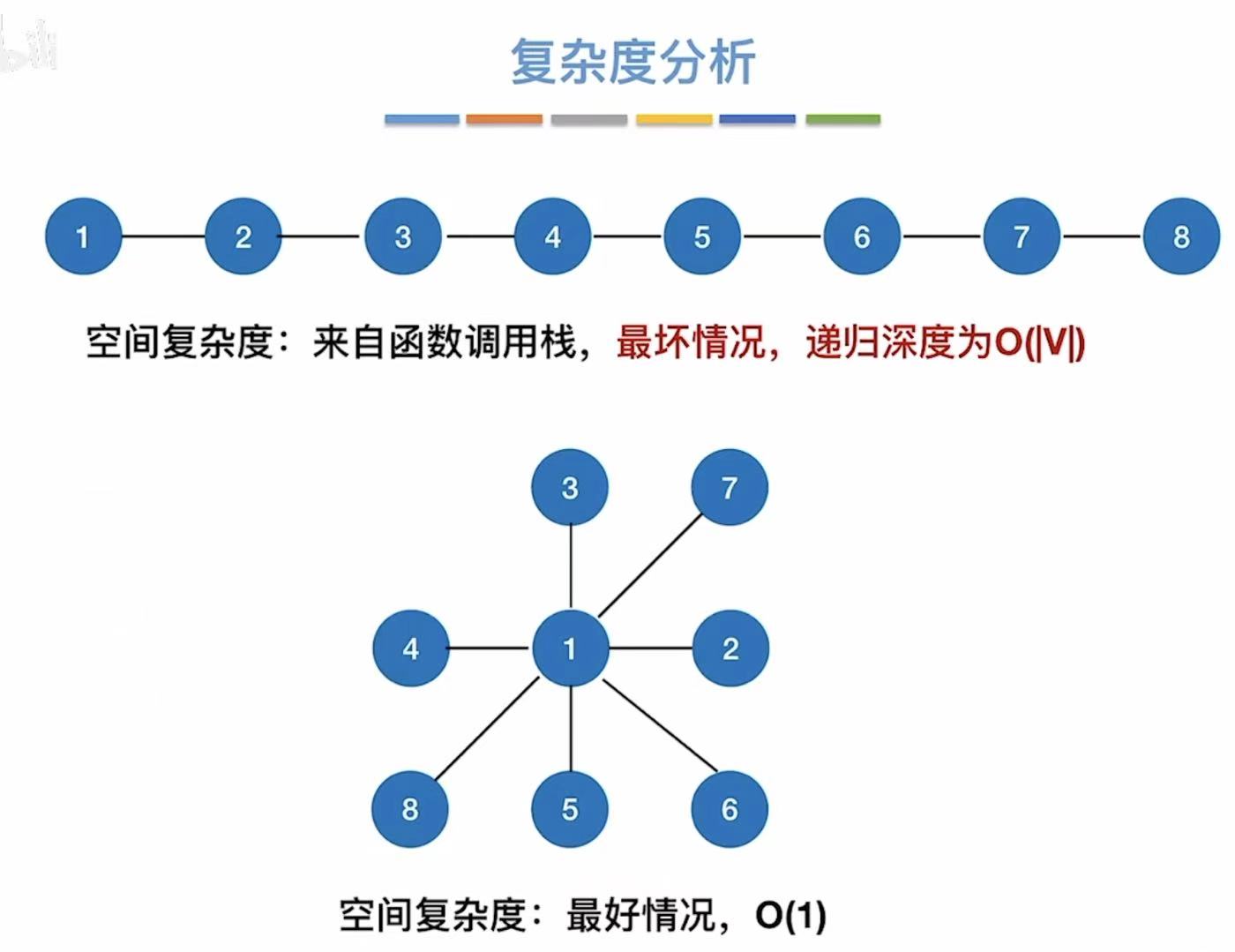
空间复杂度：

最坏：因为是最深，一直顺着到头，所以最坏肯定就是一排到头。
最好：肯定就是八面玲珑，看完2的看3的，看完4的看5的，像买鸡排一样把摊主围起来。

2.4 遍历序列

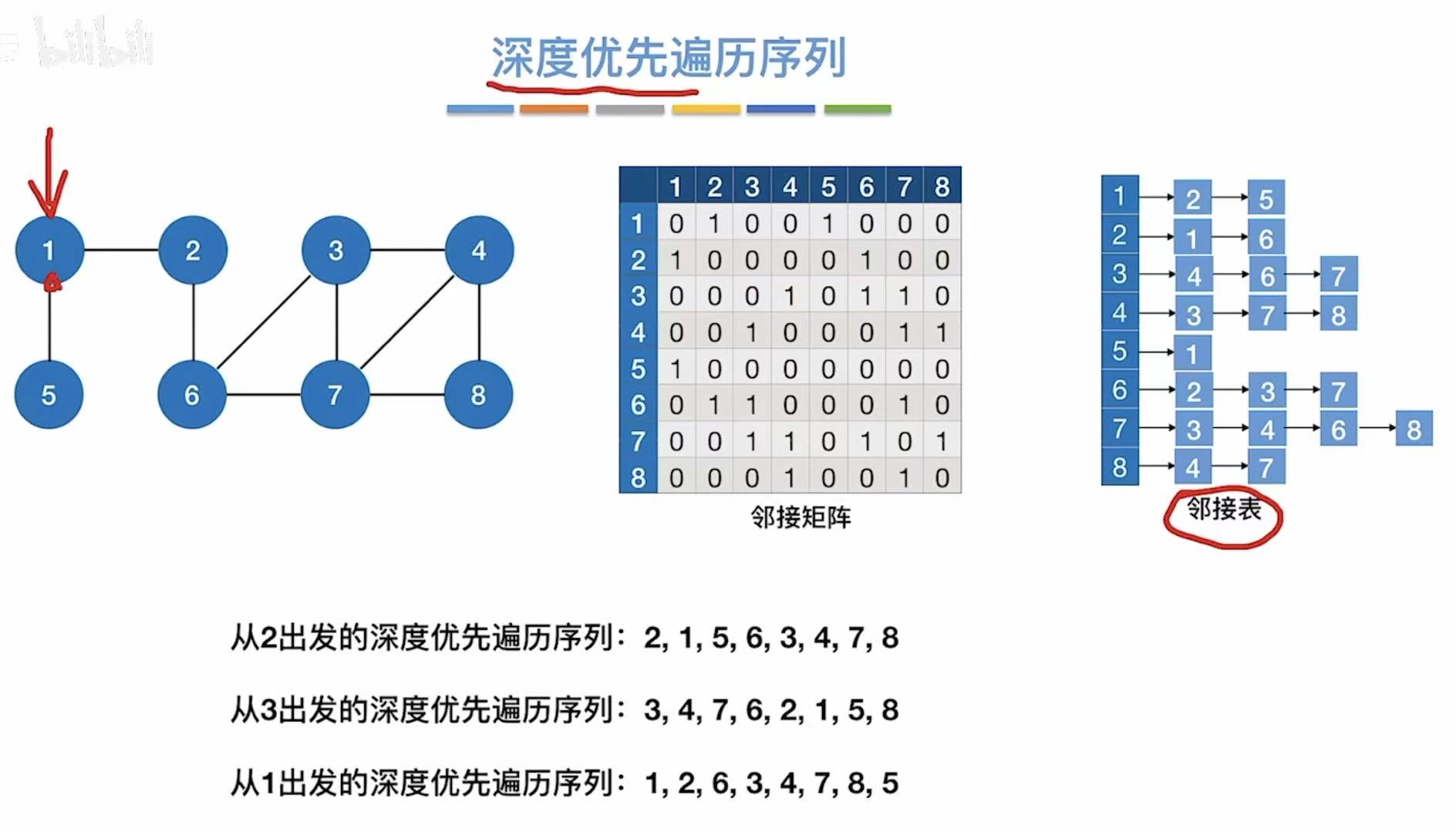
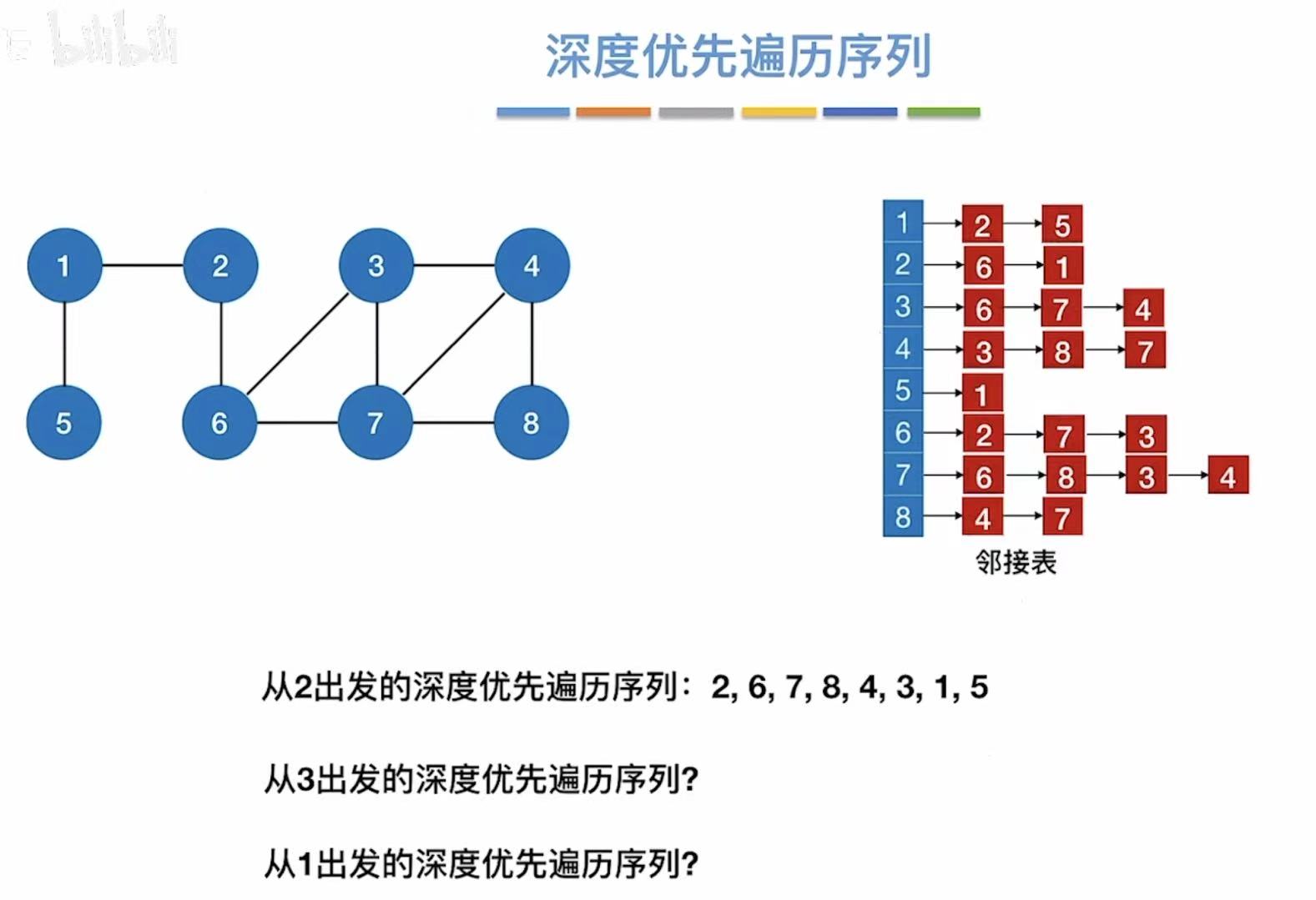
邻接矩阵：因为就0和1来表示，顶点都是按数字顺序排列的，所以表示方式唯一。
邻接表：因为后面用链表链接的序号可以随意排序，所以表示方式并不唯一。

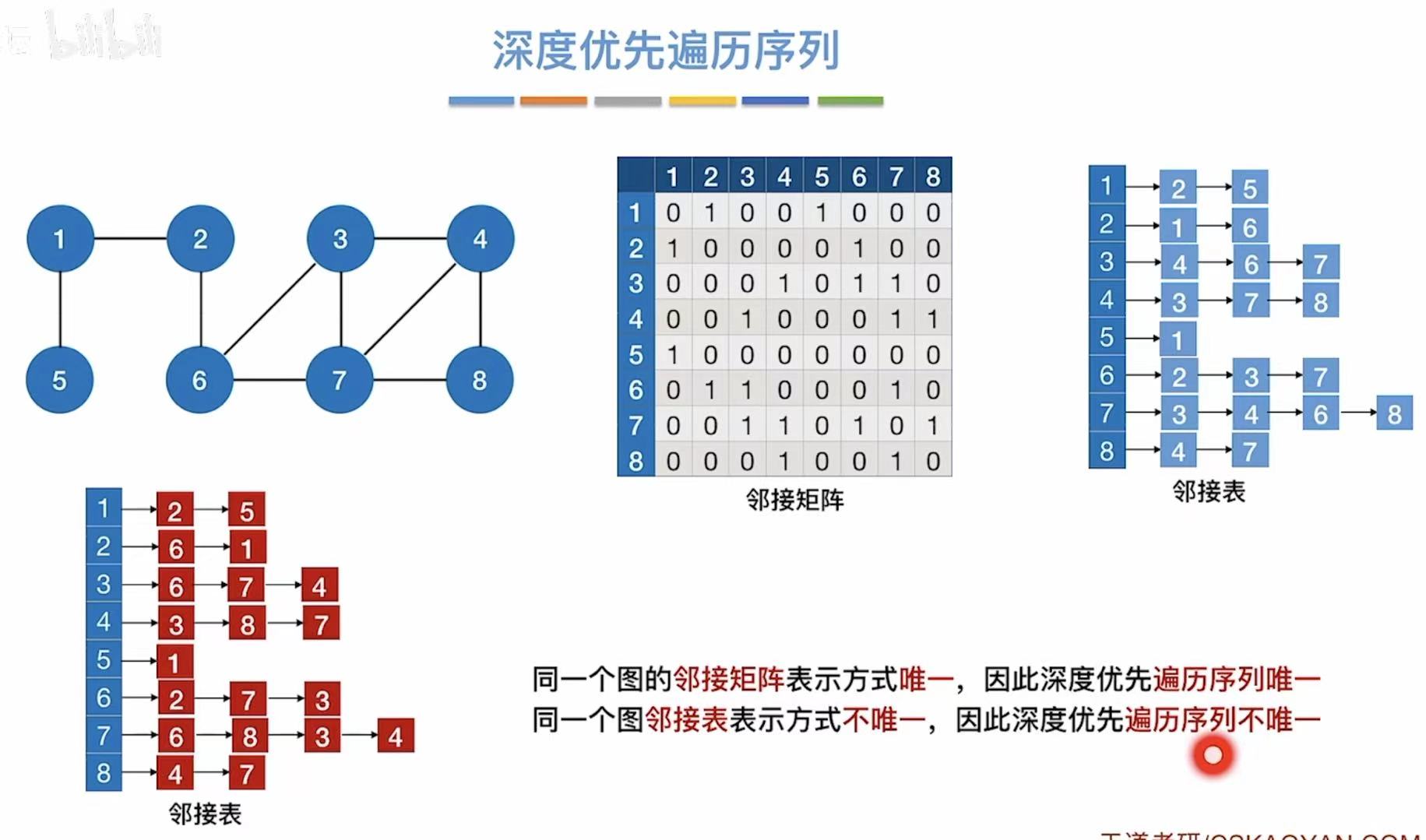
2.5 深度优先生成树

同上。

考研408--数据结构--day10--图的存储、基本操作和遍历

目录

图

1. 基本概念

1.1 定义

1.2 应用

1.3 普通图

1.4 顶点相关

1.5 (强)连通分量

1.6 生成树/森林

1.7 边的权

2. 特殊的图

3. 小结

图的存储

1. 邻接矩阵

1.1 概念

1.2 带权图

1.3 性能分析

1.4 性质

1.5 小结

2. 邻接表

2.1 概念

2.2 小结

3. 十字链表法

4. 邻接多重表

图的基本操作

1. Adjavent-->边存在

2. Neighbors-->邻接边

3. InsertVertex-->插入点

4. DeleteVertex-->删除点

5. RemoveEdge-->删除边

6. FirstNeighbor-->第一个邻接点

7. NextNeighbor-->下一个邻接点

8. 获取/设置权值

图的遍历

1. 广度优先遍历（BFS）

1.1 与树的广度优先遍历之间的联系

1.2 代码实现

1.3 遍历序列

1.4 最终实现

1.5 复杂度分析

1.6 广度优先生成树

1.7 小结

2. 深度优先遍历（DFS）

2.1 概念

2.2 最终实现

2.3 复杂度分析

2.4 遍历序列

2.5 深度优先生成树

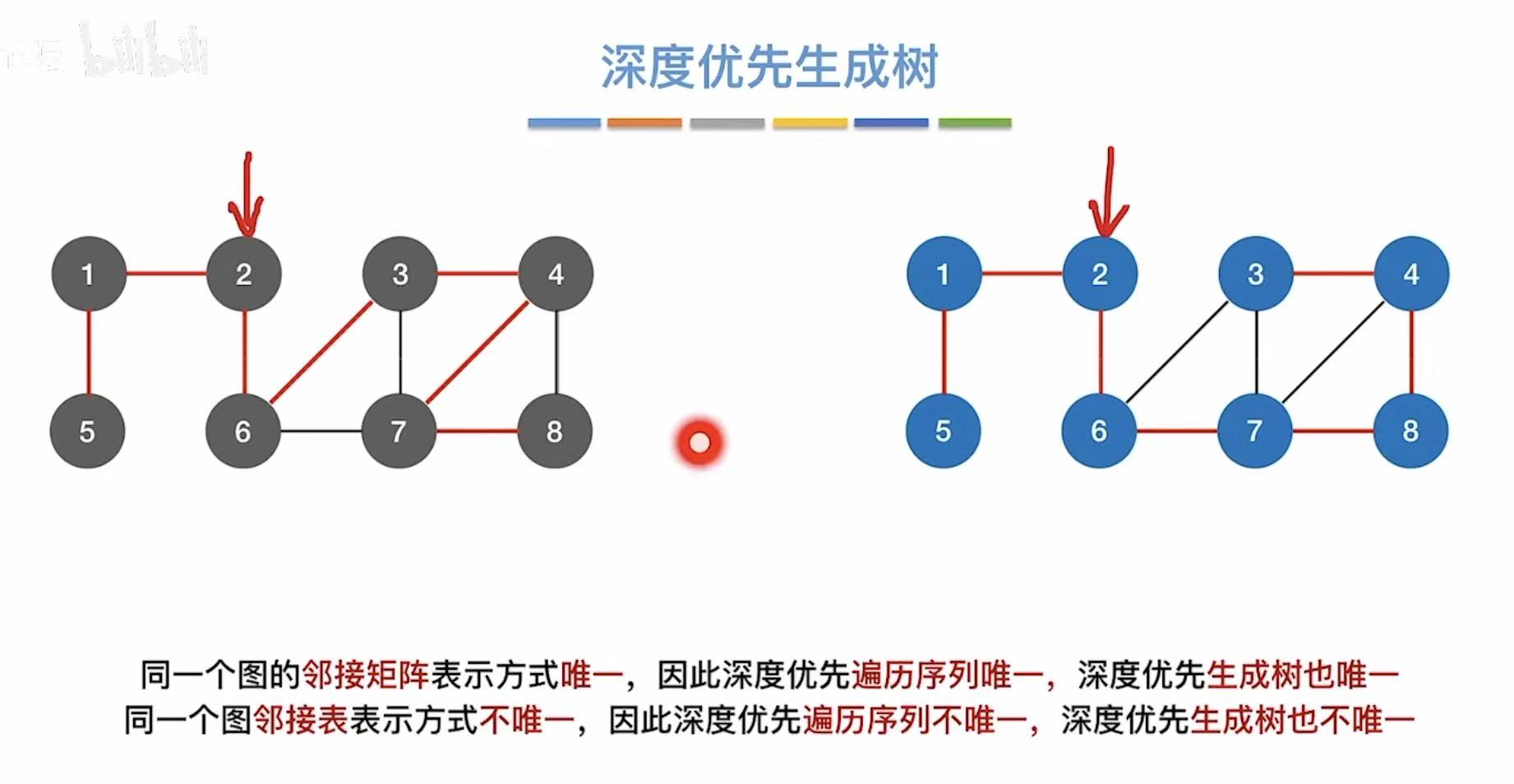
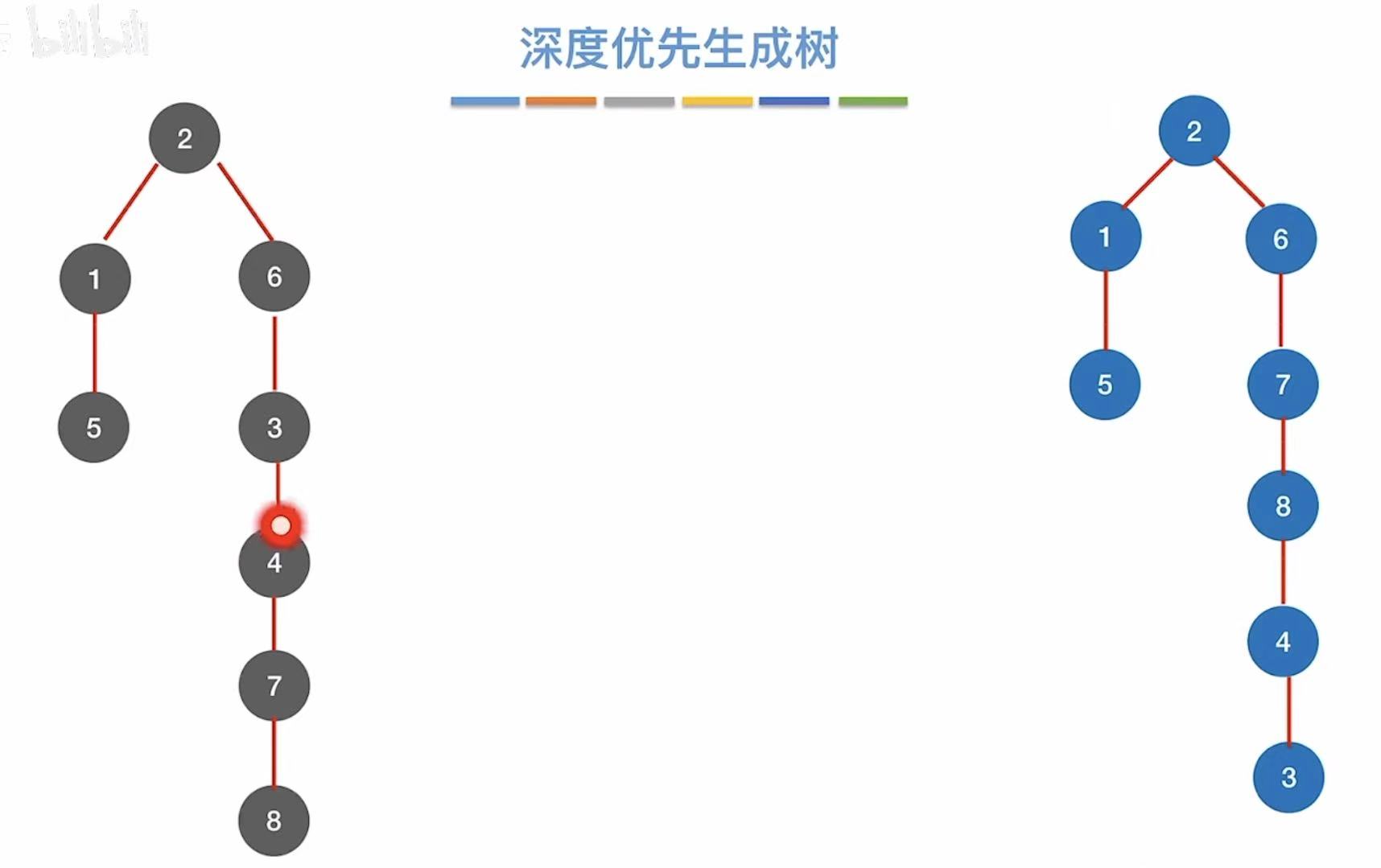
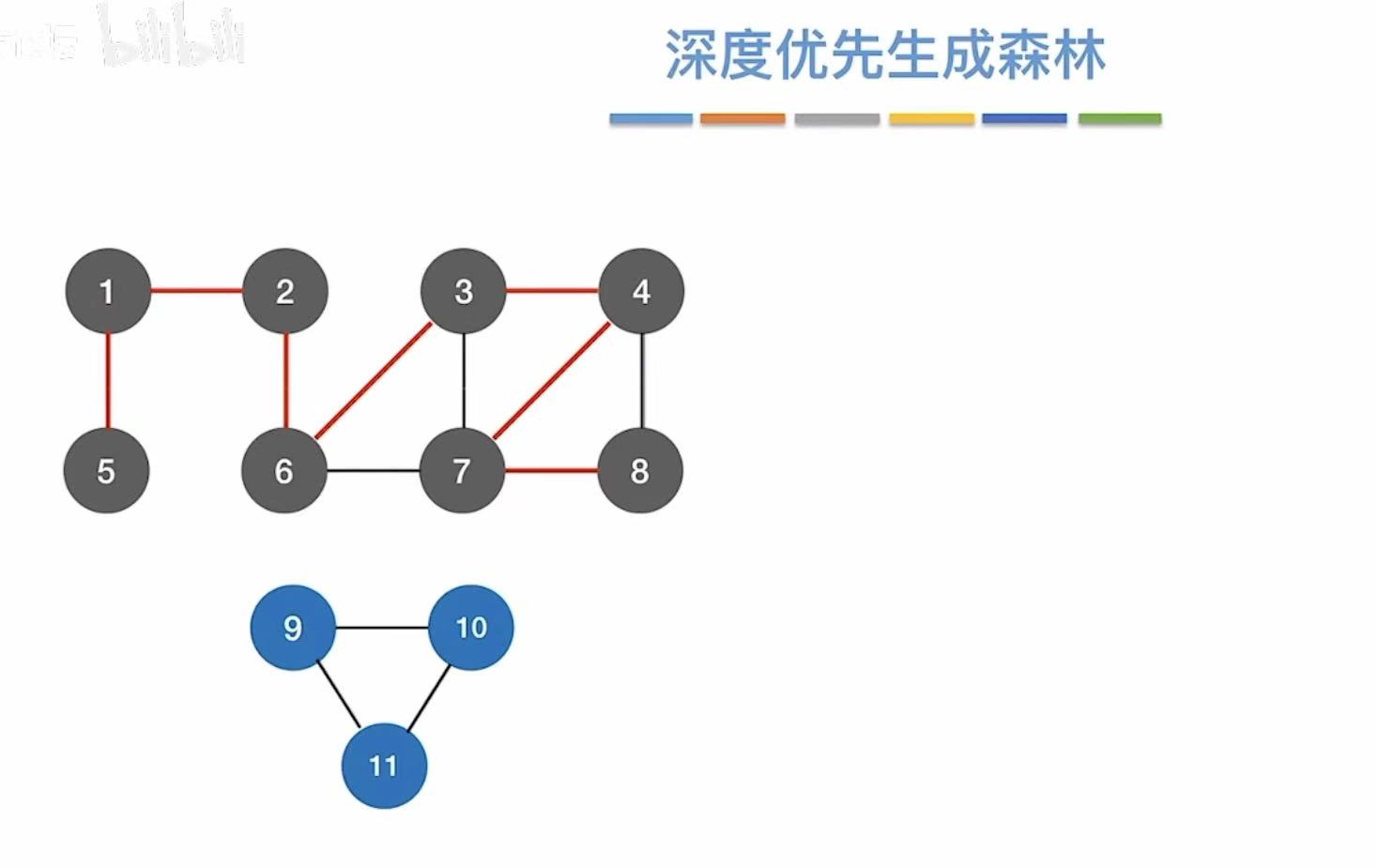
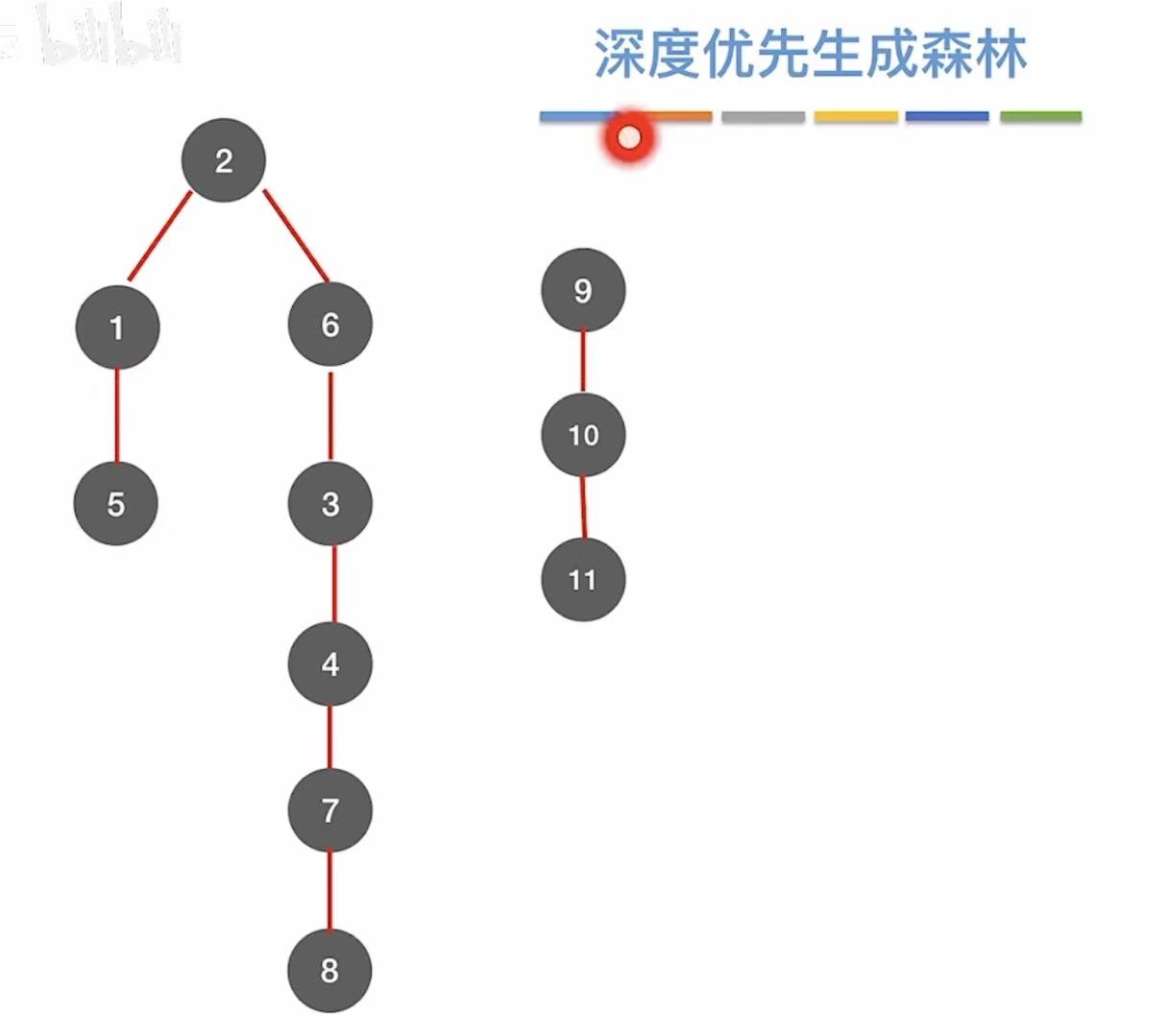
2.6 图的遍历与图的连通性

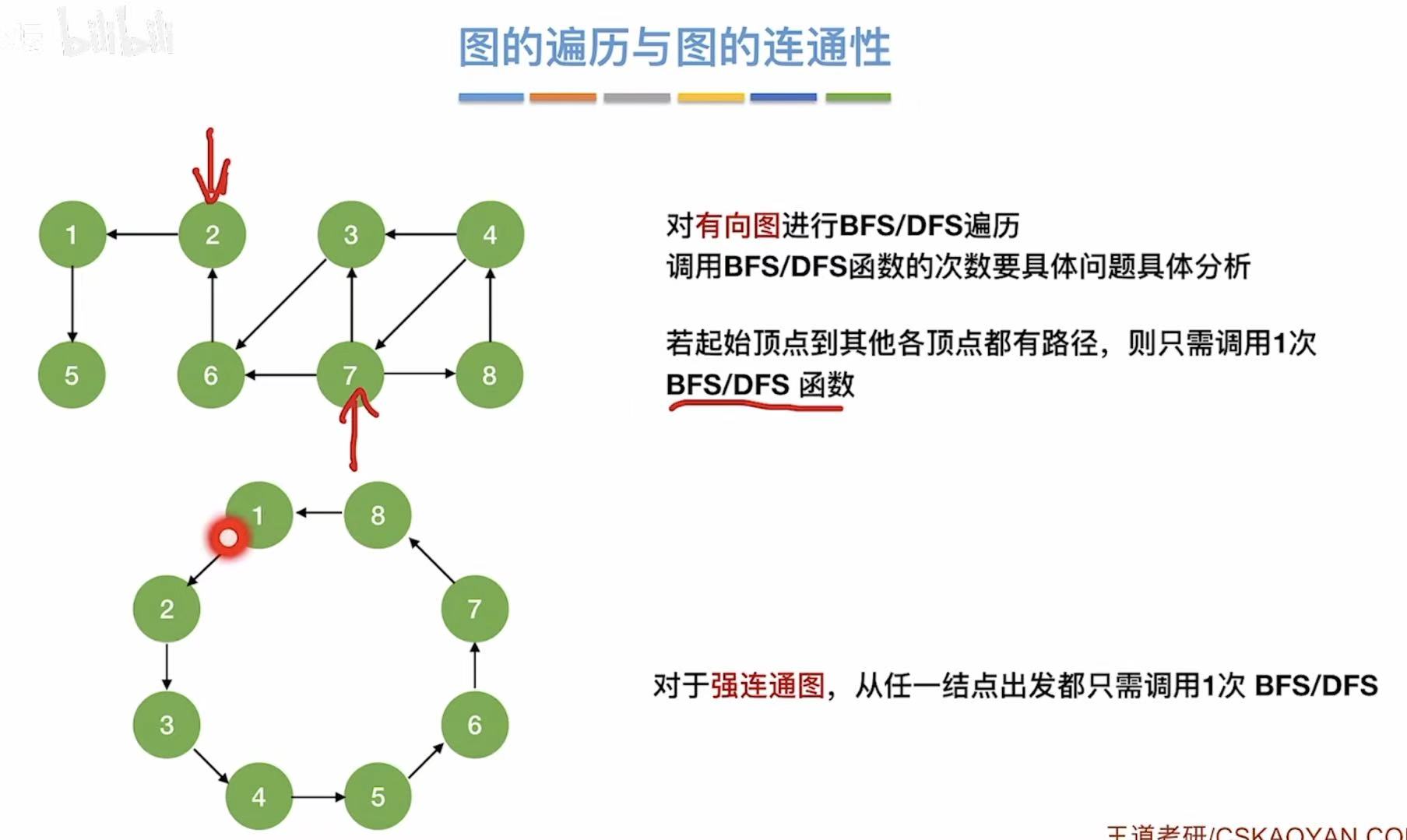
2.7 小结