数据结构：队列与二叉树精讲

typedef int DATATYPE;

typedef struct queue

{

DATATYPE *array;

int head;

int tail;

int tlen;

} SeqQueue;

SeqQueue *CreateSeqQueue(int len);

int EnterSeqQueue(SeqQueue *queue, DATATYPE *data);

int QuitSeqQueue(SeqQueue *queue);

DATATYPE *GetHeadSeqQueue(SeqQueue *queue);

int IsEmptySeqQueue(SeqQueue *queue);

int IsFullSeqQueue(SeqQueue *queue);

int DestroySeqQueue(SeqQueue *queue);

创建

cpp 复制代码

/**
 * @brief 创建 循环队列
 *
 * @param len  循环队列的容量
 * @return SeqQueue*  返回循环队列表头的指针   NULL 失败
 */
SeqQueue *CreateSeqQueue(int len)
{
    SeqQueue* sq=malloc(sizeof(SeqQueue));
    if(NULL==sq)
    {
        printf("CreateSeqQueue 1malloc error\n");
        return NULL;
    }
    sq->array=malloc(sizeof(DATATYPE)*len);
    if(NULL==sq->array)
    {
        printf("CreateSeqQueue 2malloc error\n");
        return NULL;
    }
    sq->head=0;
    sq->tail=0;
    sq->tlen=len;
    return sq;
}

入队

cpp 复制代码

/**
 * @brief 入队 循环队列 ，新增数据
 *
 * @param queue 需要操作队列的指针
 * @param data 需要新增的数据
 * @return int 0 成功 1 失败
 */
int EnterSeqQueue(SeqQueue *queue, DATATYPE *data)
{
    if(IsFullSeqQueue(queue))
    {
        printf("EnterSeqQueue error\n");
        return 1;
    }
    memcpy(&queue->array[queue->tail],data,sizeof(DATATYPE));
    queue->tail=(queue->tail+1)%queue->tlen;
    return 0;
}

出队

cpp 复制代码

/**
 * @brief 出队 循环队列 ，删除数据
 *
 * @param queue 需要操作队列的指针
 * @return int 0 成功 1 失败
 */
int QuitSeqQueue(SeqQueue *queue)
{
    if(IsEmptySeqQueue(queue))
    {
        printf("QuitSeqQueue error\n");
        return 1;
    }
    queue->head=(queue->head+1)%queue->tlen;
    return 0;
}

获得队头元素

cpp 复制代码

DATATYPE *GetHeadSeqQueue(SeqQueue *queue)
{
    if(IsEmptySeqQueue(queue))
    {
        printf("GetHeadSeqQueue error\n");
        return NULL;
    }
    return &queue->array[queue->head];
}

是否为空

cpp 复制代码

int IsEmptySeqQueue(SeqQueue *queue)
{
    return queue->head==queue->tail;
}

是否为满

cpp 复制代码

int IsFullSeqQueue(SeqQueue *queue)
{
    return (queue->tail+1)%queue->tlen ==queue->head;
}

树

一对多

n（n>=0）个结点的有限集合。n=0为空树

在任意一个非空树中

有且只有一个根结点
当n>1，其余结点可以分为m个互不相交的有限集合，其中每一个集合又是一颗树也就是子树。

结点拥有子树的个数称谓结点的度。度为0的结点称谓叶结点。度不为0，称谓分支结点。

树的度数是指，这棵树中，最大的结点的度数，称谓树的度数。

树的深度或高度，从根开始，根为第一层，根的孩子为第二层。

树的存储，顺序结构，链式结构。

二叉树（binary tree）

n个结点的有限集合，集合要么为空树，要么由一个根结点和两棵互不相交，分别称谓根结点的左子树和右子树的二叉树组成。

特点

1，每个结点最多两个子树。

2，左子树和右子树是有顺序的，次序不能颠倒。

3，如果某个结点只有一个子树，也要区分左，右子树。

特殊的二叉树

1，斜树，所有的结点都只有左子树，左斜树，所有结点都只有右子树，右树。

2，满二叉树，所有的分支结点都存在左右子树，并且叶子都在同一层上。

3，完全二叉树，对于一颗有n个结点的二叉树按层序编号，如果编号i（1<=i<=n）的结点于同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这可树为完全二叉树。

特性

1，在二叉树的第i层上最多有2^(i-1)个结点 i>=1

2,深度为k的二叉树至多有2^k -1 个结点 k>=1

3,任意一个二叉树T，如果其叶子结点的个数是n0,度数为2的结点数为n2， n0 = n2 +1;

4,有n个结点的完全二叉树深度为(logn/log 2) +1;

层序，广度遍历

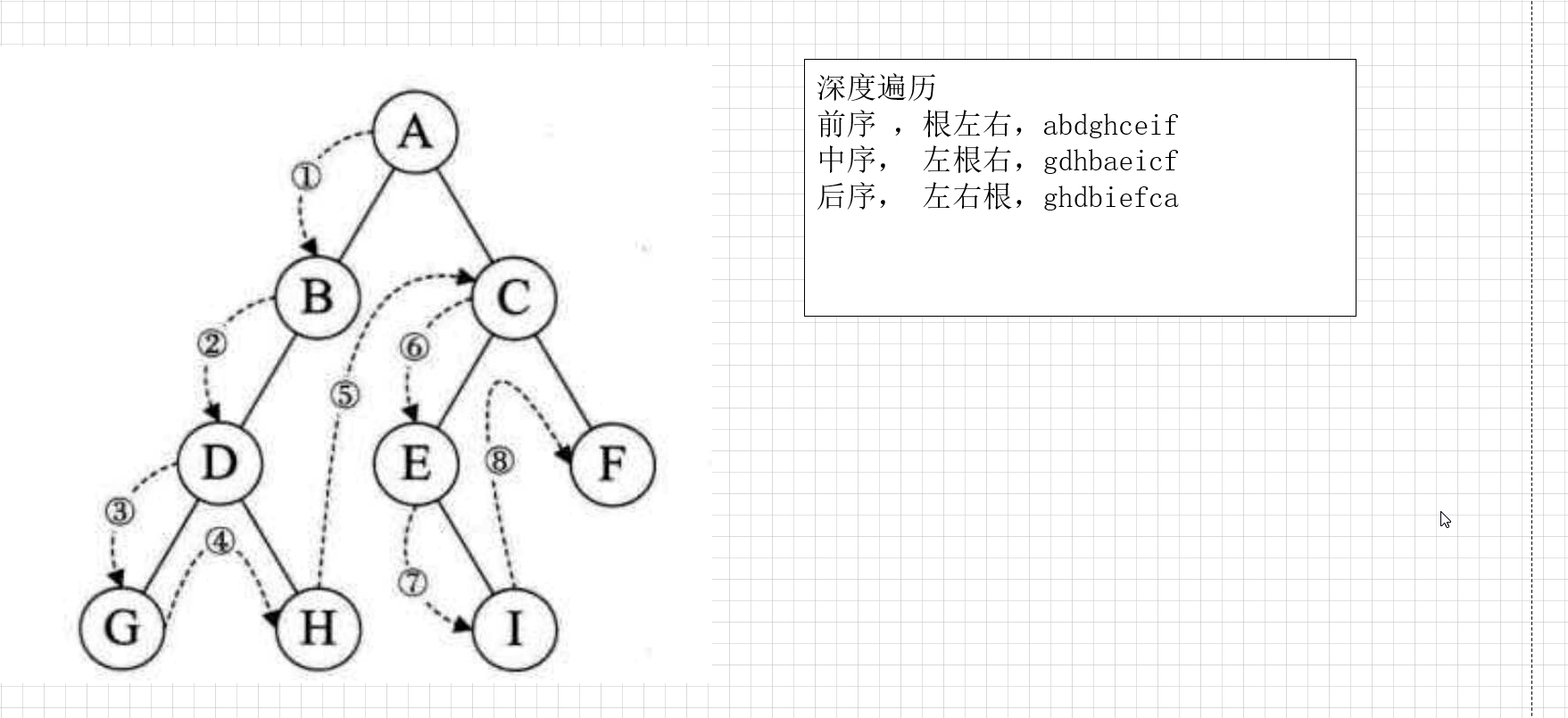
深度遍历
前序，根左右，先访问根，然访问左，访问右。
中序，左根右，先从根开始（不是先访问根），从左开始访问，在访问根，在访问右结点。
后序，左右根，先从根开始（不是先访问根），先访问左，在访问右。在访问根。

ADT

typedef struct BiTNode /* 结点结构 */

{

TElemType data; /* 结点数据 */

struct BiTNode *lchild,*rchild; /* 左右孩子指针 */

}BiTNode,*BiTree;

BiTNode *node;

struct BiTNode ** node;

CreateBiTree();

DestroyBiTree();

PreOrderTraverse();

void InOrderTraverse(BiTree T);

void PostOrderTraverse(BiTree T);

前序例题

用代码实现下面这棵树

cpp 复制代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef char DATATYPE;

typedef struct BiTNode /* 结点结构 */
{
    DATATYPE data;                   /* 结点数据 */
    struct BiTNode *lchild, *rchild; /* 左右孩子指针 */
} BiTNode;


char data[]="abd##eg###c#fh###";
int i=0;
void CreateTree(BiTNode** root)
{
    char c=data[i++];
    if('#'==c)
    {
        *root=NULL;
        return;
    }
    else
    {
        *root=malloc(sizeof(BiTNode));
        if(NULL==*root)
        {
            printf("malloc error\n");
            return;
        }
        (*root)->data=c;
        CreateTree(&(*root)->lchild);
        CreateTree(&(*root)->rchild);
    }
    return;
}

void PreOrderTranverse(BiTNode* root)
{
    if(NULL==root)
    {
        return;
    }
    printf("%c",root->data);
    PreOrderTranverse(root->lchild);
    PreOrderTranverse(root->rchild);
}

void INOrderTranverse(BiTNode* root)
{
    if(NULL==root)
    {
        return;
    }
    INOrderTranverse(root->lchild);
    printf("%c",root->data);
    INOrderTranverse(root->rchild);
}

void PostOrderTranverse(BiTNode* root)
{
    if(NULL==root)
    {
        return;
    }
    PostOrderTranverse(root->lchild);
    PostOrderTranverse(root->rchild);
    printf("%c",root->data);
}

void DestroyTree(BiTNode* root)
{
  if (NULL == root)
  {
    return;
  }
  DestroyTree(root->lchild);
  DestroyTree(root->rchild);
  free(root);
}


int main(int argc, char** argv)
{
  BiTNode* root = NULL;
  CreateTree(&root);
  //---------------------------前序---------------------------------------
  PreOrderTranverse(root);
  printf("\n");
  //-----------------------------中序---------------------------------------
  INOrderTranverse(root);
  printf("\n");
  //----------------------------后序--------------------------------------
  PostOrderTranverse(root);
  printf("\n");
  //-----------------------------销毁-------------------------------------
  DestroyTree(root);
  return 0;
}